Analysis of the Effect of Simultaneous Melt Shearing and Cooling on Grain Formation and Rheology of A356 Aluminum Alloy

Abstract

Despite the dozens of earlier research verifications, the contribution of shearing of molten metallic alloys during their solidification to grain formation is still ambiguous. Also, modeling of this phenomenon has received very little attention. Experiments were conducted in this study to investigate the effect of the shear rate on the density, size, and shape factor of the formed grains up to a solid fraction of 0.15 for the solidifying A356 aluminum alloy in the coaxial cylinder viscometer. The rheology of the formed semisolid slurry was studied as well. Results exhibited morphological evolution and grain refinement. The grain number density increased from 5 × 10⁸ m⁻³ in the absence of melt shearing to reach 4 × 10⁹ m⁻³ at the shear rate of 250 s⁻¹. Also, the shape factor was improved to reach 0.78. Based on the experimental investigations, the grain number density under shearing was correlated to the shear rate and the grain number density in the absence of shearing via an empirical formula. A shear-dependent grain multiplication factor was deduced. The alloy exhibited a shear-thinning behavior where the viscosity obeyed the power law with a constant and an exponent of 0.9264 and 0.468, respectively. Moreover, the measured data were fitted to several proposed viscosity models and the model of Hirai et al. showed the best fit; therefore, it was recommended for predicting the viscosity of semisolid slurries.

1. Introduction

During the solidification process, many hydrodynamic conditions involve important effects: some are favorable whereas the others result in solidification defects. Experimental evidence showed that free natural thermal, solutal, or thermosolutal convection could not be avoided during the solidification of alloys [1]. Furthermore, the mechanical vibrations and ultrasonic shocks [2,3,4] and other external means are used to encourage the convection intensity, e.g., mechanical or electromagnetic stirring. After the thixotropic behavior findings of the semisolid metals by Spencer [5], the need for the knowledge of the formation and solidification of the primary solid particles under convective shear field arises. Researchers tried a long time ago to find an explanation for the mechanisms causing grain refinement in the undercooled melts that are subjected to mechanical or electromagnetic stirring.

Flemings [6,7] summarized the fragmentation mechanisms in six possible types: (1) a dendrite arm fracture as a result of shearing forces; (2) remelting at the dendrite arm root as a result of ripening; (3) remelting as in (2) but enhanced with the perturbations of the thermal convection; (4) remelting as in (2) but accelerated by the shear stress induced at the root; (5) as in (3) but enhanced with the higher solute concentration at the root; (6) recrystallization as a result of the stress induced by the shear flow, where the liquid penetrates the newly formed grain boundaries. He suggested the first mechanism since the particle size at a given cooling rate tends to be about equal to what the dendrite arm spacing would be in an unstirred melt, suggesting that the frequency of dendrite fragmentation is related to the number of growing dendrite arms in the solidification front. However, mechanical shearing of dendrites arms was of less importance and dismissed by C. Paradies et al. [8], while the mechanism (2) above was seen more likely to take place. In contrast to the mechanisms (1–3) above, Pilling and Hellawell [9] concluded after an example calculation based on the dendrite arm junction that the flow resulting from thermosolutal convection (with a speed around 10 mm/s) is not strong enough to cause mechanical bending or breaking of dendrite arms.

Several years later, following these classical studies, Fan and his colleagues [10,11,12,13] introduced a new aspect based on what is called “effective nucleation”. This term resembles the 100% nuclei survival rate which can be achieved by creating the following conditions: (1) a uniform temperature and chemical composition throughout the entire liquid; (2) well-dispersed heterogeneous nucleation agents; (3) a rapid dissipation of latent heat to prevent recalescence. Their work on Al–Mg alloys [14,15,16] revealed that intensive melt shearing leads to significant grain refinement due to the dispersion of the refining particles MgAl₂O₄. A planetary stirring was applied to A356 aluminum alloy. It resulted in a remarkable refinement and globularization of the formed grains [17]. In addition to its grain refinement effect, intensive melt shearing during solidification influences the thickness of the halo of the secondary phase formed on the primary phase particles. Experiments at a high shear rate [18] showed that the Zn-rich halos disappeared from the Al-rich phase during the primary solidification and the eutectic solidification of the Zn-Al alloys.

Melt shearing with a wide range of shear rates is inadvertently associated with all metal casting processes. Thermal and solutal convection exist in sand and gravity die casting. However, relatively higher shearing/cooling rates may occur within the billet and slab in continuous casting processes. Higher shearing and cooling rates of ca. respectively 103 Ks⁻¹ and 105 s⁻¹ may arise during high pressure die casting, rheocasting and semisolid metal forming [19].

Despite the dozens of earlier inventions of the various mechanisms of grain refinement during solidification under shearing, none of them introduced a consistent quantitative model of the phenomenon. Such studies were based on analyzing the final experimental observations rather than real-time investigations of the morphological evolutions taking place during the shearing process. Therefore, contradictions arise between the presented hypotheses, leading to difficulties in modeling the phenomenon. Consequently, the modeling of shearing effect on grain refinement has received little concern except for a few models [20,21,22,23,24,25,26,27,28] that missed the simplicity, validity, and consistency.

The viscosity of molten alloys and their semisolid slurries is a very crucial property. It governs mold filling, casting soundness, solute and phase distribution, and the segregation pattern within castings. Prediction of solidification structures during casting is highly affected by using the proper viscosity model. Several models will also be presented and evaluated in the current study.

The current work attempts to lay an empirical model for grain multiplication during the application of mechanical shearing and cooling to A356 aluminum alloy based on experimental outcomes. Experiments were conducted in the coaxial cylinder rotational (Couette) rheometer to investigate the shear contribution to grain formation and to correlate the grain number density to the shear rate and to the grain number density that can be obtained in the absence of shear (under the effect of melt undercooling alone). In addition, the rheological behavior of the solidifying alloy was investigated and the most relevant viscosity model to the experiments was suggested. The obtained correlations can be utilized for modeling alloy solidification in the presence of shear and can provide more accurate predictions for the formation of cast structures.

2. Methodology

A series of experiments were carried out on the aluminum casting alloy A356 with the composition provided in

Table 1. 1 Spectrometer analysis of A356 aluminum alloy.

Element	Si	Fe	Cu	Mg	Zn	Ti	Sr	Al
(wt.%)	7.12	0.148	0.014	0.358	0.012	0.082	0.035	Rest

. Elements with concentration less than 0.01 wt.% were ignored. The molten alloy is poured into the annular gap between the rotor and the stationary cup of the coaxial cylinder viscometer with the geometry illustrated in Figure 1. The pouring continues until 15 mm above the upper surface of the rotor. The viscometer utilizes a rotating inner cylinder with 30 mm diameter concentric with an outer fixed cup with 38 mm inner diameter. Both parts are made of graphite to ensure a good thermal conductivity and to reduce the reaction with the liquid metal. The inner cylinder is rotated at a preset speed to exert a certain shear rate on the liquid metal in the gap. The rotor surface is corrugated to avoid wall slippage. The rheometer is placed inside a furnace to provide a constant controlled cooling rate of −5.5 °C/min inside the annular gap of the viscometer during the shearing operation. Argon atmosphere was applied during the experiment to prevent oxidation of the graphite and the liquid metal.

The shearing of the superheated melt started at 650 °C and was set at a constant rotational speed corresponding to shear rates ($\dot{\gamma })$, of 0, 50, 100, 150, 200, 250 s⁻¹. Melt cooling/shearing was continued until 606 °C which corresponds to a solid fraction, $f_s\approx 0.15$. The sample was quenched in water after that to capture the obtained morphology. The zero shear-rate sample was chosen as a reference one to be compared to the other samples in order to distinguish the contribution of shear to the formation of the grain. The quenched samples were then cut at the middle of the shear gap, polished, and etched in Barker’s solution. After that, a microstructure characterization was conducted using the polarized optical microscope and computer-aided image analyzer to determine the planar grain number density and grain size in addition to the shape factor of individual particles. The shape factor, $F$, was calculated according to [12] as $F=4\pi A/P^2$ where $A$ and $P$ are the total area and the peripheral length of the primary particles, respectively. The assessment was performed for a 120° sector of the annular section of each sample. Parts of the examined areas were depicted in Figure 2. The viscosity was determined using the shear stress and shear rates calculated according to the constitutive equations of the viscometer given in Appendix A.

3. Results

The microstructure of the reference sample (Figure 2a) exhibited a fully equiaxed dendritic morphology of the primary solid phase. The liquid phase transforms by quenching into fine dendrites of the eutectic phase, which can be observed in the background. At a shear rate of 50 s⁻¹ (Figure 2b), a mixture of untransformed dendrites, cramped dendrites, and rosette-like grains of the primary phase were observed. By increasing the shear rate to 100 s⁻¹ (Figure 2c), dendrites diminished and a mixture of cramped dendrites, rosette-like grains, and many fine-dispersed particles were obtained. As the shear rate was increased (Figure 2d–f), dendrites vanished, and the number of individual globular particles increased. Moreover, the size of the rosettes became smaller and several coarse agglomerated globules were notable.

The calculated planar grain number density (m⁻²) from Figure 2 was converted to the spatial grain number density (m⁻³) using the stereological relationship [29]. Results were plotted versus the shear rate as shown in Figure 3. The data fit well in a linear correlation with a maximum error of 10% and a coefficient of determination of 0.984. It is obvious that $N$ is directly proportional to the applied shear rate. The measured size and the shape factor of the formed grains versus the shear rate were also plotted as shown in Figure 4. In general, as the shear rate increases, the grain size decreases and the shape factor increases. However, the initial rate of change (for shear rates < 150 s⁻¹) is much faster due to the notable transformation from the dendritic morphology. At higher shear rates (>150 s⁻¹), the rate of change is notably less. It is generally considered that a shape factor less than 0.3 is respective for a fully dendritic morphology, from 0.3 up to 0.6 for rosette formation and more 0.6 for globular morphology [30].

The resulting viscosity during the period of continuous cooling/shearing from the liquid state was plotted versus shearing time as shown in Figure 5. The viscosity of liquid alloy is almost constant for a specific shear rate with respect to shearing time. However, the liquid viscosity rises as the shear rate increases, as depicted in the magnified portion of Figure 5. This can be attributed to the end effect of the shearing body and the Taylor vortices that may form within the 4 mm shear gap. The average results of liquid viscosity agree with the earlier results. After solidification, the mixture viscosity increases gradually due to the increasing solid fraction. In contrast to the viscosity of the liquid, the viscosity of the semisolid mixture decreases as the shear rate increases. This can be attributed to the shear-thinning behavior known for semisolid slurries and the morphological evolutions taking place during simultaneous solidification and shearing.

4. Analysis of the Results

From the grain number density results demonstrated in Figure 3, a linear relationship between the grain density and the shear rate can be deduced as given in Equation (1), where $\dot{\gamma }$ is the shear rate and n_s and n_o are the volumetric grain densities in the presence and in the absence of shearing, respectively. The nucleation density, $n_o$, is independent of the shear rate and is affected only by the cooling rate. It can be predicted simply by the application of the probabilistic Gaussian model as described in [31].

$$n_s=\left(1.4\times {10}^7\right)\hspace{0.33em}\dot{\gamma }+n_o$$

(1)

The fundamental nature of the nucleation mechanism under melt shearing is not sufficiently understood by researchers, as discussed above. Therefore, there has been no comprehensive mathematical model for this phenomenon introduced until now. It is also self-evident that melt shearing alone cannot produce any nuclei unless the necessary undercooling for grain nucleation is achieved. Accordingly, it will be assumed here that the shear forces applied to the supercooled melt cause multiplication of the formed crystals only after the onset of undercooling-dependent nucleation. As cooling continues and the undercooling increases, a new class of nuclei will be formed in the melt according to the heterogeneous nucleation theory. The newly born crystals are assumed to be multiplied with a rate that is proportional to $\dot{\gamma }$ as given in Equation (1).

In an earlier study, Ahmadein et al. [31] correlated the undercooling to the cooling rate of A356 casting alloy during solidification. The estimated undercooling for the current experiments was about 2.5 °C. When the equilibrium liquidus temperature of the alloy was 615 °C and the alloy was cooled down to 606 °C, the effective temperature range for production of the grain densities obtained was 6.5 °C (the equivalent solidification time = 71 s) (Figure 3). The grain densities obtained during this period are attributed to the dual effect of melt undercooling/shearing. The effect of melt undercooling alone can be calculated using the Gaussian nucleation model [31]. However, the effect of shearing on grain density can be tackled in any of these two approaches: either as a constant grain addition rate or as a constant grain multiplication rate. The first approach seems to be misleading since it adds a constant number of grains to the melt regardless of how many grains were already achieved by the thermosolutal undercooling. In other words, the regions exhibiting high nucleation rate due to large undercooling receive the same shear contribution as those exhibiting too low nucleation rates. It also introduces grains to the sheared melt before the onset of nucleation. However, the latter approach seems to be more realistic because the grains reproduced by shearing are related to the grains formed by the melt undercooling.

Based on the above argument, a grain multiplication factor, M, was suggested. It is calculated for each shear rate with respect to the undercooling-dependent grain density, n_o, obtained in the absence of shearing. M was plotted versus $\dot{\gamma }$ and fitted to a second-order equation as shown in Figure 6. It was reported in [6,20,32] that increasing the shear rate has two counteracting actions: one of them increases the grain reproduction and the other reduces the grain density due to the agglomeration of grains/fragments caused by the increased collision rate. Analogous to the experimental results of Ji and Fan [10] for the Sn-15%Pb alloy, it is expected here that the collision effect on reducing the reproduction rate is more evident at higher shear rates. Therefore, the second-order Equation (2) was derived to fit the experimental data plotted in Figure 6. It is obvious from the extrapolated section of the trend line ( at shear rates higher than 300 s⁻¹) that the rate of grain multiplication decreases as the shear rate increases. The empirical multiplication factor introduced in Equation (2) can be applied to the simulation codes for the prediction of the grain number density of A356 alloy during all casting and thixoforming processes. The source term of the shear contribution to the grain density, $N_s$, is simply correlated to the grains produced by the instantaneous melt undercooling (the source term of undercooling-induced nucleation), $N_0$, and to the shear rate as given in Equation (3).

$$M=-1.39\times {10}^{-5}\hspace{0.33em}{\dot{\gamma }}^2+0.031\dot{\gamma }$$

(2)

$$N_s=M{\times N}_0$$

(3)

A wide spectrum of measured viscosity values for Al alloys of the order of 400% variation has been reported in the literature, depending on the measurement method [33] and the applied shear rate. The liquid viscosity (~0.04 Pas) obtained in the current study is close to some published results [34,35,36]. The obtained viscosity of the semisolid A356 shown in Figure 5 agrees well with earlier studies on the shear-thinning behavior of the slurry. However, the current measured viscosity may vary depending on the experimental conditions and the design of the viscometer.

Several models for mixture viscosity, ${\eta }_{mix}$, were introduced by researchers. The most common model in this regard is the power law given in its simplest form in Equation (4) where $K$ is the consistence index (a measure for the average liquid viscosity) and n is the power law index (a measure for the deviation from the Newtonian; $n=1$ for Newtonian, n < 1 for pseudo-plastics, and n > 1 for dilatants). Some authors deduced values for the consistence and the power law indices, $K$ and $n$, respectively, for some alloys [37,38,39]. However, these values cover only a limited range of solid fractions and shear rates. H. Moon [40] tried to combine the effect of solid fraction and shear rate into one model. He deduced an exponential correlation (Equation (5)) with two shear rate-dependent and cooling rate-dependent coefficients: $A=2.08\times 10^{-5}\dot{\gamma }+0.0563$ and $B=-0.0113\dot{\gamma }+19.025$ for Al-6.5% Si alloy. Hirai et al. [41] proposed an empirical relationship based on experimental results (Equation (6)), with $\alpha =203 C^{1/3}$, $\beta =19.0 C^{1/3}$, $C$: volume rate of transformation ($\frac{d{f}_s}{dt}\approx 0.001$ s⁻¹), and ${\eta }_l$ and ${\rho }_l$ as the viscosity and density of liquid alloy, respectively. Z. Zhang et al. [34] deduced a model (Equation (7)) based on his own experiments on A356 aluminum. Their model was valid for $f_s$ from 0 up to 0.36.

Power law model [37,38,39]:

$${\eta }_{mix}=K {\dot{\gamma }}^{\left(n-1\right)}$$

(4)

H. Moon model [40]:

$${\eta }_{mix}=A e^{\left(B·f_s\right)}$$

(5)

Hirai et al. [41]:

$${\eta }_{mix}={\eta }_l\left\{1+\frac{\alpha {\rho }_l{C}^{1/3}{\dot{\gamma }}^{-4/3}}{2\left[(1/f_s)-(1/(0.72-\beta C^{1/3}{\dot{\gamma }}^{-1/3}\left)\right)\right]}\right\}$$

(6)

Z. Zhang et al. [34]:

$${\eta }_{mix}=\left(0.8432+0.0063f_s+75.176f_s^2\right)·{\dot{\gamma }}^{\left(-0.5422-2.354f_s+3.7253f_s^2\right)}$$

(7)

The measured viscosity of the semisolid A356 alloy from the current experiments was fitted to the above models. They are plotted at the same solid fraction and the other experimental conditions versus the shear rate as shown in Figure 7. In comparison, H. Moon’s model (Equation (5)) deviates greatly from the current experimental viscosity. The power law model (Equation (4)) with $K=54$ and $n=-0.2$ provides relatively higher apparent viscosity compared to the experiments, particularly at low shear rates. The model of Zhang et al. (Equation (7)) exhibits a good fit, but it disregarded the viscosity of liquid. On the other hand, the model of Hirai et al. [41] incorporated the liquid viscosity, liquid density, and solute concentration into the alloy, in addition to the solid fraction and shear rate as well. This model has a good fit with the experimental data as shown in Figure 7. The perfect fitting line represents the power law function given in Equation (8) with $K=0.9264$ and $n=0.468$. While this relationship fits well with the viscosity results of the current experiments, it should be applied with care when predicting viscosity at another $f_s$, shear rate, or for another alloy composition.

During the production of semisolid slurry, simultaneous cooling/shearing results in a variable solid fraction (0 to 0.45). Furthermore, thixoforming processes exhibit high shear rates (>2000 s⁻¹) and a solid fraction of about 0.5. Under such conditions, the need arises for a comprehensive and consistent viscosity model that is able to cover a wide range of shear rates and solid fractions, at least for individual alloys. Further investigations are recommended before applying this formula:

$${\eta }_{mix}=0.9264\hspace{0.33em}{\dot{\gamma }}^{-0.532}$$

(8)

5. Conclusions

(1)

Morphological evolution:

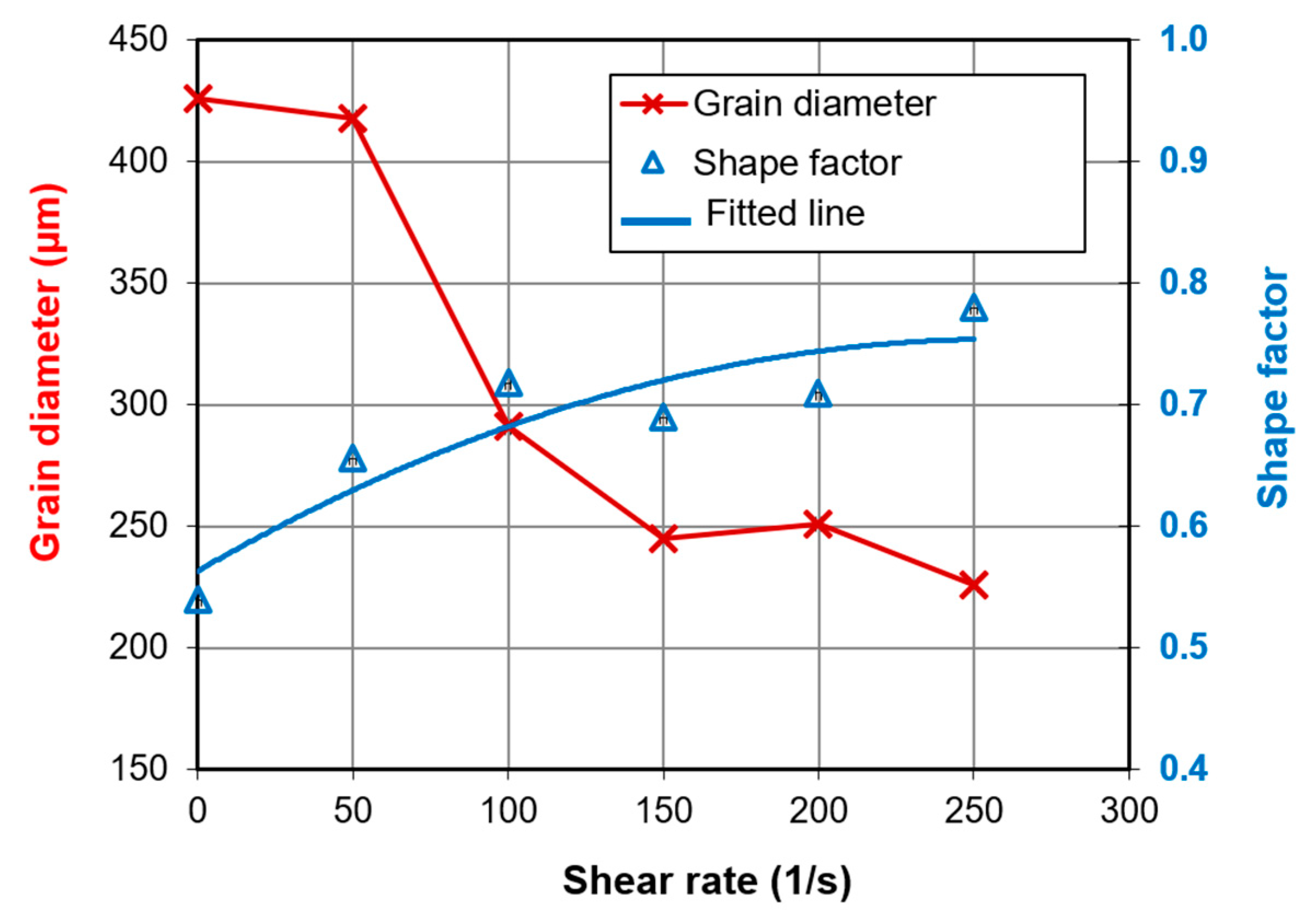
• The alloy A356 undergoes several morphological evolutions under shearing. Low shear rates provided a mixture of dispersed dendrites, cramped dendrites, and rosette-like grains. At higher shear rates, fine individual globular particles replaced the dendrites.
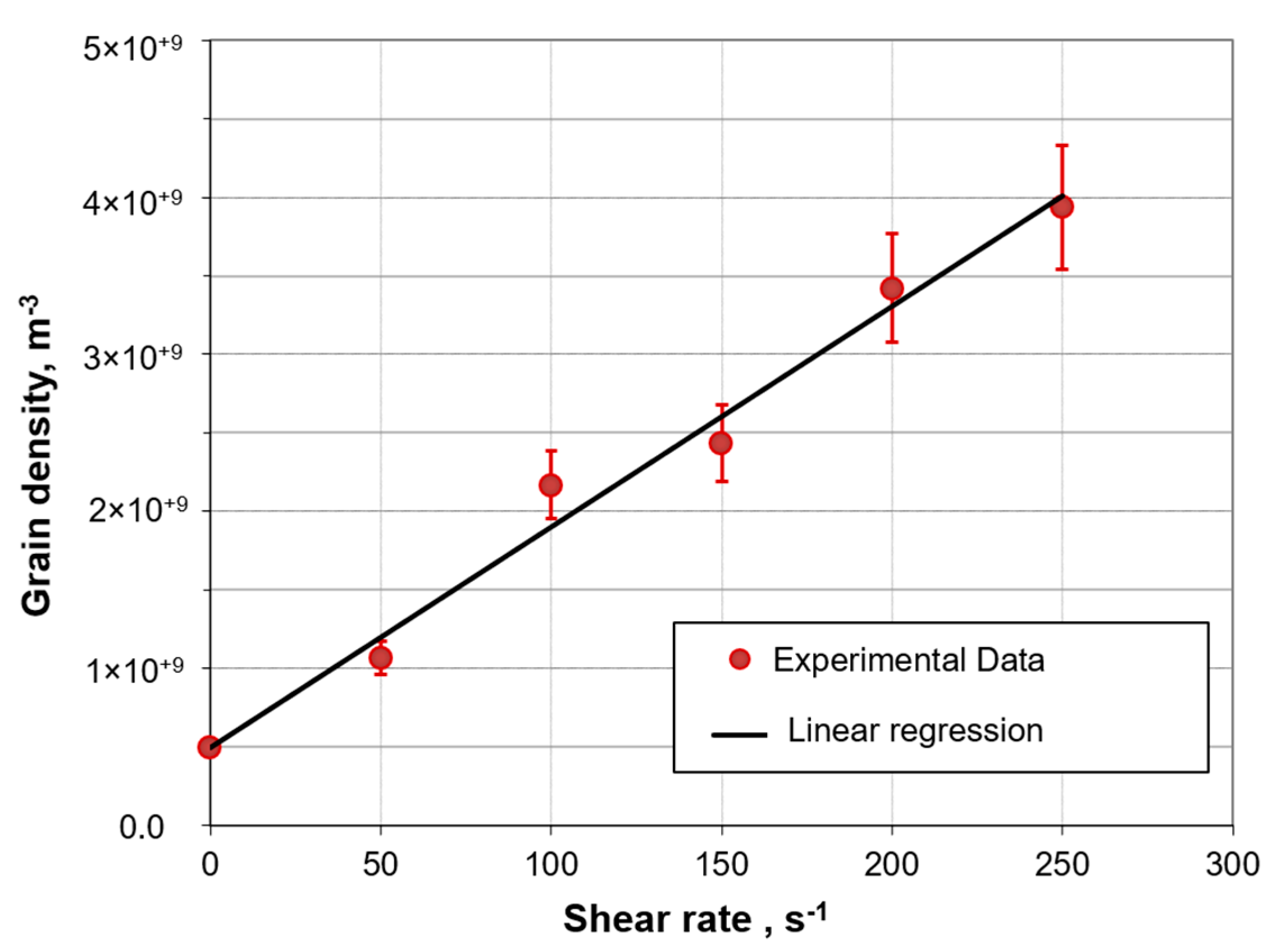
• Experiments showed an increasing grain number density, grain size refinement, and improved shape factor by increasing the shear rate.
• An empirical formula, $n_s=\left(1.4\times {10}^7\right)\hspace{0.33em}\dot{\gamma }+n_o$, correlated to the applied shear rate and the undercooling-dependent grain density in the absence of shearing.
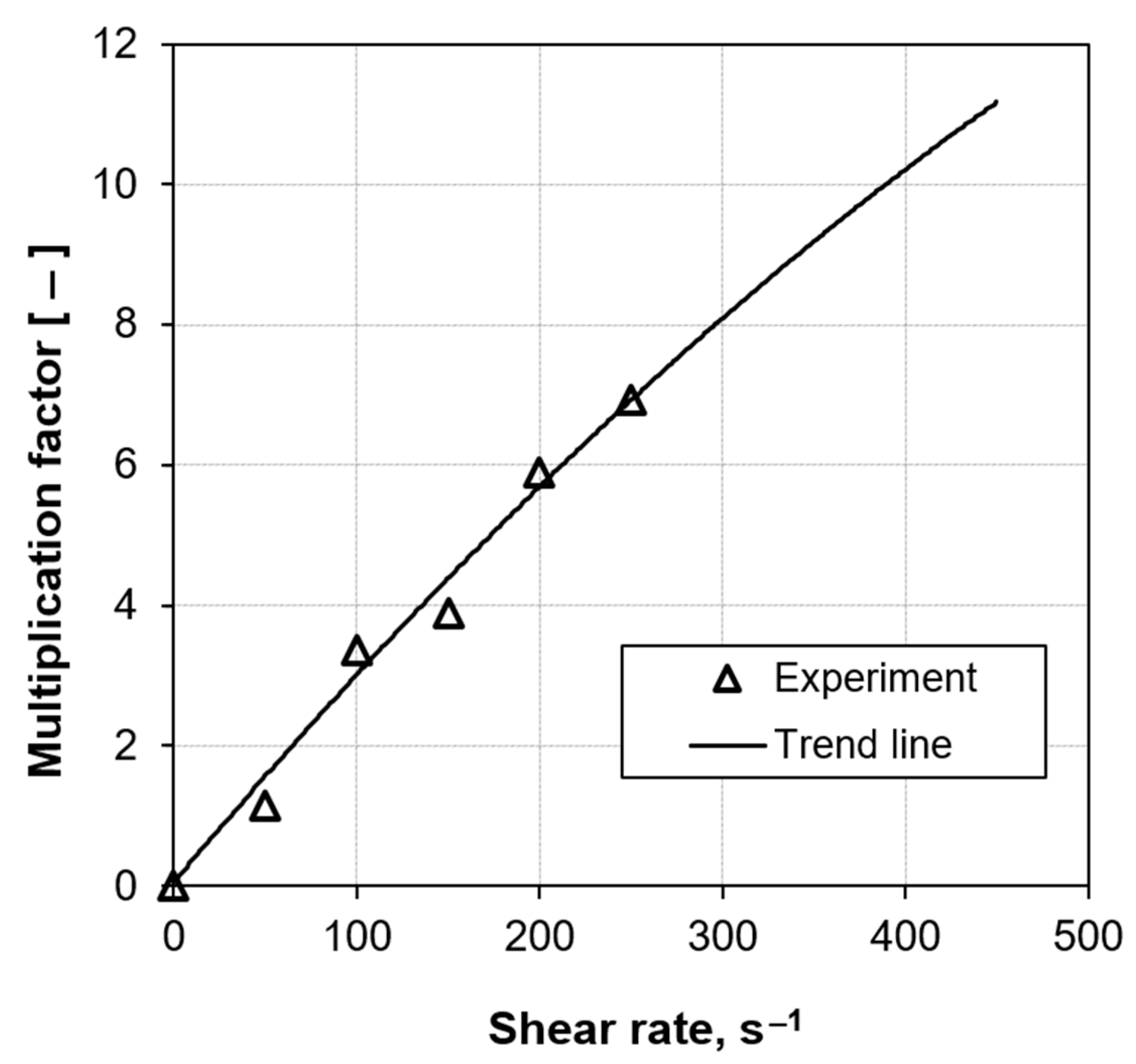
• A grain multiplication factor, $M=-1.39\times {10}^{-5}\hspace{0.33em}{\dot{\gamma }}^2+0.031\dot{\gamma }$, was suggested to account for the grains produced due to a shear rate increment. It would be very helpful in predicting grain density for when alloy mixture is transported between regions of different shear rates.

(2)

Rheology:

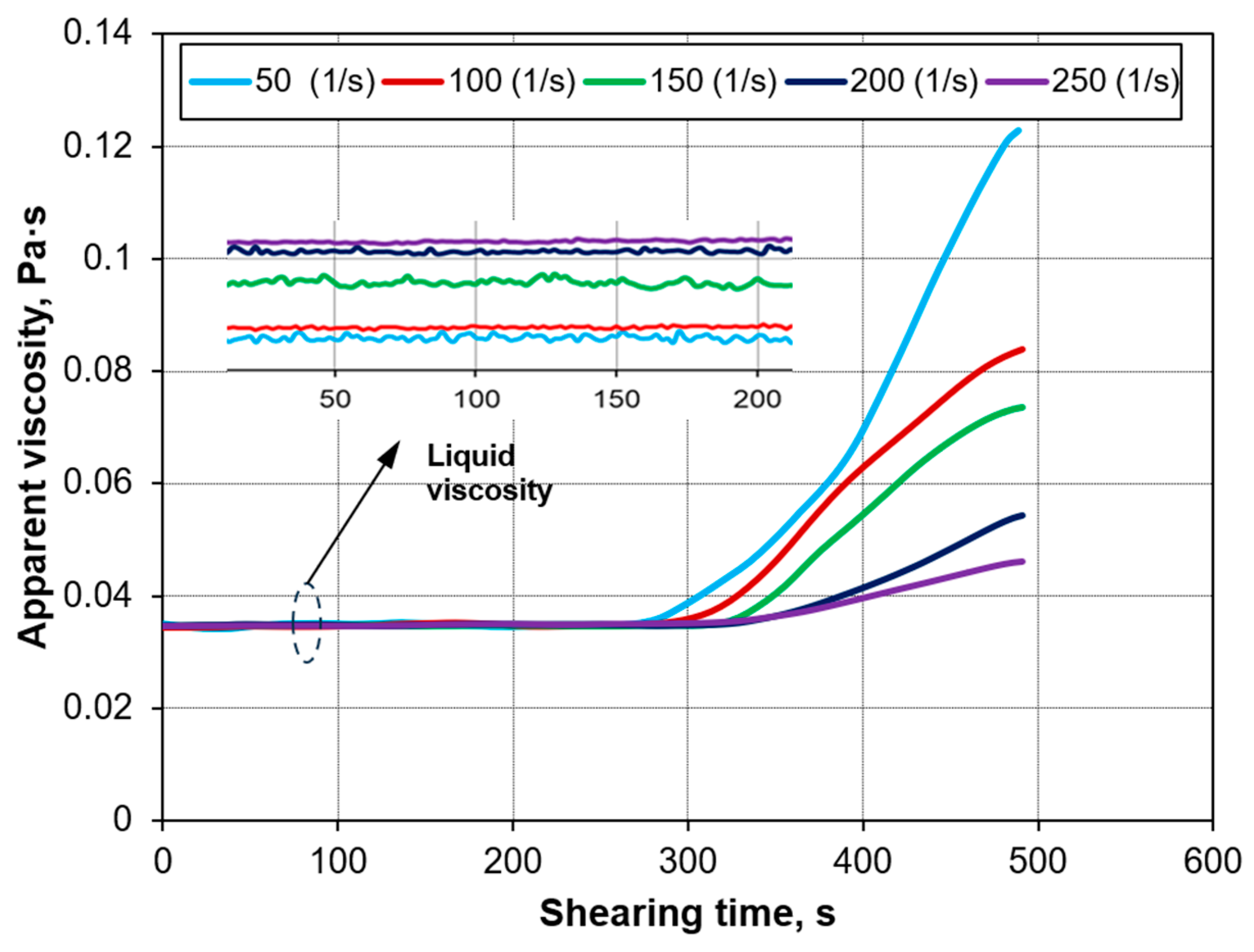
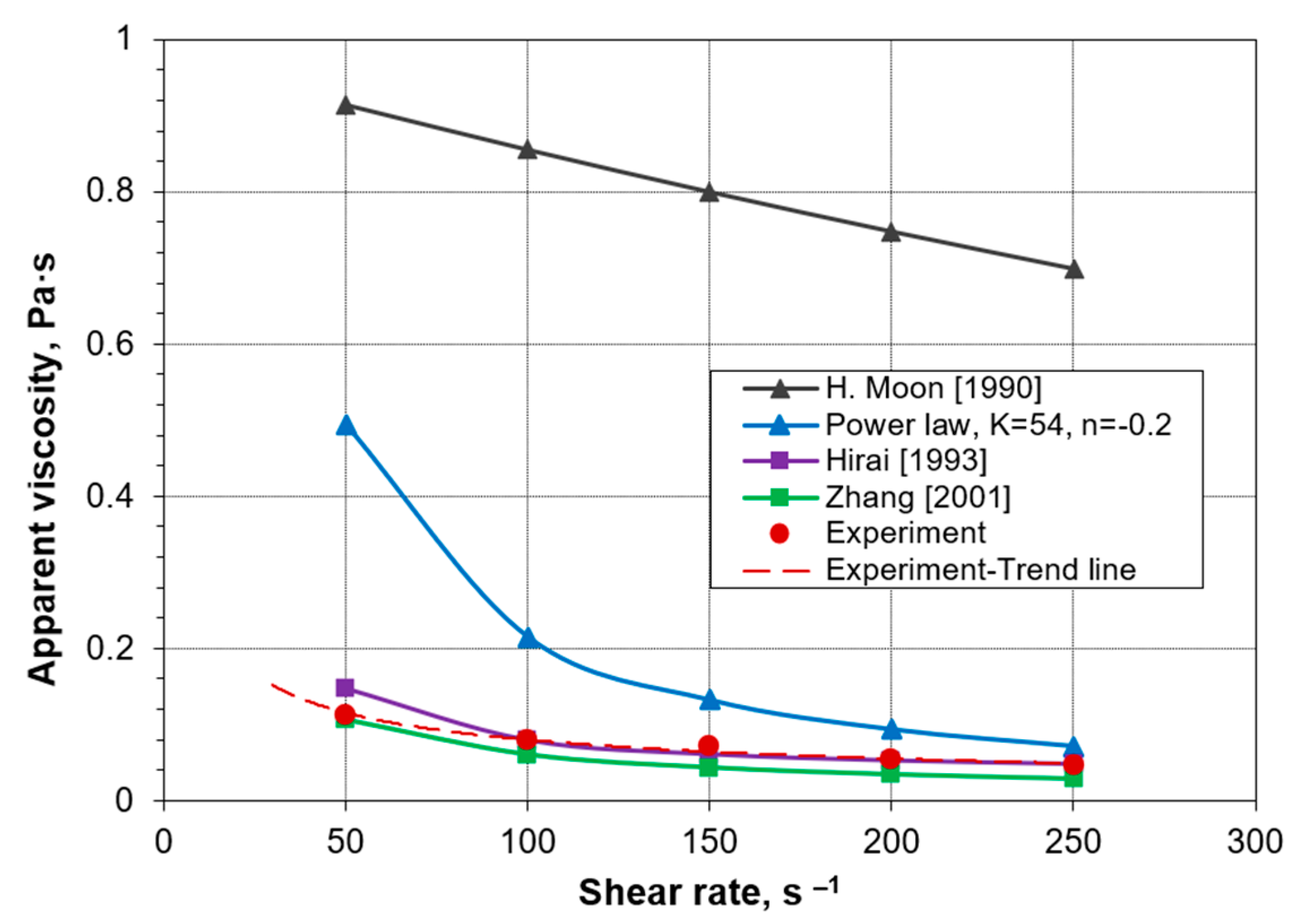
• The alloy exhibited a shear-thinning behavior where the viscosity obeyed the power law, ${\eta }_{mix}=0.9264\hspace{0.33em}{\dot{\gamma }}^{-0.532}$.
• The measured viscosity showed a best fitting mixture viscosity model Hirai et al. [41]. Therefore, it was recommended for use in predicting the viscosity of semisolid slurries.

(3)

Outlook: Experiments can be expanded to cover higher solid fractions and shear rates in a trial to achieve a more comprehensive model. In situ observation of morphological evolutions during shearing of undercooled melts is highly recommended to accurately specify the involved mechanisms, which may lead to progress in modeling solidification under convective fields.