Nucleation and Growth Kinetics of Sodium Chloride Crystallization from Water and Deuterium Oxide
Abstract
:1. Introduction
1.1. Primary Nucleation, Secondary Nucleation, and Crystal Growth
1.2. Crystallization Characterization: Solubility, Metastable Zone Width, and Growth Rates
2. Materials and Methods
2.1. Solubility and Metastable Zone Width Determination
2.2. Unseeded Crystallization: Induction Times at Different Sample Scales and Agitation Conditions
2.3. Analysis of Unseeded Induction Time Distributions: Primary Nucleation Rates
2.4. Seeded Crystallization
Seeded Secondary Nucleation Rate
2.5. Crystal Growth Rates
3. Results and Discussion
3.1. Solubility and Metastable Zone
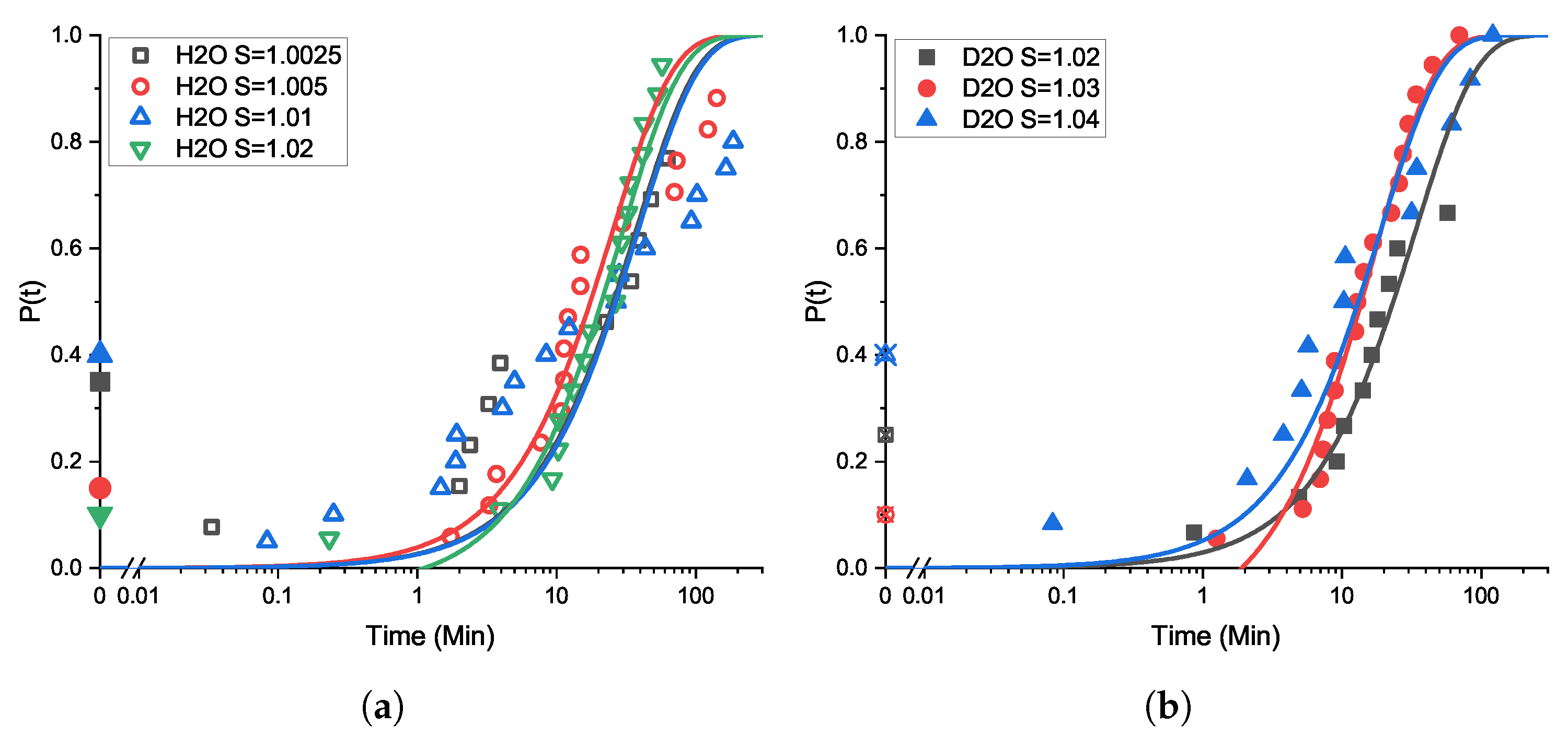
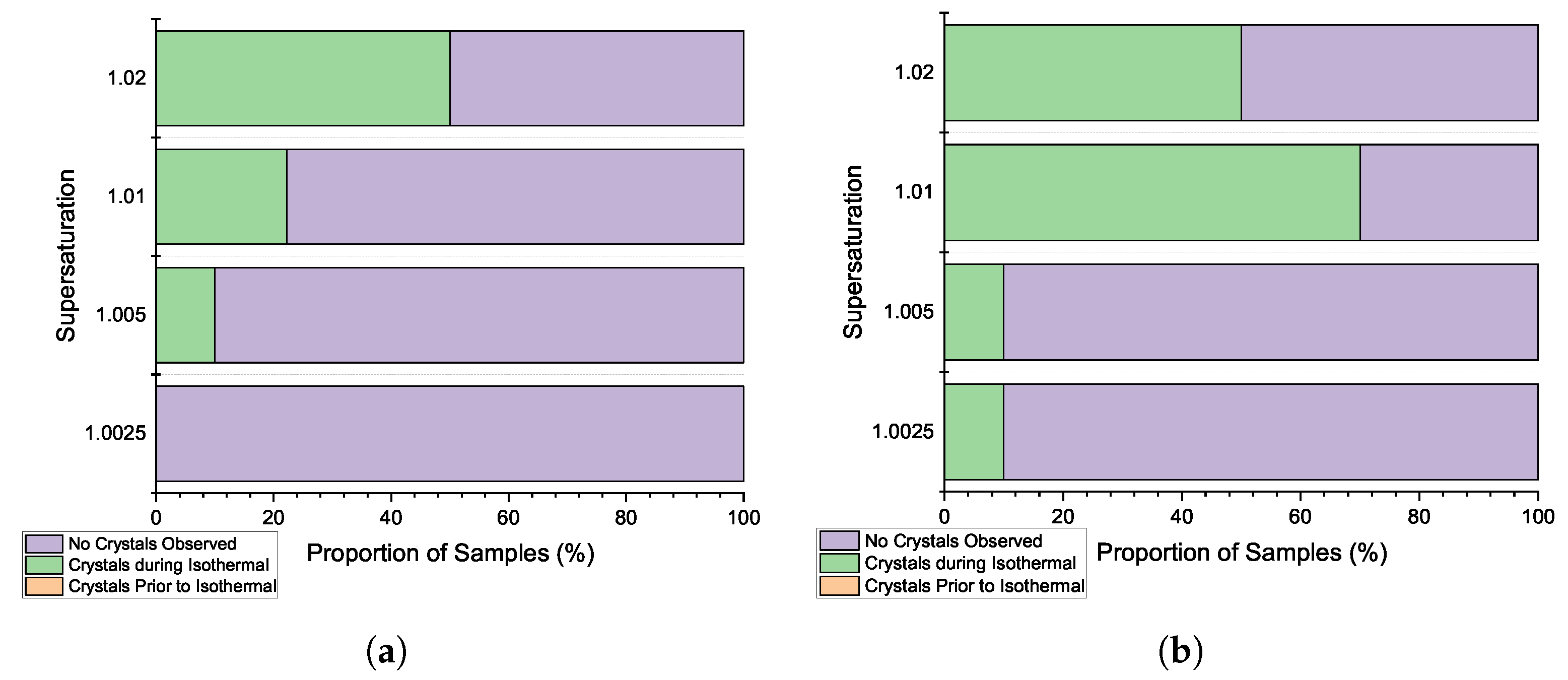
3.2. Induction Time Distributions: Effect of Agitation
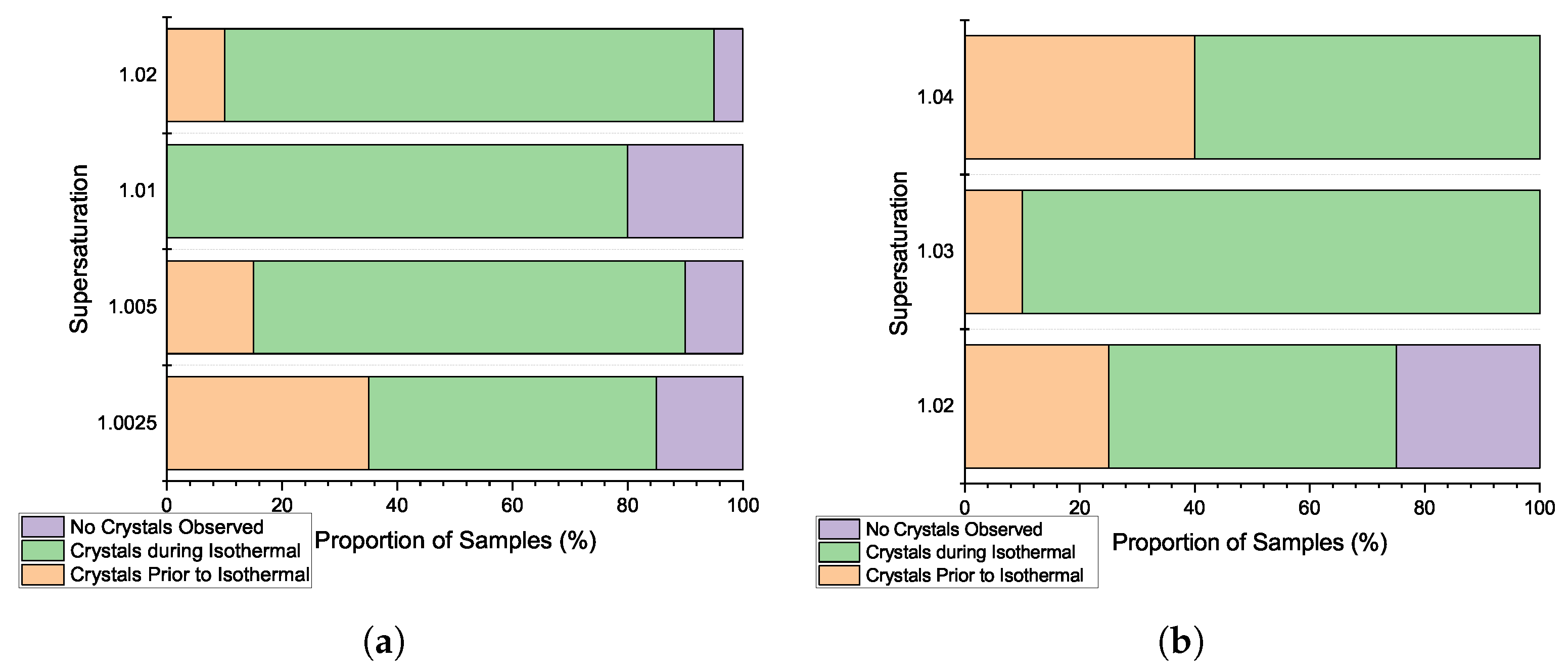
3.3. Induction Time Distributions: Pre-Isothermal Nucleation
3.4. Primary Nucleation
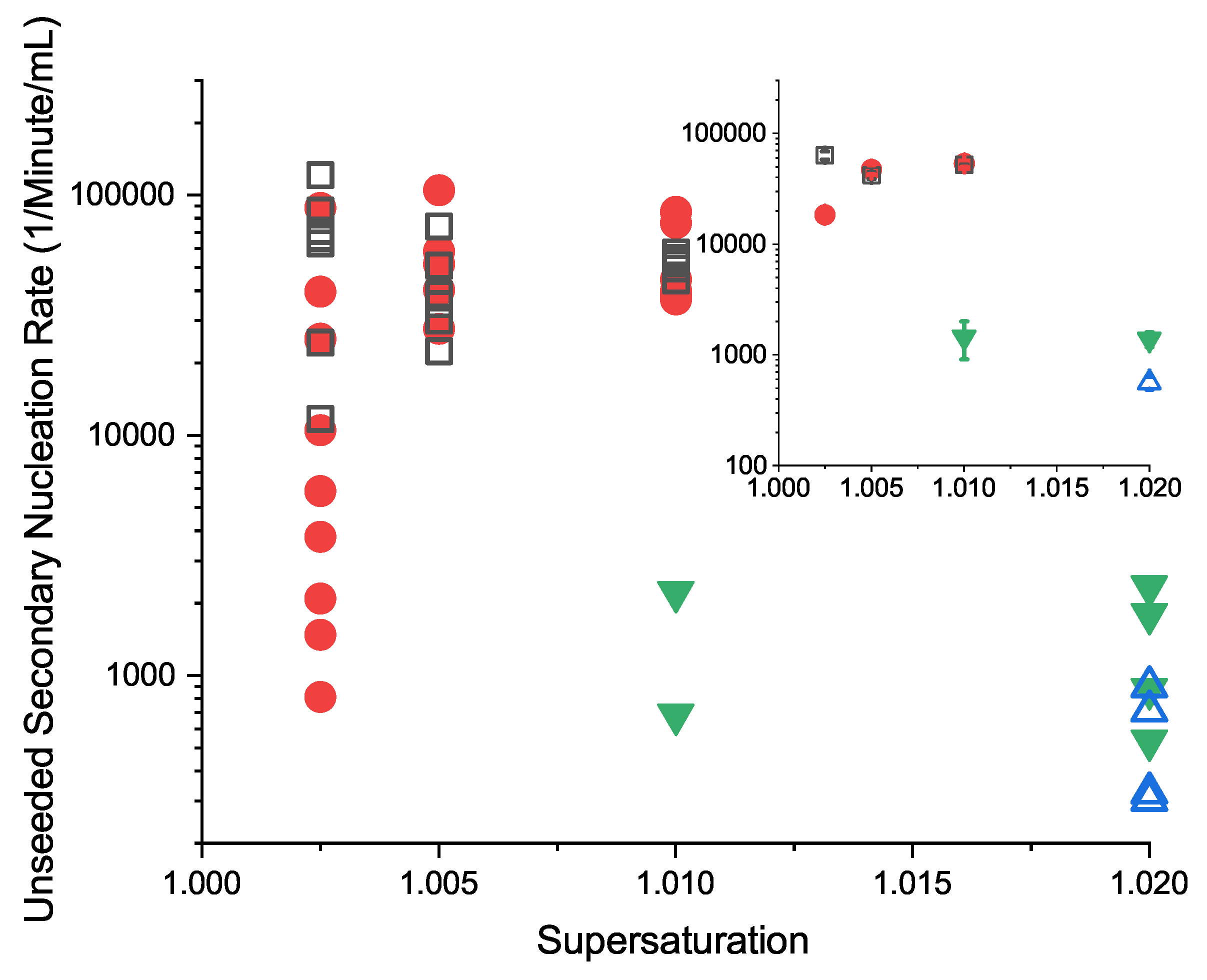
3.5. Secondary Nucleation
3.5.1. Unseeded Secondary Nucleation Rates
3.5.2. Seeded Secondary Nucleation Rates
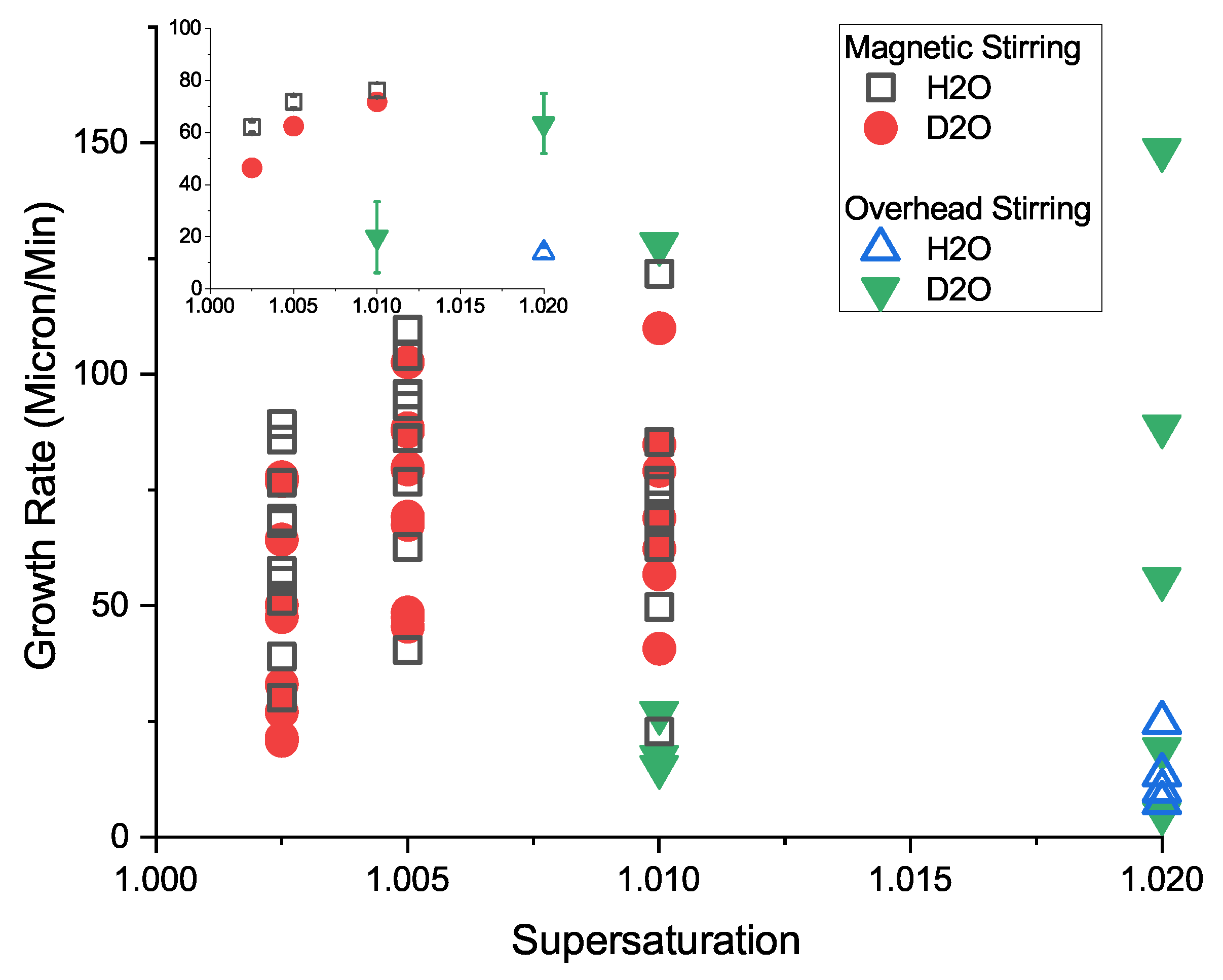
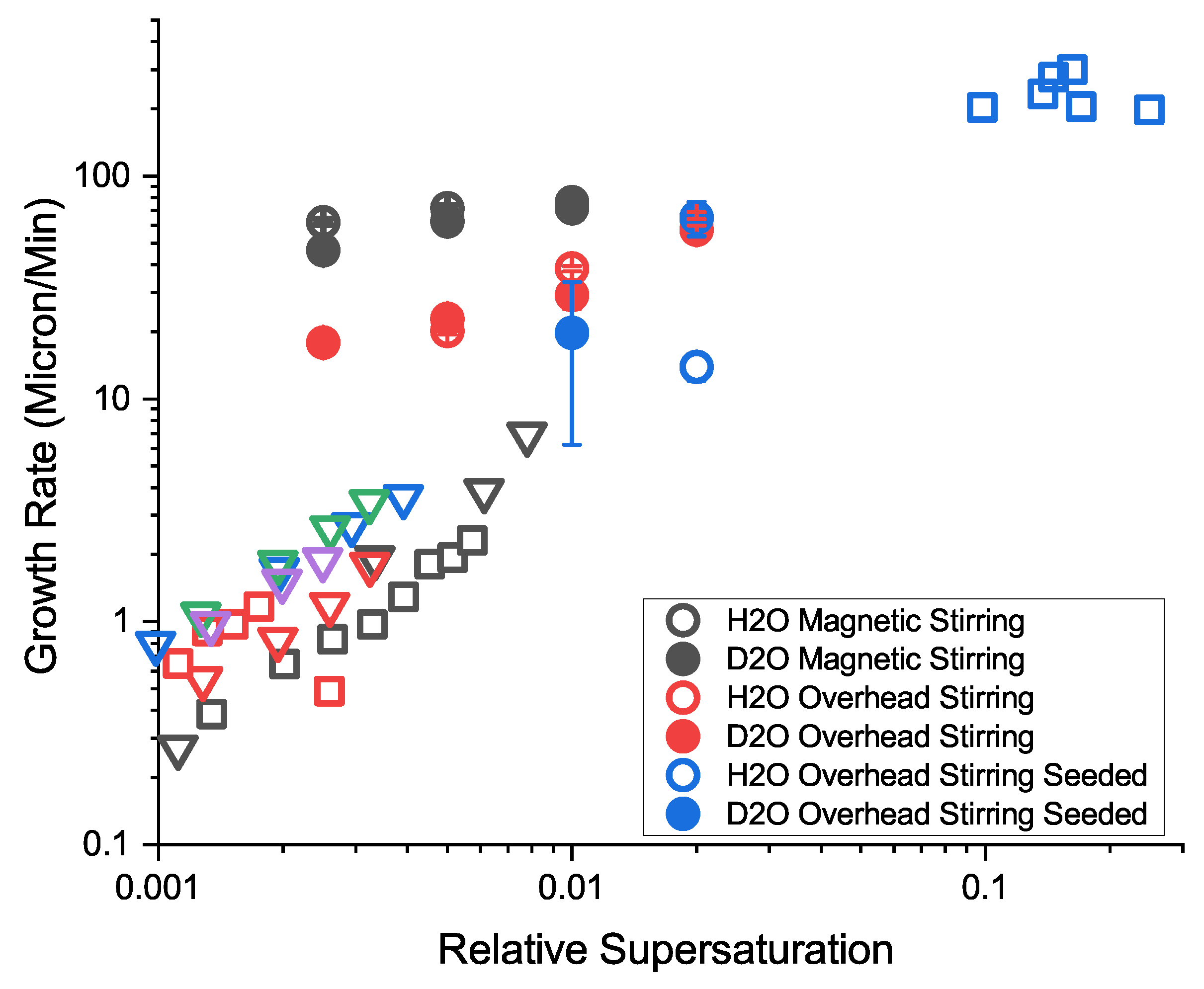
3.6. Crystal Growth Rates
Comparison with Previous Measures of Growth Rate
3.7. Seed Activation Period
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schoen, H.M.; Grove, C.S.; Palermo, J.A. The early history of crystallization. J. Chem. Educ. 1956, 33, 373–375. [Google Scholar] [CrossRef]
- de Coppet, L.C. Study on the solubility of chlorides, bromides and iodides of potassium and sodium. Ann. Chim. Phys. 1883, 30, 411–429. [Google Scholar]
- Blasdale, W.C. Equilibria in solutions containing mixtures of salts. I—the system water and the sulfates and chlorides of sodium and potassium. Ind. Eng. Chem. 1918, 10, 344–347. [Google Scholar] [CrossRef]
- Antropoff, A. The Solubilities in the ternary Systems Sodium Chloride-Sodium Hydroxide-Water and Potassium Chloride-Potassium Hydroxide-Water. Z. Elektrochem. Angew. Phys. Chem. 1924, 30, 457–467. [Google Scholar]
- Eddy, R.D.; Menzies, A.W.C. The solubilities of certain inorganic compounds in ordinary water and in deuterium water. J. Phys. Chem. 1940, 44, 207–235. [Google Scholar] [CrossRef]
- Menzies, A.W.C. A method of Solubility Measurement. Solubilities in the System SrCl2-H2O from 20 to 200°. J. Am. Chem. Soc. 1936, 58, 934–937. [Google Scholar] [CrossRef]
- Briuglia, M.L.; Sefcik, J.; ter Horst, J.H. Measuring Secondary Nucleation through Single Crystal Seeding. Cryst. Growth Des. 2019, 19, 421–429. [Google Scholar] [CrossRef]
- Cashmore, A.; Miller, R.; Jolliffe, H.; Brown, C.J.; Lee, M.; Haw, M.D.; Sefcik, J. Rapid Assessment of Crystal Nucleation and Growth Kinetics: Comparison of Seeded and Unseeded Experiments. Cryst. Growth Des. 2023, 23, 4779–4790. [Google Scholar] [CrossRef] [PubMed]
- Erdemir, D.; Lee, A.Y.; Myerson, A.S. Nucleation of crystals from solution: Classical and two-step models. Accounts Chem. Res. 2009, 42, 621–629. [Google Scholar] [CrossRef]
- Deck, L.T.; Mazzotti, M. Conceptual Validation of Stochastic and Deterministic Methods To Estimate Crystal Nucleation Rates. Cryst. Growth Des. 2023, 23, 899–914. [Google Scholar] [CrossRef]
- Jiang, S.; ter Horst, J.H. Crystal nucleation rates from probability distributions of induction times. Cryst. Growth Des. 2011, 11, 256–261. [Google Scholar] [CrossRef]
- Lee, A.Y.; Erdemir, D.; Myerson, A.S. Crystals and Crystal Growth. In Handbook of Industrial Crystallization; Cambridge University Press: Cambridge, UK, 2019; pp. 32–75. [Google Scholar] [CrossRef]
- Myerson, A.S.; Erdemir, D.; Lee, A.Y. Crystal nucleation. In Handbook of Industrial Crystallization; Butterworth-Heinemann: Oxford, UK, 2019; pp. 76–114. [Google Scholar] [CrossRef]
- Kadam, S.S.; Kramer, H.J.M.; ter Horst, J.H. Combination of a single primary nucleation event and secondary nucleation in crystallization processes. Cryst. Growth Des. 2011, 11, 1271–1277. [Google Scholar] [CrossRef]
- Cui, Y.; Myerson, A.S. Experimental evaluation of contact secondary nucleation mechanisms. Cryst. Growth Des. 2014, 14, 5152–5157. [Google Scholar] [CrossRef]
- Xu, S.; Wang, Y.; Hou, Z.; Chuai, X. Overview of secondary nucleation: From fundamentals to application. Ind. Eng. Chem. Res. 2020, 59, 18335–18356. [Google Scholar] [CrossRef]
- Anwar, J.; Khan, S.; Lindfors, L. Secondary crystal nucleation: Nuclei breeding factory uncovered. Angew. Chem.-Int. Ed. 2015, 54, 14681–14684. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, J.; Flannigan, J.; Cashmore, A.; Briuglia, M.L.; Steendam, R.R.E.; Gerard, C.J.J.; Haw, M.D.; Sefcik, J.; ter Horst, J.H. The unexpected dominance of secondary over primary nucleation. Faraday Discuss. 2022, 235, 109–131. [Google Scholar] [CrossRef]
- Kulkarni, S.A.; Meekes, H.; ter Horst, J.H. Polymorphism control through a single nucleation event. Cryst. Growth Des. 2014, 14, 1493–1499. [Google Scholar] [CrossRef]
- Forsyth, C.; Mulheran, P.A.; Forsyth, C.; Haw, M.D.; Burns, I.S.; Sefcik, J. Influence of controlled fluid shear on nucleation rates in glycine aqueous solutions. Cryst. Growth Des. 2015, 15, 94–102. [Google Scholar] [CrossRef]
- McLeod, J.S.; Paterson, A.H.J.; Bronlund, J.E.; Jones, J.R. The effect of agitation on the nucleation of α-lactose monohydrate. Int. Dairy J. 2016, 61, 114–119. [Google Scholar] [CrossRef]
- Debuysschere, R.; Rimez, B.; Zaccone, A.; Scheid, B. Experimental and Theoretical Investigation of Nonclassical Shear-Induced Nucleation Mechanism for Small Molecule. Cryst. Growth Des. 2023, 23, 4979–4989. [Google Scholar] [CrossRef]
- Vesga, M.J.; McKechnie, D.; Mulheran, P.A.; Johnston, K.; Sefcik, J. Conundrum of γ glycine nucleation revisited: To stir or not to stir? Cryst. Eng. Commn. 2019, 21, 2234–2243. [Google Scholar] [CrossRef]
- Tai, C.Y.; McCabe, W.L.; Rousseau, R.W. Contact nucleation of various crystal types. AIChE J. 1975, 21, 351–358. [Google Scholar] [CrossRef]
- Wang, M.L.; Huang, H.T.; Estrin, J. Secondary nucleation of citric acid due to fluid forces in a Couette flow crystallizer. AIChE J. 1981, 27, 312–315. [Google Scholar] [CrossRef]
- Selwood, P.W.; Frost, A.A. Some Properties of Heavy Water. J. Am. Chem. Soc. 1933, 55, 4335–4336. [Google Scholar] [CrossRef]
- Vidulich, G.A.; Evans, D.F.; Kay, R.L. The dielectric constant of water and heavy water between 0 and 40 degree. J. Phys. Chem. 1967, 71, 656–662. [Google Scholar] [CrossRef]
- Chaplin, M. Water’s Hydrogen Bond Strength. arXiv 2007, arXiv:0706.1355. [Google Scholar]
- Van Hook, W.A.; Rebelo, L.P.N. Isotope Effects on Solubility. In Developments and Applications in Solubility; Letcher, T.M., Ed.; Royal Society of Chemistry: London, UK, 2007. [Google Scholar]
- Noonan, E.C. Solubility of Salts in Deuterium Oxide. J. Am. Chem. Soc. 1948, 70, 2915–2918. [Google Scholar] [CrossRef] [PubMed]
- Jelińska-Kazimierczuk, M.; Szydłowski, J. Isotope effect on the solubility of amino acids in water. J. Solut. Chem. 1996, 25, 1175–1184. [Google Scholar] [CrossRef]
- Rungsimanon, T.; Yuyama, K.I.; Sugiyama, T.; Masuhara, H.; Tohnai, N.; Miyata, M. Control of crystal polymorph of glycine by photon pressure of a focused continuous wave near-infrared laser beam. J. Phys. Chem. Lett. 2010, 1, 599–603. [Google Scholar] [CrossRef]
- Suzuki, S.; Shimanouchi, T.; Tsuboi, M. Normal vibrations of glycine and deuterated glycine molecules. Spectrochim. Acta 1963, 19, 1195–1208. [Google Scholar] [CrossRef]
- Technobis. Application Note 3-Solubility Measurements. Technical Report.
- Xinding, Y.; Jinju, M.; Ruina, F.; Qishan, Y.; Wei, L. Measurement and Correlation of the Solubility, Dissolution Enthalpy, and Entropy of R-2[4-(6-Chloro-2-benzoxazolyloxy)phenoxy]propanoic Acid in Different Pure Solvents. Russ. J. Phys. Chem. A 2019, 93, 2340–2348. [Google Scholar] [CrossRef]
- Mack, C.; Hoffmann, J.; Sefcik, J.; ter Horst, J.H. Phase Diagram Determination and Process Development for Continuous Antisolvent Crystallizations. Crystals 2022, 12, 1102. [Google Scholar] [CrossRef]
- Olalere, O.H. Phase Behaviour and Crystal Nucleation in Complex Multicomponent system. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2019. [Google Scholar]
- Mullin, J.W. Crystallization, 4th ed.; Butterworth-Heinemann: Boston, MA, USA, 2001. [Google Scholar]
- Bharmoria, P.; Gupta, H.; Mohandas, V.P.; Ghosh, P.K.; Kumar, A. Temperature invariance of NaCl solubility in water: Inferences from salt-water cluster behavior of NaCl, KCl, and NH4Cl. J. Phys. Chem. B 2012, 116, 11712–11719. [Google Scholar] [CrossRef]
- Yerdelen, S.; Yang, Y.; Quon, J.; Papageorgiou, C.D.; Mitchell, C.; Houson, I.; Sefcik, J.; ter Horst, J.H.; Florence, A.J.; Brown, C.J. Machine Learning-Derived Correlations for Scale-Up and Technology Transfer of Primary Nucleation Kinetics. Cryst. Growth Des. 2023, 23, 681–693. [Google Scholar] [CrossRef] [PubMed]
- Chianese, A.; Di Cave, S.; Mazzarotta, B. Solubility and metastable zone width of sodium chloride in water-diethylene glycol mixtures. J. Chem. Eng. Data 1986, 31, 329–332. [Google Scholar] [CrossRef]
- Ginde, R.M.; Myerson, A.S. Effect of impurities on cluster growth and nucleation. J. Cryst. Growth 1993, 126, 216–222. [Google Scholar] [CrossRef]
- Yousuf, M.; Frawley, P.J. Experimental Evaluation of Fluid Shear Stress Impact on Secondary Nucleation in a Solution Crystallization of Paracetamol. Cryst. Growth Des. 2018, 18, 6843–6852. [Google Scholar] [CrossRef]
- Cashmore, A.; Boyle, C.; Haw, M.D.; Lee, M.; Sefcik, J. The effect of fluid shear on secondary nucleation in alpha-glycine. 2023; preparation. [Google Scholar]
- Na, H.S.; Arnold, S.; Myerson, A.S. Cluster formation in highly supersaturated solution droplets. J. Cryst. Growth 1994, 139, 104–112. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, L.E.; Chen, S.B. Efflorescence relative humidity of mixed sodium chloride and sodium sulfate particles. J. Phys. Chem. 2007, 111, 10660–10666. [Google Scholar] [CrossRef]
- Desarnaud, J.; Derluyn, H.; Carmeliet, J.; Bonn, D.; Shahidzadeh, N. Metastability limit for the nucleation of NaCl crystals in confinement. J. Phys. Chem. Lett. 2014, 5, 890–895. [Google Scholar] [CrossRef]
- Zimmermann, N.E.R.; Vorselaars, B.; David, Q.; Peters, B. Nucleation of NaCl from Aqueous Solution: Critical Sizes, Ion-Attachment Kinetics, and Rates. J. Am. Chem. Soc. 2015, 137, 13352–13361. [Google Scholar] [CrossRef]
- Zimmermann, N.E.R.; Vorselaars, B.; Espinosa, J.R.; Quigley, D.; Smith, W.R.; Sanz, E.; Vega, C.; Peters, B. NaCl nucleation from brine in seeded simulations: Sources of uncertainty in rate estimates. J. Chem. Phys. 2018, 148, 222838. [Google Scholar] [CrossRef]
- Jiang, H.; Haji-Akbari, A.; Debenedetti, P.G.; Panagiotopoulos, A.Z. Forward flux sampling calculation of homogeneous nucleation rates from aqueous NaCl solutions. J. Chem. Phys. 2018, 148, 044505. [Google Scholar] [CrossRef]
- Lanaro, G.; Patey, G.N. Molecular dynamics simulation of NaCl dissolution. J. Phys. Chem. B 2015, 119, 4275–4283. [Google Scholar] [CrossRef]
- Luo, L.; Chang, J.; Chung, T.S. Cooling Crystallization of Sodium Chloride via Hollow Fiber Devices to Convert Waste Concentrated Brines to Useful Products. Ind. Eng. Chem. Res. 2017, 56, 10183–10192. [Google Scholar] [CrossRef]
- Pratola, F. Micro-Mechanics of Agglomerative Crystallization Processes. Ph.D. Thesis, University College London, London, UK, 2004. [Google Scholar]
- Johnston, T.L.; Stokes, R.J.; Li, C.H. The ductile-brittle transition in ionic solids. Philos. Mag. 1959, 4, 1316–1324. [Google Scholar] [CrossRef]
- Threlfall, T.L.; Coles, S.J. A perspective on the growth-only zone, the secondary nucleation threshold and crystal size distribution in solution crystallisation. CrystEngComm 2016, 18, 369–378. [Google Scholar] [CrossRef]
- Grootscholten, P.A.M.; De Leer, B.G.M.; De Jong, E.J.; Asselbergs, C.J. Factors affecting secondary nucleation rate of sodium chloride in an evaporative crystallizer. AIChE J. 1982, 28, 728–737. [Google Scholar] [CrossRef]
- Zheng, D.; Zou, W.; Yan, J.; Peng, C.; Fu, Y.; Li, B.; Zeng, L.; Huang, T.; Zhang, F. Coupling of Contact Nucleation Kinetics with Breakage Model for Crystallization of Sodium Chloride Crystal in Fluidized Bed Crystallizer. J. Chem. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Noyes, A.A.; Whitney, W.R. The rate of solution of solid substances in their own solutions. J. Am. Chem. Soc. 1897, 19, 930–934. [Google Scholar] [CrossRef]
- Duroudier, J.P. Dispersions and Dissolutions of Powders. In Solid-Solid, Fluid-Solid, Fluid-Fluid Mixers; ISTE Press: London, UK, 2016. [Google Scholar]
- Rodriguez-Clemente, R. Crystal Growth Kinetics of Sodium Chloride from Solution. In Industrial Crystallization; Springer: Boston, MA, USA, 1976; pp. 187–199. [Google Scholar] [CrossRef]
- Jones, C.M. Characterizing Growth Rates and Growth Rate Dispersion of Secondary Nuclei as a Fraction of Supersaturation. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 1999. [Google Scholar]
- Millero, F.J.; Dexter, R.; Hoff, E. Density and Viscosity of Deuterium Oxide Solutions from 5–70 °C. J. Chem. Eng. Data 1971, 16, 85–87. [Google Scholar] [CrossRef]
- Offermann, H.; Von Brachel, G.; Al-Sabbagh, A.; Farelo, F. Crystallization Kinetics of NaCl in Multicomponent Solutions. Cryst. Res. Technol. 1995, 30, 651–658. [Google Scholar] [CrossRef]
- Al-Jibbouri, S.; Ulrich, J. The growth and dissolution of sodium chloride in a fluidized bed crystallizer. J. Cryst. Growth 2002, 234, 237–246. [Google Scholar] [CrossRef]
- Zhang, S.B.; Yuan, J.J.; Mohameed, H.A.; Ulrich, J. The effect of different inorganic salts on the growth rate of NaCl crystallized from sea water. Cryst. Res. Technol. 1996, 31, 19–25. [Google Scholar] [CrossRef]
- Ulrich, J.; Mohameed, H.; Zhang, S.B.; Yuan, J.J. Effect of Additives on the Crystal Growth Rates: Case Study NaCl. Bull. Soc. Sea Water Sci. Jpn. 1997, 51, 73–77. [Google Scholar] [CrossRef]
- Desarnaud, J.; Derluyn, H.; Carmeliet, J.; Bonn, D.; Shahidzadeh, N. Hopper Growth of Salt Crystals. J. Phys. Chem. Lett. 2018, 9, 2961–2966. [Google Scholar] [CrossRef]
- Schiele, S.A.; Hupfer, R.; Luxenburger, F.; Briesen, H. Growth of Abraded Crystals Tracked in Three Dimensions. Cryst. Growth Des. 2021, 21, 6373–6384. [Google Scholar] [CrossRef]
- Tominaga, Y.; Maruyama, M.; Yoshimura, M.; Koizumi, H.; Tachibana, M.; Sugiyama, S.; Adachi, H.; Tsukamoto, K.; Matsumura, H.; Takano, K.; et al. Promotion of protein crystal growth by actively switching crystal growth mode via femtosecond laser ablation. Nat. Photonics 2016, 10, 723–726. [Google Scholar] [CrossRef]
- Brown, C.J.; McGlone, T.; Yerdelen, S.; Srirambhatla, V.; Mabbott, F.; Gurung, R.; Briuglia, M.L.; Ahmed, B.; Polyzois, H.; McGinty, J.; et al. Enabling precision manufacturing of active pharmaceutical ingredients: Workflow for seeded cooling continuous crystallisations. Mol. Syst. Des. Eng. 2018, 3, 518–549. [Google Scholar] [CrossRef]
- Briuglia, M.L. Primary and Secondary Crystal Nucleation of Pharmaceutics. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2017. [Google Scholar]
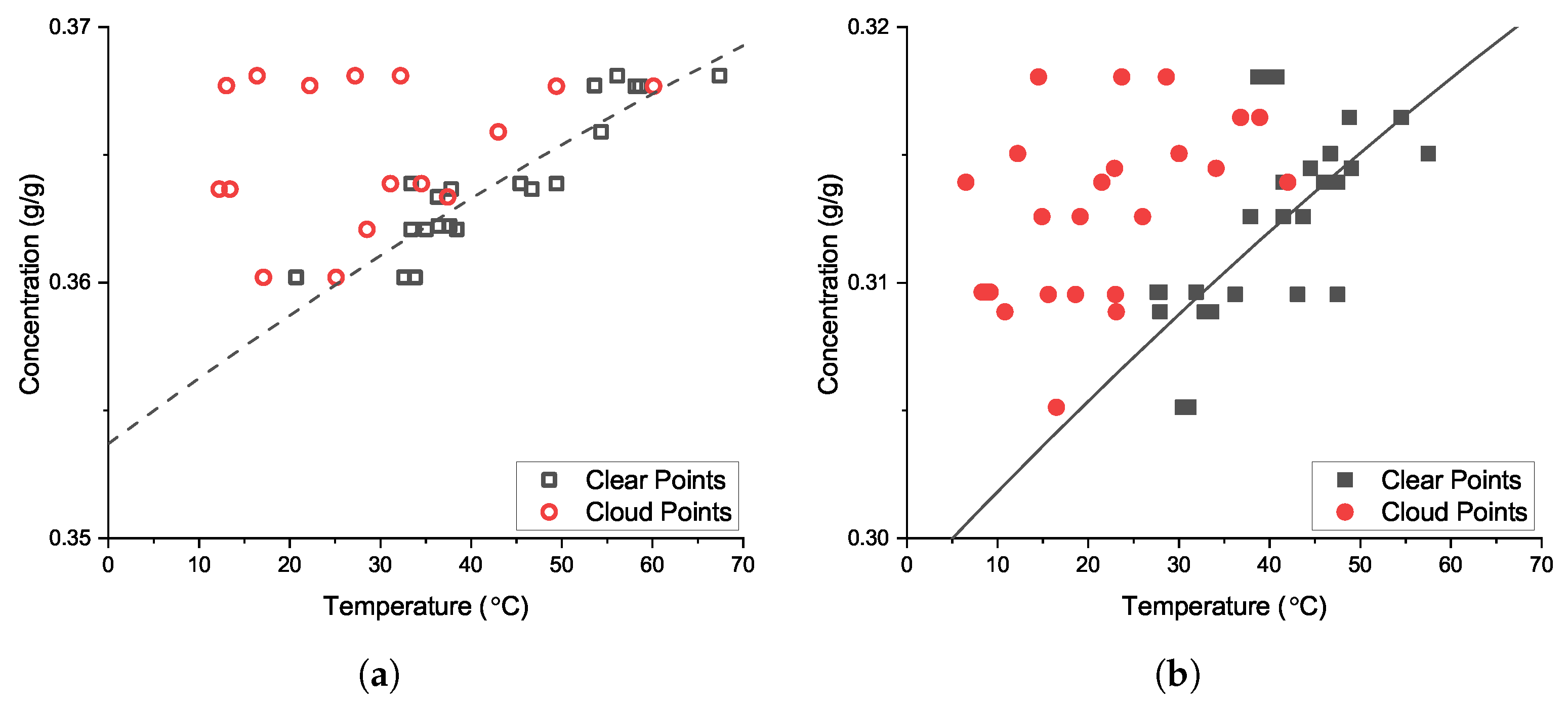
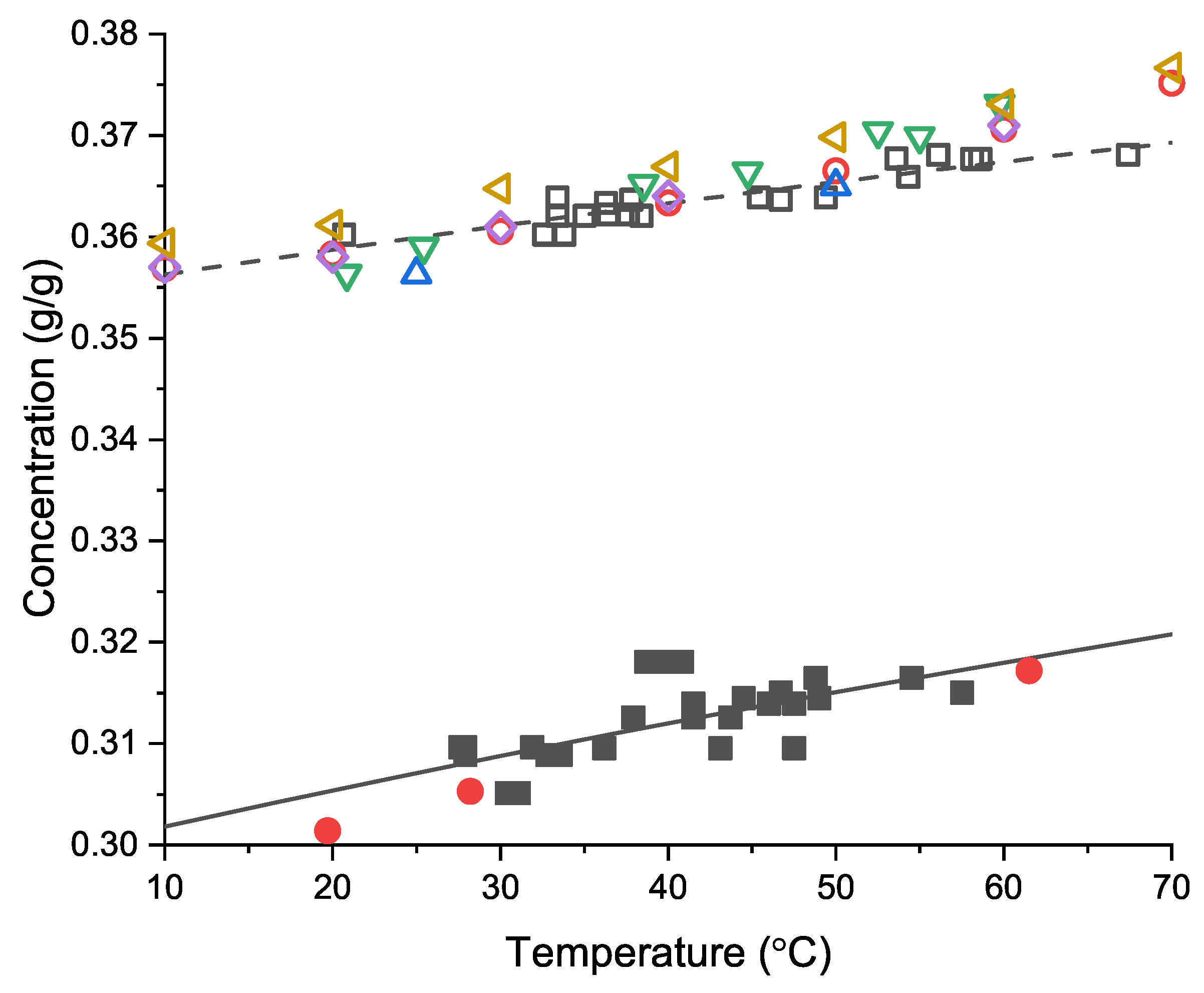








| Solvent | C (gSolute/gSolvent) | S at 25 C |
|---|---|---|
| H2O | 0.3608 | 1.0025 |
| 0.3617 | 1.005 | |
| 0.3635 | 1.01 | |
| 0.3671 | 1.02 | |
| D2O | 0.3079 | 1.0025 |
| 0.3086 | 1.005 | |
| 0.3102 | 1.01 | |
| 0.3132 | 1.02 | |
| 0.3163 | 1.03 | |
| 0.3194 | 1.04 |
| Solvent | Scale | S | Agitation Type | J (m−3 s−1) | tg (min) |
|---|---|---|---|---|---|
| H2O | C16 | 1.0025 | MS | 450 ± 99 | 0 ± 2.85 |
| H2O | C16 | 1.005 | MS | 660 ± 141 | 0 ± 2.12 |
| H2O | C16 | 1.01 | MS | 434 ± 123 | 0 ± 2.91 |
| H2O | C16 | 1.02 | MS | 580 ± 37 | 1.12 ± 0.95 |
| D2O | C16 | 1.02 | MS | 550 ± 74 | 0 ± 1.79 |
| D2O | C16 | 1.03 | MS | 1084 ± 63 | 1.90 ± 0.51 |
| D2O | C16 | 1.04 | MS | 981 ± 207 | 0 ± 1.40 |
| H2O | Crystalline | 1.0025 | MS | 358 ± 56 | 0 ± 1.27 |
| H2O | Crystalline | 1.005 | MS | 646 ± 144 | 0 ± 1.07 |
| H2O | Crystalline | 1.01 | MS | 619 ± 118 | 0 ± 0.78 |
| H2O | Crystalline | 1.02 | MS | [-] | [-] |
| D2O | Crystalline | 1.0025 | MS | 81 ± 6 | 2.37 ± 2.83 |
| D2O | Crystalline | 1.005 | MS | 375 ± 35 | 0.75 ± 0.76 |
| D2O | Crystalline | 1.01 | MS | 90 ± 7 | 6.13 ± 2.6 |
| D2O | Crystalline | 1.02 | MS | 1952 ± 267 | 0.27 ± 0.21 |
| H2O | Crystalline | 1.0025 | OS | [-] | [-] |
| H2O | Crystalline | 1.005 | OS | [-] | [-] |
| H2O | Crystalline | 1.01 | OS | [-] | [-] |
| H2O | Crystalline | 1.02 | OS | 17 ± 5 | 0 ± 29.0 |
| D2O | Crystalline | 1.0025 | OS | [-] | [-] |
| D2O | Crystalline | 1.005 | OS | [-] | [-] |
| D2O | Crystalline | 1.01 | OS | 22 ± 5 | 15.1 ± 29.4 |
| D2O | Crystalline | 1.02 | OS | 15 ± 3 | 0 ± 30.2 |
| Symbol | Source | Solvent | Conditions | Measurement Method |
|---|---|---|---|---|
 | This Work | H2O | Unseeded, Magnetic Stirring 700 RPM | D-90 Change Rate |
 | This Work | D2O | Unseeded, Magnetic Stirring 700 RPM | D-90 Change Rate |
 | This Work | H2O | Unseeded, Overhead Stirring 1250 RPM | D-90 Change Rate |
 | This Work | D2O | Unseeded, Overhead Stirring 1250 RPM | D-90 Change Rate |
 | This Work | H2O | Seeded, Overhead Stirring 1250 RPM | D-90 Change Rate |
 | This Work | D2O | Seeded, Overhead Stirring 1250 RPM | D-90 Change Rate |
 | Offerman [63] | H2O | Fluidized Bed | Change in Mass |
 | Al-Jibbouri [64] | H2O | Fluidized Bed | Change in Mass |
 | Langer [64] | H2O | Fluidized Bed | Unknown, Secondary Source |
 | Al-Sabbagh [64] | H2O | Fluidized Bed | Unknown, Secondary Source |
 | Stepanski [64] | H2O | Fluidized Bed | Unknown, Secondary Source |
 | Zhang [65] | H2O | Quiescent | Single Crystal Microscope Observation, |
 | Ulrich [66] | H2O | Quiescent | Single Crystal Microscope Observation, |
 | Desarnaud [67] | H2O | Quiescent | Single Crystal Microscope Observation, |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flannigan, J.M.; MacIver, D.; Jolliffe, H.; Haw, M.D.; Sefcik, J. Nucleation and Growth Kinetics of Sodium Chloride Crystallization from Water and Deuterium Oxide. Crystals 2023, 13, 1388. https://doi.org/10.3390/cryst13091388
Flannigan JM, MacIver D, Jolliffe H, Haw MD, Sefcik J. Nucleation and Growth Kinetics of Sodium Chloride Crystallization from Water and Deuterium Oxide. Crystals. 2023; 13(9):1388. https://doi.org/10.3390/cryst13091388
Chicago/Turabian StyleFlannigan, James M., Daniel MacIver, Hikaru Jolliffe, Mark D. Haw, and Jan Sefcik. 2023. "Nucleation and Growth Kinetics of Sodium Chloride Crystallization from Water and Deuterium Oxide" Crystals 13, no. 9: 1388. https://doi.org/10.3390/cryst13091388
APA StyleFlannigan, J. M., MacIver, D., Jolliffe, H., Haw, M. D., & Sefcik, J. (2023). Nucleation and Growth Kinetics of Sodium Chloride Crystallization from Water and Deuterium Oxide. Crystals, 13(9), 1388. https://doi.org/10.3390/cryst13091388






