Design and Performance Enhancement of a Piezoelectric Micromachined Ultrasonic Transducer Based on NBBT Lead-Free Piezoelectric Single-Crystal Thin Film
Abstract
:1. Introduction
2. Modeling and Simulation of PMUT
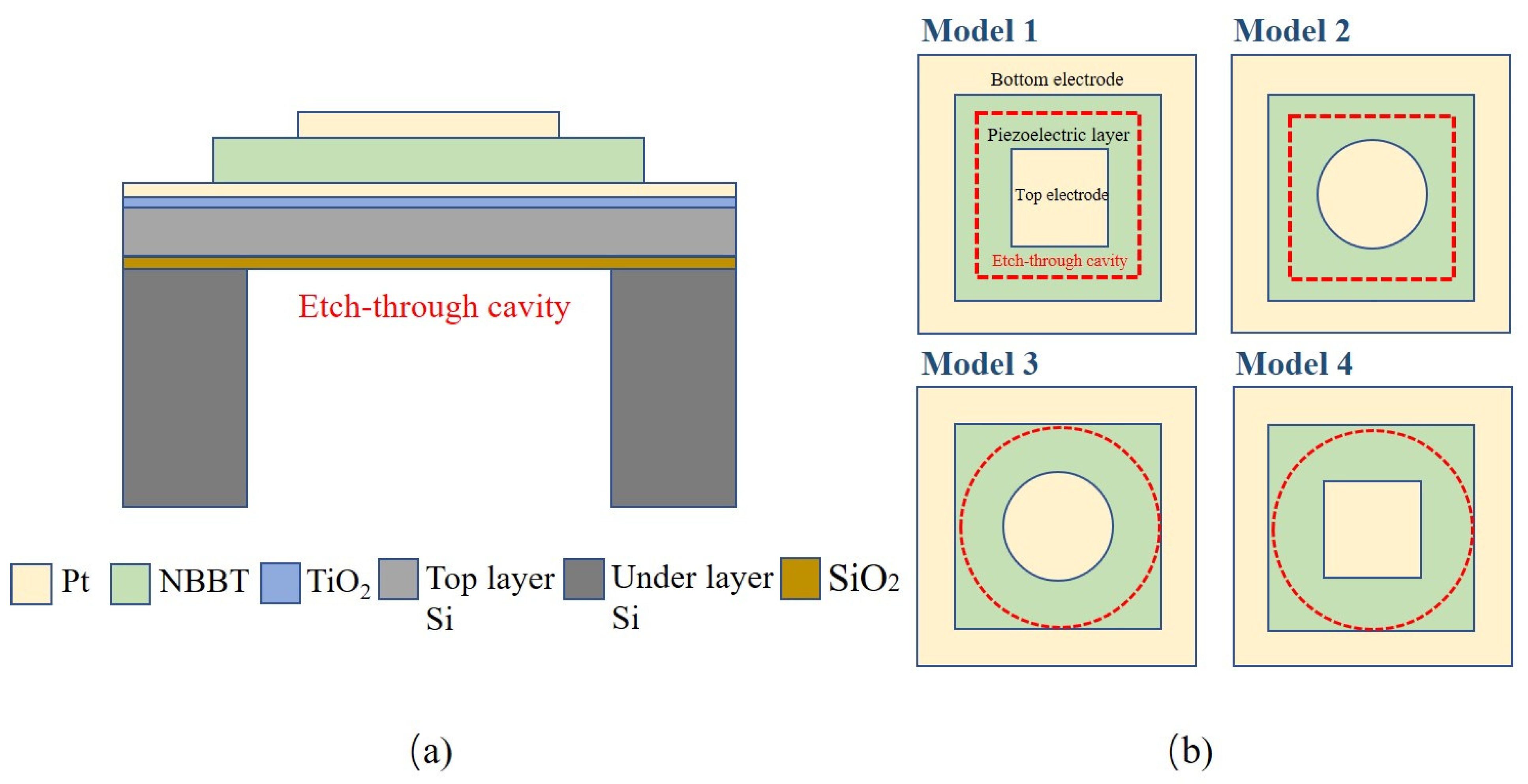
2.1. Design of PMUT Components for Structures
2.2. Mode Shape Selection
2.3. PMUT Property Evaluation
3. Results and Discussion
3.1. Static Analysis
3.1.1. General Features of PMUTs
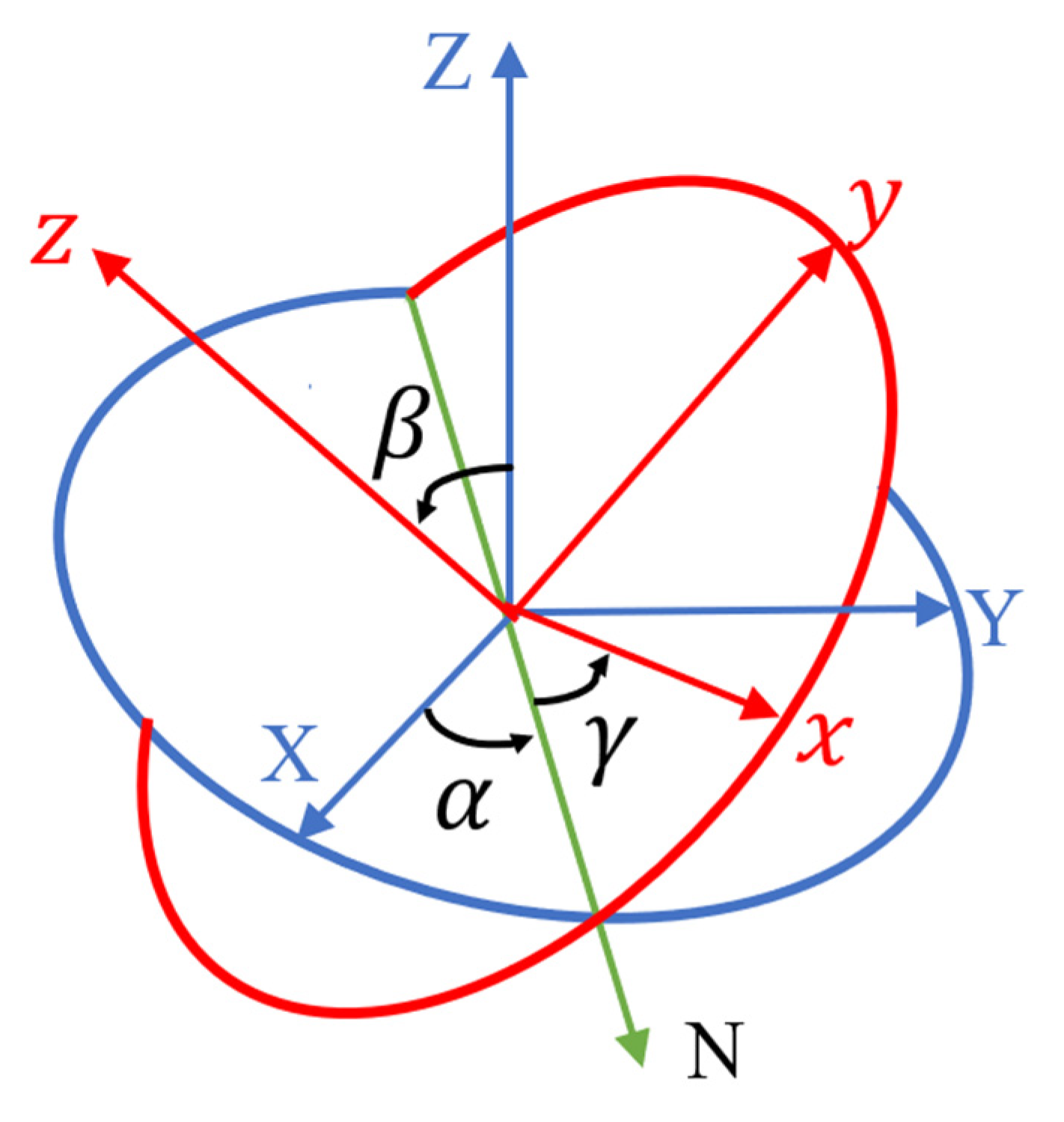
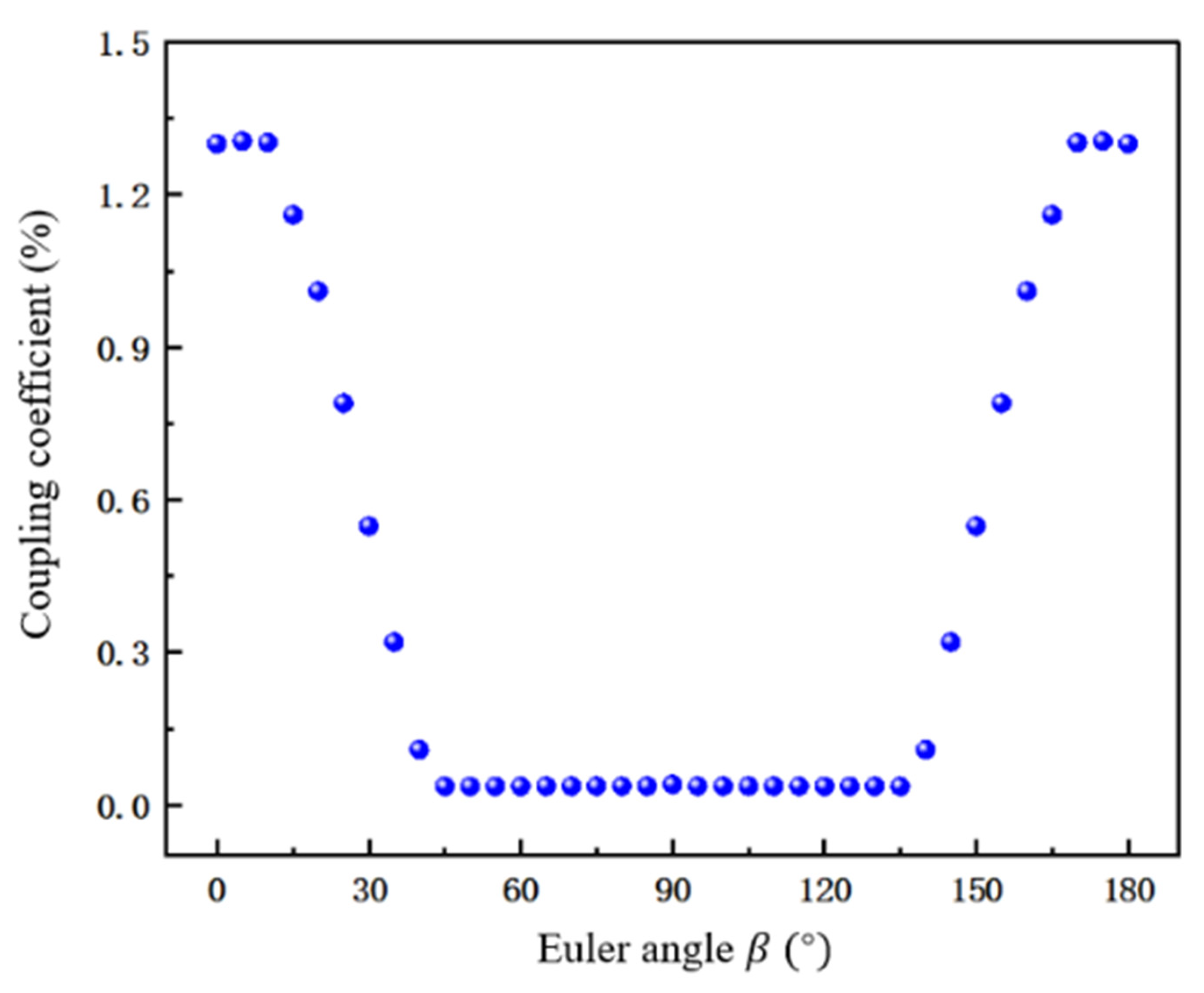
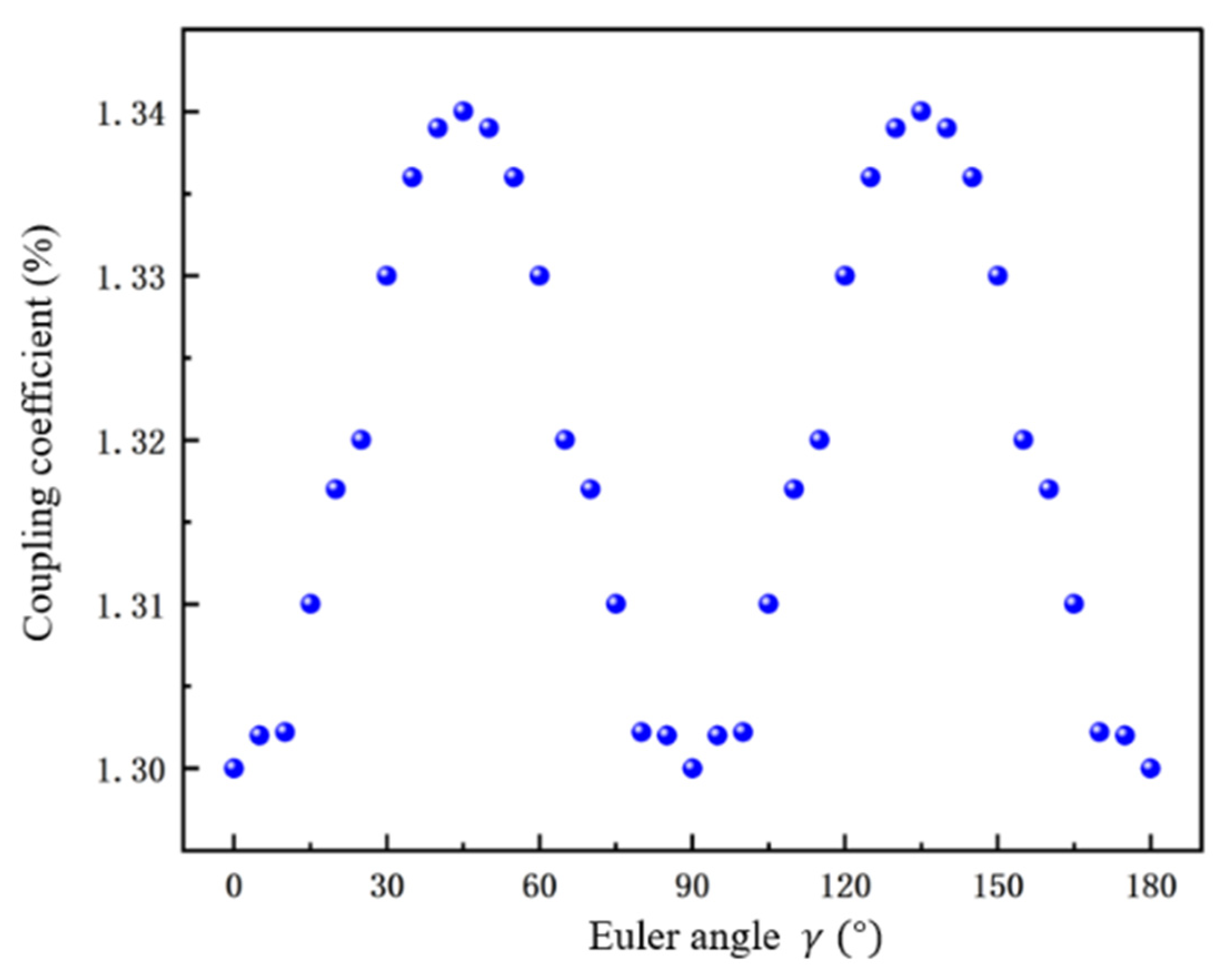
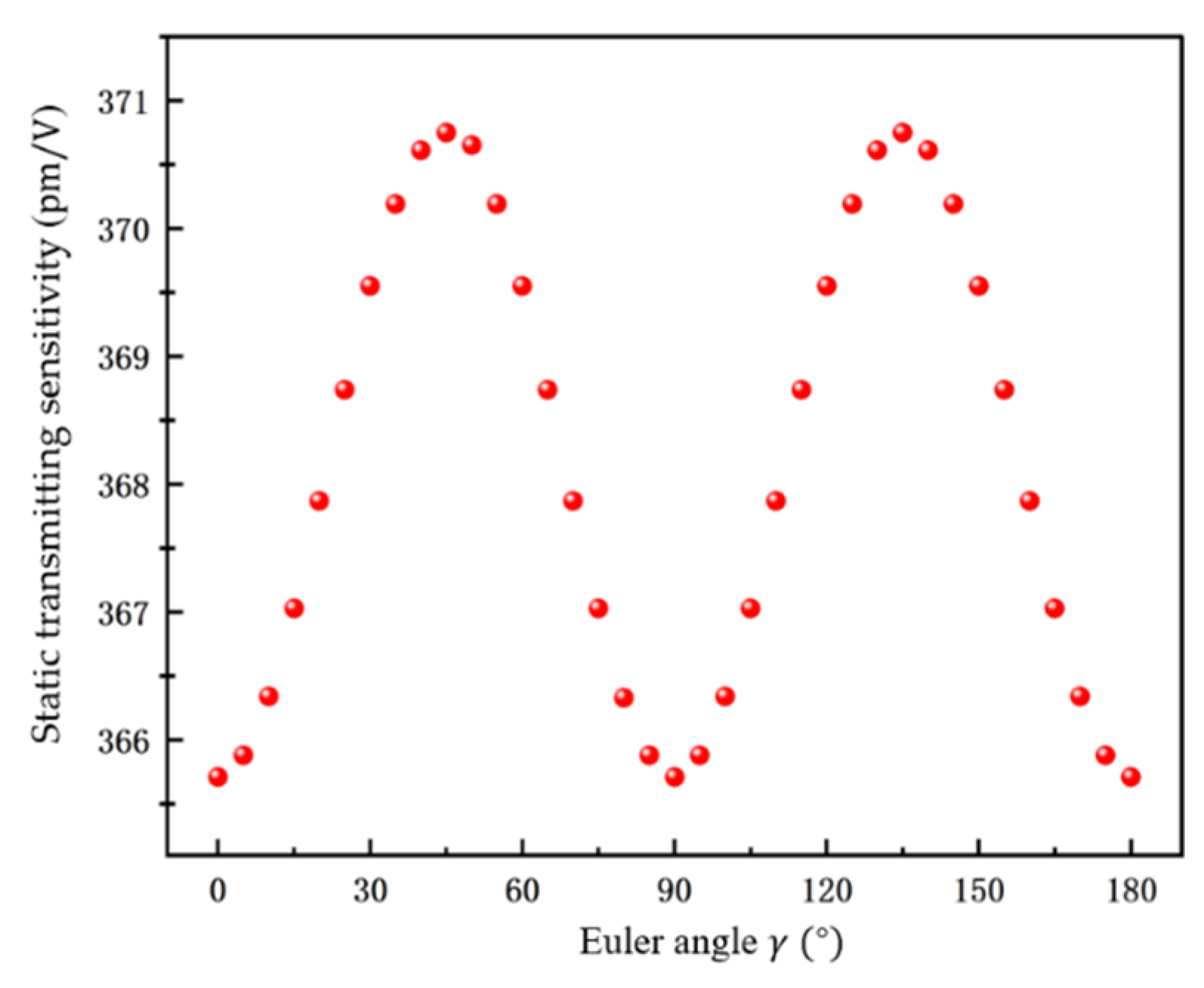
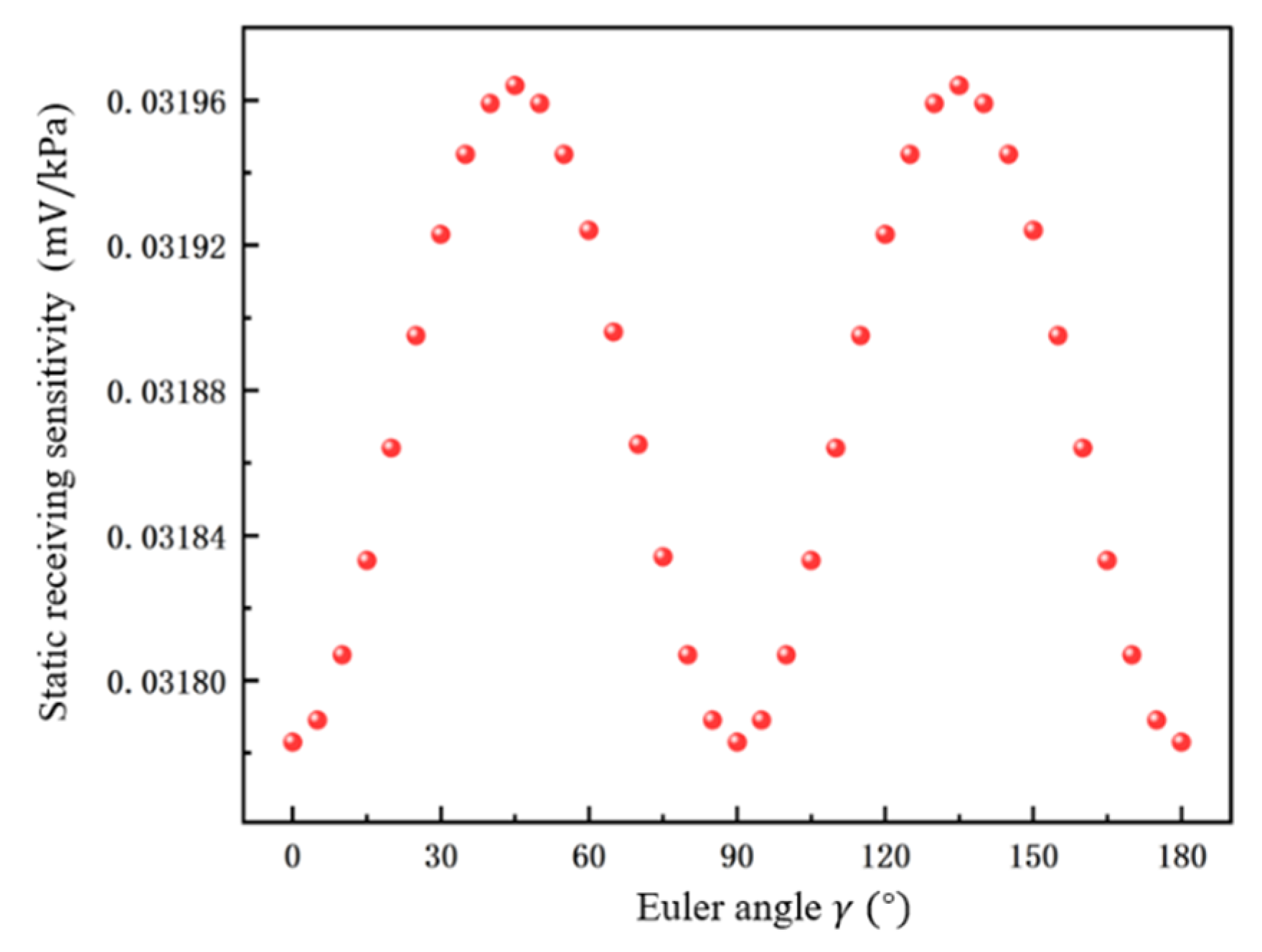
3.1.2. Influence of Euler Angle on the Performance of PMUT
3.1.3. Influence of Different Euler Angles on the Performance of PMUT
3.2. Analyzing Dynamism
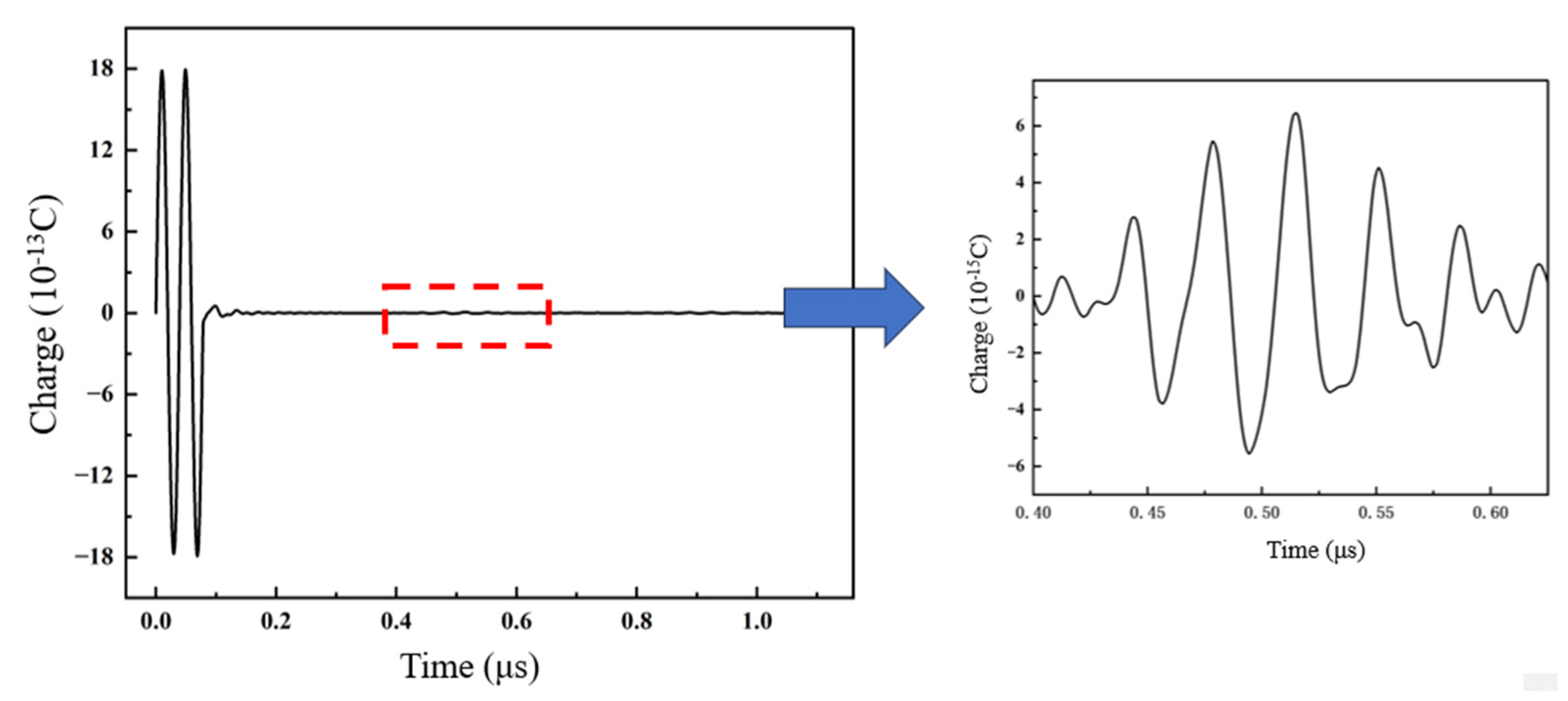
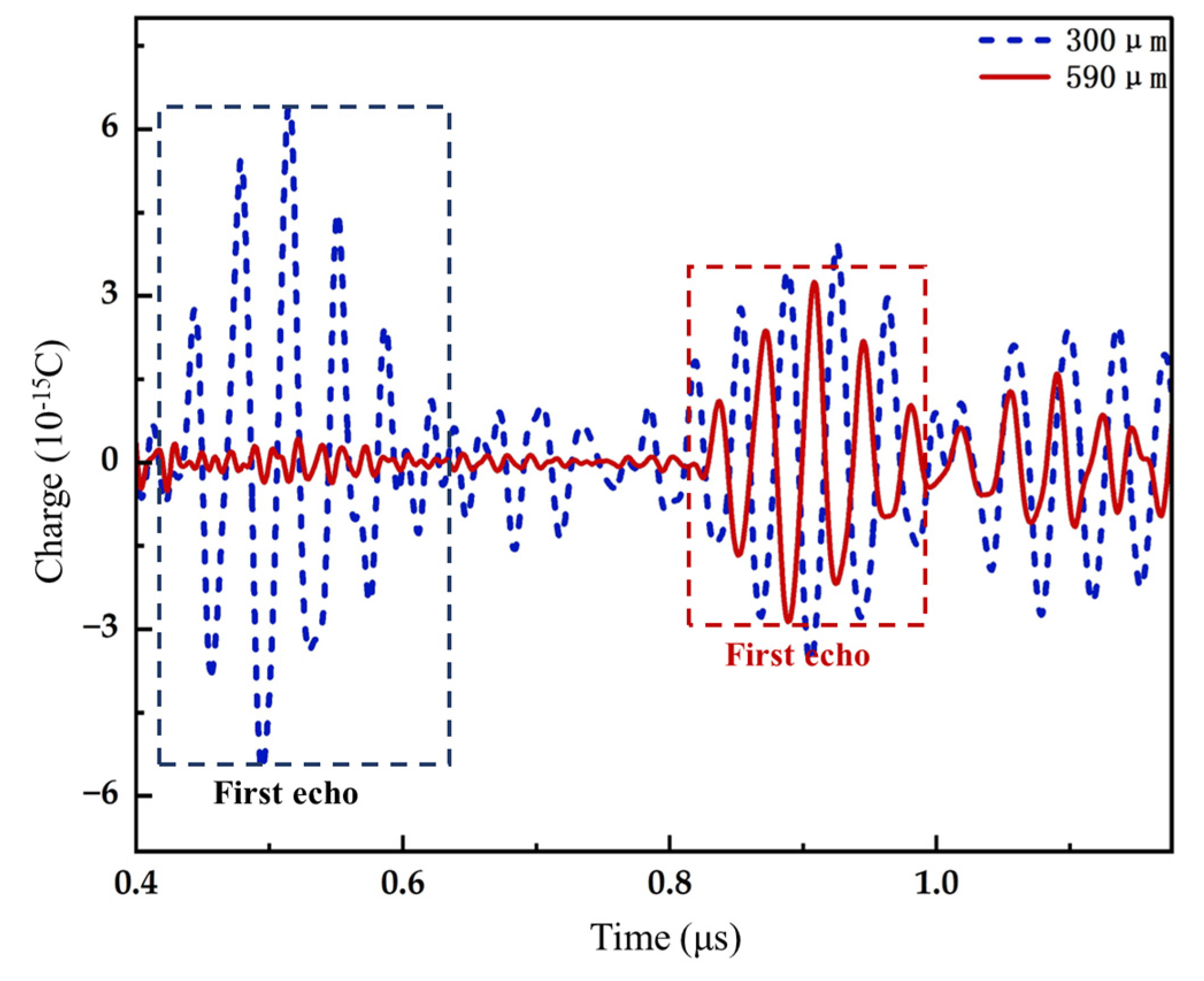
3.2.1. Pulse-Echo Sensitivity of PMUT
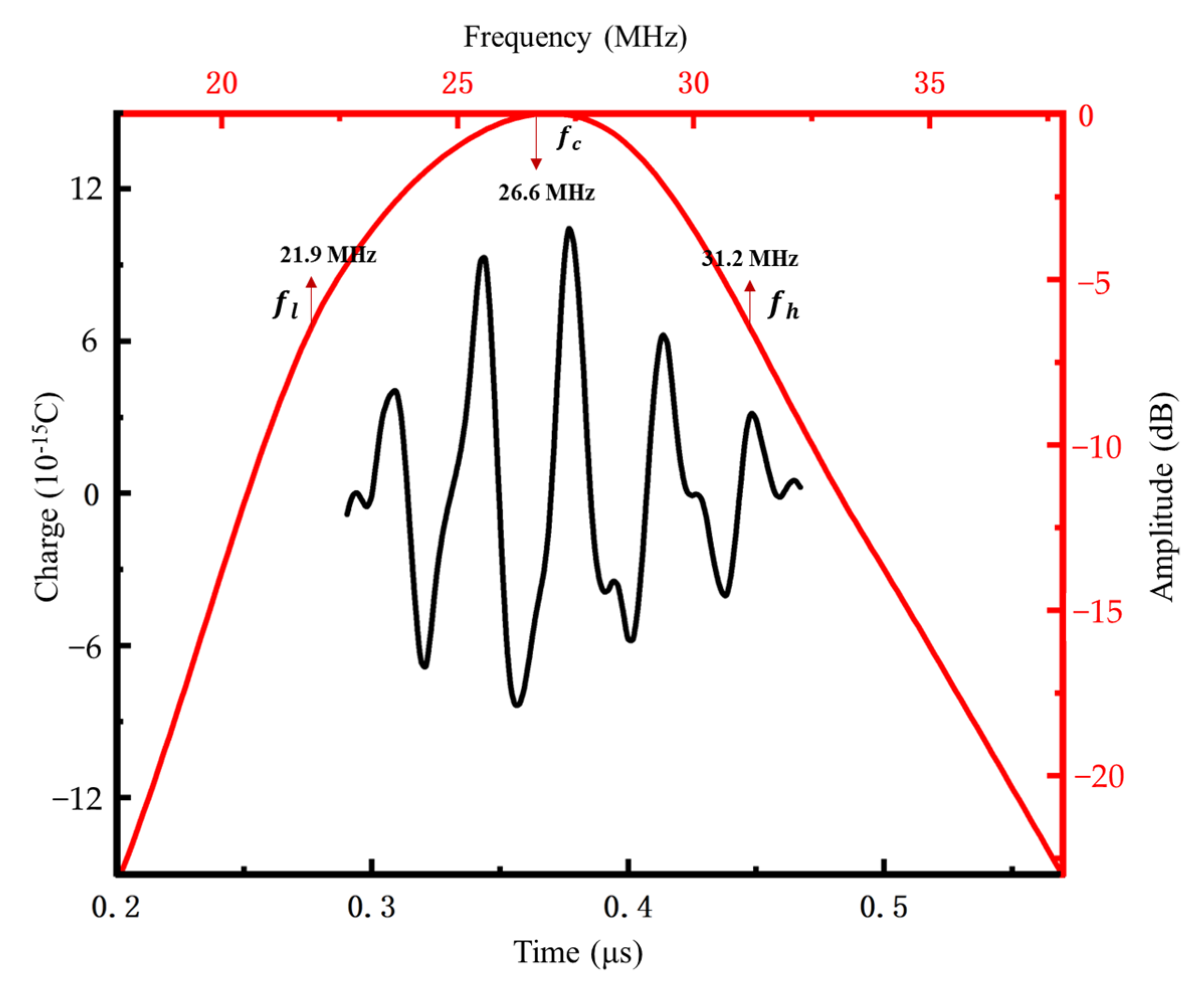
3.2.2. Frequencies and Bandwidths of PMUTs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lamberti, N.; Caliano, G.; Iula, A.; Savoia, A.S. A high frequency CMUT probe for ultrasound imaging of fingerprints. Sens. Actuators A Phys. 2011, 172, 561–569. [Google Scholar]
- Li, S.; Tian, J.; Jiang, X. A micromachined Pb (Mg1/3Nb2/3) O3-PbTiO3 single crystal composite circular array for intravascular ultrasound imaging. J. Eng. Sci. Med. Diagn. Ther. 2019, 2, 2. [Google Scholar]
- Kim, J.; Li, S.; Kasoji, S.; Dayton, P.A.; Jiang, X. Phantom evaluation of stacked-type dual-frequency 1–3 composite transducers: A feasibility study on intracavitary acoustic angiography. Ultrasonics 2015, 63, 7–15. [Google Scholar]
- Lockwood, G.R.; Turnball, D.H.; Christopher, D.A.; Foster, F.S. Beyond 30 MHz applications of high-frequency ultrasound imaging. IEEE Eng. Med. Biol. Mag. 1996, 15, 60–71. [Google Scholar]
- Takenaka, T.; Nagata, H. Current status and prospects of lead-free piezoelectric ceramics. J. Eur. Ceram. Soc. 2005, 25, 2693–2700. [Google Scholar]
- Fei, C.; Yang, Y.; Guo, F.; Lin, P.; Chen, Q.; Zhou, Q.; Sun, L. PMN-PT single crystal ultrasonic transducer with half-concave geometric design for IVUS imaging. IEEE Trans. Biomed. Eng. 2017, 65, 2087–2092. [Google Scholar]
- Lee, W.; Roh, Y. Ultrasonic transducers for medical diagnostic imaging. Biomed. Eng. Lett. 2017, 7, 91–97. [Google Scholar] [PubMed]
- Muralt, P.; Ledermann, N.; Paborowski, J.; Barzegar, A.; Gentil, S.; Belgacem, B.; Setter, N. Piezoelectric micromachined ultrasonic transducers based on PZT thin films. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 2276–2288. [Google Scholar]
- Sano, K.H.; Karasawa, R.; Yanagitani, T. ScAlN thick-film ultrasonic transducer in 40–80 MHz. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 2097–2102. [Google Scholar]
- Dausch, D.E.; Castellucci, J.B.; Chou, D.R.; Von Ramm, O.T. Theory and operation of 2-D array piezoelectric micromachined ultrasound transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2484–2492. [Google Scholar] [CrossRef]
- Tressler, J.F.; Alkoy, S.; Newnham, R.E. Piezoelectric sensors and sensor materials. J. Electroceramics 1998, 2, 257–272. [Google Scholar] [CrossRef]
- Akhbari, S.; Sammoura, F.; Shelton, S.; Yang, C.; Horsley, D.; Lin, L. Highly responsive curved aluminum nitride pMUT. In Proceedings of the 2014 IEEE 27th International Conference on Micro Electro Mechanical Systems (MEMS), San Francisco, CA, USA, 13 March 2014. [Google Scholar]
- Jung, J.; Annapureddy, V.; Hwang, G.T.; Song, Y.; Lee, W.; Kang, W.; Choi, H. 31-mode piezoelectric micromachined ultrasonic transducer with PZT thick film by granule spraying in vacuum process. Appl. Phys. Lett. 2017, 110, 212903. [Google Scholar] [CrossRef]
- Przybyla, R.; Izyumin, I.; Kline, M.; Boser, B.; Shelton, S.; Guedes, A.; Horsley, D. An ultrasonic rangefinder based on an AlN piezoelectric micromachined ultrasound transducer. In Proceedings of the Sensors, San Francisco, CA, USA, 26–30 January 2014. [Google Scholar]
- Wang, X.X.; Tang, X.G.; Chan, H.L.W. Electromechanical and ferroelectric properties of (Bi1/2Na1/2) TiO3–(Bi1/2 K1/2) TiO3–BaTiO3 lead-free piezoelectric ceramics. Appl. Phys. Lett. 2004, 85, 91–93. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, X.; Wang, Y.; Zhang, H.; Deng, H.; Li, X.; Luo, H. Giant strain and electric-field-induced phase transition in lead-free (Na0.5Bi0.5) TiO3-BaTiO3-(K0.5Na0.5) NbO3 single crystal. Appl. Phys. Lett. 2016, 108, 022903. [Google Scholar] [CrossRef]
- Saito, Y.; Takao, H.; Tani, T.; Nonoyama, T.; Takatori, K.; Homma, T.; Nakamura, M. Lead-free piezoceramics. Nature 2004, 432, 84–87. [Google Scholar] [CrossRef]
- Lin, D.; Kwok, K.W.; Lam, K.H.; Chan, H.L.W. Phase structure and electrical properties of K0.5Na0.5 (Nb0.94Sb0.06) O3-LiTaO3 lead-free piezoelectric ceramics. J. Phys. D Appl. Phys. 2008, 41, 052002. [Google Scholar] [CrossRef]
- Chiang, Y.M.; Farrey, G.W.; Soukhojak, A.N. Lead-free high-strain single-crystal piezoelectrics in the alkaline–bismuth–titanate perovskite family. Appl. Phys. Lett. 1998, 73, 3683–3685. [Google Scholar] [CrossRef]
- Lu, Y.; Reusch, M.; Kurz, N.; Ding, A.; Christoph, T.; Prescher, M.; Žukauskaitė, A. Elastic modulus and coefficient of thermal expansion of piezoelectric Al1−xScxN (up to x = 0.41) thin films. APL Mater. 2018, 6, 076105. [Google Scholar] [CrossRef]
- Jo, W.; Daniels, J.E.; Jones, J.L.; Tan, X.; Thomas, P.A.; Damjanovic, D.; Rödel, J. Evolving morphotropic phase boundary in lead-free (Bi1/2 Na1/2) TiO3–BaTiO3 piezoceramics. J. Appl. Phys. 2011, 109, 014110. [Google Scholar] [CrossRef]
- Takenaka, T.; Maruyama, K.I.M.K.I.; Sakata, K.S.K. (Bi1/2Na1/2) TiO3-BaTiO3 system for lead-free piezoelectric ceramics. Jpn. J. Appl. Phys. 1991, 30, 2236. [Google Scholar] [CrossRef]
- Chu, B.J.; Chen, D.R.; Li, G.R.; Yin, Q.R. Electrical properties of Na1/2Bi1/2TiO3–BaTiO3 ceramics. J. Eur. Ceram. Soc. 2002, 22, 2115–2121. [Google Scholar] [CrossRef]
- Caro, M.A.; Zhang, S.; Riekkinen, T.; Ylilammi, M.; Moram, M.A.; Lopez-Acevedo, O.; Laurila, T. Piezoelectric coefficients and spontaneous polarization of ScAlN. J. Phys. Condens. Matter 2015, 27, 245901. [Google Scholar] [CrossRef]
- Zheng, L.; Yi, X.; Zhang, S.; Jiang, W.; Yang, B.; Zhang, R.; Cao, W. Complete set of material constants of 0.95 (Na0.5Bi0.5) TiO3-0.05 BaTiO3 lead-free piezoelectric single crystal and the delineation of extrinsic contributions. Appl. Phys. Lett. 2013, 103, 122905. [Google Scholar] [CrossRef]
- Liu, W.; He, L.; Wang, X.; Zhou, J.; Xu, W.; Smagin, N.; Ren, J. 3D FEM analysis of high-frequency AlN-based PMUT arrays on cavity SOI. Sensors 2019, 19, 4450. [Google Scholar] [CrossRef]
- Jiang, X.; Lu, Y.; Tang, H.Y.; Tsai, J.M.; Ng, E.J.; Daneman, M.J.; Horsley, D.A. Monolithic ultrasound fingerprint sensor. Microsyst. Nanoeng. 2017, 3, 17059. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.Z.; Zhang, Q.Z.; Zhao, X.Y.; Wang, F.F. Modeling and simulation of aluminium nitride-based piezoelectric micromachined ultrasonic transducer for ultrasound imaging. In Proceedings of the 2019 14th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Shijiazhuang, China, 1–4 November 2019. [Google Scholar]
- Wilm, M.; Reinhardt, A.; Laude, V.; Armati, R.; Daniau, W.; Ballandras, S. Three-dimensional modelling of micromachined-ultrasonic-transducer arrays operating in water. Ultrasonics 2005, 43, 457–465. [Google Scholar] [CrossRef] [PubMed]
- Meeker, T.R. Publication and proposed revision of ANSI/IEEE standard 176-1987. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1996, 43, 717–772. [Google Scholar]
- Guo, J.Q.; Liu, C.C.; Han, T.; Miao, J.M. Model of scandium doped aluminum nitride based PMUT with high transmitting performance. In Proceedings of the 2017 Symposium on Piezoelectricity, Acoustic Waves, and Device Applications (SPAWDA), Chengdu, China, 27–30 October 2017. [Google Scholar]
- Przybyla, R.J.; Shelton, S.E.; Guedes, A.; Izyumin, I.I.; Kline, M.H.; Horsley, D.A.; Boser, B.E. In-air rangefinding with an AlN piezoelectric micromachined ultrasound transducer. IEEE Sens. J. 2011, 11, 2690–2697. [Google Scholar] [CrossRef]
- Lu, Y.; Tang, H.Y.; Fung, S.; Boser, B.E.; Horsley, D.A. Pulse-echo ultrasound imaging using an AlN piezoelectric micromachined ultrasonic transducer array with transmit beam-forming. J. Microelectromech. Syst. 2015, 25, 179–187. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, Q.; Zhao, X.; Wang, F.; Liu, H.; Li, B.; Luo, H. Design and analysis of piezoelectric micromachined ultrasonic transducer using high coupling PMN-PT single crystal thin film for ultrasound imaging. Smart Mater. Struct. 2021, 30, 055006. [Google Scholar] [CrossRef]
- Li, X.; Zhang, R.; Huang, N.; Lü, T.; Cao, W. Surface acoustic wave propagation in Y-and Z-cut 0.67 PbMgNbO3–0.33 PbTiO3 single crystals. J. Appl. Phys. 2009, 106, 054110. [Google Scholar] [CrossRef] [PubMed]
- Gijsenbergh, P.; Halbach, A.; Jeong, Y.; Torri, G.B.; Billen, M.; Demi, L.; Rochus, V. Characterization of polymer-based piezoelectric micromachined ultrasound transducers for short-range gesture recognition applications. J. Micromech. Microeng. 2019, 29, 074001. [Google Scholar] [CrossRef]




| Material Coefficient | AlN [24] | [001] Poled NBBT [25] |
|---|---|---|
| Parameter | Value |
|---|---|
| Thickness of the top Pt | 200 nm |
| Thickness of the NBBT | 1 μm |
| Thickness of the bottom Pt | 200 nm |
| Thickness of TiO2 | 30 nm |
| Thickness of SiO2 | 200 nm |
| Thickness of the top Si | 10 μm |
| Side length of the NBBT | 50 μm |
| Side length of the top Pt (models 1 and 4) | 30 μm |
| Radius of the top Pt (models 2 and 3) | 16.93 μm |
| Side length of the cavity (models 1 and 2) | 44.3 μm |
| Radius of the cavity (models 3 and 4) | 25 μm |
| 15.9 | 9.5 | 7.5 | 8.1 | 7.5 | 7.8 | 16.0 | 9.6 | 7.1 | 11.4 | 9.4 | 7.8 |
| Elastic compliance constants: | |||||||||||
| 12.2 | −3.4 | −8.2 | 27.7 | 13.4 | 12.9 | 10.8 | −4.8 | −3.7 | 13.3 | 10.7 | 12.9 |
| Piezoelectric coefficients: | |||||||||||
| 12.1 | −1.7 | 12.0 | 162 | −113 | 360 | 16.7 | −12.5 | 39.8 | 15.6 | −3.9 | 27.7 |
| Dielectric constants: | Electromechanical coupling factors | ||||||||||
| 1099 | 1021 | 877 | 489 | 9.1 | 9.8 | 11.4 | 20.4 | 0.449 | 0.341 | 0.720 | 0.540 |
| Configurations Properties | Model 1 Square Top Electrode | Model 2 Circular Top Electrode | Model 3 Circular Top Electrode | Model 4 Square Top Electrode |
|---|---|---|---|---|
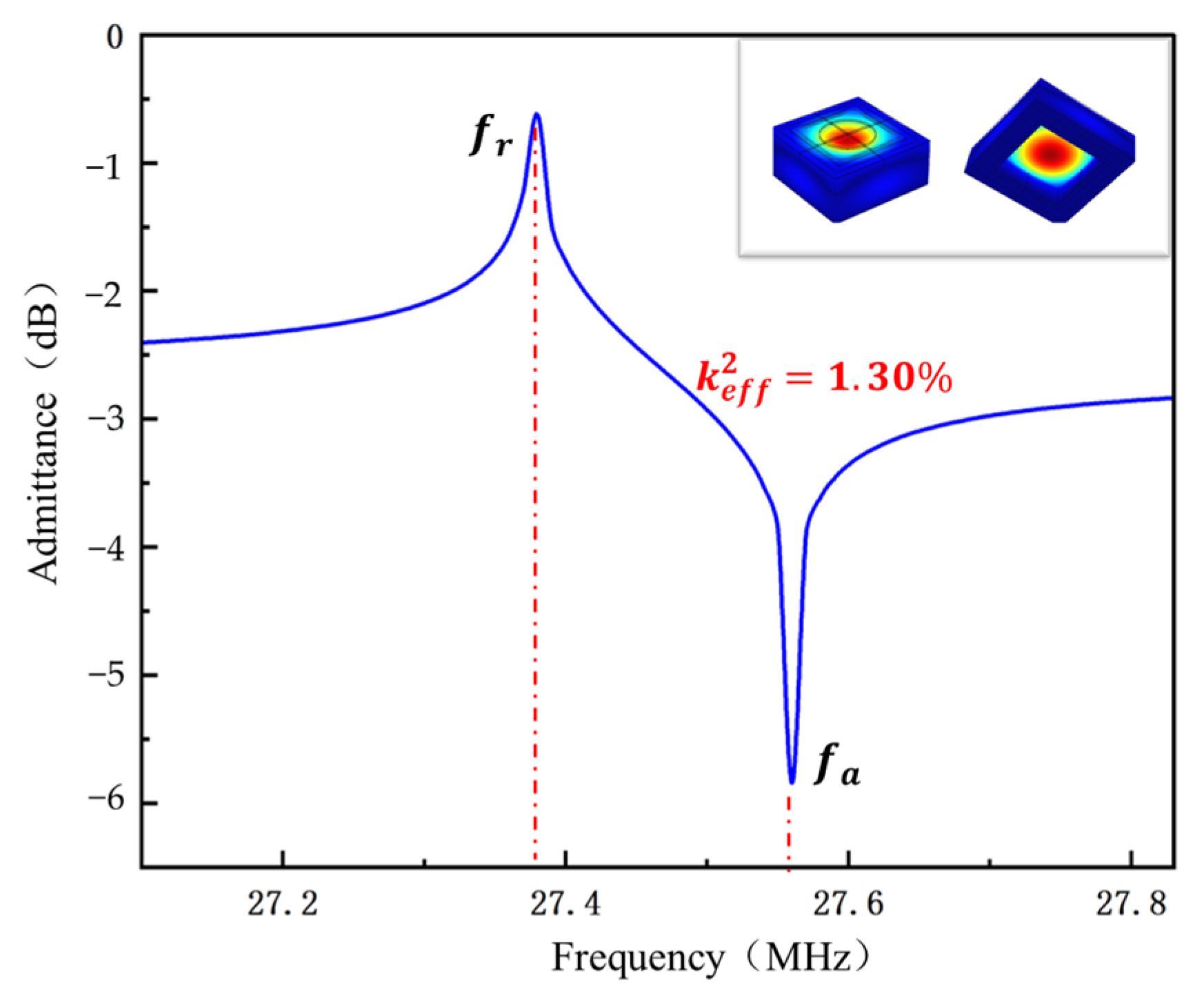
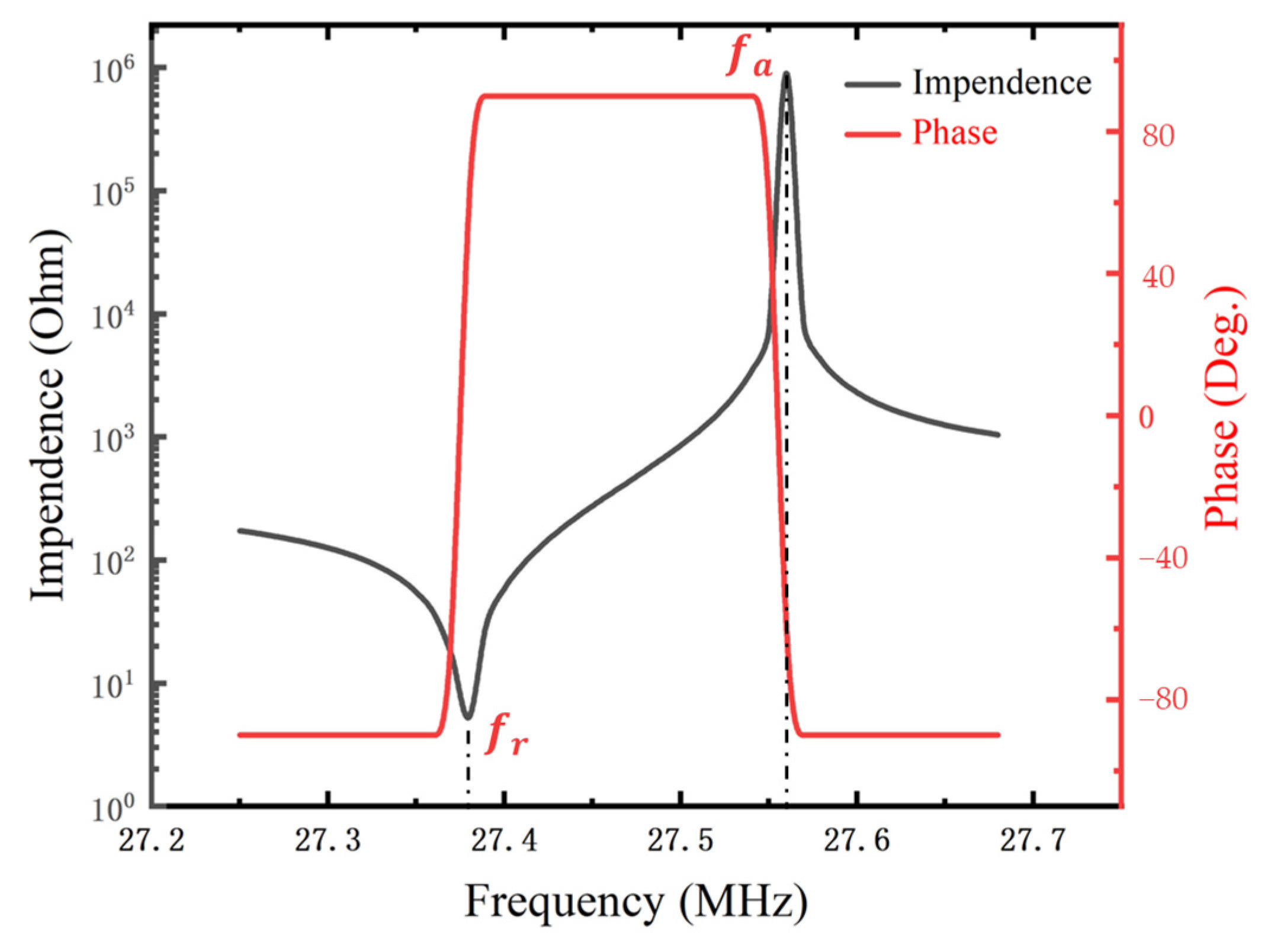
| Resonant frequency (MHz) | 28.46 | 28.41 | 27.38 | 27.38 |
| Effective electromechanical coupling (%) | 1.22 | 1.19 | 1.30 | 1.26 |
| Static transmitting sensitivity | 314.1 | 471.4 | 365.7 | 379.2 |
| Static receiving sensitivity | 0.0282 | 0.0393 | 0.0318 | 0.0315 |
| Square electrode cavity | Circular electrode cavity | |||
| Piezoelectric Materials. Properties for PMUT | NBBT | AlN |
|---|---|---|
| Resonant frequency (MHz) | 27.38 | 29.63 |
| Effective Electromechanical coupling (%) | 1.30 | 0.40 |
| Static transmitting sensitivity | 365.71 | 27.09 |
| Static receiving Sensitivity | 0.0318 | 0.271 |
| NBBT | AlN | |
|---|---|---|
| Relative pulse-echo sensitivity level (dB) | −47 | −54 |
| Lower/upper −6 dB (MHz) | 21.9/30.9 | 25.5/33.4 |
| Center freq. (MHz) | 26.4 | 29.5 |
| Bandwidth (−6 dB) | 34.1% | 26.8% |
| Before Rotation | After Rotation | |
|---|---|---|
| Relative pulse-echo sensitivity level (dB) | −47 | −46 |
| Lower/upper −6 dB (MHz) | 21.9/30.9 | 21.9/31.2 |
| Center freq. (MHz) | 26.4 | 26.6 |
| Bandwidth (−6 dB) | 34.1% | 35% |
| Effective Electromechanical coupling (%) | 1.3 | 1.34 |
| Static transmitting sensitivity | 365.71 | 370.75 |
| Static receiving sensitivity | 0.0318 | 0.032 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhang, Q.; Chen, M.; Liu, X.; Yang, J.; Wang, F.; Tang, Y.; Miao, B.; Li, J.; Zhao, X. Design and Performance Enhancement of a Piezoelectric Micromachined Ultrasonic Transducer Based on NBBT Lead-Free Piezoelectric Single-Crystal Thin Film. Crystals 2023, 13, 1394. https://doi.org/10.3390/cryst13091394
Liu Y, Zhang Q, Chen M, Liu X, Yang J, Wang F, Tang Y, Miao B, Li J, Zhao X. Design and Performance Enhancement of a Piezoelectric Micromachined Ultrasonic Transducer Based on NBBT Lead-Free Piezoelectric Single-Crystal Thin Film. Crystals. 2023; 13(9):1394. https://doi.org/10.3390/cryst13091394
Chicago/Turabian StyleLiu, Yaqi, Qiaozhen Zhang, Mingzhu Chen, Xiaonan Liu, Jiye Yang, Feifei Wang, Yanxue Tang, Bin Miao, Jiadong Li, and Xiangyong Zhao. 2023. "Design and Performance Enhancement of a Piezoelectric Micromachined Ultrasonic Transducer Based on NBBT Lead-Free Piezoelectric Single-Crystal Thin Film" Crystals 13, no. 9: 1394. https://doi.org/10.3390/cryst13091394
APA StyleLiu, Y., Zhang, Q., Chen, M., Liu, X., Yang, J., Wang, F., Tang, Y., Miao, B., Li, J., & Zhao, X. (2023). Design and Performance Enhancement of a Piezoelectric Micromachined Ultrasonic Transducer Based on NBBT Lead-Free Piezoelectric Single-Crystal Thin Film. Crystals, 13(9), 1394. https://doi.org/10.3390/cryst13091394








