In-Gap Edge and Domain-Wall States in Largely Perturbed Phononic Su–Schrieffer–Heeger Lattices
Abstract
:1. Introduction
2. Results and Discussion
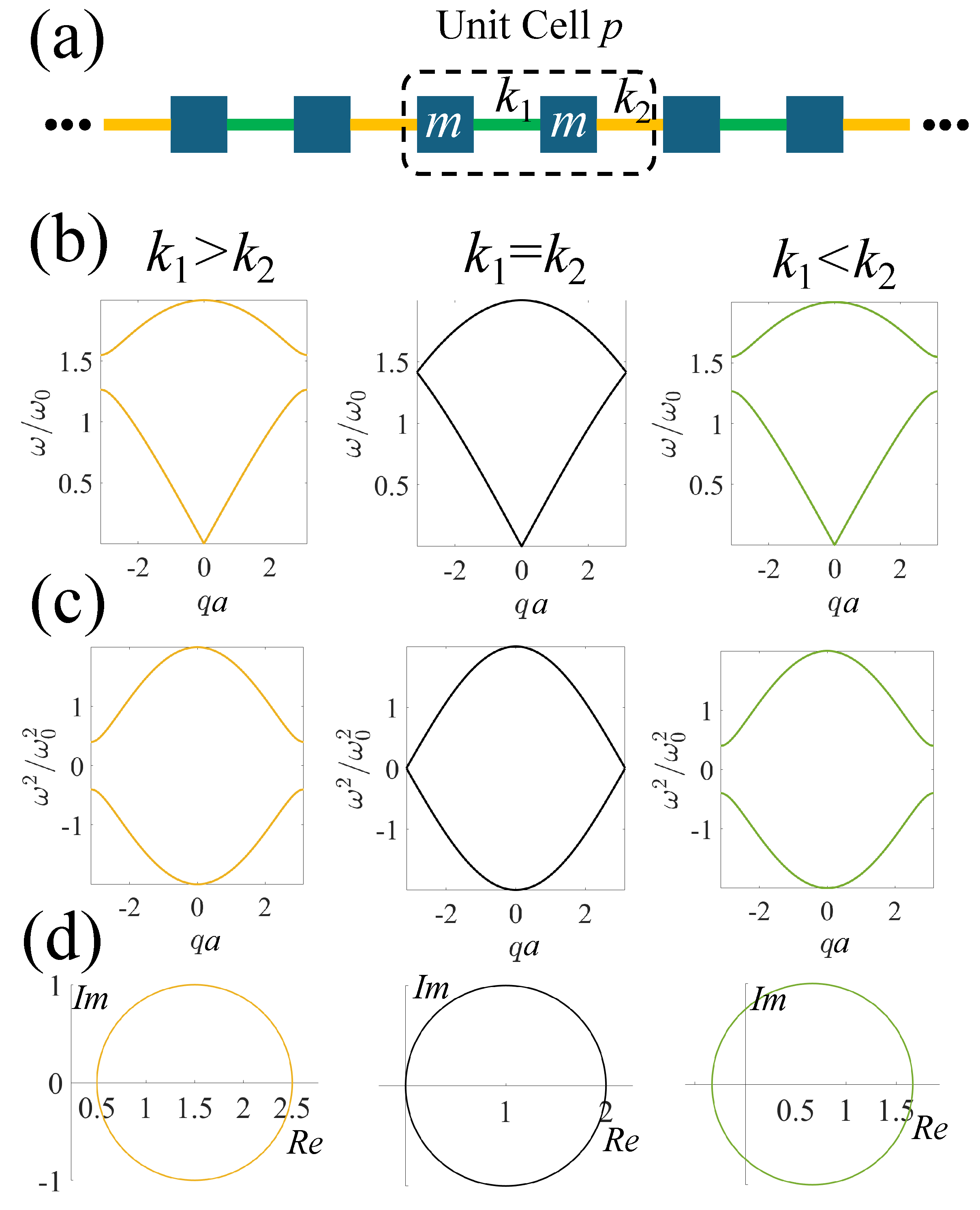
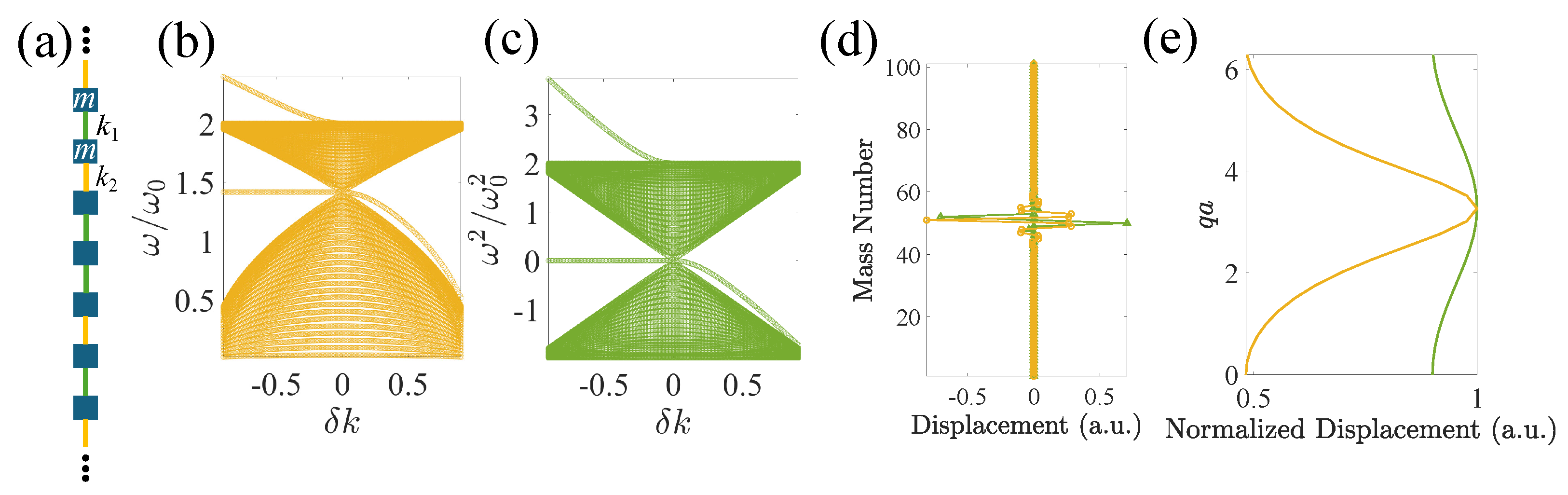
2.1. Su–Schrieffer–Heeger Systems with Nearest-Neighbor Interactions
2.1.1. In-Gap Edge States in Finite Lattices
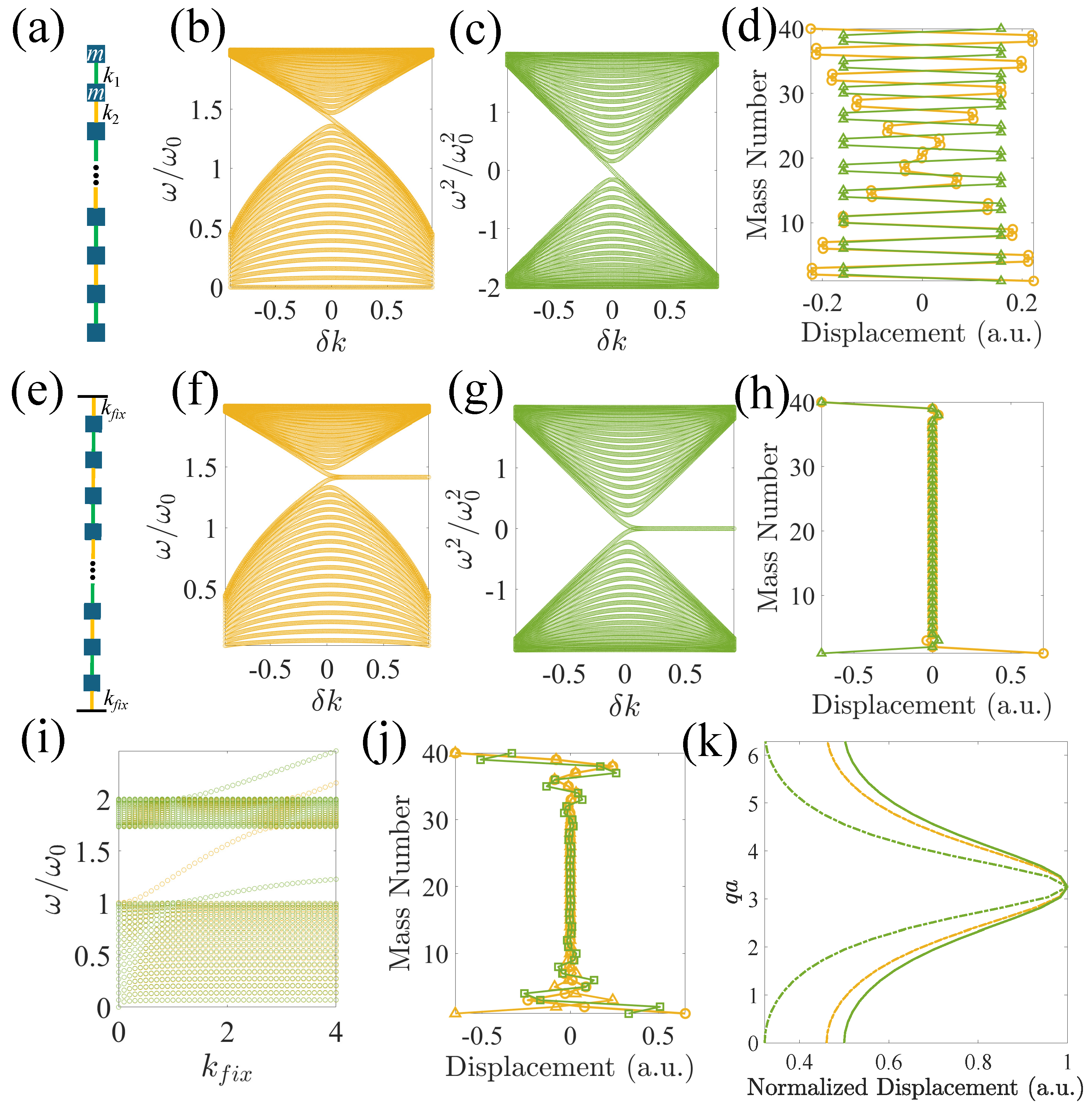
2.1.2. In-Gap Domain-Wall States in Infinite Lattices
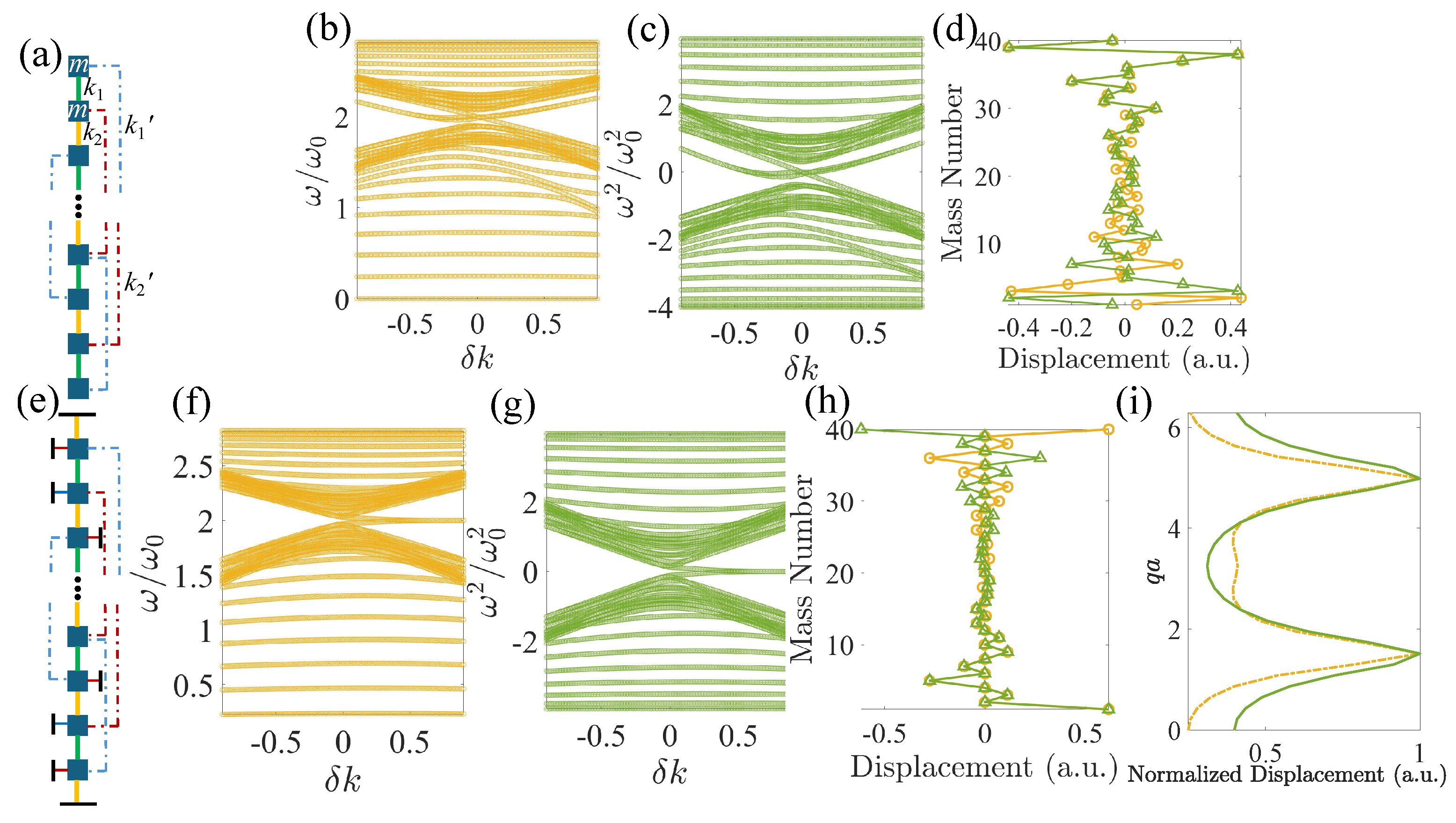
2.2. Su–Schrieffer–Heeger Systems with Beyond-Nearest-Neighbor Interactions
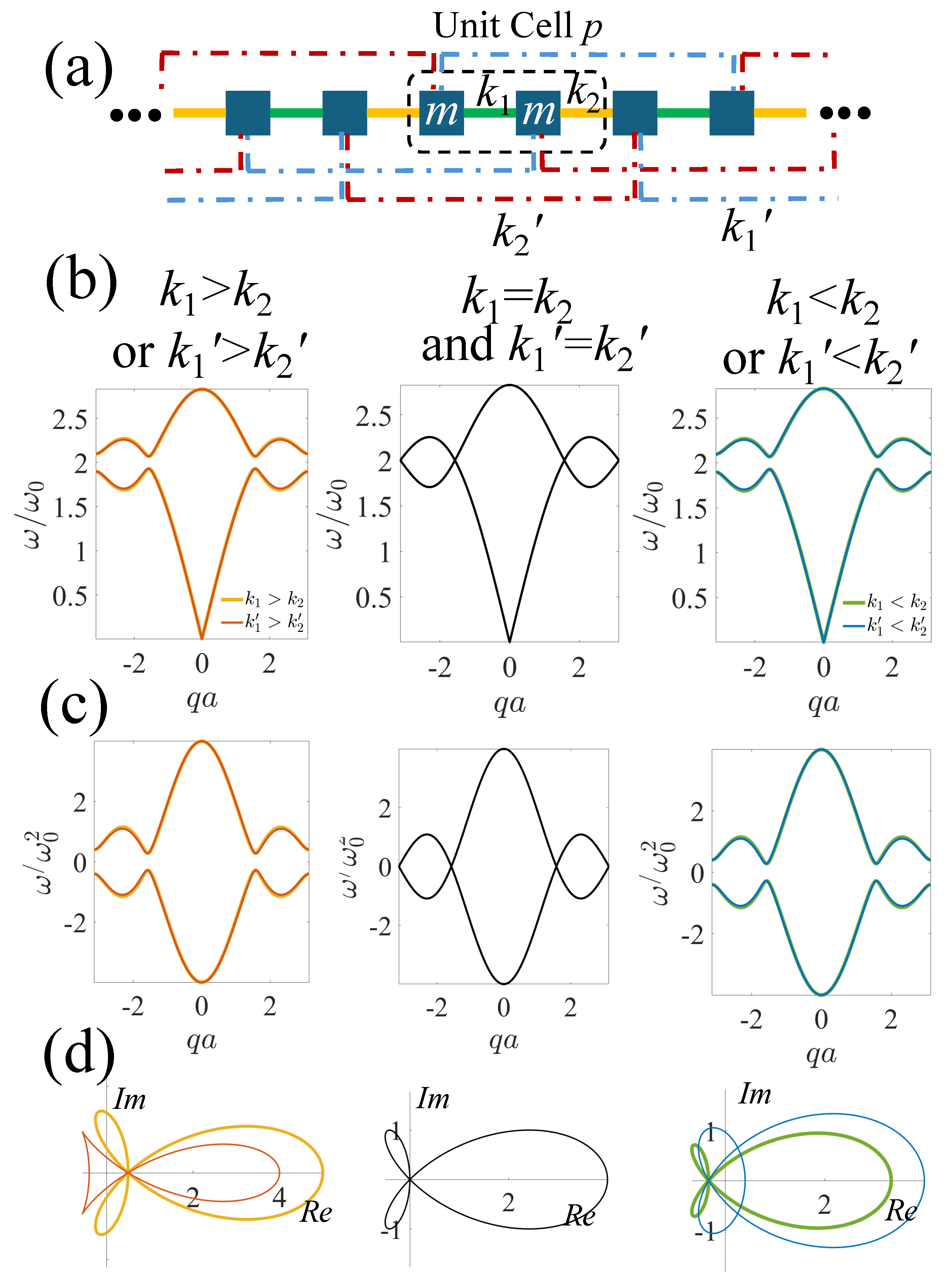
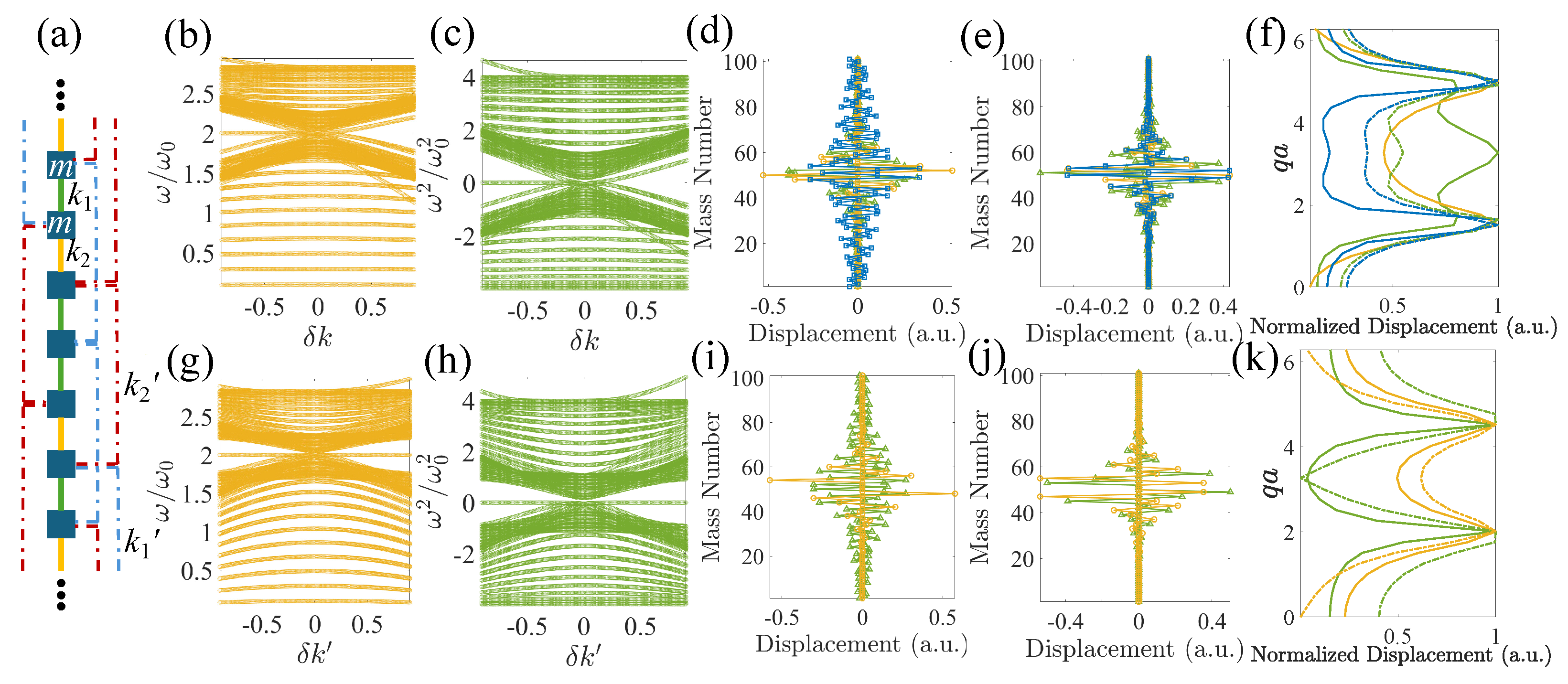
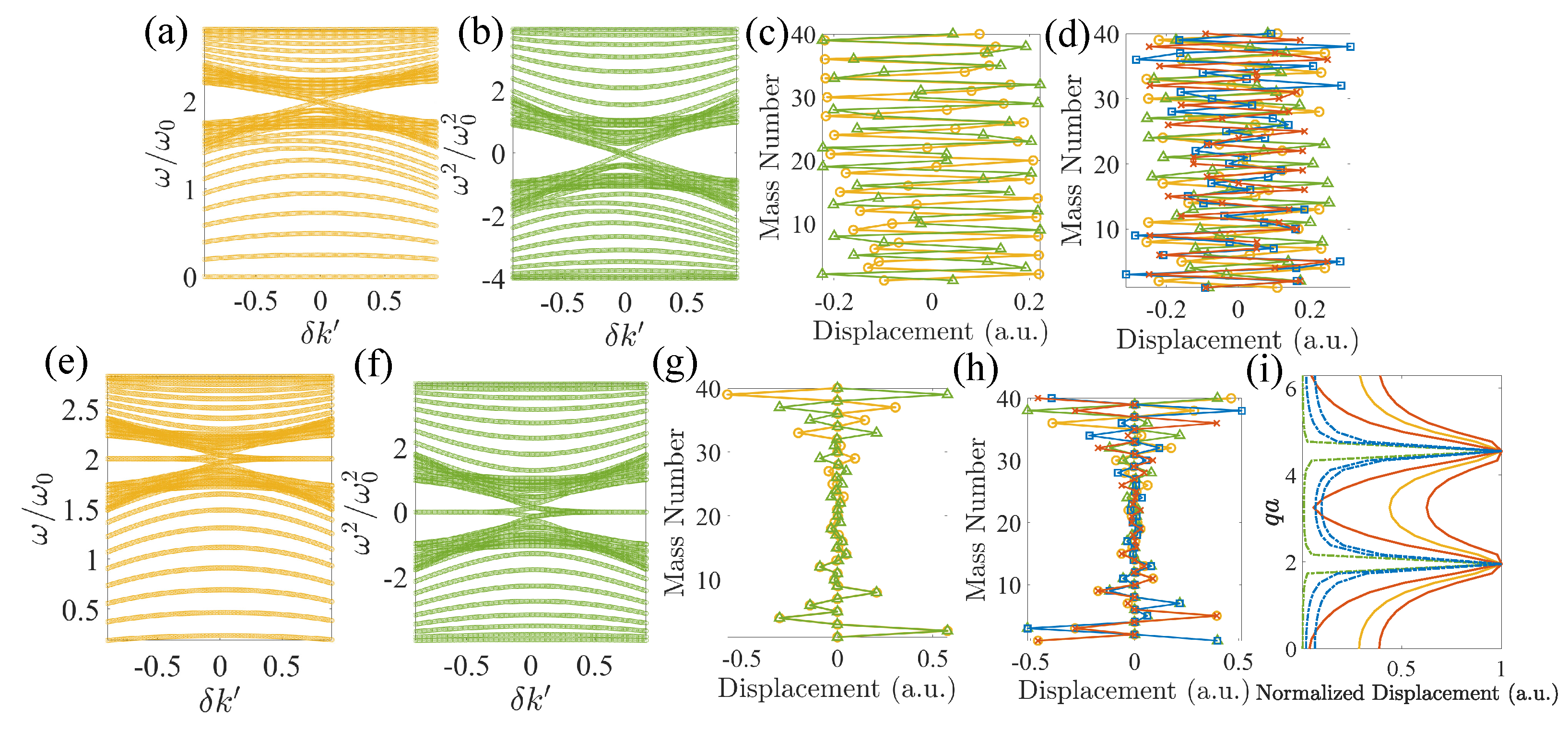
2.2.1. In-Gap Edge States in Finite Lattices with Third-Nearest Neighbors
2.2.2. In-Gap Domain-Wall States in Infinite Lattices with Third-Nearest Neighbors
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TI | Topological insulator |
| 1D | One-dimension(al) |
| SSH | Su–Schrieffer–Heeger |
| TPES | Topologically protected edge state |
| TPDWS | Topologically protected domain-wall state |
| BNN | Beyond-nearest neighbor |
| TNN | Third-nearest neighbor |
| SIS | Space-inversion symmetry |
| IBZ | Irreducible Brillouin zone |
References
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- He, M.; Sun, H.; He, Q.L. Topological insulator: Spintronics and quantum computations. Front. Phys. 2019, 14, 43401. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821–829. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y.F.; Xu, T.; Wang, H.X.; Jiang, J.H.; Hu, X.; Hang, Z.H. Visualization of a unidirectional electromagnetic waveguide using topological photonic crystals made of dielectric materials. Phys. Rev. Lett. 2018, 120, 217401. [Google Scholar] [CrossRef]
- Wang, H.; Gupta, S.K.; Xie, B.; Lu, M. Topological photonic crystals: A review. Front. Optoelectron. 2020, 13, 50–72. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.J.; He, X.T.; Shi, F.L.; Liu, J.W.; Chen, X.D.; Dong, J.W. Topological photonic crystals: Physics, designs, and applications. Laser Photonics Rev. 2022, 16, 2100300. [Google Scholar] [CrossRef]
- Hafezi, M.; Mittal, S.; Fan, J.; Migdall, A.; Taylor, J. Imaging topological edge states in silicon photonics. Nat. Photonics 2013, 7, 1001–1005. [Google Scholar] [CrossRef]
- Zhang, R.X.; Liu, C.X. Topological magnetic crystalline insulators and corepresentation theory. Phys. Rev. B 2015, 91, 115317. [Google Scholar] [CrossRef]
- Tokura, Y.; Yasuda, K.; Tsukazaki, A. Magnetic topological insulators. Nat. Rev. Phys. 2019, 1, 126–143. [Google Scholar] [CrossRef]
- Malki, M.; Uhrig, G. Topological magnetic excitations. Europhys. Lett. 2020, 132, 20003. [Google Scholar] [CrossRef]
- Wang, P.; Lu, L.; Bertoldi, K. Topological phononic crystals with one-way elastic edge waves. Phys. Rev. Lett. 2015, 115, 104302. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z.; Shen, C.; Li, J.; Reit, E.; Bachman, H.; Socolar, J.E.; Cummer, S.A.; Jun Huang, T. Dispersion tuning and route reconfiguration of acoustic waves in valley topological phononic crystals. Nat. Commun. 2020, 11, 762. [Google Scholar] [CrossRef]
- Ma, J. Phonon Engineering of Micro-and Nanophononic Crystals and Acoustic Metamaterials: A Review. Small Sci. 2023, 3, 2200052. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, D.; Sun, K.; Mao, X.; Gonella, S. Edge modes and asymmetric wave transport in topological lattices: Experimental characterization at finite frequencies. Phys. Rev. Lett. 2018, 121, 094301. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Sun, K.; Gonella, S. Valley hall in-plane edge states as building blocks for elastodynamic logic circuits. Phys. Rev. Appl. 2019, 12, 044015. [Google Scholar] [CrossRef]
- Zhou, D.; Ma, J.; Sun, K.; Gonella, S.; Mao, X. Switchable phonon diodes using nonlinear topological Maxwell lattices. Phys. Rev. B 2020, 101, 104106. [Google Scholar] [CrossRef]
- Rajabpoor Alisepahi, A.; Sarkar, S.; Sun, K.; Ma, J. Breakdown of conventional winding number calculation in one-dimensional lattices with interactions beyond nearest neighbors. Commun. Phys. 2023, 6, 334. [Google Scholar] [CrossRef]
- Kane, C.L.; Lubensky, T.C. Topological boundary modes in isostatic lattices. Nat. Phys. 2014, 10, 39–45. [Google Scholar] [CrossRef]
- Paulose, J.; Chen, B.G.G.; Vitelli, V. Topological modes bound to dislocations in mechanical metamaterials. Nat. Phys. 2015, 11, 153–156. [Google Scholar] [CrossRef]
- Rocklin, D.Z.; Zhou, S.; Sun, K.; Mao, X. Transformable topological mechanical metamaterials. Nat. Commun. 2017, 8, 14201. [Google Scholar] [CrossRef]
- Rocklin, D.Z.; Chen, B.G.G.; Falk, M.; Vitelli, V.; Lubensky, T. Mechanical Weyl modes in topological Maxwell lattices. Phys. Rev. Lett. 2016, 116, 135503. [Google Scholar] [CrossRef] [PubMed]
- Bilal, O.R.; Süsstrunk, R.; Daraio, C.; Huber, S.D. Intrinsically polar elastic metamaterials. Adv. Mater. 2017, 29, 1700540. [Google Scholar] [CrossRef] [PubMed]
- Süsstrunk, R.; Huber, S.D. Observation of phononic helical edge states in a mechanical topological insulator. Science 2015, 349, 47–50. [Google Scholar] [CrossRef] [PubMed]
- Nash, L.M.; Kleckner, D.; Read, A.; Vitelli, V.; Turner, A.M.; Irvine, W.T. Topological mechanics of gyroscopic metamaterials. Proc. Natl. Acad. Sci. USA 2015, 112, 14495–14500. [Google Scholar] [CrossRef]
- Mousavi, S.H.; Khanikaev, A.B.; Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 2015, 6, 8682. [Google Scholar] [CrossRef]
- Pal, R.K.; Ruzzene, M. Edge waves in plates with resonators: An elastic analogue of the quantum valley Hall effect. New J. Phys. 2017, 19, 025001. [Google Scholar] [CrossRef]
- Al Ba’ba’a, H.; Nouh, M.; Singh, T. Formation of local resonance band gaps in finite acoustic metamaterials: A closed-form transfer function model. J. Sound Vib. 2017, 410, 429–446. [Google Scholar] [CrossRef]
- Bastawrous, M.V.; Hussein, M.I. Closed-form existence conditions for bandgap resonances in a finite periodic chain under general boundary conditions. J. Acoust. Soc. Am. 2022, 151, 286–298. [Google Scholar] [CrossRef]
- Allein, F.; Anastasiadis, A.; Chaunsali, R.; Frankel, I.; Boechler, N.; Diakonos, F.K.; Theocharis, G. Strain topological metamaterials and revealing hidden topology in higher-order coordinates. Nat. Commun. 2023, 14, 6633. [Google Scholar] [CrossRef]
- Rosa, M.I.; Davis, B.L.; Liu, L.; Ruzzene, M.; Hussein, M.I. Material vs. structure: Topological origins of band-gap truncation resonances in periodic structures. Phys. Rev. Mater. 2023, 7, 124201. [Google Scholar] [CrossRef]
- Kuo, J.Y.; Lee, T.Y.; Chiu, Y.C.; Liao, S.R.; Kao, H.C. SSH coupled-spring systems. arXiv 2023, arXiv:2310.00547. [Google Scholar]
- Coutant, A.; Sivadon, A.; Zheng, L.; Achilleos, V.; Richoux, O.; Theocharis, G.; Pagneux, V. Acoustic Su-Schrieffer-Heeger lattice: Direct mapping of acoustic waveguides to the Su-Schrieffer-Heeger model. Phys. Rev. B 2021, 103, 224309. [Google Scholar] [CrossRef]
- Li, X.; Meng, Y.; Wu, X.; Yan, S.; Huang, Y.; Wang, S.; Wen, W. Su-Schrieffer-Heeger model inspired acoustic interface states and edge states. Appl. Phys. Lett. 2018, 113, 203501. [Google Scholar] [CrossRef]
- Joubaneh, E.F.; Ma, J. Symmetry effect on the dynamic behaviors of sandwich beams with periodic face sheets. Compos. Struct. 2022, 289, 115406. [Google Scholar] [CrossRef]
- Yang, S.; Chang, H.; Wang, Y.; Yang, M.; Sun, T. A phononic crystal suspension for vibration isolation of acoustic loads in underwater gliders. Appl. Acoust. 2024, 216, 109731. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Hussein, M.I.; Hamza, K.; Hulbert, G.M.; Saitou, K. Optimal synthesis of 2D phononic crystals for broadband frequency isolation. Waves Random Complex Media 2007, 17, 491–510. [Google Scholar] [CrossRef]
- Chen, Y.; Kadic, M.; Wegener, M. Roton-like acoustical dispersion relations in 3D metamaterials. Nat. Commun. 2021, 12, 3278. [Google Scholar] [CrossRef]
- Iglesias Martínez, J.A.; Groß, M.F.; Chen, Y.; Frenzel, T.; Laude, V.; Kadic, M.; Wegener, M. Experimental observation of roton-like dispersion relations in metamaterials. Sci. Adv. 2021, 7, eabm2189. [Google Scholar] [CrossRef]
- Iorio, L.; De Ponti, J.M.; Maspero, F.; Ardito, R. Roton-like dispersion via polarisation change for elastic wave energy control in graded delay-lines. J. Sound Vib. 2024, 572, 118167. [Google Scholar] [CrossRef]
- Cui, J.G.; Yang, T.; Niu, M.Q.; Chen, L.Q. Tunable roton-like dispersion relation with parametric excitations. J. Appl. Mech. 2022, 89, 111005. [Google Scholar] [CrossRef]
- Wang, K.; Chen, Y.; Kadic, M.; Wang, C.; Wegener, M. Nonlocal interaction engineering of 2D roton-like dispersion relations in acoustic and mechanical metamaterials. Commun. Mater. 2022, 3, 35. [Google Scholar] [CrossRef]
- Zhu, Z.; Gao, Z.; Liu, G.G.; Ge, Y.; Wang, Y.; Xi, X.; Yan, B.; Chen, F.; Shum, P.P.; Sun, H.X.; et al. Observation of multiple rotons and multidirectional roton-like dispersion relations in acoustic metamaterials. New J. Phys. 2022, 24, 123019. [Google Scholar] [CrossRef]
- Grundmann, M. Topological States Due to Third-Neighbor Coupling in Diatomic Linear Elastic Chains. Phys. Status Solidi B 2020, 257, 2000176. [Google Scholar] [CrossRef]
- Chen, H.; Nassar, H.; Huang, G. A study of topological effects in 1D and 2D mechanical lattices. J. Mech. Phys. Solids 2018, 117, 22–36. [Google Scholar] [CrossRef]
- Liu, H.; Huang, X.; Yan, M.; Lu, J.; Deng, W.; Liu, Z. Acoustic Topological Metamaterials of Large Winding Number. Phys. Rev. Appl. 2023, 19, 054028. [Google Scholar] [CrossRef]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747. [Google Scholar] [CrossRef] [PubMed]
- Jackiw, R.; Rebbi, C. Solitons with fermion number 1/2. Phys. Rev. D 1976, 13, 3398. [Google Scholar] [CrossRef]
- Vanden-Hehir, S.; Tipping, W.J.; Lee, M.; Brunton, V.G.; Williams, A.; Hulme, A.N. Raman imaging of nanocarriers for drug delivery. Nanomaterials 2019, 9, 341. [Google Scholar] [CrossRef]
- Yeo, L.Y.; Friend, J.R.; McIntosh, M.P.; Meeusen, E.N.; Morton, D.A. Ultrasonic nebulization platforms for pulmonary drug delivery. Expert Opin. Drug Deliv. 2010, 7, 663–679. [Google Scholar] [CrossRef]
- Bienfait, A.; Satzinger, K.J.; Zhong, Y.; Chang, H.S.; Chou, M.H.; Conner, C.R.; Dumur, É.; Grebel, J.; Peairs, G.A.; Povey, R.G.; et al. Phonon-mediated quantum state transfer and remote qubit entanglement. Science 2019, 364, 368–371. [Google Scholar] [CrossRef]
- Al Ba’ba’a, H.B.; Willey, C.L.; Chen, V.W.; Juhl, A.T.; Nouh, M. Theory of Truncation Resonances in Continuum Rod-Based Phononic Crystals with Generally Asymmetric Unit Cells. Adv. Theory Simul. 2023, 6, 2200700. [Google Scholar] [CrossRef]
- Kuznetsov, S.V. Guided waves in FG plates: Appearing phase velocity gaps. Z. Angew. Math. Und Phys. 2022, 73, 127. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajabpoor Alisepahi, A.; Ma, J. In-Gap Edge and Domain-Wall States in Largely Perturbed Phononic Su–Schrieffer–Heeger Lattices. Crystals 2024, 14, 102. https://doi.org/10.3390/cryst14010102
Rajabpoor Alisepahi A, Ma J. In-Gap Edge and Domain-Wall States in Largely Perturbed Phononic Su–Schrieffer–Heeger Lattices. Crystals. 2024; 14(1):102. https://doi.org/10.3390/cryst14010102
Chicago/Turabian StyleRajabpoor Alisepahi, Amir, and Jihong Ma. 2024. "In-Gap Edge and Domain-Wall States in Largely Perturbed Phononic Su–Schrieffer–Heeger Lattices" Crystals 14, no. 1: 102. https://doi.org/10.3390/cryst14010102
APA StyleRajabpoor Alisepahi, A., & Ma, J. (2024). In-Gap Edge and Domain-Wall States in Largely Perturbed Phononic Su–Schrieffer–Heeger Lattices. Crystals, 14(1), 102. https://doi.org/10.3390/cryst14010102






