Basic Modelling of General Strength and Creep Properties of Alloys
Abstract
:1. Introduction
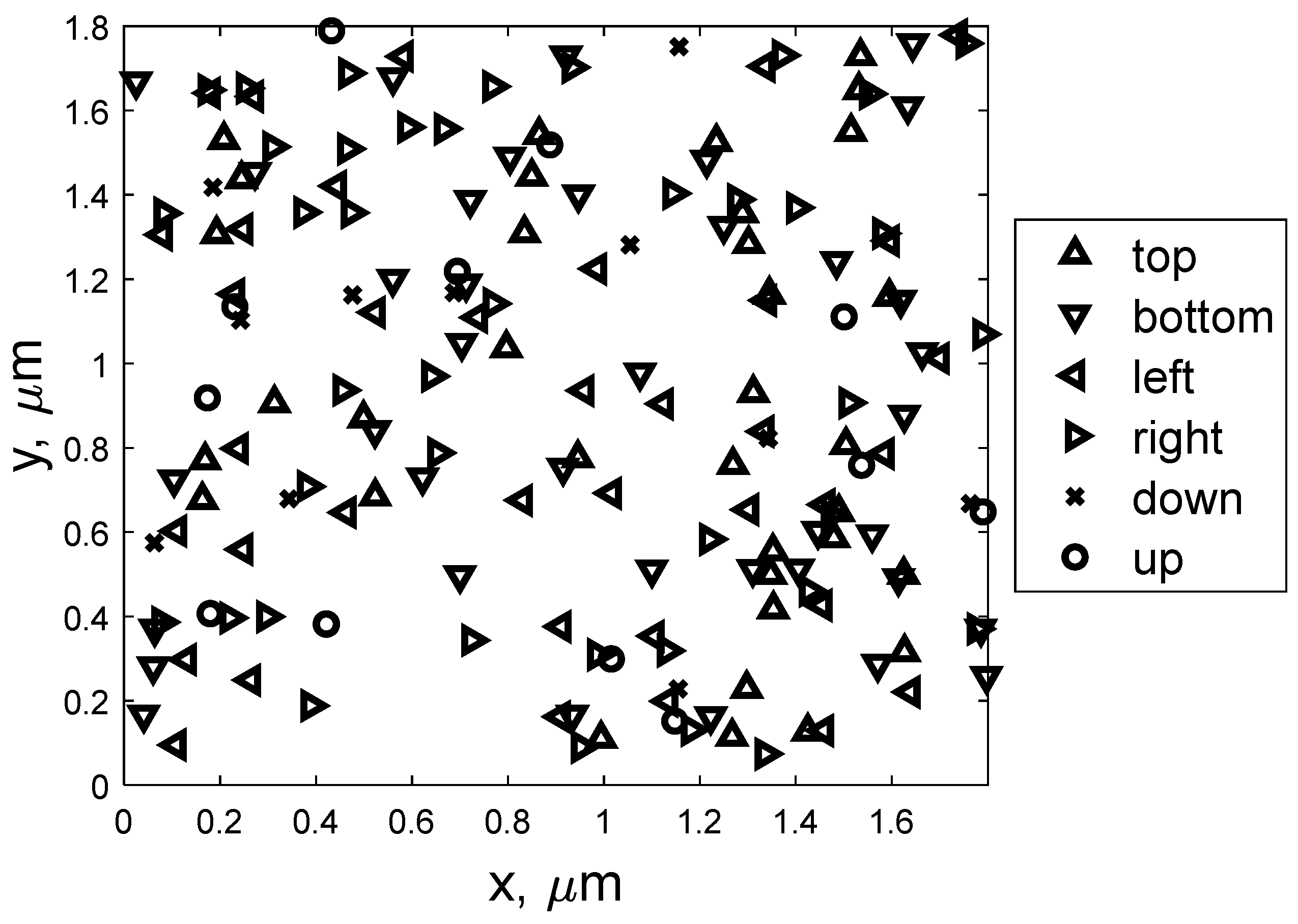
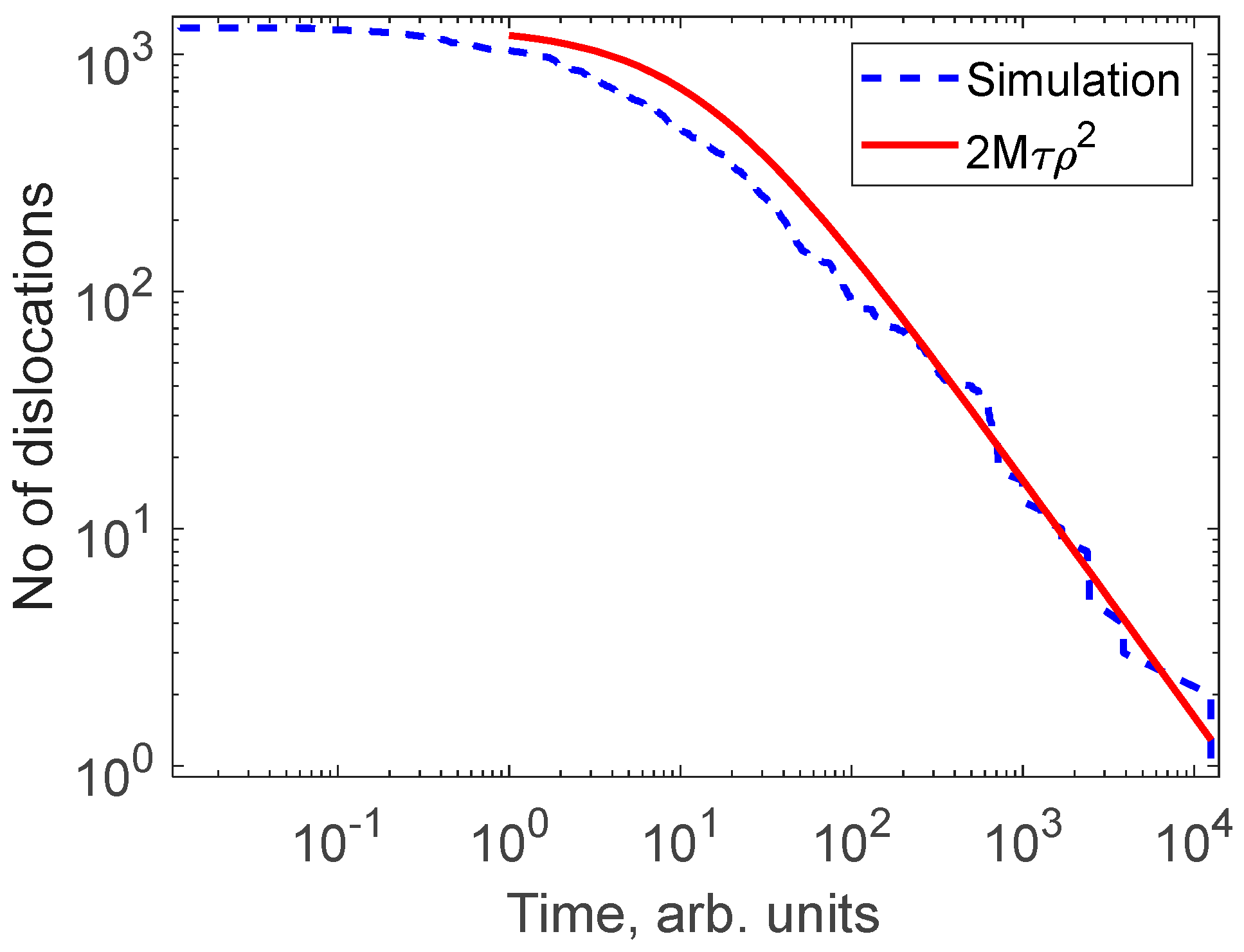
2. Dislocation Model
3. Stress–Strain Curves
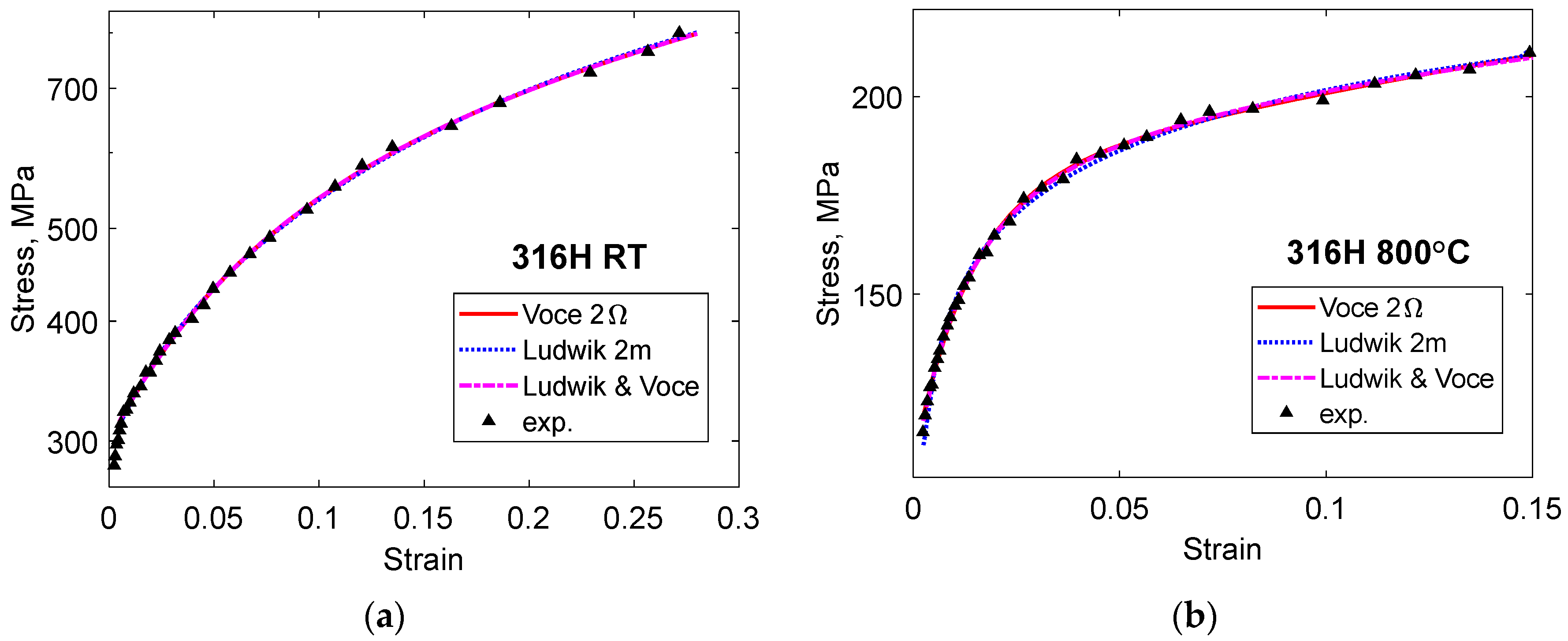
3.1. Empirical Models
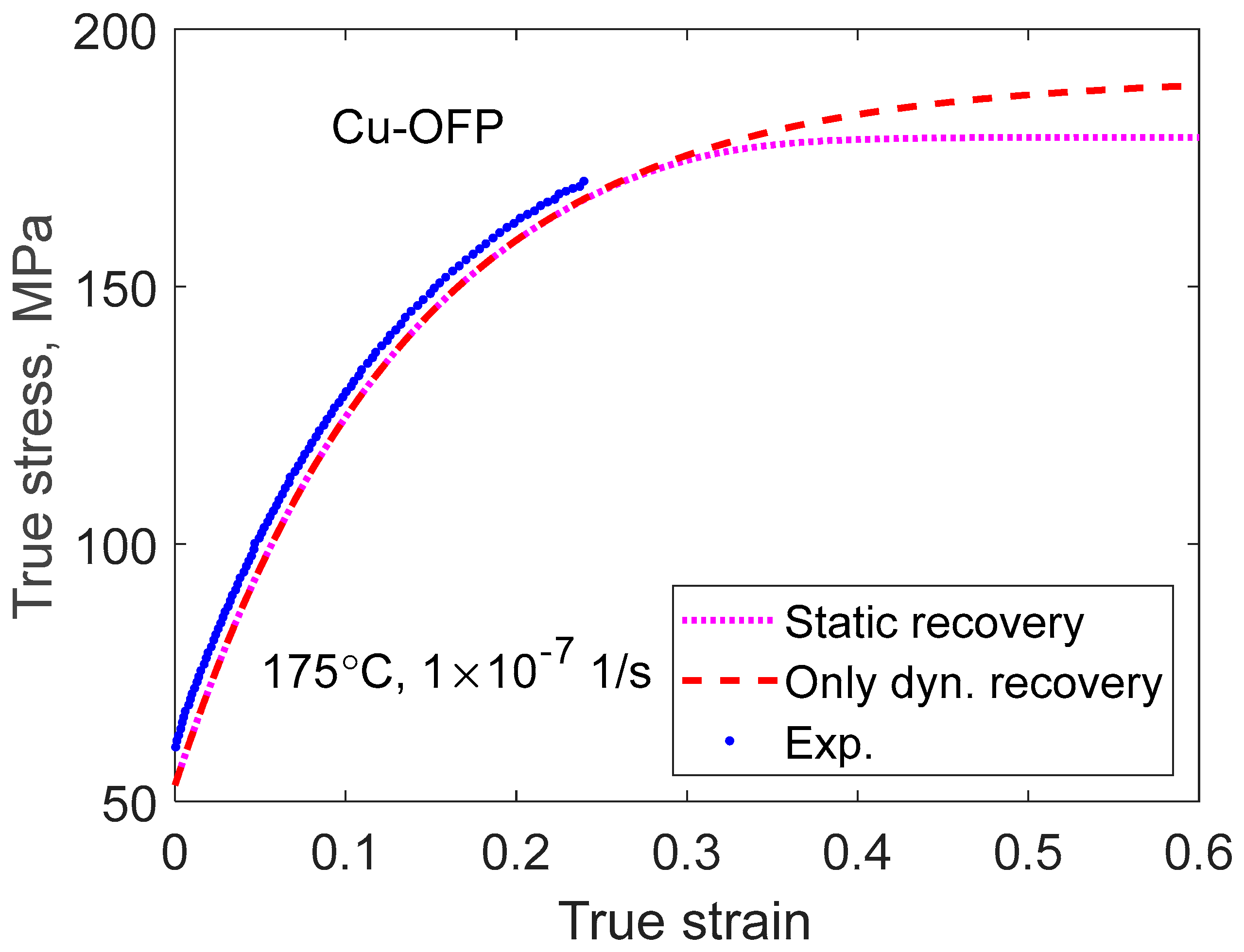
3.2. Basic Model
4. Stationary Creep
4.1. Basic Model for Stationary Creep
4.2. Application to Aluminium
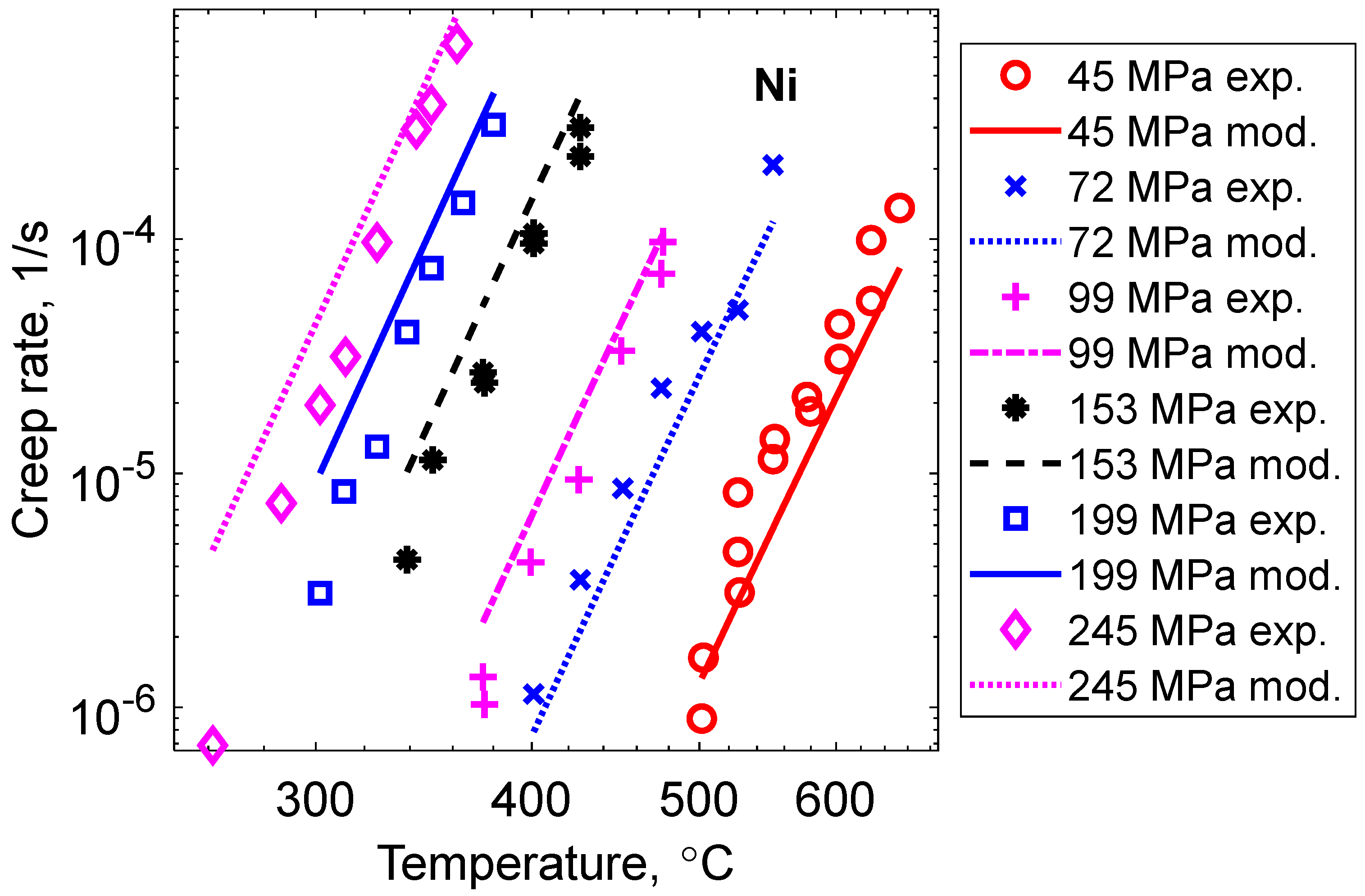
4.3. Application to Nickel
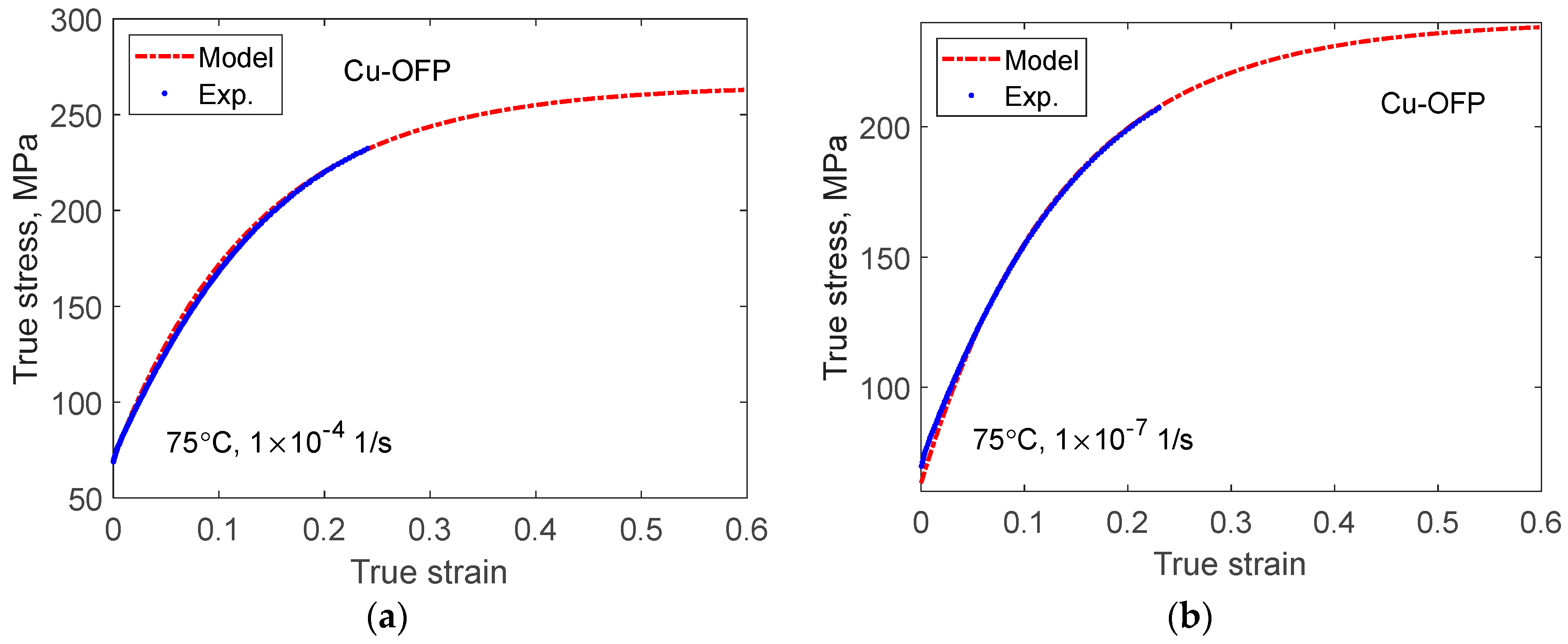
5. Primary Creep
5.1. The 2σ Model
5.2. The Stress Adaption Model
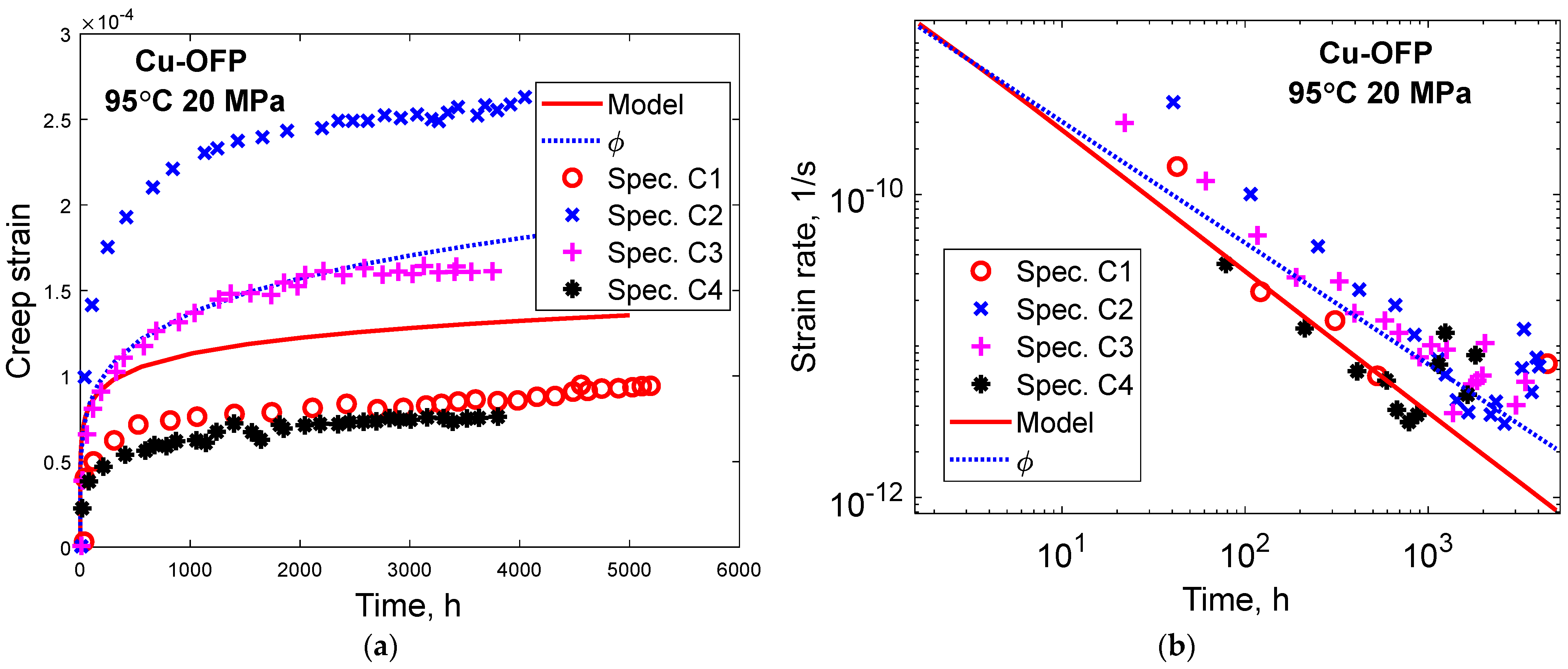
5.3. Cu-OFP at Low Stresses at 95 °C
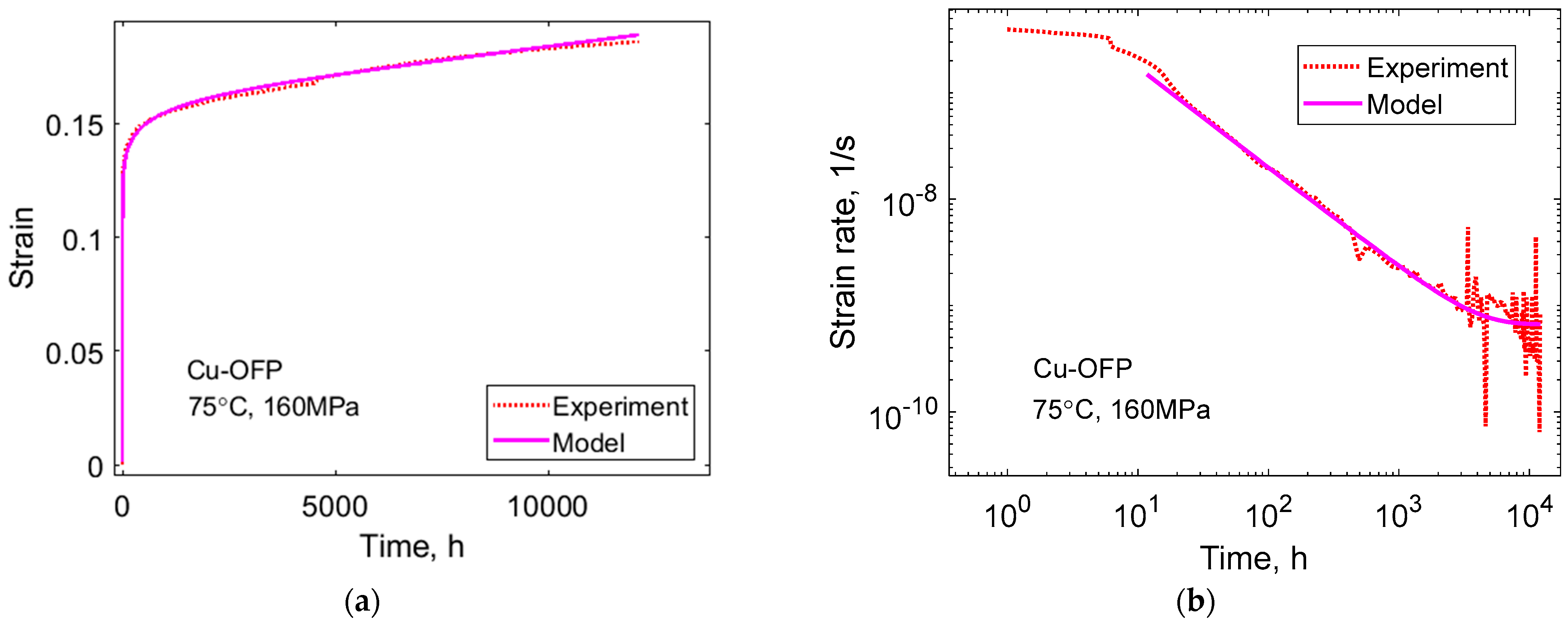
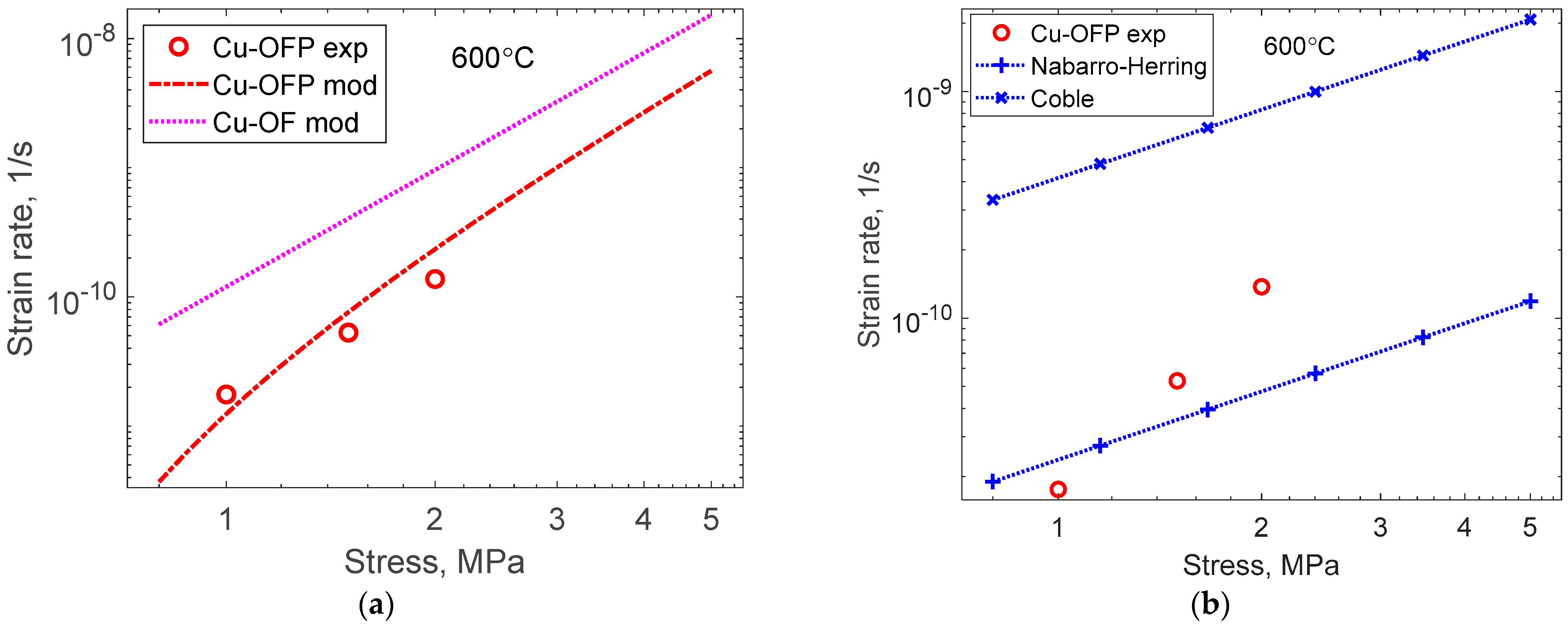
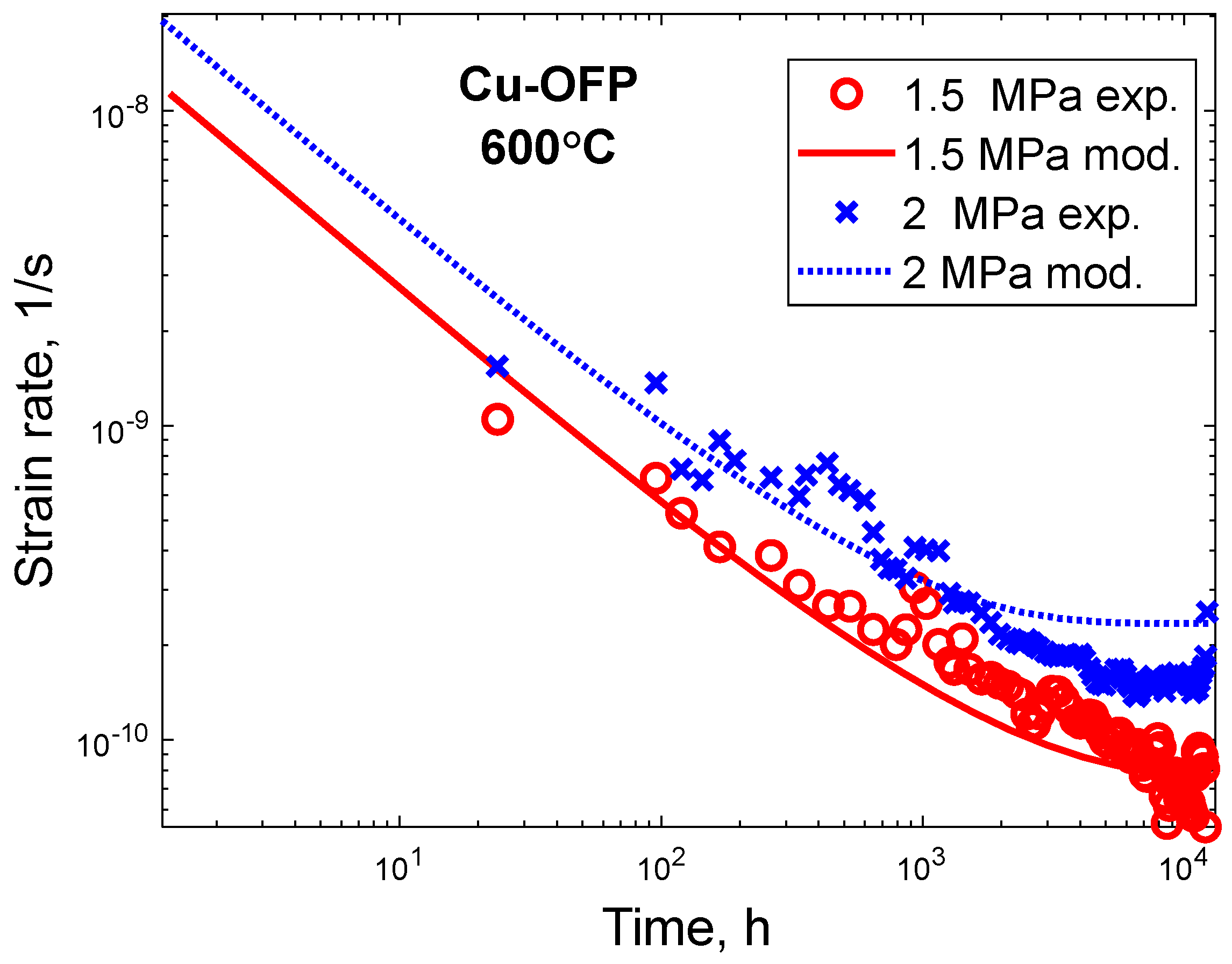
5.4. Creep of Cu-OFP at 600 °C
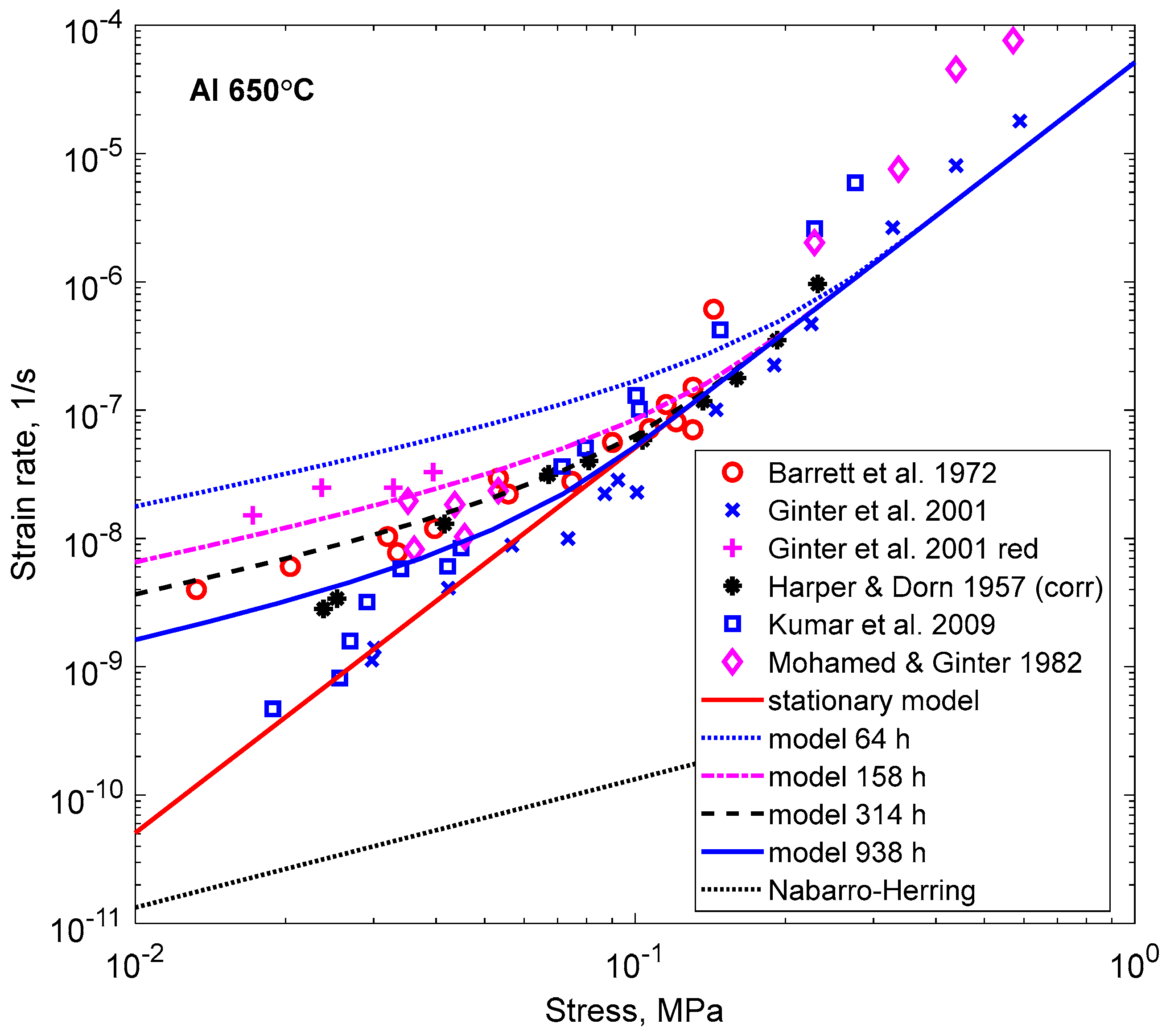
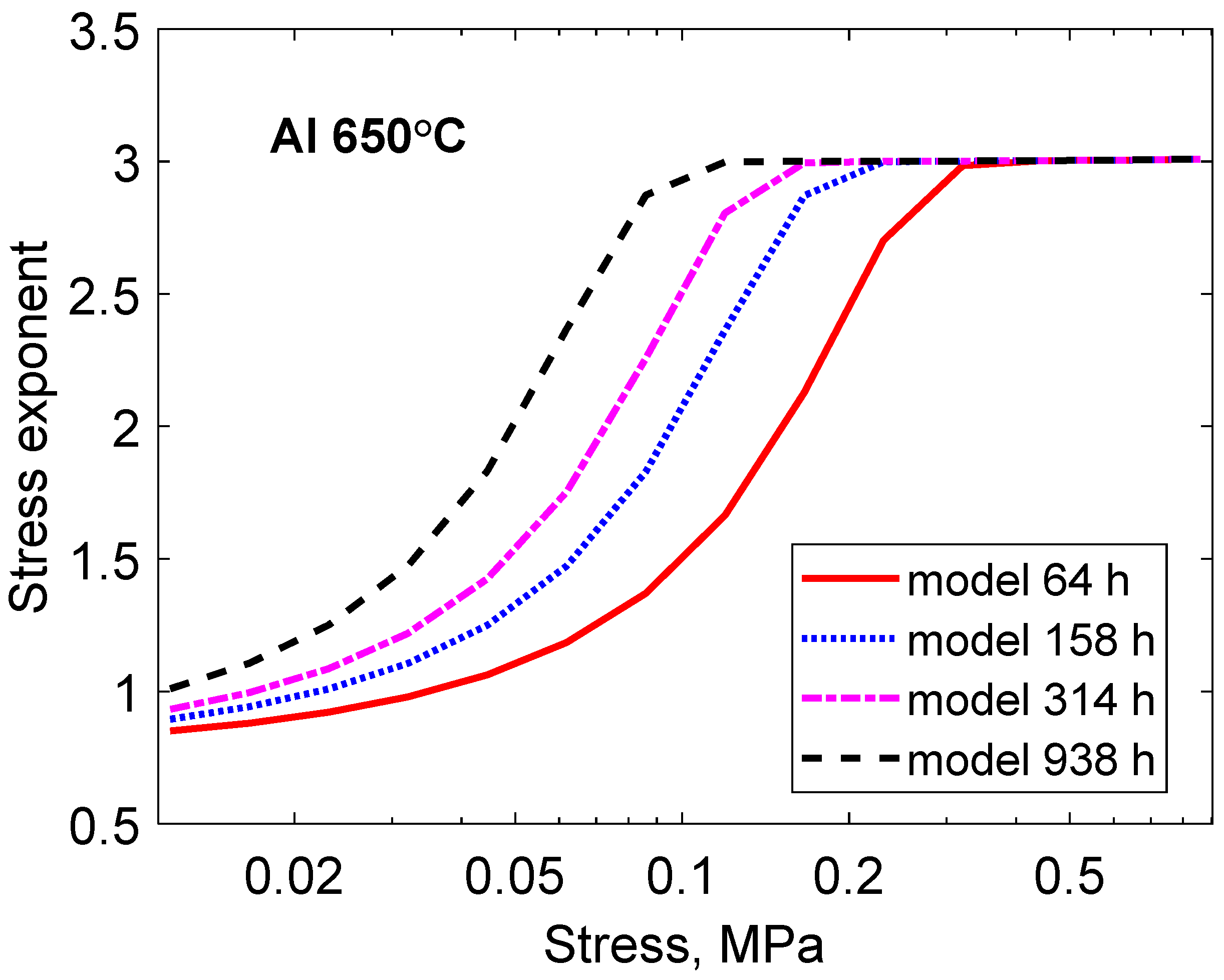
5.5. Aluminium at Low Stresses; Harper–Dorn Creep
6. Discussion
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ikeda, Y.; Grabowski, B.; Körmann, F. Ab initio phase stabilities and mechanical properties of multicomponent alloys: A comprehensive review for high entropy alloys and compositionally complex alloys. Mater. Charact. 2019, 147, 464–511. [Google Scholar] [CrossRef]
- Ladha, D.G. A review on density functional theory–based study on two-dimensional materials used in batteries. Mater. Today Chem. 2019, 11, 94–111. [Google Scholar] [CrossRef]
- Zhang, Y. First-principles Debye–Callaway approach to lattice thermal conductivity. J. Mater. 2016, 2, 237–247. [Google Scholar] [CrossRef]
- De Luca, G.; Basile, A. 17—Assessment of the key properties of materials used in membrane reactors by quantum computational approaches. In Handbook of Membrane Reactors; Woodhead Publishing: Sawston, UK, 2013; pp. 598–626. [Google Scholar]
- Maurice, V.; Marcus, P. Passive films at the nanoscale. Electrochim. Acta 2012, 84, 129–138. [Google Scholar] [CrossRef]
- David, M.; Prillieux, A.; Monceau, D.; Connétable, D. First-principles study of the insertion and diffusion of interstitial atoms (H, C, N and O) in nickel. J. Alloys Compd. 2020, 822, 153555. [Google Scholar] [CrossRef]
- Sandström, R. Fundamental Models for the Creep of Metals. In Creep; IntechOpen: London, UK, 2017. [Google Scholar]
- Choudhary, B.K.; Samuel, E.I.; Rao, K.B.S.; Mannan, S.L. Tensile stress–strain and work hardening behaviour of 316LN austenitic stainless steel. Mater. Sci. Technol. 2001, 17, 223–231. [Google Scholar] [CrossRef]
- Sandström, R. Cavitation during creep-fatigue loading. Mater. High Temp. 2023, 40, 174–183. [Google Scholar] [CrossRef]
- Sandström, R. Basic Creep-Fatigue Models Considering Cavitation. Trans. Indian Natl. Acad. Eng. 2022, 7, 583–591. [Google Scholar] [CrossRef]
- Orowan, E. Fracture and strength of solids. Rep. Prog. Phys. 1949, 12, 185–232. [Google Scholar] [CrossRef]
- Kocks, U.F. The relation between polycrystal deformation and single-crystal deformation. Met. Mater. Trans. 1970, 1, 1121–1143. [Google Scholar] [CrossRef]
- Kuhlmann-Wilsdorf, D.; Van Der Merwe, J. Theory of dislocation cell sizes in deformed metals. Mater. Sci. Eng. 1982, 55, 79–83. [Google Scholar] [CrossRef]
- Staker, M.R.; Holt, D.L. The dislocation cell size and dislocation density in copper deformed at temperatures between 25 and 700Â °C. Acta Metall. 1972, 20, 569–579. [Google Scholar] [CrossRef]
- Orlová, A. On the relation between dislocation structure and internal stress measured in pure metals and single phase alloys in high temperature creep. Acta Met. Mater. 1991, 39, 2805–2813. [Google Scholar] [CrossRef]
- Kocks, U.F. Laws for Work-Hardening and Low-Temperature Creep. J. Eng. Mater. Technol. Trans. ASME 1976, 98, 76–85. [Google Scholar] [CrossRef]
- Roberts, W.; Bergström, Y. The stress-strain behaviour of single crystals and polycrystals of face-centered cubic metals—A new dislocation treatment. Acta Met. 1973, 21, 457–469. [Google Scholar] [CrossRef]
- Roters, F.; Raabe, D.; Gottstein, G. Work hardening in heterogeneous alloys—A microstructural approach based on three internal state variables. Acta Mater. 2000, 48, 4181–4189. [Google Scholar] [CrossRef]
- Sandström, R. Basic model for primary and secondary creep in copper. Acta Mater. 2012, 60, 314–322. [Google Scholar] [CrossRef]
- Wang, R.; Wang, S.; Wu, X. Edge dislocation core structures in FCC metals determined from ab initio calculations combined with the improved Peierls-Nabarro equation. Phys. Scr. 2011, 83, 045604. [Google Scholar] [CrossRef]
- Sandström, R.; Hallgren, J. The role of creep in stress strain curves for copper. J. Nucl. Mater. 2012, 422, 51–57. [Google Scholar] [CrossRef]
- Bergström, Y. A dislocation model for the stress-strain behaviour of polycrystalline α-Fe with special emphasis on the variation of the densities of mobile and immobile dislocations. Mater. Sci. Eng. 1970, 5, 193–200. [Google Scholar] [CrossRef]
- Bergström, Y.; Roberts, W. A dislocation model for dynamical strain ageing of α-iron in the jerky-flow region. Acta Met. 1971, 19, 1243–1251. [Google Scholar] [CrossRef]
- Mohamadnejad, S.; Basti, A.; Ansari, R. Analyses of Dislocation Effects on Plastic Deformation. Multiscale Sci. Eng. 2020, 2, 69–89. [Google Scholar] [CrossRef]
- Friedel, J. Dislocations; Addison-Wesley: Reading, MA, USA, 1964. [Google Scholar]
- Lagneborg, R. Dislocation mechanisms in creep. Int. Metall. Rev. 1972, 17, 130–146. [Google Scholar] [CrossRef]
- Magnusson, H.; Sandström, R. Creep Strain Modeling of 9 to 12 Pct Cr Steels Based on Microstructure Evolution. Met. Mater. Trans. A 2007, 38, 2033–2039. [Google Scholar] [CrossRef]
- Lavrentev, F. The type of dislocation interaction as the factor determining work hardening. Mater. Sci. Eng. 1980, 46, 191–208. [Google Scholar] [CrossRef]
- Evans, R.W.; Wilshire, D. Creep of Metals and Alloy; Institute of Metals: London, UK, 1985. [Google Scholar]
- Herring, C. Diffusional Viscosity of a Polycrystalline Solid. J. Appl. Phys. 1950, 21, 437–445. [Google Scholar] [CrossRef]
- Coble, R.L. A Model for Boundary Diffusion Controlled Creep in Polycrystalline Materials. J. Appl. Phys. 1963, 34, 1679–1682. [Google Scholar] [CrossRef]
- Sandström, R. Creep at low stresses in aluminium (Harper-Dorn) and in an austenitic stainless steel with a stress exponent of 1. Mater. Today Commun. 2023, 36, 106558. [Google Scholar] [CrossRef]
- Sandström, R. Primary creep at low stresses in copper. Mater. Sci. Eng. A 2023, 873, 144950. [Google Scholar] [CrossRef]
- Langdon, T. A unified approach to grain boundary sliding in creep and superplasticity. Acta Met. Mater. 1994, 42, 2437–2443. [Google Scholar] [CrossRef]
- Sandström, R.; He, J. Survey of Creep Cavitation in fcc Metals. In Study of Grain Boundary Character; IntechOpen: London, UK, 2017. [Google Scholar]
- Korzhavyi, P.; Sandström, R. First-principles evaluation of the effect of alloying elements on the lattice parameter of a 23Cr25NiWCuCo austenitic stainless steel to model solid solution hardening contribution to the creep strength. Mater. Sci. Eng. A 2015, 626, 213–219. [Google Scholar] [CrossRef]
- Sui, F.; Sandström, R. Creep strength contribution due to precipitation hardening in copper–cobalt alloys. J. Mater. Sci. 2019, 54, 1819–1830. [Google Scholar] [CrossRef]
- He, J.; Sandström, R. Application of Fundamental Models for Creep Rupture Prediction of Sanicro 25 (23Cr25NiWCoCu). Crystals 2019, 9, 638. [Google Scholar] [CrossRef]
- He, J.; Sandström, R. Basic modelling of creep rupture in austenitic stainless steels. Theor. Appl. Fract. Mech. 2017, 89, 139–146. [Google Scholar] [CrossRef]
- Sandström, R.; Zhang, J. Modeling the Creep of Nickel. J. Eng. Mater. Technol. 2021, 143, 041011. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; Krieger: Malabar, FL, USA, 1982. [Google Scholar]
- Blum, W.; Eisenlohr, P.; Breutinger, F. Understanding creep—A review. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2002, 33, 291–303. [Google Scholar] [CrossRef]
- Ruano, O.A.; Miller, A.K.; Sherby, O.D. The influence of pipe diffusion on the creep of fine-grained materials. Mater. Sci. Eng. 1981, 51, 9–16. [Google Scholar] [CrossRef]
- Spigarelli, S.; Sandström, R. Basic creep modelling of aluminium. Mater. Sci. Eng. A 2018, 711, 343–349. [Google Scholar] [CrossRef]
- Shin, I.; Carter, E.A. Possible origin of the discrepancy in Peierls stresses of fcc metals: First-principles simulations of dislocation mobility in aluminum. Phys. Rev. B-Condens. Matter Mater. Physic 2013, 88, 064106. [Google Scholar] [CrossRef]
- Servi, I.S.; Grant, N.J. Creep and stress rupture behaviour of aluminium as a function of purity. Trans. AIME 1951, 191, 909–916. [Google Scholar]
- Norman, E.; Duran, S. Steady-state creep of pure polycrystalline nickel from 0.3 to 0.55 Tm. Acta Met. 1970, 18, 723–731. [Google Scholar] [CrossRef]
- Sui, F.; Sandström, R. Basic modelling of tertiary creep of copper. J. Mater. Sci. 2018, 53, 6850–6863. [Google Scholar] [CrossRef]
- Sandström, R. Basic Analytical Modeling of Creep Strain Curves. Materials 2023, 16, 3542. [Google Scholar] [CrossRef] [PubMed]
- Sandström, R. The role of cell structure during creep of cold worked copper. Mater. Sci. Eng. A 2016, 674, 318–327. [Google Scholar] [CrossRef]
- Norton, F.H. The Creep of Steel at High Temperatures; McGraw-Hill Book Co.: New York, NY, USA, 1929. [Google Scholar]
- Wu, R.; Sandström, R.; Seitisleam, F. Influence of Extra Coarse Grains on the Creep Properties of 9 Percent CrMoV (P91) Steel Weldment. J. Eng. Mater. Technol. 2004, 126, 87–94. [Google Scholar] [CrossRef]
- Ho, E.T.C. A Study of Creep Behaviour of Oxygen-Free Phosphorus-Doped Copper under Low-Temperture and Low-Stress Test Conditions. In Report No: 06819-REP-01200-10031-R00; Ontario Power Technologies: Toronto, ON, Canada, 2000. [Google Scholar]
- Sandström, R. Formation of a dislocation back stress during creep of copper at low temperatures. Mater. Sci. Eng. A 2017, 700, 622–630. [Google Scholar] [CrossRef]
- Sandstrom, R. Extrapolation of Creep Strain Data for Pure Copper. J. Test. Eval. 1999, 27, 31–35. [Google Scholar]
- Harper, J.; Dorn, J. Viscous creep of aluminum near its melting temperature. Acta Met. 1957, 5, 654–665. [Google Scholar] [CrossRef]
- Kassner, M.E.; Kumar, P.; Blum, W. Harper–Dorn creep. Int. J. Plast. 2007, 23, 980–1000. [Google Scholar] [CrossRef]
- Kumar, P.; Kassner, M.E.; Blum, W.; Eisenlohr, P.; Langdon, T.G. New observations on high-temperature creep at very low stresses. Mater. Sci. Eng. A 2009, 510–511, 20–24. [Google Scholar] [CrossRef]
- Ginter, T.; Chaudhury, P.; Mohamed, F. An investigation of Harper–Dorn creep at large strains. Acta Mater. 2001, 49, 263–272. [Google Scholar] [CrossRef]
- Mohamed, F.A.; Ginter, T.J. On the nature and origin of Harper-Dorn creep. Acta Met. 1982, 30, 1869–1881. [Google Scholar] [CrossRef]
- Barrett, C.; Muehleisen, E.; Nix, W. High temperature-low stress creep of Al and Al+0.5%Fe. Mater. Sci. Eng. 1972, 10, 33–42. [Google Scholar] [CrossRef]
- Sandström, R. Fundamental Models for Creep Properties of Steels and Copper. Trans. Indian Inst. Met. 2016, 69, 197–202. [Google Scholar] [CrossRef]



| Temperature, °C | Stress, MPa | Creep Rate Ratio, Stress | Creep Rate Ratio, Temperature |
|---|---|---|---|
| 75 | 1.5->165 | 4 × 1018 | |
| 600 | 1.5->165 | 3 × 1011 | |
| 75->600 | 1.5 | 6 × 1015 | |
| 75->600 | 165 | 4 × 1010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandström, R. Basic Modelling of General Strength and Creep Properties of Alloys. Crystals 2024, 14, 21. https://doi.org/10.3390/cryst14010021
Sandström R. Basic Modelling of General Strength and Creep Properties of Alloys. Crystals. 2024; 14(1):21. https://doi.org/10.3390/cryst14010021
Chicago/Turabian StyleSandström, Rolf. 2024. "Basic Modelling of General Strength and Creep Properties of Alloys" Crystals 14, no. 1: 21. https://doi.org/10.3390/cryst14010021





