Abstract
In past years, optical lattices have been demonstrated as an excellent platform for making, understanding, and controlling quantum matters at nonlinear and fundamental quantum levels. Shrinking experimental observations include matter-wave gap solitons created in ultracold quantum degenerate gases, such as Bose–Einstein condensates with repulsive interaction. In this paper, we theoretically and numerically study the formation of one-dimensional gap soliton molecules and clusters in ultracold coherent atom ensembles under electromagnetically induced transparency conditions and trapped by an optical lattice. In numerics, both linear stability analysis and direct perturbed simulations are combined to identify the stability and instability of the localized gap modes, stressing the wide stability region within the first finite gap. The results predicted here may be confirmed in ultracold atom experiments, providing detailed insight into the higher-order localized gap modes of ultracold bosonic atoms under the quantum coherent effect called electromagnetically induced transparency.
1. Introduction
In the context of optics, it is commonly known that linear diffraction can greatly spread waves, and dispersion is able to separate the light of colors by refraction or diffraction (with the appearance or formation of optical frequency spectrum), eliminating and destroying the propagation of light with well-conserved shapes [1]. In order to overcome such problems, optical nonlinearities in the forms of Kerr (cubic) nonlinear terms and other higher-order ones or their combination are usually introduced to the strong laser light propagation, and in such instances, a graceful balance between the inherent linear diffraction (or dispersion) and the material’s nonlinearity like the Kerr one could be reached; therefore, solitons or localized modes/waves (in a much wider range of circumstances that do not permit analytical solutions) can be created [2,3]. Solitons are nonlinear waves exhibiting three unique properties that are only affiliated to nonlinear (physical) dynamical systems: (i) keeps the same velocity; (ii) the shape conserves; (iii) quasi-elastic collision happen for two solitons—they keep their original propagating direction and do not change their shapes and velocities. As a matter of fact, owing to these three unique properties, optical solitons are widely considered to be ideal candidates for low-loss or lossless nonlinear light propagation in modern optics communications [4,5]. It is relevant to point out that solitons are one of the ubiquitous nonlinear emergent phenomena in nonlinear physical systems and beyond [6,7,8,9,10].
Within past years, considerable research interest has been focused on periodic potentials, such as photonic crystals/lattices in optics and optical lattices in Bose–Einstein condensates (BECs), because of their tunable band-gap engineering and the control of light and matter waves in both linear and nonlinear processes [11,12,13,14,15,16,17,18]. In periodic potentials, by tuning the strength, periodicity, and structure of the periodic structures, one can obtain controllable finite forbidden gaps of the underlying linear Bloch-wave spectrum, and particularly, as far as optics are concerned, the light waves with frequencies lying within such finite gaps are not allowed to be propagated due to the strong Bragg scattering, while those waves with frequencies lying inside the linear Bloch bands (but not the finite gaps) can be freely propagated as a carrier of both energy and information, enabling the versatile applications in modern optics communications. Diverse localized modes (no matter the matter waves or classical waves), including fundamental solitons, gap solitons, and vortices, have been found with the help of periodic potentials and under nonlinear regimes [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]; the latter two modes combine the finite gap’s strong localization and materials’s nonlinearity, enabling the formation and control of robust localized gap modes. Recently, the localization of light and matters has been extended to a novel twisted structure named Moiré superlattices that can be tuned to periodic form under the Pythagorean angle and an aperiodic one for other angles [34,35,36,37,38,39,40,41]; particularly, soliton formation and gap solitons and vortical ones have been addressed in such settings [28,39,40,41,42,43]. It is deserved to be emphasized that twisted structures such as Moiré optical lattices can be made easily in optics and condensed matter physics experiments, providing a new controllable (twisted angle) degree of freedom in studying the linear, nonlinear, and quantum properties of light and matter waves.
In recent years, searching for novel types of localized modes as various solitons is also a topic gaining intense attention in the nonlinear science domain [3,44]. An interesting experimental observation in recent years is the discovery of soliton molecules in mode-locked laser and other fiber lasers under various nonlinear ultrafast transient processes [45,46], revealing novel ultrafast transient processes and interesting nonlinear emergent soliton phenomena in real complex nonlinear physical systems. It deserves to be mentioned that a stable soliton molecule’s birth dynamics were observed and confirmed to experience five different stages, which are raised relaxation oscillation, beating dynamics, transient single pulse stage, transient bound state, and lastly the stable bound state, according to Ref. [45], where it is also found the buildup dynamics of soliton molecules is very sensitive to two experimental conditions: the intracavity light’s polarization state and the fluctuation of pump power. In addition to that, it was observed in Ref. [46] that the stable optical soliton molecular complexes formed by two soliton-pair molecules (the constitution of two strongly bound optical solitons) can highlight the important differences between the intramolecular bonds and intermolecular ones of the soliton molecular complexes, stressing that the strong intramolecular bond may be considered as a dynamical attractor of focus type with strength being lowly sensitive to external perturbations, and conversely, the intermolecular bond (a weaker attractor of limit-cycle type that is usually more sensitive to environmental perturbations) works over a distance thrice larger than that of the intramolecular one and can be characterized by a sliding relative phase. On the theoretical side, soliton molecules have been found in different nonlinear physical systems, containing both uniform media and periodic ones [47,48,49,50].
Very recently, quantum droplets, a novel liquid state of matter existing under a precise balance between the competing focusing (attractive) inter- and defocusing (repulsive) intraspecies forces and beyond-mean-field term called Lee–Huang–Yang corrections, describing quantum fluctuations of many-body atoms (physics) [51,52,53,54], were also found to be a good system for creating metastable ring-shaped clusters [55]. We would like to point out that quantum droplets are the self-bound state existing without the help of any external potentials, and in such droplets, the underlying physical model can be approximated as a mean-field one in the framework of the Gross–Pitaevskii equation, which, surprisingly, includes both the nonlinear effect and quantum many-body terms, thus within where the quantum nonlinear effects can be researched. In addition, other soliton clusters have also been predicted in different nonlinear systems [56,57,58,59,60,61,62,63]. One point deserving to be emphasized is that the internal dynamics of two- and three-soliton bound states (femtosecond soliton molecules) over hundreds of thousands of consecutive cavity round trips was tracked experimentally in the cavity of a few-cycle mode-locked laser, highlighting the importance of real-time spectral interferometry detection in resolving internal interactions in complex nonlinear physical systems, enabling the probe of the transient dynamics of soliton bound states, breathers, and rogue waves [57]. It is safe to conclude that although soliton clusters and gap soliton clusters have been widely studied in various nonlinear physical systems, the gap soliton molecules and clusters in coherent atomic media where the multilevel atoms are tuned to a electromagnetically induced transparency (EIT) regime are still missing. In the context of quantum optics, EIT is a quantum interference effect induced by a control laser field to eliminate the absorption of a probe laser field in a resonant atomic system, and previous studies have demonstrated that the EIT effect could lead to many intriguing physical properties, i.e., the giant reduction of group velocity, a remarkable enhancement of Kerr nonlinearity with ultra-low-power light fields [64].
We here reveal the existence, property, and dynamics of one-dimensional matter-wave gap soliton molecules and clusters in optical lattice-trapped coherently ultracold atoms ensembles with a -type three-level configuration that are tuned to the EIT condition. Here, the optical lattice (i.e., external potential) is formed by a pair of counter-propagating far-detuned Stark laser fields. In previous works with similar physical systems, we have predicted the formations and evolutionary dynamics of one-dimensional (1D) fundamental matter-wave gap solitons (single mode) and dipole ones [25] and also the gap vortices in two-dimensional scenarios [26]. In the present work particularly, we show that the gap soliton clusters could be built as different forms, including one called gap waves, which have been experimentally confirmed in ultracold Bose–Einstein atoms loaded into deep optical lattices and in nonlinear optics backgrounds with moderate-depth periodic potential. The stability and instability of the localized gap modes in the first finite gap are identified numerically by linear stability analysis and direct perturbed simulations. The localized gap modes predicted here can be readily confirmed in experiments, providing an insightful understanding of soliton physics and nonlinear dynamics in ultracold atoms. It is necessary to note that, although our physical description is based on the three-level coherently ultracold atoms ensembles, other atomic systems with more complex electronic level configurations like the four-level one are also good candidates. On the other hand, in addition to ultracold atoms, hot atoms under room temperature can be operated to the EIT regime, and thus the nonlinear physics and dynamics revealed here could emerge too. We would like to state that the predicted gap soliton molecules and clusters could be implemented in ultracold atom experiments and may lead to promising applications in modern optical communications and quantum information processing.
The rest of this article is arranged in the following way. In Section 2, we first put forward the theoretical model under study, and give a detailed description of our numerical methods for solving such a model. In Section 3, we present our numerical results for the gap soliton molecules and clusters of two types: equal-height type and dipole one; the shapes, linear stability eigenvalues, and stability regions of these gap soliton clusters are also shown. Lastly, in Section 4, we make a conclusion of this article and give a brief prospect.
2. Theoretical Model and Numerical Methods
The physical model under study is a lifetime-broadened and ultracold atomic gas with a -type three-level configuration interacting resonantly with two laser fields (i.e., the pulsed weak probe field and the strong continuous-wave control field ), and working at EIT circumstances [64], as shown in Figure 1a. The probe field with frequency drives the transition , and the control field with frequency couples and . and are, respectively, the spontaneous emission decay rates of and transitions. and , respectively, denote the two- and one-detunings, where angular frequency difference with being the eigen energy of state . The atoms are initially prepared in the ground state and cooled to an ultracold temperature to eliminate center-of-mass motion. We should note that the model considered here can generate a giant enhancement of Kerr nonlinearity, because of the EIT effect, to form optical solitons [65]. In addition, the far-detuned Stark field, two counter-propagating far-detuned laser fields of angular frequency , is applied into the system to induce the 1D optical lattice (i.e., external potential) to generate the corresponding band-gap structure and obtain the gap soliton molecules and clusters.
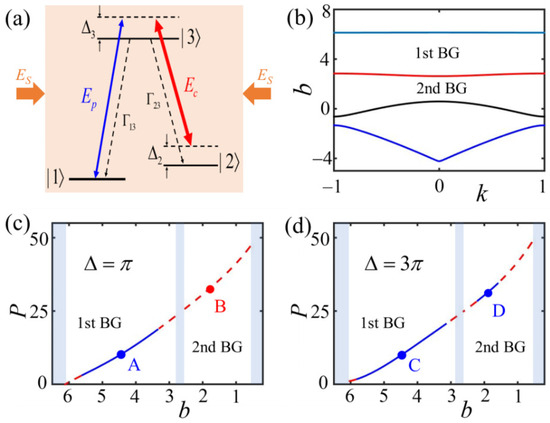
Figure 1.
(a) Excitation scheme of the -type three-level atomic system in an optical lattice induced by two counter-propagating far-detuned laser fields (see the brown arrows). The other physical parameters are described in the main text. (b) The relevant linear band-gap spectrum of the corresponding optical lattice with . The 1st BG and 2nd BG represent the first and second band gaps, respectively. (c,d) represent the power P of equal-height type [or (1, 1, 1, 1)-type] localized gap modes versus propagation constant b with spatial distance and , respectively. Stability and instability regions for gap soliton clusters in panels (c,d) are respectively marked by blue solid and red dashed lines. The profiles of gap soliton clusters marked by points (A, B) and (C, D) whose corresponding propagation constants b are (4.5, 1.9) and (4.5, 1.9) will be depicted below.
We would like to point out that the theoretical model taken here can be realized in realistic physical systems, e.g., for ultracold 87Rb atomic ensembles tuned to D1-line transition. Then, the atomic energy levels , , and depicted in Figure 1a can be selected respectively as , , and [66]. In theory, the Maxwell–Bloch equation, depicting the interaction between light laser fields and atoms, can be obtained under the electric-dipole and rotation wave approximations in the interaction picture. Therefore, the evolution of the probe field in our model can be described by dimensionless nonlinear envelope equations (i.e., nonlinear Schrödinger equation), which is derived and obtained by employing the method of multiple scales based on Maxwell–Bloch equation [65]. The governing nonlinear envelope equation in dimensionless form with defocusing Kerr nonlinearity for probe field amplitude , yields [25]
where is time, is a coordinate in the transverse plane, and represents the 1D optical lattice induced by the far-detuned Stark fields. and R are, respectively, the typical pulse duration and beam radius of the probe field. is the strength of the optical lattice, and we set throughout. We stress that detailed theoretical derivations and descriptions and selected physical parameters of such a model can be referred to in our previous publication in [25]. According to Ref. [25], we can estimate that the group velocity of the probe field envelope is around (c being the light speed in vacuum), which is obviously ultraslow. Deserved to be mentioned is the choice of the physical model (Equation (1)), particularly for nonlinear light propagation in coherent multilevel atoms loaded onto optical lattices. Such a model is unique since almost all previous studies talk about ground-state ultracold atoms (which are assumed to be tuned to ground state) despite still being trapped by optical lattices; we progress earlier soliton studies with this model to form, consolidate, and establish our particular research contents and characteristics. It is also relevant to highlight that the physical model (Equation (1)) shares the similarity of the mean-field Gross–Pitaevskii equation describing ultracold atoms such as BECs loaded onto a 1D optical lattice, and the generalized nonlinear Schrödinger equation for modeling the nonlinear light propagation in 1D photonic crystal gratings or photonic lattices, the only difference being the negative sign of the optical lattice in Equation (1). Therefore, the localized gap soliton molecules and clusters predicted here could also be observed in the contexts of BECs and conventional nonlinear optics.
To proceed with the outcome of the linear Bloch-wave spectrum of the optical lattice given in Equation (1), we first describe the numerical method for producing such a spectrum. In solid-state physics, the atomic lattices possess translational symmetry so that the unit cell for the lattice can repeat its cycle and shape completely after some spatial displacement. According to this fact, the linear Bloch theorem could be used to exactly characterize the band-gap structure of the periodic potentials like atomic lattices. This theorem is then extended to the optics domain for mapping the optical forbidden gaps and allowed bands of optical periodic potentials, including the photonic crystals (waveguides and fibers) and photonic lattices. Upon using such a theorem, we can easily build the linear Bloch band-gap structure with a discarding Kerr nonlinear effect, which is shown in Figure 1b for an optical lattice with moderate strength (considering that fact that we have set such strength as throughout). In the figure, we can see that the Bloch spectrum has a wide first finite gap and a narrow second gap. The first BG and second BG in Figure 1 represent the first and second band gaps, respectively.
We then turn to search stationary solution of field amplitude , with b being propagation constant. Submitting the form of the stationary solution into Equation (1), then it becomes
The power of gap soliton clusters is defined as versus propagation constant b, which can be obtained from integrating Equation (2).
Linear stability is a key issue in analyzing the stability property of the stationary solution (i.e., the localized gap solutions). Therefore, we take the perturbed amplitude as . It should be noted that U is the undisturbed field amplitude found from Equation (2) by adopting the modified squared-operator method (MSOM) [67], and and are small perturbations at eigenvalue . Substituting such expression into Equation (1), we then obtain the following linear eigenvalue problem:
where . By solving the eigenvalue Equation (3) with the Fourier collocation method [67], we can obtain the eigenvalues that determine the stability of the perturbed localized solutions. Specifically, the solutions are stable when the real parts of corresponding eigenvalues are zero, i.e., Re; otherwise, they are unstable since they are affected by very small perturbations. The stability of these solutions are rechecked via direct numerical simulations of the perturbed evolution in Equation (1) using the split-step Fourier method based on fourth-order Runge–Kutta.
3. Numerical Results
This section reports the numerical results of gap soliton clusters of two types, which we call equal-height type and dipole. The formation, structural property, and dynamics of these gap soliton clusters are presented. For the sake of discussion, we focus our attention on just four-peak gap soliton clusters; obviously, the extension to such gap soliton clusters but with more peaks is natural. On the other hand, while we here only report the numerical results for optical lattices with moderate strength, it is straightforward to introduce the deep optical lattices and consider the gap soliton molecules and clusters therein.
3.1. Gap Soliton Clusters of Equal-Height Type
The simplest type of soliton clusters consists of identical solitons with equal height. For convenience, the structures of identical solitons are called (1, 1, 1, 1)-type solitons, where all branches of U are located on the upper-half plane of (, U). The adjacent distance between the identical solitons is adjustable and tuned to an integer that is a multiple of the lattice period that is set to for the given optical lattice with . After performing a great many numerical simulations, we identify the stability regions, expressed by power P versus propagation constant b, of such gap soliton clusters with two different spatial distances and in Figure 1c,d, demonstrating the instability of soliton clusters near the edge of finite gaps and that the former case is always unstable when being created in the second finite gap, although the stability region for the latter contracts sharply. Note that the stability and instability regions for (1, 1, 1, 1)-type gap soliton clusters in Figure 1c,d are, respectively, marked by blue solid and red dashed lines. The shapes of the stable and unstable (1, 1, 1, 1)-type gap soliton clusters (labeled by A and B in Figure 1c) are shown in Figure 2a,b by simulating Equation (2) via MSOM, which resemble a novel type of gap mode called gap waves or truncated nonlinear Bloch waves [22,68,69,70]. Increasing the adjacent distance , as depicted in Figure 2c,d (labeled by C and D in Figure 1d), each soliton of the gap soliton clusters could be considered as a fundamental gap soliton, and the interaction or tunneling between each soliton becomes weak. The orange solid lines in Figure 2a–d denote the shape of the optical lattice. The middle line of Figure 2 depicts the eigenvalue spectra of these four gap soliton clusters obtained by means of linear stability analysis via solving the eigenvalue problem (Equation (3)). We show that of the second mode (Figure 2b) with , and is nonzero, which indicates the mode is unstable. Meanwhile, the other modes (Figure 2a,c,d) are stable due to their corresponding real parts of eigenvalue being zero. We then turn to utilize the direct perturbed simulation to integrate Equation (1) for investigating the dynamical propagation of gap modes. The results displayed in the bottom line of Figure 2 are identical to the eigenvalue problem. Particularly, the unstable one in Figure 2j diverges and oscillates, and the stable ones in Figure 2i,k,l keep their shapes unchanged in the course of evolution.
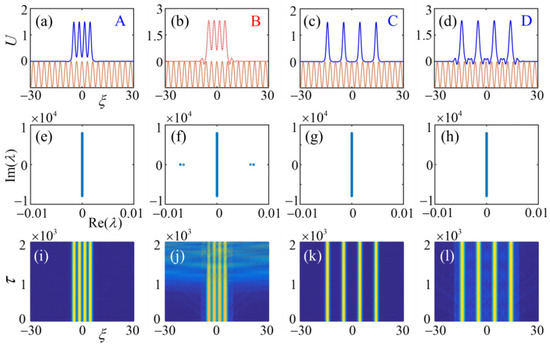
Figure 2.
Profiles, eigenvalues, and perturbed evolutions of equal-height type (or (1, 1, 1, 1)-type) gap soliton clusters modes. Profiles of (1, 1, 1, 1)-type gap soliton clusters modes obtained by simulating Equation (2) via MSOM, with different propagation constants b: (a) and (b) marked as (A, B) in Figure 1c, and (c) and (d) marked as (C, D) in Figure 1d. The blue solid lines, red dashed line, and orange solid lines in panels (a–d) respectively denote the stable profiles, unstable profile, and shape of optical lattice. Panels (e–l) show the corresponding eigenvalues and perturbed evolutions of the equal-height type gap soliton clusters exhibited in panels (a–d). The eigenvalue spectra and the perturbed dynamical propagation of these gap soliton clusters modes are matched well.
3.2. Dipole-Type Gap Soliton Clusters
The second type of gap soliton clusters is the composite pattern consisting of dipole gap solitons, i.e., two branches of U are located on the down half plane of (, U). In their forms, the dipole-type gap soliton clusters can be made as (1, 1, −1, −1)-type or (1, −1, 1, −1)-type ones. The stability regions, dependence , for the dipole-type gap soliton clusters of both forms with spatial distance are displayed in Figure 3a (for (1, 1, −1, −1)-type mode) and Figure 3d (for (1, −1, 1, −1)-type mode), respectively. We find that the power P of (1, 1, −1, −1)-type and (1, −1, 1, −1)-type localized gap modes decrease with propagation constant b, which obey satisfies the well-known anti-Vakhitov–Kolokolov criterion, , a necessary but not sufficient condition for stable solitons supported by defocusing nonlinearity. Here, the blue solid and red dashed lines in Figure 3a,d, respectively, indicate the stability and instability regions for dipole-type gap soliton clusters. By adopting MSOM to simulate Equation (2), the stable and unstable shapes of (1, 1, −1, −1)-type gap soliton clusters are shown in Figure 3b,c, which are labeled by E and F in Figure 3a, and the profiles of (1, −1, 1, −1)-type gap soliton clusters labeled by G and H in Figure 3d are shown in Figure 3e,f.
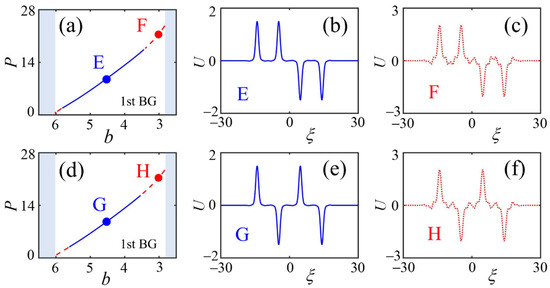
Figure 3.
(a,d), respectively, represent the power P of (1, 1, −1, −1)-type and (1, −1, 1, −1)-type localized gap modes versus propagation constant b with spatial distance in the first finite gap. (b,e) and (c,f) are, respectively, the corresponding profiles of the marked points (E, G) and (F, H) by simulating Equation (2) via MSOM. Note that the blue solid and red dashed lines in all panels, respectively, indicate the stable and unstable dipole-type gap soliton clusters modes.
We emphasize that the stable dipole-type gap soliton clusters of both forms could only be prepared within the first finite gap of the underlying linear Bloch spectra, compared to their equal-height type in Figure 1d where the existence of stable gap soliton clusters is also within the second finite gap. In the top line of Figure 4, we have shown the corresponding linear stability eigenvalue spectra of these four soliton clusters. The real parts of the eigenvalue, i.e., , for stable gap modes of marked points (E, G) with are zero, while for unstable gap modes of marked points (F, H) with , they are nonzero. Utilizing the direct perturbed simulation to integrate Equation (1), the evolutional dynamical propagation of the corresponding gap modes is depicted in the bottom line of Figure 4, where it is seen that an agreement is once again made between the both. For stable gap soliton clusters, their shapes and amplitudes remain constant during a long-time evolution, while the unstable ones in Figure 4f,h diverge and oscillate, which behave as the equal-height type in Figure 2j.
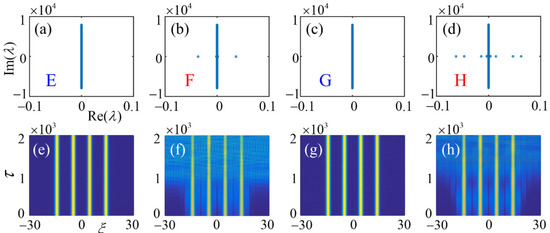
Figure 4.
Eigenvalues and perturbed evolutions of (1, 1, −1, −1)-type and (1, −1, 1, −1)-type gap soliton clusters modes. (a–d) display the eigenvalues of (1, 1, −1, −1)-type and (1, −1, 1, −1)-type gap soliton clusters shown in Figure 3b,c,e,f by solving the eigenvalue Equation (3) with the Fourier collocation method. Panels (e–h) are the corresponding perturbed evolutions by utilizing the direct perturbed simulation to integrate Equation (1). The stable gap soliton clusters keep their shapes and amplitudes unchanged during a long-time evolution, while the unstable ones diverge and oscillate.
4. Conclusions
In this article, using numerical ways relying on linear stability analysis and direct simulations, we have revealed briefly the existence, structural property, and perturbed dynamics of one-dimensional gap soliton molecules and clusters loaded onto optical lattice-trapped coherently atoms ensembles working on the electromagnetically induced transparency regime, and in the framework of generalized nonlinear Schrödinger equation. We find that both the equal-height and dipole types of gap soliton molecules and clusters could be formed in such a physical setting, and they are mostly stable within the first finite gap of the underlying linear Bloch-wave spectrum. Strikingly, the spatial distance between each adjacent peak of the soliton clusters could be tuned to an integer multiple of the spatial period of optical lattices; with a larger distance, the stability expands. Our linear stability analysis results agree well with the results produced by direct perturbed simulations. We are optimistic to believe that the gap soliton molecules and clusters predicted here may be readily observed in ultracold atom experiments, providing detailed insight into higher-order localized gap modes of coherent atomic gas and laying the foundation for their promising applications in optical communications and quantum information processing.
The natural extension of this article includes the consideration of other types of gap soliton clusters with more peaks or wider spatial distance , and in two-component coupled equations. It is an obvious theme to investigate the appearance of gap soliton molecules and clusters as well as gap vortex soliton clusters in a similar model but with two-dimensional spatial coordinates. For the experimental observation, the one-dimensional soliton molecules and clusters can also be observed in the context of nonlinear optics for nonlinear laser light propagation through photonic crystals and fiber Bragg gratings.
Author Contributions
Conceptualization, Z.C. and H.X.; methodology, Z.C. and Q.Z.; software, Z.C. and J.Z.; validation, Z.C., H.X., Q.Z. and J.Z.; formal analysis, Z.C., H.X., and J.Z.; investigation, Z.C., H.X., Q.Z., and J.Z.; resources, Z.C. and J.Z.; data curation, Z.C., Q.Z., and J.Z.; writing—original draft preparation, Z.C. and J.Z.; writing—review and editing, Z.C., H.X., Q.Z. and J.Z.; visualization, Z.C. and J.Z.; supervision, J.Z.; project administration, J.Z.; funding acquisition, Z.C., H.X. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (12264002, 12074423, 12074063, and 12264003), the Jiangxi Provincial Natural Science Foundation (20202BABL211013, 20232BAB201041, and 20232ACB211007), and the Young Scholar of Chinese Academy of Sciences in western China (XAB2021YN18).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chiao, R.Y.; Garmire, E.; Townes, C.H. Self-trapping of optical beams. Phys. Rev. Lett. 1964, 13, 479–482. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Agrawal, G.P. Optical Solitons: From Fibers to Photonic Crystals; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Malomed, B.A. Multidimensional Solitons, 1st ed.; AIP Publishing (Online): New York, NY, USA, 2022. [Google Scholar]
- Malomed, B.A.; Mihalache, D. Nonlinear waves in optical and matter-wave media: A topical survey of recent theoretical and experimental results. Rom. J. Phys. 2019, 64, 106. [Google Scholar]
- Mihalache, D. Localized structures in optical and matter-wave media: A selection of recent studies. Rom. Rep. Phys. 2021, 73, 403. [Google Scholar]
- Wang, W.; Wang, L.; Zhang, W. Advances in soliton microcomb generation. Adv. Photon. 2020, 2, 034001. [Google Scholar] [CrossRef]
- Rozenman, G.G.; Shemer, L.; Arie, A. Observation of accelerating solitary wavepackets. Phys. Rev. E 2020, 101, 050201. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Chen, H.-J.; Wang, W.; Yao, L.; Wang, Y.; Yu, Y.; Little, B.E.; Chu, S.T.; Gong, Q.; Zhao, W.; et al. Synthesized soliton crystals. Nat. Commun. 2021, 12, 3179. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Yang, S.; Wang, J.; Li, L.; Bai, Z.; Wang, Y.; Lv, Z. Recent advance of emerging low-dimensional materials for vector soliton generation in fiber lasers. Mater. Today Phys. 2022, 23, 100622. [Google Scholar] [CrossRef]
- Rozenman, G.G.; Schleich, W.P.; Shemer, L.; Arie, A. Periodic wave trains in nonlinear media: Talbot revivals, Akhmediev breathers, and asymmetry breaking. Phys. Rev. Lett. 2022, 128, 214101. [Google Scholar] [CrossRef]
- Eiermann, B.; Anker, T.; Albiez, M.; Taglieber, M.; Treutlein, P.; Marzlin, K.P.; Oberthaler, M.K. Bright Bose-Einstein gap solitons of atoms with repulsive interaction. Phys. Rev. Lett. 2004, 92, 230401. [Google Scholar] [CrossRef]
- Morsch, O.; Oberthaler, M. Dynamics of Bose-Einstein condensates in optical lattices. Rev. Mod. Phys. 2006, 78, 179–215. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Torner, L. Solitons in nonlinear lattices. Rev. Mod. Phys. 2011, 83, 247–305. [Google Scholar] [CrossRef]
- Garanovich, I.L.; Longhi, S.; Sukhorukov, A.A.; Kivshar, Y.S. Light propagation and localization in modulated photonic lattices and waveguides. Phys. Rep. 2012, 518, 1–79. [Google Scholar] [CrossRef]
- Eckardt, A. Colloquium: Atomic quantum gases in periodically driven optical lattices. Rev. Mod. Phys. 2017, 89, 011004. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Astrakharchik, G.E.; Malomed, B.A.; Torner, L. Frontiers in multidimensional self-trapping of nonlinear fields and matter. Nat. Rev. Phys. 2019, 1, 185–197. [Google Scholar] [CrossRef]
- Panajotov, K.; Tlidi, M.; Song, Y.; Zhang, H. Discrete vector light bullets in coupled nonlinear cavities. Chaos Solitons Fractals 2022, 163, 112532. [Google Scholar] [CrossRef]
- Kengne, E.; Liu, W.-M.; Malomed, B.A. Spatiotemporal engineering of matter-wave solitons in Bose-Einstein condensates. Phys. Rep. 2021, 899, 1–62. [Google Scholar] [CrossRef]
- Huang, C.; Dong, L. Gap solitons in the nonlinear fractional Schrödinger equation with an optical lattice. Opt. Lett. 2016, 41, 5636–5639. [Google Scholar] [CrossRef]
- Huang, C.; Li, C.; Deng, H.; Dong, L. Gap Solitons in fractional dimensions with a quasi-periodic lattice. Ann. Phys. 2019, 531, 1900056. [Google Scholar] [CrossRef]
- Xie, J.; Zhu, X.; He, Y. Vector solitons in nonlinear fractional Schrödinger equations with parity-time-symmetric optical lattices. Nonlinear Dyn. 2019, 97, 1287–1294. [Google Scholar] [CrossRef]
- Zeng, L.; Zeng, J. Gap-type dark localized modes in a Bose-Einstein condensate with optical lattices. Adv. Photon. 2019, 1, 046004. [Google Scholar] [CrossRef]
- Zeng, L.; Zeng, J. Preventing critical collapse of higher-order solitons by tailoring unconventional optical diffraction and nonlinearities. Commun. Phys. 2020, 3, 26. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Zeng, J. Matter-wave gap solitons and vortices in three-dimensional parity-time-symmetric optical lattices. iScience 2022, 25, 104026. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zeng, J. Localized gap modes of coherently trapped atoms in an optical lattice. Opt. Express 2021, 29, 3011–3025. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zeng, J. Two-dimensional optical gap solitons and vortices in a coherent atomic ensemble loaded on optical lattices. Commun. Nonlinear Sci. Numer. Simulat. 2021, 102, 105911. [Google Scholar] [CrossRef]
- Chen, Z.; Zeng, J. Nonlinear localized modes in onedimensional nanoscale dark-state optical lattices. Nanophotonics 2022, 11, 3465–3474. [Google Scholar] [CrossRef]
- Kartashov, Y.V. Light bullets in moiré lattices. Opt. Lett. 2022, 47, 4528–4531. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wu, Z.; Zeng, J. Light gap bullets in defocusing media with optical lattices. Chaos Solitons Fractals 2023, 174, 113785. [Google Scholar] [CrossRef]
- Ye, F.; Kartashov, Y.V.; Hu, B.; Torner, L. Light bullets in Bessel optical lattices with spatially modulated nonlinearity. Opt. Express 2009, 17, 11328. [Google Scholar] [CrossRef]
- Hang, C.; Huang, G. Stern-Gerlach effect of weak-light ultraslow vector solitons. Phys. Rev. A 2012, 86, 043809. [Google Scholar] [CrossRef]
- Hang, C.; Konotop, V.V.; Huang, G. Spatial solitons and instabilities of light beams in a three-level atomic medium with a standing-wave control field. Phys. Rev. A 2009, 79, 033826. [Google Scholar] [CrossRef]
- Dong, L.; Kartashov, Y.V.; Torner, L.; Ferrando, A. Vortex Solitons in Twisted Circular Waveguide Arrays. Phys. Rev. Lett. 2022, 129, 123903. [Google Scholar] [CrossRef]
- Huang, C.; Ye, F.; Chen, X.; Kartashov, Y.V.; Konotop, V.V.; Torner, L. Localization-delocalization wavepacket transition in Pythagorean aperiodic potentials. Sci. Rep. 2016, 6, 32546. [Google Scholar] [CrossRef]
- Wang, P.; Zheng, Y.; Chen, X.; Huang, C.; Kartashov, Y.V.; Torner, L.; Konotop, V.V.; Ye, F. Localization and delocalization of light in photonic moiré lattices. Nature 2020, 577, 42–46. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, X.; Zeng, J. Electromagnetically induced moire optical lattices in a coherent atomic gas. Front. Phys. 2022, 17, 42508. [Google Scholar] [CrossRef]
- Mao, X.R.; Shao, Z.K.; Luan, H.Y.; Wang, S.L.; Ma, R.M. Magic-angle lasers in nanostructured moiré superlattice. Nat. Nanotechnol. 2021, 16, 1099. [Google Scholar] [CrossRef]
- González-Tudela, A.; Cirac, J.I. Cold atoms in twistedbilayer optical potentials. Phys. Rev. A 2019, 100, 053604. [Google Scholar] [CrossRef]
- Fu, Q.; Wang, P.; Huang, C.; Kartashov, Y.V.; Torner, L.; Konotop, V.V.; Ye, F. Optical soliton formation controlled by angle twisting in photonic moiré lattices. Nat. Photon. 2020, 14, 663–668. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Ye, F.; Konotop, V.V.; Torner, L. Multifrequency Solitons in Commensurate-Incommensurate Photonic Moiré Lattices. Phys. Rev. Lett. 2021, 127, 163902. [Google Scholar] [CrossRef]
- Arkhipova, A.A.; Kartashov, Y.V.; Ivanov, S.K.; Zhuravitskii, S.A.; Skryabin, N.N.; Dyakonov, I.V.; Kalinkin, A.A.; Kulik, S.P.; Kompanets, V.O.; Chekalin, S.V.; et al. Observation of Linear and Nonlinear Light Localization at the Edges of Moiré Arrays. Phys. Rev. Lett. 2023, 130, 083801. [Google Scholar] [CrossRef]
- Ivanov, S.K.; Konotop, V.V.; Kartashov, Y.V.; Torner, L. Vortex solitons in moire optical lattices. Opt. Lett. 2023, 48, 3797–3800. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zeng, J. Gap solitons in parity-time symmetric moiré optical lattices. Photonics Res. 2023, 11, 196–202. [Google Scholar] [CrossRef]
- Malomed, B.A. Optical Solitons and Vortices in Fractional Media: A Mini-Review of Recent Results. Photonics 2021, 8, 353. [Google Scholar] [CrossRef]
- Liu, X.; Yao, X.; Cui, Y. Real-Time Observation of the Buildup of Soliton Molecules. Phys. Rev. Lett. 2018, 121, 023905. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Nithyanandan, K.; Coillet, A.; Tchofo-Dinda, P.; Grelu, P. Optical soliton molecular complexes in a passively mode-locked fibre laser. Nat. Commun. 2019, 10, 830. [Google Scholar] [CrossRef]
- Zhu, W.; He, Y.; Malomed, B.A.; Mihalache, D. Two-dimensional solitons and clusters in dissipative lattices. J. Opt. Soc. Am. B 2014, 31, A1–A5. [Google Scholar] [CrossRef]
- Zeng, L.; Zeng, J. Modulated solitons, soliton and vortex clusters in purely nonlinear defocusing media. Ann. Phys. 2020, 421, 168284. [Google Scholar] [CrossRef]
- Qin, L.; Hang, C.; Malomed, B.A.; Huang, G. Stable High-Dimensional Weak-Light Soliton Molecules and Their Active Control. Laser Photon. Rev. 2022, 16, 2100297. [Google Scholar] [CrossRef]
- Zhong, M.; Yan, Z. Formation of multi-peak gap solitons and stable excitations for double-Lévy-index and mixed fractional NLS equations with optical lattice potentials. Proc. R. Soc. A 2023, 479, 20230222. [Google Scholar] [CrossRef]
- Lee, T.D.; Huang, K.; Yang, C.N. Eigenvalues and Eigenfunctions of a Bose System of Hard Spheres and Its Low-Temperature Properties. Phys. Rev. 1957, 106, 1135–1145. [Google Scholar] [CrossRef]
- Petrov, D.S. Quantum Mechanical Stabilization of a Collapsing Bose-Bose Mixture. Phys. Rev. Lett. 2015, 115, 155302. [Google Scholar] [CrossRef]
- Dong, L.; Kartashov, Y.V. Rotating Multidimensional Quantum Droplets. Phys. Rev. Lett. 2021, 126, 244101. [Google Scholar] [CrossRef]
- Ma, Y.; Peng, C.; Cui, X. Borromean Droplet in Three-Component Ultracold Bose Gases. Phys. Rev. Lett. 2021, 127, 043002. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Malomed, B.A.; Torner, L. Metastability of Quantum Droplet Clusters. Phys. Rev. Lett. 2019, 122, 193902. [Google Scholar] [CrossRef]
- Desyatnikov, A.S.; Kivshar, Y.S. Rotating Optical Soliton Clusters. Phys. Rev. Lett. 2002, 88, 053901. [Google Scholar] [CrossRef]
- Herink, G.; Kurtz, F.; Jalali, B.; Solli, D.R.; Ropers, C. Real-time spectral interferometry probes the internal dynamics of femtosecond soliton molecules. Science 2017, 356, 50. [Google Scholar] [CrossRef]
- Song, L.; Yang, Z.; Li, X.; Zhang, S. Controllable Gaussian-shaped soliton clusters in strongly nonlocal media. Opt. Express 2018, 26, 19182–19198. [Google Scholar] [CrossRef]
- Zeng, L.; Belić, M.R.; Mihalache, D.; Shi, J.; Li, J.; Li, S.; Lu, X.; Cai, Y.; Li, J. Families of gap solitons and their complexes in media with saturable nonlinearity and fractional diffraction. Nonlinear Dyn. 2022, 108, 1671–1680. [Google Scholar] [CrossRef]
- Reyna, A.S.; Baltar, H.T.M.C.M.; Bergmann, E.; Amaral, A.M.; Falcão-Filho, E.L.; Brevet, P.-F.; Malomed, B.A.; de Araújo, C.B. Observation and analysis of creation, decay, and regeneration of annular soliton clusters in a lossy cubic-quintic optical medium. Phys. Rev. A 2020, 102, 033523. [Google Scholar] [CrossRef]
- Weng, W.; Bouchand, R.; Lucas, E.; Obrzud, E.; Herr, T.; Kippenberg, T.J. Heteronuclear soliton molecules in optical microresonators. Nat. Commun. 2020, 11, 2402. [Google Scholar] [CrossRef]
- Kurtz, F.; Ropers, C.; Herink, G. Resonant excitation and all-optical switching of femtosecond soliton molecules. Nat. Photonics 2020, 14, 9. [Google Scholar] [CrossRef]
- Wang, Q.; Liang, G. Vortex and cluster solitons in nonlocal nonlinear fractional Schrödinger equation. J. Opt. 2020, 22, 055501. [Google Scholar] [CrossRef]
- Fleischhauer, M.; Imamoǧlu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. [Google Scholar] [CrossRef]
- Huang, G.; Deng, L.; Payne, M.G. Dynamics of ultraslow optical solitons in a cold three-state atomic system. Phys. Rev. E 2005, 72, 016617. [Google Scholar] [CrossRef]
- Steck, D.A. Rubidium 87 D Line Data. Revision 2.2.2. Available online: http://steck.us/alkalidata (accessed on 9 July 2021).
- Yang, J. Nonlinear Waves in Integrable and Nonintegrable Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2010. [Google Scholar]
- Anker, T.; Albiez, M.; Gati, R.; Hunsmann, S.; Eiermann, B.; Trombettoni, A.; Oberthaler, M.K. Nonlinear self-trapping of matter waves in periodic potentials. Phys. Rev. Lett. 2005, 94, 020403. [Google Scholar] [CrossRef]
- Alexander, T.J.; Ostrovskaya, E.A.; Kivshar, Y.S. Self-trapped nonlinear matter waves in periodic potentials. Phys. Rev. Lett. 2006, 96, 040401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wu, B. Composition relation between gap solitons and bloch waves in nonlinear periodic systems. Phys. Rev. Lett. 2009, 102, 093905. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).