3D Optical Wedge and Movable Optical Axis LC Lens
Abstract
:1. Introduction
2. Principle
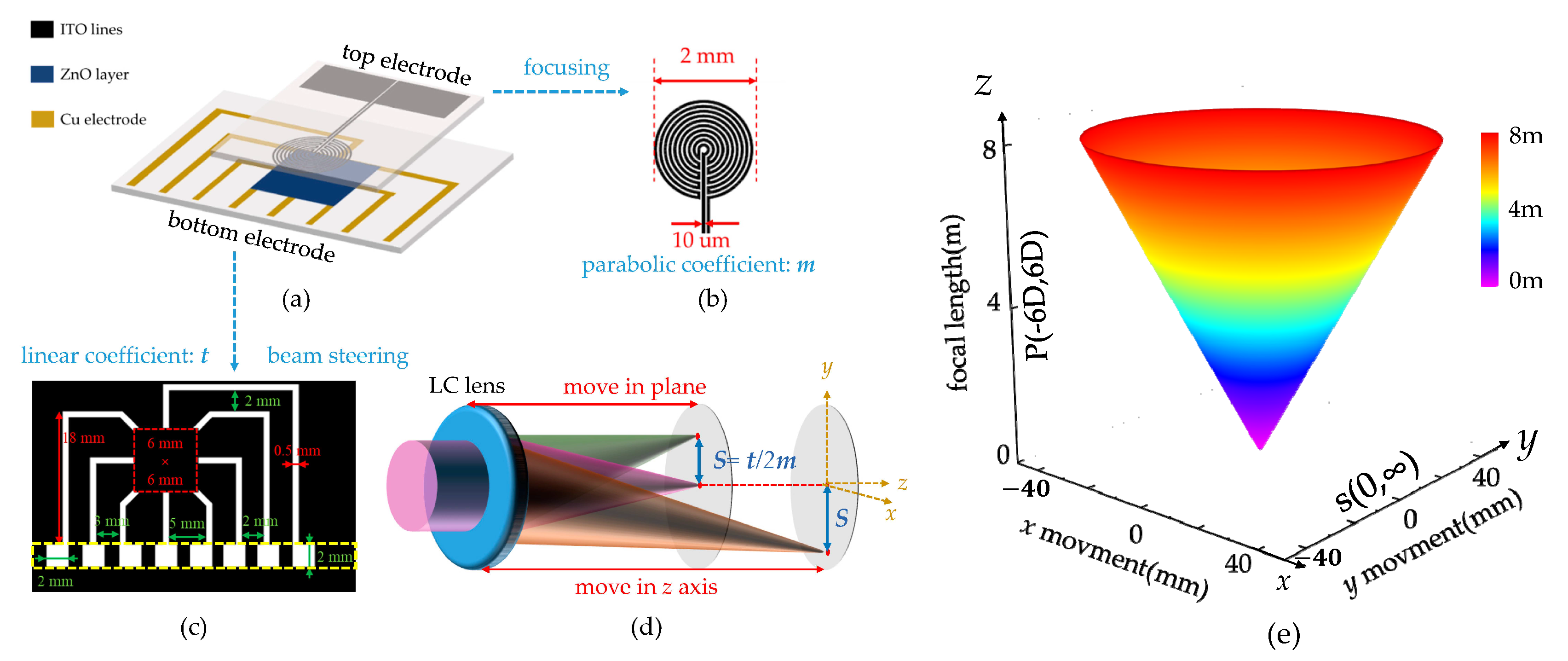
2.1. Electrode Structure and Process
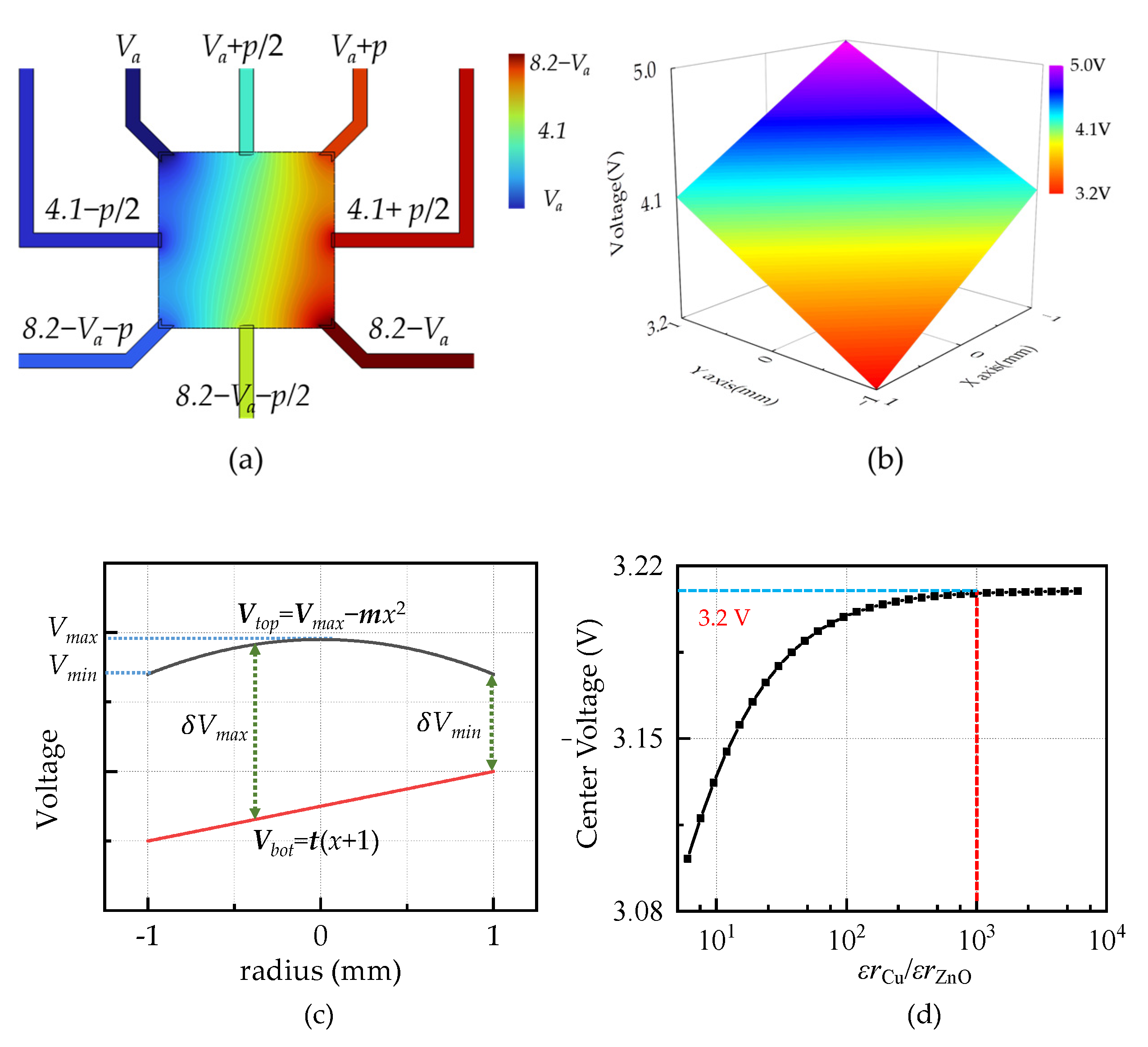
2.2. Function and Working Principle
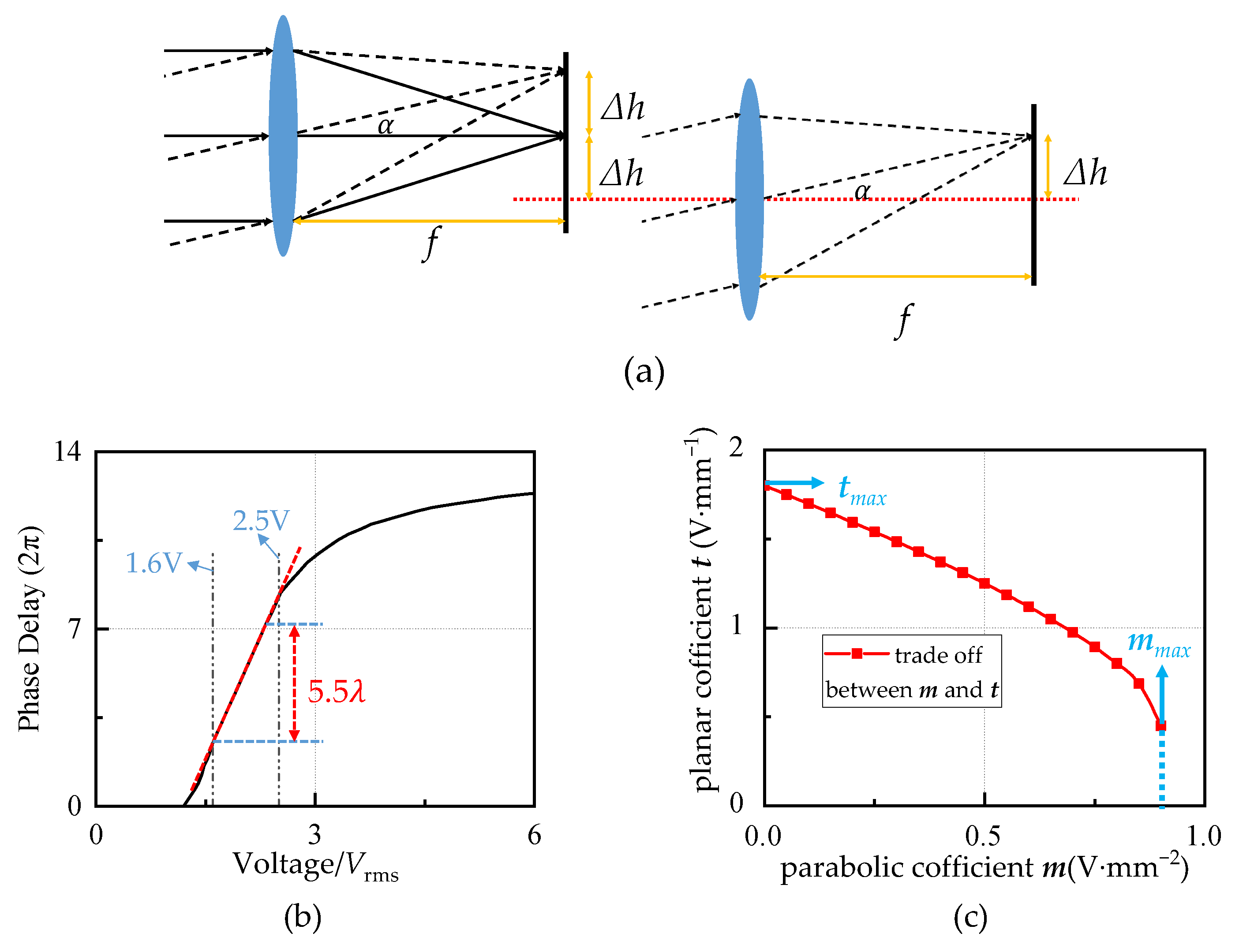
2.3. Driving Voltage Condition
3. Experiment and Result
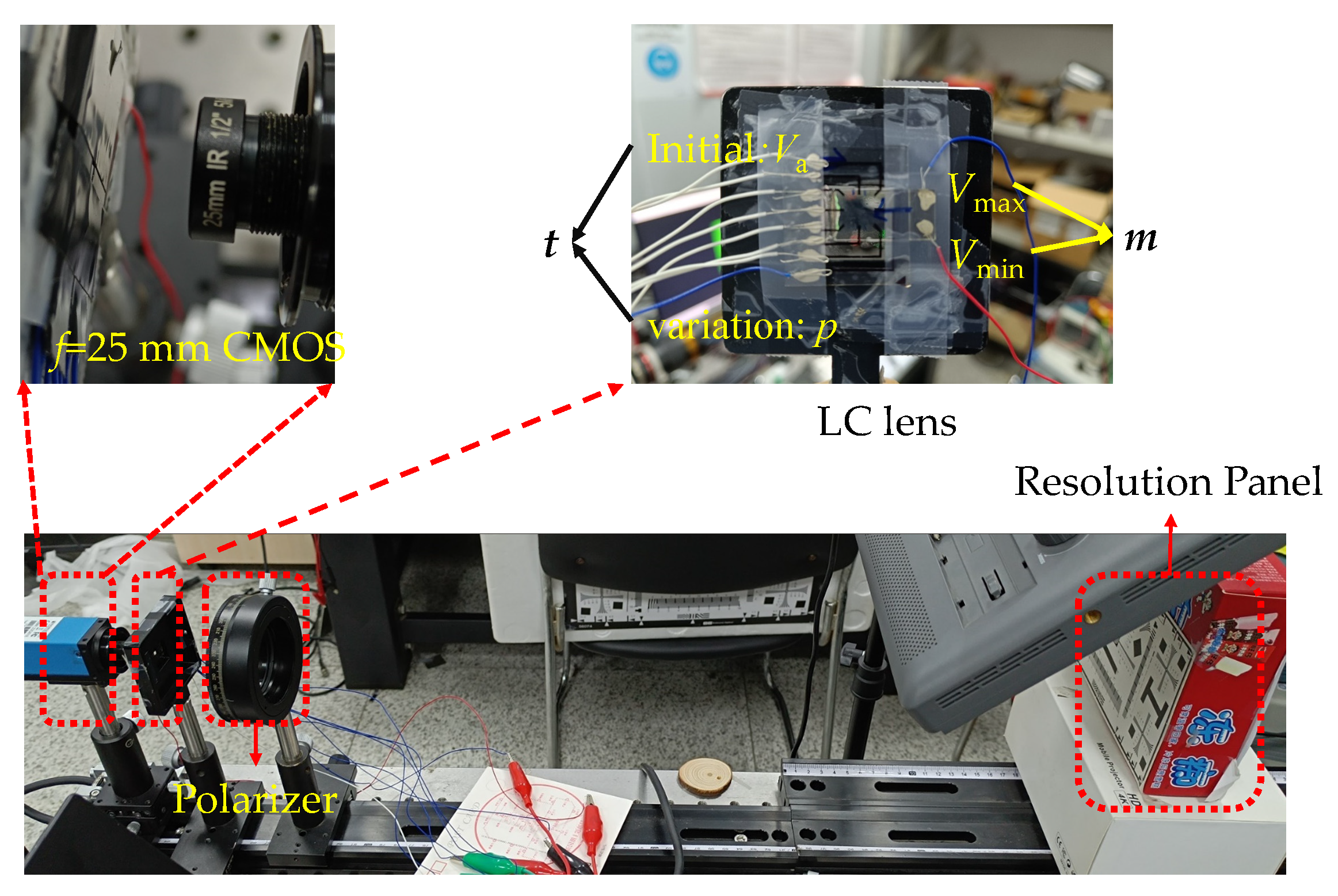
3.1. Experimental Setup
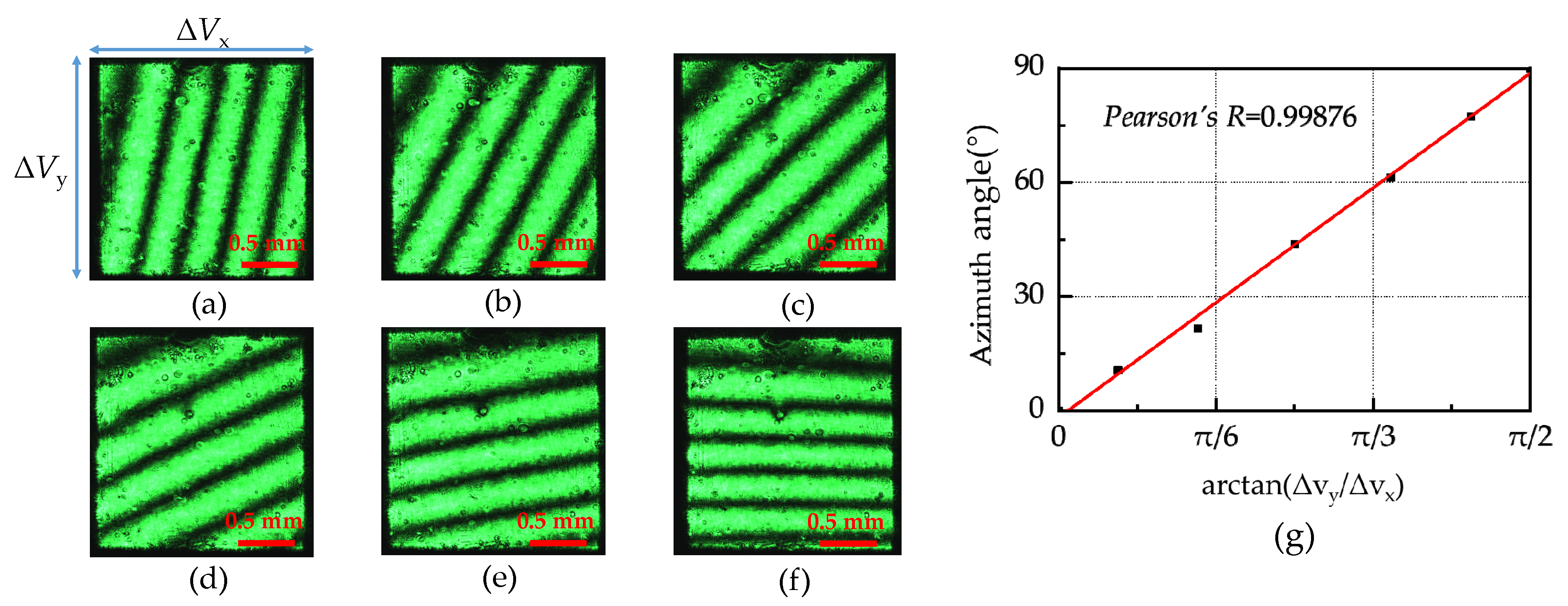
3.2. Analysis of Light Deflection Experiment
3.3. Analysis of Off-Axis Focusing Experiment
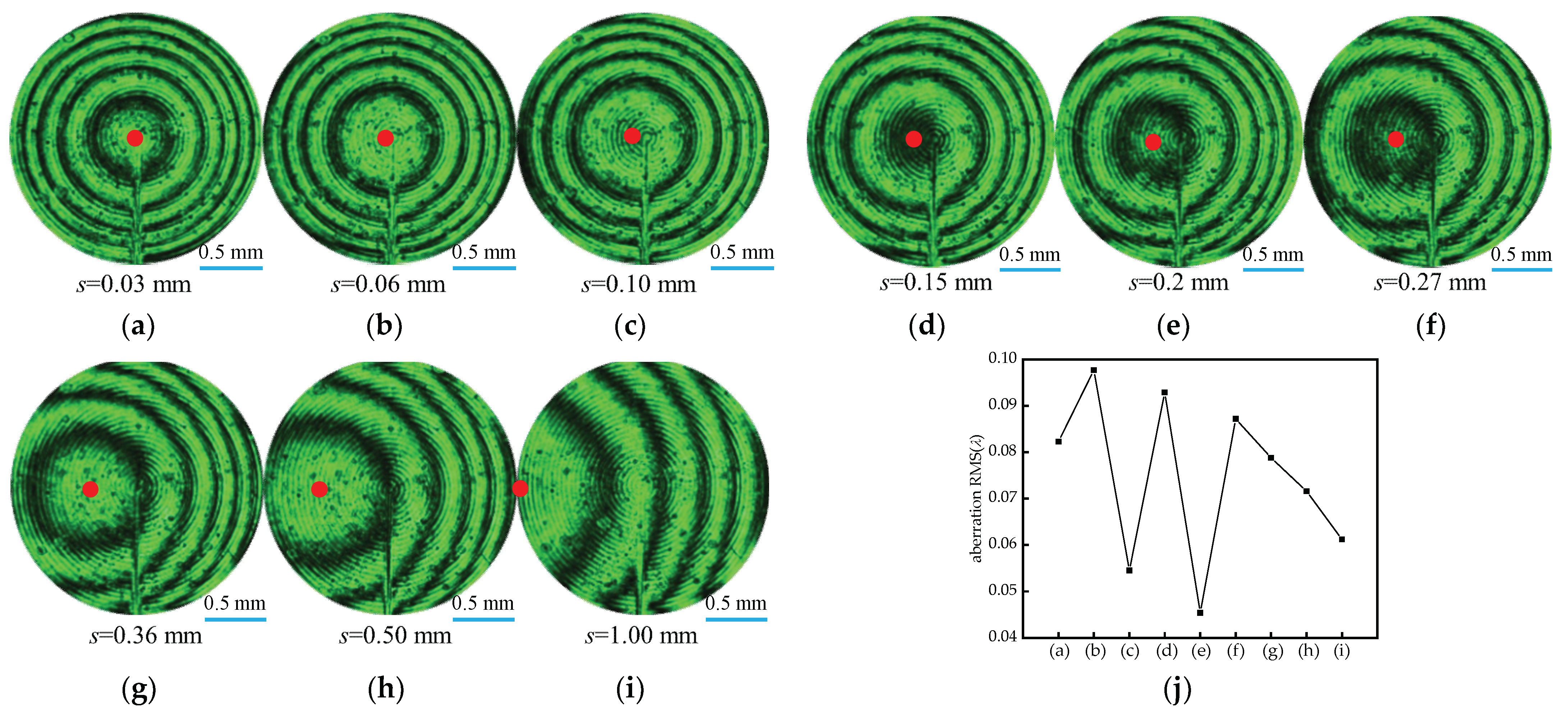
3.3.1. m and t at the Critical Condition
3.3.2. Fixed m, Gradual t, Fixed Focal Length OAM Lens with Equal Movement
3.3.3. Changing m and t, Fixed OAM Lens with Changed Focal Length
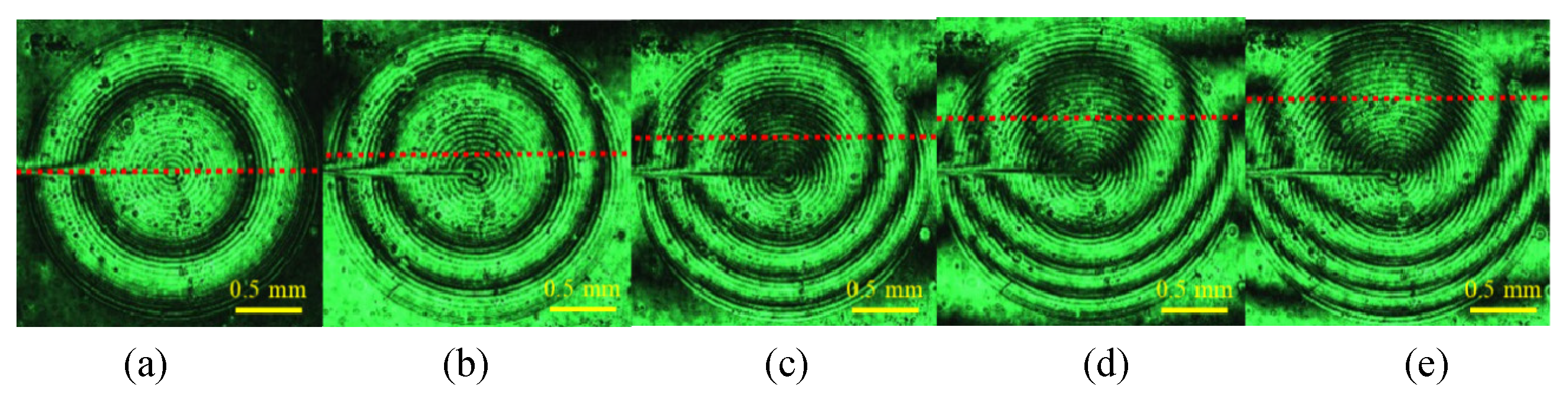
3.3.4. Fixed m and t, the OMA Lens Moves within the Aperture in Multiple Directions
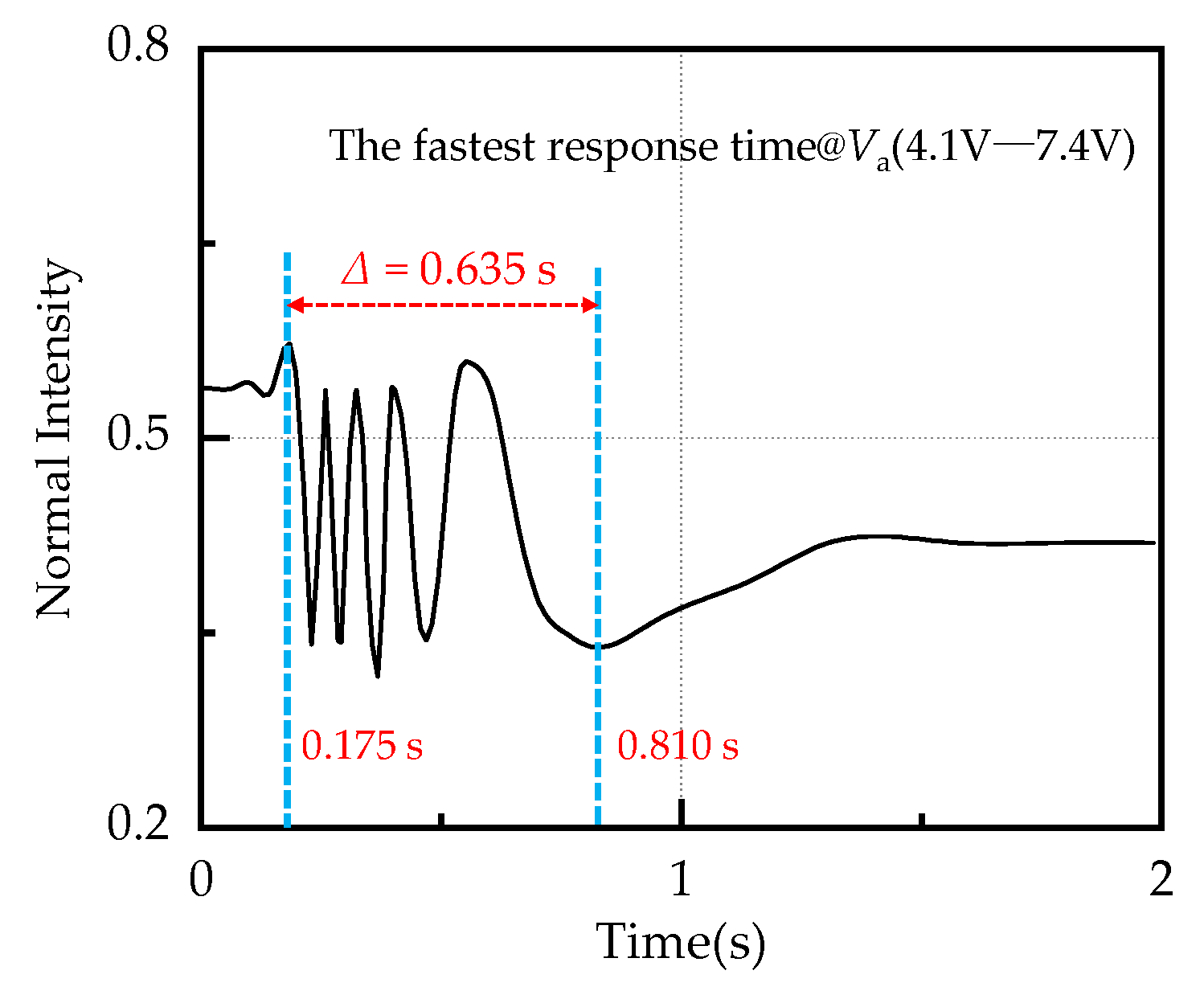
3.4. Phase Delay Response Time
4. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, M.; Feng, Y.; Wang, Y.; Huang, W.; Su, S. Design, Analysis and Experiment of a Bridge-Type Piezoelectric Actuator for Infrared Image Stabilization. Micromachines 2021, 12, 1197. [Google Scholar] [CrossRef] [PubMed]
- Bleier, B.J.; Yezer, B.A.; Freireich, B.J.; Anna, S.L.; Walker, L.M. Droplet-Based Characterization of Surfactant Efficacy in Colloidal Stabilization of Carbon Black in Nonpolar Solvents. J. Colloid Interface Sci. 2017, 493, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Karasikov, N.; Peled, G.; Yasinov, R.; Feinstein, A. Piezo-Based, High Dynamic Range, Wide Bandwidth Steering System for Optical Applications; Pham, T., Kolodny, M.A., Eds.; SPIE: Anaheim, CA, USA, 2017; p. 101901C. [Google Scholar]
- Zheng, Y.; Fu, Y.G.; He, W.J.; Wang, J.K.; Zhang, L. Opto-Mechanical Structure Design of the Image Stabilization Collimator. Key Eng. Mater. 2013, 552, 79–84. [Google Scholar] [CrossRef]
- Meng, Z.; Huang, W.; Zhang, L.; Zhou, X.; Zhao, K.; Pu, D.; Chen, L. Large Aperture and Defect-Free Liquid Crystal Planar Optics Enabled by High-Throughput Pulsed Polarization Patterning. Opt. Express 2023, 31, 30435. [Google Scholar] [CrossRef]
- Yoshida, S.; Schmid, W.; Vo, N.; Calabrase, W.; Kisley, L. Computationally-Efficient Spatiotemporal Correlation Analysis Super-Resolves Anomalous Diffusion. Opt. Express 2021, 29, 7616. [Google Scholar] [CrossRef]
- Sun, Z.; Yuan, Z.; Nikita, A.; Kwok, H.; Srivastava, A.K. Fast-Switchable, High Diffraction-Efficiency Ferroelectric Liquid Crystal Fibonacci Grating. Opt. Express 2021, 29, 13978. [Google Scholar] [CrossRef]
- Cheng, K.; Li, Z.; Wu, J.; Hu, Z.-D.; Wang, J. Super-Resolution Imaging Based on Radially Polarized Beam Induced Superoscillation Using an All-Dielectric Metasurface. Opt. Express 2022, 30, 2780. [Google Scholar] [CrossRef]
- Chen, H.; Yu, S. A Stereo Camera Tracking Algorithm Used in Glass-Free Stereoscopic Display System. J. Comput. -Aided Des. Comput. Graph. 2017, 29, 436–443. [Google Scholar]
- Li, R.; Zhang, H.; Chu, F.; Wang, Q. Compact Integral Imaging 2D/3D Compatible Display Based on Liquid Crystal Micro-Lens Array. Liq. Cryst. 2022, 49, 512–522. [Google Scholar] [CrossRef]
- Dong, J.; Li, Z.; Liu, X.; Zhong, W.; Wang, G.; Liu, Q.; Song, X. High-Speed Real 3D Scene Acquisition and 3D Holographic Reconstruction System Based on Ultrafast Optical Axial Scanning. Opt. Express 2023, 31, 21721. [Google Scholar] [CrossRef]
- Juodkazis, S.; Shikata, M.; Takahashi, T.; Matsuo, S.; Misawa, H. Fast Optical Switching by a Laser-Manipulated Microdroplet of Liquid Crystal. Appl. Phys. Lett. 1999, 74, 3627–3629. [Google Scholar] [CrossRef]
- Kawamura, M.; Ye, M.; Sato, S. Optical Tweezers System by Using a Liquid Crystal Optical Device. Mol. Cryst. Liq. Cryst. 2007, 478, 135–891. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, H.; Jia, D.; Liu, T. Recent Development of Tunable Optical Devices Based on Liquid. Molecules 2022, 27, 8025. [Google Scholar] [CrossRef] [PubMed]
- Maksymova, I.; Greiner, P.; Wiesmeier, J.; Darrer, F.M.; Druml, N. A MEMS Mirror Driver ASIC for Beam-Steering in Scanning MEMS-Based LiDAR. In Proceedings of the Laser Beam Shaping XIX, San Diego, CA, USA, 11–12 August 2019; Dudley, A., Laskin, A.V., Eds.; SPIE: San Diego, CA, USA, 2019; p. 11. [Google Scholar]
- Galaktionov, I.; Kudryashov, A.; Sheldakova, J.; Nikitin, A. Laser Beam Focusing through the Dense Multiple Scattering Suspension Using Bimorph Mirror. In Proceedings of the Adaptive Optics and Wavefront Control for Biological Systems V, San Diego, CA, USA, 3–4 February 2019; Bifano, T.G., Gigan, S., Ji, N., Eds.; SPIE: San Francisco, CA, USA, 2019; p. 44. [Google Scholar]
- Wlodarczyk, K.L.; Bryce, E.; Schwartz, N.; Strachan, M.; Hutson, D.; Maier, R.R.J.; Atkinson, D.; Beard, S.; Baillie, T.; Parr-Burman, P.; et al. Scalable Stacked Array Piezoelectric Deformable Mirror for Astronomy and Laser Processing Applications. Rev. Sci. Instrum. 2014, 85, 024502. [Google Scholar] [CrossRef]
- Verpoort, S.; Wittrock, U. Unimorph Deformable Mirror for Telescopes and Laser Applications. In Proceedings of the International Conference on Space Optics—ICSO 2010, Rhodes Island, Greece, 4–8 October 2010; Armandillo, E., Cugny, B., Karafolas, N., Eds.; SPIE: Rhodes Island, Greece, 2019; p. 527. [Google Scholar]
- Salter, P.S.; Booth, M.J. Adaptive Optics in Laser Processing. Light Sci. Appl. 2019, 8, 10. [Google Scholar] [CrossRef]
- Nose, T.; Sato, S. A Liquid Crystal Microlens Obtained with a Non-Uniform Electric Field. Liq. Cryst. 1989, 5, 1425–1433. [Google Scholar] [CrossRef]
- Morris, R.; Jones, C.; Nagaraj, M. Liquid Crystal Devices for Beam Steering Applications. Micromachines 2021, 12, 247. [Google Scholar] [CrossRef]
- He, Z.; Gou, F.; Chen, R.; Yin, K.; Zhan, T.; Wu, S.-T. Liquid Crystal Beam Steering Devices: Principles, Recent Advances, and Future Developments. Crystals 2019, 9, 292. [Google Scholar] [CrossRef]
- Sato, S. Applications of Liquid Crystals to Variable-Focusing Lenses. Opt. Rev. 1999, 6, 471–485. [Google Scholar] [CrossRef]
- Reshetnyak, V.Y.; Sova, O.; Wang, Y.-J.; Lin, Y.-H. Modeling Liquid Crystal Lenses. In Proceedings of the Emerging Liquid Crystal Technologies XV, San Diego, CA, USA, 3–5 February 2020; Chien, L.-C., Broer, D.J., Eds.; SPIE: San Francisco, CA, USA, 2020; p. 3. [Google Scholar]
- Love, G.D.; Major, J.V.; Purvis, A. Liquid-Crystal Prisms for Tip-Tilt Adaptive Optics. Opt. Lett. 1994, 19, 1170. [Google Scholar] [CrossRef]
- Hands, P.J.W.; Tatarkova, S.A.; Kirby, A.K.; Love, G.D. Modal Liquid Crystal Devices in Optical Tweezing: 3D Control and Oscillating Potential Wells. Opt. Express 2006, 14, 4525. [Google Scholar] [CrossRef] [PubMed]
- Kotova, S.P.; Patlan, V.V.; Samagin, S.A. Tunable Liquid-Crystal Focusing Device. 2. Experiment. Quantum Electron. 2011, 41, 65–70. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, Y.; Liu, Z.; Ye, M. Driving Method for Adjustable Liquid Crystal Optical Wedge with Four Electrodes. Acta Opt. Sin. 2022, 42, 1323001. [Google Scholar] [CrossRef]
- Ye, M.; Sato, S. Liquid Crystal Lens with Focus Movable along and off Axis. Opt. Commun. 2003, 225, 277–280. [Google Scholar] [CrossRef]
- Ye, M.; Wang, B.; Sato, S. Liquid Crystal Lens with Focus Movable in Focal Plane. Opt. Commun. 2006, 259, 710–722. [Google Scholar] [CrossRef]
- Ye, M.; Wang, B.; Uchida, M.; Yanase, S.; Takahashi, S.; Yamaguchi, M.; Sato, S. Low-Voltage-Driving Liquid Crystal Lens. Jpn. J. Appl. Phys. 2010, 49, 100204. [Google Scholar] [CrossRef]
- Bennis, N.; Jankowski, T.; Strzezysz, O.; Pakuła, A.; Zografopoulos, D.C.; Perkowski, P.; Sánchez-Pena, J.M.; López-Higuera, J.M.; Algorri, J.F. A High Birefringence Liquid Crystal for Lenses with Large Aperture. Sci. Rep. 2022, 12, 14603. [Google Scholar] [CrossRef]
- Bennis, N.; Jankowski, T.; Morawiak, P.; Spadlo, A.; Zografopoulos, D.C.; Sánchez-Pena, J.M.; López-Higuera, J.M.; Algorri, J.F. Aspherical Liquid Crystal Lenses Based on a Variable Transmission Electrode. Opt. Express 2022, 30, 12237. [Google Scholar] [CrossRef]
- Algorri, J.F.; Love, G.D.; Urruchi, V. Modal Liquid Crystal Array of Optical Elements. Opt. Express 2013, 21, 24809. [Google Scholar] [CrossRef]
- Algorri, J.F.; Morawiak, P.; Zografopoulos, D.C.; Bennis, N.; Spadlo, A.; Rodríguez-Cobo, L.; Jaroszewicz, L.R.; Sánchez-Pena, J.M.; López-Higuera, J.M. Multifunctional Light Beam Control Device by Stimuli-Responsive Liquid Crystal Micro-Grating Structures. Sci. Rep. 2020, 10, 13806. [Google Scholar] [CrossRef]
- Algorri, J.F.; Morawiak, P.; Bennis, N.; Zografopoulos, D.C.; Urruchi, V.; Rodríguez-Cobo, L.; Jaroszewicz, L.R.; Sánchez-Pena, J.M.; López-Higuera, J.M. Positive-Negative Tunable Liquid Crystal Lenses Based on a Microstructured Transmission Line. Sci. Rep. 2020, 10, 10153. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Liu, Z.; Liu, H.; Ye, M. Design of Tunable Liquid Crystal Lenses with a Parabolic Phase Profile. Crystals 2022, 13, 8. [Google Scholar] [CrossRef]
- Cao, F.; Liu, Z.; Ye, M. Modulated Beam Deflection by Liquid Crystal Optical Wedge Arrays. Acta Opt. Sin. 2024, 44, 251–257. [Google Scholar] [CrossRef]
- Elston, S.J. Optics and Nonlinear Optics of Liquid Crystals. J. Mod. Opt. 1994, 41, 1517–1518. [Google Scholar] [CrossRef]
- Feng, W.; Liu, Z.; Ye, M. Positive-Negative Tunable Cylindrical Liquid Crystal Lenses. Optik 2022, 266, 169613. [Google Scholar] [CrossRef]
- Xu, S.; Li, Y.; Liu, Y.; Sun, J.; Ren, H.; Wu, S.-T. Fast-Response Liquid Crystal Microlens. Micromachines 2014, 5, 300–324. [Google Scholar] [CrossRef]
- Yang, D.-K.; Wu, S.-T. Fundamentals of Liquid Crystal Devices; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]





| (a) | (b) | (c) | (d) | (e) | (f) | |
|---|---|---|---|---|---|---|
| Va | 0.8 V | 0.8 V | 0.8 V | 0.8 V | 0.8 V | 0.8 V |
| p | 1.1 V | 2.2 | 3.3 | 4.4 | 5.5 | 6.6 |
| θa | 77.6 | 61.3 | 43.8 | 26.3 | 10.6 | 0 |
| θw | 0.17° | 0.17° | 0.17° | 0.17° | 0.17° | 0.17° |
| m (V·mm−2) | t (V·mm−1) | s (mm) | Sfigure (mm) | Va (V) |
|---|---|---|---|---|
| 1.70 | 0.10 | 0.029 | 0.03 | 3.73 |
| 1.59 | 0.20 | 0.063 | 0.07 | 3.37 |
| 1.48 | 0.30 | 0.101 | 0.11 | 3.00 |
| 1.37 | 0.40 | 0.146 | 0.16 | 2.63 |
| 1.25 | 0.50 | 0.200 | 0.22 | 2.27 |
| 1.12 | 0.60 | 0.268 | 0.27 | 1.90 |
| 0.97 | 0.70 | 0.361 | 0.38 | 1.53 |
| 0.45 | 0.80 | 0.500 | 0.52 | 1.17 |
| 0.45 | 0.90 | 1.000 | 0.98 | 0.80 |
| (a) | (b) | (c) | (d) | (e) | |
|---|---|---|---|---|---|
| Vmin (V) | 7.3 | 7.5 | 7.7 | 7.9 | 8.1 |
| Vmax (V) | 8.1 | 8.3 | 8.5 | 8.7 | 8.9 |
| m (V·mm−2) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| t (V·mm−1) | 0 | 0.2 | 0.4 | 0.17° | 0.17° |
| s (mm) | 0 | 0.125 | 0.250 | 0.375 | 0.500 |
| Sfigure (mm) | 0 | 0.126 | 0.251 | 3.780 | 0.495 |
| s (mm) | m (V·mm−2) | t (V·mm−1) | Va (V) |
|---|---|---|---|
| 0.25 | 0.40 | 0.20 | 3.37 |
| 0.60 | 0.30 | 3.00 | |
| 0.80 | 0.40 | 2.63 | |
| 1.00 | 0.50 | 2.27 | |
| 0.50 | 0.40 | 0.40 | 2.63 |
| 0.50 | 0.50 | 2.27 | |
| 0.60 | 0.60 | 1.90 | |
| 0.70 | 0.70 | 1.53 | |
| 1.00 | 0.30 | 0.60 | 1.90 |
| 0.35 | 0.70 | 1.53 | |
| 0.40 | 0.80 | 1.17 | |
| 0.45 | 0.90 | 0.80 |
| m (V·mm−2) | t (V·mm−1) | s (mm) | Vleftup (V) | p (V) | Azimuth Angle |
|---|---|---|---|---|---|
| 1.0 | 0.60 | 0.30 | 1.90 | 2.20 | 45° (left up) |
| 1.0 | 0.60 | 0.30 | 4.10 | 2.20 | 45° (left down) |
| 1.0 | 0.60 | 0.30 | 4.10 | 0 | 0° |
| 1.0 | 0.60 | 0.30 | 4.10 | 2.20 | 45° (right up) |
| 1.0 | 0.60 | 0.30 | 1.90 | 2.20 | 45° (right down) |
| LC Devices | Beam Deflectors | OAM Lens | Response Time | ||||
|---|---|---|---|---|---|---|---|
| Angle | Dimension | Thickness | Movement | Dimension | Aberration | ||
| Hands [26] | 0.024° | 3D | 50 μm | — | — | — | 2–3 s |
| Ye [13] | 0.1° | 2D | 130 μm | — | — | — | — |
| J.F.Algorri [35] | 0.008° | 2D | 50 μm | — | — | — | — |
| Feng [37] | — | — | 50 μm | 1.0 mm | 1D | 2–3 s | |
| This paper | 0.164° | 3D | 30 μm | 0~∞ (firstly) | 2D | 0.635–3 s | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Zhang, H.; Jia, D.; Liu, T. 3D Optical Wedge and Movable Optical Axis LC Lens. Crystals 2024, 14, 843. https://doi.org/10.3390/cryst14100843
Wu Q, Zhang H, Jia D, Liu T. 3D Optical Wedge and Movable Optical Axis LC Lens. Crystals. 2024; 14(10):843. https://doi.org/10.3390/cryst14100843
Chicago/Turabian StyleWu, Qi, Hongxia Zhang, Dagong Jia, and Tiegen Liu. 2024. "3D Optical Wedge and Movable Optical Axis LC Lens" Crystals 14, no. 10: 843. https://doi.org/10.3390/cryst14100843
APA StyleWu, Q., Zhang, H., Jia, D., & Liu, T. (2024). 3D Optical Wedge and Movable Optical Axis LC Lens. Crystals, 14(10), 843. https://doi.org/10.3390/cryst14100843









