Weld Pool Flow Characteristics in Double-Wire Arc Welding of Aluminum Alloys: Research by Numerical Simulations
Abstract
:1. Introduction
2. Numerical Model
3. Results and Discussion
3.1. The Development of Double-Wire Liquid Bridge Transfer Model
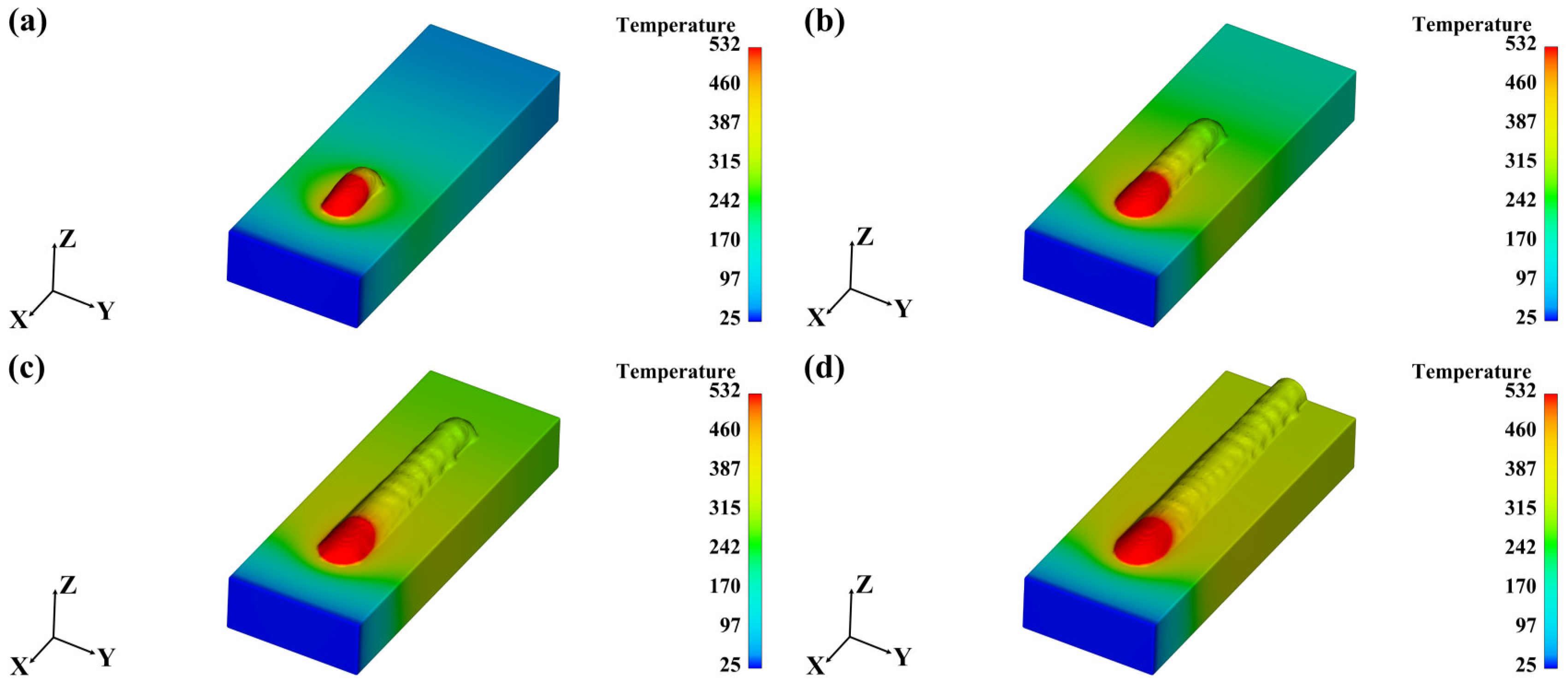
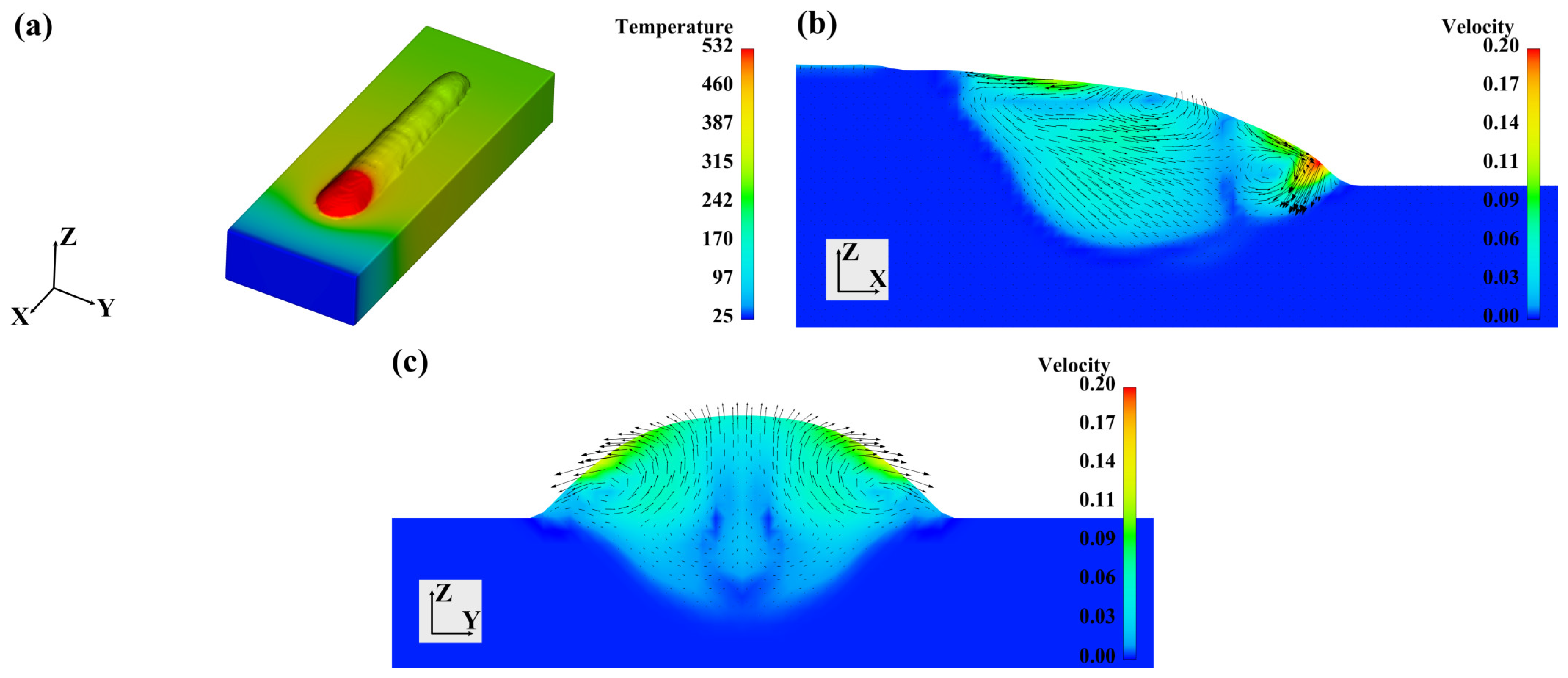
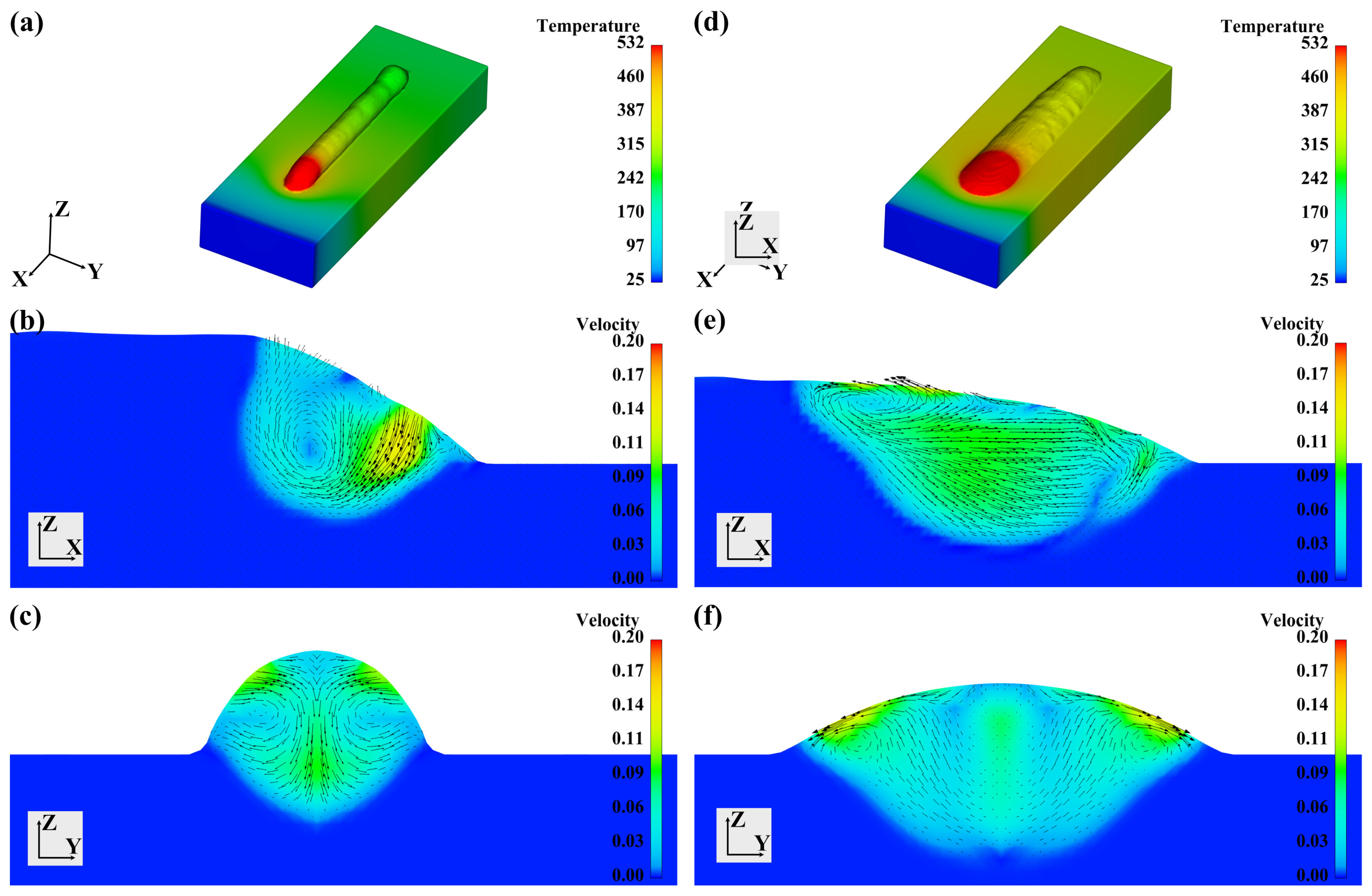
3.2. Basic Weld Pool Flow Characteristics in Double-Wire Arc Welding
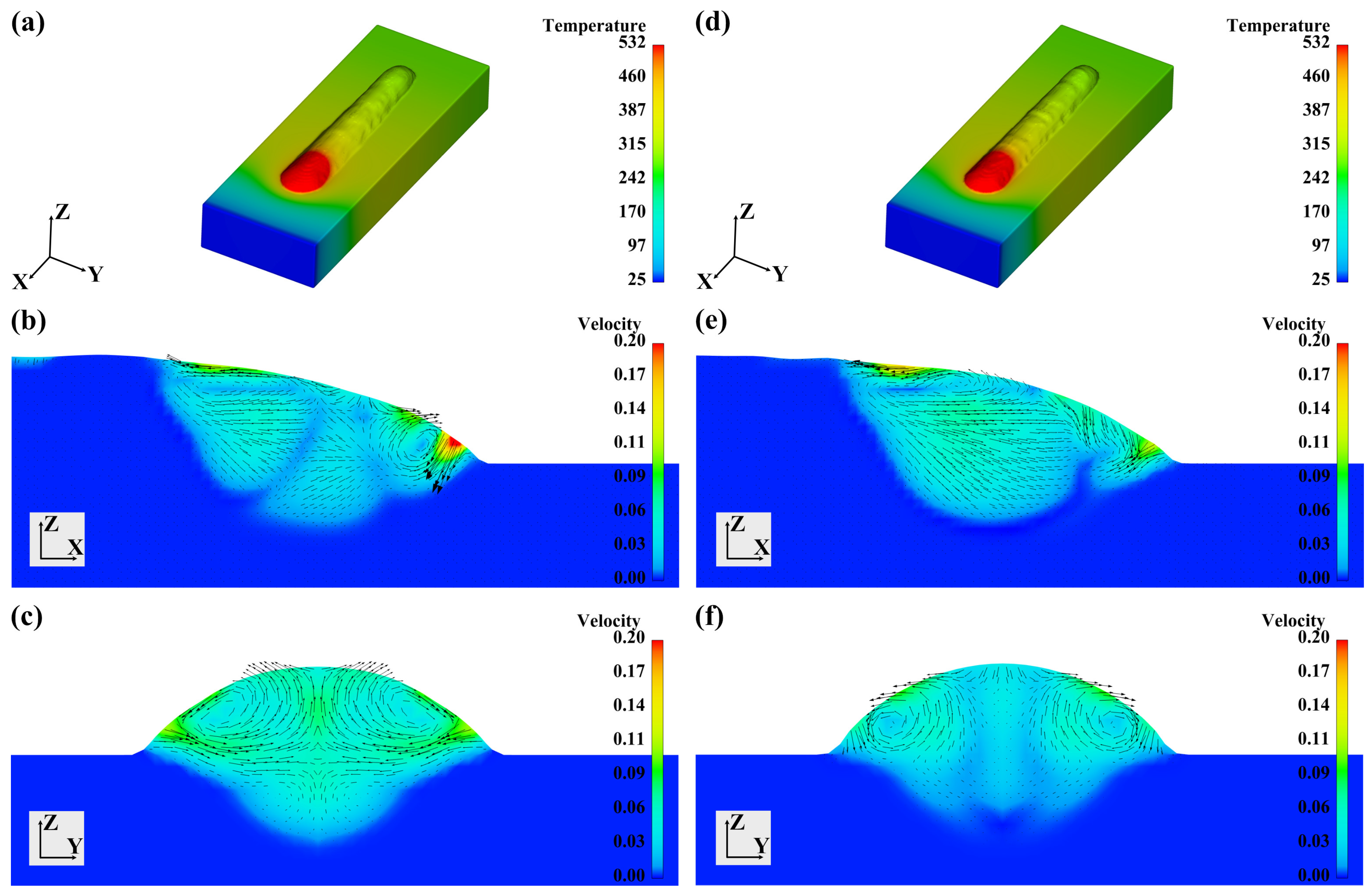
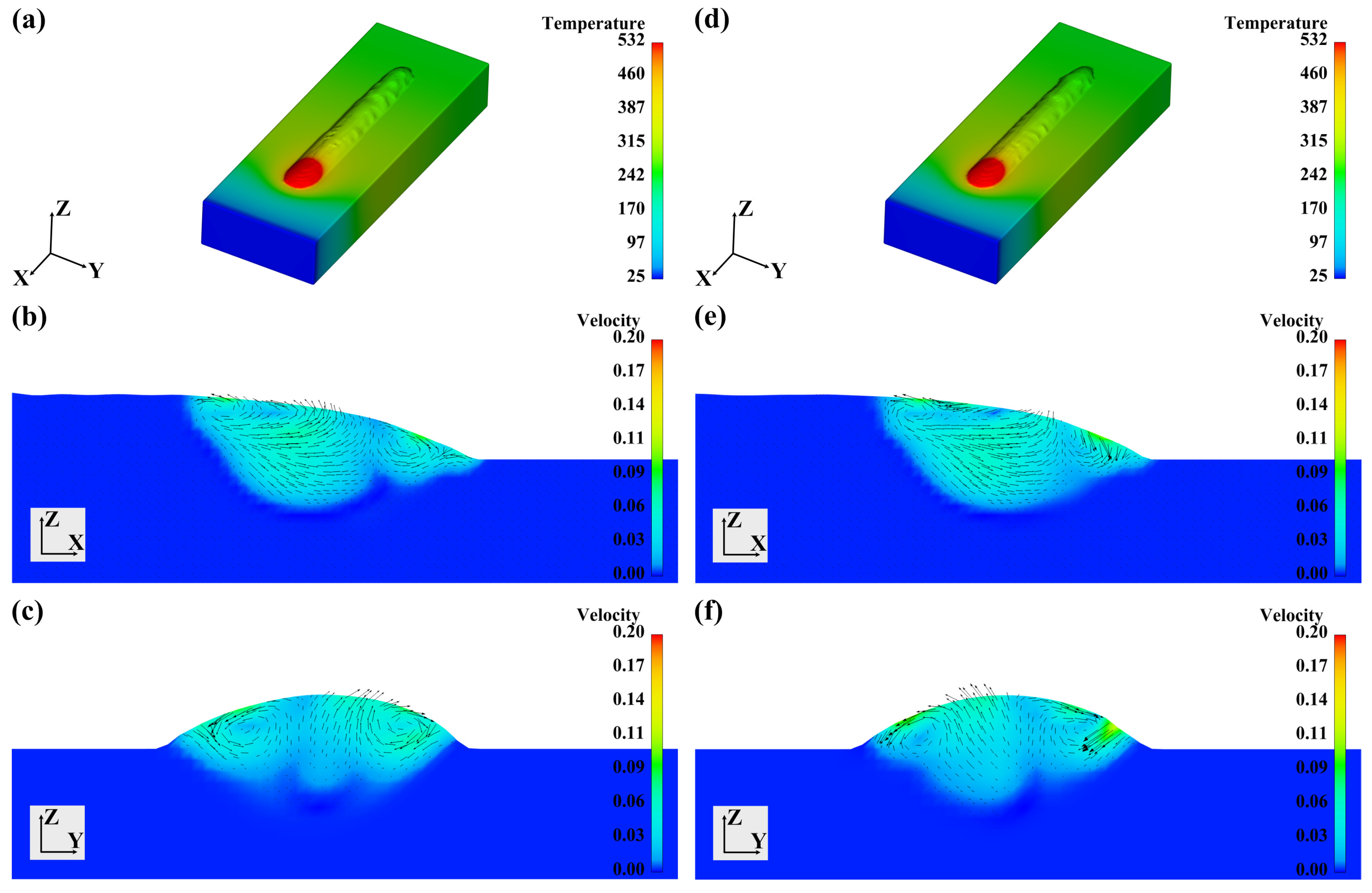
3.3. The Effects of Processing Conditions on the Flow Characteristics
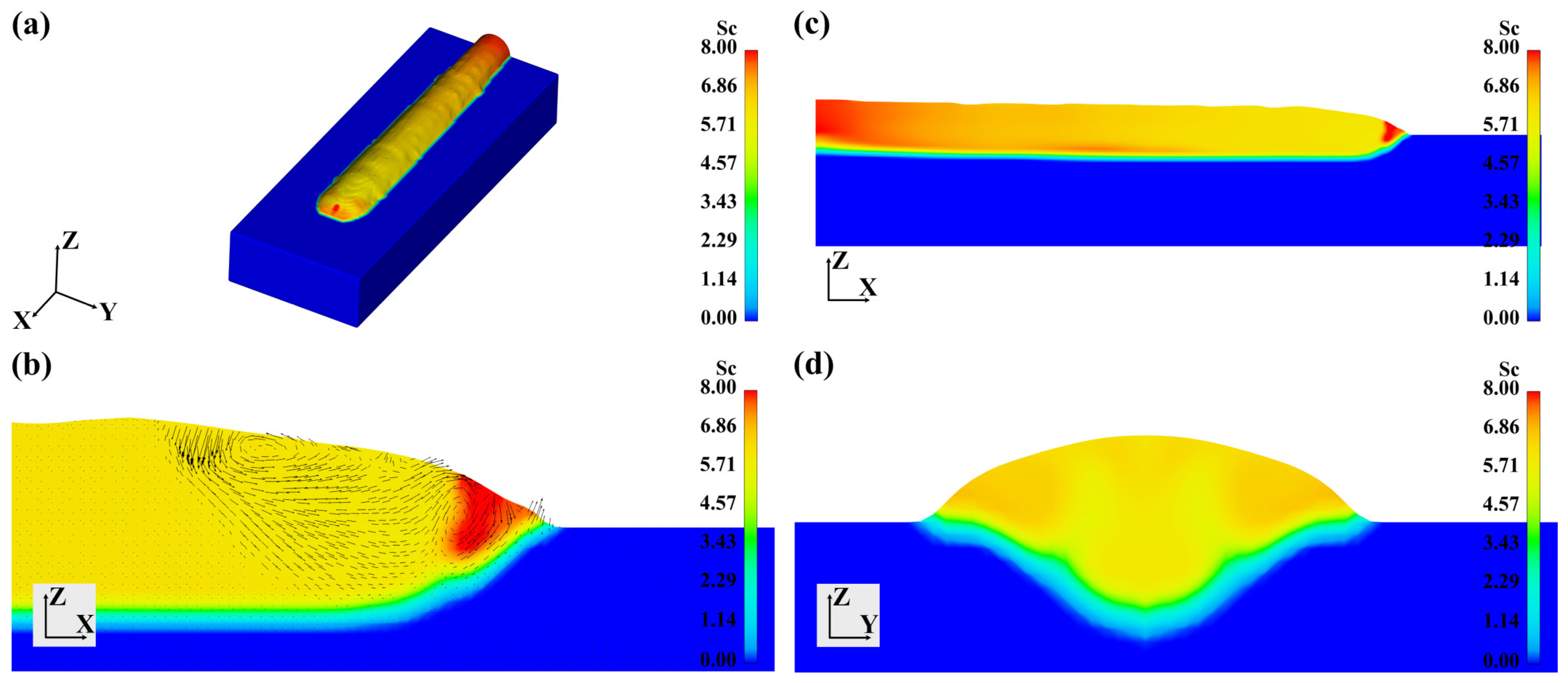
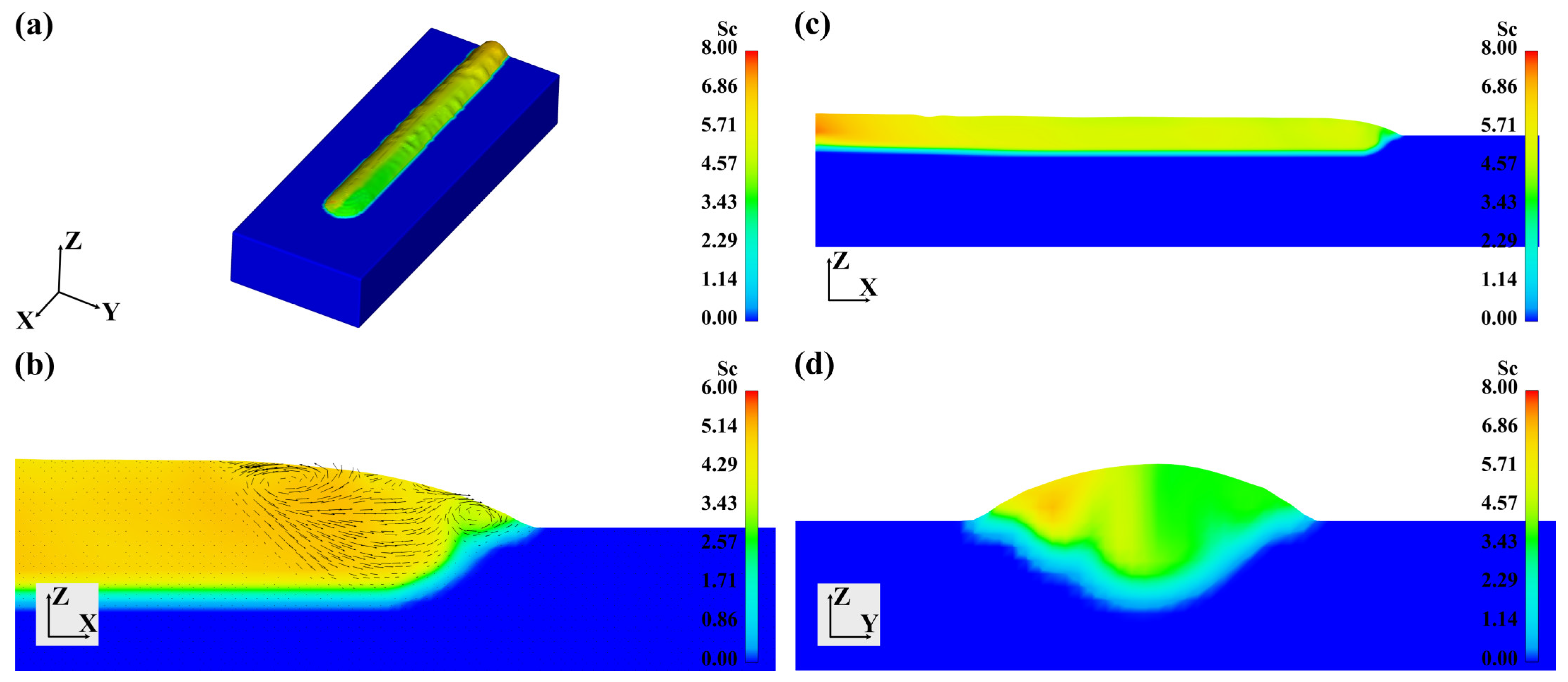
3.4. Mass Transfer in Heterogeneous Double-Wire Arc Welding
4. Conclusions
- (1)
- The bead-forming appearances and flow characteristics of double-wire arc welding show no significant differences from single-wire arc welding. The melted liquid, driven by the Marangoni effects, shows an outward tendency from the molten pool center to the boundary, forming opposite outward vortexes on both longitudinal sections and cross-sections.
- (2)
- Welding current and welding speed have significant effects on the weld bead dimensions. With a low welding current, the fluid flow in molten pools is mainly driven by the feedstock transfer. With a high welding current, the Marangoni forces take the initiative. Welding speed shows no significant influences on the metal liquid flow.
- (3)
- Wire feed XOZ angles show no significant influences on weld bead forming appearances and molten pool flow characteristics. Wire feed XOY angles influence the symmetry of the weld bead and the fluid flow.
- (4)
- In 5B71/7055 heterogeneous double-wire arc welding, achieving a uniform distribution of alloy elements is difficult due to the complex convection patterns within the molten pool. The alloy element concentration shows inhomogeneity in longitudinal, transverse, and height directions. Changing the wire feed XOY angles aggravates the inhomogeneity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, F.; Peng, S.; Zhang, G.; Xu, B.; Cai, X.; Chen, S.; Zhang, P. Investigation of Arc Behavior and Welding Formation for a Novel Vector Gas Regulated Plasma Arc Welding. J. Manuf. Process. 2024, 119, 768–780. [Google Scholar] [CrossRef]
- Wang, L.; Gu, Y.; Quan, M.; Liu, A.; Wu, C.; Yang, X.; Liang, Z.; Wang, D.; Liu, Y.; Peng, Z.; et al. The Arc Stability and Droplet Transfer Characteristics of an Alternating Current Heterogeneous Twin-Wire Indirect Arc Welding. J. Mater. Process. Technol. 2024, 332, 118570. [Google Scholar] [CrossRef]
- Wu, K.; Zeng, Y.; Zhang, M.; Hong, X.; Xie, P. Effect of High-Frequency Phase Shift on Metal Transfer and Weld Formation in Aluminum Alloy Double-Wire DP-GMAW. J. Manuf. Process. 2022, 75, 301–319. [Google Scholar] [CrossRef]
- Cui, G.; Yang, C. Formation and Strengthening Mechanism of Equiaxial Cellular Grain Zone in AA2195-T8 Al–Cu–Li Alloy Twin-Wire P-VPPA Welded Joint with Ti–Zr Microalloying. Mater. Sci. Eng. A 2024, 896, 146278. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, M.; Wang, J.; Lu, T.; Ma, S.; Liu, C. Research on High Efficiency Deposition Method of Titanium Alloy Based on Double-Hot-Wire Arc Additive Manufacturing and Heat Treatment. J. Manuf. Process. 2022, 79, 60–69. [Google Scholar] [CrossRef]
- Meng, Y.; Li, J.; Gao, M.; Chen, H. Preparation of Ni–Al Intermetallic Compounds by Plasma Arc Melting Deposition through Double-Wire Feeding. J. Mater. Res. Technol. 2023, 24, 6174–6186. [Google Scholar] [CrossRef]
- Kong, H.; Liu, Y.; Ren, H.; Li, F.; Kang, K.; Tao, Y.; Sun, Q. Surface Modification of Mild Steel via Heterogeneous Double-Wire Arc Directed Energy Deposition: Microstructure and Performance of Cladding Layer. Surf. Coat. Technol. 2024, 482, 130751. [Google Scholar] [CrossRef]
- Hou, X.; Zhao, L.; Ren, S.; Peng, Y.; Ma, C.; Tian, Z.; Qu, X. Effect of Sc and Zr Addition on Microstructure and Mechanical Properties of High Strength 7A52 Aluminum Alloy Welded Joints Fabricated by Double-Wire Gas Metal Arc Welding. Mater. Today Commun. 2024, 38, 108341. [Google Scholar] [CrossRef]
- Wan, Z.; Zhao, Y.; Zhang, S.; Zhao, T.; Li, Q.; Shan, J.; Wu, A. Novel Weld Composition to Improve Mechanical Properties of 2219-T8 Aluminum Alloy Joint Using Double-Wire TIG Welding. Mater. Charact. 2024, 209, 113764. [Google Scholar] [CrossRef]
- Feng, J.; Luo, C.; Liu, J.; Liu, H.; Zhang, Y.; Chen, X.; Jiang, M.; Tian, Y. Narrow Gap Multi-Pass Laser Welding with 52M/308L Double Wires Filler Addition for SA508/316L Dissimilar Metals. Int. J. Press. Vessel. Pip. 2024, 211, 105286. [Google Scholar] [CrossRef]
- Huang, Y.; Xin, D.; Chen, X. Microstructure and Properties of NiTi Shape Memory Alloy Fabricated by Double-Wire Plasma Arc Additive Manufacturing with a Nearly Equal Atomic Ratio. Mater. Lett. 2024, 354, 135406. [Google Scholar] [CrossRef]
- Wang, D.; Lu, H. Numerical Analysis of Internal Flow of Molten Pool in Pulsed Gas Tungsten Arc Welding Using a Fully Coupled Model with Free Surface. Int. J. Heat Mass Transf. 2021, 165, 120572. [Google Scholar] [CrossRef]
- Cai, C.; He, Y.; Xie, J.; Yu, J.; Xu, L.; Chen, Z.; Li, Z.; Wang, E.; Chen, H. Porosity Suppression Mechanism Analysis in Narrow-Gap Oscillating Laser-MIG Hybrid Welding of Aluminum Alloys Based on Keyhole Stability and Molten Pool Flow Behavior. J. Mater. Res. Technol. 2024, 32, 502–518. [Google Scholar] [CrossRef]
- Fan, D.; Wang, Y.; Zhang, C.; Huang, J.; Li, D. Numerical Analysis of Arc-Droplet-Pool Coupling Behavior in Magnetically Controlled High Current MIG Welding. J. Manuf. Process. 2024, 126, 402–412. [Google Scholar] [CrossRef]
- Hao, H.; Gao, J.; Huang, H. Numerical Simulation for Dynamic Behavior of Molten Pool in Tungsten Inert Gas Welding with Reserved Gap. J. Manuf. Process. 2020, 58, 11–18. [Google Scholar] [CrossRef]
- Lang, R.; Han, Y.; Bai, X.; Bao, X. Influence of the Metal Flow in the Keyhole Molten Pool on the Molten Pool Stability in Continuous Variable Polarity Plasma Arc Keyhole Vertical-up Welding. J. Manuf. Process. 2022, 76, 195–209. [Google Scholar] [CrossRef]
- Xu, L.; He, J.; Pan, X.; Ji, Y.; Wu, Q.; Jin, S. Numerical and Experimental Study on Oscillation Mechanism of Molten Pool during Pulsed Microplasma Arc Welding Ultrathin Sheets. Results Phys. 2022, 35, 105359. [Google Scholar] [CrossRef]
- Han, S.; Liu, G.; Tang, X.; Xu, L.; Cui, H.; Shao, C. Effect of Molten Pool Behaviors on Welding Defects in Tandem NG-GMAW Based on CFD Simulation. Int. J. Heat Mass Transf. 2022, 195, 123165. [Google Scholar] [CrossRef]
- Han, S.; Li, J.; Shao, C.; Cui, H.; Tang, X. Numerical Evaluation of Interwire Angle Influence on Molten Pool Fluid Dynamics and Weld Defects in Tandem NG-GMAW of 5083 Aluminum Alloy. J. Manuf. Process. 2024, 124, 1112–1123. [Google Scholar] [CrossRef]
- Jia, H.; Cao, L.; Fu, S.; Wen, H.; Ma, G. Numerical Simulation and Experiment for the Dynamic Behavior of Molten Pool in Ultrasonic-Assisted MIG Welding. Int. J. Heat Mass Transf. 2023, 215, 124469. [Google Scholar] [CrossRef]
- Lang, R.; Han, Y.; Bao, X.; Fan, J. Stability Mechanism of the Molten Pool in Variable Polarity Plasma Arc Welding of Medium Thickness Aluminum Alloy. J. Mater. Process. Technol. 2023, 321, 118127. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhang, Y.; Zong, R. Numerical Analysis of the Behavior of Molten Pool and the Suppression Mechanism of Undercut Defect in TIG-MIG Hybrid Welding. Int. J. Heat Mass Transf. 2024, 218, 124757. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J.; Tashiro, S.; Tanaka, M. Study of Molten Pool Dynamics in Keyhole TIG Welding by Numerical Modelling. J. Manuf. Process. 2024, 119, 827–841. [Google Scholar] [CrossRef]
- Esmati, P.; Flint, T.; Akyel, F.; Olschok, S.; Reisgen, U.; Cardiff, P.; Larrosa, N.O.; Grilli, N. Simulating Chemical Mixing and Molten Pool Shape in Dissimilar Welds Using Thermal Fluid Dynamics. Int. J. Heat Mass Transf. 2024, 226, 125449. [Google Scholar] [CrossRef]
- Cai, X.; Dong, B.; Lin, S.; Li, X.; Fan, C. Forming Characteristics and Mechanism of Variable Polarity TIG-Based Wire Arc Additive Manufacturing of Al-Mg-Zn-Cu Alloy. Int. J. Adv. Manuf. Technol. 2022, 123, 3007–3020. [Google Scholar] [CrossRef]
- Dong, B.; Cai, X.; Chen, F.; Lin, S.; Zong, Y.; Shan, D. Twinned Dendrites Growth in Wire Arc Directed Energy Deposition of Al-Zn-Mg-Cu Alloy. Mater. Des. 2023, 228, 111821. [Google Scholar] [CrossRef]
- Luo, H.; Liu, W.; Ma, Y.; Xiao, D.; Liang, C. Unraveling L12 Al3X (X=Ti, Zr, Hf) Nano-Precipitate Evolution in Aluminum Alloys via Multi-Scale Diffusion Simulation. J. Mater. Res. Technol. 2024, 30, 7104–7114. [Google Scholar] [CrossRef]
- Xu, D.; Li, Z.; Wang, G.; Li, X.; Lv, X.; Zhang, Y.; Fan, Y.; Xiong, B. Phase Transformation and Microstructure Evolution of an Ultra-High Strength Al-Zn-Mg-Cu Alloy during Homogenization. Mater. Charact. 2017, 131, 285–297. [Google Scholar] [CrossRef]
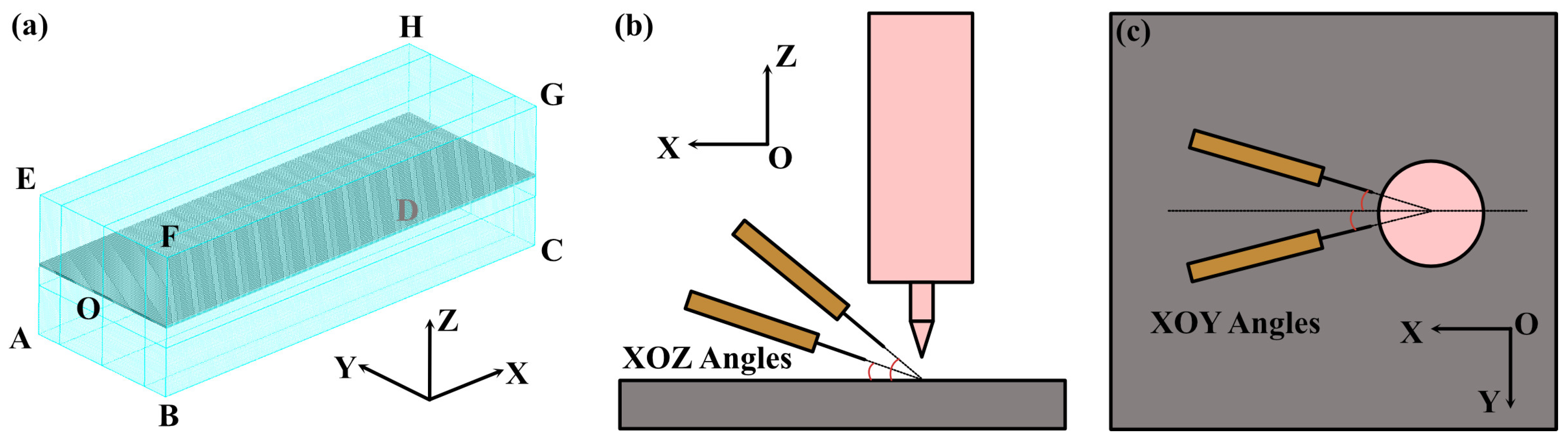
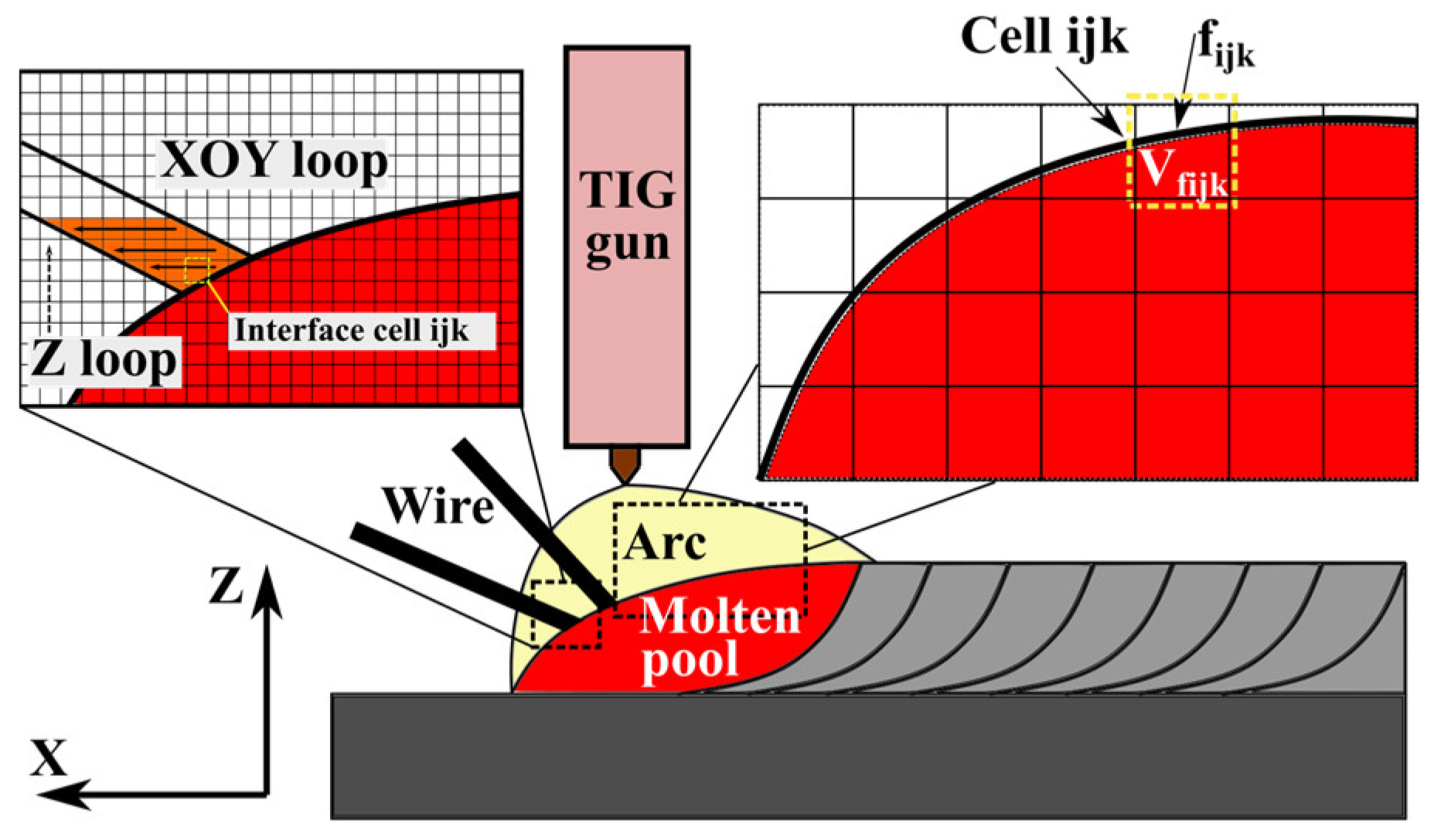




| Plane | T | p | u | v | w |
| CDHG | - | ||||
| BCGF | |||||
| ABFE | - | - | |||
| ADHE | |||||
| EFHG | |||||
| ABCD | - | - | - |
| Case No. | EP Current (A) | EN Current (A) | EP/EN Ratio | Frequency (Hz) | Welding Velocity (mm/min) | Wire Feed Speed (mm/min) | Wire Feed Angle (XOZ, °) | Wire Feed Angle (XOY, °) |
|---|---|---|---|---|---|---|---|---|
| 1 | 220 | 120 | 25% | 100 | 180 | 600 + 600 | 30, 60 | 0, 0 |
| 2 | 220 | 120 | 25% | 100 | 180 | 1200 | 30 | - |
| 3 | 190 | 90 | 25% | 100 | 180 | 600 + 600 | 30, 60 | 0, 0 |
| 4 | 250 | 150 | 25% | 100 | 180 | 600 + 600 | 30, 60 | 0, 0 |
| 5 | 220 | 120 | 25% | 100 | 210 | 600 + 600 | 30, 60 | 0, 0 |
| 6 | 220 | 120 | 25% | 100 | 240 | 600 + 600 | 30, 60 | 0, 0 |
| 7 | 220 | 120 | 25% | 100 | 180 | 600 + 600 | 30, 45 | 0, 0 |
| 8 | 220 | 120 | 25% | 100 | 180 | 600 + 600 | 30, 75 | 0, 0 |
| 9 | 220 | 120 | 25% | 100 | 180 | 600 + 600 | 30, 60 | 0, 30 |
| 10 | 220 | 120 | 25% | 100 | 180 | 600 + 600 | 30, 60 | 0, 60 |
| 11 | 220 | 120 | 25% | 100 | 180 | 600 + 600 | 30, 60 | 0, 0 |
| 12 | 220 | 120 | 25% | 100 | 180 | 600 + 600 | 30, 60 | −30, 30 |
| 13 | 220 | 120 | 25% | 100 | 180 | 600 + 600 | 30, 60 | −60, 60 |
| Alloy | Zn | Mg | Cu | Sc | Al |
|---|---|---|---|---|---|
| 7055 | 8.05 | 2.09 | 2.32 | - | Bal. |
| 5B71 | 0.05 | 6.3 | - | 0.35 | Bal. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, B.; Xia, Y.; Ni, Z.; Cai, X.; Lin, S. Weld Pool Flow Characteristics in Double-Wire Arc Welding of Aluminum Alloys: Research by Numerical Simulations. Crystals 2024, 14, 881. https://doi.org/10.3390/cryst14100881
Dong B, Xia Y, Ni Z, Cai X, Lin S. Weld Pool Flow Characteristics in Double-Wire Arc Welding of Aluminum Alloys: Research by Numerical Simulations. Crystals. 2024; 14(10):881. https://doi.org/10.3390/cryst14100881
Chicago/Turabian StyleDong, Bolun, Yunhao Xia, Zhida Ni, Xiaoyu Cai, and Sanbao Lin. 2024. "Weld Pool Flow Characteristics in Double-Wire Arc Welding of Aluminum Alloys: Research by Numerical Simulations" Crystals 14, no. 10: 881. https://doi.org/10.3390/cryst14100881
APA StyleDong, B., Xia, Y., Ni, Z., Cai, X., & Lin, S. (2024). Weld Pool Flow Characteristics in Double-Wire Arc Welding of Aluminum Alloys: Research by Numerical Simulations. Crystals, 14(10), 881. https://doi.org/10.3390/cryst14100881







