The Melt–Crystal Interface in the Production of Monocrystalline Sapphire via Heat Exchanger Method—Numerical Simulation Aspects
Abstract
1. Introduction
2. Model
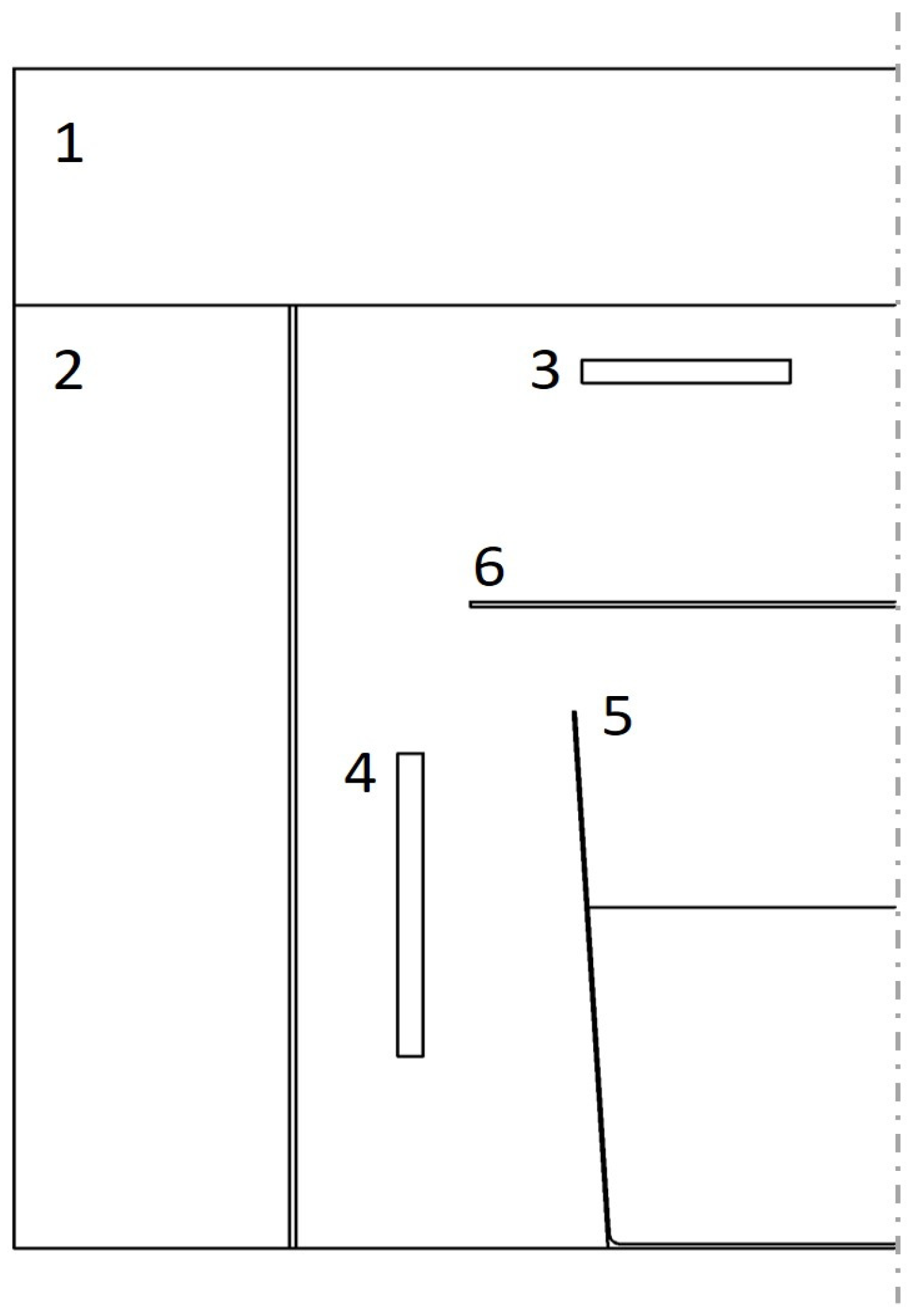
2.1. Geometry and Mesh
2.2. Governing Equations
2.3. Boundary Conditions
3. Results
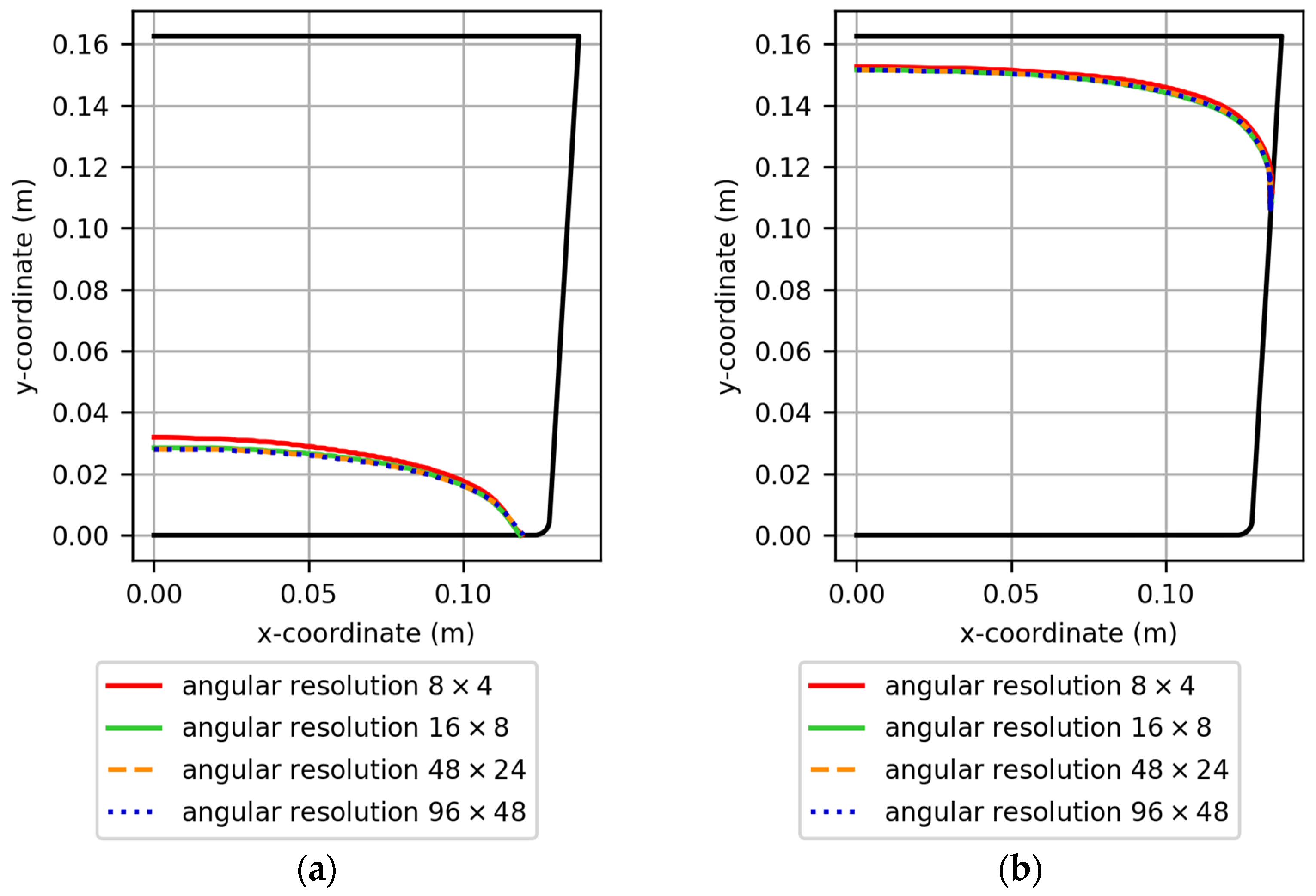
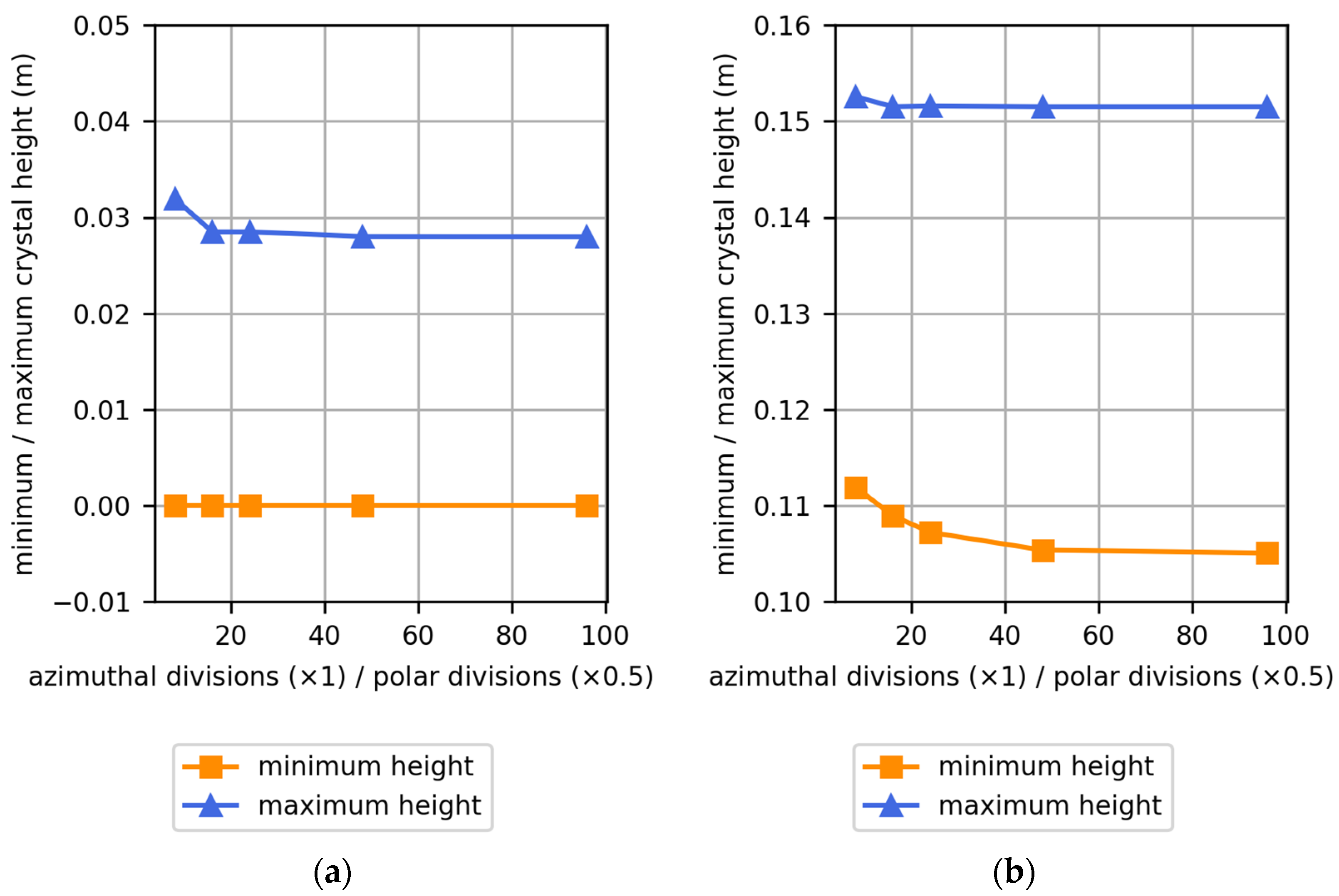
3.1. Influence of the Angular Discretization
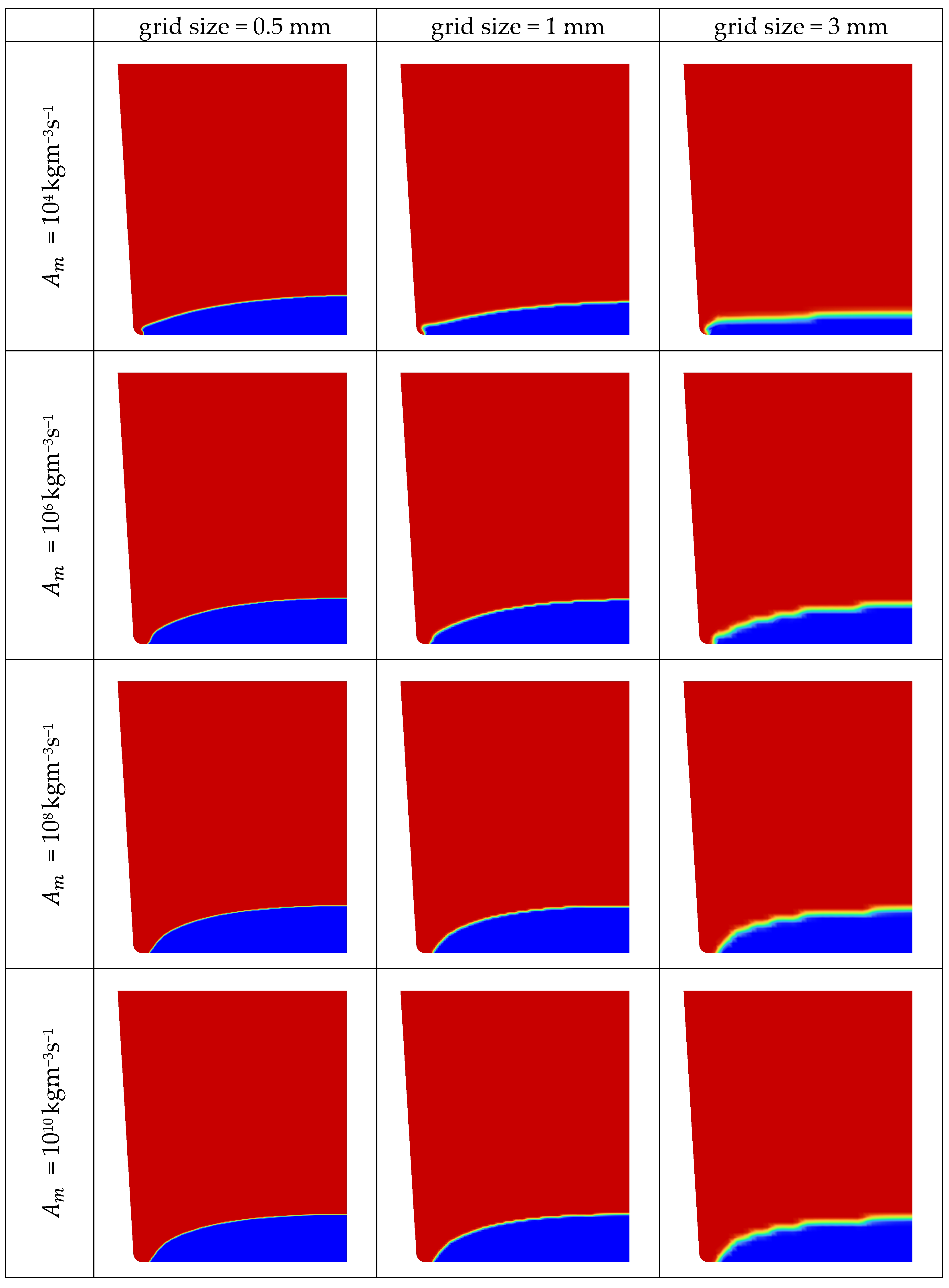
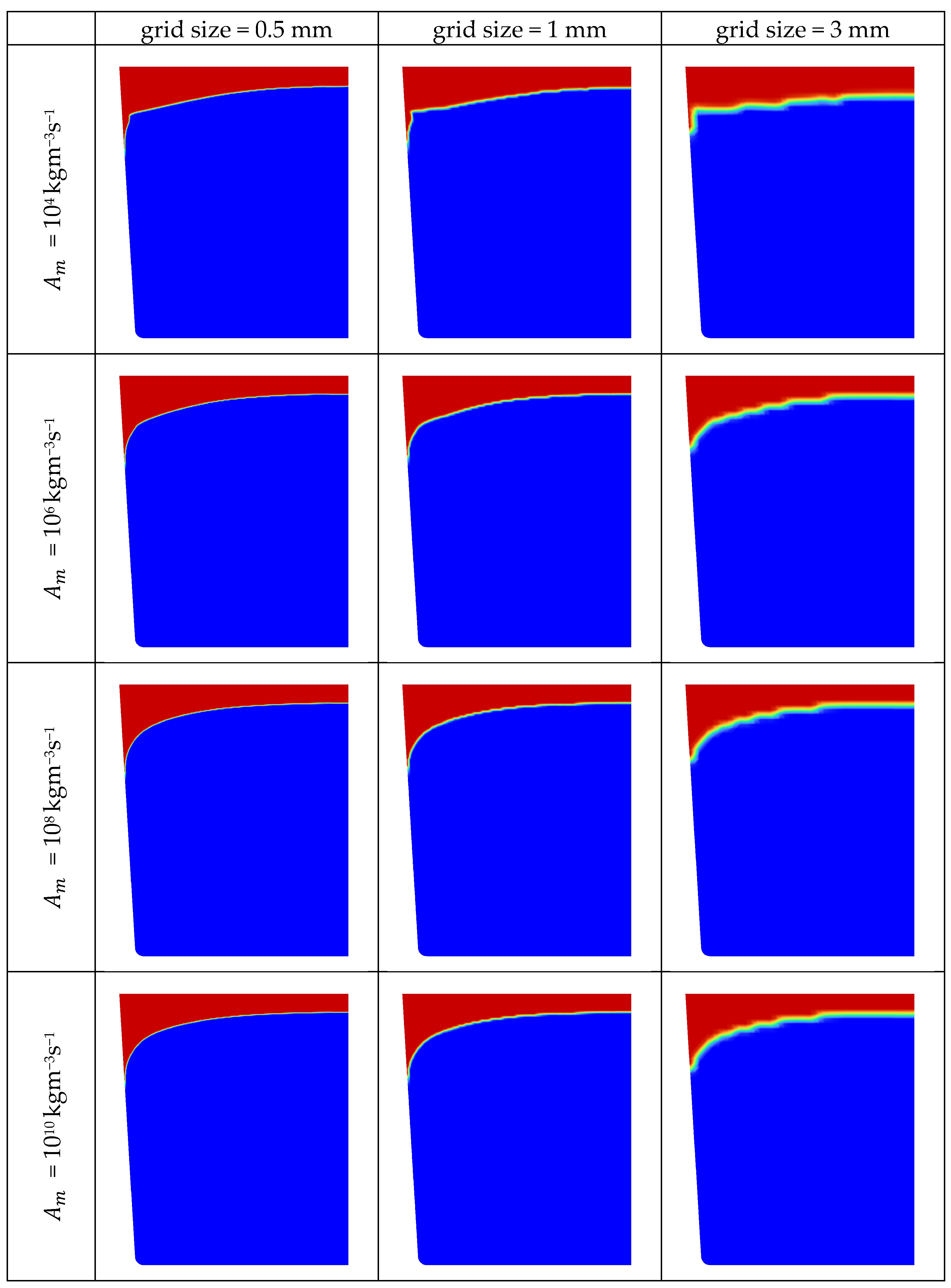
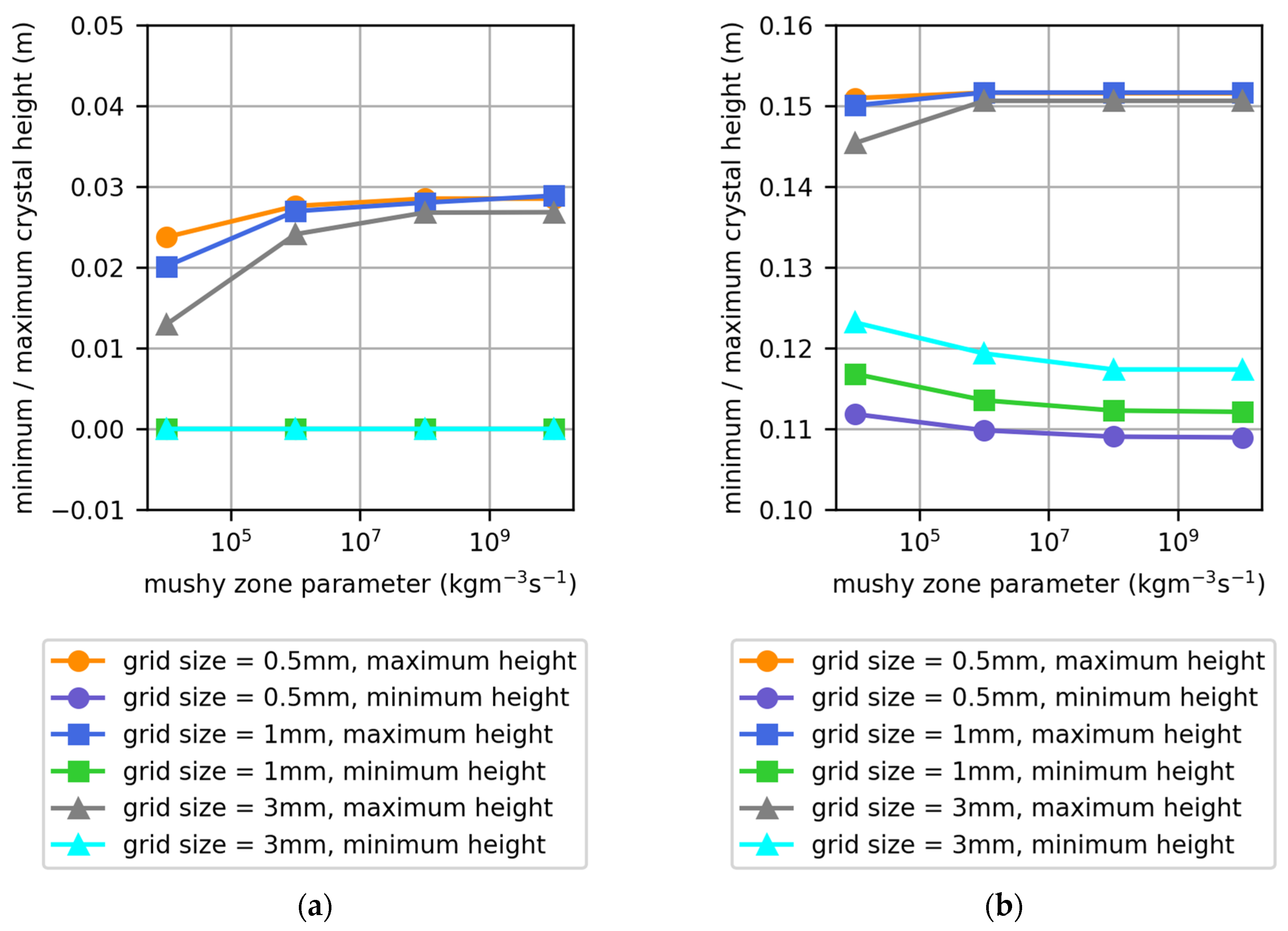
3.2. Combined Influence of Grid and Mushy Zone Parameter
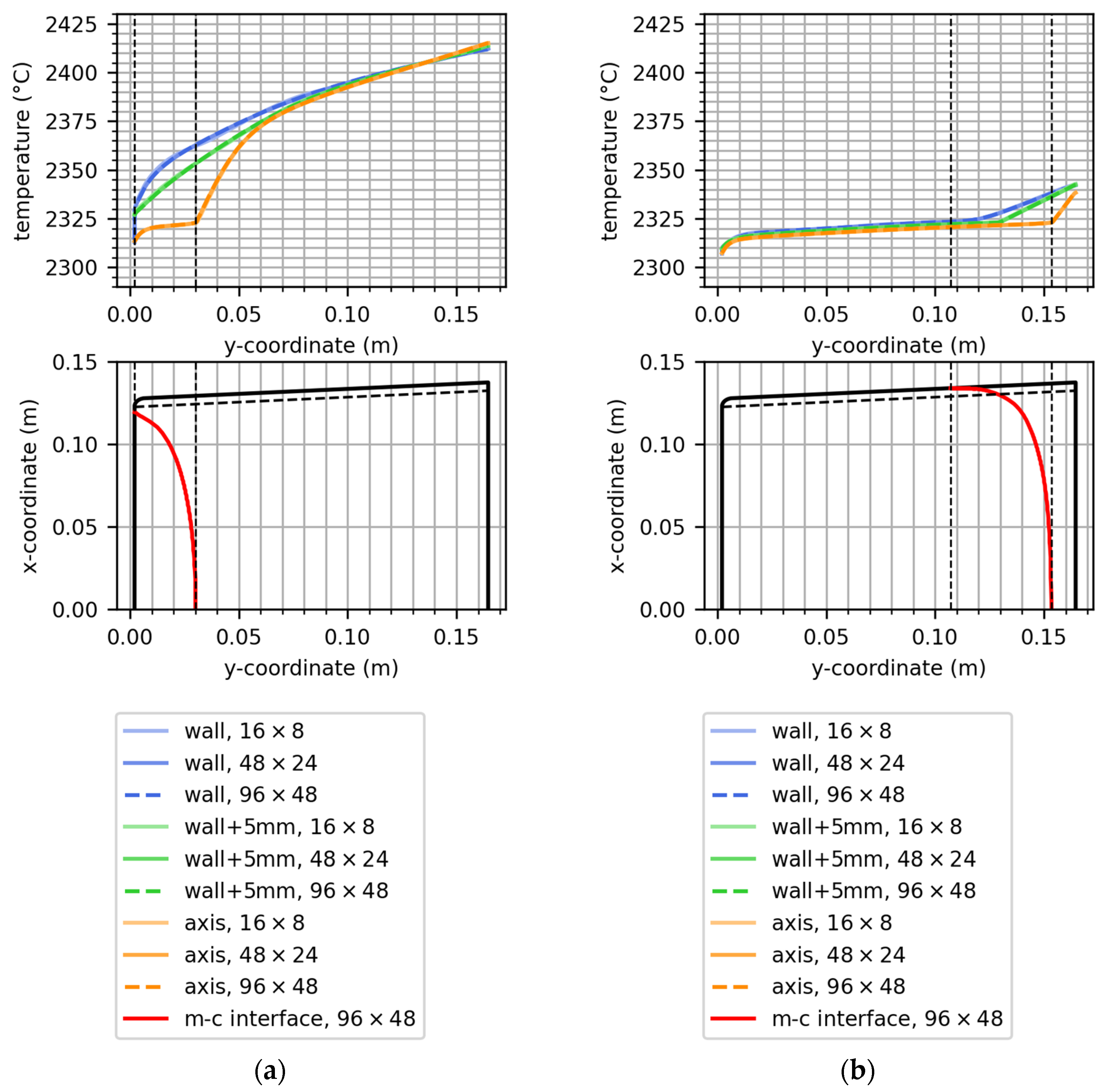
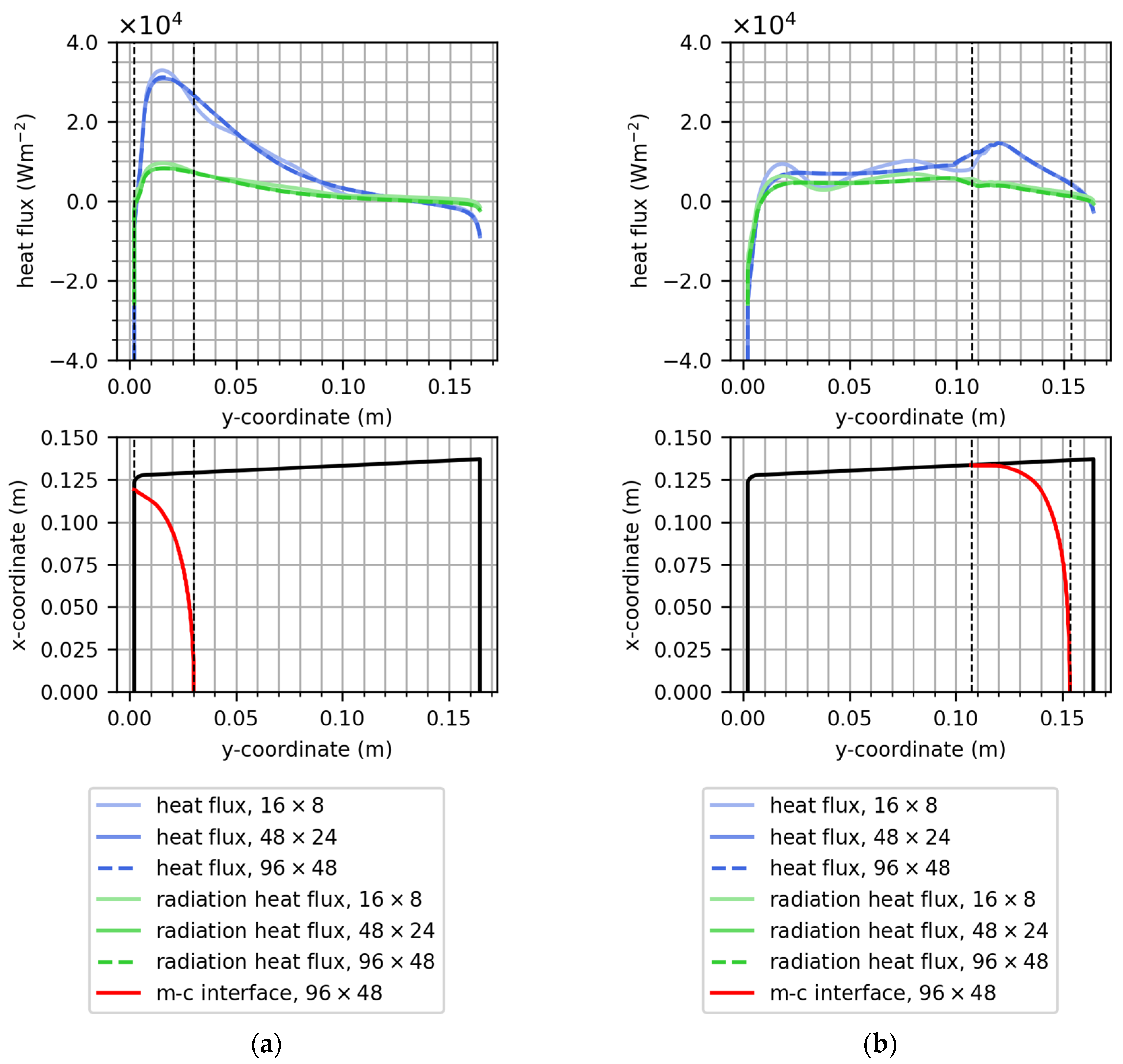
3.3. Physically Determined Interface Shape
3.4. Thermal Analysis of Process States
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akselrod, M.S.; Bruni, F.J. Modern trends in crystal growth and new applications of sapphire. J. Cryst. Growth 2012, 360, 134–145. [Google Scholar] [CrossRef]
- Bruni, F.J. Crystal growth of sapphire for substrates for high-brightness, light emitting diodes. Cryst. Res. Technol. 2015, 50, 133–142. [Google Scholar] [CrossRef]
- Kappers, M.J.; Moram, M.A.; Sridhara Rao, D.V.; McAleese, C.; Humphreys, C.J. Low dislocation density GaN growth on high-temperature AlN buffer layers on (0 0 0 1) sapphire. J. Cryst. Growth 2010, 312, 363–367. [Google Scholar] [CrossRef]
- Klunnikova, Y.V.; Malyukov, S.P.; Filomonov, A.V.; Zhang, N. Analysis of heat transfer processes for sapphire growth by horizontal directed crystallization method. J. Adv. Dielectr. 2020, 10, 2060001. [Google Scholar] [CrossRef]
- Hu, K.; Zheng, L.; Zhang, H. Control of interface shape during high melting sesquioxide crystal growth by HEM technique. J. Cryst. Growth 2018, 483, 175–182. [Google Scholar] [CrossRef]
- Tang, H.; Li, H.; Xu, J. Growth and development of sapphire crystal for LED applications. In Advanced Topics on Crystal Growth; Ferreira, S., Ed.; InTech: Rijeka, Croatia, 2013; pp. 307–333. [Google Scholar]
- Wu, M.; Zhao, W.; Liu, L.; Yang, Y.; Ma, W. Yuan Wang Effects of crucible cover on heat transfer during sapphire crystal growth by heat exchanger method. J. Cryst. Growth 2014, 404, 130–135. [Google Scholar] [CrossRef]
- He, Y.; Hua, Z.; Chen, M.; Tang, T.; Han, J. Numerical simulation of the sapphire growth process using a self-regulating thermal boundary condition method. Appl. Therm. Eng. 2018, 132, 87–94. [Google Scholar] [CrossRef]
- Ma, W.; Zhao, L.; Ding, G.; Yang, Y.; Lv, T.; Wu, M.; Liu, L. Numerical study of heat transfer during sapphire crystal growth by heat exchanger method. Int. J. Heat Mass Transf. 2014, 72, 452–460. [Google Scholar] [CrossRef]
- Zhang, N.; Park, H.G.; Derby, J.J. Simulation of heat transfer and convection during sapphire crystal growth in a modified heat exchanger method. J. Cryst. Growth 2013, 367, 27–34. [Google Scholar] [CrossRef]
- Chen, J.-C.; Lu, C.-W. Influence of the crucible geometry on the shape of the melt–crystal interface during growth of sapphire crystal using a heat exchanger method. J. Cryst. Growth 2004, 266, 239–245. [Google Scholar] [CrossRef]
- Lu, C.-W.; Chen, J.-C. Numerical computation of sapphire crystal growth using heat exchanger method. J. Cryst. Growth 2001, 225, 274–281. [Google Scholar] [CrossRef]
- Wu, M.; Liu, L.; Ma, W. Control of melt-crystal interface shape during sapphire crystal growth by heat exchanger method. J. Cryst. Growth 2017, 474, 31–36. [Google Scholar] [CrossRef]
- Demina, S.E.; Bystrova, E.N.; Postolov, V.S.; Eskov, E.V.; Nikolenko, M.V.; Marshanin, D.A.; Yuferev, V.S.; Kalaev, V.V. Use of numerical simulation for growing high-quality sapphire crystals by the Kyropoulos method. J. Cryst. Growth 2008, 310, 1443–1447. [Google Scholar] [CrossRef]
- Liu, W.; Lu, J.; Chen, H.; Yan, W.; Min, C.; Lian, Q.; Wang, Y.; Cheng, P.; Liu, C.; Xu, Y. Study on crystal-melt interface shape of sapphire crystal growth by the KY method. J. Cryst. Growth 2015, 431, 15–23. [Google Scholar] [CrossRef]
- Miyagawa, C.; Kobayashi, T.; Taishi, T.; Hoshikawa, K. Demonstration of crack-free c-axis sapphire crystal growth using the vertical Bridgman method. J. Cryst. Growth 2013, 372, 95–99. [Google Scholar] [CrossRef]
- Hoshikawa, K.; Taishi, T.; Ohba, E.; Miyagawa, C.; Kobayashi, T.; Yanagisawa, J.; Shinozuka, M. Vertical Bridgman growth of sapphire crystals, with thin-neck formation process. J. Cryst. Growth 2014, 401, 146–149. [Google Scholar] [CrossRef]
- Tavakoli, M.H. Numerical Study of Heat Transport and Fluid Flow of Melt and Gas during the Seeding Process of Sapphire Czochralski Crystal Growth. J. Cryst. Growth 2008, 310, 3107–3112. [Google Scholar] [CrossRef]
- Qi, X.; Ma, W.; Liu, L. Effect of Internal Radiation on Heat Transfer during Ti:sapphire Crystal Growth Process by Heat Exchanger Method. Int. J. Heat Mass Transf. 2021, 170, 121000. [Google Scholar] [CrossRef]
- Trasca, R.A.; Sistaninia, M.; Reiss, G.; Eßl, W.; Raninger, P.; Lohrasbi, S. Coupled Thermal Solidification Process Simulation of Sapphire Growth. Integr. Mater. Manuf. Innov. 2024, 13, 1–13. [Google Scholar] [CrossRef]
- Wu, M.; Liu, L.; Yang, Y.; Zhao, W.; Ma, W. Effect of Crucible Location on Heat Transfer in Sapphire Crystal Growth by Heat Exchanger Method. Heat Transf. Eng. 2016, 37, 332–340. [Google Scholar] [CrossRef]
- Ma, W.; Zhao, W.; Wu, M.; Ding, G.; Liu, L. Temperature and thermal stress evolutions in sapphire crystal during the cooling process by heat exchanger method. J. Cryst. Growth 2017, 474, 37–42. [Google Scholar] [CrossRef]
- Ma, W.; Liu, L. Role of Internal Radiation in Oxide Crystal Growth by Heat Exchanger Method. Crystals 2017, 7, 18. [Google Scholar] [CrossRef]
- Vogel, J.; Felbinger, J.; Johnson, M. Natural convection in high temperature flat plate latent heat thermal energy storage systems. Appl. Energy 2016, 184, 184–196. [Google Scholar] [CrossRef]
- Fadl, M.; Eames, P.C. Numerical investigation of the influence of mushy zone parameter Amush on heat transfer characteristics in vertically and horizontally oriented thermal energy storage systems. Appl. Therm. Eng. 2019, 151, 90–99. [Google Scholar] [CrossRef]
- Ezzat, Y.; Sakr, R.Y.; Abdel-Rehim, A.A. Numerical investigation of the effect of thermal expansion coefficient and mushy zone constant on modelling of the phase change process to provide reliable selection criteria of modelling parameters. J. Energy Storage 2023, 72, 108771. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Kleijn, C.R.; Richardson, I.M. Sensitivity of Numerical Predictions to the Permeability Coefficient in Simulations of Melting and Solidification Using the Enthalpy-Porosity Method. Energies 2019, 12, 4360. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys Fluent Theory Guide 2021 R2; ANSYS Inc.: Canonsburg, PA, USA, 2021. [Google Scholar]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Mencinger, J. Numerical simulation of melting in two-dimensional cavity using adaptive grid. J. Comput. Phys. 2004, 198, 243–264. [Google Scholar] [CrossRef]
- Barbar, G.; Ebner, R.; Park, J.K.; Sen, G. Process for Manufacturing a Monocrystalline Crystal, in Particular a Sapphire. EP4271856A1, 28 January 2021. [Google Scholar]
- Ebner, R.; Park, J.; Sen, G.; Lohrasbi, S.; Bürscher, M. Device and Method for Producing an Artificial Sapphire Single Crystal. WO2023212765A1, 5 May 2023. [Google Scholar]
- Ma, W.; Liu, L. Investigation of heat transfer and thermal stress during sapphire crystal growth process by heat exchanger method: Evaluation of radiation models. J. Cryst. Growth 2017, 468, 909–913. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eßl, W.; Reiss, G.; Trasca, R.A.; Sistaninia, M.; Raninger, P.; Lohrasbi, S. The Melt–Crystal Interface in the Production of Monocrystalline Sapphire via Heat Exchanger Method—Numerical Simulation Aspects. Crystals 2024, 14, 1036. https://doi.org/10.3390/cryst14121036
Eßl W, Reiss G, Trasca RA, Sistaninia M, Raninger P, Lohrasbi S. The Melt–Crystal Interface in the Production of Monocrystalline Sapphire via Heat Exchanger Method—Numerical Simulation Aspects. Crystals. 2024; 14(12):1036. https://doi.org/10.3390/cryst14121036
Chicago/Turabian StyleEßl, Werner, Georg Reiss, Raluca Andreea Trasca, Masoud Sistaninia, Peter Raninger, and Sina Lohrasbi. 2024. "The Melt–Crystal Interface in the Production of Monocrystalline Sapphire via Heat Exchanger Method—Numerical Simulation Aspects" Crystals 14, no. 12: 1036. https://doi.org/10.3390/cryst14121036
APA StyleEßl, W., Reiss, G., Trasca, R. A., Sistaninia, M., Raninger, P., & Lohrasbi, S. (2024). The Melt–Crystal Interface in the Production of Monocrystalline Sapphire via Heat Exchanger Method—Numerical Simulation Aspects. Crystals, 14(12), 1036. https://doi.org/10.3390/cryst14121036






