Ultrathin Encapsulation Strategies with Predefined Gate Dielectric Surface Area for Flexible Crystalline Silicon Nanomembrane-Based MOS Capacitors

Abstract

Ultrathin encapsulation strategies show huge potential in wearable and implantable electronics. However, insightful efforts are still needed to improve the electrical and mechanical characteristics of encapsulated devices. This work introduces Al₂O₃/alucone nanolaminates using hybrid atomic/molecular layer deposition for ultrathin encapsulation structures employed in crystalline silicon nanomembrane (Si NM)-based metal-oxide-semiconductor capacitors (MOSCAPs). The comprehensive electrical and mechanical analysis focused on the encapsulated and bare MOSCAPs with three gate dielectric diameters (Ø) under planar and bending conditions, including concave bending radii of 110.5 mm and 85 mm as well as convex bending radii of 77.5 mm and 38.5 mm. Combined with the Ø-related mechanical analysis of the maximum strain in the critical layers and the practical investigations of electrical parameters, the encapsulated MOSCAPs with Ø 160 μm showed the most stable electro-mechanical performance partly due to the optimized position of the neutral mechanical plane. Comparison of the electrical changes in Al₂O₃/alucone-encapsulated MOSCAPs with Ø 160 μm, Ø 240 μm, and Ø 320 μm showed that it is beneficial to define the gate dielectric surface area of 0.02 to 0.05 mm² for Si NM-based wearable electronics. These findings are significant for leveraging the practical applications in ultrathin encapsulation strategies for reliable operations of crystalline Si NM-based integrated circuits.

1. Introduction

Thin film encapsulation is indispensable in the prevailing Internet of Things due to its practical applications in biomedical engineering, precision medicine, and brain–computer interfaces [1,2]. Considerable efforts have been made to improve the lifetime of wearable and implantable devices such as thin film electrodes [3], field-effect transistors [4], and organic electrochemical transistors [5]. Because of their advantages of high performance, high areal density, and low cost, crystalline silicon nanomembranes (Si NMs) show excellent mechanical and electrical properties as active electrodes recording the signals from the human body through advanced complementary metal-oxide-semiconductor (CMOS) techniques, which has huge potential for medical bioelectronics [6,7]. To achieve long-term reliable operation for crystalline Si NM-based CMOS devices, it is important to use optimized thin film encapsulation strategies to maintain durability in curvilinear, soft, and wet environments. Benefiting from the advancements in techniques of atomic layer deposition (ALD) and molecular layer deposition (MLD), the conformality, scalability, and CMOS compatibility for thin film encapsulation have been promoted and ultrathin film has started to attract more attention [8,9]. Al₂O₃ is an excellent encapsulation material and the water vapor transmission rate (WVTR) of 50 nm ALD-Al₂O₃ film is 3.77 × 10⁻⁴ g/m²/day [10]. The barrier performance can be improved through double stacks using Al₂O₃ and ALD oxides such as ALD-Al₂O₃/HfO₂ and Al₂O₃/ZrO₂ [11,12]. However, the ALD oxides are too brittle to enhance the bending stability while maintaining the barrier performance. The most beneficial strategy is to insert organic film such as alucone into the Al₂O₃ layer through ALD/MLD; the reported WVTR value of alternated Al₂O₃/alucone structures decreased by one magnitude to 7.1 × 10⁻⁵ g/m²/day using only 4 nm alucone equally inserted into the 45 nm Al₂O₃ layer, and the barrier performance remained stable after bending tests [10]. The previous research showed outstanding barrier and bending performance of Al₂O₃/alucone nanolaminates, but it is challenging to verify this ultrathin encapsulation structure on practical CMOS devices.

As for the ultrathin encapsulation strategies of crystalline Si NM-based metal-oxide-semiconductor field-effect transistors (MOSFETs), the gate dielectric surface area is the primary factor to be considered in the design of implantable and multiplexed transistor arrays [13]. The precise surface area of the gate terminal substantially affects the capacitive coupling between the tissue and flexible electronics encapsulated by ultrathin encapsulation, and especially varies the gate controls in CMOS devices with the top gate top contact configuration. The evaluation of ultrathin encapsulation should not only rely on the barrier performance, but also the practical use in wearable and implantable Si NM-based MOSFETs, which is unsolved in the existing research. MOSCAPs are the building blocks for MOSFETs; thus, it is critical to combine the advanced ultrathin encapsulation structure such as Al₂O₃/alucone with crystalline Si NM-based MOSCAPs to qualitatively investigate the electrical and mechanical performances along with different gate dielectric surface areas.

The content of this paper is arranged as follows: Section 2 reveals the maximum strain versus bending radii relationship in every investigated layer for encapsulated and bare MOSCAPs with three anode diameters (Ø). Section 3 analyzes the C-V and I-V properties under a planar state for encapsulated and bare MOSCAPs with different Ø. Section 4 comparatively depicts Ø-related electrical parameters with variations in both oxide layers and interfacial properties under five conditions of planar, concave, and convex bending states.

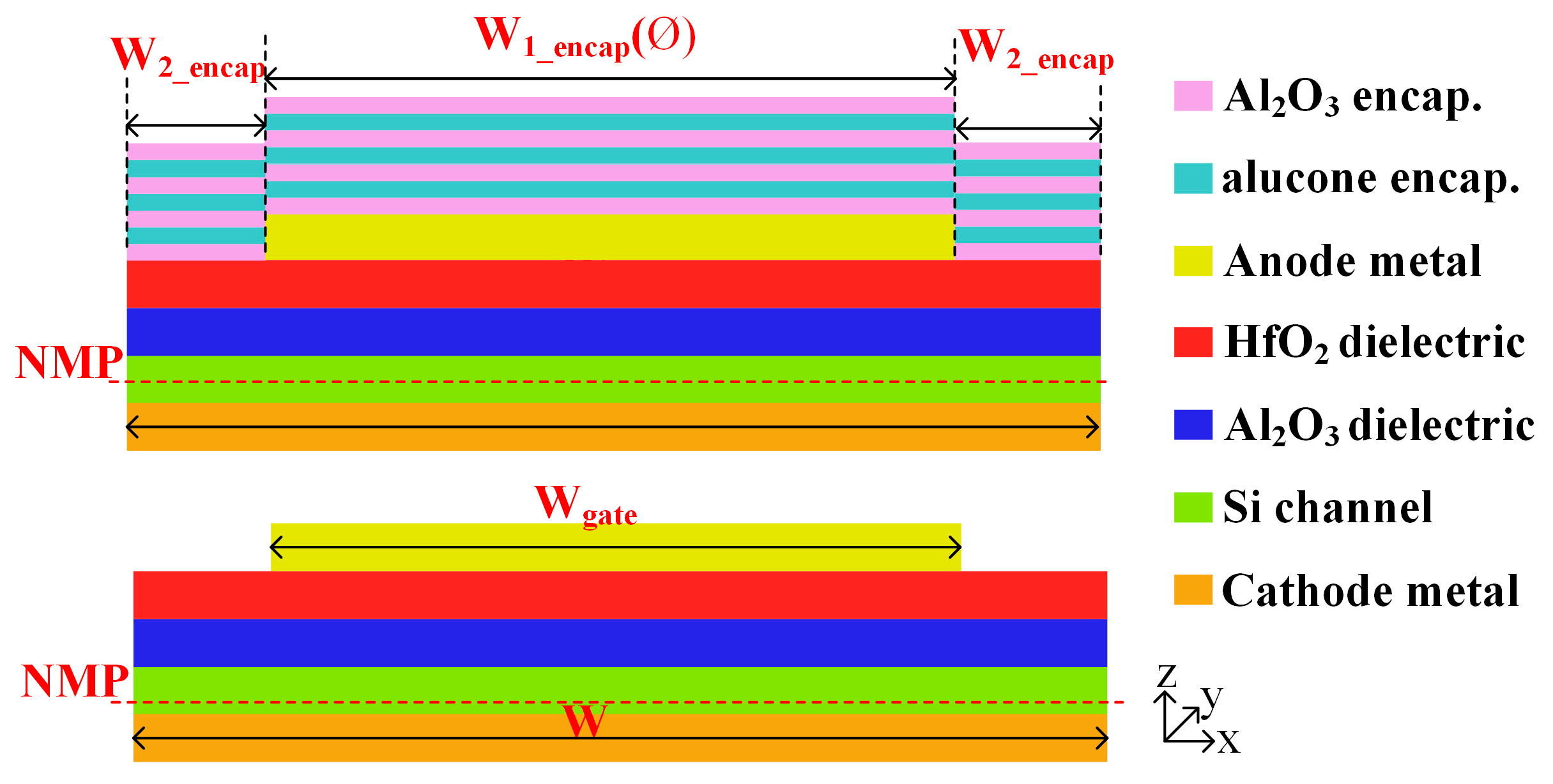
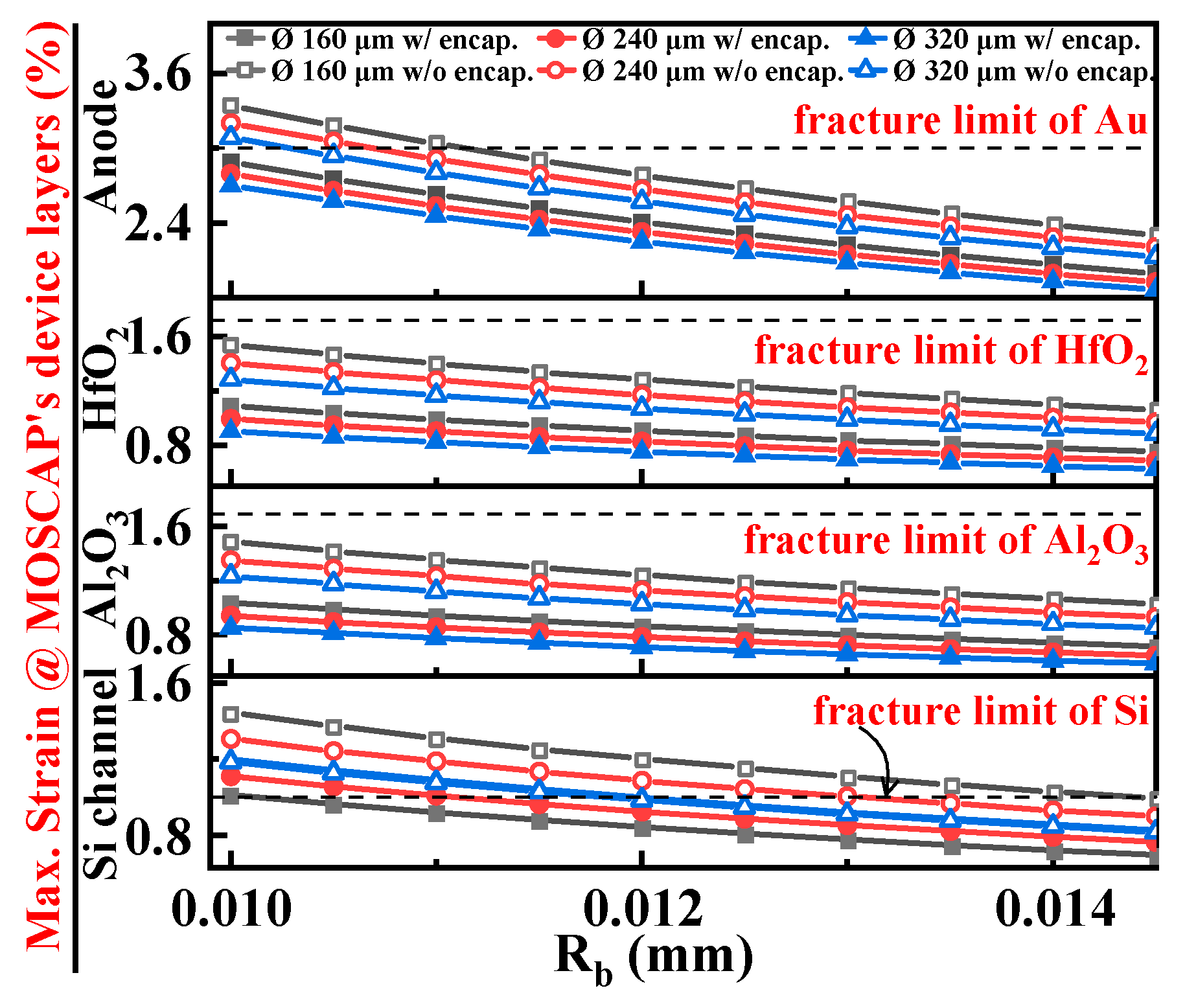
2. Maximum Strain Analysis in the Device Layer for Al₂O₃/Alucone-Encapsulated and Bare MOSCAPs with Different Ø

Figure 1 explicitly illustrates the cross-sectional view of MOSCAPs with (w/) and without (w/o) 3.5 dyads (one Al₂O₃ layer and one alucone layer) of Al₂O₃/alucone encapsulation, with the multi-layered structures defined as composite beams. Notably, the width of encapsulation layers includes two parts (i.e., W_{1_encap.} and W_{2_encap.}) with specifications as follows: (1) Alternating 11 nm Al₂O₃ and 3.5 nm alucone to generate 3.5 dyad nanolaminates on the anode metal of circular MOSCAPs through atomic/molecular layer deposition (ALD/MLD). (2) The total thickness of the ultrathin encapsulation layer (54.5 nm) is less than the thickness of the anode metal film (180 nm). W denotes the width of the beam, W_gate denotes the width of the anode (i.e., the Ø of the anode), W_{1_encap} is equal to W_gate, and W_{2_encap} is equal to (W-W_gate)/2. From the layout design, W is 500 μm and W_gate is defined as 160 μm, 240 μm, and 320 μm. The mechanical performances of Al₂O₃/alucone-encapsulated and bare MOSCAPs in configurations of different Ø under extreme bending conditions were comparatively investigated using mathematical models. The neutral mechanical plane (NMP) conceptually represents the surface in the beam where the bending stress is zero. The W_gate-related location of the NMP in encapsulated and bare MOSCAPs and the corresponding strain in the multi-layered structures are given by [14]

$$\left\{\begin{array}{l}{\mathrm{z}}_0=\frac{{\displaystyle \sum _{i=1}^N{\overline{E}}_{\mathrm{i}}{A}_i\left[\left({\displaystyle \sum _{j=1}^i{h}_j}\right)-\frac{h_i}{2}\right]}}{{\displaystyle \sum _{i=1}^N{\overline{E}}_{\mathrm{i}}{A}_i}}\\ \epsilon =\frac{z-z_0}{R}\end{array}\right.$$

(1)

where ${\mathrm{z}}_0$ is the distance from the NMP to the bottom surface of the composite beam, N is the total number of layers, ${\mathrm{A}}_{\mathrm{i}}$ is the cross-sectional area for every investigated layer, and ${\overline{\mathrm{E}}}_{\mathrm{i}}$ and ${\mathrm{h}}_{\mathrm{i}}$, respectively, represent the plane-strain modulus and thickness for the i^th layer. ${\overline{\mathrm{E}}}_{\mathrm{i}}$ is calculated by ${\mathrm{E}}_{\mathrm{i}}$/(1−υ²), $\mathsf{\epsilon }$ is the strain in the beam, R is the bending radius, and z is the distance from the position of interest to the bottom surface. Specifically, for encapsulated MOSCAPs with different Ø of 160 μm, 240 μm, and 320 μm, the distance from the NMP to the bottom surface of the Si channel layer is 101.13 nm, 110.87 nm, and 119.7 nm. For bare MOSCAPs with Ø of 160 μm, 240 μm, and 320 μm, the distance from the NMP to the bottom surface of the Si channel layer is 55.96 nm, 69.53 nm, and 81.67 nm. As for the original state in encapsulated MOSCAPs with Ø of 160 μm, the NMP position is moved towards the mid-surface of the Si channel compared to the bare MOSCAPs. Afterward, the location of NMP further increase in encapsulated and bare MOSCAPs as the Ø increases to 240 μm and 320 μm. This phenomenon leads to the difference in applied strain in the device layer varying with R, as plotted in Figure 2.

It is important to explore the strain in flexible multi-layered devices, especially under extreme bending conditions to understand the effect of the encapsulation layer on MOSCAPs with different Ø. In general, the applied strain versus R curve monotonically decreases with increasing Ø for encapsulated and bare MOSCAPs in the anode layer and dielectric bilayers. The difference occurs in the Si channel layer of encapsulated MOSCAPs, i.e., the applied strain employed by increasing Ø exhibits a positive correlation in strain versus R curves. This is mainly attributed to the maximum strain in encapsulated MOSCAPs with Ø of 240 μm and 320 μm appearing at the bottom surface of the Si channel, for which the distance between NMP and the calculated position is larger than the related distance in the device with Ø 160 μm. Moreover, the strain of the fracture limit is represented by the black dashed line in Figure 2 for every critical layer, highlighting the huge difference between Al₂O₃/alucone-encapsulated and bare MOSCAPs that are equipped with different Ø. At the anode metal layer, the applied strain at R = 11 μm for bare MOSCAPs with Ø 160 μm reaches the fracture limit of Au (i.e., 3%). However, the applied strain could be kept below 3% even at R = 10 μm for encapsulated MOSCAPs with the same Ø. As the Ø increases to 240 μm and 320 μm, the applied strain is less than 3% for encapsulated MOSCAPs, but for bare MOSCAPs, the applied strain at 240 μm and 320 μm exceeds 3% at R = 10 μm.

On the HfO₂ and Al₂O₃ dielectric layer, the strain versus R relation for the bare MOSCAPs with Ø 160 μm has the greatest increase, approaching the strain of the fracture limit (i.e., 1.72% for HfO₂ and 1.69% for Al₂O₃). Importantly, it can be concluded that the variations in maximum strain on the bilayered dielectric layer decrease 0.45%, 0.41%, and 0.38% for encapsulated MOSCAPs with Ø 160 μm, 240 μm, and 320 μm, in comparison to bare MOSCAPs. Compared to the other four curves, the strain versus R curves on the Si channel reflect unique and favorable behavior for encapsulated MOSCAPs with Ø 160 μm. The applied strain is kept beneath the strain of the fracture limit in the Si channel (i.e., 1%) because the optimized NMP for Al₂O₃/alucone-encapsulated MOSCAPs in the configuration of Ø 160 μm is almost located on the mid-surface of the Si channel. Thus, these calculations prove that the Ø, as the form factor, substantially affects the bending radii-related mechanisms for Al₂O₃/alucone-encapsulated and bare MOSCAPs. This emphasizes that the NMP optimization of the critical layer in MOSCAPs with ultrathin encapsulation should be carefully designed for the ultrathin Si channel-based devices. The mechanical parameters for each layer in the numerical analysis are summarized in the Appendix A.

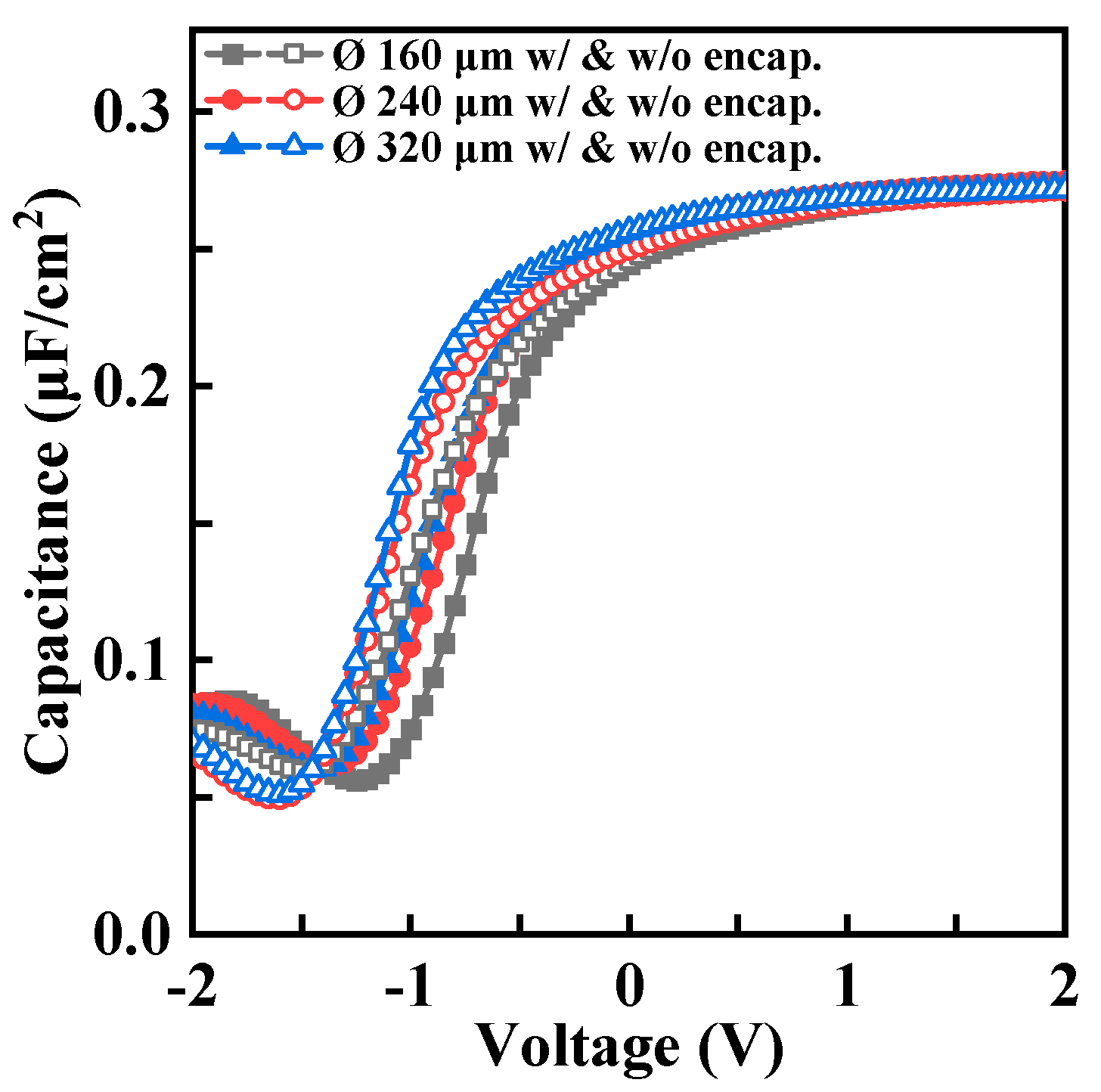
3. C-V and J-V Characteristics in the Planar State for Encapsulated and Bare MOSCAPs with Different Ø

Figure 3 illustrates the convex bending test for a real sample of encapsulated MOSCAPs as well as the optical images for encapsulated and bare devices with Ø 160 μm, Ø 240 μm, and Ø 320 μm. Fabrication of Al₂O₃/alucone-encapsulated MOSCAPs began with a silicon-on-insulator wafer with a 200 nm device layer and a 150 nm buried oxide layer. Opening the photolithographically patterned holes using reactive ion etching and removing the photoresist yielded arrays of hollow square patterns on the Si NM/SiO₂ vertical structure. This was soaked in 49% hydrofluoric acid to fully dissolve the SiO₂ sacrificial layer via holes and the Ti/Au (10/170 nm) metal stacks on suspended Si NM were immediately evaporated using e-beam evaporation, and served as the cathode electrode. The flipping transfer approach delivered multi-layer structures from the handling silicon wafer onto adhesive SU-8 photoresist-coated polyethylene terephthalate substrate; then, the critical structures were permanently bonded to the plastic substrate via ultraviolet exposure. Standard CMOS fabrication steps were performed on the transferred Si NM/cathode structure, including mesa isolation, dielectric deposition, anode deposition, and dielectric etching. The flexible MOSCAPs were instantly taped on an uploading chuck and transmitted into the ALD/MLD chamber for depositing a 3.5 dyad encapsulation structure of Al₂O₃/alucone at 120 °C. One hybrid cycle of Al₂O₃/alucone comprised a pulse of one hundred small cycles (trimethylaluminum (TMA) for 0.1 s, N₂ purging for 10 s, H₂O pulse for 0.1 s, N₂ purging for 20 s) and ten small cycles (TMA pulse for 0.2 s, N₂ purging for 10 s, ethylene glycol pulse for 0.5 s, N₂ purging for 20 s) with the deposition ratio of 10:1. The predefined gate surface area of circular MOSCAPs was 0.02 mm², 0.05 mm², and 0.08 mm² according to the Ø of 160 μm, 240 μm, and 320 μm.

To begin with, the original C-V characteristics obtained in the planar state for encapsulated and bare MOSCAPs with three values of Ø are shown in Figure 4. Figures 6–8 show the changes in the C-V curves as the planar and different bending conditions change to depict the variations in encapsulated and bare MOSCAPs with Ø 160, Ø 240, and Ø 320 μm. Figure 4 depicts the measured capacitance versus voltage curves at 100 kHz when the voltage swept from −2 V to +2 V for different Ø of circular MOSCAPs w/ and w/o Al₂O₃/alucone encapsulation, from which three viewpoints can be clarified. Firstly, the MOSCAPs are clearly distinguished from depletion to inversion until the maximum capacitance of encapsulated and bare devices consistently reaches 0.27 to 0.28 μF/cm². Secondly, it is obvious that the flatband voltage (V_fb) negatively shifts in bare and encapsulated MOSCAPs with different Ø from 160 μm to 320 μm. This phenomenon is due to both the operational point of MOSCAPs and the amounts of charges in the oxide layer being controlled by different gate dielectric surface areas. Thirdly, compared to the bare MOSCAPs with the same Ø, Al₂O₃/alucone-encapsulated devices maintain a similar slope, indicating that the presence of ultrathin encapsulation nanolaminates ensures the stability in interfacial characteristics at the planar state. Figure 5 depicts the change in the current density versus voltage (J-V) curves as a function of Ø for encapsulated and bare MOSCAPs. Notably, the current density decreased with the increase in Ø of circular MOSCAPs. Specifically, the gate leakage current density (J_g) is effective in valuing ultrathin dielectric islands in encapsulated Si NM-based MOSCAPs with different Ø. In the planar state, J_g values at 0.5 V for encapsulated circular MOSCAPs with Ø of 160 μm, 240 μm, and 320 μm are 3.95 × 10⁻⁹ A/cm², 3.48 × 10⁻⁹ A/cm², and 2.61 × 10⁻⁹ A/cm². However, the J_g synchronously increased to 5.22 × 10⁻⁹ A/cm², 5.11 × 10⁻⁹ A/cm², and 3.30 × 10⁻⁹ A/cm² for bare MOSCAPs with the same Ø. It can be concluded from the C-V and J-V results for encapsulated and bare MOSCAPs that, in the planar state, the Ø of circular MOSCAPs varied from 160 μm to 320 μm, facilitating the more negative shift in V_fb accompanied by decreased Jg. Overall, the investigation of electrical properties is worth undertaking to further explore the effect of different Ø values on circular MOSCAPs w/ and w/o ultrathin encapsulation under bending deformations.

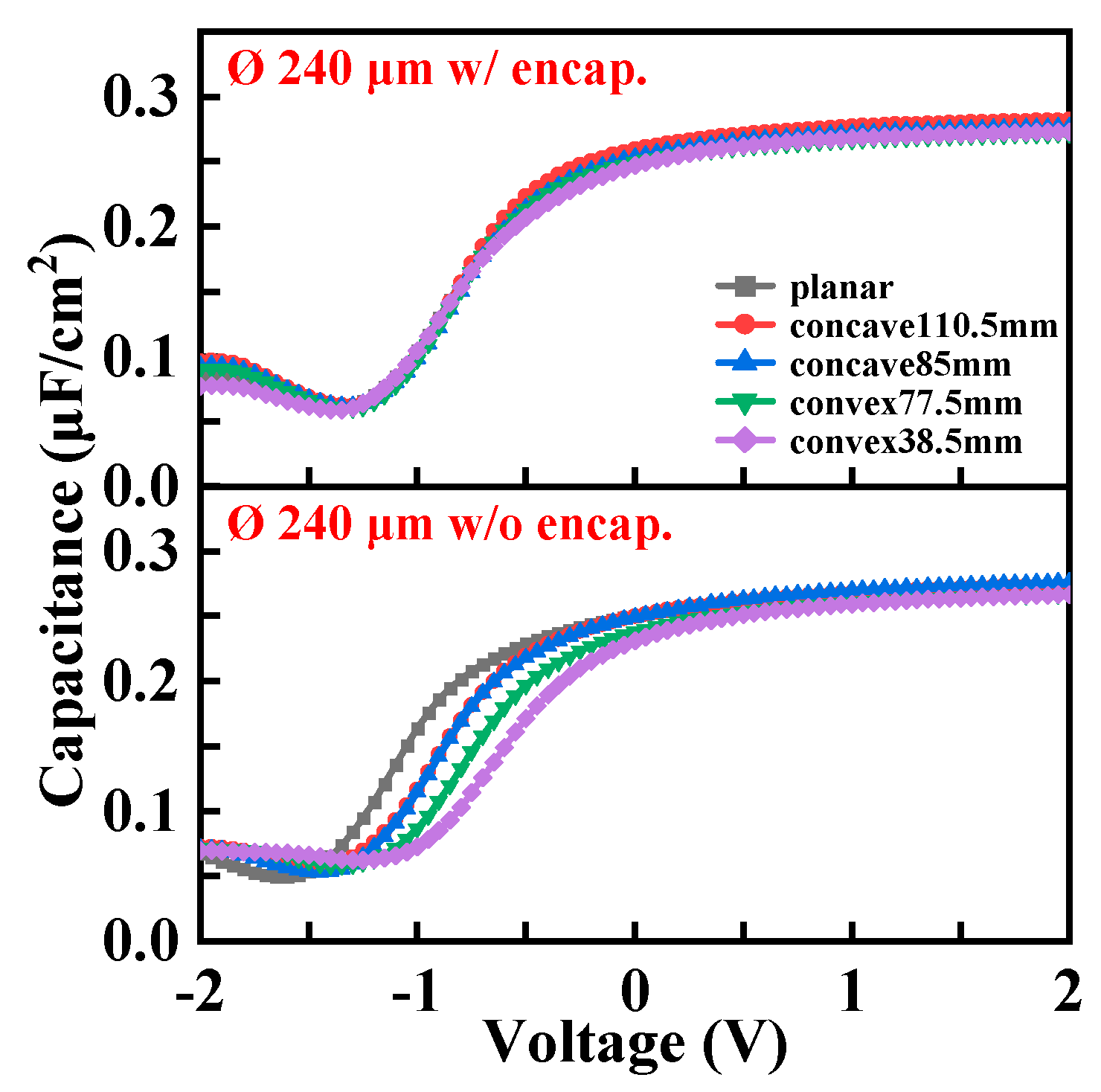
4. Electro-Mechanical Analysis under Bending Conditions for Encapsulated and Bare MOSCAPs with Different Ø

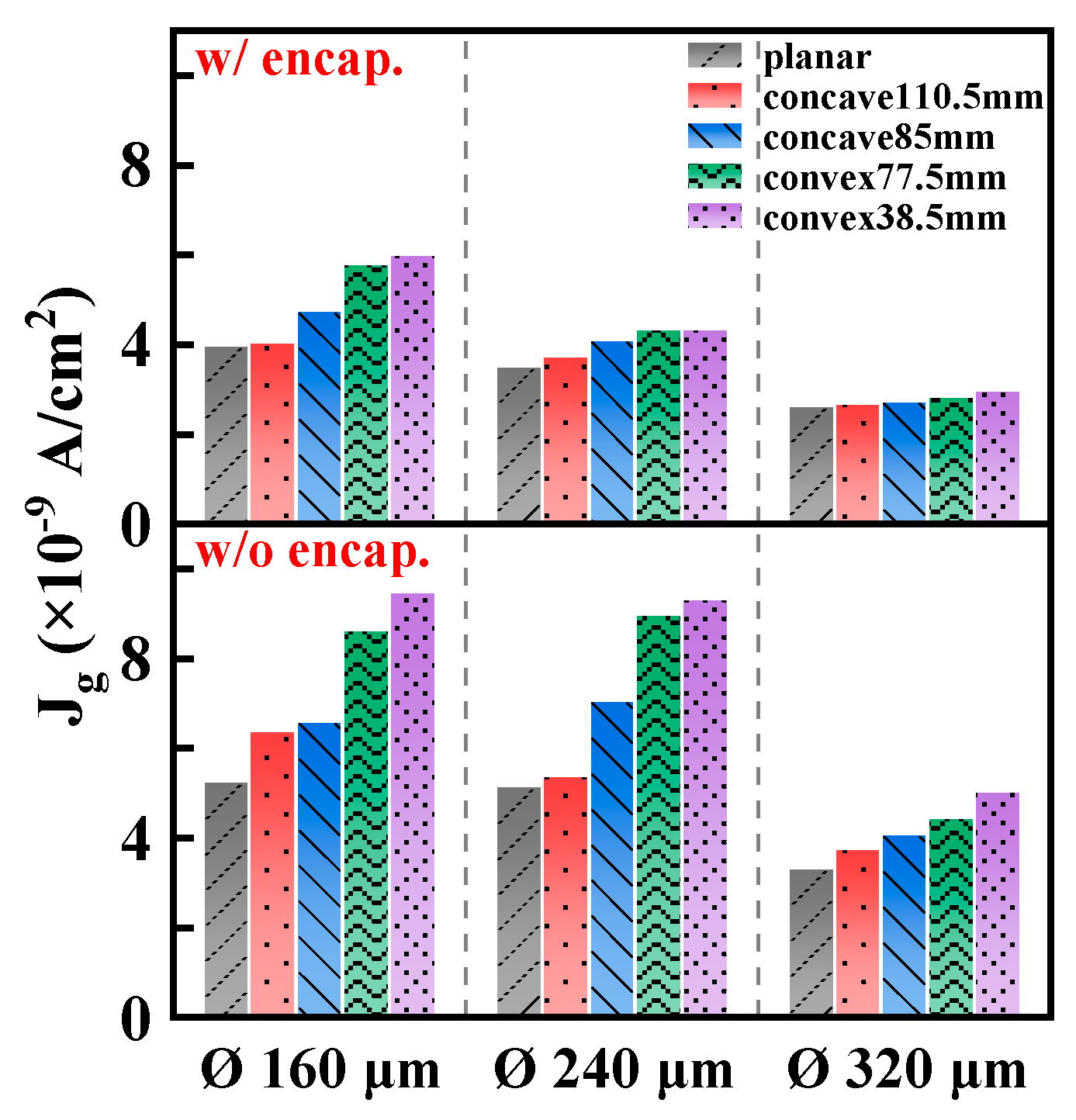
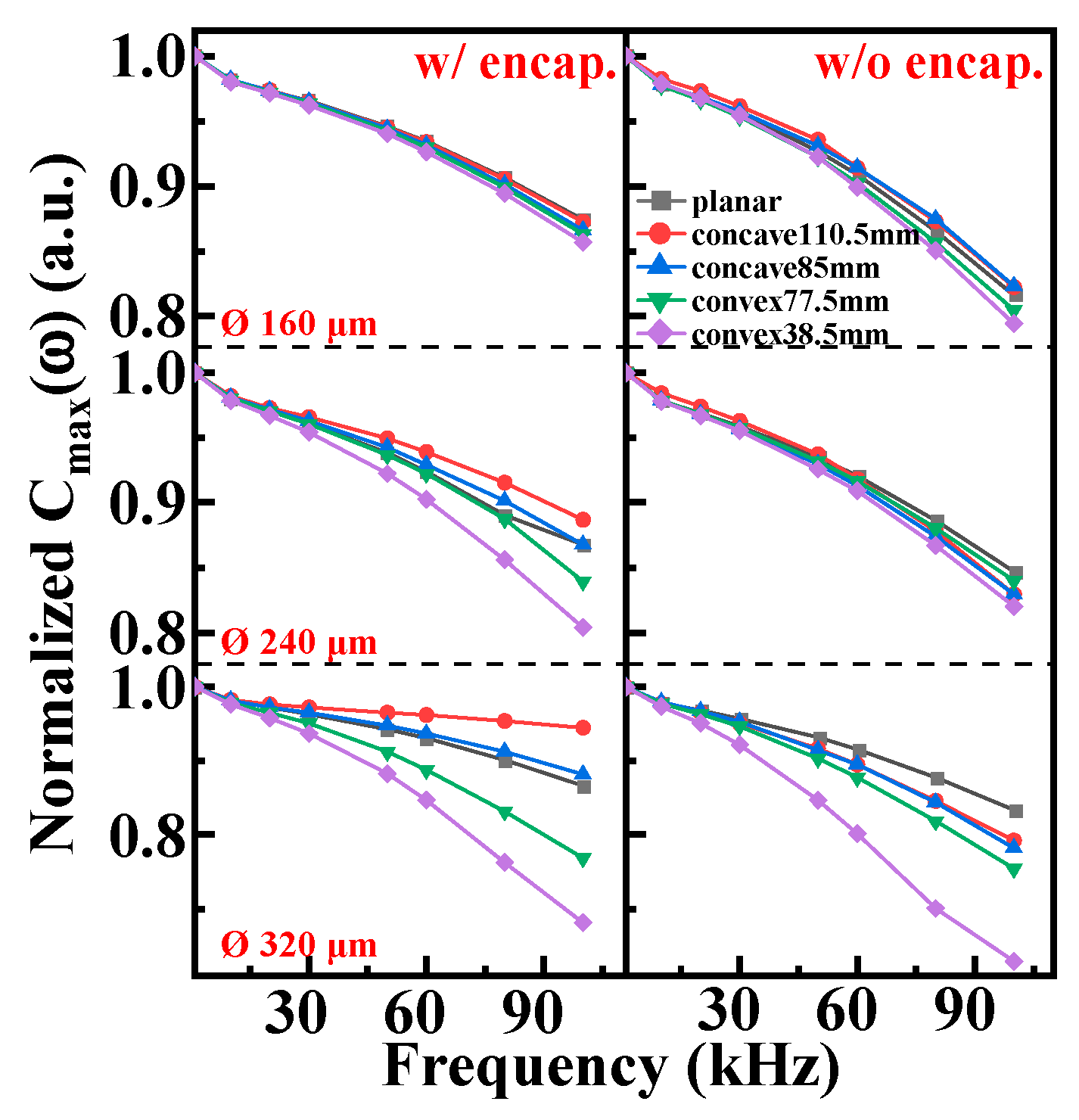
4.1. Comparative Analysis on Basic Electrical Properties

Bending tests were thoroughly implemented on circular MOSCAPs with three values of Ø simultaneously for the encapsulated and bare flexible devices. The flat state denotes that the bending radius is infinite. Based on the previous investigation on MOSCAPs using flexible monocrystalline Si NM, the bending radii carefully adopted the concave bending radii of 110.5 mm and 85 mm (i.e., (−)110.5 mm and (−)85 mm), as well as the convex bending radii of 77.5 mm and 38.5 mm (i.e., (+)77.5 mm and (+)38.5 mm). Figure 6 depicts the dynamic changes in C-V curves under bending deformations for Ø 160 μm circular MOSCAPs w/ and w/o ultrathin Al₂O₃/alucone nanolaminates. For comparison, the C-V results influenced by bending radii for Al₂O₃/alucone-encapsulated and bare circular MOSCAPs with Ø of 240 μm and 320 μm are shown in Figure 7 and Figure 8, respectively. Figure 9 depicts the comparative analysis of maximum capacitance (C_max) with different Ø values for encapsulated and bare MOSCAPs.

The changes in C_max of encapsulated MOSCAPs with three values of Ø varied from −3.5% to +2.7% with concave bending radii of (−)110.5 mm and (−)85 mm. The changes in C_max of encapsulated MOSCAPs with Ø 160 μm and Ø 240 μm varied from −0.5% to +0.9% with convex bending radii of (+)77.5 mm and (+)38.5 mm. However, a significant reduction in C_max appeared in encapsulated MOSCAPs with Ø 320 μm and convex bending radii, namely −16.5% at (+)77.5 mm and −20.5% at (+)38.5 mm. According to the applied voltage, the obvious “stretch-out” phenomenon occurred in encapsulated MOSCAPs with Ø 320 μm, which denotes the presence of interface states and changes under the different bending conditions. Compared to the encapsulated MOSCAPs, the C_max in bare MOSCAPs behaved undesirablely at the smallest and largest Ø. A relatively large reduction in C_max of Ø 160 μm and Ø 320 μm was found with −2% and −7.9% and a high concave bending deformation of 85 mm, when the variations reached −3.6% and −26.3% at a high convex bending deformation of 38.5 mm. At Ø of 240 μm, the C_max of bare MOSCAPs was relatively stable, with variations ranging from −1.9% to +1.8% with four bending radii.

In addition, it is observed that V_fb of bare devices with Ø of 160, 240, and 320 μm shifted positively as a function of bending radii. These observations of C-V results illustrate that the Al₂O₃/alucone-encapsulated MOSCAPs with Ø of 160, 240, and 320 μm can effectively promote the stability of C_max under bending deformations, compared to the same Ø of bare devices. However, the Ø-related mechanisms for Al₂O₃/alucone-encapsulated and bare MOSCAPs are not monotonically changed with the increase in Ø; thus, it is supposed that this is because of multi-dimensional factors, such as the reliability of the dielectric layer and the interface in dielectric/Si NM.

Figure 10 comparatively illustrates the J-V curves of circular MOSCAPs w/ and w/o Al₂O₃/alucone encapsulation under bending deformations that changed with three values of Ø at 160 μm, 240 μm, and 320 μm. As the bending deformations increased, the J-V curves gradually increased for encapsulated and bare MOSCAPs with three predefined gate surface areas. It is noticeable from the J-V characteristics that the performance of Al₂O₃/alucone-encapsulated MOSCAPs with Ø 320 μm is most favorable under bending deformations compared to the other two. Importantly, the J_g values were analyzed to investigate the stability of the gate dielectric manipulated by both bending radii and gate surface area, as shown in Figure 11.

Compared to the planar state, the variations in J_g at 0.5 V of encapsulated MOSCAPs with Ø 240 μm increased to 1.07, 1.17, 1.24, and 1.24 times for the four bending radii, whereas they increased to 1.05, 1.37, 1.75, and 1.82 times in bare MOSCAPs with Ø 240 μm corresponding to the same bending deformation. This indicates that the Ø 240 μm of encapsulated MOSCAPs can reliably inhibit the growth of J_g in bare MOSCAPs under bending deformations. This was followed by the variations in J_g for Ø 320 μm, which increased to 1.01, 1.04, 1.07, and 1.13 times in encapsulated devices, while they increased to 1.13, 1.23, 1.34, and 1.51 times in bare devices under four bending conditions when compared with the planar state. Although the variations in J_g are also inhibited by encapsulated MOSCAPs with Ø 160 μm, the magnitude of the difference is inferior to that of the Ø 240 μm and Ø 320 μm of encapsulated devices. Hence, the J-V results under bending deformations indicate that the Al₂O₃/alucone-encapsulated MOSCAPs with Ø 320 μm and Ø 240 μm take the leading role in both stabilizing J_g and relieving the increase in J_g under bending deformations when compared to the bare MOSCAPs.

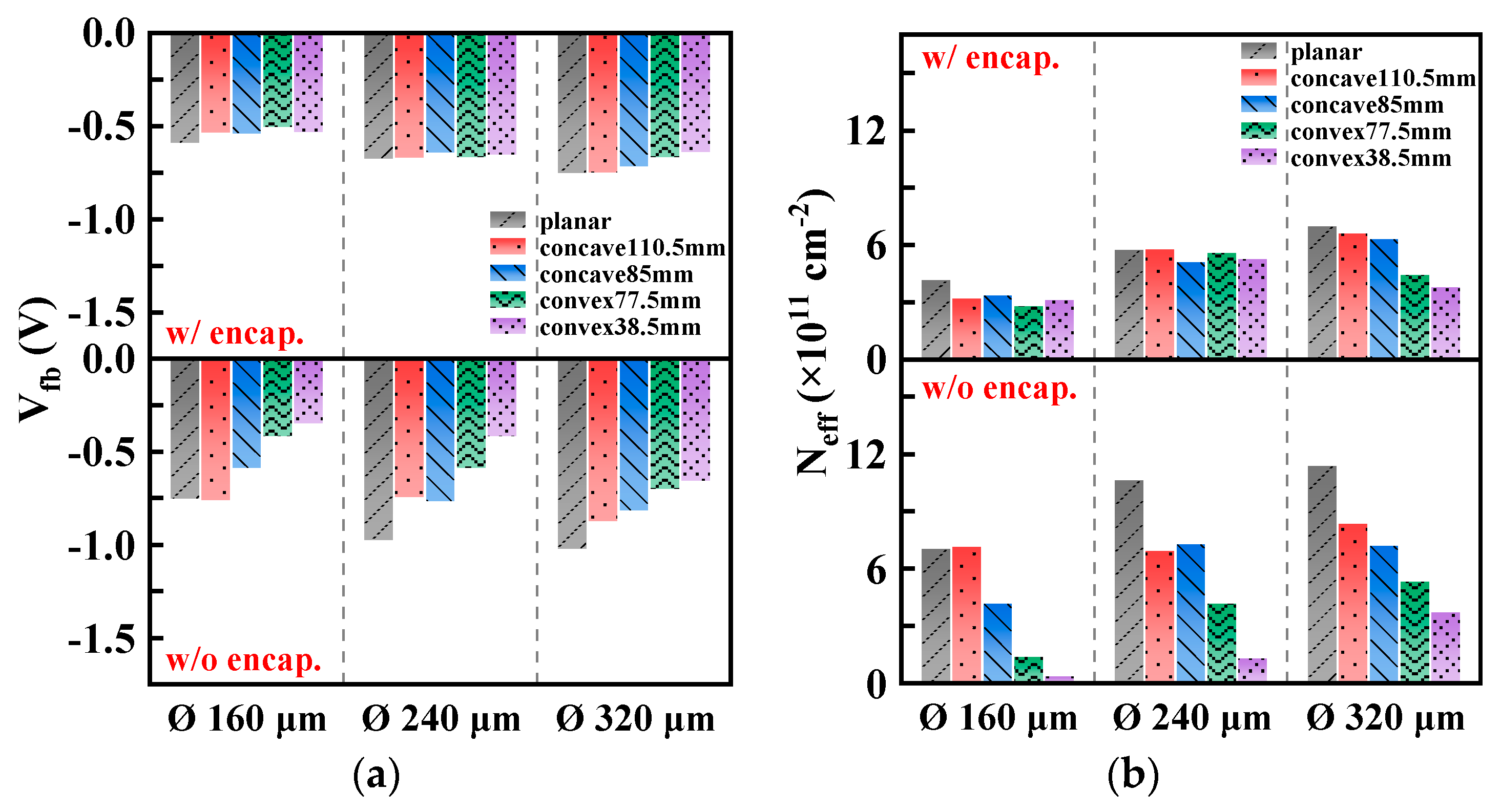
4.2. Comparative Analysis of Extracted Parameters

The variations in V_fb for encapsulated and bare MOSCAPs are positively shifted with the increase in bending deformations under concave and convex conditions, as mentioned in Section 4.1. This may be attributed to more electrons being injected by increasing mechanical strains, but the behavior of the fluctuating magnitude of V_fb from planar to bent states varies with Ø for MOSCAPs w/ and w/o encapsulation. It is significant to compare the V_fb and effective oxide charge (N_eff) in encapsulated and bare MOSCAPs. The V_fb corresponding to C_fb is extracted from C-V curves, and C_fb and N_eff are calculated as follows [15]:

$$\left\{\begin{array}{l}{C}_{fb}=\frac{C_{\max }}{1+\frac{(C_{\max }/C_{\min })-1}{2\sqrt{\ln (\left|N_A-N_D\right|/n_i)}}}\\ N_{eff}=\frac{C_{\max }\times \Delta V_{fb}}{q\times A}\end{array}\right.$$

(2)

where C_max and C_min are the maximum and minimum capacitance of measured C-V curves, N_A is the acceptor concentration, N_D is the donor concentration, n_i is the intrinsic carrier concentration, ΔV_fb is the theoretical V_fb minus extracted V_fb, q is the electron charge, and A is the gate surface area of MOSCAPs.

Figure 12 summarizes the V_fb and N_eff for encapsulated and bare MOSCAPs with Ø from 160 μm to 320 μm under bending conditions. Compared to the encapsulated devices with Ø 160 μm and Ø 320 μm, the encapsulated MOSCAP of Ø 240 μm presents the most desirable ability to alleviate the instability of V_fb in bare devices. Specifically, the precise variations of V_fb with four bending radii of (−)110.5 mm, (−)85 mm, (+)77.5 mm, and (+)38.5 mm minus V_fb in the planar state (i.e., V_fb–V_fb,o) were extracted to be as small as 0.005 V, 0.034 V, 0.009 V, and 0.023 V. This shows that the encapsulated MOSCAP with Ø 240 μm can beneficially relieve the strain in the gate dielectric layer, leading to the enhancement of stability of J_g and V_fb. In the planar state, N_eff in encapsulated MOSCAPs with Ø of 160 μm, 240 μm, and 320 μm is 4.14 × 10¹¹ cm⁻², 5.74 × 10¹¹ cm⁻², and 6.99 × 10¹¹ cm⁻². N_eff increased to 7.0 × 10¹¹ cm⁻², 10.61 × 10¹¹ cm⁻², and 11.38 × 10¹¹ cm⁻² for bare MOSCAPs with Ø of 160 μm, 240 μm, and 320 μm. However, as the bending deformations are applied, the decrease in N_eff is obvious in the bare MOSCAPs, probably because the physical thickness of the gate dielectric layer with a larger size is more sensitive to being altered and affected by bending strains without the protection of the ultrathin encapsulation layer.

Figure 13 illustrates the change in C_max divided by C_max at 1 kHz (i.e., normalized C_max (ω)) with Ø of 160 μm, 240 μm, and 320 μm in encapsulated and bare MOSCAPs. Figure 14 illustrates the extracted values of frequency dispersion according to the varied Ø under bending conditions. Notably, the frequency dispersion from Ø 160 μm to Ø 320 μm is 9.19%/Dec, 7.67%/Dec, and 8.3%/Dec in the planar state for bare MOSCAPs, which is relatively large and fluctuating. However, the frequency dispersion in the planar state is extremely stable for encapsulated MOSCAPs from Ø 160 μm to Ø 320 μm, and is 6.29%/Dec, 6.63%/Dec, and 6.68%/Dec. Among the three values of Ø in encapsulated MOSCAPs, Ø 160 μm maximally maintains stability of frequency dispersion under the four bending conditions, but the larger areas of Ø 240 μm and Ø 320 μm only performed better under concave bending conditions, rather than convex. The C_max performances for encapsulated MOSCAPs with Ø 320 μm under concave and convex bending deformations are consistent with the properties of the frequency dispersion, while the increased frequency dispersion for encapsulated MOSCAPs with Ø 240 μm denotes the substantial changes in interface states.

In addition, compared to Ø 160 μm and Ø 320 μm, the frequency dispersion of bare MOSCAPs with Ø 240 μm is most stable under bending deformations, which is due to the robustness of both C_max and interfacial properties. Hence, the results of frequency dispersion indicate that the smallest Ø of 160 μm is the favorable choice in ultrathin encapsulation strategies, but it needs optimization of the strain insensitivity of both the ultrathin dielectric layer and the interface between the dielectric and ultrathin channels as Ø increases.

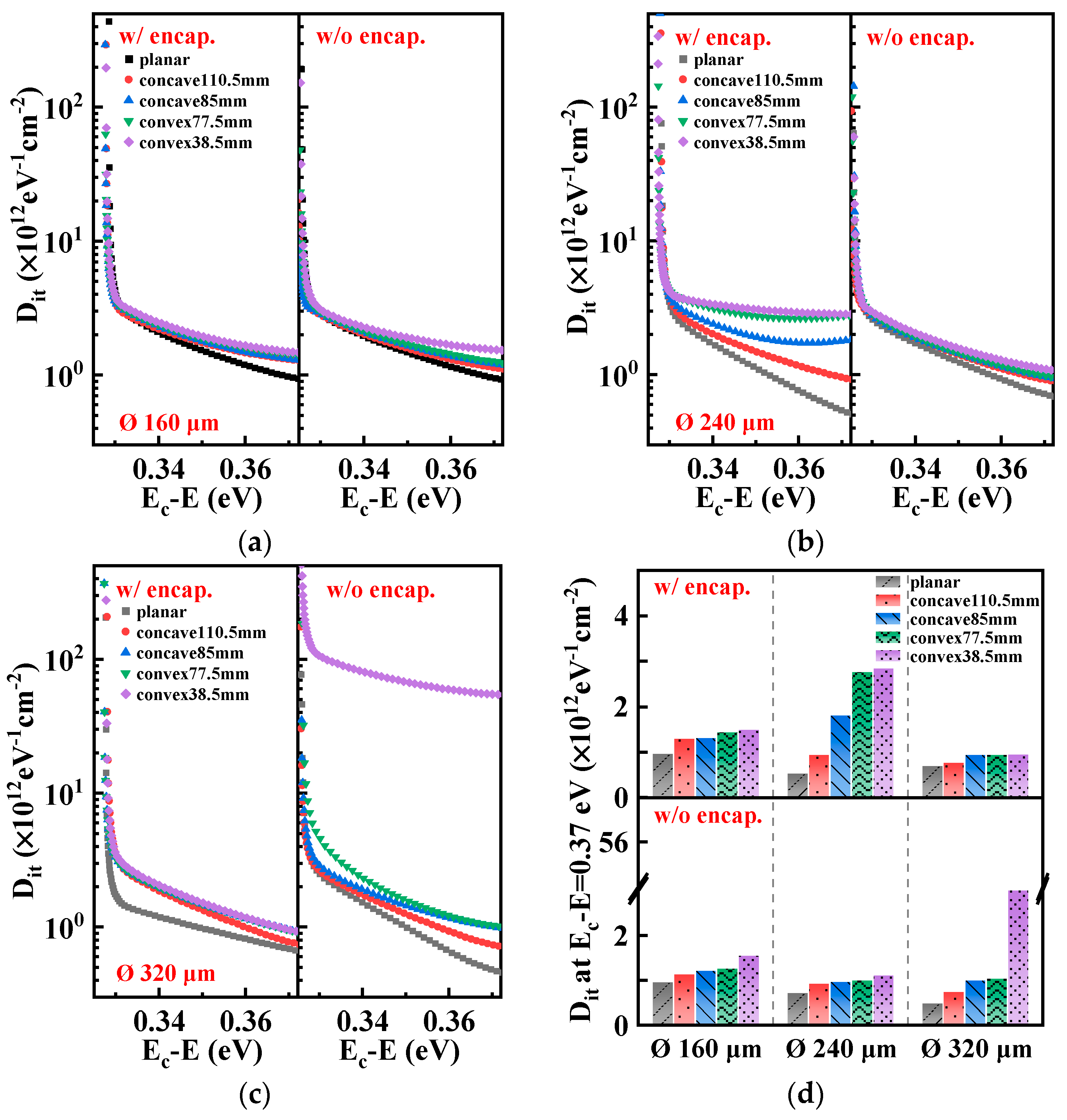
4.3. Comparative Analysis on Interfacial Characteristics

Figure 15a illustrates the D_it distribution for Al₂O₃/alucone-encapsulated and bare MOSCAPs with Ø 160 μm under bending conditions. The D_it values were extracted using the methods of Terman [16]. The encapsulated MOSCAPs with Ø 160 μm exhibit similar changes in bending strains related to D_it distribution compared to the bare device with the same Ø of 160 μm, which is probably because the optimized NMP position in the Si channel uses ultrathin encapsulation strategies. When Ø increased, the variations in D_it distribution differed between 240 μm and 320 μm, as shown in Figure 15b,c. For Ø 240 μm of encapsulated and bare MOSCAPs, the obvious increase in D_it according to the bending strain is verified in the former. However, the relatively stable performance in the latter is due to the reliability of both C_max and frequency dispersion. When the Ø further increased to 320 μm for bare MOSCAPs, the D_it values at investigated E_c-E entirely increased by two orders of magnitude under high deformation of (+)38.5 mm. Hence, the encapsulated MOSCAPs with Ø 320 μm can maintain the stability of D_it distributions under bending conditions. Moreover, in encapsulated MOSCAPs with Ø 320 μm, D_it values distributed at 0.33 eV beneath the conduction band (E_c) at bending states notably increased to 2 times in the planar state.

Importantly, the D_it values for encapsulated and bare MOSCAPs with three values of Ø are representative of the energy level of E_c − E = 0.37 eV (i.e., 0.19 eV above the mid-gap), which changed with different Ø under bending deformations, as shown in Figure 15d. Compared to the planar state, the variations in D_it at the energy level of E_c − E = 0.37 eV of MOSCAPs with Ø 160 μm increased to 1.3, 1.4, 1.5, and 1.6 times in encapsulated devices with the four bending radii. However, they increased to 1.2, 1.3, 1.3, and 1.6 times in bare devices corresponding to the same bending deformation. The variations are continually stable for larger Ø of 240 μm in bare MOSCAPs, and increased to 1.3, 1.4, 1.4, and 1.6 times. However, the values rose rapidly for the largest Ø of 320 μm in bare MOSCAPs, and increased to 1.6, 2.1, 2.2, and 116.2 times under the four bending conditions compared with the planar state. On the other hand, for encapsulated MOSCAPs with Ø 240 μm, the variations corresponding to the four bending states on D_it at the energy level of E_c − E = 0.37 eV increased to 1.8, 3.4, 5.3, and 5.4 times. The variations in D_it at the reference energy level in encapsulated MOSCAPs with Ø 320 μm importantly and stably increased to 1.1, 1.4, 1.4, and 1.4 times under the four bending conditions. From the thorough analysis of D_it results, it can be carefully speculated that the interfacial characteristics of MOSCAPs with different gate dielectric surface areas under bending deformations are promoted/maintained overall through ultrathin encapsulation strategies of Al₂O₃/alucone nanolaminates.

The circular gate dielectric surface areas equipped with three values of Ø at 160 μm, 240 μm, and 320 μm performed using different mechanisms under bending conditions. Encapsulated MOSCAPs with Ø of 160 μm can maintain the stability of C_max and frequency dispersion under concave and convex bending conditions, as well as having a certain ability to inhibit the growth of J_g compared to the bare MOSCAPs with the same Ø. As Ø increased to 240 μm, the stability of C_max was not only maintained, but the reliability of J_g and V_fb was strengthened, while the performance of the frequency dispersion accompanied with interfacial properties under convex bending deformations was supposed to have been further optimized. The interfacial characteristics were enhanced under concave and convex bending conditions for encapsulated MOSCAPs at the largest Ø of 320 μm. However, the C_max deteriorated due to the high convex bending deformations, and the performance of J_g was satisfactory in this configuration. In addition to the above, the long-term stability of the device was also studied. The encapsulated and bare devices were tested again after being stored in the air for three months. It was found that the performance of the packaged device did not change, while C_max of the bare device dropped by 10%. It can be seen that this work has considered long-term stability. The performance of the encapsulated device did not degrade although the performance of the bare device degraded, indicating that the Al₂O₃/alucone encapsulation structure is conducive to improving the long-term stability of the device.

5. Conclusions

In conclusion, ultrathin encapsulation strategies of Al₂O₃/alucone nanolaminates combined with different gate dielectric surface areas were employed in flexible monocrystalline Si NM-based MOSCAPs, and the electrical properties of encapsulated MOSCAPs with different gate dielectric islands were explored and evaluated under the planar and different bending deformations. To improve the electro-mechanical stability of wearable and implantable electronics, it is recommended to use an Al₂O₃/alucone ultrathin encapsulation structure. To maintain/improve the stability of the oxide layer and the interfacial characteristics of the encapsulated device under bending conditions, it is recommended to adopt a design with a diameter range of 160 to 240 μm, namely, a gate dielectric surface area of 0.02 to 0.05 mm². The CMOS devices have scalability, and the encapsulation process uses ALD/MLD technology with precise and controllable thickness. These are all standard CMOS process steps. Therefore, the encapsulation process also has the same scalability, in addition to having promising commercial prospects. The findings highlight that variations in the gate dielectric surface area, as a form factor, significantly influence the electrical performance in Si NM-based MOSCAPs w/ and w/o encapsulation according to the concave and convex bending deformations.