A Multiband and Multifunctional Metasurface for Linear and Circular Polarization Conversion in Reflection Modes
Abstract
:1. Introduction
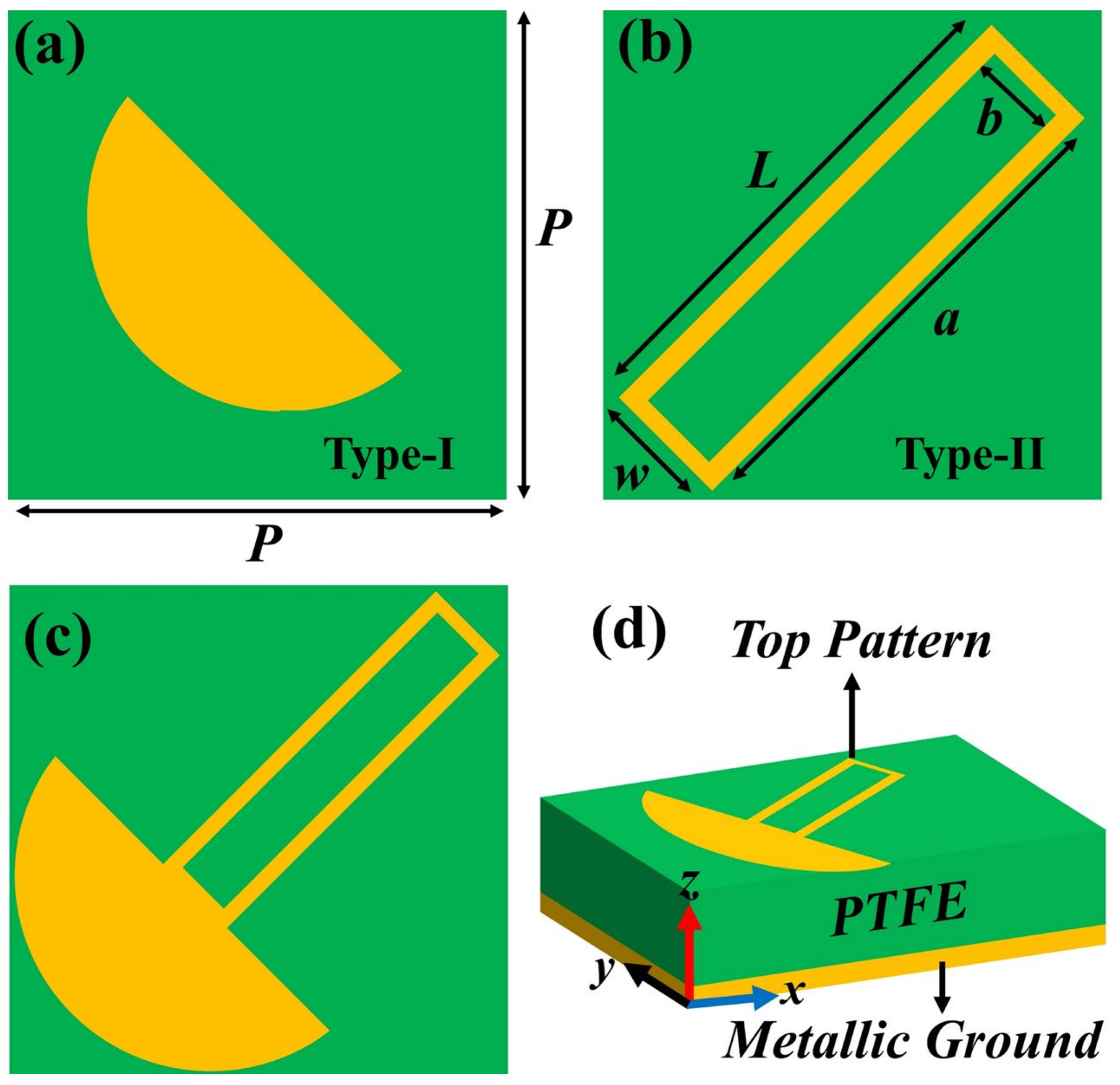
2. Unit Cell Design
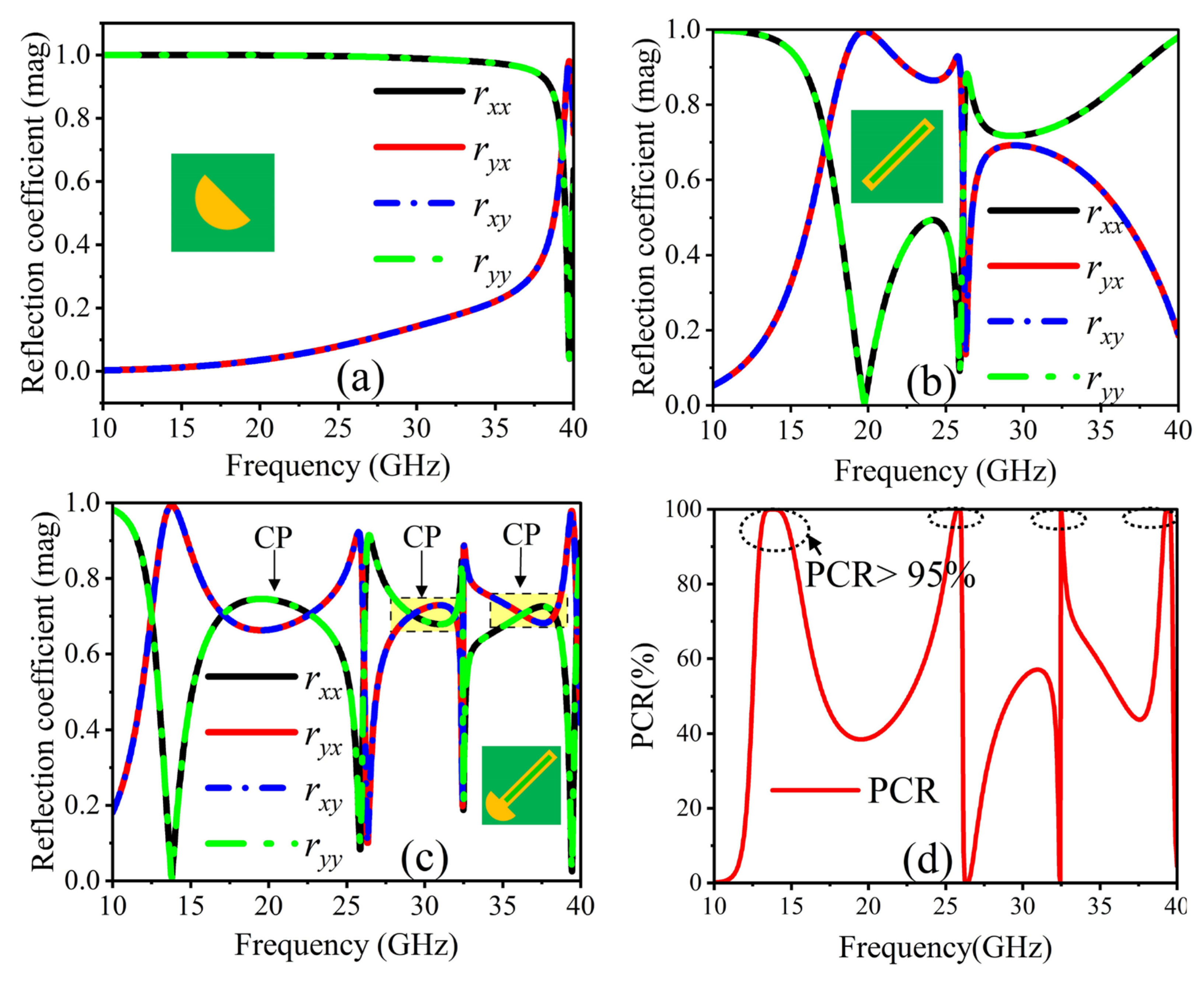
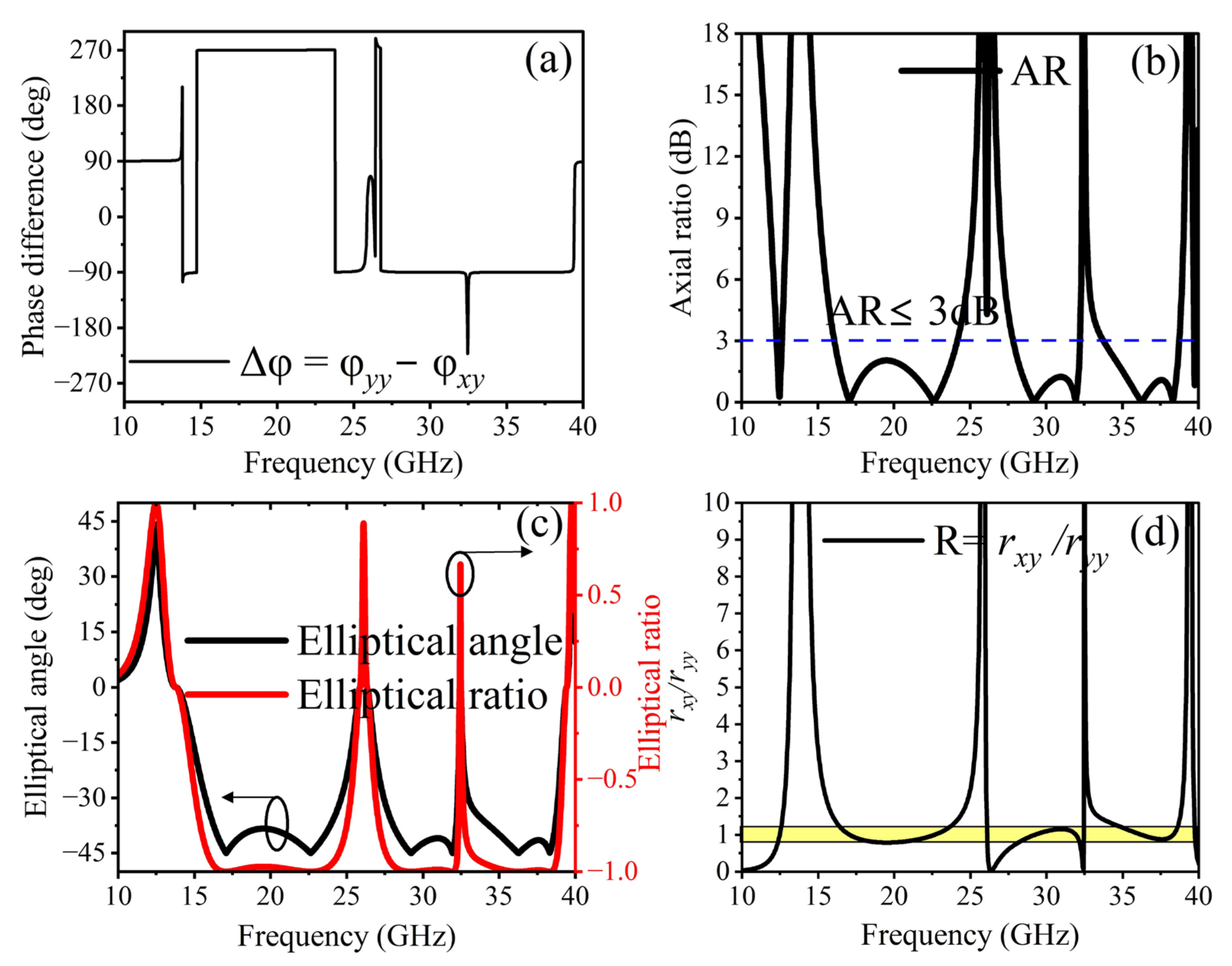
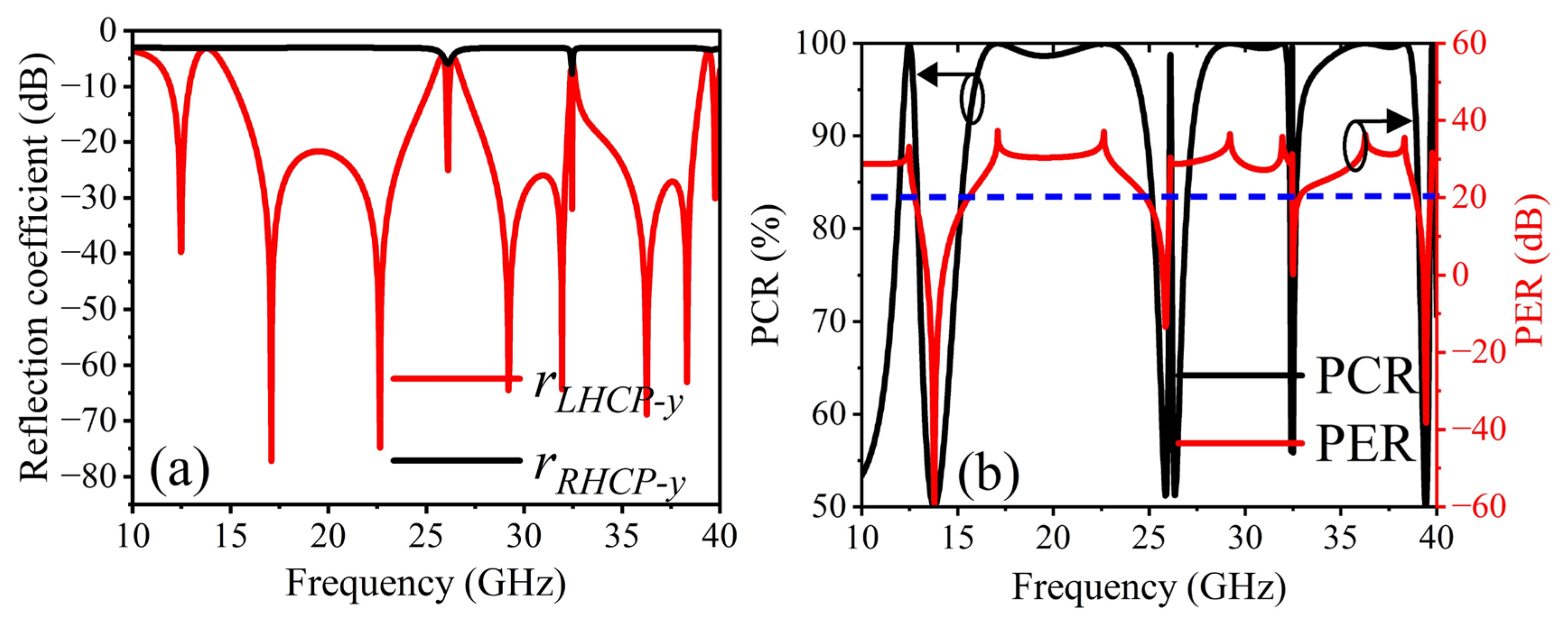
3. Simulated Results and Discussion
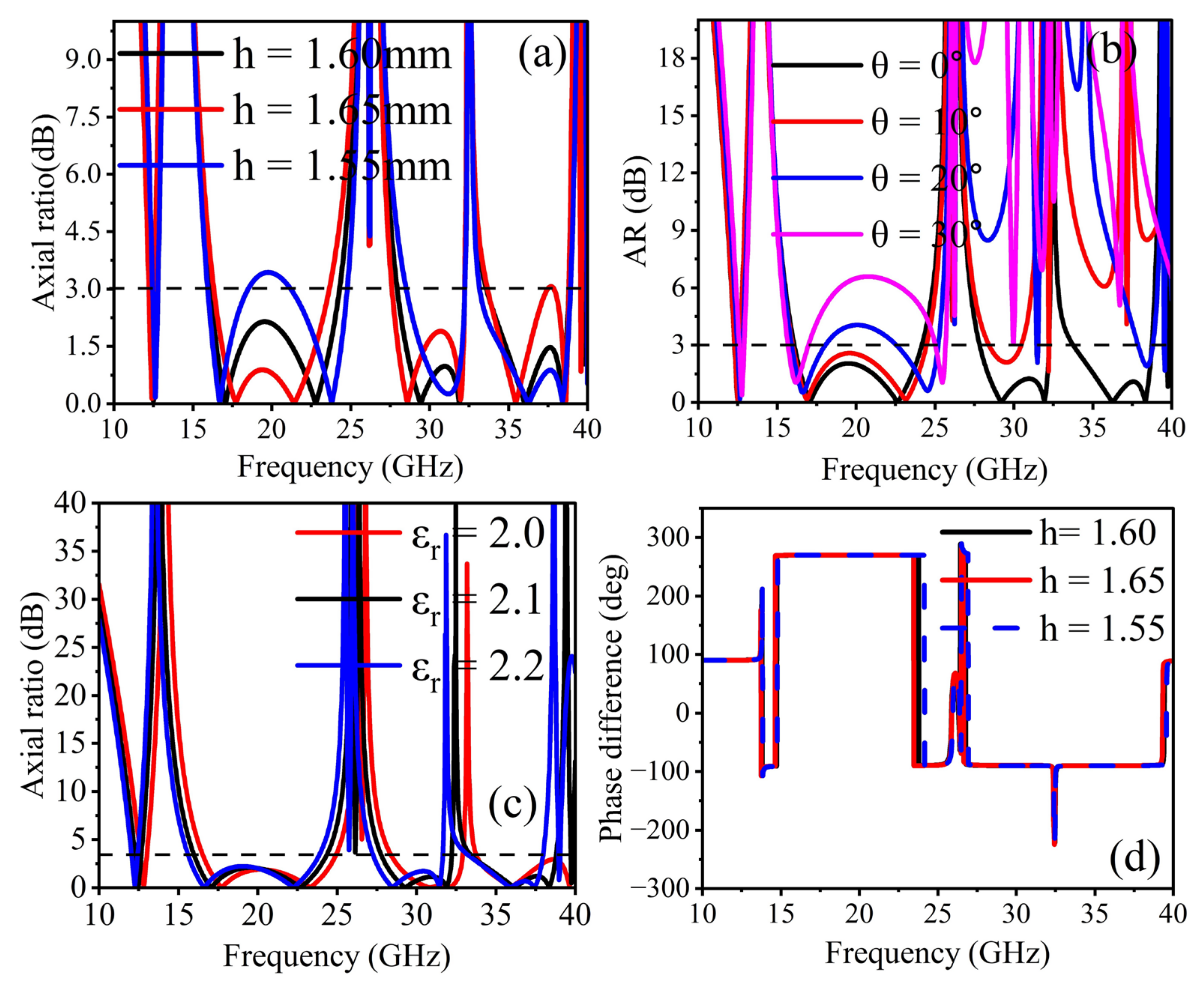
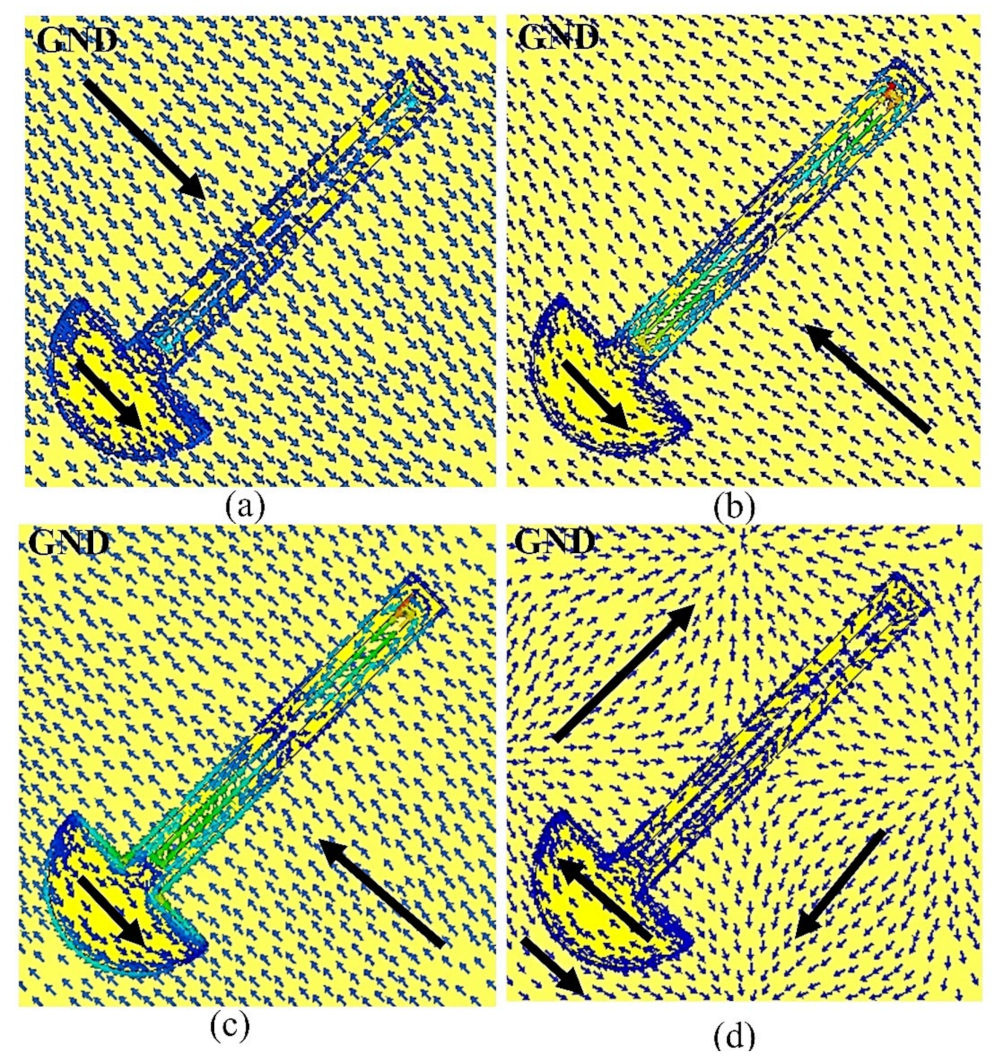
4. Parametric Analysis
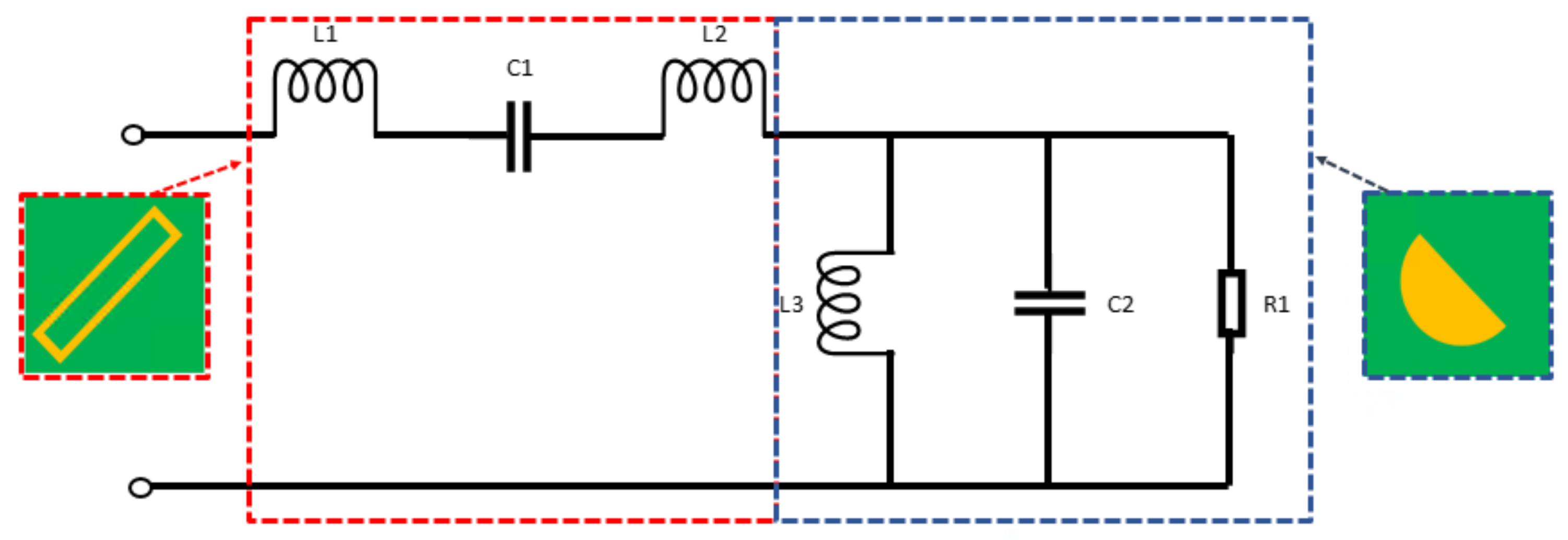
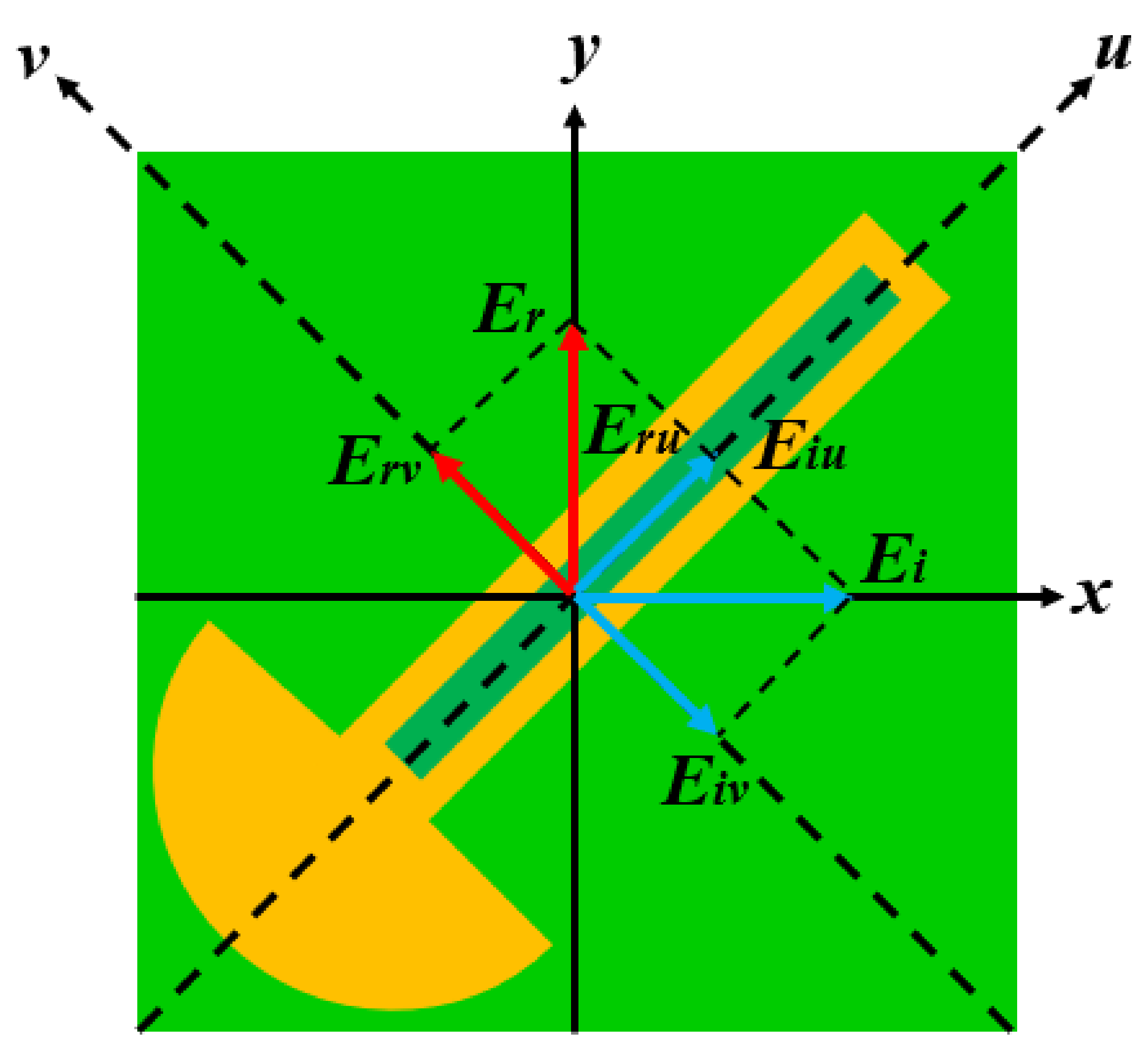
5. Theoretical Analysis
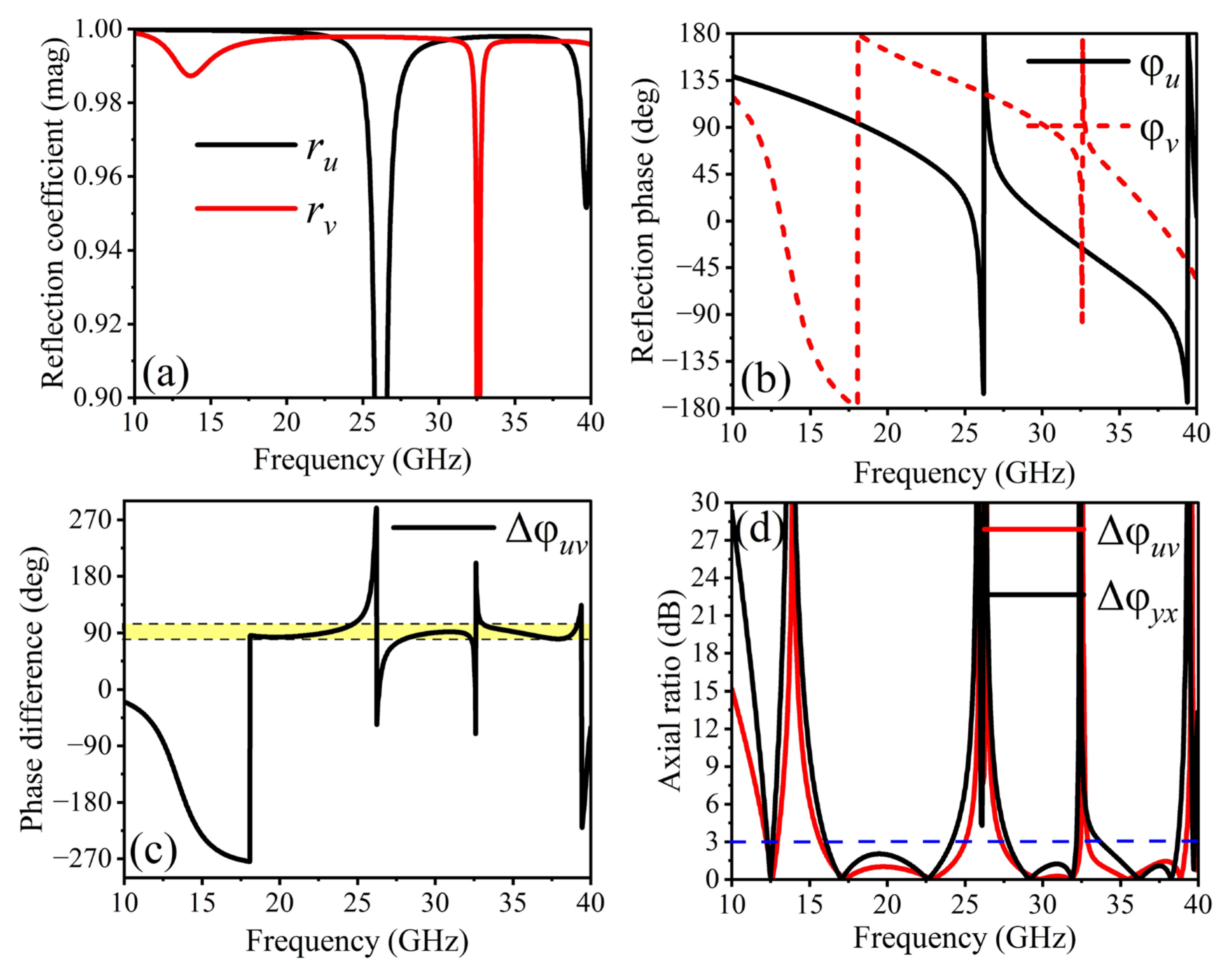
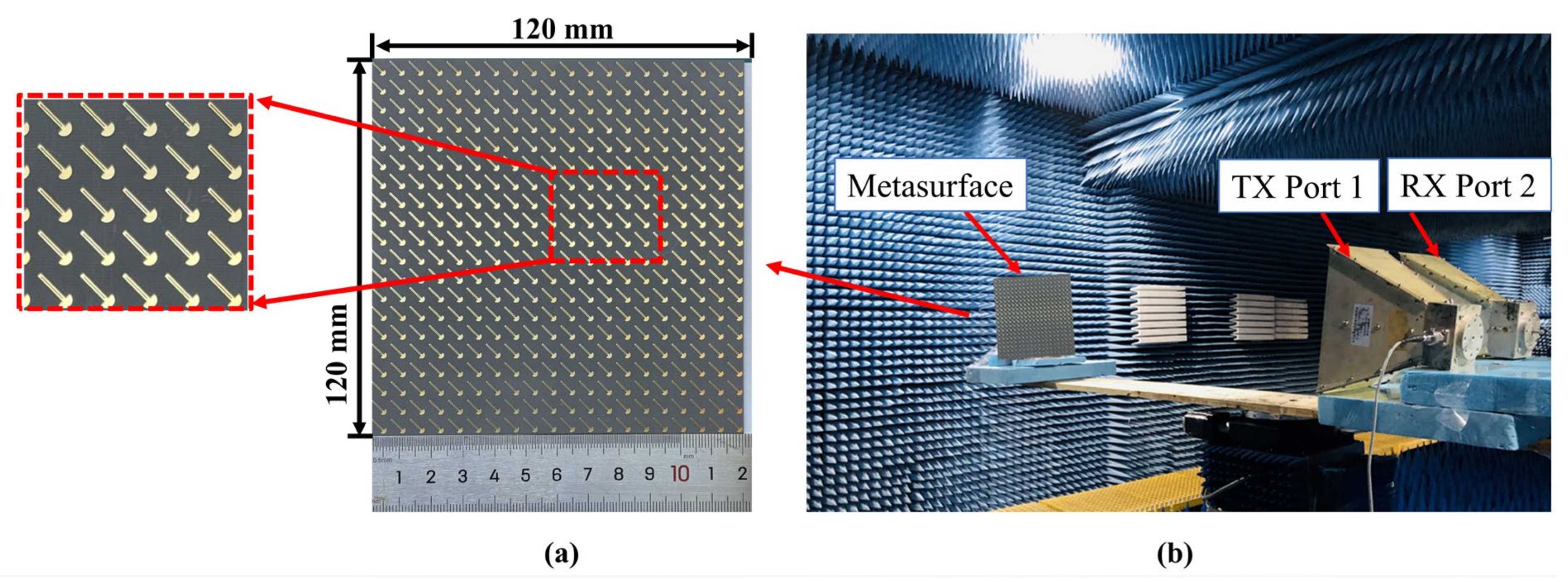
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fahad, A.K.; Ruan, C.; Nazir, R.; Hassan, B. Transmissive Polarizer Metasurfaces: From Microwave to Optical Regimes. Nanomaterials 2022, 12, 1705. [Google Scholar] [CrossRef]
- Ding, F.; Tang, S.W.; Bozhevolnyi, S.I. Recent advances in polarization-encoded optical metasurface. Adv. Photon. Res. 2021, 2, 2000173. [Google Scholar] [CrossRef]
- Faniayeu, I.; Asadchy, V.; Fanyaev, I. Polarization Control with Helical Metasurfaces. Crystals 2020, 10, 726. [Google Scholar] [CrossRef]
- Badri, S.H.; Gilarlue, M.M.; Saeid, N.S.; Kim, J.S. Narrowband-to-broadband switchable and polarization-insensitive terahertz metasurface absorber enabled by phase-change material. J. Opt. 2022, 24, 025101. [Google Scholar] [CrossRef]
- Maral, G.; Bousquet, M.; Sun, Z. Satellite Communications Systems: Systems, Techniques, and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Nilotpal Nama, L.; Bhattacharyya, S.; Chakrabarti, P. A metasurface-based broadband quasi nondispersive cross polarization converter for far infrared region. Int. J. RF Microw. Comp. Aided. Eng. 2019, 29, e21889. [Google Scholar] [CrossRef]
- Jeyaraj, J.P.G.; Swaminathan, A. An efficient reflective polarization rotation meta surface for broadband RCS reduction. Int. J. RF Microw. Comp. Aided. Eng. 2018, 28, e21474. [Google Scholar] [CrossRef]
- Cheng, Z.; Cheng, Y. A multi-functional polarization convertor based on chiral metamaterial for terahertz waves. Opt. Commun. 2019, 435, 178–182. [Google Scholar] [CrossRef]
- Majeed, A.; Zhang, J.; Ashraf, M.A.; Memon, S.; Mohammadani, K.H.; Ishfaq, M.; Sun, M. An ultra-wideband linear-to-circular polarization converter based on a circular, pie-shaped reflective metasurface. Electronics 2022, 11, 1681. [Google Scholar] [CrossRef]
- Chen, L.; Ma, Q.; Luo, S.S.; Ye, F.J.; Cui, H.Y.; Cui, T.J. Touch-Programmable Metasurface for Various Electromagnetic Manipulations and Encryptions. Small 2022, 18, 2203871. [Google Scholar] [CrossRef]
- Ma, Q.; Gao, W.; Xiao, Q.; Ding, L.; Gao, T.; Zhou, Y.; Gao, X.; Yan, T.; Liu, C.; Gu, Z.; et al. Directly wireless communication of human minds via non-invasive brain-computer-metasurface platform. eLight 2022, 2, 11. [Google Scholar] [CrossRef]
- Bilal, R.M.H.; Baqir, M.A.; Choudhury, P.K.; Ali, M.M.; Rahim, A.A. On the specially designed fractal metasurface-based dual-polarization converter in the THz regime. Results Phys. 2020, 19, 103358. [Google Scholar] [CrossRef]
- Wen, D.; Yue, F.; Li, G.; Zheng, G.; Chan, K.; Chen, S.; Chen, M.; Li, K.F.; Wong, P.W.H.; Cheah, K.W.; et al. Helicity multiplexed broadband metasurface holograms. Nat. Commun. 2015, 6, 8241. [Google Scholar] [CrossRef] [PubMed]
- Majeed, A.; Zhang, J. A study of linear-to-linear (LTL) cross-polarization conversion metasurface (CPCM) in microwave regime. Optik 2023, 274, 170497. [Google Scholar] [CrossRef]
- Long, F.; Yu, S.; Kou, N.; Zhang, C.; Ding, Z.; Zhang, Z. Efficient broadband linear polarization conversion metasurface based on %-shape. Microw. Opt. Technol. Lett. 2020, 62, 226–232. [Google Scholar] [CrossRef]
- Das, P.; Mandal, K. Polarization converter surface integrated MIMO antenna for simultaneous reduction of RCS and mutual coupling. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 1782–1786. [Google Scholar] [CrossRef]
- Majeed, A.; Zhang, J.; Awan, Z.A.; Memon, S.; Ishfaq, M.; Wang, C. A high-efficiency dual-band linear-to-circular polarization converter based on rectangular-slot reflective metasurface. Appl. Sci. 2022, 12, 9172. [Google Scholar] [CrossRef]
- Lin, B.Q.; Huang, W.Z.; Lv, L.T.; Guo, J.X.; Huang, S.Q.; Zhu, R. An ultra-wideband linear-to-circular polarization conversion realized by an 8-shaped metasurface. Plasmonics 2021, 62, 629–634. [Google Scholar] [CrossRef]
- Khan, M.I.; Chen, Y.; Hu, B.; Ullah, N.; Bukhari, S.H.R.; Iqbal, S. Multiband linear and circular polarization rotating metasurface based on multiple plasmonic resonances for C, X and K band applications. Sci. Rep. 2020, 10, 17981. [Google Scholar] [CrossRef]
- Lin, B.; Lv, L.; Guo, J.; Liu, Z.; Ji, X.; Wu, J. An ultra-wideband reflective linear-to-circular polarization converter based on anisotropic Metasurface. IEEE Access 2020, 8, 82732–82740. [Google Scholar] [CrossRef]
- Markovich, D.L.; Andryieuski, A.; Zalkovskij, M.; Malureanu, R.; Lavrinenko, A.V. Metamaterial polarization converter analysis: Limits of performance. Appl. Phys. B 2013, 112, 143–152. [Google Scholar] [CrossRef]
- Dutta, R.; Ghosh, J.; Yang, Z.; Zhang, X. Multi-band and multifunctional metasurface-based reflective polarization converter for linear and circular polarization. IEEE Access 2021, 9, 152738–152748. [Google Scholar] [CrossRef]
- Qiu, L.; Xiao, G.; Kong, X.; Xiong, C. Broadband, polarization insensitive low-scattering metasurface based on lossy Pancharatnam-Berry phase particles. Optics Express 2019, 27, 21226–21238. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, J. Manipulating terahertz wave and reducing radar cross section (RCS) by combining a Pancharatnam–Berry phase with a coding metasurface. Laser Phys. 2019, 29, 075403. [Google Scholar] [CrossRef]
- Tang, Y.; Liang, Y.; Yao, J.; Chen, M.K.; Lin, S.; Wang, Z.; Zhang, J.; Huang, X.G.; Yu, C.; Tsai, D.P. Chiral bound states in the continuum in plasmonic metasurfaces. Laser Photonics Rev. 2023, 17, 2200597. [Google Scholar] [CrossRef]
- Gryb, D.; Wendisch, F.J.; Aigner, A.; Gölz, T.; Tittl, A.; Menezes, L.d.S.; Maier, S.A. Two-Dimensional Chiral Metasurfaces Obtained by Geometrically Simple Meta-atom Rotations. Nano Lett. 2023, 23, 8891–8897. [Google Scholar] [CrossRef] [PubMed]
- Lalbakhsh, A.; Afzal, M.U.; Hayat, T.; Esselle, K.P.; Mandal, K. All-metal wideband metasurface for near-field transformation of medium-to-high gain electromagnetic sources. Sci. Rep. 2021, 11, 9421. [Google Scholar] [CrossRef]
- Karamirad, M.; Ghobadi, C.; Nourinia, J. Metasurfaces for wideband and efficient polarization rotation. IEEE Trans. Antennas Propag. 2020, 69, 1799–1804. [Google Scholar] [CrossRef]
- Pouyanfar, N.; Nourinia, J.; Ghobadi, C.; Nayyeri, V. Low-profile reflective surface for multi-band linear-to-linear and linear-to-circular polarization conversion. IEEE Access 2023, 11, 135159–135165. [Google Scholar] [CrossRef]
- Shukoor, M.A.; Bini, T.S.; Kunju, N.; Dey, S. Wideband dual-polarized linear-circular and linear-cross angular stable THz reflective polarizer based on a modified square loop FSS. Appl. Opt. 2022, 61, 6476–6482. [Google Scholar] [CrossRef]
- Xu, G.; Gao, L.; Chen, Y.; Ding, Y.; Wang, J.; Fang, Y.; Wu, X.; Sun, Y. Broadband polarization manipulation based on W-shaped metasurface. Front. Mater. 2022, 9, 850020. [Google Scholar] [CrossRef]
- Cao, W.; Yang, X.; Gao, J. Broadband polarization conversion with anisotropic plasmonic metasurfaces. Sci. Rep. 2017, 7, 8841. [Google Scholar] [CrossRef] [PubMed]
- Kundu, D.; Singh, J.; Singh, D.; Chakrabarty, A. Design and analysis of broadband ultrathin reflective linear-to-circular polarization converter using polygon-based anisotropic-impedance surface. IEEE Trans. Antennas Propag. 2021, 69, 5154–5159. [Google Scholar] [CrossRef]
- Coskun, A.; Hasar, U.C.; Ozmen, A.; Ertugrul, M. Easy-to-implement Ultra-thin, wideband, and multi-functional polarization converter for K and Ka-band applications. Adv. Theory Simul. 2022, 5, 2100543. [Google Scholar] [CrossRef]
- Pouyanfar, N.; Nourinia, J.; Ghobadi, C. Multiband and multifunctional polarization converter using an asymmetric metasurface. Sci. Rep. 2021, 11, 9306. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Dang, R.; Li, L. Dual-linear-to-circular polarization converter-based polarization-twisting metasurface antenna for generating dual band dual circularly polarized radiation in Ku-band. IEEE Trans. Antennas Propag. 2022, 70, 9877–9881. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghosh, J.; Singh, M.S.; Sarkhel, A. A low-profile multifunctional metasurface reflector for multiband polarization transformation. IEEE Trans. Circuits Syst. II 2023, 70, 76–80. [Google Scholar] [CrossRef]
- Zhang, J.W.; Liang, J.C.; Xia, J.; Zhang, J. A conformal coding metasurface for dual polarization conversion and radar cross-section (RCS) reduction. J. Opt. 2023, 25, 125102. [Google Scholar]

| P | r | w | L | a | b |
|---|---|---|---|---|---|
| 6 | 1.1 | 0.52 | 5.0 | 4.40 | 0.20 |
| Reference | Substrate Height h (mm) | Periodic Unit Cell p (mm) | 3 dB AR (%) | PCR (%) | Substrate Layer | Performance Polarization | No. of Bands |
|---|---|---|---|---|---|---|---|
| Ref. [9] | 1.6 | 6.0 | 50.8 | 90 | Single layer | LP–CP | 1 |
| Ref. [17] | 1.6 | 6.0 | 35.23/ 26.62 | NG | Single layer | LP–CP | 2 |
| Ref. [18] | 3.5 | 9.5 | 69.51 | NG | Single layer | LP–CP | 1 |
| Ref. [30] | 1.0 | 8.0 | 13.3/31.8/ 23.9 | NG | Single layer | LP–CP | 3 |
| Ref. [37] | 1.57 | 10.0 | 0.9/1.6/ 1.7/1.72 | NG | Bi-layer | LP–CP | 4 |
| This paper | 1.6 | 6.0 | 40.15/14.6/ 13.76/2.7/0.2 | 95 | Single layer | LP–CP LP–LP | 5 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hafeez, S.; Yu, J.; Umrani, F.A.; Yun, W.; Ishfaq, M. A Multiband and Multifunctional Metasurface for Linear and Circular Polarization Conversion in Reflection Modes. Crystals 2024, 14, 266. https://doi.org/10.3390/cryst14030266
Hafeez S, Yu J, Umrani FA, Yun W, Ishfaq M. A Multiband and Multifunctional Metasurface for Linear and Circular Polarization Conversion in Reflection Modes. Crystals. 2024; 14(3):266. https://doi.org/10.3390/cryst14030266
Chicago/Turabian StyleHafeez, Saima, Jianguo Yu, Fahim Aziz Umrani, Wang Yun, and Muhammad Ishfaq. 2024. "A Multiband and Multifunctional Metasurface for Linear and Circular Polarization Conversion in Reflection Modes" Crystals 14, no. 3: 266. https://doi.org/10.3390/cryst14030266
APA StyleHafeez, S., Yu, J., Umrani, F. A., Yun, W., & Ishfaq, M. (2024). A Multiband and Multifunctional Metasurface for Linear and Circular Polarization Conversion in Reflection Modes. Crystals, 14(3), 266. https://doi.org/10.3390/cryst14030266








