Next Article in Journal
On the Energy Dependence of the PL of RE Ions in LuBO3:RE (RE = Ce, Eu, Gd, or Tb)
Previous Article in Journal
Endowing Ferroelectric Properties of Tetragonal Lysozyme Crystals through C60 Doping
Previous Article in Special Issue
L-Glutamine Coating on Antibacterial Cu Surface by Density Functional Theory
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 14
Issue 4
10.3390/cryst14040340
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Hafnium Carbide: Prediction of Crystalline Structures and Investigation of Mechanical Properties

by
Jelena Zagorac
1,2,*,
Johann Christian Schön
3,*,
Branko Matović
1,2,
Svetlana Butulija
1,2 and
Dejan Zagorac
1,2
1
Materials Science Laboratory, Institute of Nuclear Sciences Vinča, Belgrade University, 11000 Belgrade, Serbia
2
Center for Synthesis, Processing and Characterization of Materials for Application in the Extreme Conditions-CextremeLab, Materials Science Laboratory, Institute of Nuclear Sciences Vinča, 11000 Belgrade, Serbia
3
Max Planck Institute for Solid State Research, Heisenbergstr. 1, 70569 Stuttgart, Germany
*
Authors to whom correspondence should be addressed.
Crystals 2024, 14(4), 340; https://doi.org/10.3390/cryst14040340
Submission received: 9 March 2024 / Revised: 19 March 2024 / Accepted: 25 March 2024 / Published: 2 April 2024
(This article belongs to the Special Issue Density Functional Theory (DFT) of Two-Dimensional Materials)
Browse Figures
Versions Notes

Abstract

:
Hafnium carbide (HfC) is a refractory compound known for its exceptional mechanical, thermal, and electrical properties. This compound has gained significant attention in materials science and engineering due to its high melting point, extreme hardness, and excellent thermal stability. This study presents crystal structure prediction via energy landscape explorations of pristine hafnium carbide supplemented by data mining. Apart from the well-known equilibrium rock salt phase, we predict eight new polymorphs of HfC. The predicted HfC phases appear in the energy landscape with known structure types such as the WC type, NiAs type, 5-5 type, sphalerite (ZnS) type, TlI type, and CsCl type; in addition, we predict two new structure types denoted as ortho_HfC and HfC_polytype, respectively. Moreover, we have investigated the structural characteristics and mechanical properties of hafnium carbide at the DFT level of computation, which opens diverse applications in various technological domains.

1. Introduction

The lack of predictability in solid-state synthesis and crystallography makes it difficult to discover new crystalline structures and design new materials. This is of particular concern since new types of crystal structures can exhibit special physical and chemical properties, while their realization as new materials is of great technological interest. To enhance crystal structure and materials discovery by providing promising synthesis targets in given chemical systems, the prediction of possible crystal structures in a chemical system and the computation of their physical properties are therefore of vital importance [1]. Here, crystal structure prediction (CSP) refers to the determination of the feasible crystalline modifications of solids from first principles, i.e., without input from experiments, where a large variety of search methods have been employed [1,2,3,4,5,6,7,8,9]; these a priori-type methods are frequently supplemented by data mining procedures that suggest starting configurations for local minimizations on the landscape. The ability to perform such predictions is based on the underlying mathematical structure of the chemical system, the energy landscape [10], where the time evolution and dynamics of the system occur, and where stable compounds correspond to locally ergodic regions on the landscape [2]. Thus, the study of the energy landscape of a chemical system provides insight into metastable chemical compounds capable of existence on various observational time scales [10] ranging from simple molecules and clusters [11], biomolecules [11], monolayers and nanotubes [12], bulk crystalline [7], and amorphous solids [11] to phase diagrams of multinary chemical systems [13] including both thermodynamically stable and metastable phases [14]. The energy landscape concepts and their applications in extreme conditions [15] are especially important for investigating materials such as hafnium carbide, where not only the potential energy landscape but also the potential enthalpy landscapes [10] at high non-zero pressures are relevant.
Hafnium carbide (HfC) belongs to the family of transition metal carbides and exhibits a wide range of remarkable properties including high strength, wear resistance, anti-oxidation, anti-corrosion, and biocompatibility, which make it a promising candidate for advanced materials applications [16]. It also ranks among the hardest materials, with a Vickers hardness value exceeding 20 GPa, making it a possible substitute for industrial diamonds [17]. Its high melting point, approximately 3900 °C, has attracted interest since a superior level of hardness can be inferred from a high melting point [18]. HfC can form solid solutions with various chemical systems, e.g., with TaC [19], ZrC [20], SiC [21], uranium monocarbide (UC) [22], and more complex ones like (Hf, Ta)C/SiC, and (Hf, Ti)C/SiC [23], SiC/(Hf, Ta)C(N)/(B)C [24], etc.
Several methods have been developed for synthesizing hafnium carbide, including carbothermic reduction, low-temperature synthesis, sol–gel polycondensation, chemical vapor deposition (CVD), and spark plasma sintering (SPS) [25,26,27,28]. In all of these experiments, as well as most of the calculations reported in the literature, hafnium carbide adopts a face-centered cubic (FCC) crystal structure, similar to that of the rock salt (NaCl) type [17,29,30,31]. In most of the earlier theoretical work, the equilibrium NaCl structure has been investigated for its mechanical properties, especially regarding the Vickers hardness [32,33,34,35,36]. There is only one study, by Zeng et al. [35], that deals with other HfC phases; however, the stable hafnium carbides discussed exhibit stoichiometries different from HfC.
In the current study, we go beyond this earlier work in a systematic fashion by performing a priori structure prediction in pristine hafnium carbide. We identify novel HfC modifications and compute their mechanical properties, thus providing promising targets for the synthesis of new HfC-based materials.

2. Computational Details

In the first part of our study, crystal structure prediction of hafnium carbide was carried out using global optimization (GS) of the energy landscape for identifying local minima of the potential energy or enthalpy. This exploration was supplemented by results from data mining-based searches, followed by local optimizations on the ab initio level of the most promising candidate structures, similar to the general procedure used in earlier work [37].
The enthalpy landscape of the HfC compound was explored for several pressures, including extremely high values up to 1.6 × 106 GPa (0, 0.16, 1.6, 16, 160, 1600, 16,000, 160,000 and 1,600,000 GPa). Here, we employed simulated annealing as an algorithm for the global search, combined with periodic local optimizations along the search trajectory, carried out with the G42+ code [38]. The global searches were performed for four formula units of HfC, and the moveclass of the random walk included shifts in randomly selected atoms only (65%), exchange of randomly chosen pairs of atoms (10%), and changes in the cell parameters with and without atom movements (25%). To perform the global searches with a reasonable computational effort, a fast computable empirical two-body potential consisting of Lennard–Jones and exponentially damped Coulomb terms was employed. In this fashion, ca. 27,000 structure candidates exhibiting a great variety of structures and structure types were generated.
The global search was supplemented with data-mining-based explorations of the ICSD database [39,40], which were restricted to the common AB structure prototypes found in our previous studies [41,42]. The data mining confirmed the equilibrium rock salt (NaCl), cesium chloride (CsCl), and sphalerite (ZnS) types of structures that had been obtained from the global searches as feasible modifications, and added the tungsten carbide (WC) type as a structure candidate in the HfC system via analogy to known crystallographic structure types.
The final step of the structure prediction part of the study was accomplished by locally minimizing all promising structure candidates on an ab initio level with the CRYSTAL17 code, based on linear combinations of atomic orbitals [43,44]. Analytical gradients were used for the local optimization [45,46]. DFT calculations were performed using two different functionals and approximations: the local density approximation (LDA) with the Perdew–Zunger (PZ) correlation functional [47], and the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional [48]. Previous studies have shown that the choice of these DFT functionals produces reliable structure prediction results [37,41]. For the integration over the Brillouin zone, a k-point mesh of 8 × 8 × 8 was generated using the Monkhorst–Pack scheme [49], and the energy convergence tolerance was set as 10−7 eV/atom [50].
Basis set choice is very important for the correct DFT structure optimization [51]. For hafnium, a Hf_ECP_Stevens_411d31G_munoz_2007 effective core pseudopotential was employed [52]. In the case of carbon, the C_6-21G*_catti_1993 all-electron basis set based on Gaussian-type orbitals was used [53,54].
Subsequently, the symmetries of the computed structures were determined using the program KPLOT [55], and the structures were visualized using the Vesta code [56]. Next, the energy was computed as a function of volume for the most promising modifications predicted, and possible high-temperature and high-pressure or effective negative-pressure phases were identified.
Finally, in the second part of this study, the mechanical properties of selected particularly interesting crystalline HfC structure candidates were calculated using the computational strategy implemented in the CRYSTAL17 solid-state quantum-chemical program [57]. A full elastic tensor has been generated using the keyword ELASTCON [58].

3. Results and Discussion

3.1. Energy Landscape and Energetic Properties

The most common candidate we observe on the enthalpy landscapes of HfC appears in the rock salt (NaCl) structure, which is the lowest energy minimum (global minimum) on the empirical potential energy landscape of HfC. After local optimization on the DFT level using LDA-PZ and GGA-PBE functionals, the NaCl type modification continues to be the lowest energy structure, shown on the computed energy vs. volume, E(V), curves (Figure 1) as well as in the energy ranking (Table 1). This is in agreement with the experimental observations [17] where it has been observed that NaCl is the equilibrium structure at standard thermodynamic conditions.
Apart from the NaCl modification, we note three predicted structures possibly appearing for effective negative pressures: the new ortho_HfC type, the 5-5 type, and the ZnS type (Figure 1 and Table 1). Similarly, several new polymorphs for the HfC system are predicted that might be feasible at high pressures or in the high-temperature region of the phase diagram, exhibiting the TlI type, the NiAs type, the WC type, and a new HfC_polytype. The CsCl type only appears on the enthalpy landscape for extremely high pressures and is energetically quite high compared to the other predicted modifications (Figure 1 and Table 1), suggesting that it might be difficult to reach even in high-pressure experiments, in contrast to, e.g., the case of most alkali metal halides [42]. We note that the energy ranking of these HfC polymorphs remains the same regardless of the computational ab initio approach employed, with only a slight variation between the WC and the ZnS type at the GGA-PBE level (Table 1).

3.2. Crystal Structure Prediction and Polymorphs of HfC

The predicted structures of hafnium carbide are visualized in Figure 2, while full structural details computed using LDA and GGA are presented in Table 2. The global minimum is found in the rock salt (NaCl) type of structure (Figure 2a) and appears in the cubic symmetry with the space group Fm-3m (no. 225), which is the known equilibrium phase of hafnium carbide. We note that the computed unit cell parameters (LDA a = 4.62 Å, GGA a = 4.67 Å, Table 2) are in excellent agreement with previous experimental observations [16,59,60,61,62] and DFT calculations [34,63,64,65,66,67,68,69].
The so-called 5-5 type is predicted to be thermodynamically stable in the negative pressure region (Figure 1). The transition negative pressure is expected to be around −20 GPa. The 5-5 structure type appears in the hexagonal symmetry with space group P63/mmc (no. 194). This type of structure can be described as a mutual fivefold coordination of cation A by anion B in a hexagonal lattice with ABAB stacking, where the A-atoms form trigonal bipyramids around B-atoms, and vice versa (Figure 2b) [70]. This structure has been found on the energy landscape of various AB chemical systems in the past [42,70,71,72].
The new predicted ortho_HfC type of structure appears in orthorhombic symmetry with space group Cmcm (no. 63) (Table 2). This new structure type can be visualized as a combination of the NaCl and 5-5 types of structure, where six fold octahedra are edge connected to the five fold trigonal bipyramids (Figure 2c), reminiscent of an intergrowth type of structure. Such a combination of structural features has reduced symmetry to the orthorhombic lattice; however, it should be feasible to synthesize it on the NaCl → 5-5 transition route. This is supported by the observation that very similar kinds of combinations of octahedra and trigonal bipyramids have been observed as local minima on the energy landscape of other ionic systems, such as for bulk NaCl (c.f., Figure 3 in reference [70]) or monolayers of MgO on sapphire (c.f., Figure 3d in reference [38]). Another novel structure type has also been found as a polytypic form of hafnium carbide, which is the first report of its kind. The HfC_polytype modification appears in the R3m (no. 160) space group in the trigonal crystal system (Figure 2d). The polytypic structure consists of edge-connected six-fold octahedra and trigonal prisms, which we might consider as a combination of NiAs and WC structural features. The trigonal symmetry of the HfC_polytype remains high and can easily be transformed into a hexagonal setting (shown in Table 2 and Figure 2d). The polytypic behavior has previously been experimentally observed in various chemical systems [73,74,75] and theoretically computed [76,77] in various chemical systems; in the HfC compound, it appears in high-temperature conditions as a metastable phase (Figure 1).
The TlI structure type is predicted to appear as a high-temperature form of hafnium carbide (Figure 1, Table 1). Although the TlI modification exhibits the same orthorhombic space group Cmcm (no. 63) as the newly predicted ortho_HfC type, these two structures are different. Unit cell and structural parameters differ (Table 2) and the TlI structure shows a sevenfold coordination of Hf by C atoms. The orthorhombic TlI type can be considered to be a rather distorted NaCl structure type, described as a chain of monocapped trigonal prisms sharing common rectangular faces (Figure 2e). There are possible synthesis routes for the TlI type of structure since it has previously been found along the NaCl → CsCl transition route in other chemical systems [41,78,79,80].
NiA modification appears in the same hexagonal P63/mmc (no. 194) space group as the 5-5 type structure; however, they are structurally very different. The NiAs type shows sixfold coordination of hafnium by carbon forming ABAB layers of octahedra, while the 5-5 type is fivefold coordinated with trigonal bipyramids (Figure 2b,f), reminiscent of an ionic analog of the h-BN type structure. The NiAs type has been found in previous theoretical searches for various AB systems [42,70,71,78], but this is the first indication of this type in the hafnium carbide system.
The tungsten carbide (WC) type of structure shows a hexagonal lattice with space group P-6m2 (no. 187) (Table 2). The WC modification can be visualized as edge-connected trigonal prisms formed by the six-fold coordination of Hf atoms by C atoms (Figure 2g). The WC type of hafnium carbide has previously been theoretically investigated for its hardness and elastic properties [81], as well as for semi-metal and electronic properties [82]. We note that the calculated cell parameters for the WC structure (LDA a = 3.20 Å; c = 2.90 Å, GGA a = 3.24 Å; c = 2.93 Å) are in good agreement with previous DFT calculations (LDA a = 3.227 Å; c = 2.915Å, GGA a = 3.267 Å; c = 2.942 Å) [81,82].
Finally, we predict two cubic phases, exhibiting the ZnS and CsCl type, respectively, as structure candidates in the HfC system. Both commonly appear on the energy landscape of AB compounds [70]; however, they are structurally very different. The sphalerite (ZnS) type appears in the space group F-43m (no. 216) and the CsCl type in the space group Pm-3m (no. 221), respectively. The ZnS-like phase shows fourfold coordination of Hf ions by C ions, while in the CsCl-like one, the Hf ion is eightfold coordinated by C ions (Figure 2h,i). Yang et al. carried out first-principles calculations of mechanical properties of cubic 5d transition metal monocarbides, where they predicted a stable ZnS type and an unstable CsCl type modification of hafnium carbide [33]. Our DFT calculations of the unit cell parameters (Table 2) concur with this study [33].

3.3. Mechanical Properties of Hafnium Carbide

The mechanical properties of hafnium carbide have been computed on the DFT-LDA level including elastic tensor constants (Cxy), bulk modulus (K), shear modulus (G), Young modulus (E), Poisson ratio (v), and Vickers hardness (VH) as shown in Table 3 and Table A1. The bulk modulus, shear modulus, and Vickers hardness were calculated using the Voigt–Reuss–Hill (VRH) approximation expressed in GPa. The Voigt–Reuss–Hill (VRH) approximation is a useful scheme by which anisotropic single-crystal elastic constants can be converted into isotropic polycrystalline elastic moduli, and where the validity of the VRH approximation is established in the literature [58,83]. Table 3 shows only three of the mechanically stable modifications of HfC, the NaCl type, the ortho_HfC type, and the NiAs type, and a comparison with previous experimental and theoretical observations where available. In addition, we will describe the computed mechanical properties of the mechanically unstable structures and compare them with previous reports in the literature. Here, instability was indicated by negative values of some of the computed elastic constants or/and mechanical moduli; we note that even though all structures investigated here corresponded to local minima of the energy and exhibited a positive bulk modulus (see Table A1 in Appendix A), such an instability can appear in the calculations due to the choice of approximation for the computation of the moduli and the finite atom displacements involved in the numerical computation of the moduli when the structure is already close to a possible phase transformation.
The computed value of the bulk modulus for the rock salt phase of HfC (K = 261.54 GPa) is in agreement with previous experimental (K = 242–263 GPa) and theoretical findings (233–278 GPa) (Table 3). Similarly, the computed values of the shear modulus (G = 192.73 GPa) and the Young modulus (E = 466.11 GPa) concur with experimental findings (G = 195 GPa and E = 461 GPa); here, the earlier calculations in the literature show a wide range of values (G = 166–230 GPa and E = 404–537 GPa). The computed Vickers hardness (VH = 27.22 GPa) is slightly overestimated compared to the data from experiment (VH = 18–26.1 GPa) but concurs with previously reported theoretical reports (VH = 26.2–29.08 GPa).
The computed bulk modulus (K = 225.48 GPa and 229.27 GPa), shear modulus (G = 161.71 GPa and 139.67 GPa), and Young modulus (E = 391.53 GPa and 348.29 GPa) for the predicted ortho_HfC-type and NiAs-type-HfC modifications are significantly lower than the values measured and computed for the equilibrium rock salt phase (Table 3). On the other hand, the computed Poisson ratio for these two predicted phases (v = 0.21 and 0.25) is higher than the one computed for the NaCl type modification. Finally, if one were to manage to synthesize the ortho_HfC type and the NiAs type of hafnium carbide, these would correspond to less hard phases compared to the rock salt type modification, and they thus might have versatile technological applications.
For the mechanically unstable structures (see Table A1 in Appendix A), we computed the value of the bulk modulus and compared it to previous calculations for the WC type, ZnS type, and CsCl type in the literature. Our LDA calculations of the bulk modulus of the WC type modification (K = 222.69 GPa) slightly underestimate the calculated values reported in the literature (K = 239 [81]), while for the ZnS type (K = 175.95 GPa) and the CsCl type (K = 227.16 GPa), we obtained slightly larger values (K = 165 GPa and K = 214 GPa [33]). We can conclude that our LDA-PZ calculations of the mechanical properties are in agreement with previous experimental and theoretical data, where available, and the values of the predicted mechanical properties of the new feasible HfC modifications should thus be realistic.

4. Conclusions

Hafnium carbide is a known compound with exceptional mechanical, thermal, and electrical properties. Here, we have performed crystal structure prediction of HfC using global optimization on enthalpy landscapes of the system supplemented by data mining searches in the ICSD database. Local optimizations of the obtained structure candidates have been performed using DFT, specifically employing the LDA-PZ and GGA-PBE functionals. Apart from the NaCl-type phase corresponding to the thermodynamically stable phase in standard conditions, we predict eight new polymorphs of hafnium carbide: the WC-type, NiAs-type, 5-5-type, ZnS-type, TlI-type, CsCl-type, ortho_HfC-type, and HfC_polytype polymorphs. Moreover, we have investigated the structural characteristics and mechanical properties of these predicted modifications of hafnium carbide at the ab initio level of computation. Our LDA-PZ calculations of the mechanical properties are in agreement with previous experimental and theoretical data, where available. The predicted values for the previously unknown HfC polymorphs suggest a certain degree of versatility for technological applications, making such modifications promising targets of chemical syntheses.

Author Contributions

D.Z., B.M. and J.C.S. conceived the idea; the global search optimization was performed by J.C.S., and the ab initio structure optimizations and the computation of the mechanical properties were performed by J.Z. and D.Z.; S.B. collected and analyzed the literature and the computational data. All authors contributed to the discussion and writing of the paper. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia through Contract No. 451-03-47/2023-01/200017.

Data Availability Statement

Data are contained within the article.

Acknowledgments

The authors are grateful to R. Dovesi, K. Doll, and Crystal Solutions for software support with CRYSTAL code.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Table A1. Bulk modulus (K) for the nine most promising predicted HfC structure types, calculated using the Voigt–Reuss–Hill (VRH) approximation, expressed in GPa.
Table A1. Bulk modulus (K) for the nine most promising predicted HfC structure types, calculated using the Voigt–Reuss–Hill (VRH) approximation, expressed in GPa.
NaCl_TypeOrtho_HfC _Type5-5_TypeHfC_polytypeTlI_TypeNiAs_TypeWC_TypeZnS_TypeCsCl_Type
Bulk modulus KV261.54228.12208.70237.89209.70230.53224.23179.95227.16
Bulk modulus KR261.54222.84205.11237.86131.91228.01221.16175.95227.16
Bulk modulus KH261.54225.48206.90237.87170.80229.27222.69175.95227.16
Exp242 [84]
263 [85]		n.a.n.a.n.a.n.a.n.a.n.a.n.a.n.a.
Theory233 [63]
238 [86]
247 [33]
248 [87]
262.5 [68]
270 [36]
276.3 [34]
278 [35]		n.a.n.a.n.a.n.a.n.a.239 [81]165 [33]214 [33]
Elastic tensor constants (GPa)C11 = 560
C12 = 112
C44 = 175		C11 = 363
C22 = 458
C33 = 580
C44 = 163
C55 = 141
C66 = 232
C12 = 147
C13 = 77
C23 = 103		C11 = 253
C12 = 241
C13 = 86
C33 = 550
C44 = 142		C11 = 438
C12 = 134
C13 = 124
C33 = 444
C44 = −31		C11 = 525
C22 = 166
C33 = 520
C44 = 165
C55 = 235
C66 = −833
C12 = 18
C13 = 164
C23 = 152		C11 = 417
C12 = 155
C13 = 74
C33 = 630
C44 = 108		C11 = 420
C12 = 146
C13 = 57
C33 = 661
C44 = −70.29		C11 = 187
C12 = 170
C44 = 54		C11 = 83
C12 = 299
C44 = −252

References

  1. Schön, J.C.; Jansen, M. First Step Towards Planning of Syntheses in Solid-State Chemistry: Determination of Promising Structure Candidates by Global Optimization. Angew. Chem. Int. Ed. Engl. 1996, 35, 1286–1304. [Google Scholar] [CrossRef]
  2. Schön, J.C.; Jansen, M. Determination, prediction, and understanding of structures, using the energy landscapes of chemical systems—Part I. Z. Für Krist.-Cryst. Mater. 2001, 216, 307–325. [Google Scholar] [CrossRef]
  3. Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
  4. Wales, D.J. Energy Landscapes and Structure Prediction Using Basin-Hopping. In Modern Methods of Crystal Structure Prediction; Oganov, A.R., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 29–54. [Google Scholar]
  5. Lyakhov, A.O.; Oganov, A.R.; Valle, M. Crystal Structure Prediction Using Evolutionary Approach. In Modern Methods of Crystal Structure Prediction; Oganov, A.R., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 147–180. [Google Scholar]
  6. Woodley, S.M.; Catlow, R. Crystal structure prediction from first principles. Nat. Mater. 2008, 7, 937–946. [Google Scholar] [CrossRef] [PubMed]
  7. Zurek, E. Discovering New Materials via A Priori Crystal Structure Prediction. Rev. Comput. Chem. 2016, 29, 274–326. [Google Scholar]
  8. Oganov, A.; Pickard, C.; Zhu, Q.; Needs, R. Structure prediction drives materials discovery. Nat. Rev. Mater. 2019, 4, 331–348. [Google Scholar] [CrossRef]
  9. Woodley, S.M.; Day, G.M.; Catlow, R. Structure prediction of crystals, surfaces and nanoparticles, Philosophical Transactions of the Royal Society A: Mathematical. Phys. Eng. Sci. 2020, 378, 20190600. [Google Scholar]
  10. Schön, J.C. 3.11—Energy landscapes in inorganic chemistry. In Comprehensive Inorganic Chemistry III, 3rd ed.; Reedijk, J., Poeppelmeier, K.R., Eds.; Elsevier: Oxford, UK, 2023; Volume 3, pp. 262–392. [Google Scholar]
  11. Wales, D. (Ed.) Introduction. In Energy Landscapes: Applications to Clusters, Biomolecules and Glasses; Cambridge University Press: Cambridge, UK, 2004; pp. 1–118. [Google Scholar]
  12. Schön, J.C. Structure prediction in low dimensions: Concepts, issues and examples. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2023, 381, 20220246. [Google Scholar] [CrossRef] [PubMed]
  13. Schön, J.C.; Jansen, M. Prediction, determination and validation of phase diagrams via the global study of energy landscapes. Int. J. Mater. Res. 2009, 100, 135–152. [Google Scholar] [CrossRef]
  14. Jansen, M.; Pentin, I.V.; Schön, J.C. A Universal Representation of the States of Chemical Matter Including Metastable Configurations in Phase Diagrams. Angew. Chem. Int. Ed. 2012, 51, 132–135. [Google Scholar] [CrossRef]
  15. Schön, J.C. Energy Landscape Concepts for Chemical Systems under Extreme Conditions. J. Innov. Mater. Extrem. Cond. 2021, 2, 5–57. [Google Scholar]
  16. Nakamura, K.; Yashima, M. Crystal structure of NaCl-type transition metal monocarbides MC (M=V, Ti, Nb, Ta, Hf, Zr), a neutron powder diffraction study. Mater. Sci. Eng. B 2008, 148, 69–72. [Google Scholar] [CrossRef]
  17. Cotter, P.G.; Kohn, J.A. Industrial Diamond Substitutes: I, Physical and X-Ray Study of Hafnium Carbide. J. Am. Ceram. Soc. 1954, 37, 415–420. [Google Scholar] [CrossRef]
  18. Cedillos-Barraza, O.; Manara, D.; Boboridis, K.; Watkins, T.; Grasso, S.; Jayaseelan, D.D.; Konings, R.J.M.; Reece, M.J.; Lee, W.E. Investigating the highest melting temperature materials: A laser melting study of the TaC-HfC system. Sci. Rep. 2016, 6, 37962. [Google Scholar] [CrossRef]
  19. Cedillos-Barraza, O.; Grasso, S.; Nasiri, N.A.; Jayaseelan, D.D.; Reece, M.J.; Lee, W.E. Sintering behaviour, solid solution formation and characterisation of TaC, HfC and TaC–HfC fabricated by spark plasma sintering. J. Eur. Ceram. Soc. 2016, 36, 1539–1548. [Google Scholar] [CrossRef]
  20. Ghaffari, S.A.; Faghihi-Sani, M.A.; Golestani-Fard, F.; Nojabayy, M. Diffusion and solid solution formation between the binary carbides of TaC, HfC and ZrC. Int. J. Refract. Met. Hard Mater. 2013, 41, 180–184. [Google Scholar] [CrossRef]
  21. Wen, Q.; Yu, Z.; Riedel, R.; Ionescu, E. Significant improvement of high-temperature oxidation resistance of HfC/SiC ceramic nanocomposites with the incorporation of a small amount of boron. J. Eur. Ceram. Soc. 2020, 40, 3499–3508. [Google Scholar] [CrossRef]
  22. Krikorian, N.H.; Witteman, W.G.; Bowman, M.G. The Mutual Solid Solubility of Hafnium Carbide and Uranium Monocarbide. J. Electrochem. Soc. 1963, 110, 560. [Google Scholar] [CrossRef]
  23. Wen, Q.; Riedel, R.; Ionescu, E. Significant improvement of the short-term high-temperature oxidation resistance of dense monolithic HfC/SiC ceramic nanocomposites upon incorporation of Ta. Corros. Sci. 2018, 145, 191–198. [Google Scholar] [CrossRef]
  24. Bernauer, J.; Petry, N.-C.; Thor, N.; Kredel, S.A.; Teppala, D.T.; Galetz, M.; Lepple, M.; Pundt, A.; Ionescu, E.; Riedel, R. Exceptional Hardness and Thermal Properties of SiC/(Hf,Ta)C(N)/(B)C Ceramic Composites Derived from Single-Source Precursor. Adv. Eng. Mater. 2024, 2301864. [Google Scholar] [CrossRef]
  25. Yudin, S.N.; Kasimtsev, A.V.; Volodko, S.S.; Alimov, I.A.; Markova, G.V.; Sviridova, T.A.; Tabachkova, N.Y.; Buinevich, V.S.; Nepapushev, A.A.; Moskovskikh, D.O. Low-temperature synthesis of ultra-high-temperature HfC and HfCN nanoparticles. Materialia 2022, 22, 101415. [Google Scholar] [CrossRef]
  26. Sacks, M.D.; Wang, C.-A.; Yang, Z.; Jain, A. Carbothermal reduction synthesis of nanocrystalline zirconium carbide and hafnium carbide powders using solution-derived precursors. J. Mater. Sci. 2004, 39, 6057–6066. [Google Scholar] [CrossRef]
  27. Ha, D.; Kim, J.; Han, J.; Kang, S. Synthesis and properties of (Hf1-xTax)C solid solution carbides. Ceram. Int. 2018, 44, 19247–19253. [Google Scholar] [CrossRef]
  28. Teppala, D.T.; Kredel, S.A.; Ionescu, E.; Matović, B. A Review of the Synthesis of Compositionally Complex Ultra-High-Temperature Ceramics. J. Innov. Mater. Extrem. Cond. 2023, 4, 77–103. [Google Scholar]
  29. Elliott, R.O.; Kempter, C.P. Thermal Expansion of Some Transition Metal Carbides. J. Phys. Chem. 1958, 62, 630–631. [Google Scholar] [CrossRef]
  30. Jun, C.K. Thermal Expansion of NbC, HfC, and TaC at High Temperatures. J. Appl. Phys. 2003, 41, 5081. [Google Scholar] [CrossRef]
  31. Jun, C.K.; Shaffer, P.T.B. Thermal expansion of niobium carbide, hafnium carbide and tantalum carbide at high temperatures. J. Less Common Met. 1971, 24, 323–327. [Google Scholar] [CrossRef]
  32. Lu, X.-G.; Selleby, M.; Sundman, B. Calculations of thermophysical properties of cubic carbides and nitrides using the Debye–Grüneisen model. Acta Mater. 2007, 55, 1215–1226. [Google Scholar] [CrossRef]
  33. Yang, J.; Gao, F. First principles calculations of mechanical properties of cubic 5d transition metal monocarbides. Phys. B Condens. Matter 2012, 407, 3527–3534. [Google Scholar] [CrossRef]
  34. Li, H.; Zhang, L.; Zeng, Q.; Guan, K.; Li, K.; Ren, H.; Liu, S.; Cheng, L. Structural, elastic and electronic properties of transition metal carbides TMC (TM=Ti, Zr, Hf and Ta) from first-principles calculations. Solid State Commun. 2011, 151, 602–606. [Google Scholar] [CrossRef]
  35. Zeng, Q.; Peng, J.; Oganov, A.R.; Zhu, Q.; Xie, C.; Zhang, X.; Dong, D.; Zhang, L.; Cheng, L. Prediction of stable hafnium carbides: Stoichiometries, mechanical properties, and electronic structure. Phys. Rev. B 2013, 88, 214107. [Google Scholar] [CrossRef]
  36. He, L.F.; Lin, Z.J.; Wang, J.Y.; Bao, Y.W.; Zhou, Y.C. Crystal structure and theoretical elastic property of two new ternary ceramics Hf3Al4C6 and Hf2Al4C5. Scr. Mater. 2008, 58, 679–682. [Google Scholar] [CrossRef]
  37. Skundric, T.; Schön, J.C.; Zarubica, A.; Fonovic, M.; Zagorac, D. Exploring the energy landscape and crystal structures of CrSi2N4. Z. Für Anorg. Und Allg. Chem. 2023, 649, e202300130. [Google Scholar] [CrossRef]
  38. Schön, J.C. Nanomaterials—What energy landscapes can tell us. Process. Appl. Ceram. 2015, 9, 157–168. [Google Scholar] [CrossRef]
  39. Bergerhoff, G.; Brown, I.D. Crystallographic Databases; International Union of Crystallography: Chester, UK, 1987. [Google Scholar]
  40. Zagorac, D.; Muller, H.; Ruehl, S.; Zagorac, J.; Rehme, S. Recent developments in the Inorganic Crystal Structure Database: Theoretical crystal structure data and related features. J. Appl. Crystallogr. 2019, 52, 918–925. [Google Scholar] [CrossRef]
  41. Zagorac, D.; Doll, K.; Zagorac, J.; Jordanov, D.; Matović, B. Barium Sulfide under Pressure: Discovery of Metastable Polymorphs and Investigation of Electronic Properties on ab Initio Level. Inorg. Chem. 2017, 56, 10644–10654. [Google Scholar] [CrossRef]
  42. Čančarević, Ž.P.; Schön, J.C.; Jansen, M. Stability of Alkali Metal Halide Polymorphs as a Function of Pressure. Chem.—Asian J. 2008, 3, 561–572. [Google Scholar] [CrossRef]
  43. Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. WIREs Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
  44. Dovesi, R.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.; D’Arco, P.; Noël, Y.; Rérat, M.; Carbonnière, P.; et al. The CRYSTAL code, 1976–2020 and beyond, a long story. J. Chem. Phys. 2020, 152, 204111. [Google Scholar] [CrossRef] [PubMed]
  45. Doll, K.; Saunders, V.R.; Harrison, N.M. Analytical Hartree–Fock gradients for periodic systems. Int. J. Quantum Chem. 2001, 82, 1–13. [Google Scholar] [CrossRef]
  46. Doll, K.; Dovesi, R.; Orlando, R. Analytical Hartree-Fock gradients with respect to the cell parameter for systems periodic in three dimensions. Theor. Chem. Acc. 2004, 112, 394–402. [Google Scholar] [CrossRef]
  47. Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
  48. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  49. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  50. Dovesi, R.; Saunders, V.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.; Bush, I. CRYSTAL17 User’s Manual; University of Torino: Torino, Italy, 2017. [Google Scholar]
  51. Doll, K. Gaussian Basis Sets for Solid State Calculations. In Basis Sets in Computational Chemistry; Perlt, E., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 157–181. [Google Scholar]
  52. Ramo, D.M.; Gavartin, J.L.; Shluger, A.L.; Bersuker, G. Spectroscopic properties of oxygen vacancies in monoclinic HfO2 calculated with periodic and embedded cluster density functional theory. Phys. Rev. B 2007, 75, 205336. [Google Scholar] [CrossRef]
  53. Catti, M.; Pavese, A.; Dovesi, R.; Saunders, V.R. Static lattice and electron properties of MgCO3 (magnesite) calculated by ab initio periodic Hartree-Fock methods. Phys. Rev. B Condens. Matter 1993, 47, 9189–9198. [Google Scholar] [CrossRef] [PubMed]
  54. Skundric, T.; Matovic, B.; Zarubica, A.; Chudoba, D.; Zagorac, D. Data Mining Ab Initio Study of Gypsum CaCO3 Modifications at Standard and Extreme Conditions. J. Innov. Mater. Extrem. Cond. 2023, 4, 38–51. [Google Scholar]
  55. Hundt, R. KPLOT, A Program for Plotting and Analyzing Crystal Structures; Technicum Scientific Publishing: Stuttgart, Germany, 2016. [Google Scholar]
  56. Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  57. Perger, W.F.; Criswell, J.; Civalleri, B.; Dovesi, R. Ab-initio calculation of elastic constants of crystalline systems with the CRYSTAL code. Comput. Phys. Commun. 2009, 180, 1753–1759. [Google Scholar] [CrossRef]
  58. Erba, A.; Mahmoud, A.; Orlando, R.; Dovesi, R. Elastic properties of six silicate garnet end members from accurate ab initio simulations. Phys. Chem. Miner. 2014, 41, 151–160. [Google Scholar] [CrossRef]
  59. Krikorian, N.H.; Wallace, T.C.; Anderson, J.L. Low-Temperature Thermal Expansion of the Group 4a Carbides. J. Electrochem. Soc. 1963, 110, 587. [Google Scholar] [CrossRef]
  60. Aigner, K.; Lengauer, W.; Rafaja, D.; Ettmayer, P. Lattice parameters and thermal expansion of Ti(CxN1−x), Zr(CxN1−x), Hf(CxN1−x) and TiN1−x from 298 to 1473 K as investigated by high-temperature X-ray diffraction. J. Alloys Compd. 1994, 215, 121–126. [Google Scholar] [CrossRef]
  61. Lengauer, W.; Binder, S.; Aigner, K.; Ettmayer, P.; Guillou, A.; Debuigne, J.; Groboth, G. Solid state properties of group IVb carbonitrides. J. Alloys Compd. 1995, 217, 137–147. [Google Scholar] [CrossRef]
  62. Zhang, H.; Hedman, D.; Feng, P.; Han, G.; Akhtar, F. A high-entropy B4(HfMo2TaTi)C and SiC ceramic composite. Dalton Trans. 2019, 48, 5161–5167. [Google Scholar] [CrossRef] [PubMed]
  63. Feng, W.; Cui, S.; Hu, H.; Zhang, G.; Lv, Z. Electronic structure and elastic constants of TiCxN1−x, ZrxNb1−xC and HfCxN1−x alloys: A first-principles study. Phys. B Condens. Matter 2011, 406, 3631–3635. [Google Scholar] [CrossRef]
  64. Razumovskiy, V.I.; Popov, M.N.; Ding, H.; Odqvist, J. Formation and interaction of point defects in group IVb transition metal carbides and nitrides. Comput. Mater. Sci. 2015, 104, 147–154. [Google Scholar] [CrossRef]
  65. Yang, Y.; Ma, L.; Gan, G.-Y.; Wang, W.; Tang, B.-Y. Investigation of thermodynamic properties of high entropy (TaNbHfTiZr)C and (TaNbHfTiZr)N. J. Alloys Compd. 2019, 788, 1076–1083. [Google Scholar] [CrossRef]
  66. Chang, Y.H.R.; Yoon, T.L. Effects of nitrogen addition and growth condition on the enhanced mechanical properties of transition metal carbides TMC (TM = Zr, Hf). Ceram. Int. 2020, 46, 1124–1136. [Google Scholar] [CrossRef]
  67. Jiang, S.; Shao, L.; Fan, T.-W.; Duan, J.-M.; Chen, X.-T.; Tang, B.-Y. Elastic and thermodynamic properties of high entropy carbide (HfTaZrTi)C and (HfTaZrNb)C from ab initio investigation. Ceram. Int. 2020, 46, 15104–15112. [Google Scholar] [CrossRef]
  68. Krasnenko, V.; Brik, M. First-principles calculations of the structural, elastic and electronic properties of MNxC1−x (M=Ti, Zr, Hf; 0<x<1) carbonitrides at ambient and elevated hydrostatic pressure. Solid State Sci. 2013, 28, 1–8. [Google Scholar]
  69. Kim, J.; Kwon, H.; Kim, B.; Suh, Y. Finite temperature thermal expansion and elastic properties of (Hf1-xTax)C ultrahigh temperature ceramics. Ceram. Int. 2019, 45, 10805–10809. [Google Scholar] [CrossRef]
  70. Schön, J.C.; Jansen, M. Determination of candidate structures for simple ionic compounds through cell optimisation. Comput. Mater. Sci. 1995, 4, 43–58. [Google Scholar] [CrossRef]
  71. Zagorac, D.; Zagorac, J.; Fonović, M.; Prikhna, T.; Matović, B. Novel boron-rich aluminum nitride advanced ceramic materials. Int. J. Appl. Ceram. Technol. 2023, 20, 174–189. [Google Scholar] [CrossRef]
  72. Haq, B.U.; AlFaify, S.; Alrebdi, T.A.; Ahmed, R.; Al-Qaisi, S.; Taib, M.F.M.; Naz, G.; Zahra, S. Investigations of optoelectronic properties of novel ZnO monolayers: A first-principles study. Mater. Sci. Eng. B 2021, 265, 115043. [Google Scholar] [CrossRef]
  73. Guinier, A.; Bokij, G.B.; Boll-Dornberger, K.; Cowley, J.M.; Durovic, S.; Jagodzinski, H.; Krishna, P.; de Wolff, P.M.; Zvyagin, B.B.; Cox, D.E.; et al. Nomenclature of polytype structures. Report of the International Union of Crystallography Ad hoc Committee on the Nomenclature of Disordered, Modulated and Polytype Structures. Acta Crystallogr. Sect. A 1984, 40, 399–404. [Google Scholar] [CrossRef]
  74. Kelly, J.F.; Fisher, G.R.; Barnes, P. Correlation between layer thickness and periodicity of long polytypes in silicon carbide. Mater. Res. Bull. 2005, 40, 249–255. [Google Scholar] [CrossRef]
  75. Aksenov, S.M.; Charkin, D.O.; Banaru, A.M.; Banaru, D.A.; Volkov, S.N.; Deineko, D.V.; Kuznetsov, A.N.; Rastsvetaeva, R.K.; Chukanov, N.V.; Shkurskii, B.B.; et al. Modularity, polytypism, topology, and complexity of crystal structures of inorganic compounds (Review). J. Struct. Chem. 2023, 64, 1797–2028. [Google Scholar]
  76. Zagorac, D.; Schön, J.C.; Zagorac, J.; Jansen, M. Theoretical investigations of novel zinc oxide polytypes and in-depth study of their electronic properties. RSC Adv. 2015, 5, 25929–25935. [Google Scholar] [CrossRef]
  77. Menad, A.; Benmalti, M.E.; Zaoui, A.; Ferhat, M. Impact of polytypism on the ground state properties of zinc oxide: A first-principles study. Results Phys. 2020, 18, 103316. [Google Scholar] [CrossRef]
  78. Zagorac, D.; Doll, K.; Schön, J.C.; Jansen, M. Ab initio structure prediction for lead sulfide at standard and elevated pressures. Phys. Rev. B 2011, 84, 045206. [Google Scholar] [CrossRef]
  79. Mudring, A.-V. Thallium Halides—New Aspects of the Stereochemical Activity of Electron Lone Pairs of Heavier Main-Group Elements. Eur. J. Inorg. Chem. 2007, 2007, 882–890. [Google Scholar] [CrossRef]
  80. Lowndes, R.P.; Perry, C.H. Molecular structure and anharmonicity in thallium iodide. J. Chem. Phys. 1973, 58, 271–278. [Google Scholar] [CrossRef]
  81. Yang, J.; Gao, F. Hardness calculations of 5d transition metal monocarbides with tungsten carbide structure. Phys. Status Solidi B 2010, 247, 2161–2167. [Google Scholar] [CrossRef]
  82. Yu, R.; Wu, Q.; Fang, Z.; Weng, H. From Nodal Chain Semimetal to Weyl Semimetal in HfC. Phys. Rev. Lett. 2017, 119, 036401. [Google Scholar] [CrossRef]
  83. Chung, D.H.; Buessem, W.R. The Voigt-Reuss-Hill Approximation and Elastic Moduli of Polycrystalline MgO, CaF2, β-ZnS, ZnSe, and CdTe. J. Appl. Phys. 1967, 38, 2535–2540. [Google Scholar] [CrossRef]
  84. Brown, H.L.; Armstrong, P.E.; Kempter, C.P. Elastic Properties of Some Polycrystalline Transition-Metal Monocarbides. J. Chem. Phys. 1966, 45, 547–549. [Google Scholar] [CrossRef]
  85. Nartowski, A.M.; Parkin, I.P.; MacKenzie, M.; Craven, A.J.; MacLeod, I. Solid state metathesis routes to transition metal carbides. J. Mater. Chem. 1999, 9, 1275–1281. [Google Scholar] [CrossRef]
  86. Isaev, E.I.; Simak, S.I.; Abrikosov, I.A.; Ahuja, R.; Vekilov, Y.K.; Katsnelson, M.I.; Lichtenstein, A.I.; Johansson, B. Phonon related properties of transition metals, their carbides, and nitrides: A first-principles study. J. Appl. Phys. 2007, 101, 123519. [Google Scholar] [CrossRef]
  87. Zaoui, A.; Bouhafs, B.; Ruterana, P. First-principles calculations on the electronic structure of TiCxN1−x, ZrxNb1−xC and HfCxN1−x alloys. Mater. Chem. Phys. 2005, 91, 108–115. [Google Scholar] [CrossRef]
  88. Krajewski, A.; D’Alessio, L.; De Maria, G. Physico-Chemical and Thermophysical Properties of Cubic Binary Carbides. Cryst. Res. Technol. 1998, 33, 341–374. [Google Scholar] [CrossRef]
  89. Pierson, H.O. 4—Carbides of Group IV: Titanium, Zirconium, and Hafnium Carbides. In Handbook of Refractory Carbides and Nitrides; Pierson, H.O., Ed.; William Andrew Publishing: Westwood, NJ, USA, 1996; pp. 55–80. [Google Scholar]
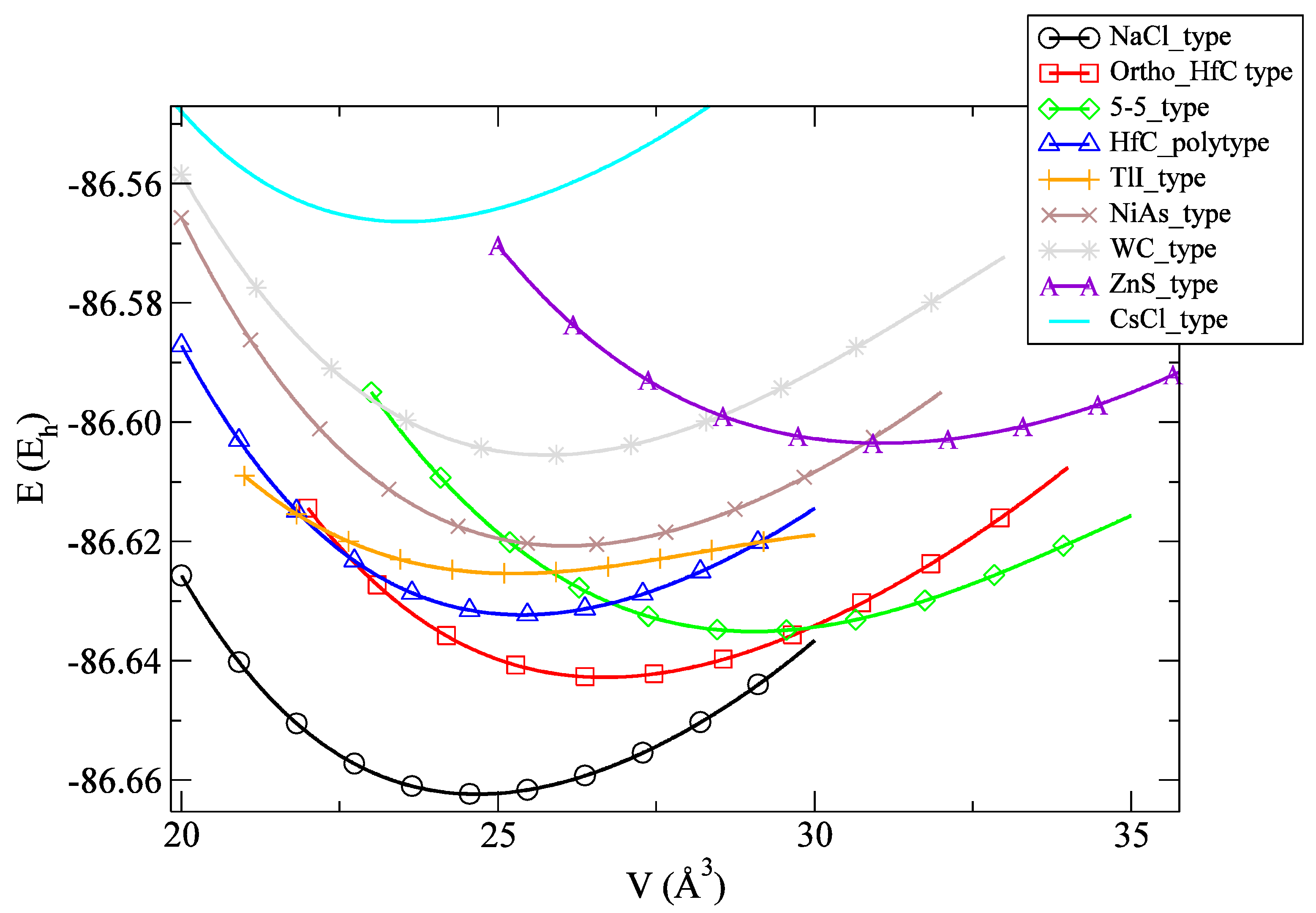
Crystals 14 00340 g001
Figure 1. Energy vs. volume, E(V), curves for the nine most stable and energetically favorable structure candidates in the HfC system obtained using the LDA functional. Energies per formula unit are given in Hartree (Eh).
Figure 1. Energy vs. volume, E(V), curves for the nine most stable and energetically favorable structure candidates in the HfC system obtained using the LDA functional. Energies per formula unit are given in Hartree (Eh).
Crystals 14 00340 g001
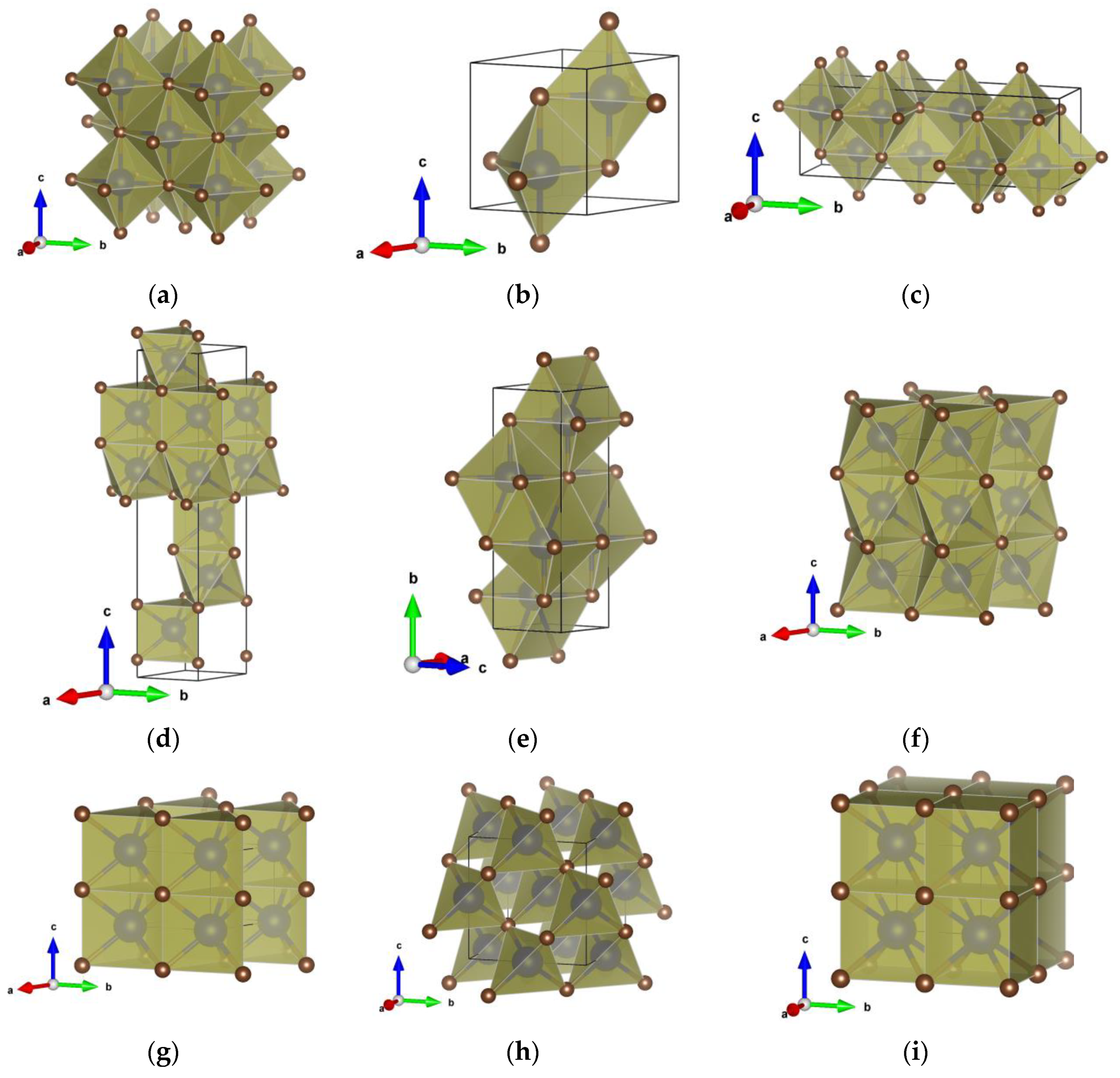
Crystals 14 00340 g002
Figure 2. Predicted HfC structure candidates from global search: (a) NaCl_type; (b) 5-5_type: (c) Ortho_HfC_type; (d) HfC_polytype; (e) TlI_type; (f) NiAs_type; (g) WC_type; (h) ZnS_type; (i) CsCl_type. Hf ions are shown as large blue spheres inside the coordination polyhedra, and C ions are shown as small golden spheres at the corners of the coordination polyhedra.
Figure 2. Predicted HfC structure candidates from global search: (a) NaCl_type; (b) 5-5_type: (c) Ortho_HfC_type; (d) HfC_polytype; (e) TlI_type; (f) NiAs_type; (g) WC_type; (h) ZnS_type; (i) CsCl_type. Hf ions are shown as large blue spheres inside the coordination polyhedra, and C ions are shown as small golden spheres at the corners of the coordination polyhedra.
Crystals 14 00340 g002
Table 1. Energy ranking of the crystalline structure candidates after ab initio optimization. The total energy (in Eh) is computed using the LDA-PZ and GGA-PBE functional.
Table 1. Energy ranking of the crystalline structure candidates after ab initio optimization. The total energy (in Eh) is computed using the LDA-PZ and GGA-PBE functional.
ModificationLDAPBE
NaCl_type−86.6624−87.0498
Ortho_HfC_type−86.6428−87.0319
5-5_type−86.6352−87.0261
HfC_polytype−86.6324−87.0203
TlI_type−86.6251−87.0135
NiAs_type−86.6209−87.0104
WC_type−86.6055−86.9942
ZnS_type−86.6034−86.9968
CsCl_type−86.5664−86.9519
Table 2. Structure type, space group, unit cell parameters (Å), unit cell volume (Å3), and atomic positions for the most relevant HfC polymorphs.
Table 2. Structure type, space group, unit cell parameters (Å), unit cell volume (Å3), and atomic positions for the most relevant HfC polymorphs.
Structure CandidatesLDAPBE
NaCl_typeFm-3m (225)
a = 4.62; V = 98.51
Hf 0 0 0
C 1/2 0 0		Fm-3m (225)
a = 4.67; V = 101.91
Hf 0 0 0
C 1/2 0 0
Ortho_HfC typeCmcm (63)
a = 3.40; b = 13.66; c = 4.59; V = 213.30
Hf1 0 0.6862 1/4
Hf2 0 0.9200 1/4
C1 0 0.3144 1/4
C2 0 0.0799 1/4		Cmcm (63)
a = 3.45; b = 13.81
c = 4.64; V = 220.66
Hf1 0 0.6857 1/4
Hf2 0 0.9201 1/4
C1 0 0.3149 1/4
C2 0 0.0799 1/4
5-5_typeP63/mmc (194)
a = 3.82; c = 4.60; V = 58.01
Hf 1/3 2/3 3/4
C 2/3 1/3 3/4		P63/mmc (194)
a = 3.86; c = 4.65
V = 60.02
Hf 1/3 2/3 3/4
C 2/3 1/3 3/4
HfC_polytypeR3m (160)
a = 3.24; c = 16.73; V = 152.34
Hf1 0 0 0.8085
Hf2 0 0 0.6344
C1 0 0 0.2234
C2 0 0 0.0541		R3m (160)
a = 3.28; c = 16.90
V = 157.70
Hf1 0 0 0.8085
Hf2 0 0 0.6345
C1 0 0 0.2234
C2 0 0 0.0540
TlI_typeCmcm (63)
a = 3.15; b = 9.54; c = 3.34; V = 100.52
Hf 0 0.6343 1/4
C 0 0.8697 1/4		Cmcm (63)
a = 3.20; b = 9.92
c = 3.35; V = 106.16
Hf 0 0.6367 1/4
C 0 0.8649 1/4
NiAs_typeP63/mmc (194)
a = 3.24; c = 5.72; V = 52.03
Hf 0 0 1/2
C 1/3 2/3 3/4		P63/mmc (194)
a = 3.28; c = 5.78
V = 53.86
Hf 0 0 0.5
C 1/3 2/3 3/4
WC_typeP-6m2 (187)
a = 3.20; c = 2.90; V = 25.73
Hf 0 0 0
C 1/3 2/3 1/2		P-6m2 (187)
a = 3.24; c = 2.93
V = 26.68
Hf 0 0 0
C 1/3 2/3 1/2
ZnS_typeF-43m (216)
a = 4.99; V = 124.33
Hf 1/2 1/2 1/2
C 3/4 3/4 1/4		F-43m (216)
a = 5.05; V = 128.72
Hf 1/2 1/2 1/2
C 3/4 3/4 1/4
CsCl_typePm-3m (221)
a = 2.87; V = 23.54
Hf 0 0 0
C 1/2 1/2 1/2		Pm-3m (221)
a = 2.91; V = 24.54
Hf 0 0 0
C 1/2 1/2 1/2
Table 3. Mechanical properties of hafnium carbide computed using LDA-PZ functional. Bulk modulus (K), shear modulus (G), and Vickers hardness (VH) were calculated using the Voigt–Reuss–Hill (VRH) approximations expressed in GPa. We employed three different approximations for calculating the bulk and shear moduli and the Vickers hardness, where letters V, R, or H in the subscript denote the Voigt, Reuss, or Hill approach, respectively.
Table 3. Mechanical properties of hafnium carbide computed using LDA-PZ functional. Bulk modulus (K), shear modulus (G), and Vickers hardness (VH) were calculated using the Voigt–Reuss–Hill (VRH) approximations expressed in GPa. We employed three different approximations for calculating the bulk and shear moduli and the Vickers hardness, where letters V, R, or H in the subscript denote the Voigt, Reuss, or Hill approach, respectively.
Mechanical PropertyRock Salt (NaCl) Typeortho_HfC TypeNiAs Type
LDAExperimentTheoryLDALDA
Bulk modulus KV (GPa)261.54242 [84], 263 [85]233 [63], 238 [86], 247 [33],
248 [87], 262.5 [68], 270 [36],
276.3 [34], 278 [35]		228.12230.53
Bulk modulus KR (GPa)261.54222.84228.01
Bulk modulus KH (GPa)261.54225.48229.27
Shear modulus GV (GPa)195.08195 [84]166 [32], 181 [33], 188.8 [34],
207 [35], 230 [36]		86.10146.79
Shear modulus GR (GPa)192.38237.31132.56
Shear modulus GH (GPa)193.73161.71139.67
Young modulus E_H (GPa)466.11430 [88], 461 [84]404 [32], 437 [33], 461.3 [34],
537 [36]		391.53348.29
Poisson ratio v_H0.20n.a.n.a.0.210.25
Vickers (GPa) hardness VH_V27.5726.1 [89], 18–20 [88]26.2 [33]; 29.08 [35]1.1518.83
Vickers (GPa) hardness VH_R26.8747.4815.80
Vickers (GPa) hardness VH_H27.2223.0917.29
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zagorac, J.; Schön, J.C.; Matović, B.; Butulija, S.; Zagorac, D. Hafnium Carbide: Prediction of Crystalline Structures and Investigation of Mechanical Properties. Crystals 2024, 14, 340. https://doi.org/10.3390/cryst14040340

AMA Style

Zagorac J, Schön JC, Matović B, Butulija S, Zagorac D. Hafnium Carbide: Prediction of Crystalline Structures and Investigation of Mechanical Properties. Crystals. 2024; 14(4):340. https://doi.org/10.3390/cryst14040340

Chicago/Turabian Style

Zagorac, Jelena, Johann Christian Schön, Branko Matović, Svetlana Butulija, and Dejan Zagorac. 2024. "Hafnium Carbide: Prediction of Crystalline Structures and Investigation of Mechanical Properties" Crystals 14, no. 4: 340. https://doi.org/10.3390/cryst14040340

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop