Hafnium Carbide: Prediction of Crystalline Structures and Investigation of Mechanical Properties
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Energy Landscape and Energetic Properties
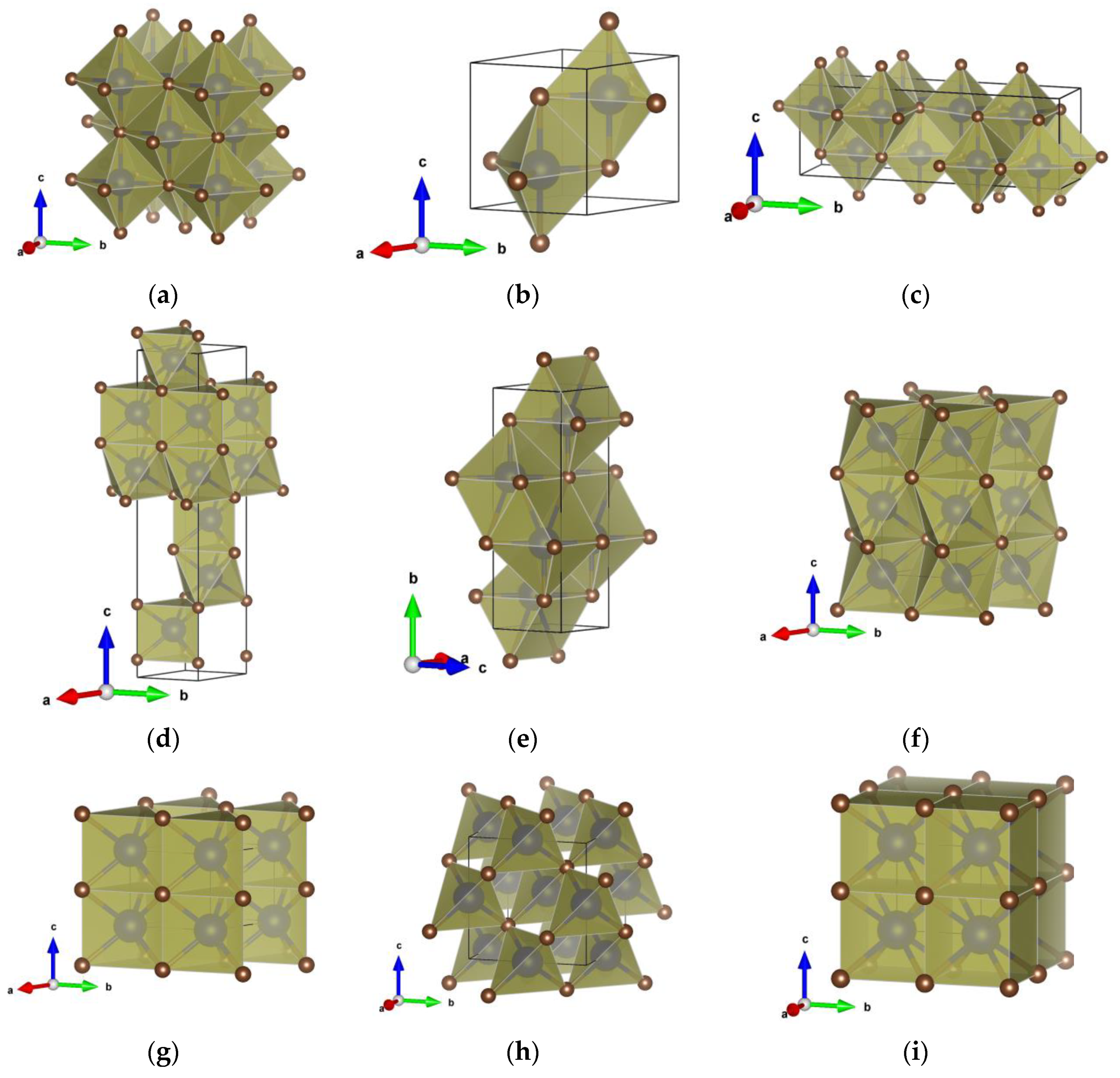
3.2. Crystal Structure Prediction and Polymorphs of HfC
3.3. Mechanical Properties of Hafnium Carbide
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| NaCl_Type | Ortho_HfC _Type | 5-5_Type | HfC_polytype | TlI_Type | NiAs_Type | WC_Type | ZnS_Type | CsCl_Type | |
|---|---|---|---|---|---|---|---|---|---|
| Bulk modulus KV | 261.54 | 228.12 | 208.70 | 237.89 | 209.70 | 230.53 | 224.23 | 179.95 | 227.16 |
| Bulk modulus KR | 261.54 | 222.84 | 205.11 | 237.86 | 131.91 | 228.01 | 221.16 | 175.95 | 227.16 |
| Bulk modulus KH | 261.54 | 225.48 | 206.90 | 237.87 | 170.80 | 229.27 | 222.69 | 175.95 | 227.16 |
| Exp | 242 [84] 263 [85] | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. | n.a. |
| Theory | 233 [63] 238 [86] 247 [33] 248 [87] 262.5 [68] 270 [36] 276.3 [34] 278 [35] | n.a. | n.a. | n.a. | n.a. | n.a. | 239 [81] | 165 [33] | 214 [33] |
| Elastic tensor constants (GPa) | C11 = 560 C12 = 112 C44 = 175 | C11 = 363 C22 = 458 C33 = 580 C44 = 163 C55 = 141 C66 = 232 C12 = 147 C13 = 77 C23 = 103 | C11 = 253 C12 = 241 C13 = 86 C33 = 550 C44 = 142 | C11 = 438 C12 = 134 C13 = 124 C33 = 444 C44 = −31 | C11 = 525 C22 = 166 C33 = 520 C44 = 165 C55 = 235 C66 = −833 C12 = 18 C13 = 164 C23 = 152 | C11 = 417 C12 = 155 C13 = 74 C33 = 630 C44 = 108 | C11 = 420 C12 = 146 C13 = 57 C33 = 661 C44 = −70.29 | C11 = 187 C12 = 170 C44 = 54 | C11 = 83 C12 = 299 C44 = −252 |
References
- Schön, J.C.; Jansen, M. First Step Towards Planning of Syntheses in Solid-State Chemistry: Determination of Promising Structure Candidates by Global Optimization. Angew. Chem. Int. Ed. Engl. 1996, 35, 1286–1304. [Google Scholar] [CrossRef]
- Schön, J.C.; Jansen, M. Determination, prediction, and understanding of structures, using the energy landscapes of chemical systems—Part I. Z. Für Krist.-Cryst. Mater. 2001, 216, 307–325. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Wales, D.J. Energy Landscapes and Structure Prediction Using Basin-Hopping. In Modern Methods of Crystal Structure Prediction; Oganov, A.R., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 29–54. [Google Scholar]
- Lyakhov, A.O.; Oganov, A.R.; Valle, M. Crystal Structure Prediction Using Evolutionary Approach. In Modern Methods of Crystal Structure Prediction; Oganov, A.R., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 147–180. [Google Scholar]
- Woodley, S.M.; Catlow, R. Crystal structure prediction from first principles. Nat. Mater. 2008, 7, 937–946. [Google Scholar] [CrossRef] [PubMed]
- Zurek, E. Discovering New Materials via A Priori Crystal Structure Prediction. Rev. Comput. Chem. 2016, 29, 274–326. [Google Scholar]
- Oganov, A.; Pickard, C.; Zhu, Q.; Needs, R. Structure prediction drives materials discovery. Nat. Rev. Mater. 2019, 4, 331–348. [Google Scholar] [CrossRef]
- Woodley, S.M.; Day, G.M.; Catlow, R. Structure prediction of crystals, surfaces and nanoparticles, Philosophical Transactions of the Royal Society A: Mathematical. Phys. Eng. Sci. 2020, 378, 20190600. [Google Scholar]
- Schön, J.C. 3.11—Energy landscapes in inorganic chemistry. In Comprehensive Inorganic Chemistry III, 3rd ed.; Reedijk, J., Poeppelmeier, K.R., Eds.; Elsevier: Oxford, UK, 2023; Volume 3, pp. 262–392. [Google Scholar]
- Wales, D. (Ed.) Introduction. In Energy Landscapes: Applications to Clusters, Biomolecules and Glasses; Cambridge University Press: Cambridge, UK, 2004; pp. 1–118. [Google Scholar]
- Schön, J.C. Structure prediction in low dimensions: Concepts, issues and examples. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2023, 381, 20220246. [Google Scholar] [CrossRef] [PubMed]
- Schön, J.C.; Jansen, M. Prediction, determination and validation of phase diagrams via the global study of energy landscapes. Int. J. Mater. Res. 2009, 100, 135–152. [Google Scholar] [CrossRef]
- Jansen, M.; Pentin, I.V.; Schön, J.C. A Universal Representation of the States of Chemical Matter Including Metastable Configurations in Phase Diagrams. Angew. Chem. Int. Ed. 2012, 51, 132–135. [Google Scholar] [CrossRef]
- Schön, J.C. Energy Landscape Concepts for Chemical Systems under Extreme Conditions. J. Innov. Mater. Extrem. Cond. 2021, 2, 5–57. [Google Scholar]
- Nakamura, K.; Yashima, M. Crystal structure of NaCl-type transition metal monocarbides MC (M=V, Ti, Nb, Ta, Hf, Zr), a neutron powder diffraction study. Mater. Sci. Eng. B 2008, 148, 69–72. [Google Scholar] [CrossRef]
- Cotter, P.G.; Kohn, J.A. Industrial Diamond Substitutes: I, Physical and X-Ray Study of Hafnium Carbide. J. Am. Ceram. Soc. 1954, 37, 415–420. [Google Scholar] [CrossRef]
- Cedillos-Barraza, O.; Manara, D.; Boboridis, K.; Watkins, T.; Grasso, S.; Jayaseelan, D.D.; Konings, R.J.M.; Reece, M.J.; Lee, W.E. Investigating the highest melting temperature materials: A laser melting study of the TaC-HfC system. Sci. Rep. 2016, 6, 37962. [Google Scholar] [CrossRef]
- Cedillos-Barraza, O.; Grasso, S.; Nasiri, N.A.; Jayaseelan, D.D.; Reece, M.J.; Lee, W.E. Sintering behaviour, solid solution formation and characterisation of TaC, HfC and TaC–HfC fabricated by spark plasma sintering. J. Eur. Ceram. Soc. 2016, 36, 1539–1548. [Google Scholar] [CrossRef]
- Ghaffari, S.A.; Faghihi-Sani, M.A.; Golestani-Fard, F.; Nojabayy, M. Diffusion and solid solution formation between the binary carbides of TaC, HfC and ZrC. Int. J. Refract. Met. Hard Mater. 2013, 41, 180–184. [Google Scholar] [CrossRef]
- Wen, Q.; Yu, Z.; Riedel, R.; Ionescu, E. Significant improvement of high-temperature oxidation resistance of HfC/SiC ceramic nanocomposites with the incorporation of a small amount of boron. J. Eur. Ceram. Soc. 2020, 40, 3499–3508. [Google Scholar] [CrossRef]
- Krikorian, N.H.; Witteman, W.G.; Bowman, M.G. The Mutual Solid Solubility of Hafnium Carbide and Uranium Monocarbide. J. Electrochem. Soc. 1963, 110, 560. [Google Scholar] [CrossRef]
- Wen, Q.; Riedel, R.; Ionescu, E. Significant improvement of the short-term high-temperature oxidation resistance of dense monolithic HfC/SiC ceramic nanocomposites upon incorporation of Ta. Corros. Sci. 2018, 145, 191–198. [Google Scholar] [CrossRef]
- Bernauer, J.; Petry, N.-C.; Thor, N.; Kredel, S.A.; Teppala, D.T.; Galetz, M.; Lepple, M.; Pundt, A.; Ionescu, E.; Riedel, R. Exceptional Hardness and Thermal Properties of SiC/(Hf,Ta)C(N)/(B)C Ceramic Composites Derived from Single-Source Precursor. Adv. Eng. Mater. 2024, 2301864. [Google Scholar] [CrossRef]
- Yudin, S.N.; Kasimtsev, A.V.; Volodko, S.S.; Alimov, I.A.; Markova, G.V.; Sviridova, T.A.; Tabachkova, N.Y.; Buinevich, V.S.; Nepapushev, A.A.; Moskovskikh, D.O. Low-temperature synthesis of ultra-high-temperature HfC and HfCN nanoparticles. Materialia 2022, 22, 101415. [Google Scholar] [CrossRef]
- Sacks, M.D.; Wang, C.-A.; Yang, Z.; Jain, A. Carbothermal reduction synthesis of nanocrystalline zirconium carbide and hafnium carbide powders using solution-derived precursors. J. Mater. Sci. 2004, 39, 6057–6066. [Google Scholar] [CrossRef]
- Ha, D.; Kim, J.; Han, J.; Kang, S. Synthesis and properties of (Hf1-xTax)C solid solution carbides. Ceram. Int. 2018, 44, 19247–19253. [Google Scholar] [CrossRef]
- Teppala, D.T.; Kredel, S.A.; Ionescu, E.; Matović, B. A Review of the Synthesis of Compositionally Complex Ultra-High-Temperature Ceramics. J. Innov. Mater. Extrem. Cond. 2023, 4, 77–103. [Google Scholar]
- Elliott, R.O.; Kempter, C.P. Thermal Expansion of Some Transition Metal Carbides. J. Phys. Chem. 1958, 62, 630–631. [Google Scholar] [CrossRef]
- Jun, C.K. Thermal Expansion of NbC, HfC, and TaC at High Temperatures. J. Appl. Phys. 2003, 41, 5081. [Google Scholar] [CrossRef]
- Jun, C.K.; Shaffer, P.T.B. Thermal expansion of niobium carbide, hafnium carbide and tantalum carbide at high temperatures. J. Less Common Met. 1971, 24, 323–327. [Google Scholar] [CrossRef]
- Lu, X.-G.; Selleby, M.; Sundman, B. Calculations of thermophysical properties of cubic carbides and nitrides using the Debye–Grüneisen model. Acta Mater. 2007, 55, 1215–1226. [Google Scholar] [CrossRef]
- Yang, J.; Gao, F. First principles calculations of mechanical properties of cubic 5d transition metal monocarbides. Phys. B Condens. Matter 2012, 407, 3527–3534. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L.; Zeng, Q.; Guan, K.; Li, K.; Ren, H.; Liu, S.; Cheng, L. Structural, elastic and electronic properties of transition metal carbides TMC (TM=Ti, Zr, Hf and Ta) from first-principles calculations. Solid State Commun. 2011, 151, 602–606. [Google Scholar] [CrossRef]
- Zeng, Q.; Peng, J.; Oganov, A.R.; Zhu, Q.; Xie, C.; Zhang, X.; Dong, D.; Zhang, L.; Cheng, L. Prediction of stable hafnium carbides: Stoichiometries, mechanical properties, and electronic structure. Phys. Rev. B 2013, 88, 214107. [Google Scholar] [CrossRef]
- He, L.F.; Lin, Z.J.; Wang, J.Y.; Bao, Y.W.; Zhou, Y.C. Crystal structure and theoretical elastic property of two new ternary ceramics Hf3Al4C6 and Hf2Al4C5. Scr. Mater. 2008, 58, 679–682. [Google Scholar] [CrossRef]
- Skundric, T.; Schön, J.C.; Zarubica, A.; Fonovic, M.; Zagorac, D. Exploring the energy landscape and crystal structures of CrSi2N4. Z. Für Anorg. Und Allg. Chem. 2023, 649, e202300130. [Google Scholar] [CrossRef]
- Schön, J.C. Nanomaterials—What energy landscapes can tell us. Process. Appl. Ceram. 2015, 9, 157–168. [Google Scholar] [CrossRef]
- Bergerhoff, G.; Brown, I.D. Crystallographic Databases; International Union of Crystallography: Chester, UK, 1987. [Google Scholar]
- Zagorac, D.; Muller, H.; Ruehl, S.; Zagorac, J.; Rehme, S. Recent developments in the Inorganic Crystal Structure Database: Theoretical crystal structure data and related features. J. Appl. Crystallogr. 2019, 52, 918–925. [Google Scholar] [CrossRef]
- Zagorac, D.; Doll, K.; Zagorac, J.; Jordanov, D.; Matović, B. Barium Sulfide under Pressure: Discovery of Metastable Polymorphs and Investigation of Electronic Properties on ab Initio Level. Inorg. Chem. 2017, 56, 10644–10654. [Google Scholar] [CrossRef]
- Čančarević, Ž.P.; Schön, J.C.; Jansen, M. Stability of Alkali Metal Halide Polymorphs as a Function of Pressure. Chem.—Asian J. 2008, 3, 561–572. [Google Scholar] [CrossRef]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. WIREs Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Dovesi, R.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.; D’Arco, P.; Noël, Y.; Rérat, M.; Carbonnière, P.; et al. The CRYSTAL code, 1976–2020 and beyond, a long story. J. Chem. Phys. 2020, 152, 204111. [Google Scholar] [CrossRef] [PubMed]
- Doll, K.; Saunders, V.R.; Harrison, N.M. Analytical Hartree–Fock gradients for periodic systems. Int. J. Quantum Chem. 2001, 82, 1–13. [Google Scholar] [CrossRef]
- Doll, K.; Dovesi, R.; Orlando, R. Analytical Hartree-Fock gradients with respect to the cell parameter for systems periodic in three dimensions. Theor. Chem. Acc. 2004, 112, 394–402. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.; Bush, I. CRYSTAL17 User’s Manual; University of Torino: Torino, Italy, 2017. [Google Scholar]
- Doll, K. Gaussian Basis Sets for Solid State Calculations. In Basis Sets in Computational Chemistry; Perlt, E., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 157–181. [Google Scholar]
- Ramo, D.M.; Gavartin, J.L.; Shluger, A.L.; Bersuker, G. Spectroscopic properties of oxygen vacancies in monoclinic HfO2 calculated with periodic and embedded cluster density functional theory. Phys. Rev. B 2007, 75, 205336. [Google Scholar] [CrossRef]
- Catti, M.; Pavese, A.; Dovesi, R.; Saunders, V.R. Static lattice and electron properties of MgCO3 (magnesite) calculated by ab initio periodic Hartree-Fock methods. Phys. Rev. B Condens. Matter 1993, 47, 9189–9198. [Google Scholar] [CrossRef] [PubMed]
- Skundric, T.; Matovic, B.; Zarubica, A.; Chudoba, D.; Zagorac, D. Data Mining Ab Initio Study of Gypsum CaCO3 Modifications at Standard and Extreme Conditions. J. Innov. Mater. Extrem. Cond. 2023, 4, 38–51. [Google Scholar]
- Hundt, R. KPLOT, A Program for Plotting and Analyzing Crystal Structures; Technicum Scientific Publishing: Stuttgart, Germany, 2016. [Google Scholar]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Perger, W.F.; Criswell, J.; Civalleri, B.; Dovesi, R. Ab-initio calculation of elastic constants of crystalline systems with the CRYSTAL code. Comput. Phys. Commun. 2009, 180, 1753–1759. [Google Scholar] [CrossRef]
- Erba, A.; Mahmoud, A.; Orlando, R.; Dovesi, R. Elastic properties of six silicate garnet end members from accurate ab initio simulations. Phys. Chem. Miner. 2014, 41, 151–160. [Google Scholar] [CrossRef]
- Krikorian, N.H.; Wallace, T.C.; Anderson, J.L. Low-Temperature Thermal Expansion of the Group 4a Carbides. J. Electrochem. Soc. 1963, 110, 587. [Google Scholar] [CrossRef]
- Aigner, K.; Lengauer, W.; Rafaja, D.; Ettmayer, P. Lattice parameters and thermal expansion of Ti(CxN1−x), Zr(CxN1−x), Hf(CxN1−x) and TiN1−x from 298 to 1473 K as investigated by high-temperature X-ray diffraction. J. Alloys Compd. 1994, 215, 121–126. [Google Scholar] [CrossRef]
- Lengauer, W.; Binder, S.; Aigner, K.; Ettmayer, P.; Guillou, A.; Debuigne, J.; Groboth, G. Solid state properties of group IVb carbonitrides. J. Alloys Compd. 1995, 217, 137–147. [Google Scholar] [CrossRef]
- Zhang, H.; Hedman, D.; Feng, P.; Han, G.; Akhtar, F. A high-entropy B4(HfMo2TaTi)C and SiC ceramic composite. Dalton Trans. 2019, 48, 5161–5167. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Cui, S.; Hu, H.; Zhang, G.; Lv, Z. Electronic structure and elastic constants of TiCxN1−x, ZrxNb1−xC and HfCxN1−x alloys: A first-principles study. Phys. B Condens. Matter 2011, 406, 3631–3635. [Google Scholar] [CrossRef]
- Razumovskiy, V.I.; Popov, M.N.; Ding, H.; Odqvist, J. Formation and interaction of point defects in group IVb transition metal carbides and nitrides. Comput. Mater. Sci. 2015, 104, 147–154. [Google Scholar] [CrossRef]
- Yang, Y.; Ma, L.; Gan, G.-Y.; Wang, W.; Tang, B.-Y. Investigation of thermodynamic properties of high entropy (TaNbHfTiZr)C and (TaNbHfTiZr)N. J. Alloys Compd. 2019, 788, 1076–1083. [Google Scholar] [CrossRef]
- Chang, Y.H.R.; Yoon, T.L. Effects of nitrogen addition and growth condition on the enhanced mechanical properties of transition metal carbides TMC (TM = Zr, Hf). Ceram. Int. 2020, 46, 1124–1136. [Google Scholar] [CrossRef]
- Jiang, S.; Shao, L.; Fan, T.-W.; Duan, J.-M.; Chen, X.-T.; Tang, B.-Y. Elastic and thermodynamic properties of high entropy carbide (HfTaZrTi)C and (HfTaZrNb)C from ab initio investigation. Ceram. Int. 2020, 46, 15104–15112. [Google Scholar] [CrossRef]
- Krasnenko, V.; Brik, M. First-principles calculations of the structural, elastic and electronic properties of MNxC1−x (M=Ti, Zr, Hf; 0<x<1) carbonitrides at ambient and elevated hydrostatic pressure. Solid State Sci. 2013, 28, 1–8. [Google Scholar]
- Kim, J.; Kwon, H.; Kim, B.; Suh, Y. Finite temperature thermal expansion and elastic properties of (Hf1-xTax)C ultrahigh temperature ceramics. Ceram. Int. 2019, 45, 10805–10809. [Google Scholar] [CrossRef]
- Schön, J.C.; Jansen, M. Determination of candidate structures for simple ionic compounds through cell optimisation. Comput. Mater. Sci. 1995, 4, 43–58. [Google Scholar] [CrossRef]
- Zagorac, D.; Zagorac, J.; Fonović, M.; Prikhna, T.; Matović, B. Novel boron-rich aluminum nitride advanced ceramic materials. Int. J. Appl. Ceram. Technol. 2023, 20, 174–189. [Google Scholar] [CrossRef]
- Haq, B.U.; AlFaify, S.; Alrebdi, T.A.; Ahmed, R.; Al-Qaisi, S.; Taib, M.F.M.; Naz, G.; Zahra, S. Investigations of optoelectronic properties of novel ZnO monolayers: A first-principles study. Mater. Sci. Eng. B 2021, 265, 115043. [Google Scholar] [CrossRef]
- Guinier, A.; Bokij, G.B.; Boll-Dornberger, K.; Cowley, J.M.; Durovic, S.; Jagodzinski, H.; Krishna, P.; de Wolff, P.M.; Zvyagin, B.B.; Cox, D.E.; et al. Nomenclature of polytype structures. Report of the International Union of Crystallography Ad hoc Committee on the Nomenclature of Disordered, Modulated and Polytype Structures. Acta Crystallogr. Sect. A 1984, 40, 399–404. [Google Scholar] [CrossRef]
- Kelly, J.F.; Fisher, G.R.; Barnes, P. Correlation between layer thickness and periodicity of long polytypes in silicon carbide. Mater. Res. Bull. 2005, 40, 249–255. [Google Scholar] [CrossRef]
- Aksenov, S.M.; Charkin, D.O.; Banaru, A.M.; Banaru, D.A.; Volkov, S.N.; Deineko, D.V.; Kuznetsov, A.N.; Rastsvetaeva, R.K.; Chukanov, N.V.; Shkurskii, B.B.; et al. Modularity, polytypism, topology, and complexity of crystal structures of inorganic compounds (Review). J. Struct. Chem. 2023, 64, 1797–2028. [Google Scholar]
- Zagorac, D.; Schön, J.C.; Zagorac, J.; Jansen, M. Theoretical investigations of novel zinc oxide polytypes and in-depth study of their electronic properties. RSC Adv. 2015, 5, 25929–25935. [Google Scholar] [CrossRef]
- Menad, A.; Benmalti, M.E.; Zaoui, A.; Ferhat, M. Impact of polytypism on the ground state properties of zinc oxide: A first-principles study. Results Phys. 2020, 18, 103316. [Google Scholar] [CrossRef]
- Zagorac, D.; Doll, K.; Schön, J.C.; Jansen, M. Ab initio structure prediction for lead sulfide at standard and elevated pressures. Phys. Rev. B 2011, 84, 045206. [Google Scholar] [CrossRef]
- Mudring, A.-V. Thallium Halides—New Aspects of the Stereochemical Activity of Electron Lone Pairs of Heavier Main-Group Elements. Eur. J. Inorg. Chem. 2007, 2007, 882–890. [Google Scholar] [CrossRef]
- Lowndes, R.P.; Perry, C.H. Molecular structure and anharmonicity in thallium iodide. J. Chem. Phys. 1973, 58, 271–278. [Google Scholar] [CrossRef]
- Yang, J.; Gao, F. Hardness calculations of 5d transition metal monocarbides with tungsten carbide structure. Phys. Status Solidi B 2010, 247, 2161–2167. [Google Scholar] [CrossRef]
- Yu, R.; Wu, Q.; Fang, Z.; Weng, H. From Nodal Chain Semimetal to Weyl Semimetal in HfC. Phys. Rev. Lett. 2017, 119, 036401. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The Voigt-Reuss-Hill Approximation and Elastic Moduli of Polycrystalline MgO, CaF2, β-ZnS, ZnSe, and CdTe. J. Appl. Phys. 1967, 38, 2535–2540. [Google Scholar] [CrossRef]
- Brown, H.L.; Armstrong, P.E.; Kempter, C.P. Elastic Properties of Some Polycrystalline Transition-Metal Monocarbides. J. Chem. Phys. 1966, 45, 547–549. [Google Scholar] [CrossRef]
- Nartowski, A.M.; Parkin, I.P.; MacKenzie, M.; Craven, A.J.; MacLeod, I. Solid state metathesis routes to transition metal carbides. J. Mater. Chem. 1999, 9, 1275–1281. [Google Scholar] [CrossRef]
- Isaev, E.I.; Simak, S.I.; Abrikosov, I.A.; Ahuja, R.; Vekilov, Y.K.; Katsnelson, M.I.; Lichtenstein, A.I.; Johansson, B. Phonon related properties of transition metals, their carbides, and nitrides: A first-principles study. J. Appl. Phys. 2007, 101, 123519. [Google Scholar] [CrossRef]
- Zaoui, A.; Bouhafs, B.; Ruterana, P. First-principles calculations on the electronic structure of TiCxN1−x, ZrxNb1−xC and HfCxN1−x alloys. Mater. Chem. Phys. 2005, 91, 108–115. [Google Scholar] [CrossRef]
- Krajewski, A.; D’Alessio, L.; De Maria, G. Physico-Chemical and Thermophysical Properties of Cubic Binary Carbides. Cryst. Res. Technol. 1998, 33, 341–374. [Google Scholar] [CrossRef]
- Pierson, H.O. 4—Carbides of Group IV: Titanium, Zirconium, and Hafnium Carbides. In Handbook of Refractory Carbides and Nitrides; Pierson, H.O., Ed.; William Andrew Publishing: Westwood, NJ, USA, 1996; pp. 55–80. [Google Scholar]
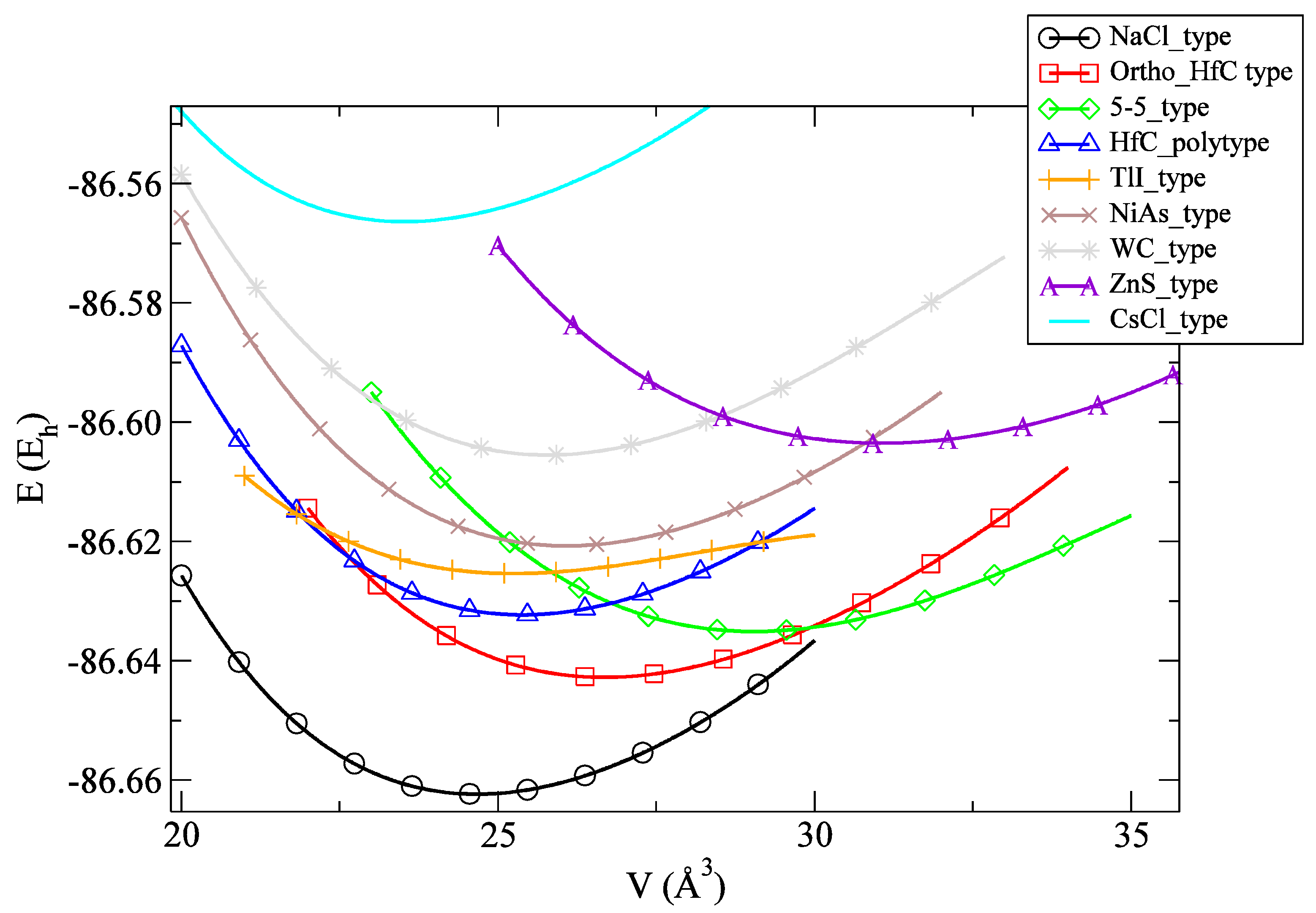
| Modification | LDA | PBE |
|---|---|---|
| NaCl_type | −86.6624 | −87.0498 |
| Ortho_HfC_type | −86.6428 | −87.0319 |
| 5-5_type | −86.6352 | −87.0261 |
| HfC_polytype | −86.6324 | −87.0203 |
| TlI_type | −86.6251 | −87.0135 |
| NiAs_type | −86.6209 | −87.0104 |
| WC_type | −86.6055 | −86.9942 |
| ZnS_type | −86.6034 | −86.9968 |
| CsCl_type | −86.5664 | −86.9519 |
| Structure Candidates | LDA | PBE |
|---|---|---|
| NaCl_type | Fm-3m (225) a = 4.62; V = 98.51 Hf 0 0 0 C 1/2 0 0 | Fm-3m (225) a = 4.67; V = 101.91 Hf 0 0 0 C 1/2 0 0 |
| Ortho_HfC type | Cmcm (63) a = 3.40; b = 13.66; c = 4.59; V = 213.30 Hf1 0 0.6862 1/4 Hf2 0 0.9200 1/4 C1 0 0.3144 1/4 C2 0 0.0799 1/4 | Cmcm (63) a = 3.45; b = 13.81 c = 4.64; V = 220.66 Hf1 0 0.6857 1/4 Hf2 0 0.9201 1/4 C1 0 0.3149 1/4 C2 0 0.0799 1/4 |
| 5-5_type | P63/mmc (194) a = 3.82; c = 4.60; V = 58.01 Hf 1/3 2/3 3/4 C 2/3 1/3 3/4 | P63/mmc (194) a = 3.86; c = 4.65 V = 60.02 Hf 1/3 2/3 3/4 C 2/3 1/3 3/4 |
| HfC_polytype | R3m (160) a = 3.24; c = 16.73; V = 152.34 Hf1 0 0 0.8085 Hf2 0 0 0.6344 C1 0 0 0.2234 C2 0 0 0.0541 | R3m (160) a = 3.28; c = 16.90 V = 157.70 Hf1 0 0 0.8085 Hf2 0 0 0.6345 C1 0 0 0.2234 C2 0 0 0.0540 |
| TlI_type | Cmcm (63) a = 3.15; b = 9.54; c = 3.34; V = 100.52 Hf 0 0.6343 1/4 C 0 0.8697 1/4 | Cmcm (63) a = 3.20; b = 9.92 c = 3.35; V = 106.16 Hf 0 0.6367 1/4 C 0 0.8649 1/4 |
| NiAs_type | P63/mmc (194) a = 3.24; c = 5.72; V = 52.03 Hf 0 0 1/2 C 1/3 2/3 3/4 | P63/mmc (194) a = 3.28; c = 5.78 V = 53.86 Hf 0 0 0.5 C 1/3 2/3 3/4 |
| WC_type | P-6m2 (187) a = 3.20; c = 2.90; V = 25.73 Hf 0 0 0 C 1/3 2/3 1/2 | P-6m2 (187) a = 3.24; c = 2.93 V = 26.68 Hf 0 0 0 C 1/3 2/3 1/2 |
| ZnS_type | F-43m (216) a = 4.99; V = 124.33 Hf 1/2 1/2 1/2 C 3/4 3/4 1/4 | F-43m (216) a = 5.05; V = 128.72 Hf 1/2 1/2 1/2 C 3/4 3/4 1/4 |
| CsCl_type | Pm-3m (221) a = 2.87; V = 23.54 Hf 0 0 0 C 1/2 1/2 1/2 | Pm-3m (221) a = 2.91; V = 24.54 Hf 0 0 0 C 1/2 1/2 1/2 |
| Mechanical Property | Rock Salt (NaCl) Type | ortho_HfC Type | NiAs Type | ||
|---|---|---|---|---|---|
| LDA | Experiment | Theory | LDA | LDA | |
| Bulk modulus KV (GPa) | 261.54 | 242 [84], 263 [85] | 233 [63], 238 [86], 247 [33], 248 [87], 262.5 [68], 270 [36], 276.3 [34], 278 [35] | 228.12 | 230.53 |
| Bulk modulus KR (GPa) | 261.54 | 222.84 | 228.01 | ||
| Bulk modulus KH (GPa) | 261.54 | 225.48 | 229.27 | ||
| Shear modulus GV (GPa) | 195.08 | 195 [84] | 166 [32], 181 [33], 188.8 [34], 207 [35], 230 [36] | 86.10 | 146.79 |
| Shear modulus GR (GPa) | 192.38 | 237.31 | 132.56 | ||
| Shear modulus GH (GPa) | 193.73 | 161.71 | 139.67 | ||
| Young modulus E_H (GPa) | 466.11 | 430 [88], 461 [84] | 404 [32], 437 [33], 461.3 [34], 537 [36] | 391.53 | 348.29 |
| Poisson ratio v_H | 0.20 | n.a. | n.a. | 0.21 | 0.25 |
| Vickers (GPa) hardness VH_V | 27.57 | 26.1 [89], 18–20 [88] | 26.2 [33]; 29.08 [35] | 1.15 | 18.83 |
| Vickers (GPa) hardness VH_R | 26.87 | 47.48 | 15.80 | ||
| Vickers (GPa) hardness VH_H | 27.22 | 23.09 | 17.29 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zagorac, J.; Schön, J.C.; Matović, B.; Butulija, S.; Zagorac, D. Hafnium Carbide: Prediction of Crystalline Structures and Investigation of Mechanical Properties. Crystals 2024, 14, 340. https://doi.org/10.3390/cryst14040340
Zagorac J, Schön JC, Matović B, Butulija S, Zagorac D. Hafnium Carbide: Prediction of Crystalline Structures and Investigation of Mechanical Properties. Crystals. 2024; 14(4):340. https://doi.org/10.3390/cryst14040340
Chicago/Turabian StyleZagorac, Jelena, Johann Christian Schön, Branko Matović, Svetlana Butulija, and Dejan Zagorac. 2024. "Hafnium Carbide: Prediction of Crystalline Structures and Investigation of Mechanical Properties" Crystals 14, no. 4: 340. https://doi.org/10.3390/cryst14040340
APA StyleZagorac, J., Schön, J. C., Matović, B., Butulija, S., & Zagorac, D. (2024). Hafnium Carbide: Prediction of Crystalline Structures and Investigation of Mechanical Properties. Crystals, 14(4), 340. https://doi.org/10.3390/cryst14040340







