Ferroelectric Smectic Liquid Crystals
Abstract
:1. Introduction
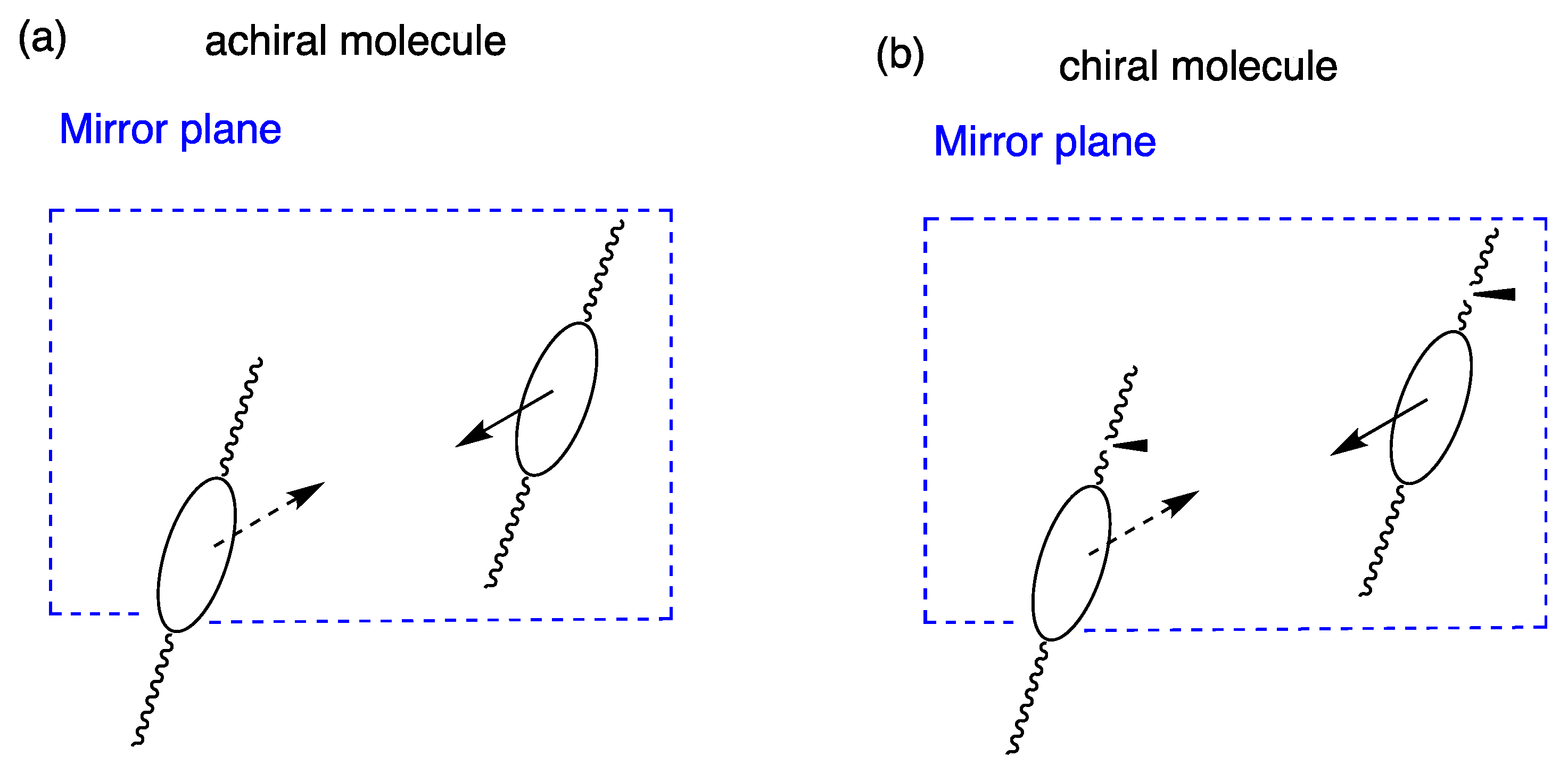
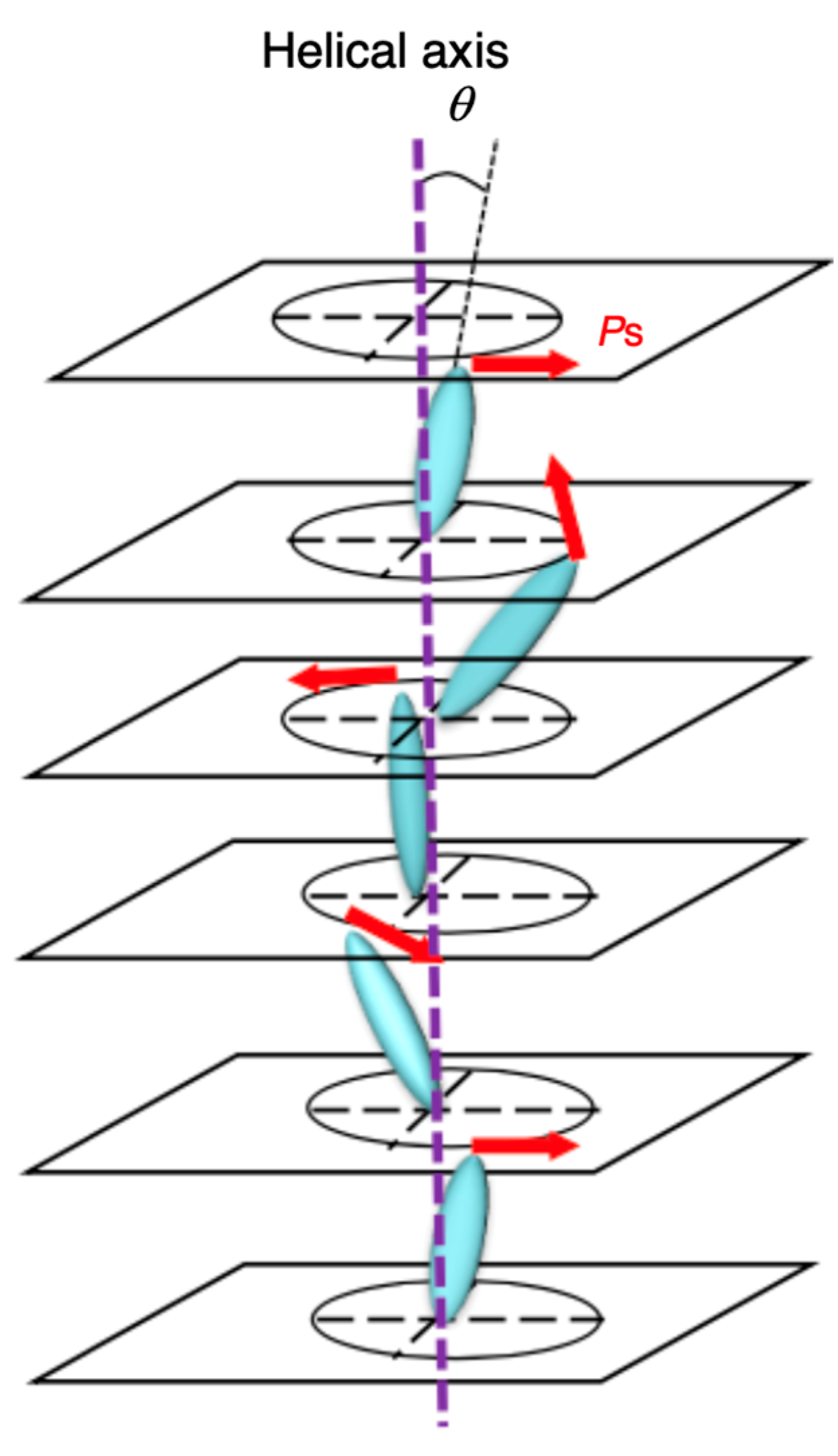
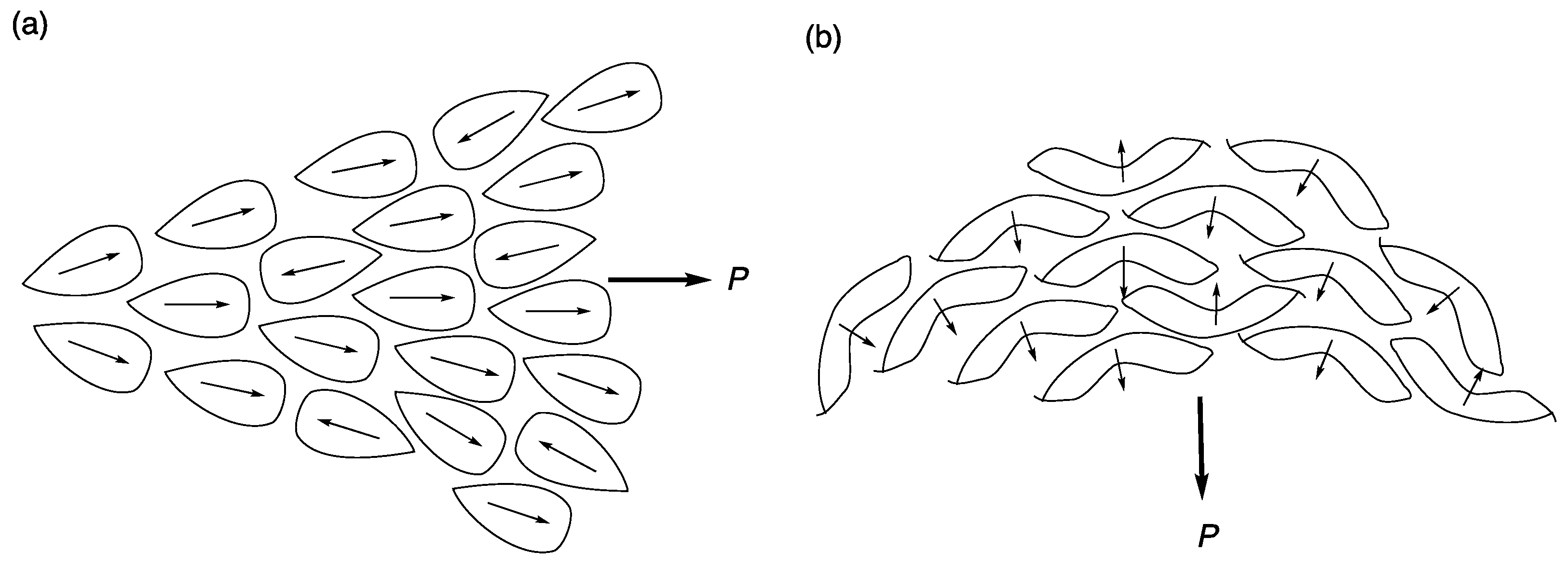
2. Ferroelectricity in Liquid Crystals
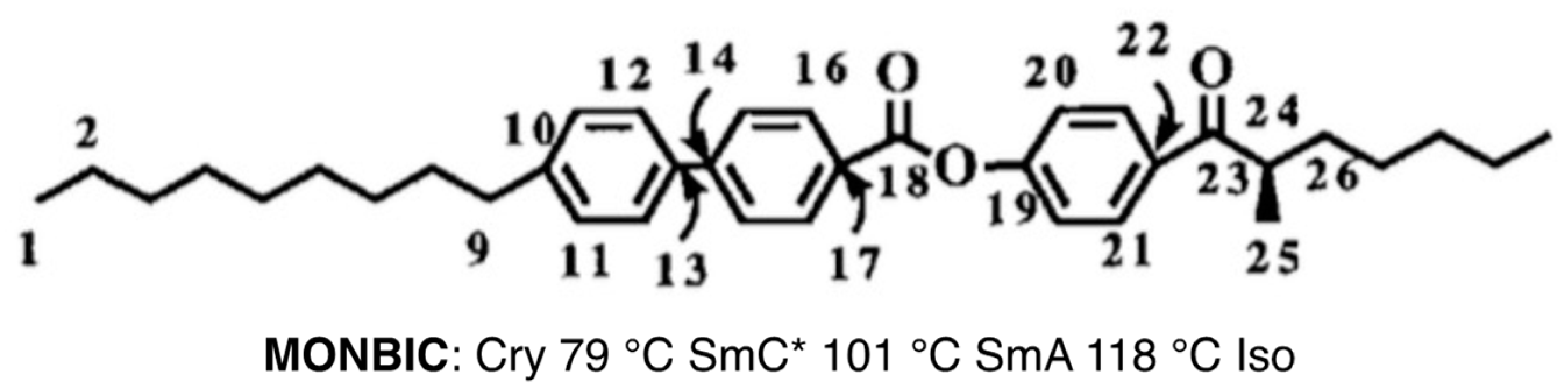
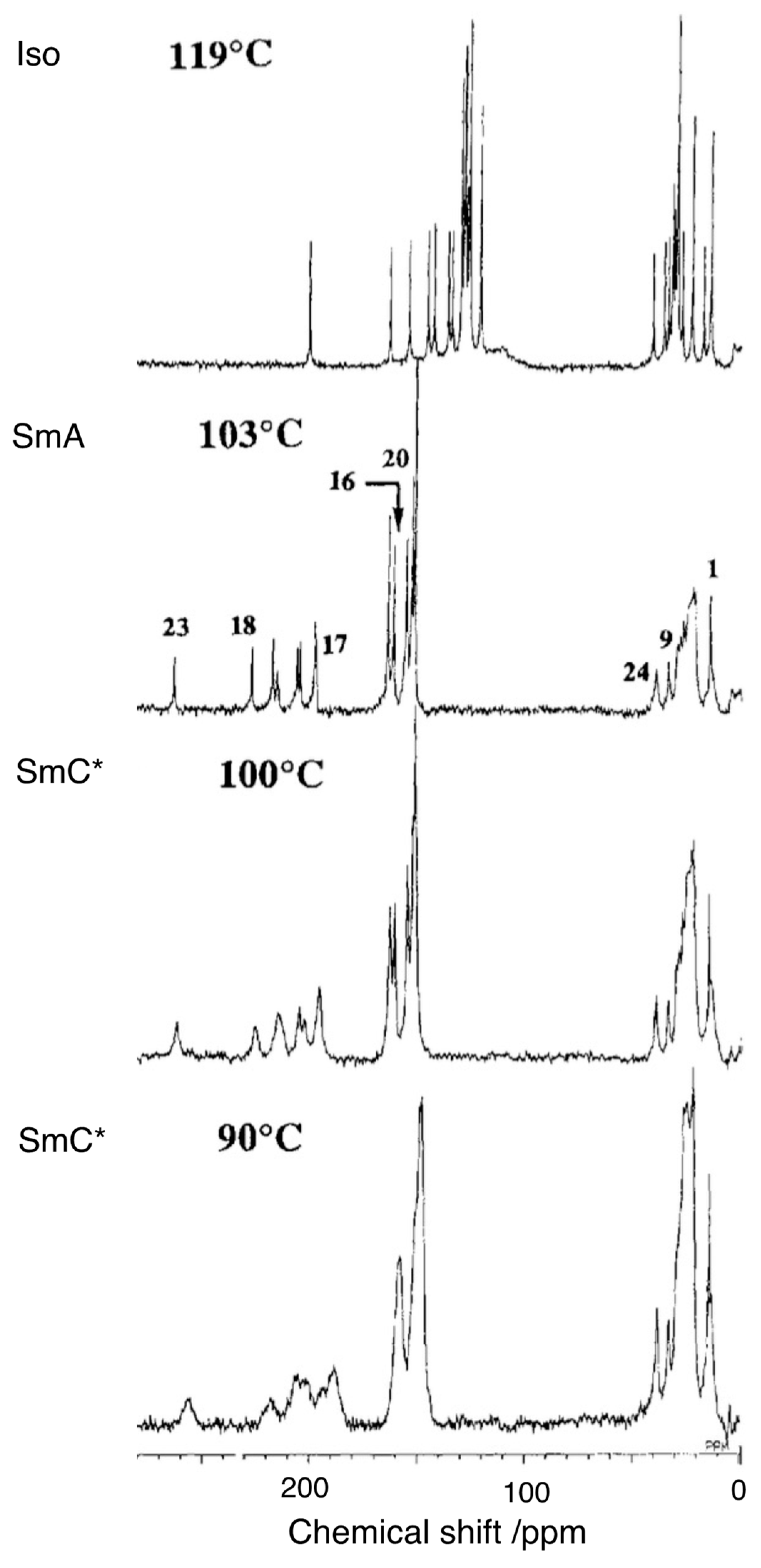
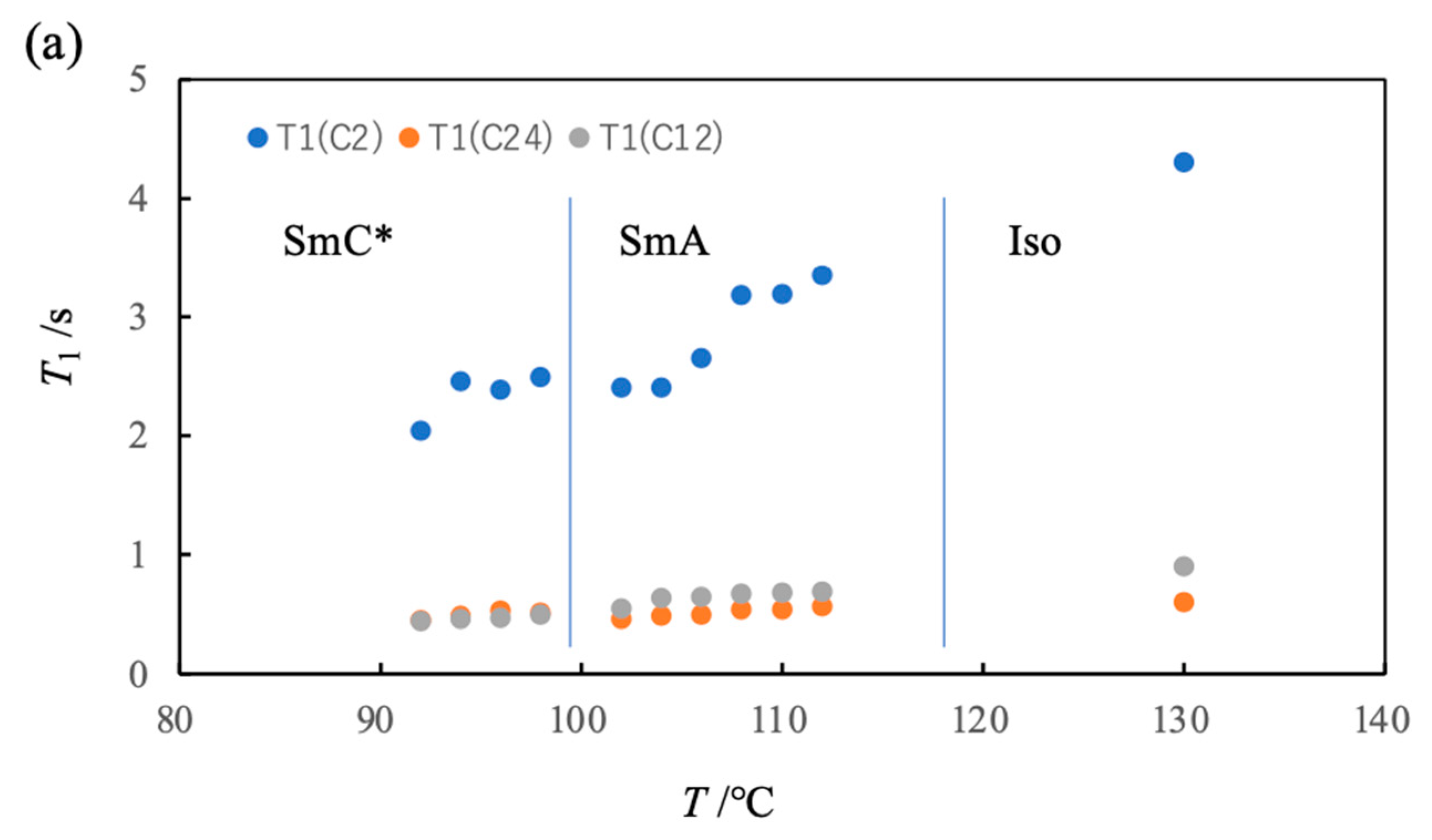
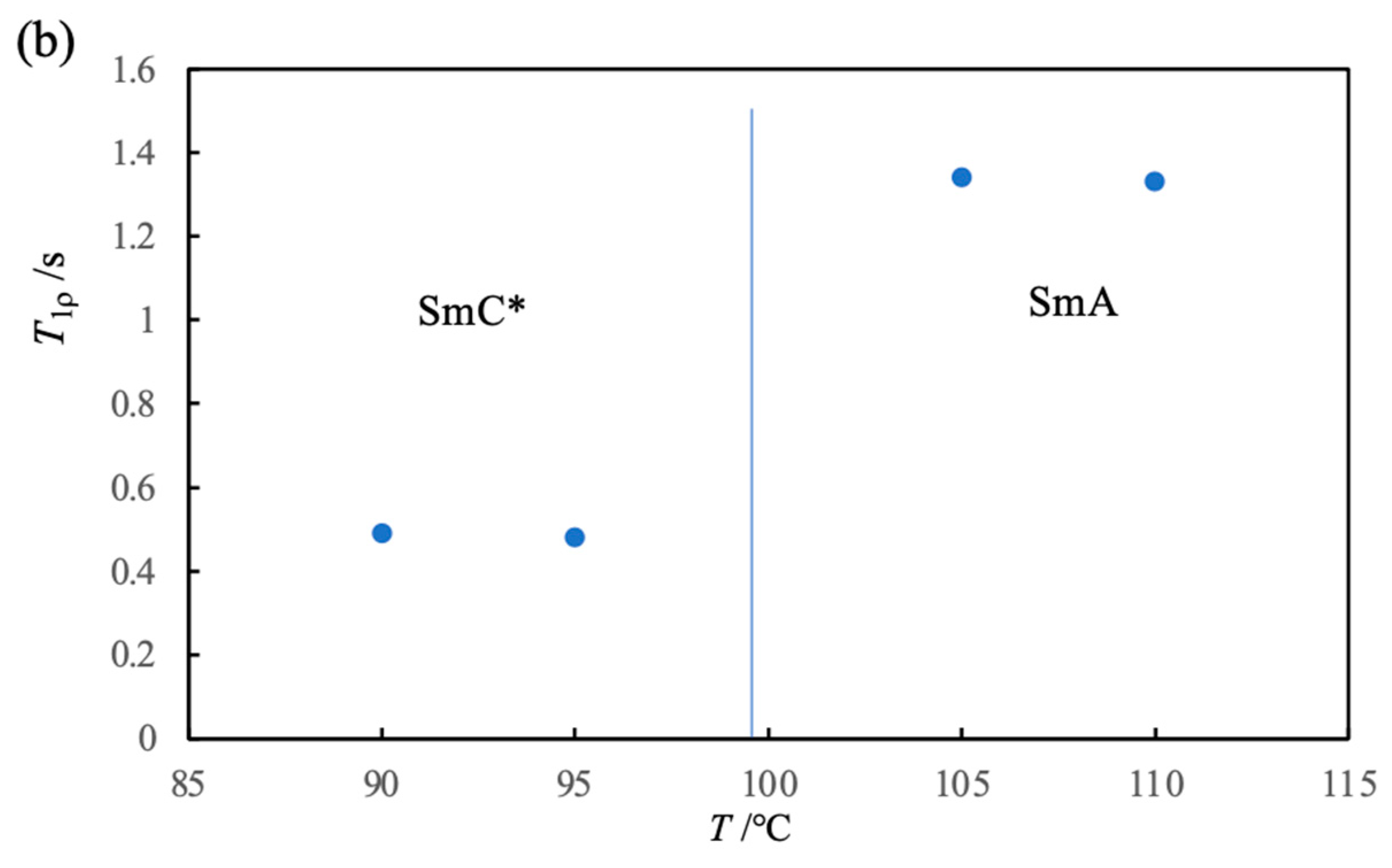
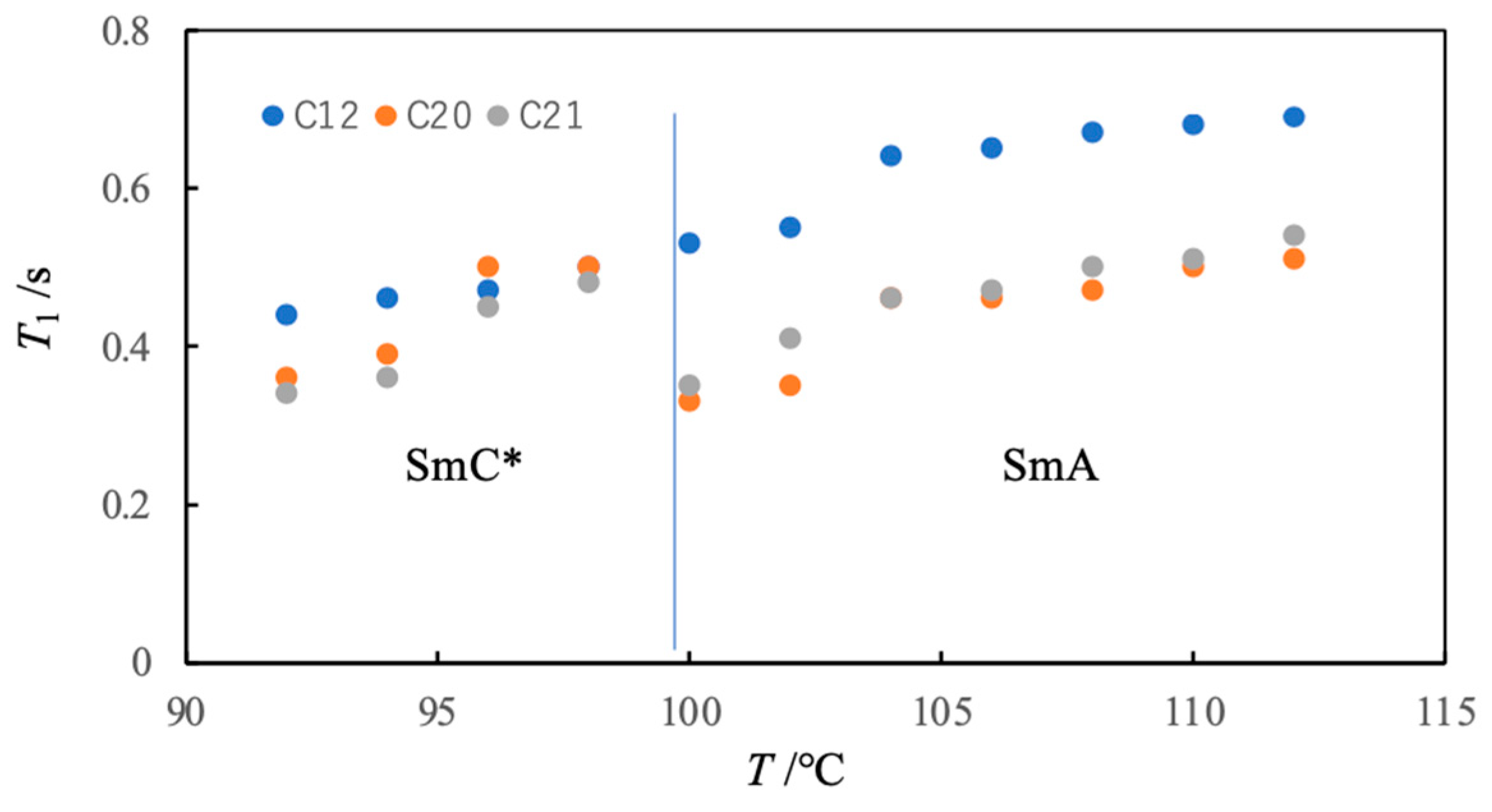
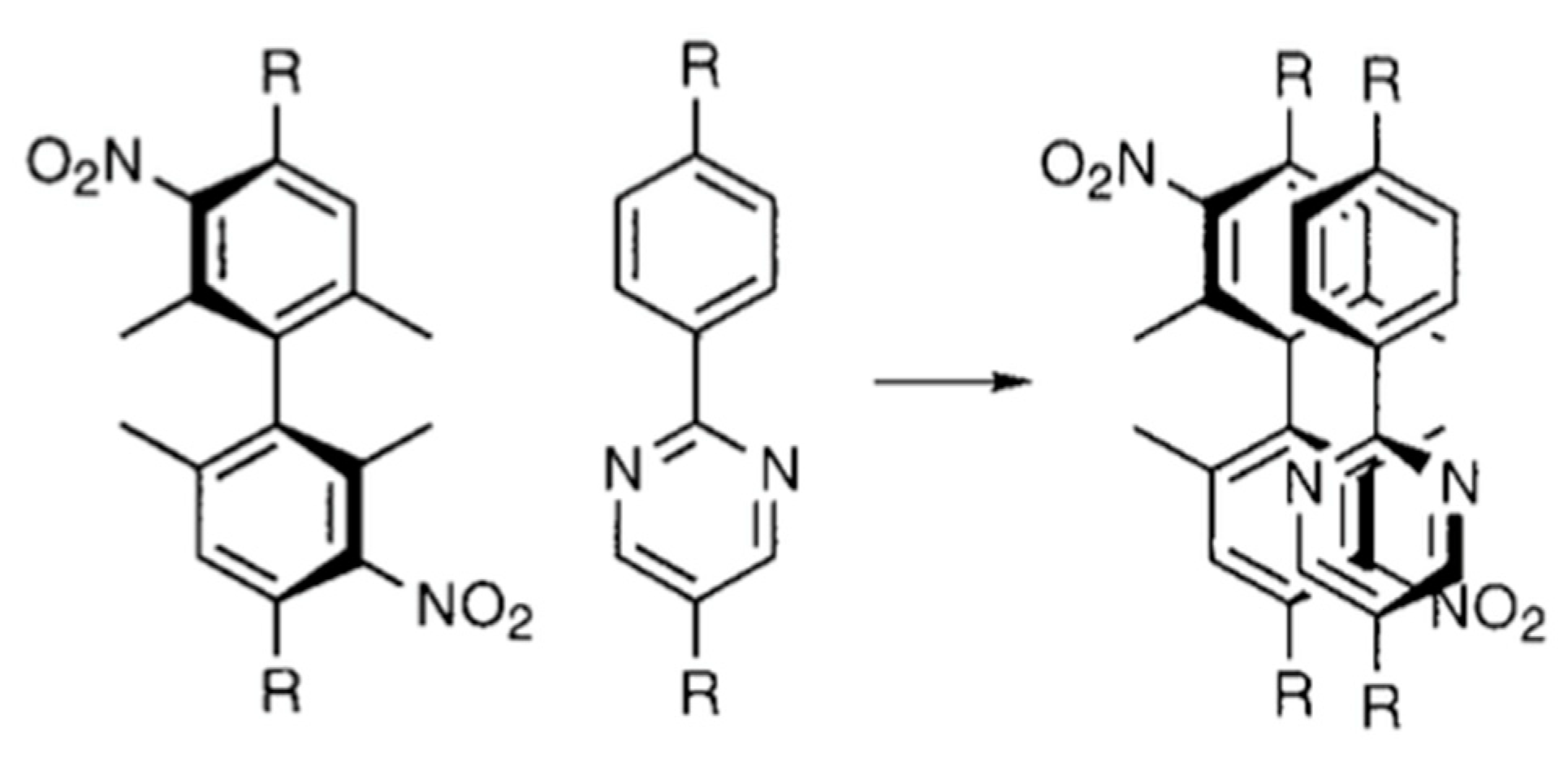
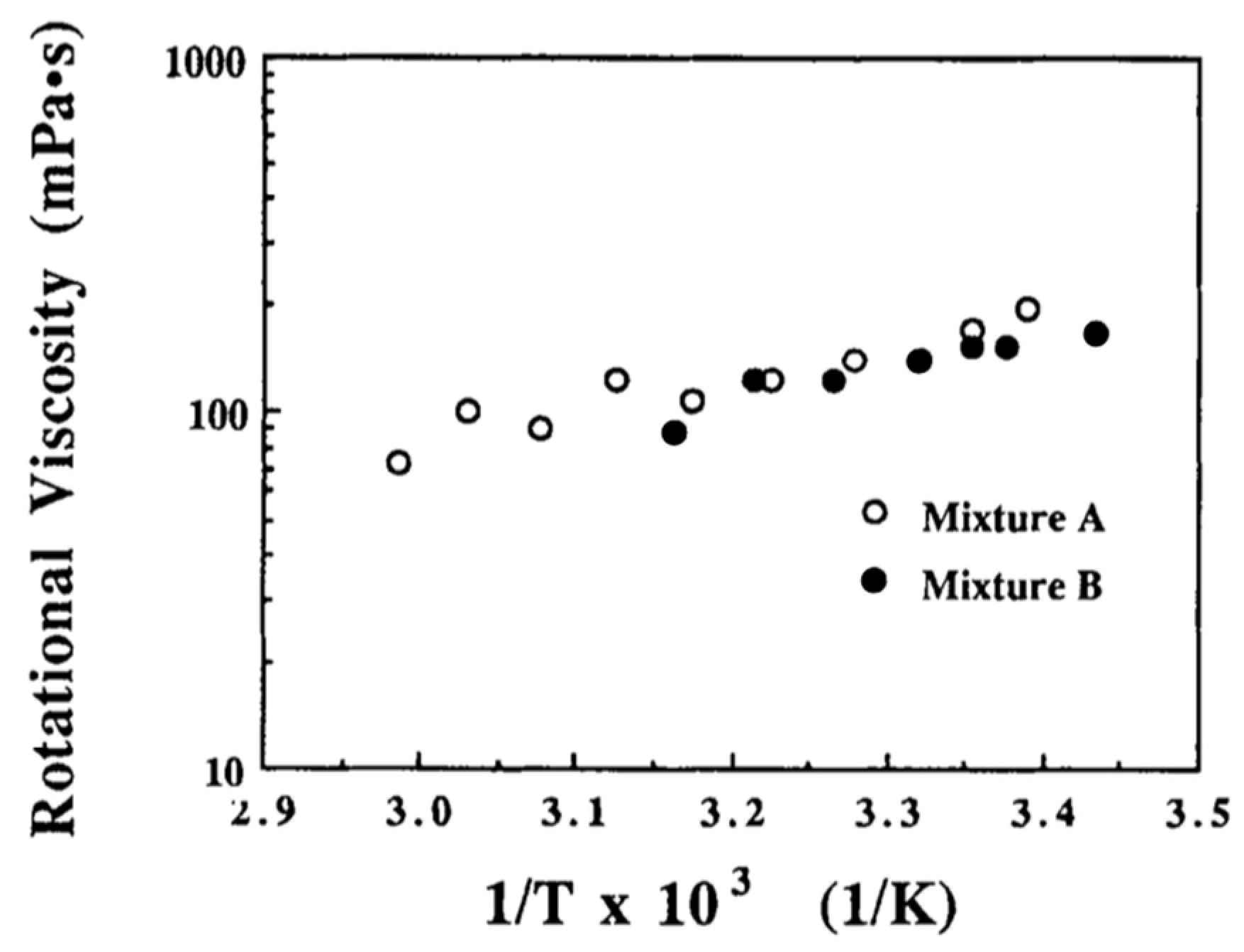
3. 13C NMR Studies on a Ferroelectric Liquid Crystal
4. Materials for Ferroelectric Liquid Crystal Displays
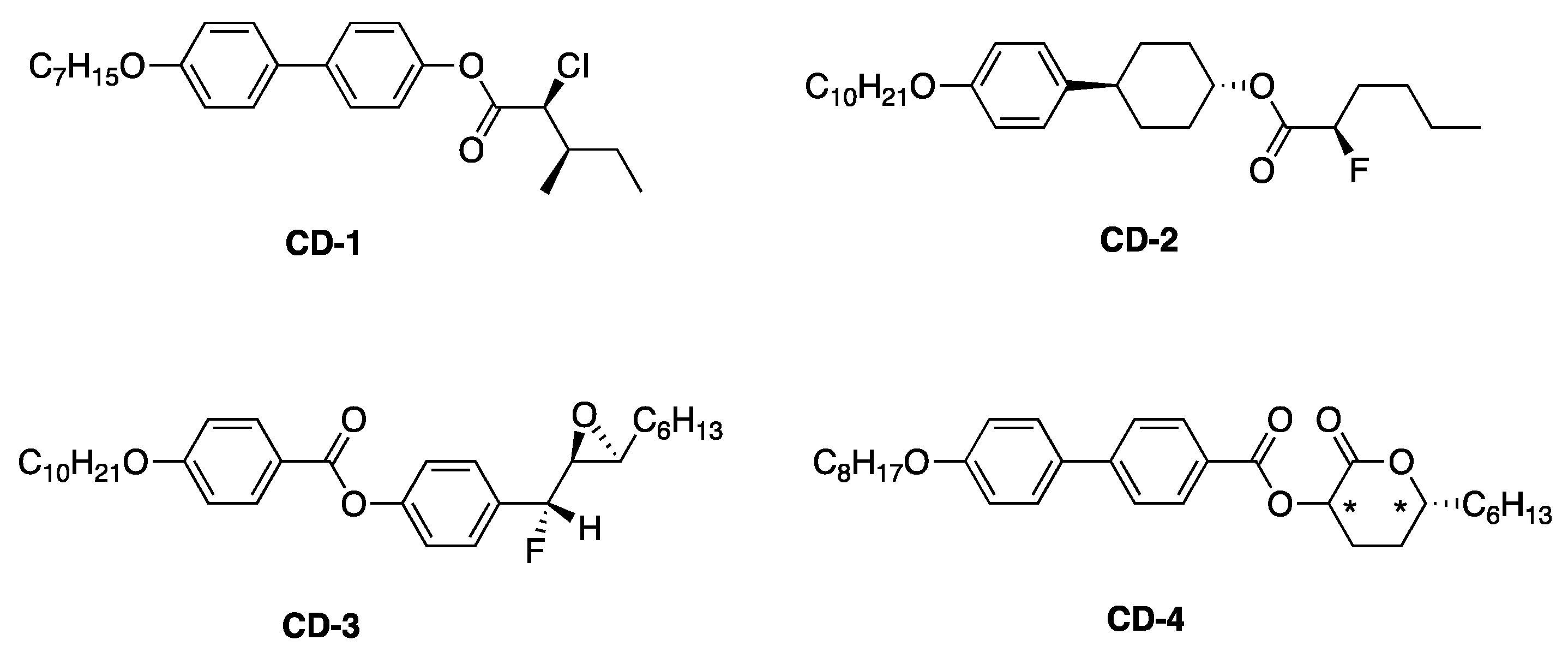
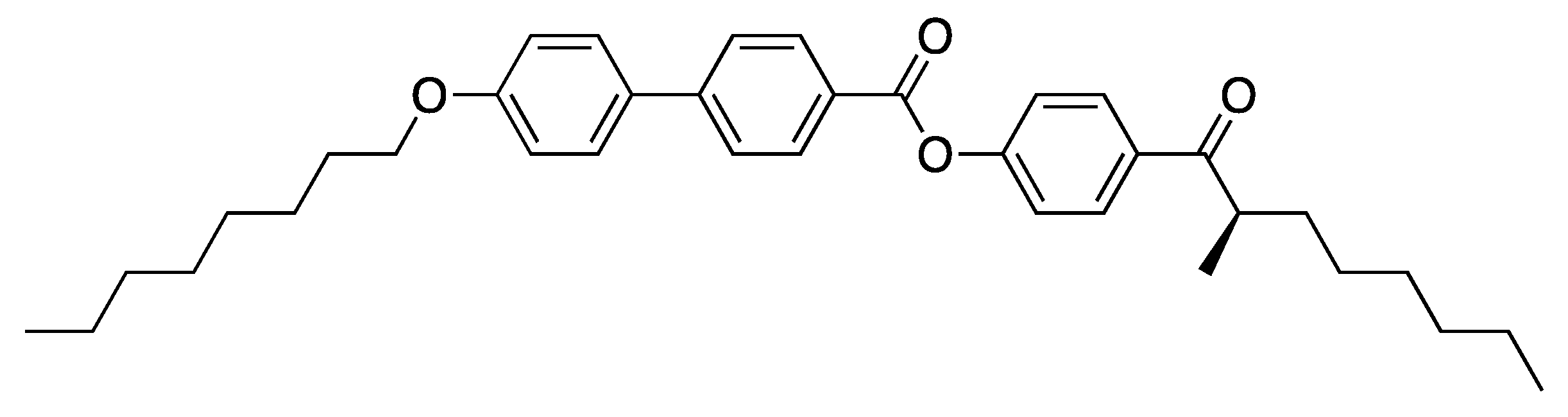
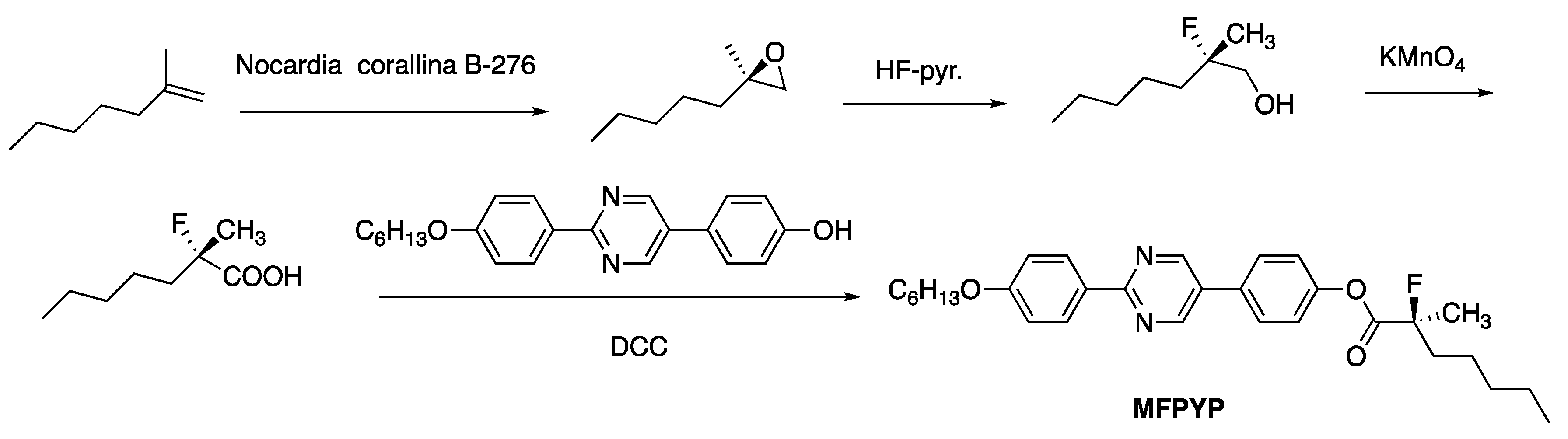
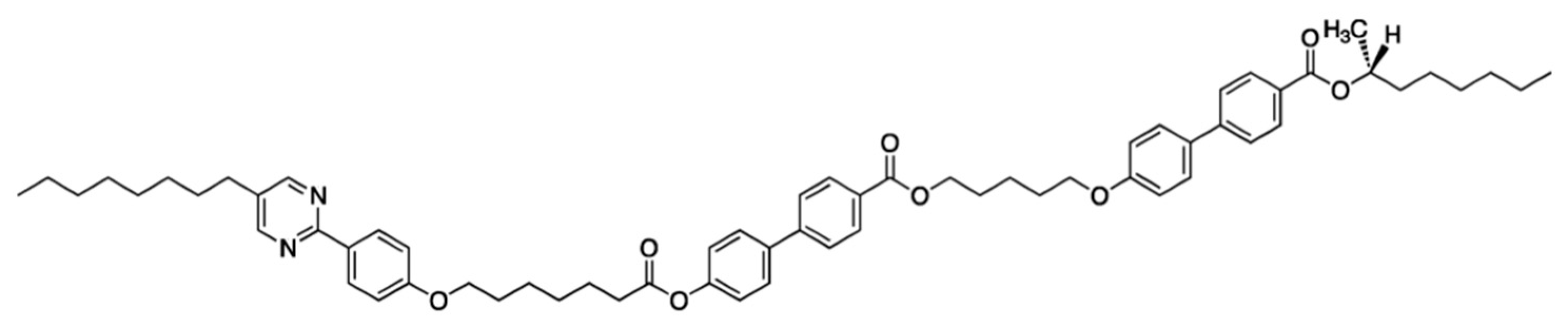
4.1. FLCs Exhibiting Large Spontaneous Polarization
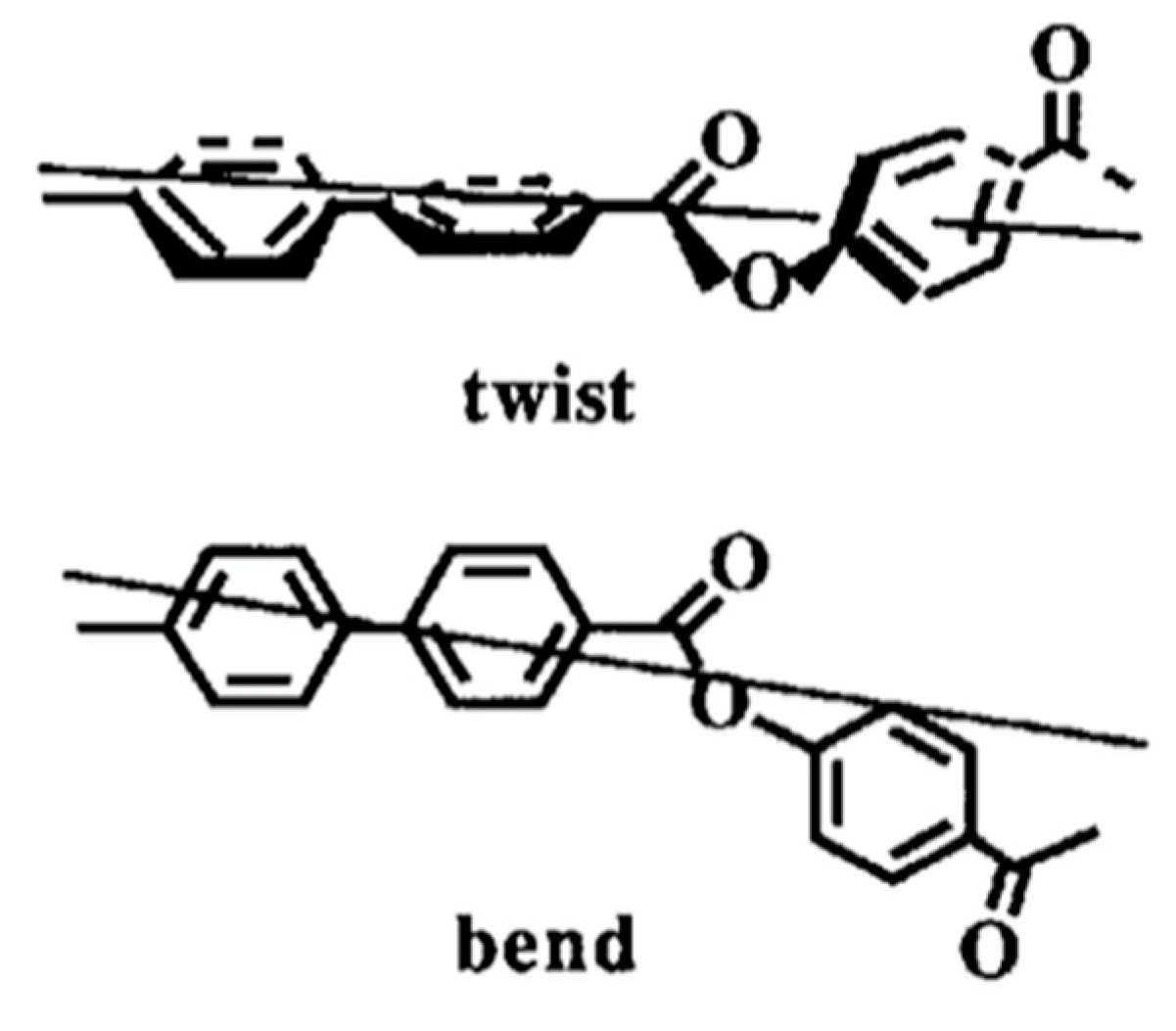
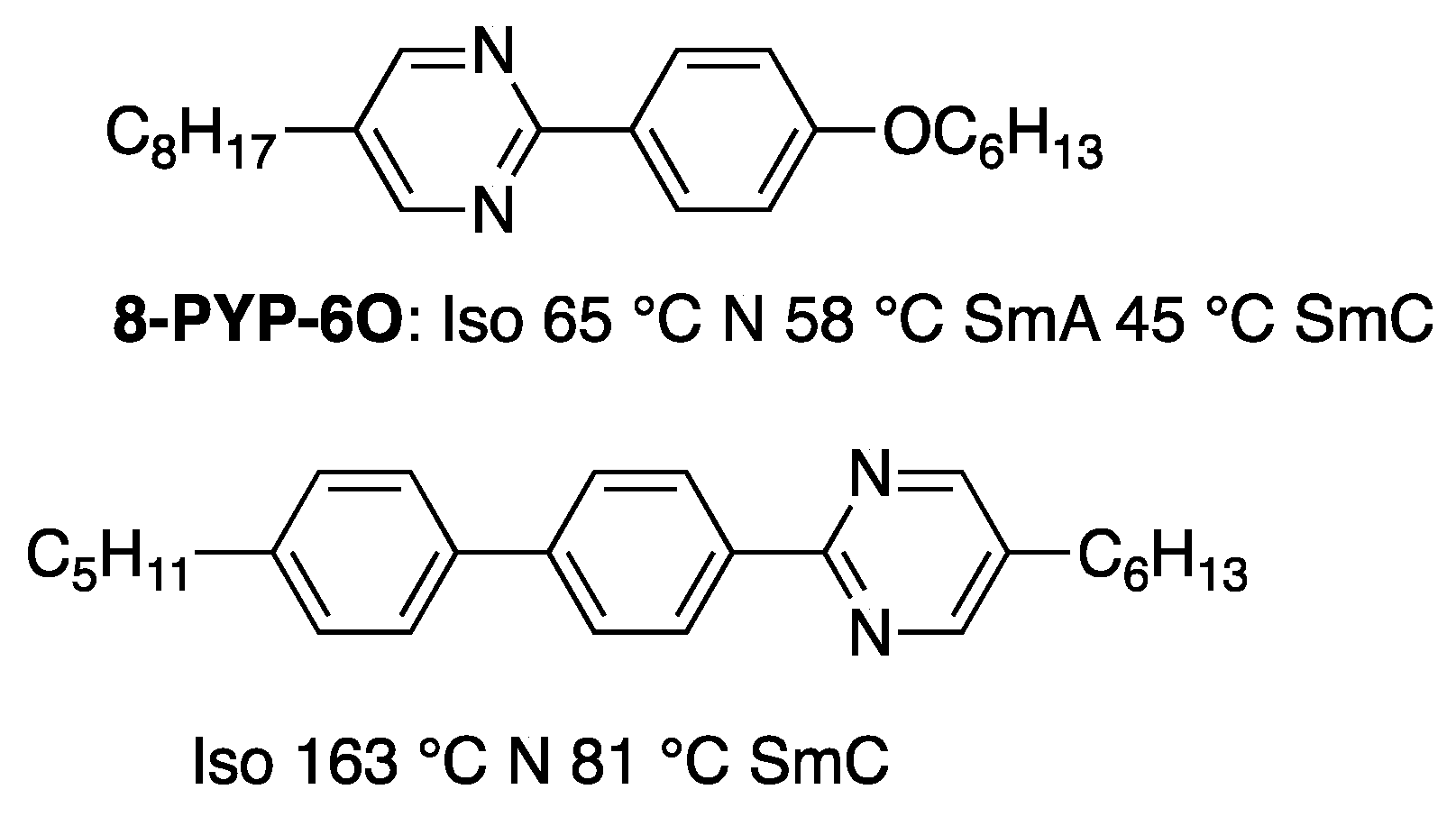
4.2. Host SmC Materials
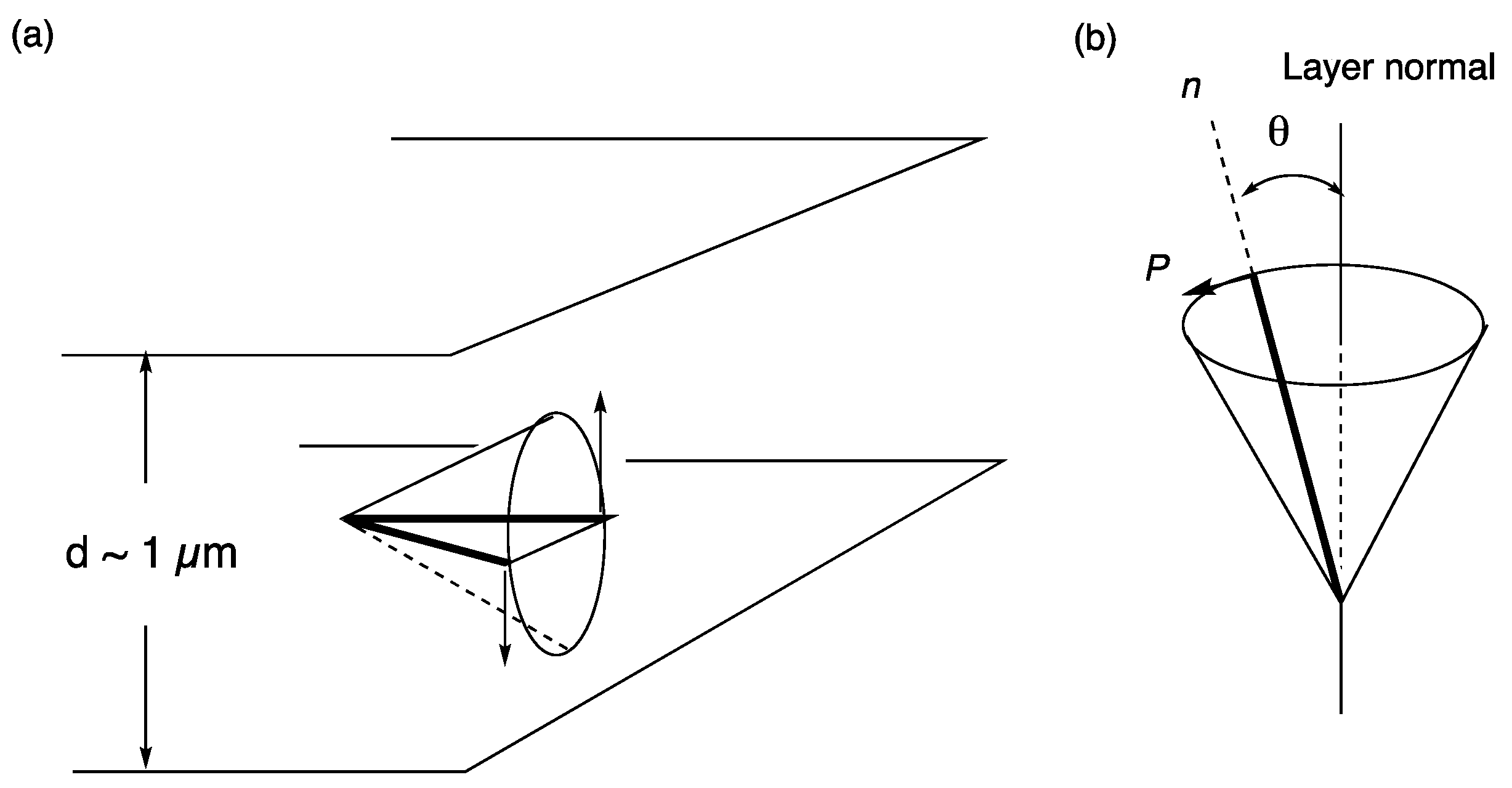
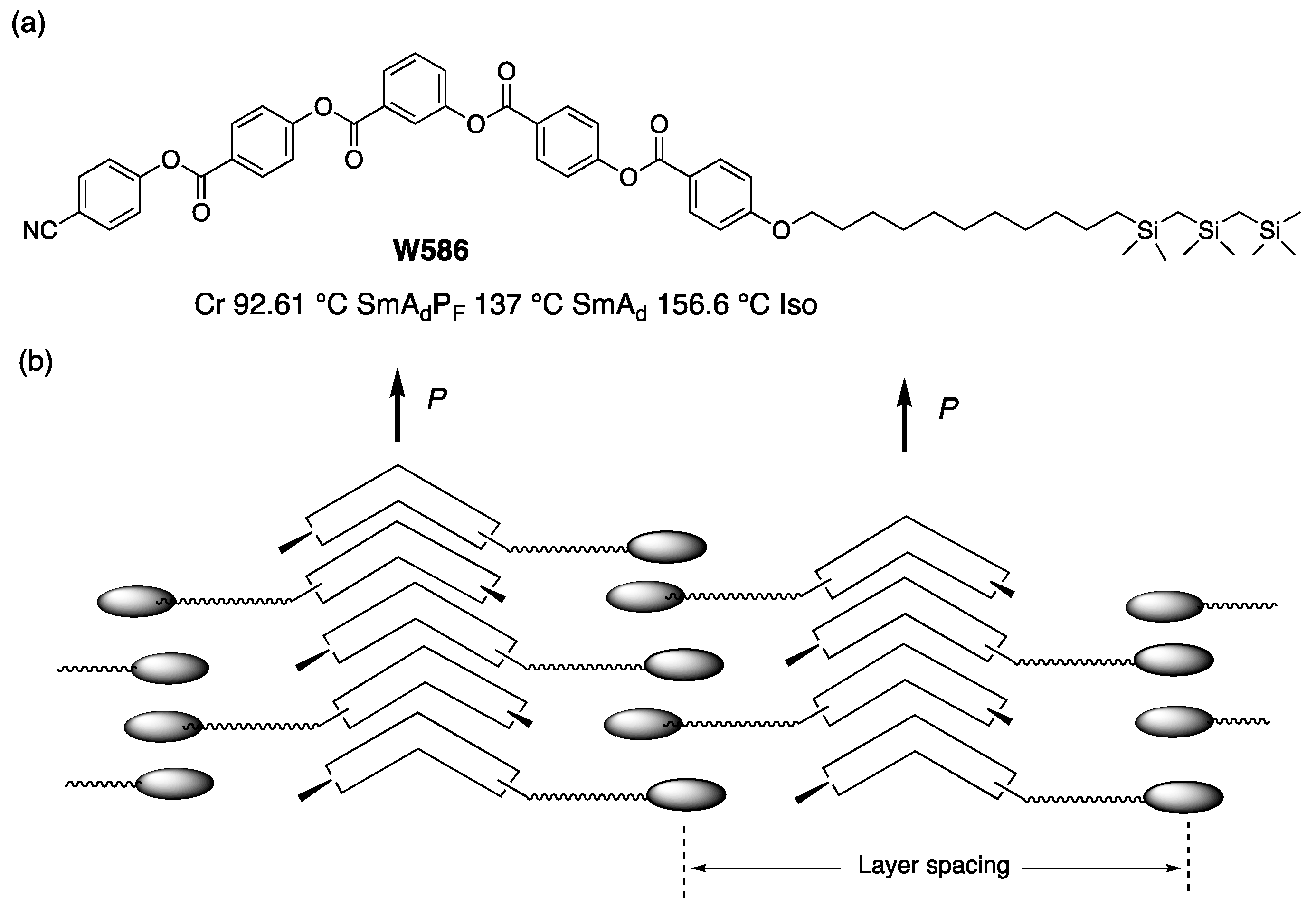
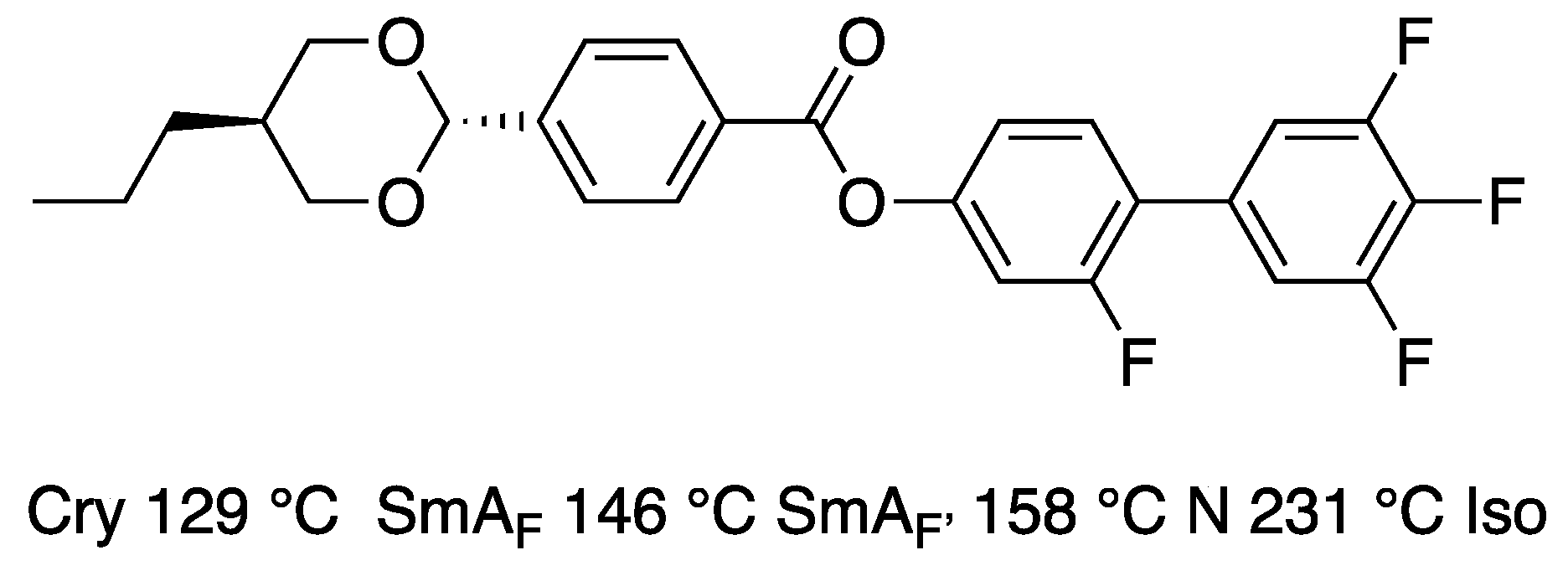
5. Electro-Optical Switching in the De Vries Smectic A Phase
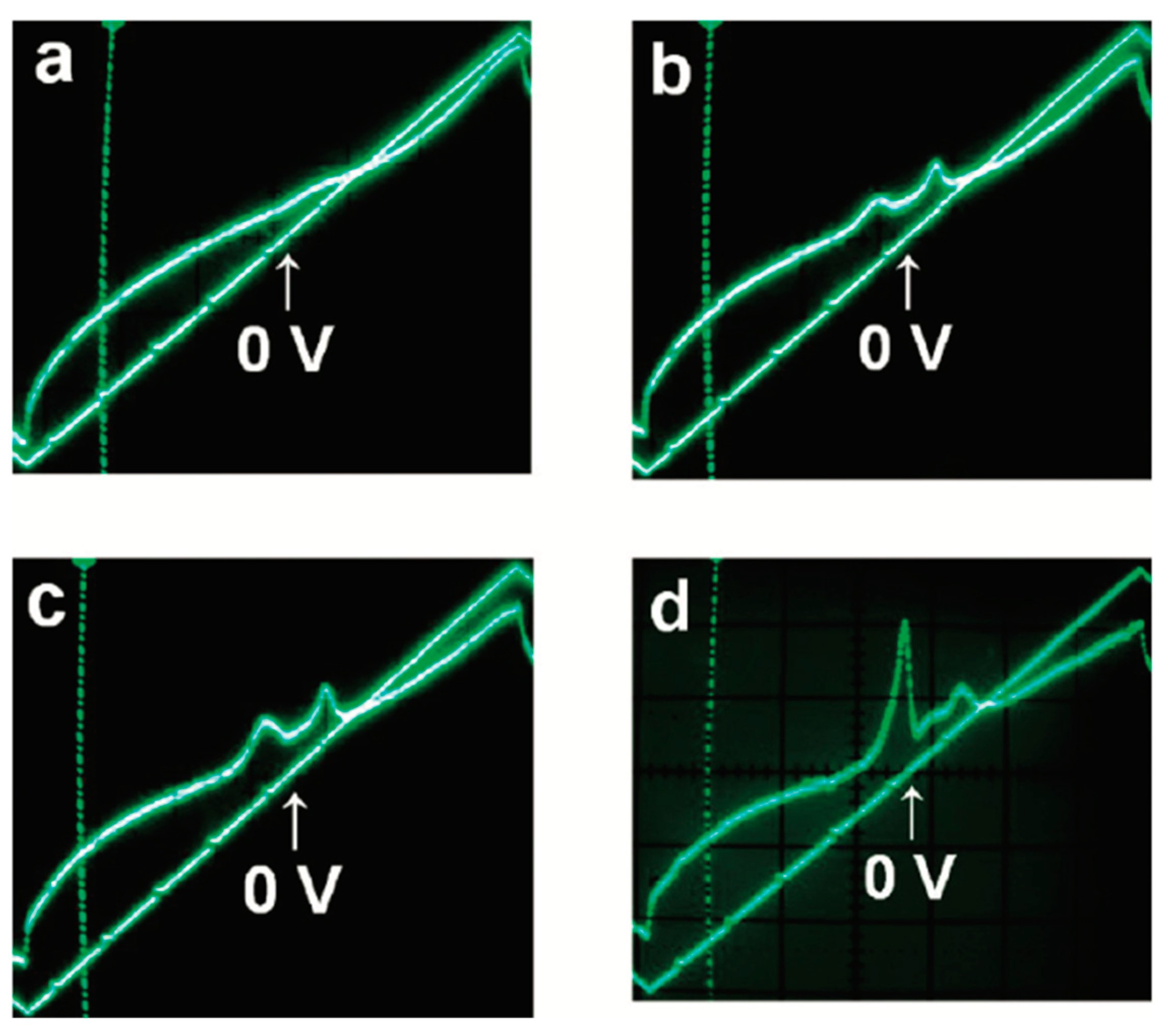
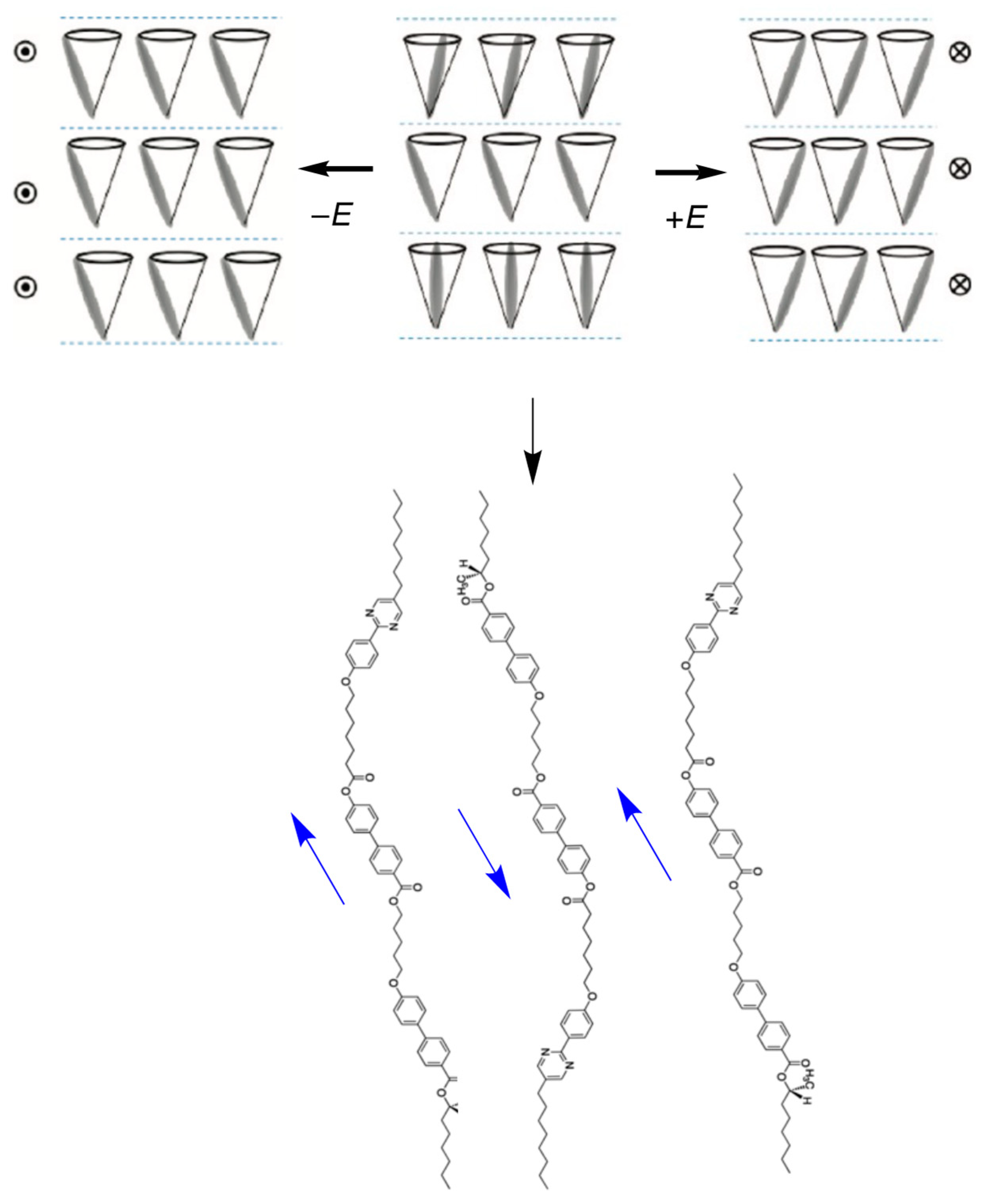
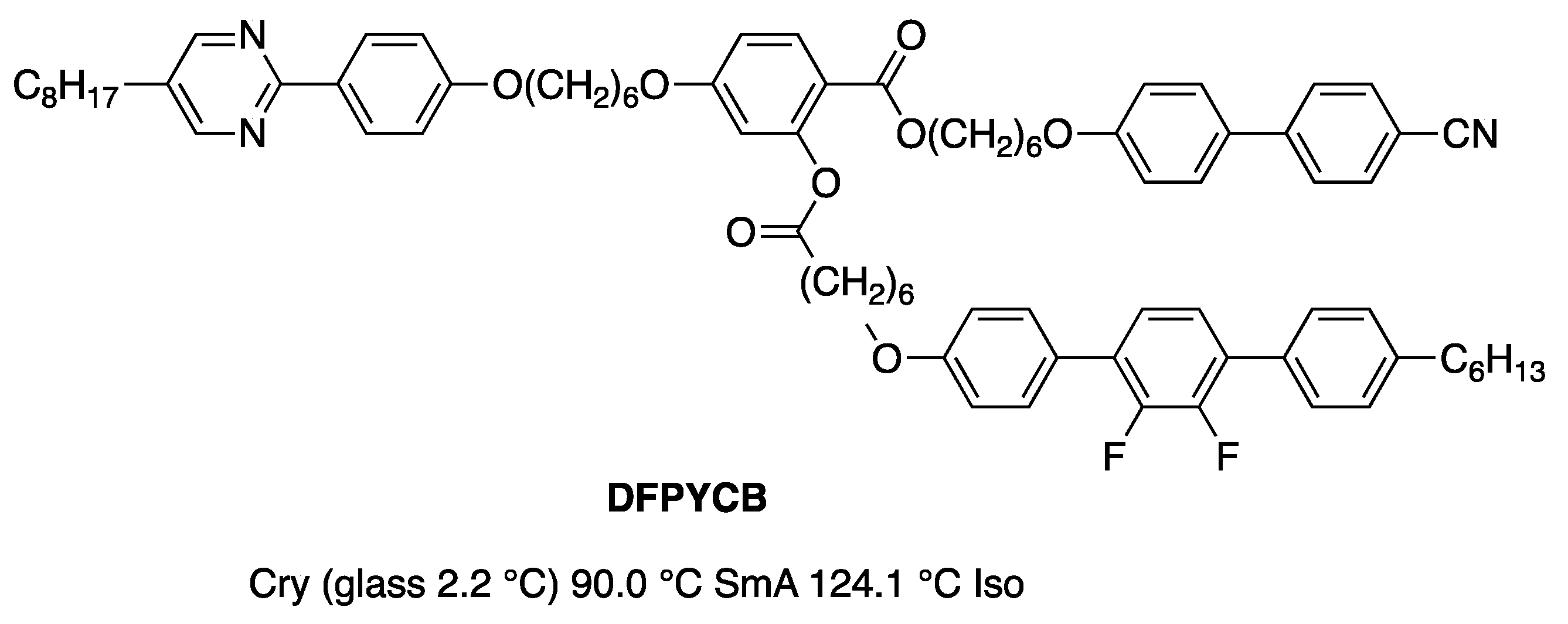
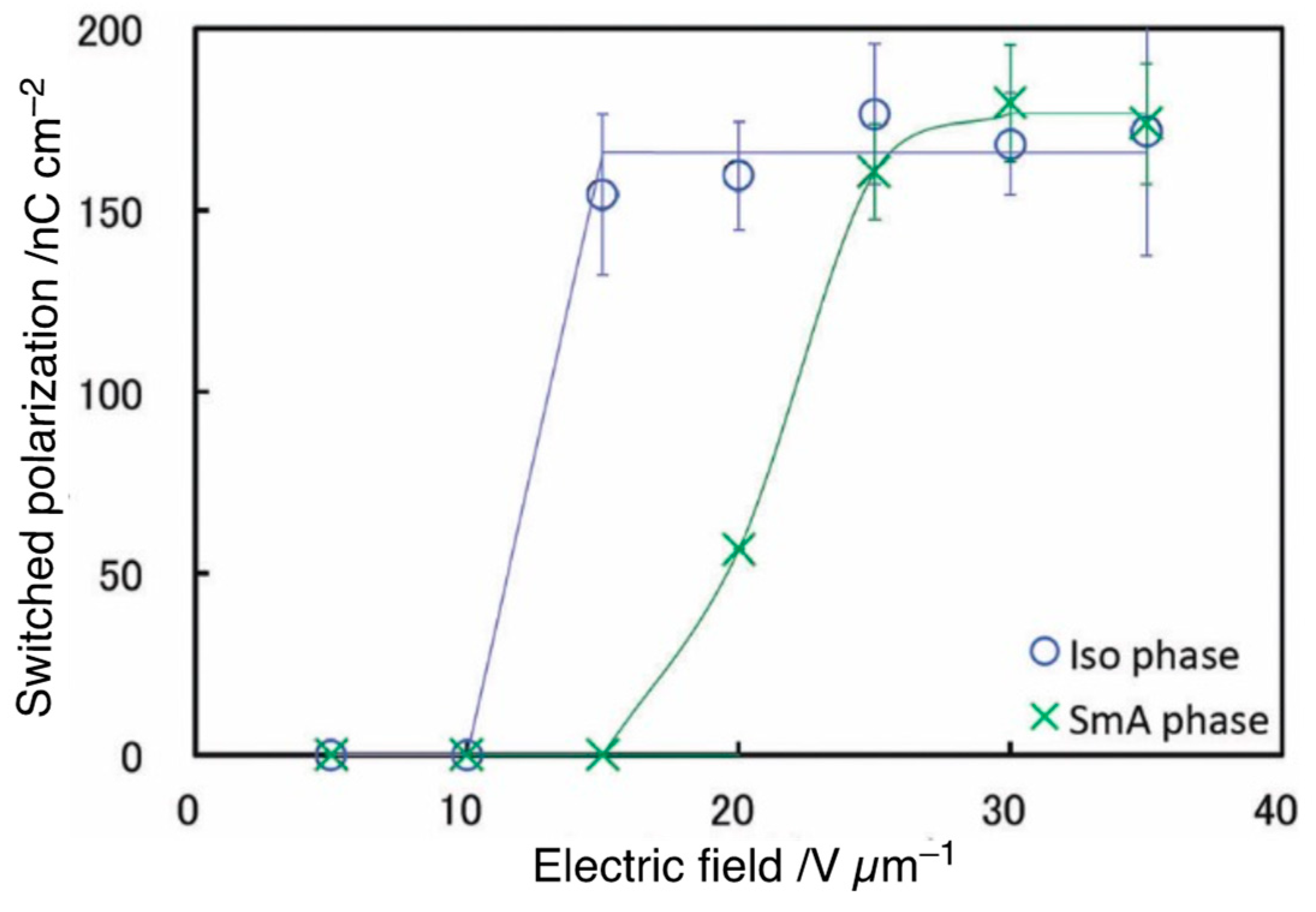
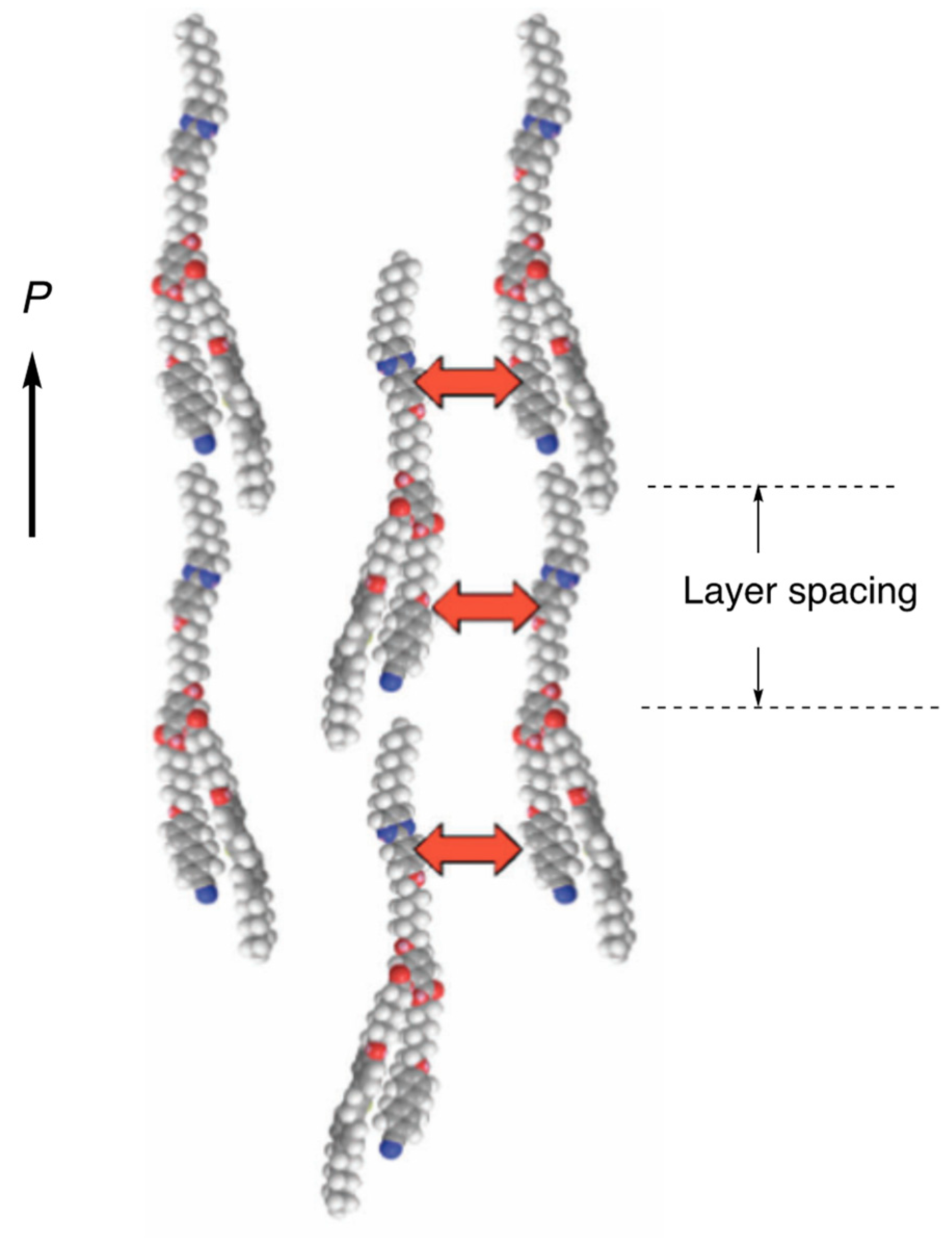
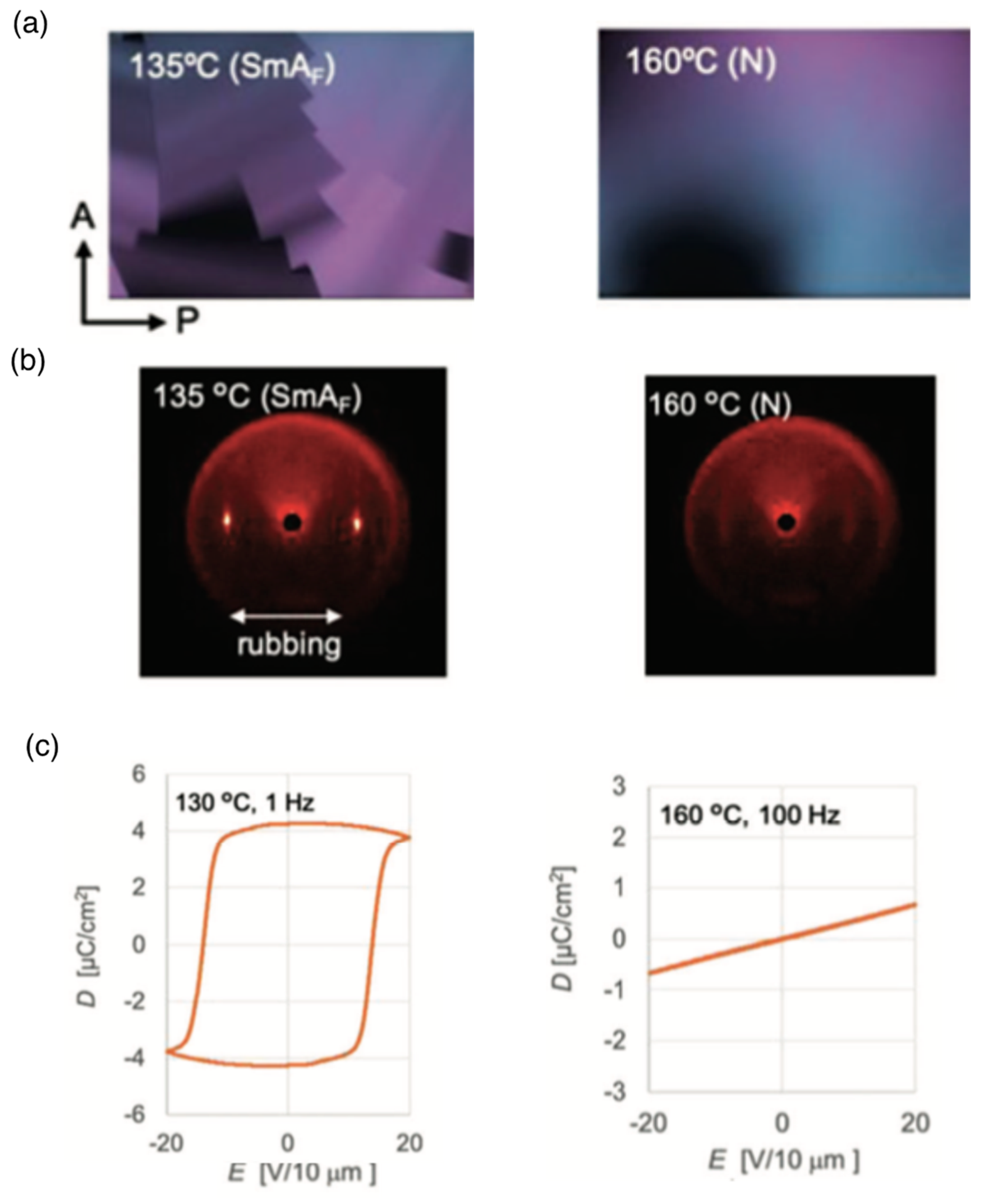
6. Polar Order in an Optically Uniaxial Smectic A Phase
7. Concluding Remarks
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meyer, R.B.; Liebert, L.; Strzelecki, L.; Keller, P. Ferroelectric liquid crystals. J. Phys. Lett. 1975, 36, L69–L71. [Google Scholar] [CrossRef]
- Clark, N.A.; Largerwall, S.T. Submicrosecond bistable electro-optic switching in liquid crystals. Appl. Phys. Lett. 1980, 36, 899–901. [Google Scholar] [CrossRef]
- Meyer, R.B. Ferroelectric liquid crystals; a review. Mol. Cryst. Liq. Cryst. 1977, 40, 33–48. [Google Scholar] [CrossRef]
- Goodby, J.W.; Blinc, R.; Clark, N.A.; Lagerwall, S.T.; Osipov, A.; Pikin, S.A.; Sakurai, T.; Yoshino, K.; Zeks, B. Ferroelectric Liquid Crystals, Principles, Properties and Applications, 1st ed.; Gordon and Breach: Philadelphia, PA, USA, 1991. [Google Scholar]
- Lagerwall, S.T. Ferroelectric liquid crystals. In Handbook of Liquid Crystals, 1st ed.; Demus, D., Goodby, J.W., Gray, G.W., Spiess, H.W., Vill, V., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1998; Volume 2B, pp. 515–664. [Google Scholar]
- Guo, Q.; Yan, K.; Chigrinov, V.; Zhao, H.; Tribelsky, M. Ferroelectric liquid crystals: Physics and applications. Crystals 2019, 9, 470. [Google Scholar] [CrossRef]
- Bahr, C. Chirality in Liquid Crystals; Kitzerow, H.-S., Bahr, C., Eds.; Springer: New York, NY, USA, 2001; pp. 223–250. [Google Scholar]
- Walba, D.M. Fast ferroelectric liquid-crystal electrooptics. Science 1995, 270, 250. [Google Scholar] [CrossRef]
- Chandani, A.D.L.; Gorecka, E.; Ouchi, Y.; Takezoe, H.; Fukuda, A. Antiferroelectric chiral smectic phases responsible for the tristable switching in MHPOBC. Jpn. J. Appl. Phys. 1989, 28, L1265–L1268. [Google Scholar] [CrossRef]
- Nishiyama, I. Antiferroelectric liquid crystals. Adv. Mater. 1993, 6, 966–970. [Google Scholar] [CrossRef]
- Fukuda, A.; Takanishi, Y.; Isozaki, T.; Ishikawa, K.; Takezoe, H. Antiferroelectric chiral smectic liquid crystals. J. Mater. Chem. 1994, 4, 997–1016. [Google Scholar] [CrossRef]
- Miyachi, K.; Fukuda, A. Antiferroelectric Liquid Crystals. In Handbook of Liquid Crystals, 1st ed.; Demus, D., Goodby, J.W., Gray, G.W., Spiess, H.W., Vill, V., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1998; Volume 2B, pp. 665–691. [Google Scholar]
- Inui, S.; Iimura, N.; Suzuki, T.; Iwane, H.; Miyachi, K.; Takanishi, Y.; Fukuda, A. Thresholdless antiferroelectricity in liquid crystals and its application to displays. J. Mater. Chem. 1996, 6, 671–673. [Google Scholar] [CrossRef]
- Niori, T.; Sekine, J.; Watanabe, J.; Furukawa, T.; Takezoe, H. Distinct ferroelectric smectic liquid crystals consisting of banana shaped achiral molecules. J. Mater. Chem. 1996, 6, 1231–1233. [Google Scholar] [CrossRef]
- Sekine, T.; Niori, T.; Sone, M.; Watanabe, J.; Choi, S.-W.; Takanishi, Y.; Takezoe, H. Origin of helix in achiral banana-shaped molecular systems. Jpn. J. Appl. Phys. 1997, 36, 6455–6463. [Google Scholar] [CrossRef]
- Reddy, R.A.; Tschierske, C. Bent-core liquid crystals: Polar order, superstructural chirality and spontaneous desymmetrisation in soft matter systems. J. Mater. Chem. 2006, 16, 907–961. [Google Scholar] [CrossRef]
- Takezoe, H.; Takanishi, Y. Bent-core liquid crystals: Their mysterious and attractive world. Jpn. J. Appl. Phys. 2006, 45, 597–625. [Google Scholar] [CrossRef]
- Cestari, M.; Diez-Berart, S.; Dunmur, D.A.; Ferrarini, M.R.; de la Fuente, M.R.; Jackson, D.J.B.; Lopez, D.O.; Luckhurst, G.R.; Perez-Jubindo, M.A.; Richardson, R.M.; et al. Phase behavior and properties of the liquid-crystal dimer 1′′,7′′-bis(4-cyanobiphenyl-4′-yl) heptane: A twist-bend nematic liquid crystal. Phys. Rev. E 2011, 84, 031704. [Google Scholar] [CrossRef] [PubMed]
- Tschierske, C.; Ungar, G. Mirror symmetry breaking by chirality synchronization in liquids and liquid crystals of achiral molecules. ChemPhysChem. 2016, 17, 9–26. [Google Scholar] [CrossRef] [PubMed]
- Yoshizawa, A. The formation of supramolecular chiral materials from achiral molecules using a liquid-crystalline system: Symmetry breaking, amplification, and transfer. Crystals 2024, 14, 97. [Google Scholar] [CrossRef]
- Reddy, R.A.; Zhu, C.; Shao, R.; Korblova, E.; Gong, T.; Shen, Y.; Garcia, E.; Glaser, M.A.; Maclennan, J.E.; Walba, D.M.; et al. Spontaneous ferroelectric order in a bent-core smectic liquid crystal of fluid orthorhombic layers. Science 2011, 332, 72–77. [Google Scholar] [CrossRef]
- Mandle, R.J.; Cowling, S.J.; Goodby, J.W. A nematic to nematic transformation exhibited by a rod-like liquid crystal. Phys. Chem. Chem. Phys. 2017, 19, 11429–11435. [Google Scholar] [CrossRef]
- Mandle, R.J.; Cowling, S.J.; Goodby, J.W. Rational design of rod-like liquid crystals exhibiting two nematic phases. Chem. A Eur. J. 2017, 23, 14554–14562. [Google Scholar] [CrossRef]
- Nishikawa, H.; Shiroshita, K.; Higuchi, H.; Okumura, Y.; Haseba, Y.; Yamamoto, S.; Sago, K.; Kikuchi, H. A fluid liquid-crystal material with highly polar order. Adv. Mater. 2017, 29, 1702354. [Google Scholar] [CrossRef]
- Chen, X.; Korblova, E.; Dong, D.P.; Wei, X.Y.; Shao, R.F.; Radzihovsky, L.; Glaser, M.A.; Maclenan, J.E.; Bedrov, D.; Walba, D.M.; et al. First-principles experimental demonstration of ferroelectricity in a thermotropic nematic liquid crystal: Polar domains and striking electro-optics. Proc. Natl. Acad. Sci. USA 2020, 117, 14021–14031. [Google Scholar] [CrossRef] [PubMed]
- Li, J.X.; Nishikawa, H.; Kougo, J.; Zhou, J.C.; Dai, S.Q.; Tang, W.T.; Zhao, X.H.; Hisai, Y.; Huang, M.J.; Aya, S.O.S. Development of ferroelectric nematic fluids with giant-e dielectricity and nonlinear optical properties. Sci. Adv. 2021, 7, eabf5047. [Google Scholar] [CrossRef] [PubMed]
- Lavrentovich, O.D. Ferroelectric nematic liquid crystal, a century in waiting. Proc. Natl. Acad. Sci. USA 2020, 117, 14629–14631. [Google Scholar] [CrossRef]
- Lalanne, J.R.; Buchert, J.; Destrade, C.; Nguyen, H.T.; Marcerou, J.P. Slowing down of molecular rotation at the smectic-A–smectic-C* transition of liquid crystals. Phys. Rev. Lett. 1989, 62, 3046–3049. [Google Scholar] [CrossRef] [PubMed]
- Kremer, F.; Vallerien, S.U.; Kapitza, H.; Zentel, R.; Fischer, E.W. Constant molecular rotation at the smectic-A to smectic-C* transition in ferroelectric liquid crystals. Phys. Rev. 1990, 42, 3667–3669. [Google Scholar] [CrossRef] [PubMed]
- Blinov, L.M.; Beresnev, L.A. Ferroelectric liquid crystals. Sov. Phys. Usp. 1984, 27, 492–514. [Google Scholar] [CrossRef]
- Berardi, R.; Ricci, M.; Zannoni, C. Ferroelectric nematic and smectic liquid crystals from Tapered molecules. ChemPhysChem 2001, 7, 443–447. [Google Scholar] [CrossRef]
- Haeni, J.H.; Irvin, P.; Chang, W.; Uecker, R.; Reiche, P.; Li, Y.L.; Choudhury, S.; Tian, W.; Hawley, M.E.; Craigo, B.; et al. Room-temperature ferroelectricity in strained SrTiO3. Nature 2004, 430, 758–761. [Google Scholar] [CrossRef]
- Damodaran, A.R.; Agar, J.C.; Pandya, S.; Chen, Z.; Dedon, L.; Xu, R.; Apgar, B.; Saremi, S.; Martin, L.W. New modalities of strain-control of ferroelectric thin films. J. Phys. Condens. Matter. 2016, 28, 263001. [Google Scholar] [CrossRef]
- Lu, X.; Chen, Z.; Cao, Y.; Tang, Y.; Xu, R.; Saremi, S.; Zhang, Z.; You, L.; Dong, Y.; Das, S.; et al. Mechanical-force-induced non-local collective ferroelectric switching in epitaxial lead-titanate thin films. Nat. Commun. 2019, 10, 3951. [Google Scholar] [CrossRef]
- Na, Y.H.; Aburaya, Y.; Orihara, H.; Hiraoka, K. Measurement of electrically induced shear strain in a chiral smectic liquid-crystal elastomer. Phys. Rev. A 2011, 83, 061709. [Google Scholar] [CrossRef] [PubMed]
- Mathe, M.T.; Himel, M.S.H.; Adaka, A.; Gleeson, J.T.; Sprunt, S.; Salamon, P.; Jakli, A. Liquid piezoelectric materials: Linear electromechanical effect in fluid ferroelectric nematic liquid crystals. Adv. Funct. Mater. 2024, 34, 2314158. [Google Scholar] [CrossRef]
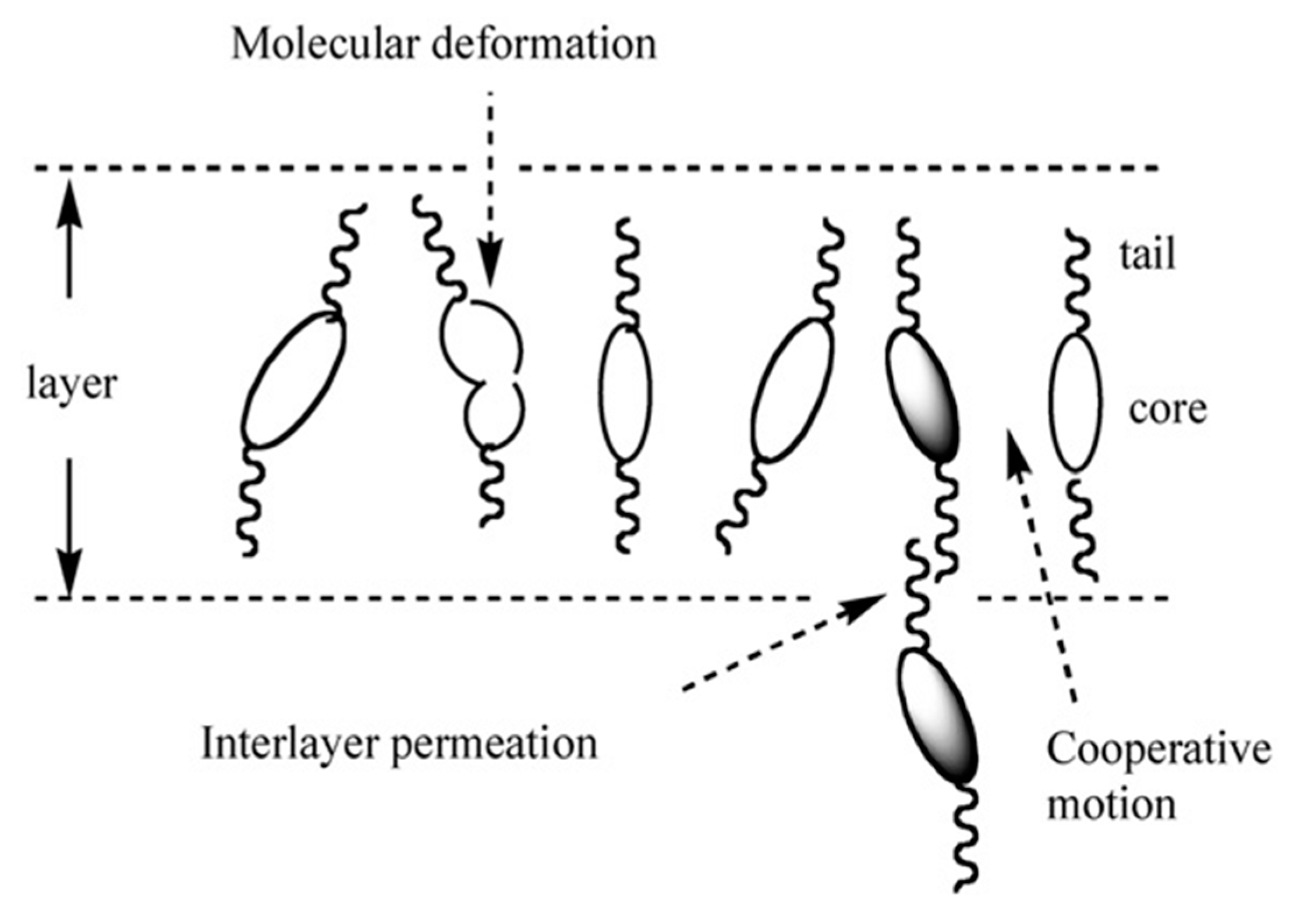
- Yoshizawa, A.; Kikuzaki, H.; Fukumasa, M. Microscopic organization of the molecules in smectic A and chiral (racemic) smectic C phases: Dynamic molecular deformation effect on the SmA to SmC* (SmC) transition. Liq. Cryst. 1995, 18, 351–366. [Google Scholar] [CrossRef]
- Walba, D.M.; Clark, N.A. Molecular design of ferroelectric liquid crystals. Ferroelectrics 1988, 84, 65–72. [Google Scholar] [CrossRef]
- Walba, D.M. Ferroelectric liquid crystals–a unique state of matter. In Advances in the Synthesis and Reactivity of Solids; Mallouck, T.E., Ed.; JAI Press: Greemwich, CT, USA, 1991; Volume 1, pp. 173–235. [Google Scholar]
- Lemieux, R.P. Chirality transfer in ferroelectric liquid crystals. Acc. Chem. Res. 2001, 34, 845–853. [Google Scholar] [CrossRef] [PubMed]
- Kelly, S.M. Synthesis of chiral smectic liquid crystals. In Handbook of Liquid Crystals, 1st ed.; Demus, D., Goodby, J.W., Gray, G.W., Spiess, H.W., Vill, V., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1998; Volume 2B, pp. 493–514. [Google Scholar]
- Sakurai, T.; Mikami, N.; Higuchi, R.; Honma, M.; Yoshino, K. Synthesis ad properties of ferroelectric liquid crystals with large spontaneous polarization. Ferroelectrics 1988, 85, 469–478. [Google Scholar] [CrossRef]
- Kelly, S.M.; Buchecker, R.; Fünfschhilling, J. a-Fluoro esters incorporating a cyclohexane ring: Some new chiral dopants for ferroelectric mixtures. J. Mater. Chem. 1994, 4, 1689–1697. [Google Scholar] [CrossRef]
- Sakashita, K.; Shindo, M.; Nakauchi, J.; Uematsu, M.; Kageyama, Y.; Hayashi, S.; Ikemoto, T.; Mori, K. Novel ferroelectric liquid crystalline d-valerolactone derivatives with very large spontaneous polarization. Mol. Cryst. Liq. Cryst. 1991, 199, 119–127. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Nishiyama, I.; Fukumasa, M.; Hirai, T.; Yamane, M. New ferroelectric liquid crystal with large spontaneous polarization. Jpn. J. Appl. Phys. 1989, 28, L1269–L1270. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Nishiyama, I.; Kikuzaki, H.; Ise, N. C-13 NMR and X-ray investigations of phase transitions in an antiferroelectric liquid crystal. Jpn. J. Appl. Phys. 1992, 31, L860–L863. [Google Scholar] [CrossRef]
- Shiratori, N.; Yoshizawa, A.; Nishiyama, I.; Fukumasa, M.; Yokoyama, A.; Hirai, T.; Yamane, M. New ferroelectric liquid crystals having 2-fluoro-2-methyl alkanoyloxy group. Mol. Cryst. Liq. Cryst. 1991, 199, 129–140. [Google Scholar] [CrossRef]
- Lemieux, R.P. Molecular recognition in chiral smectic liquid crystals: The effect of core–core interactions and chirality transfer on polar order. Chem. Soc. Rev. 2007, 36, 2033–2045. [Google Scholar] [CrossRef] [PubMed]
- Goodby, J.W. Synthesis of non-chiral smectic liquid crystals. In Handbook of Liquid Crystals, 1st ed.; Demus, D., Goodby, J.W., Gray, G.W., Spiess, H.W., Vill, V., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 1998; Volume 2A, pp. 411–440. [Google Scholar]
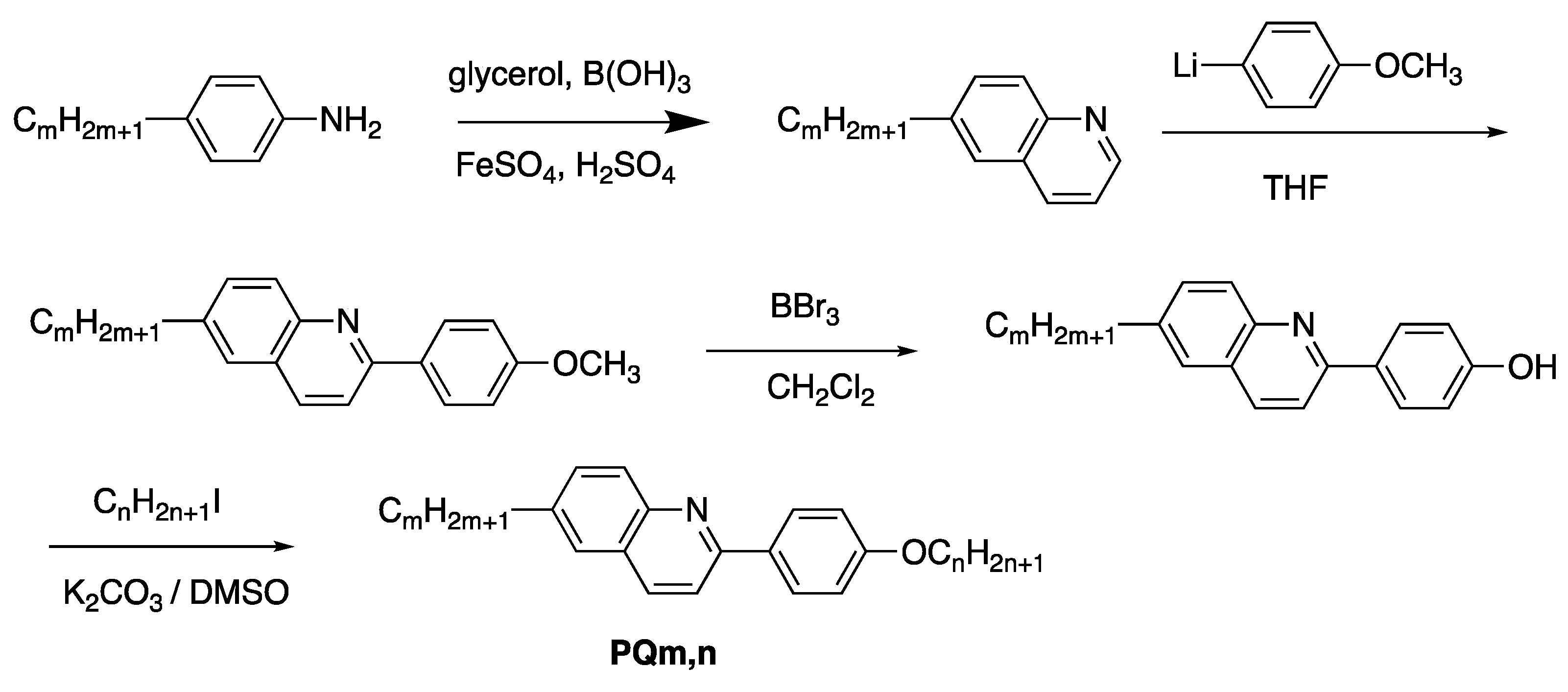
- Yokoyama, A.; Nishiyama, I.; Yoshizawa, A. 6-Alkyl-2-(4-alkyloxyphenyl)quinoline: A new smectic C base material. Ferroelectrics 1993, 148, 139–145. [Google Scholar] [CrossRef]
- Skraup, Z.H. Eine syntheses der chinolins. Monatshefte Für Chem. 1880, 1, 316–318. [Google Scholar] [CrossRef]
- Ishikawa, K.; Hashimoto, K.; Takezoe, H.; Fukuda, A.; Kuze, E. A practical method of preparing thin homogeneous ferroelectric smectic cells for electro-optical microsecond switches (II): SmA liquid crystal growth under a temperature gradient. Jpn. J. Appl. Phys. 1984, 23, L211–L213. [Google Scholar] [CrossRef]
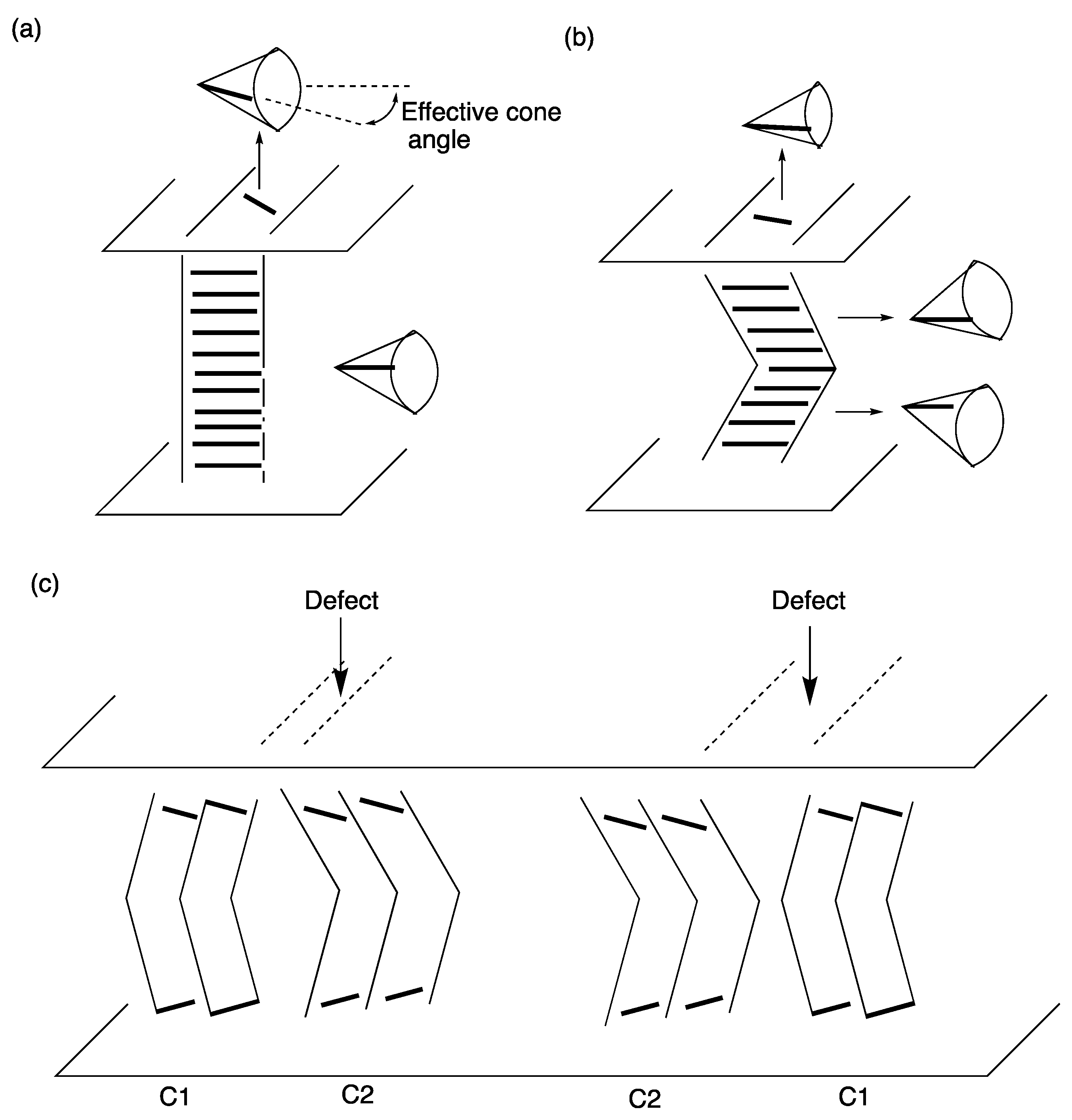
- Hiji, N.; Ouchi, Y.; Takezoe, H.; Fukuda, A. Determination of chevron direction and sign of the boat-shaped disclination in surface-stabilized ferroelectric liquid crystals. Jpn. J. Appl. Phys. 1988, 27, L1–L4. [Google Scholar] [CrossRef]
- Clark, N.A.; Rieker, T.P. Smectic-C “chevron”, a planar liquid-crystal defect: Implications for the surface-stabilized ferroelectric liquid-crystal geometry. Phys. Rev. A 1988, 37, 1053–1056. [Google Scholar] [CrossRef] [PubMed]
- Mochizuki, A.; Yoshihara, T.; Iwasaki, M.; Nakatsuka, M.; Takanishi, Y.; Ouchi, Y.; Takezoe, H.; Fukuda, A. Electro-optical switching of bookshelf structure Sc*cells. Inst. Image Inf. Telev. Eng. 1990, 14, 21–27. [Google Scholar]
- Janulis, E.P.; Osten, D.W.; Radcliff, M.D.; Novack, J.C.; Tristani-Kendra, M.; Epstein, K.A.; Keyes, M.; Johnson, G.C.; Savu, P.M.; Spawn, T.D. Fluorinated liquid crystals: An update. In SPIE 1665, Liquid Crystal Materials, Devices, and Applications; SPIE: Bellingham, DC, USA, 1992. [Google Scholar] [CrossRef]
- Rieker, T.P.; Janulis, E.P. Dimerlike smectic-A and -C phases in highly fluorinated thermotropic liquid crystals. Phys. Rev. E 1995, 52, 2688–2691. [Google Scholar] [CrossRef]
- Lagerwall, J.P.F.; Giesselmann, F. Current topics in smectic liquid crystals. ChemPhysChem 2006, 7, 20–45. [Google Scholar] [CrossRef]
- De Vries, A. X-ray photographic studies of liquid crystals: II. Apparent molecular length and thickness in three phases of ethyl-p-ethoxybenzal-p-aminobenzoate. Mol. Cryst. Liq. Cryst. 1970, 11, 361–383. [Google Scholar] [CrossRef]
- De Vries, A. Experimental evidence concerning two different kinds of smectic C to smectic A transitions. Mol. Cryst. Liq. Cryst. 1977, 41, 27–31. [Google Scholar] [CrossRef]
- De Vries, A. The description of the smectic A and C phases and the smectic A–C phase transition of TCOOB with a diffuse-cone model. J. Chem. Phys. 1979, 71, 25–31. [Google Scholar] [CrossRef]
- Spector, M.S.; Heiney, P.A.; Naciri, J.; Weslowski, B.T.; Holt, D.B.; Shashidhar, R. Electroclinic liquid crystals with large induced tilt angle and small layer contraction. Phys. Rev. E 2000, 61, 1576–1584. [Google Scholar] [CrossRef]
- Song, Q.; Nonnenmacher, D.; Giesselmann, F.; Lemieux, R.P. Tuning ‘de Vries-like’ properties in siloxane- and carbosilane-terminated smectic liquid crystals. J. Mater. Chem. C 2013, 1, 343–350. [Google Scholar] [CrossRef]
- Kaur, S.; Barthakur, A.; Mohiuddin, G.; Guta, S.P.; Dhara, S.; Pal, S.K. Observation of “de Vries-like” properties in bent-core molecules. Chem. Sci. 2022, 13, 2249–2257. [Google Scholar] [CrossRef]
- Ishida, N.; Takanishi, Y.; Yamamoto, J.; Yoshizawa, A. Amphiphilic liquid crystal exhibiting the smectic A to smectic C phase transition without layer contraction. Appl. Phys. Express 2011, 4, 021701. [Google Scholar] [CrossRef]
- Giesselmann, F.; Zugenmaier, P.; Dierking, I.; Lagerwall, S.T.; Stebler, B.; Kaspar, M.; Hamplova, V.; Glogarova, M. Smectic-A*–smectic-C* transition in a ferroelectric liquid crystal without smectic layer shrinkage. Phys. Rev. E 1999, 60, 598. [Google Scholar] [CrossRef]
- Clark, N.A.; Bellini, T.; Shao, R.-F.; Coleman, D.; Bardon, S.; Link, D.R.; Maclennan, J.E.; Chen, X.-H.; Wand, M.D.; Walba, D.M.; et al. Electro-optic characteristics of de Vries tilted smectic liquid crystals: Analog behavior in the smectic A* and smectic C* phases. Appl. Phys. Lett. 2002, 80, 4097–4099. [Google Scholar] [CrossRef]
- Naciri, J.; Carboni, C.; George, A.K. Low transition temperature organosiloxane liquid crystals displaying a de Vries smectic A phase. Liq. Cryst. 2003, 30, 219–225. [Google Scholar] [CrossRef]
- Kapernaum, N.; Walba, D.M.; Korblova, E.; Zhu, C.; Jones, C.; Shen, Y.; Clark, N.A.; Gisselmann, F. On the origin of the “giant” electroclinic effect in a “de Vries”-type ferroelectric liquid crystal material for chirality sensing applications. ChemPhysChem 2009, 10, 890–892. [Google Scholar] [CrossRef] [PubMed]
- Prasad, S.K.; Rao, D.S.S.; Sridevi, S.; Lobo, C.V.; Rarana, B.R.; Naciri, J.; Shashidhar, R. Unusual dielectric and electrical switching behavior in the de Vries smectic A phase of two organosiloxane derivatives. Phys. Rev. Lett. 2009, 102, 147802. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Nayek, P.; Roy, S.K.; Majumder, T.P.; Zurowska, M.; Dabrowski, R. Double-peak polarization current response in the unusual SmA* phase of a fluorinated high-tilt antiferroelectric liquid crystal. Eur. Phys. Lett. 2010, 89, 16001. [Google Scholar] [CrossRef]
- Garoff, S.; Meyer, R.B. Electroclinic effect at the A–C phase change in a chiral smectic liquid crystal. Phys. Rev. Lett. 1977, 38, 848–851. [Google Scholar] [CrossRef]
- Abdulhalim, I.; Moddel, G. Switching behviour and electro-optic response due to the soft mode ferroelectric effect in chiral smectic A liquid crystals. Liq. Cryst. 1991, 9, 493–518. [Google Scholar] [CrossRef]
- Tsuji, D.; Takanishi, Y.; Yamamoto, J.; Yoshizawa, A. Chiral liquid crystal trimer exhibiting an optically uniaxial smectic phase with a double-peak polarization. J. Phys. Chem. C 2012, 116, 8678–8687. [Google Scholar] [CrossRef]
- Schubert, C.P.J.; Müller, C.; Wand, M.D.; Giesselmann, F.; Lemieux, R.P. Electroclinic effect in a chiral carbosilane-terminated 5-phenylpyrimidine liquid crystal with ‘de Vries-like’ properties. Chem. Commun. 2015, 51, 12601–12604. [Google Scholar] [CrossRef] [PubMed]
- Swaminathan, V.; Panov, V.P.; Panov, A.; Rodriguez-Lojo, D.; Stevenson, P.J.; Gorecka, E.; Vij, J.K. Design and electro-optic investigations of de Vries chiral smectic liquid crystals for exhibiting broad temperature ranges of SmA* and SmC* phases and fast electro-optic switching. J. Mater. Chem. C 2020, 8, 4859–4868. [Google Scholar] [CrossRef]
- Link, D.R.; Natale, G.; Shao, R.; Maclennan, J.E.; Clark, N.A.; Körblova, E.; Walba, D.M. Spontaneous formation of macroscopic chiral domains in a fluid smectic phase of achiral molecules. Science 1997, 278, 1924–1927. [Google Scholar] [CrossRef]
- Guo, L.; Gorecka, E.; Pociecha, D.; Vaupotic, N.; Čepič, M.; Reddy, R.A.; Gornik, K.; Araoka, F.; Clark, N.A.; Walba, D.M.; et al. Ferroelectric behavior of orthogonal smectic phase made of bent-core molecules. Phys. Rev. E 2011, 84, 031706. [Google Scholar] [CrossRef]
- Kashima, S.; Chiba, M.; Takanishi, Y.; Yamamoto, J.; Yoshizawa, A. Polar order of an achiral taper-shaped liquid crystal in the uniaxial smectic A phase. J. Mater. Chem. C 2018, 6, 5521–5527. [Google Scholar] [CrossRef]
- Francescangeli, O.; Stanic, V.; Torgova, S.I.; Strigazzi, A.; Scaramuzza, N.; Ferrero, C.; Dolbnya, I.P.; Weiss, T.M.; Berardi, R.; Mucciolo, L.; et al. Ferroelectric response and induced biaxiality in the nematic phase of a bent-core mesogen. Adv. Funct. Mater. 2009, 19, 2592–2600. [Google Scholar] [CrossRef]
- Weissflog, W.; Baumeister, U.; Tamba, M.-G.; Pelzl, G.; Kresse, H.; Friedemann, R.; Hempel, G.; Kurz, R.; Roos, M.; Merzweiler, K.; et al. Unexpected liquid crystalline behaviour of three-ring bent-core mesogens: Bis(4-subst.-phenyl) 2-methyl-iso-phthalates. Soft Matter. 2012, 8, 2671–2685. [Google Scholar] [CrossRef]
- Khan, B.C.; Mukherjee, P.K. Isotropic to smectic-A phase transition in taper-shaped liquid crystal. J. Mol. Liq. 2021, 329, 115539. [Google Scholar] [CrossRef]
- Chen, X.; Korblova, E.; Glaser, M.A.; Maclennan, J.E.; Walba, D.M.; Clark, N.A. Polar in-plane surface orientation of a ferroelectric nematic liquid crystal: Polar monodomains and twisted state electro-optics. Proc. Natl. Acad. Sci. USA 2021, 118, e2104092118. [Google Scholar] [CrossRef] [PubMed]
- Caim, F.; Nava, G.; Barboza, R.; Clark, N.A.; Korblova, E.; Walba, D.M.; Bellini, T.; Lucchetti, L. Surface alignment of ferroelectric nematic liquid crystals. Soft Matter. 2021, 17, 8130–8139. [Google Scholar] [CrossRef] [PubMed]
- Kikuchi, H.; Matsukizono, H.; Iwamatsu, K.; Endo, S.; Anan, S.; Okunura, Y. Fluid layered ferroelectrics with global C∞V symmetry. Adv. Sci. 2022, 9, 2202048. [Google Scholar] [CrossRef] [PubMed]
- Chien, X.; Martinez, V.; Nacke, P.; Korblova, E.; Manabe, A.; Klasen-Memmer, M.; Freychet, G.; Zhernenkov, M.; Glaser, M.A.; Radzihovsky, L.; et al. Observation of a uniaxial ferroelectric smectic A phase. Proc. Natl. Acad. Sci. USA 2022, 119, e2210062119. [Google Scholar] [CrossRef]
- Nacke, P.; Manabe, A.; Klasen-Memmer, M.; Chen, X.; Martinez, V.; Freychet, G.; Zhernenkov, M.; Maclennan, J.E.; Clark, N.A.; Bremer, M.; et al. New examples of ferroelectric nematic materials showing evidence for the antiferroelectric smectic-Z phase. Sci. Rep. 2024, 14, 4473. [Google Scholar] [CrossRef]
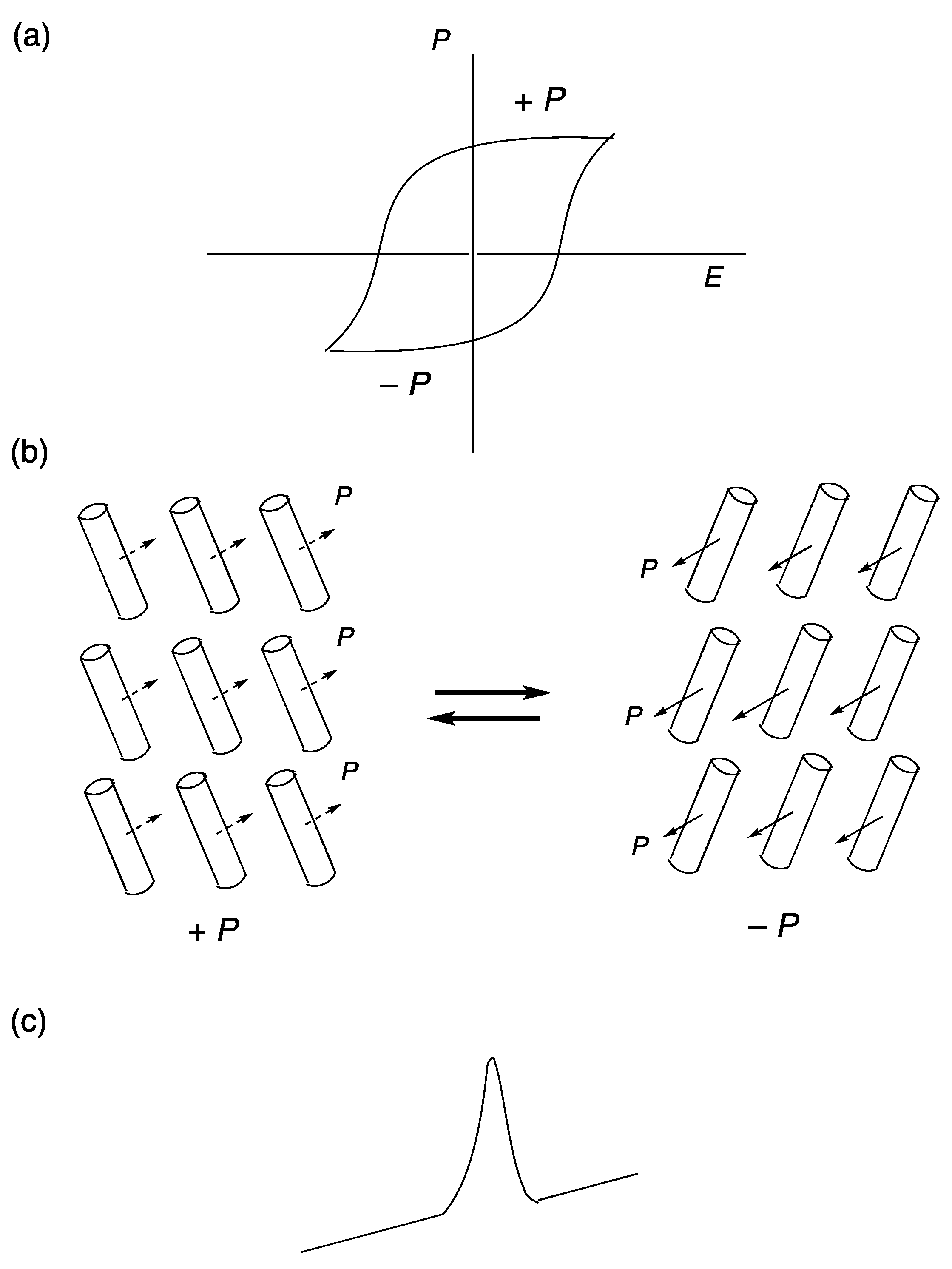

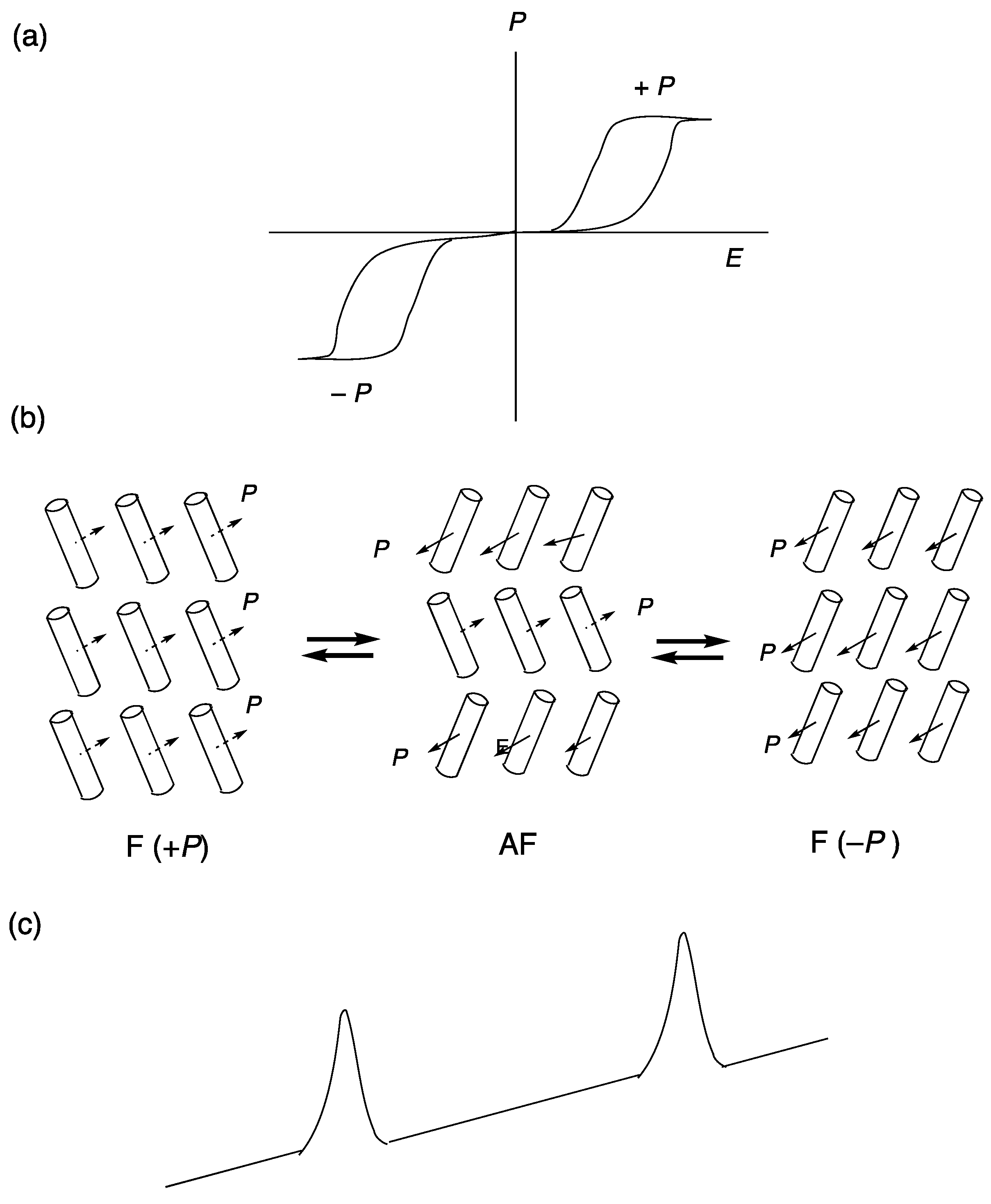
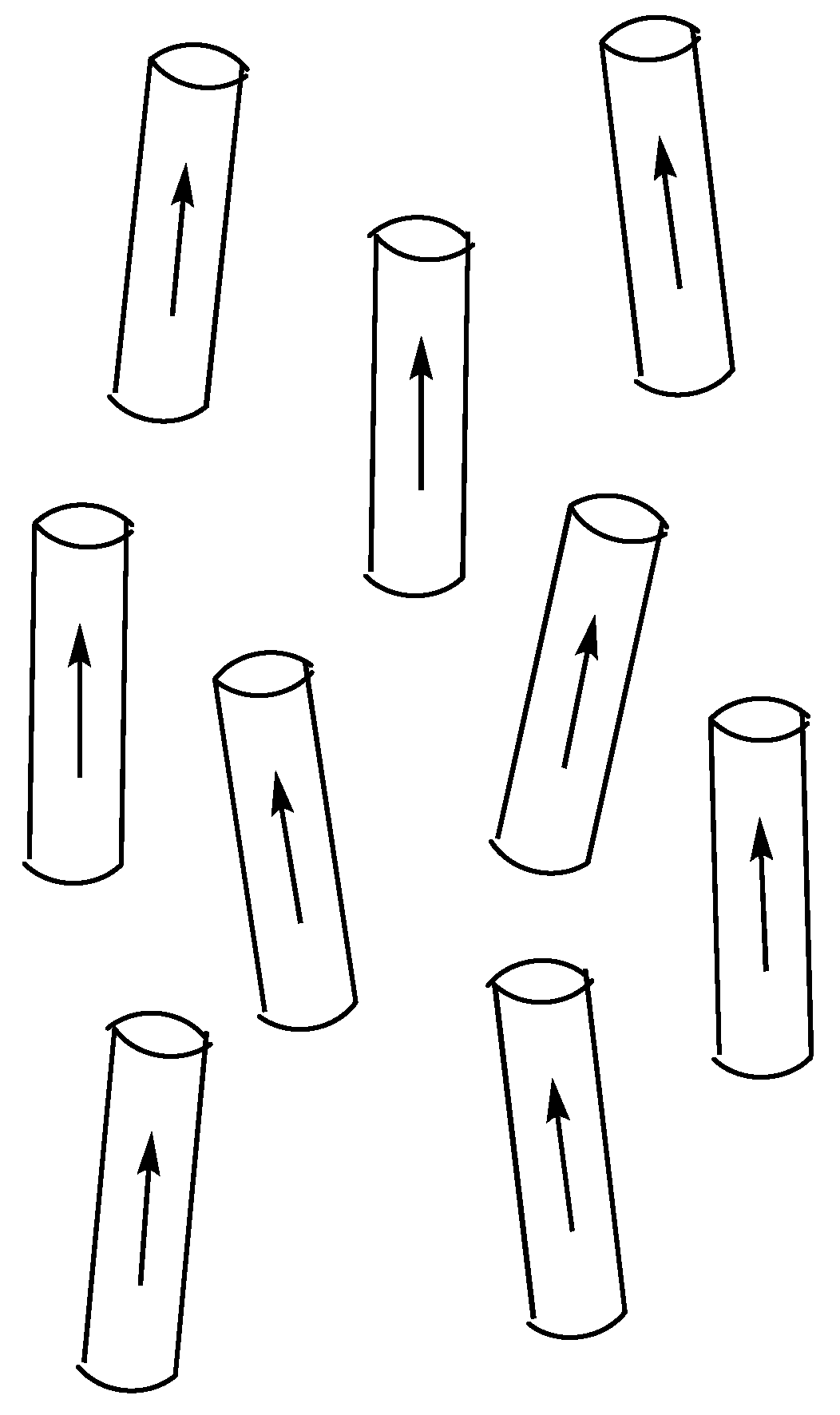
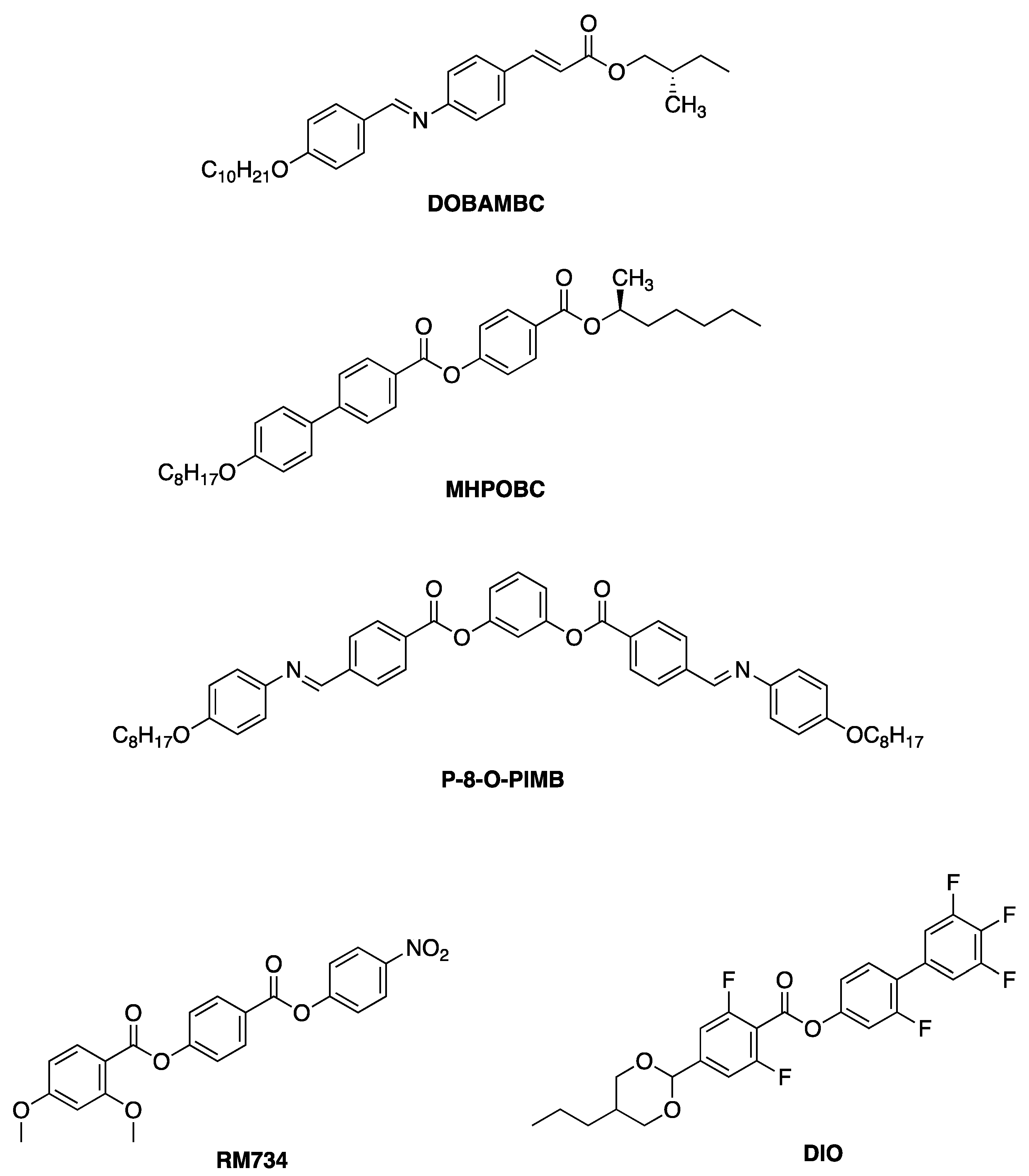











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshizawa, A. Ferroelectric Smectic Liquid Crystals. Crystals 2024, 14, 350. https://doi.org/10.3390/cryst14040350
Yoshizawa A. Ferroelectric Smectic Liquid Crystals. Crystals. 2024; 14(4):350. https://doi.org/10.3390/cryst14040350
Chicago/Turabian StyleYoshizawa, Atsushi. 2024. "Ferroelectric Smectic Liquid Crystals" Crystals 14, no. 4: 350. https://doi.org/10.3390/cryst14040350
APA StyleYoshizawa, A. (2024). Ferroelectric Smectic Liquid Crystals. Crystals, 14(4), 350. https://doi.org/10.3390/cryst14040350




