Homogeneous Organic Crystal Nucleation Rates in Solution from the Perspective of Chemical Reaction Kinetics
Abstract
:1. Introduction
2. Model
2.1. Reversible Aggregation of Solvated Solutes in Solution
2.2. Nucleation from Reversible Aggregates with First Order Kinetics
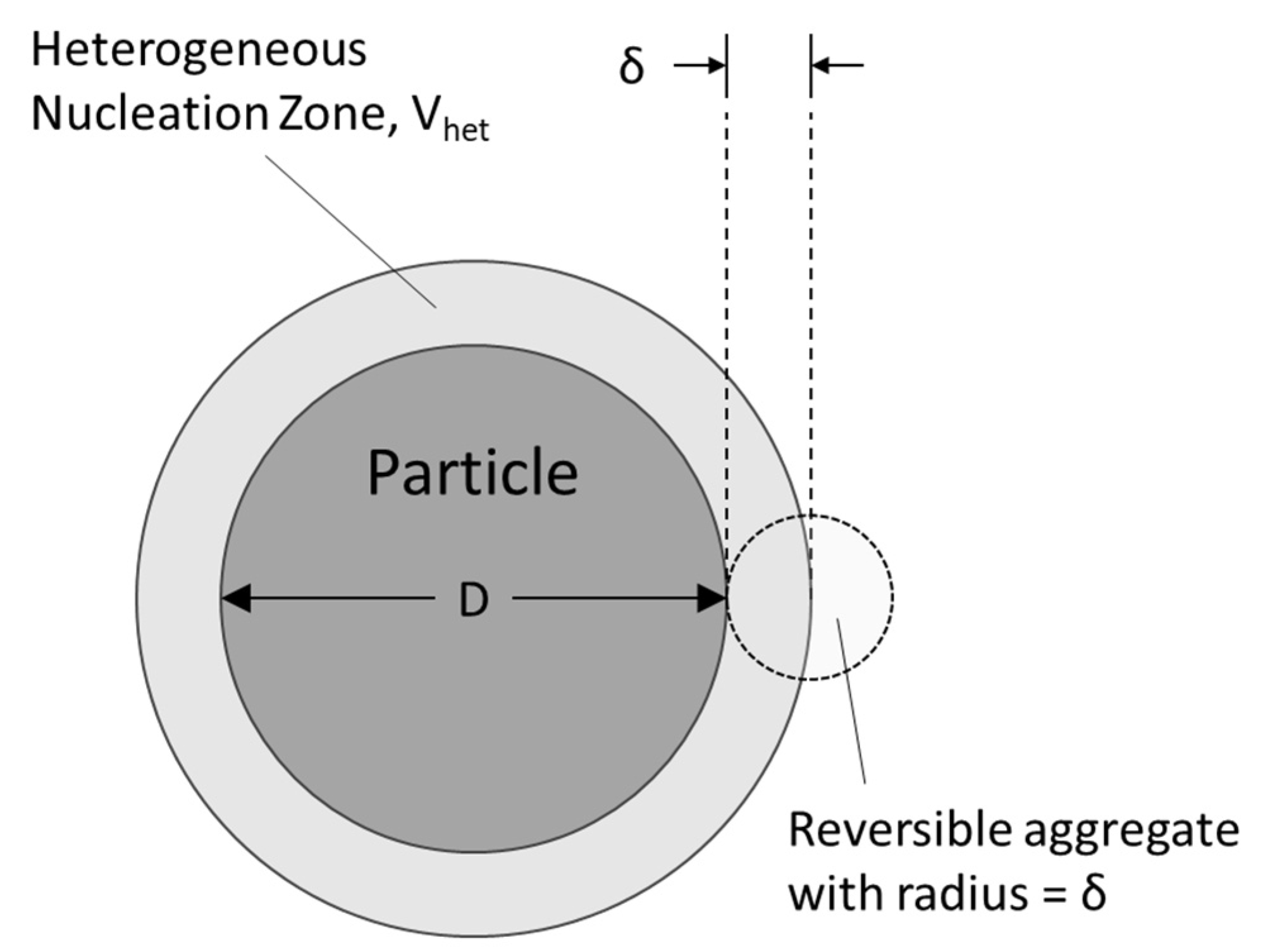
2.3. Heterogeneous Nucleation
3. Results
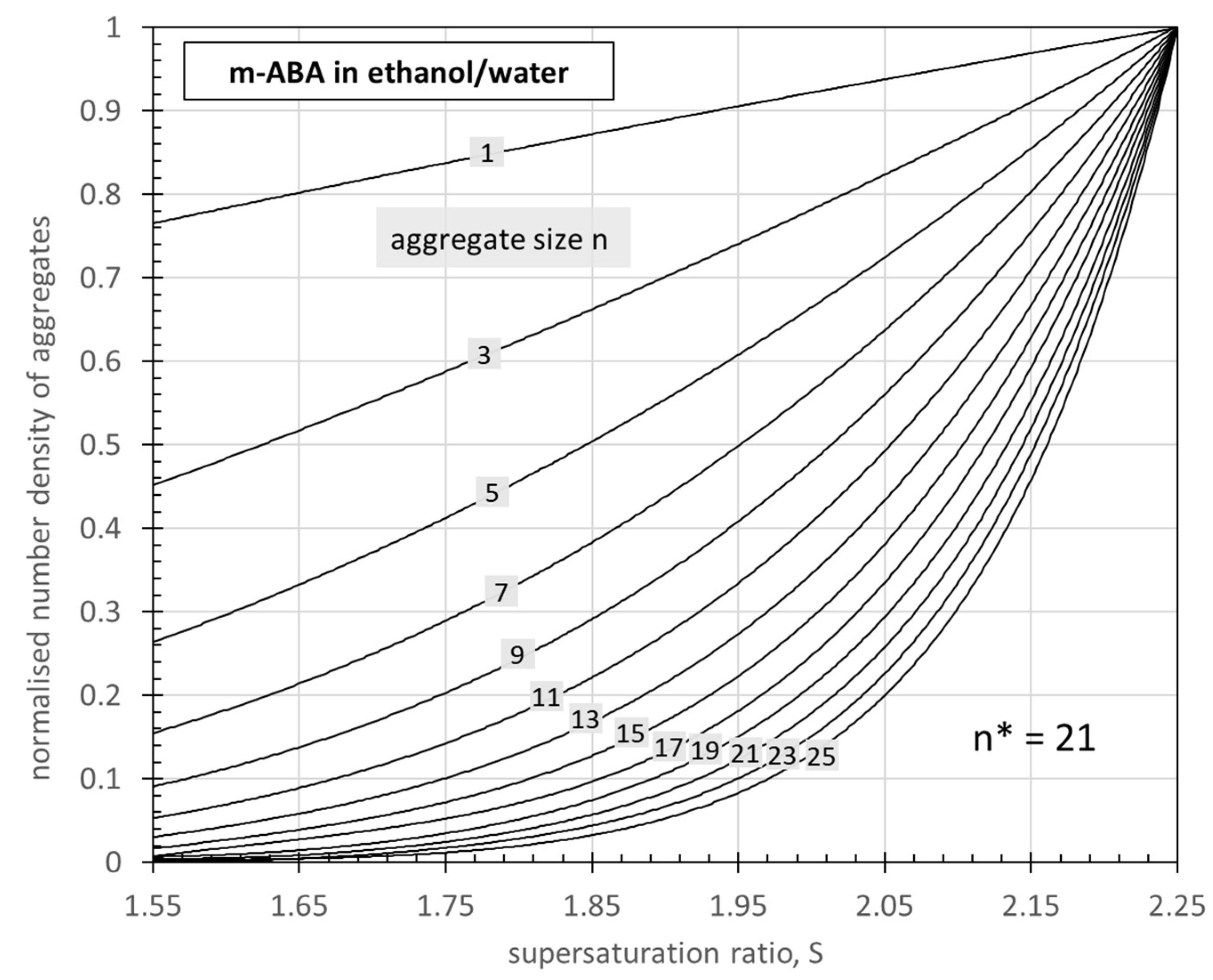
3.1. Effect of Supersaturation on the Size Distribution of Reversible Aggregates
3.2. Excess of Large Reversible Aggregates
3.3. Rate Constant Determination for m-ABA Crystallization from 50wt% Ethanol/Water
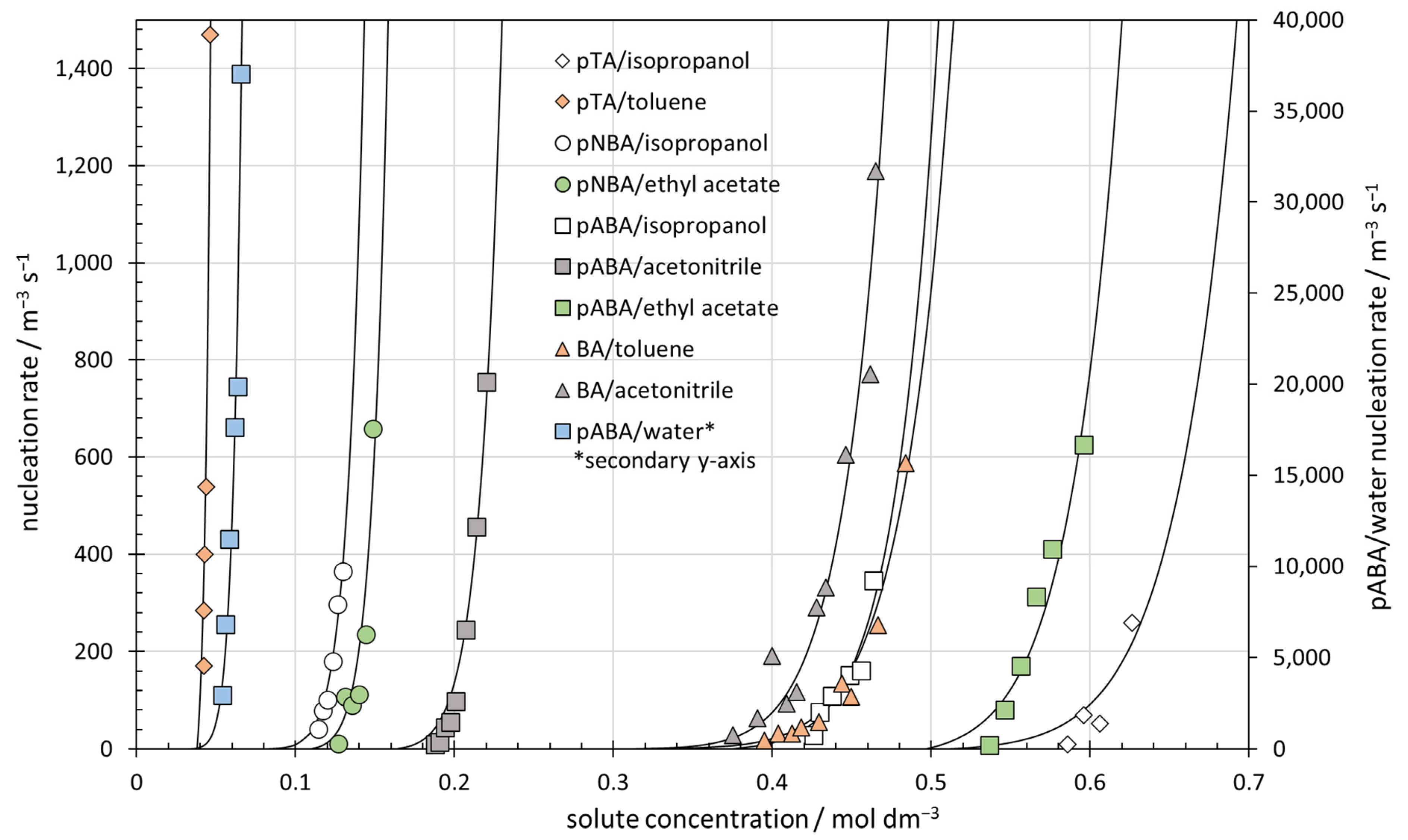
3.4. Nucleation Rates of 10 Benzoic Acid and para-Substituted Benzoic Acid Systems
3.5. Homogeneous vs. Heterogeneous Nucleation
4. Discussion
4.1. Homogeneous vs. Heterogeneous Nucleation
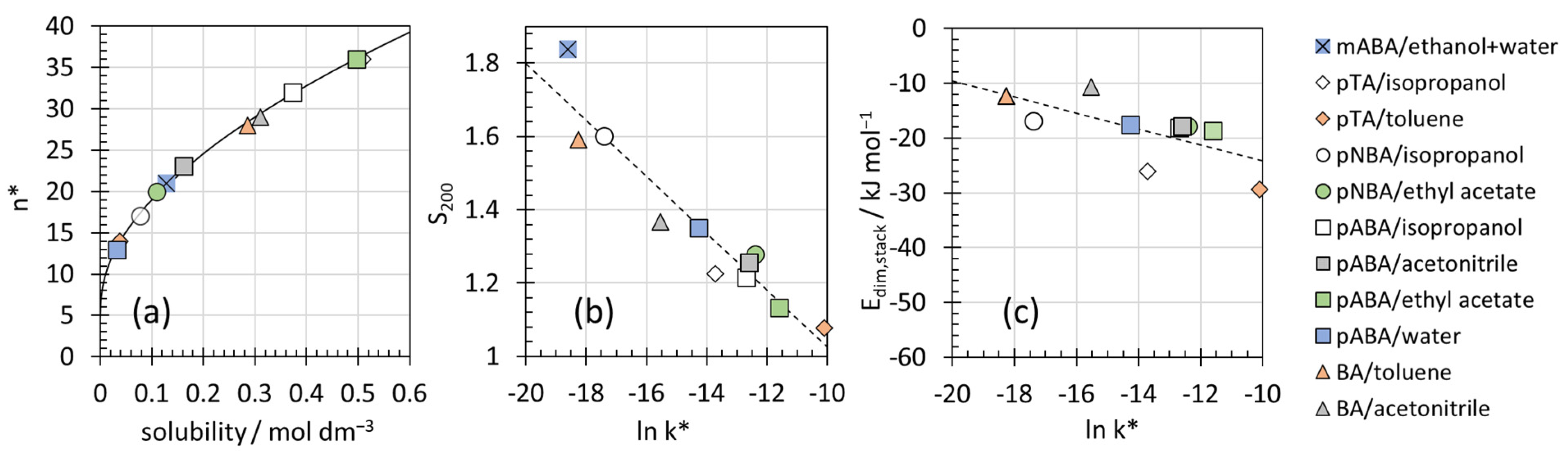
4.2. Interpretation of the Constants n* and k*
4.3. Some General Points
5. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Glasstone, S.; Laidler, K.J.; Eyring, H. The Theory of Rate Processes, 1st ed.; McGraw-Hill, Inc.: New York, NY, USA; London, UK, 1941. [Google Scholar]
- Atkins, P.W. Physical Chemistry, 6th ed.; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Laidler, K.J. Chemical Kinetics; Harper & Row: New York, NY, USA, 1987. [Google Scholar]
- Bao, J.L.; Truhlar, D.G. Variational Transition State Theory: Theoretical Framework and Recent Developments. Chem. Soc. Rev. 2017, 46, 7548–7596. [Google Scholar] [CrossRef] [PubMed]
- Laidler, K.J. Symbolism and Terminology in Chemical Kinetics. Pure Appl. Chem. 1981, 53, 753–771. [Google Scholar] [CrossRef]
- Kashchiev, D.; Van Rosmalen, G.M. Review: Nucleation in Solutions Revisited. Cryst. Res. Technol. 2003, 38, 555–574. [Google Scholar] [CrossRef]
- Davey, R.J.; Schroeder, S.L.M.; Ter Horst, J.H. Nucleation of Organic Crystals—A Molecular Perspective. Angew. Chemie-Int. Ed. 2013, 52, 2166–2179. [Google Scholar] [CrossRef] [PubMed]
- Yi, P.; Rutledge, G.C. Molecular Origins of Homogeneous Crystal Nucleation. Annu. Rev. Chem. Biomol. Eng. 2012, 3, 157–182. [Google Scholar] [CrossRef] [PubMed]
- Sosso, G.C.; Chen, J.; Cox, S.J.; Fitzner, M.; Pedevilla, P.; Zen, A.; Michaelides, A. Crystal Nucleation in Liquids: Open Questions and Future Challenges in Molecular Dynamics Simulations. Chem. Rev. 2016, 116, 7078–7116. [Google Scholar] [CrossRef]
- Kashchiev, D. Nucleation: Basic Theory with Applications; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Myerson, A.S.; Erdemir, D.; Lee, A.Y. Crystal Nucleation. In Handbook of Industrial Crystallization; Cambridge University Press: Cambridge, UK, 2019; pp. 76–114. ISBN 9781139026949. [Google Scholar]
- Li, X.; Wang, J.; Wang, T.; Wang, N.; Zong, S.; Huang, X.; Hao, H. Molecular Mechanism of Crystal Nucleation from Solution. Sci. China Chem. 2021, 64, 1460–1481. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2001. [Google Scholar]
- Volmer, M.; Weber, A. Keimbildung in Übersättigten Gebilden. Zeitschrift Fur Phys. Chemie 1926, 119, 277–301. [Google Scholar] [CrossRef]
- Becker, R.; Döring, W. Kinetische Behandlung Der Keimbildung in Übersättigten Dämpfen. Ann. Phys. 1935, 24, 719–752. [Google Scholar] [CrossRef]
- Volmer, M. Kinetik Der Phasenbildung; Steinkopff: Leipzig, Germany, 1939. [Google Scholar]
- Wu, D.T.; Gránásy, L.; Spaepen, F. Nucleation and the Solid-Liquid Interfacial Free Energy. MRS Bull. 2004, 29, 945–950. [Google Scholar] [CrossRef]
- Oxtoby, D.W. Homogeneous Nucleation—Theory and Experiment. J. Physics-Condensed Matter 1992, 4, 7627–7650. [Google Scholar] [CrossRef]
- Turnbull, D.; Fisher, J.C. Rate of Nucleation in Condensed Systems. J. Chem. Phys. 1949, 17, 71–73. [Google Scholar] [CrossRef]
- Black, S. Simulating Nucleation of Molecular Solids. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2007, 463, 2799–2811. [Google Scholar] [CrossRef]
- Jiang, S.; Ter Horst, J.H. Crystal Nucleation Rates from Probability Distributions of Induction Times. Cryst. Growth Des. 2011, 11, 256–261. [Google Scholar] [CrossRef]
- Blow, K.E.; Quigley, D.; Sosso, G.C. The Seven Deadly Sins: When Computing Crystal Nucleation Rates, the Devil Is in the Details. J. Chem. Phys. 2021, 155, 40901. [Google Scholar] [CrossRef]
- Guo, H.; Liu, K. Control of Chemical Reactivity by Transition-State and Beyond. Chem. Sci. 2016, 7, 3992–4003. [Google Scholar] [CrossRef] [PubMed]
- Polanyi, J.C.; Zewail, A.H. Direct Observation of the Transition State. Acc. Chem. Res. 1995, 28, 119–132. [Google Scholar] [CrossRef]
- Einstein, A. Über Die von Der Molekularkinetischen Theorie Der Wärme Geforderte Bewegung von in Ruhenden Flüssigkeiten Suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- von Smoluchowski, M. Zur Kinetischen Theorie Der Brownschen Molekularbewegung Und Der Suspensionen. Ann. Phys. 1906, 326, 756–780. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Stochastic Problems in Physics and Astronomy. Rev. Mod. Phys. 1943, 15, 1–89. [Google Scholar] [CrossRef]
- Bentz, J.; Nir, S. Mass Action Kinetics and Equilibria of Reversible Aggregation. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1981, 77, 1249–1275. [Google Scholar] [CrossRef]
- Jeffrey, G.C.; Ottewill, R.H. Reversible Aggregation Part 2. Kinetics of Reversible Aggregation. Colloid Polym. Sci. 1990, 268, 179–189. [Google Scholar] [CrossRef]
- Vasilev, G.A.; Filkova, A.A.; Sveshnikova, A.N. Study of Reversible Platelet Aggregation Model by Nonlinear Dynamics. Mathematics 2021, 9, 759. [Google Scholar] [CrossRef]
- Girshick, S.L.; Chiu, C.P. Kinetic Nucleation Theory: A New Expression for the Rate of Homogeneous Nucleation from an Ideal Supersaturated Vapor. J. Chem. Phys. 1990, 93, 1273–1277. [Google Scholar] [CrossRef]
- Katz, J.L.; Wiedersich, H. Nucleation Theory without Maxwell Demons. J. Colloid Interface Sci. 1977, 61, 351–355. [Google Scholar] [CrossRef]
- Katz, J.L.; Spaepen, F. A Kinetic Approach to Nucleation in Condensed Systems. Philos. Mag. B Phys. Condens. Matter; Stat. Mech. Electron. Opt. Magn. Prop. 1978, 37, 137–148. [Google Scholar] [CrossRef]
- Chiang, P.P.; Donohue, M.D.; Katz, J.L. A Kinetic Approach to Crystallization from Ionic Solution. II. Crystal Nucleation. J. Colloid Interface Sci. 1988, 122, 251–265. [Google Scholar] [CrossRef]
- Vekilov, P.G. Two-Step Mechanism for the Nucleation of Crystals from Solution. J. Cryst. Growth 2005, 275, 65–76. [Google Scholar] [CrossRef]
- Gebauer, D.; Kellermeier, M.; Gale, J.D.; Bergström, L.; Cölfen, H. Pre-Nucleation Clusters as Solute Precursors in Crystallisation. Chem. Soc. Rev. 2014, 43, 2348–2371. [Google Scholar] [CrossRef]
- Kashchiev, D.; Vekilov, P.G.; Kolomeisky, A.B. Kinetics of Two-Step Nucleation of Crystals. J. Chem. Phys. 2005, 122, 244706. [Google Scholar] [CrossRef]
- Vekilov, P.G. The Two-Step Mechanism of Nucleation of Crystals in Solution. Nanoscale 2010, 2, 2346–2357. [Google Scholar] [CrossRef] [PubMed]
- Erdemir, D.; Lee, A.Y.; Myerson, A.S. Nucleation of Crystals from Solution: Classical and Two-Step Models. Acc. Chem. Res. 2009, 42, 621–629. [Google Scholar] [CrossRef] [PubMed]
- Kashchiev, D. Classical Nucleation Theory Approach to Two-Step Nucleation of Crystals. J. Cryst. Growth 2020, 530, 125300. [Google Scholar] [CrossRef]
- Karthika, S.; Radhakrishnan, T.K.; Kalaichelvi, P. A Review of Classical and Nonclassical Nucleation Theories. Cryst. Growth Des. 2016, 16, 6663–6681. [Google Scholar] [CrossRef]
- De Yoreo, J. A Perspective on Multistep Pathways of Nucleation. ACS Symp. Ser. 2020, 1358, 1–17. [Google Scholar] [CrossRef]
- Li, J.; Deepak, F.L. In Situ Kinetic Observations on Crystal Nucleation and Growth. Chem. Rev. 2022, 122, 16911–16982. [Google Scholar] [CrossRef] [PubMed]
- Jun, Y.S.; Zhu, Y.; Wang, Y.; Ghim, D.; Wu, X.; Kim, D.; Jung, H. Classical and Nonclassical Nucleation and Growth Mechanisms for Nanoparticle Formation. Annu. Rev. Phys. Chem. 2022, 73, 453–477. [Google Scholar] [CrossRef]
- Yang, F.; Yuan, K.; Stack, A.G.; Starchenko, V. Numerical Study of Mineral Nucleation and Growth on a Substrate. ACS Earth Space Chem. 2022, 6, 1655–1665. [Google Scholar] [CrossRef]
- Gebauer, D.; Gale, J.D.; Cölfen, H. Crystal Nucleation and Growth of Inorganic Ionic Materials from Aqueous Solution: Selected Recent Developments, and Implications. Small 2022, 18, 2107735. [Google Scholar] [CrossRef]
- Smoluchowski, M.V. Versuch Einer Mathematischen Theorie Der Koagulationskinetik Kolloider Lösungen. Zeitschrift Für Phys. Chemie 1918, 92U, 129–168. [Google Scholar] [CrossRef]
- Popov, K.; Oshchepkov, M.; Kovalenko, A.; Redchuk, A.; Dikareva, J.; Pochitalkina, I. Scale Nucleation Natural Precursors: A Case Study of “Micro/Nanodust” Impurities Nature in Laboratory Aqueous Samples Obtained from Moscow Tap Water. Int. J. Corros. Scale Inhib. 2020, 9, 1097–1112. [Google Scholar] [CrossRef]
- Liu, X.Y. Heterogeneous Nucleation or Homogeneous Nucleation? J. Chem. Phys. 2000, 112, 9949–9955. [Google Scholar] [CrossRef]
- Rausch, H.; Sziklai, I.L.; Nazarov, V.M.; Bodon, P.; Erdélyvári, I.; Tóth, B. Determination of Impurities in High-Purity Solvents by Neutron Activation Analysis. J. Radioanal. Nucl. Chem. 1991, 148, 217–225. [Google Scholar] [CrossRef]
- Gebauer, D. How Can Additives Control the Early Stages of Mineralisation? Minerals 2018, 8, 179. [Google Scholar] [CrossRef]
- Nicoud, L.H.; Myerson, A.S. The Influence of Impurities and Additives on Crystallization. In Handbook of Industrial Crystallization; Cambridge University Press: Cambridge, UK, 2019; pp. 115–135. ISBN 9781139026949. [Google Scholar]
- Kulkarni, S.A.; Kadam, S.S.; Meekes, H.; Stankiewicz, A.I.; Ter Horst, J.H. Crystal Nucleation Kinetics from Induction Times and Metastable Zone Widths. Cryst. Growth Des. 2013, 13, 2435–2440. [Google Scholar] [CrossRef]
- Debye, P. Reaction Rates in Ionic Solutions. Trans. Electrochem. Soc. 1942, 82, 265–272. [Google Scholar] [CrossRef]
- Xiao, Y.; Tang, S.K.; Hao, H.; Davey, R.J.; Vetter, T. Quantifying the Inherent Uncertainty Associated with Nucleation Rates Estimated from Induction Time Data Measured in Small Volumes. Cryst. Growth Des. 2017, 17, 2852–2863. [Google Scholar] [CrossRef]
- Black, J.F.B.; Cardew, P.T.; Cruz-Cabeza, A.J.; Davey, R.J.; Gilks, S.E.; Sullivan, R.A. Crystal Nucleation and Growth in a Polymorphic System: Ostwald’s Rule,: P -Aminobenzoic Acid and Nucleation Transition States. CrystEngComm 2018, 20, 768–776. [Google Scholar] [CrossRef]
- Tang, S.K.; Davey, R.J.; Sacchi, P.; Cruz-Cabeza, A.J. Can Molecular Flexibility Control Crystallization? The Case of Para Substituted Benzoic Acids. Chem. Sci. 2021, 12, 993–1000. [Google Scholar] [CrossRef]
- Cruz-Cabeza, A.J.; Davey, R.J.; Sachithananthan, S.S.; Smith, R.; Tang, S.K.; Vetter, T.; Xiao, Y. Aromatic Stacking—A Key Step in Nucleation. Chem. Commun. 2017, 53, 7905–7908. [Google Scholar] [CrossRef]
- Sullivan, R.A. Molecules, Clusters, Crystals: The Crystallisation of p-Aminobenzoic Acid from Solution. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2015. [Google Scholar]
- Sullivan, R.A.; Davey, R.J.; Sadiq, G.; Dent, G.; Back, K.R.; Ter Horst, J.H.; Toroz, D.; Hammond, R.B. Revealing the Roles of Desolvation and Molecular Self-Assembly in Crystal Nucleation from Solution: Benzoic and p -Aminobenzoic Acids. Cryst. Growth Des. 2014, 14, 2689–2696. [Google Scholar] [CrossRef]
- Hanrahan, E.S.; Bruce, B.D. Dimerization of P-Substituted Benzoic Acids. Spectrochim. Acta Part A Mol. Spectrosc. 1967, 23, 2497–2503. [Google Scholar] [CrossRef]
- Turner, T.D.; Corzo, D.M.C.; Toroz, D.; Curtis, A.; Dos Santos, M.M.; Hammond, R.B.; Lai, X.; Roberts, K.J. The Influence of Solution Environment on the Nucleation Kinetics and Crystallisability of Para-Aminobenzoic Acid. Phys. Chem. Chem. Phys. 2016, 18, 27507–27520. [Google Scholar] [CrossRef] [PubMed]
- Trukhina, M.; Tkachenko, S.; Ryabova, A.; Oshchepkov, M.; Redchuk, A.; Popov, K. Calcium Sulfate Crystallization in Presence of Fluorecent-Tagged Polyacrylate and Some Refinement of Scale Inhibition Mechanism. Minerals 2023, 13, 559. [Google Scholar] [CrossRef]
- Katz, J.L.; Donohue, M.D. A Kinetic Approach to Homogeneous Nucleation Theory. In Advances in Chemical Physics; Prigogine, I., Rice, S.A., Eds.; John Wiley & Sons, Inc.: New York, NY, USA; Chichester, UK; Brisbane, Australia; Toronto, ON, Canada, 1979; Volume 40, pp. 137–156. [Google Scholar]
- Ruckenstein, E.; Djikaev, Y.S. Recent Developments in the Kinetic Theory of Nucleation. Adv. Colloid Interface Sci. 2005, 118, 51–72. [Google Scholar] [CrossRef] [PubMed]
- Hammond, G.S. A Correlation of Reaction Rates. J. Am. Chem. Soc. 1955, 77, 334–338. [Google Scholar] [CrossRef]
- Eaton, W.A. Modern Kinetics and Mechanism of Protein Folding: A Retrospective. J. Phys. Chem. B 2021, 125, 3452–3467. [Google Scholar] [CrossRef]


| Solute | Solvent | [M]0/mol dm−3 | T/°C | S200 | k*/s−1 | n* |
|---|---|---|---|---|---|---|
| p-toluic acid | isopropanol | 0.509 | 20 | 1.23 | 1.1 × 10−6 | 36 |
| toluene # | 0.038 # | 20 | 1.08 | 4.1 × 10−5 # | 14 # | |
| p-nitrobenzoic acid | isopropanol | 0.078 | 25 | 1.60 | 2.8 × 10−8 | 17 |
| ethyl acetate | 0.109 | 25 | 1.28 | 4.1 × 10−6 | 20 | |
| p-aminobenzoic acid | isopropanol | 0.374 | 20 | 1.22 | 3.1 × 10−6 | 32 |
| acetonitrile | 0.163 | 20 | 1.26 | 3.4 × 10−6 | 23 | |
| ethyl acetate | 0.497 | 20 | 1.13 | 9.2 × 10−6 | 36 | |
| water | 0.032 | 20 | 1.35 | 6.4 × 10−7 | 13 | |
| benzoic acid | toluene # | 0.286 # | 20 | 1.59 | 1.2 × 10−8 # | 28 # |
| acetonitrile | 0.310 | 20 | 1.37 | 1.8 × 10−7 | 29 |
| Solute | Solvent | Vm,sol cm3 | Vm,solv cm3 | Vagg 10−27 m3 | δ nm | η mPa s | τ ns | |
|---|---|---|---|---|---|---|---|---|
| p-toluic acid | isopropanol | 128.4 | 76.5 | 16.8 | 1.1 | 0.237 | 5 | 1.0 |
| toluene | 128.4 | 106.9 | 10.9 | 1.0 | 0.560 | 62 | 0.0 | |
| p-nitro-benzoic acid | isopropanol | 105.8 | 76.5 | 7.3 | 0.8 | 0.237 | 16 | 9.7 |
| ethyl acetate | 105.8 | 97.7 | 10.0 | 0.9 | 0.455 | 25 | 0.0 | |
| p-amino-benzoic acid | isopropanol | 99.8 | 76.5 | 13.4 | 1.0 | 0.237 | 6 | 0.3 |
| acetonitrile | 99.8 | 52.2 | 7.8 | 0.9 | 0.334 | 14 | 0.1 | |
| ethyl acetate | 99.8 | 97.7 | 17.6 | 1.1 | 0.455 | 10 | 0.1 | |
| water | 99.8 | 18.0 | 2.9 | 0.6 | 0.890 | 109 | 0.0 | |
| benzoic acid | toluene | 96.5 | 106.9 | 18.9 | 1.1 | 0.560 | 16 | 29.5 |
| acetonitrile | 96.5 | 52.2 | 9.7 | 0.9 | 0.334 | 9 | 2.7 | |
| m-ABA | 50wt% ethanol/water | 90.8 | 18.0 | 4.4 | 0.7 | 0.890 | 44 | 9.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schroeder, S.L.M. Homogeneous Organic Crystal Nucleation Rates in Solution from the Perspective of Chemical Reaction Kinetics. Crystals 2024, 14, 349. https://doi.org/10.3390/cryst14040349
Schroeder SLM. Homogeneous Organic Crystal Nucleation Rates in Solution from the Perspective of Chemical Reaction Kinetics. Crystals. 2024; 14(4):349. https://doi.org/10.3390/cryst14040349
Chicago/Turabian StyleSchroeder, Sven L. M. 2024. "Homogeneous Organic Crystal Nucleation Rates in Solution from the Perspective of Chemical Reaction Kinetics" Crystals 14, no. 4: 349. https://doi.org/10.3390/cryst14040349





