Crystal Plasticity Finite Element Modeling of the Influences of Ultrafine-Grained Austenite on the Mechanical Response of a Medium-Mn Steel
Abstract
:1. Introduction
2. CPFE Modeling of Medium-Mn: Dislocation Density-Based Flow and Hardening Rules
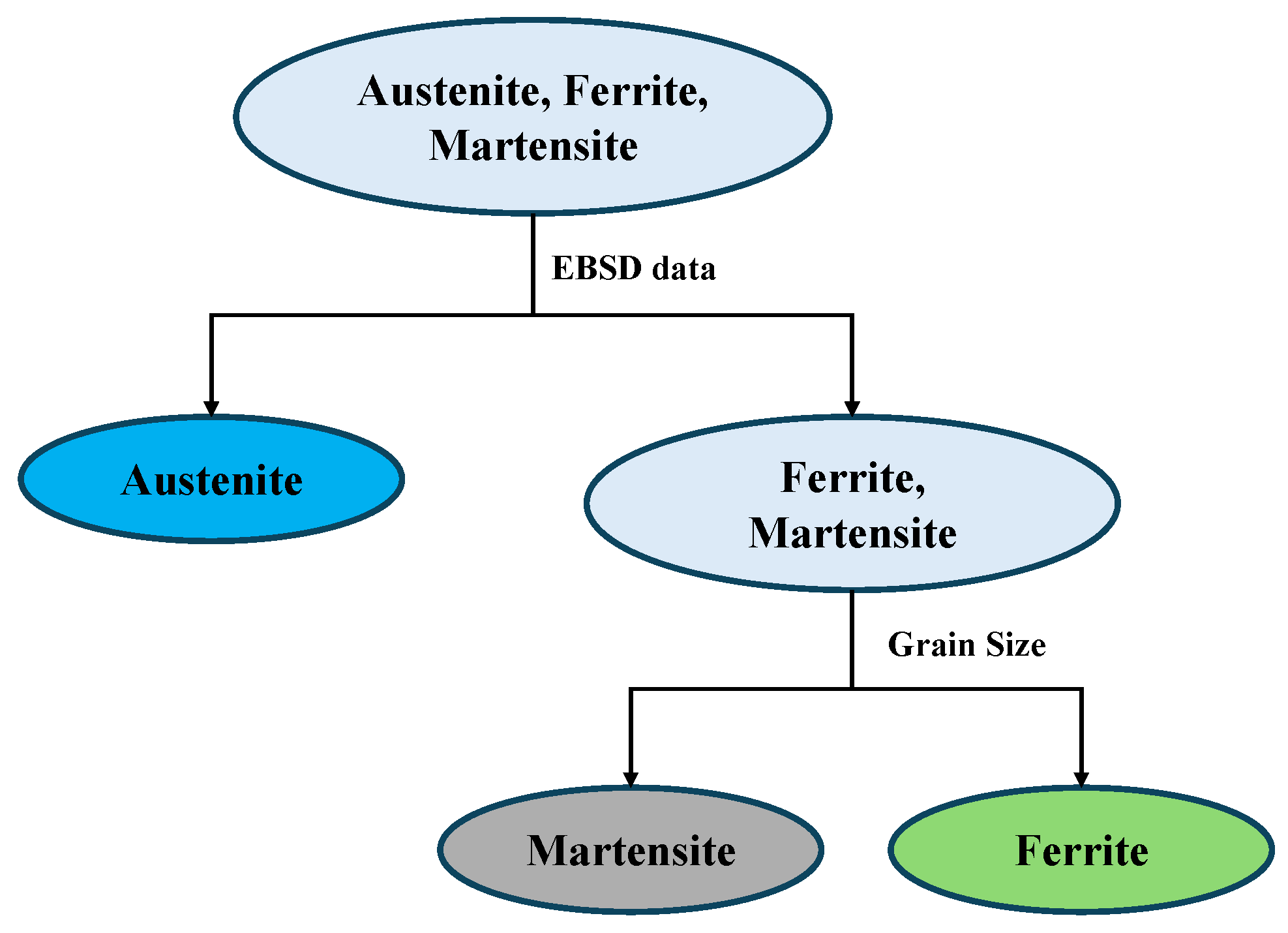
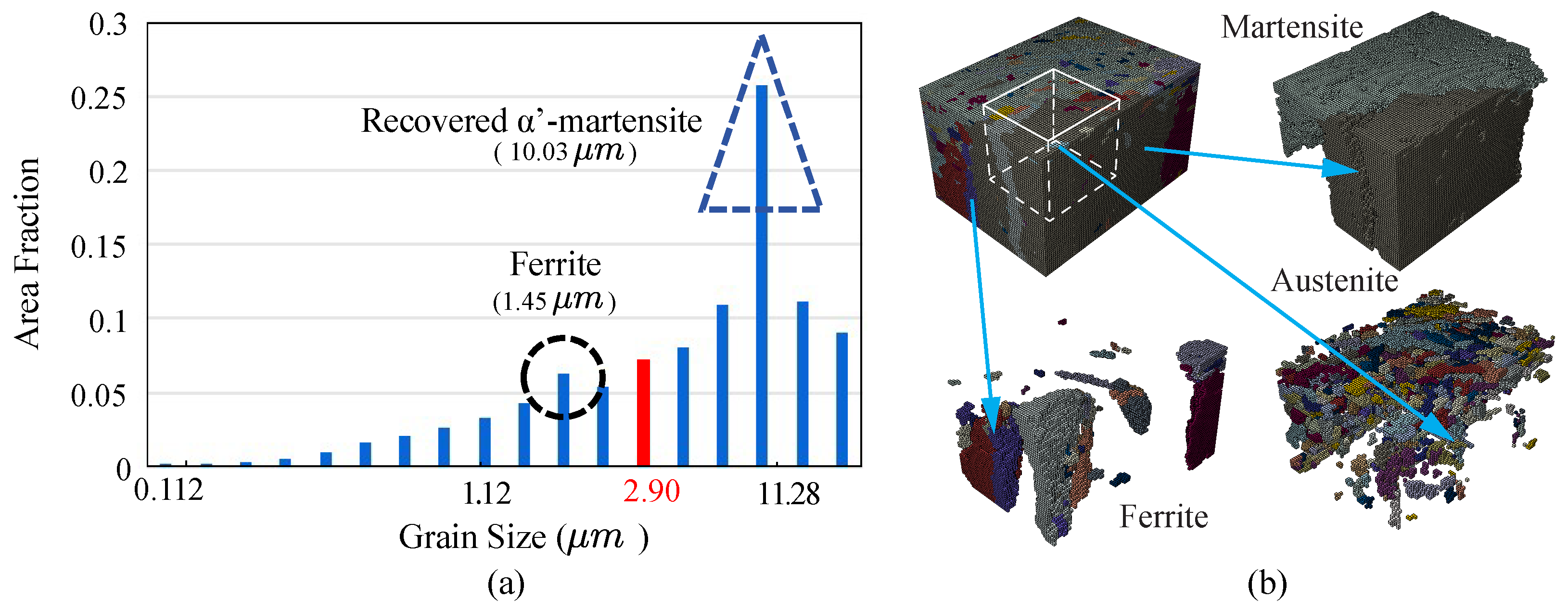
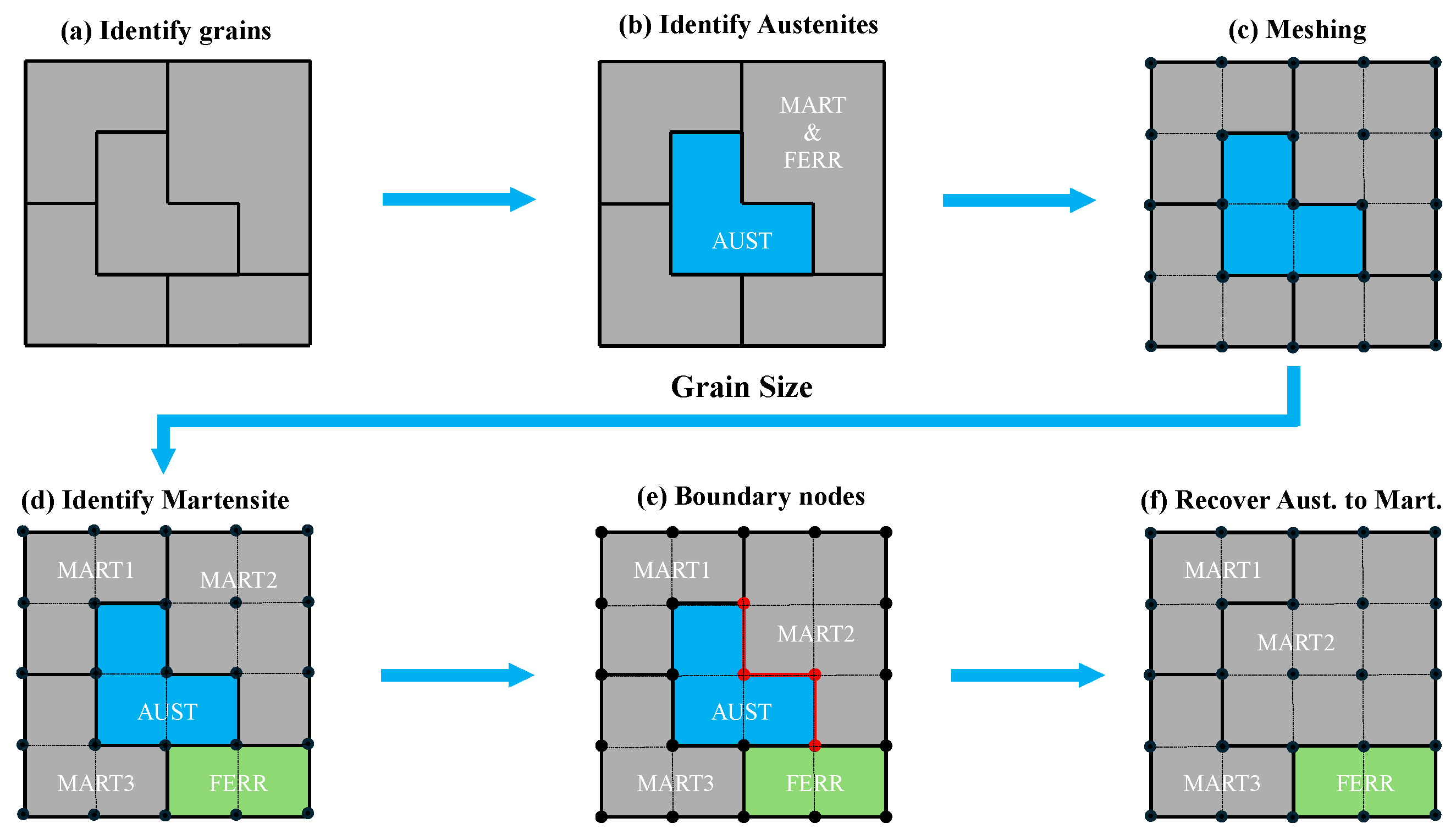
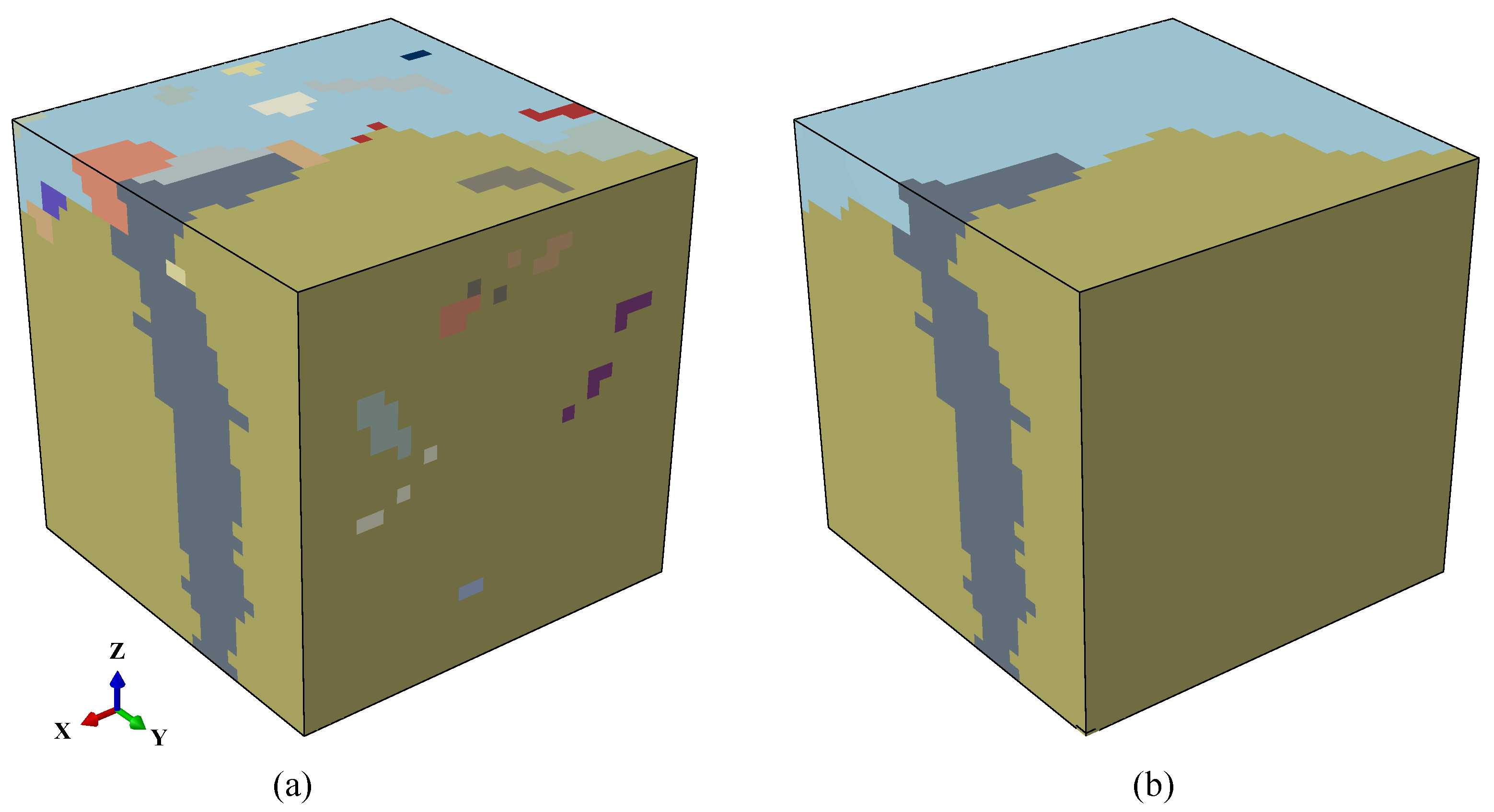
3. Microstructure Reconstruction and Phase Identification
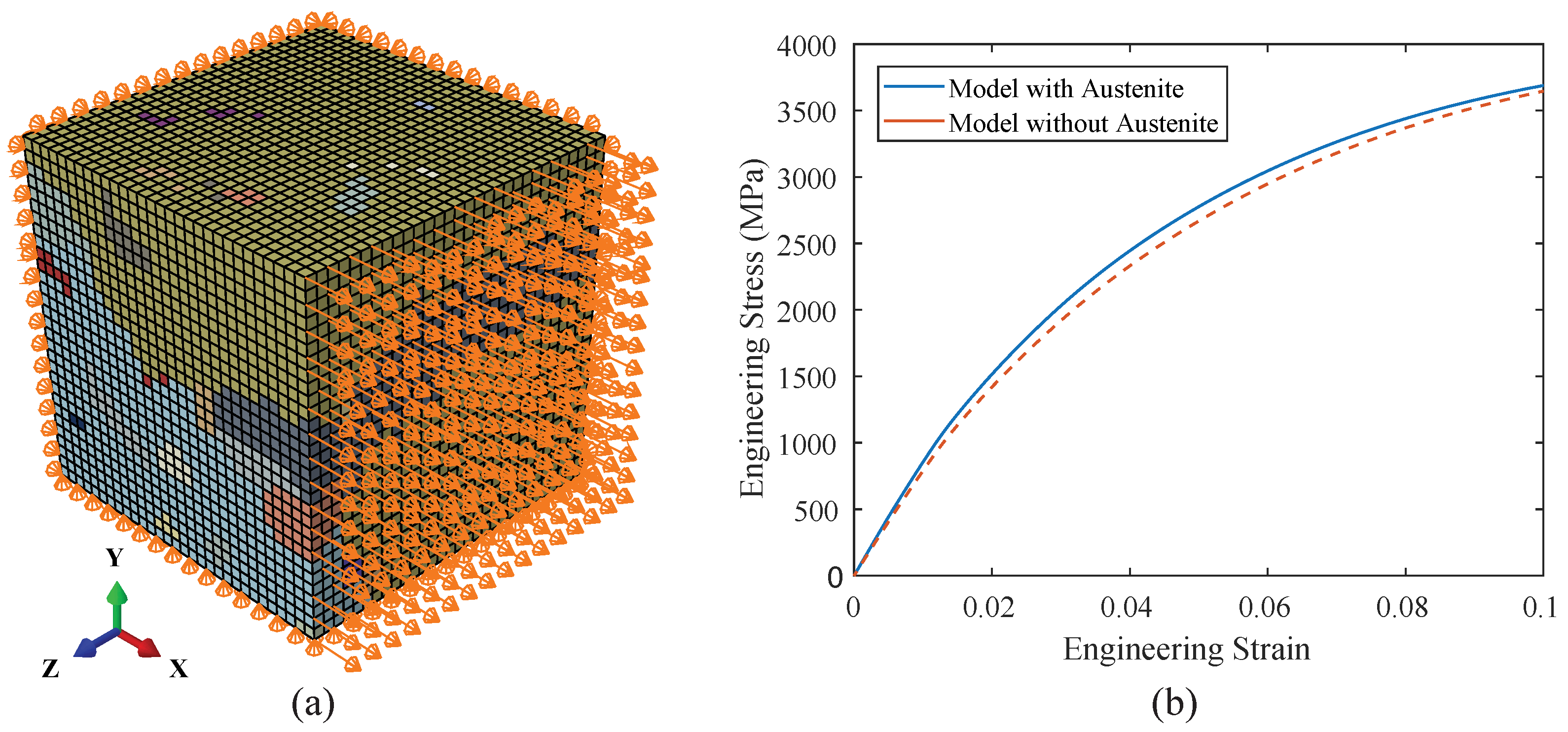
3.1. Mesh Size Convergence Study and Model Calibration
3.2. Establish a Microstructure without Austenite
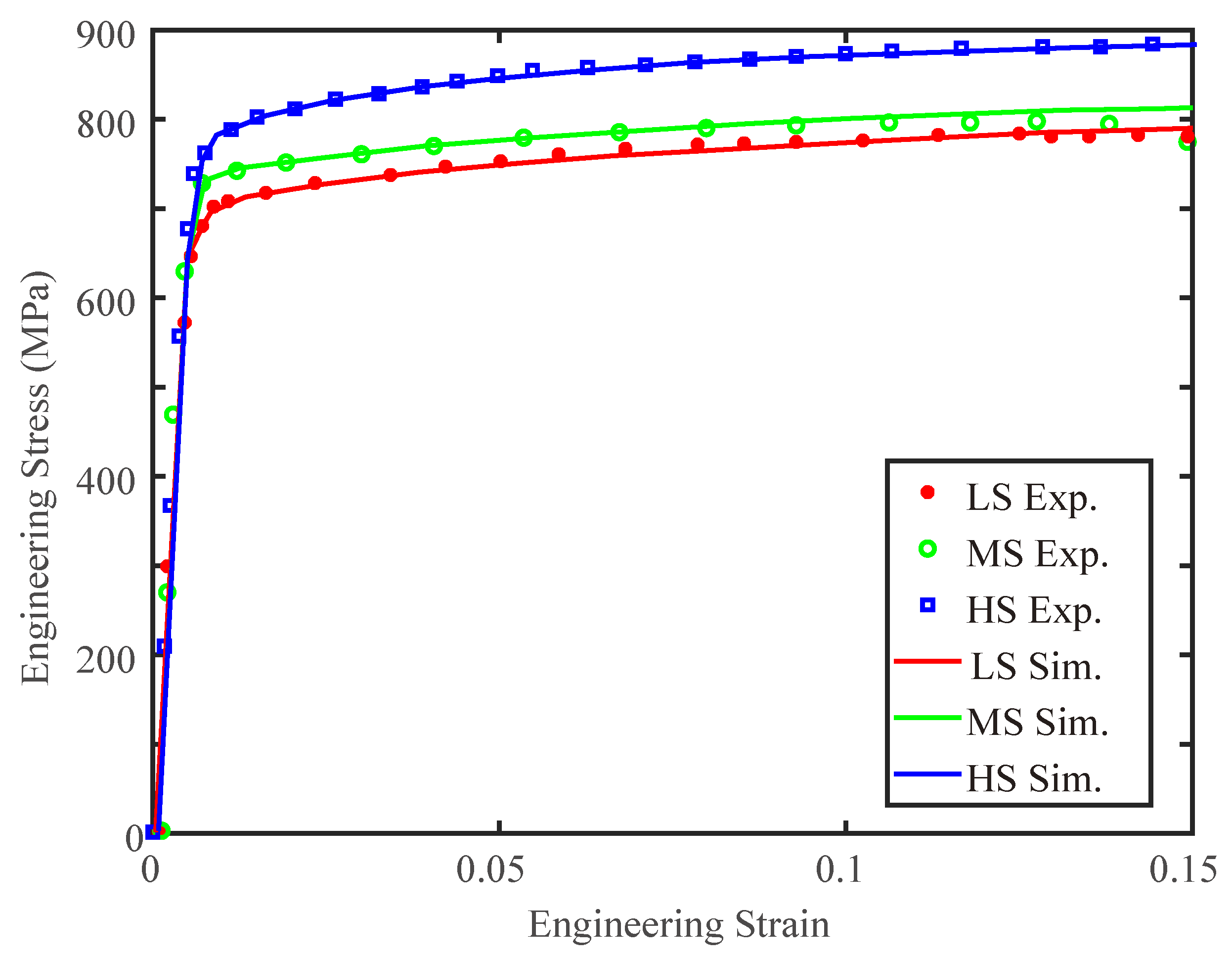
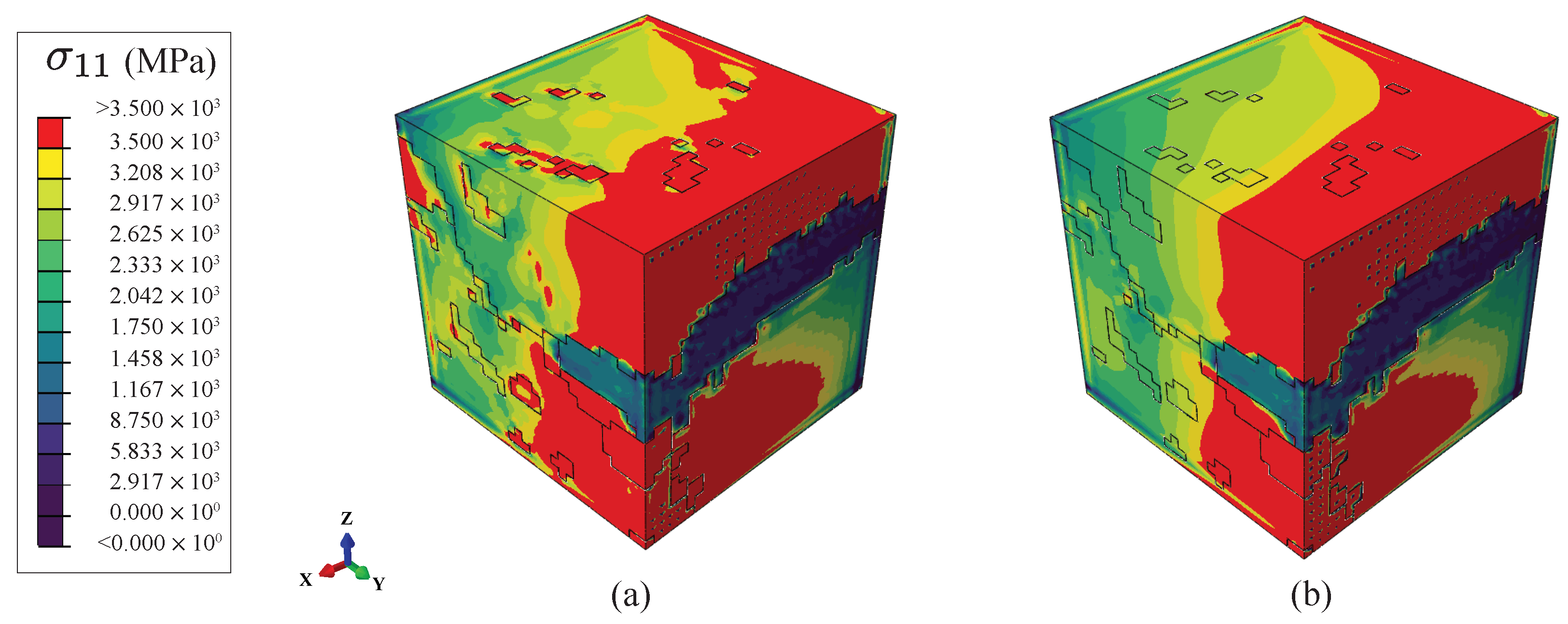
4. CPFE Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameters | Phase | |||
|---|---|---|---|---|
| Symbol | Unit | Martensite | Ferrite | Austenite |
| GPa | 169 | 175 | 174 | |
| GPa | 82 | 82 | 85 | |
| GPa | 96 | 97 | 99 | |
| m−2 | ||||
| Hz | ||||
| μm | ||||
| J | ||||
| m3 | ||||
| MPa | 1036.4 | 272.7 | 163.4 | |
| GPa | 320 | 320 | 207 | |
| 1 | 130 | 130 | 134 | |
| m−1 | ||||
| m−2 | ||||
References
- Matlock, D.K.; Speer, J.G. Processing Opportunities for New Advanced High-Strength Sheet Steels. Mater. Manuf. Process. 2010, 25, 7–13. [Google Scholar] [CrossRef]
- Hu, B.; Luo, H.; Yang, F.; Dong, H. Recent progress in medium-Mn steels made with new designing strategies, a review. J. Mater. Sci. Technol. 2017, 33, 1457–1464. [Google Scholar] [CrossRef]
- Benzing, J.T.; Kwiatkowski da Silva, A.; Morsdorf, L.; Bentley, J.; Ponge, D.; Dutta, A.; Han, J.; McBride, J.R.; Van Leer, B.; Gault, B.; et al. Multi-scale characterization of austenite reversion and martensite recovery in a cold-rolled medium-Mn steel. Acta Mater. 2019, 166, 512–530. [Google Scholar] [CrossRef]
- Lee, S.; De Cooman, B.C. Annealing Temperature Dependence of the Tensile Behavior of 10 pct Mn Multi-phase TWIP-TRIP Steel. Metall. Mater. Trans. A 2014, 45, 6039–6052. [Google Scholar] [CrossRef]
- Benzing, J.T.; Bentley, J.; McBride, J.R.; Ponge, D.; Han, J.; Raabe, D.; Wittig, J.E. Characterization of Partitioning in a Medium-Mn Third-Generation AHSS. Microsc. Microanal. 2017, 23, 402–403. [Google Scholar] [CrossRef]
- Benzing, J.T.; Liu, Y.; Zhang, X.; Luecke, W.E.; Ponge, D.; Dutta, A.; Oskay, C.; Raabe, D.; Wittig, J.E. Experimental and numerical study of mechanical properties of multi-phase medium-Mn TWIP-TRIP steel: Influences of strain rate and phase constituents. Acta Mater. 2019, 177, 250–265. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; da Silva, A.K.; Ponge, D.; Raabe, D.; Lee, S.M.; Lee, Y.K.; Lee, S.I.; Hwang, B. The effects of prior austenite grain boundaries and microstructural morphology on the impact toughness of intercritically annealed medium Mn steel. Acta Mater. 2017, 122, 199–206. [Google Scholar] [CrossRef]
- Wang, T.; Hu, J.; Misra, R.D.K. Microstructure evolution and strain behavior of a medium Mn TRIP/TWIP steel for excellent combination of strength and ductility. Mater. Sci. Eng. A 2019, 753, 99–108. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, J.M.; Sun, G.S.; Du, L.X.; Liu, Y.; Dong, Y.; Misra, R.D.K. High strength and ductility combination in nano-/ultrafine-grained medium-Mn steel by tuning the stability of reverted austenite involving intercritical annealing. J. Mater. Sci. 2019, 54, 6565–6578. [Google Scholar] [CrossRef]
- Hu, B.; Rong, X.; Tian, C.; Yu, Y.; Guo, H.; Misra, R.D.K.; Shang, C. Nanoscale precipitation and ultrafine retained austenite induced high strength-ductility combination in a newly designed low carbon Cu-bearing medium-Mn steel. Mater. Sci. Eng. A 2021, 822, 141685. [Google Scholar] [CrossRef]
- Sadeghpour, S.; Somani, M.C.; Kömi, J.; Karjalainen, L.P. A new combinatorial processing route to achieve an ultrafine-grained, multiphase microstructure in a medium Mn steel. J. Mater. Res. Technol. 2021, 15, 3426–3446. [Google Scholar] [CrossRef]
- Jia, Q.; Chen, L.; Xing, Z.; Wang, H.; Jin, M.; Chen, X.; Choi, H.; Han, H.N. Tailoring hetero-grained austenite via a cyclic thermomechanical process for achieving ultrahigh strength-ductility in medium-Mn steel. Scr. Mater. 2022, 217, 114767. [Google Scholar] [CrossRef]
- Li, J.; Xu, Y.; Lu, B.; Yu, Y.; Jing, Y.; Sun, W. Improvement of strength-ductility combination in ultra-high-strength medium-Mn Q&P steel by tailoring the characteristics of martensite/retained austenite constituents. J. Mater. Res. Technol. 2022, 18, 352–369. [Google Scholar] [CrossRef]
- Mohammed, B.; Park, T.; Pourboghrat, F.; Hu, J.; Esmaeilpour, R.; Abu-Farha, F. Multiscale crystal plasticity modeling of multiphase advanced high strength steel. Int. J. Solids Struct. 2018, 151, 57–75. [Google Scholar] [CrossRef]
- Park, T.; Kim, H.; Ryu, I.; Pourboghrat, F.; Esmaeilpour, R. A multi-scale modelling of 3rd generation advanced high strength steels to account for anisotropic evolution of yield surface and plastic potential. J. Phys. Conf. Ser. 2018, 1063, 012019. [Google Scholar] [CrossRef]
- Park, T.; Hector, L.G.; Hu, X.; Abu-Farha, F.; Fellinger, M.R.; Kim, H.; Esmaeilpour, R.; Pourboghrat, F. Crystal plasticity modeling of 3rd generation multi-phase AHSS with martensitic transformation. Int. J. Plast. 2019, 120, 1–46. [Google Scholar] [CrossRef]
- He, B.B.; Luo, H.W.; Huang, M.X. Experimental investigation on a novel medium Mn steel combining transformation-induced plasticity and twinning-induced plasticity effects. Int. J. Plast. 2016, 78, 173–186. [Google Scholar] [CrossRef]
- Kalsar, R.; Sanamar, S.; Schell, N.; Brokmeier, H.G.; Saha, R.; Ghosh, P.; Suwas, S. In-situ study of tensile deformation behaviour of medium Mn TWIP/TRIP steel using synchrotron radiation. Mater. Sci. Eng. A 2022, 857, 144013. [Google Scholar] [CrossRef]
- Nimaga, O.G.; He, B.B.; Cheng, G.J.; Yen, H.W.; Huang, M.X. Revealing orientation-dependent martensitic transformation in a medium Mn steel by micropillar compression. Int. J. Plast. 2019, 123, 165–177. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, H.; Wang, Y.; Wang, S.; Li, R.; Li, S.; Wang, Y.D. Deformation-induced martensitic transformation kinetics and correlative micromechanical behavior of medium-Mn transformation-induced plasticity steel. J. Mater. Sci. Technol. 2019, 35, 1779–1786. [Google Scholar] [CrossRef]
- Soleimani, M.; Kalhor, A.; Mirzadeh, H. Transformation-induced plasticity (TRIP) in advanced steels: A review. Mater. Sci. Eng. A 2020, 795, 140023. [Google Scholar] [CrossRef]
- Lee, Y.K.; Han, J. Current opinion in medium manganese steel. Mater. Sci. Technol. 2015, 31, 843–856. [Google Scholar] [CrossRef]
- Kwok, T.W.J.; Dye, D. A review of the processing, microstructure and property relationships in medium Mn steels. Int. Mater. Rev. 2023, 68, 1098–1134. [Google Scholar] [CrossRef]
- Liu, M.; Zhou, J.; Zhang, J.; Song, C.; Zhai, Q. Ultra-high strength medium-Mn lightweight steel by dislocation slip band refinement and suppressed intergranular κ-carbide with Cr addition. Mater. Charact. 2022, 190, 112042. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Hu, P.; Liu, Y.; Zhu, Y.; Ying, L. Crystal plasticity extended models based on thermal mechanism and damage functions: Application to multiscale modeling of aluminum alloy tensile behavior. Int. J. Plast. 2016, 86, 1–25. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Oskay, C. Multiscale Reduced-Order Modeling of a Titanium Skin Panel Subjected to Thermomechanical Loading. arXiv 2021. [Google Scholar] [CrossRef]
- Williams, J.C.; Baggerly, R.G.; Paton, N.E. Deformation behavior of HCP Ti-Al alloy single crystals. Metall. Mater. Trans. A 2002, 33, 837–850. [Google Scholar] [CrossRef]
- Ozturk, D.; Shahba, A.; Ghosh, S. Crystal plasticity FE study of the effect of thermo-mechanical loading on fatigue crack nucleation in titanium alloys. Fatigue Fract. Eng. Mater. Struct. 2016, 39, 752–769. [Google Scholar] [CrossRef]
- Venkataramani, G.; Kirane, K.; Ghosh, S. Microstructural parameters affecting creep induced load shedding in Ti-6242 by a size dependent crystal plasticity FE model. Int. J. Plast. 2008, 24, 428–454. [Google Scholar] [CrossRef]
- Oppedal, A.L.; El Kadiri, H.; Tomé, C.N.; Kaschner, G.C.; Vogel, S.C.; Baird, J.C.; Horstemeyer, M.F. Effect of dislocation transmutation on modeling hardening mechanisms by twinning in magnesium. Int. J. Plast. 2012, 30–31, 41–61. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Tomé, C.N. A dislocation-based constitutive law for pure Zr including temperature effects. Int. J. Plast. 2008, 24, 867–895. [Google Scholar] [CrossRef]
- Xia, D.; Oskay, C. Reduced order mathematical homogenization method for polycrystalline microstructure with microstructurally small cracks. Int. J. Numer. Methods Eng. 2023, 124, 3166–3190. [Google Scholar] [CrossRef]
- Madec, R.; Devincre, B.; Kubin, L.P. From Dislocation Junctions to Forest Hardening. Phys. Rev. Lett. 2002, 89, 255508. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, X.; Oskay, C. A comparative study on fatigue indicator parameters for near-α titanium alloys. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 271–294. [Google Scholar] [CrossRef]
- Kocks, U.F.; As, A.; Mf, A. Thermodynamics and Kinetics of Slip; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Williams, W.S.; Schaal, R.D. Elastic deformation, plastic flow, and dislocations in single crystals of titanium carbide. J. Appl. Phys. 1962, 33, 955–962. [Google Scholar] [CrossRef]
- Appel, F.; Lorenz, U.; Oehring, M.; Sparka, U.; Wagner, R. Thermally activated deformation mechanisms in micro-alloyed two-phase titanium amminide alloys. Mater. Sci. Eng. A 1997, 233, 1–14. [Google Scholar] [CrossRef]
- Cuitino, A.M.; Ortiz, M. Computational modelling of single crystals. Model. Simul. Mater. Sci. Eng. 1993, 1, 225. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Bronkhorst, C.A.; Anand, L. Crystallographic texture evolution in bulk deformation processing of FCC metals. J. Mech. Phys. Solids 1992, 40, 537–569. [Google Scholar] [CrossRef]
- Groeber, M.A.; Jackson, M.A. DREAM.3D: A Digital Representation Environment for the Analysis of Microstructure in 3D. Integr. Mater. Manuf. Innov. 2014, 3, 56–72. [Google Scholar] [CrossRef]
- Zhang, X.; Oskay, C. Eigenstrain based reduced order homogenization for polycrystalline materials. Comput. Methods Appl. Mech. Eng. 2015, 297, 408–436. [Google Scholar] [CrossRef]
- Zhang, X.; Oskay, C. Polycrystal plasticity modeling of nickel-based superalloy IN 617 subjected to cyclic loading at high temperature. Model. Simul. Mater. Sci. Eng. 2016, 24, 055009. [Google Scholar] [CrossRef]
- Nasirov, A.; Zhang, X.; Wagner, D.; Yeratapally, S.R.; Oskay, C. Achieving high efficiency in reduced order modeling for large scale polycrystal plasticity simulations. Finite Elem. Anal. Des. 2024, 228, 104053. [Google Scholar] [CrossRef]
- Tian, Y.; Lin, S.; Ko, J.Y.P.; Lienert, U.; Borgenstam, A.; Hedström, P. Micromechanics and microstructure evolution during in situ uniaxial tensile loading of TRIP-assisted duplex stainless steels. Mater. Sci. Eng. A 2018, 734, 281–290. [Google Scholar] [CrossRef]
- Baghdadchi, A.; Hosseini, V.A.; Karlsson, L. Identification and quantification of martensite in ferritic-austenitic stainless steels and welds. J. Mater. Res. Technol. 2021, 15, 3610–3621. [Google Scholar] [CrossRef]
- Cai, Z.H.; Zhang, D.L.; Ma, L.F.; Ding, H.; Feng, Y.; Hu, J.; Misra, R.D.K. Competing deformation mechanisms in an austenite-ferrite medium-Mn steel at different strain rates. Mater. Sci. Eng. A 2021, 818, 141357. [Google Scholar] [CrossRef]
- Benzing, J.T.; Luecke, W.E.; Mates, S.P.; Ponge, D.; Raabe, D.; Wittig, J.E. Intercritical annealing to achieve a positive strain-rate sensitivity of mechanical properties and suppression of macroscopic plastic instabilities in multi-phase medium-Mn steels. Mater. Sci. Eng. A 2021, 803, 140469. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Yu, H.; Sisson, R.D. The effect of carbon content on the c/a ratio of as-quenched martensite in Fe-C alloys. Mater. Sci. Eng. A 2017, 700, 592–597. [Google Scholar] [CrossRef]
- Cheong, K.S.; Busso, E.P. Effects of lattice misorientations on strain heterogeneities in FCC polycrystals. J. Mech. Phys. Solids 2006, 54, 671–689. [Google Scholar] [CrossRef]
- Chen, W.F.; Han, D.J.; Han, D.J. Plasticity for Structural Engineers; J. Ross Publishing: Plantation, FL, USA, 2007. [Google Scholar]
- McDowell, D.L.; Dunne, F.P.E. Microstructure-sensitive computational modeling of fatigue crack formation. Int. J. Fatigue 2010, 32, 1521–1542. [Google Scholar] [CrossRef]
- Dunne, F.P.E.; Wilkinson, A.J.; Allen, R. Experimental and computational studies of low cycle fatigue crack nucleation in a polycrystal. Int. J. Plast. 2007, 23, 273–295. [Google Scholar] [CrossRef]
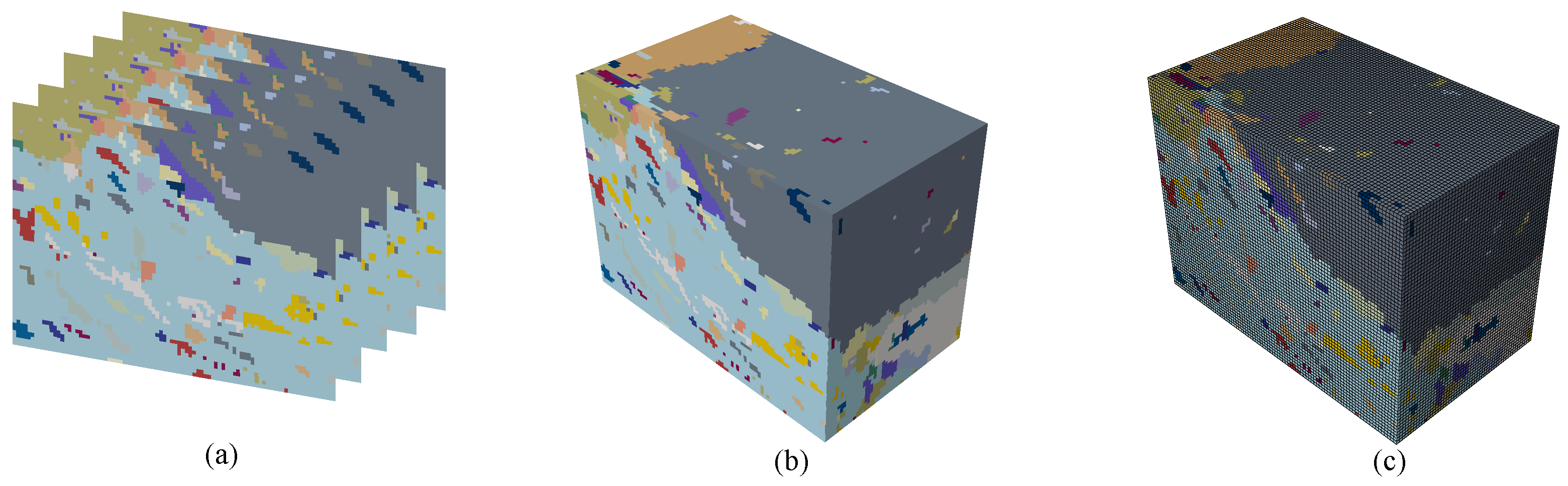


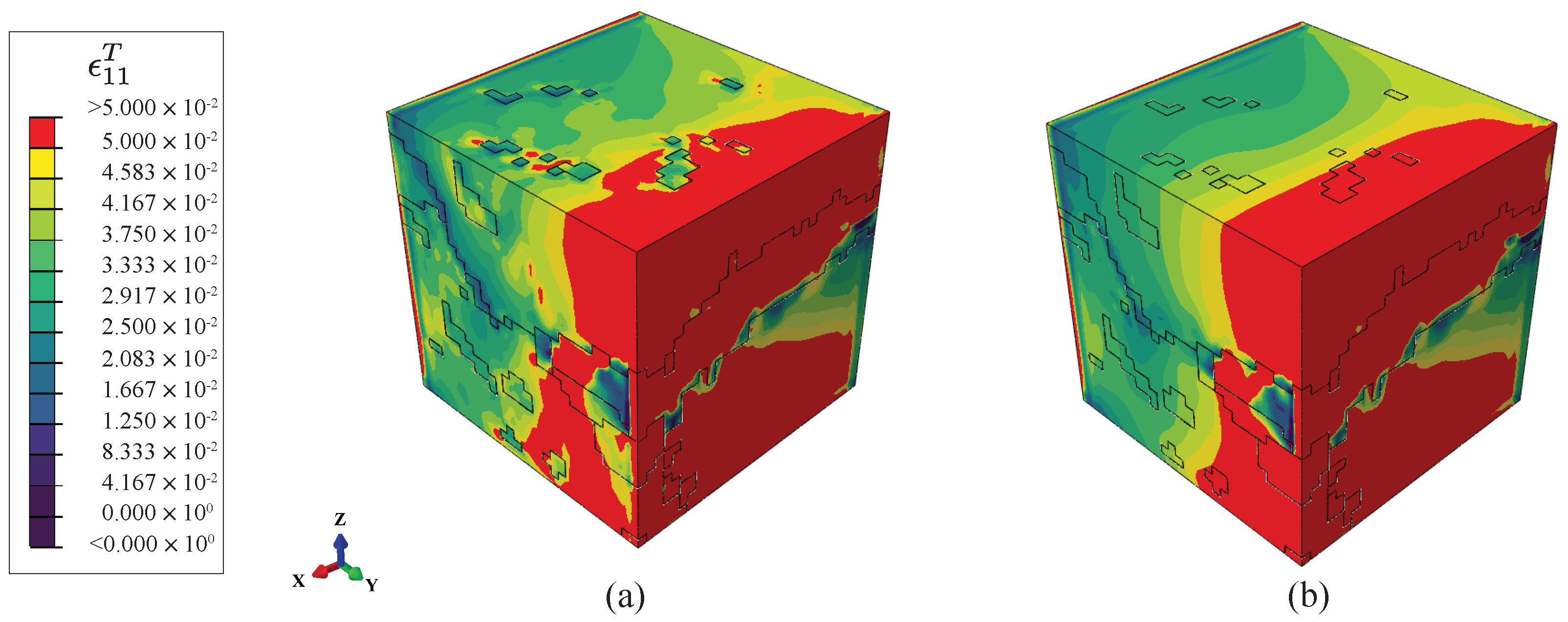
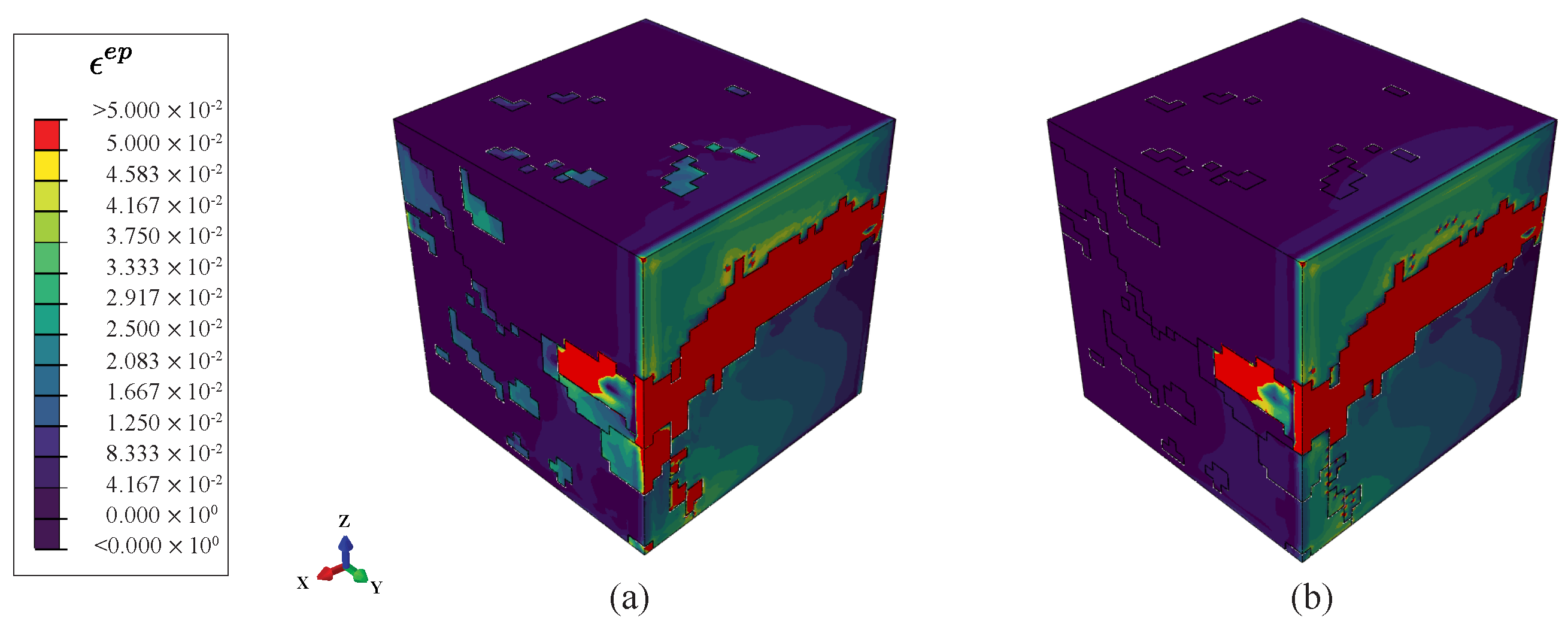
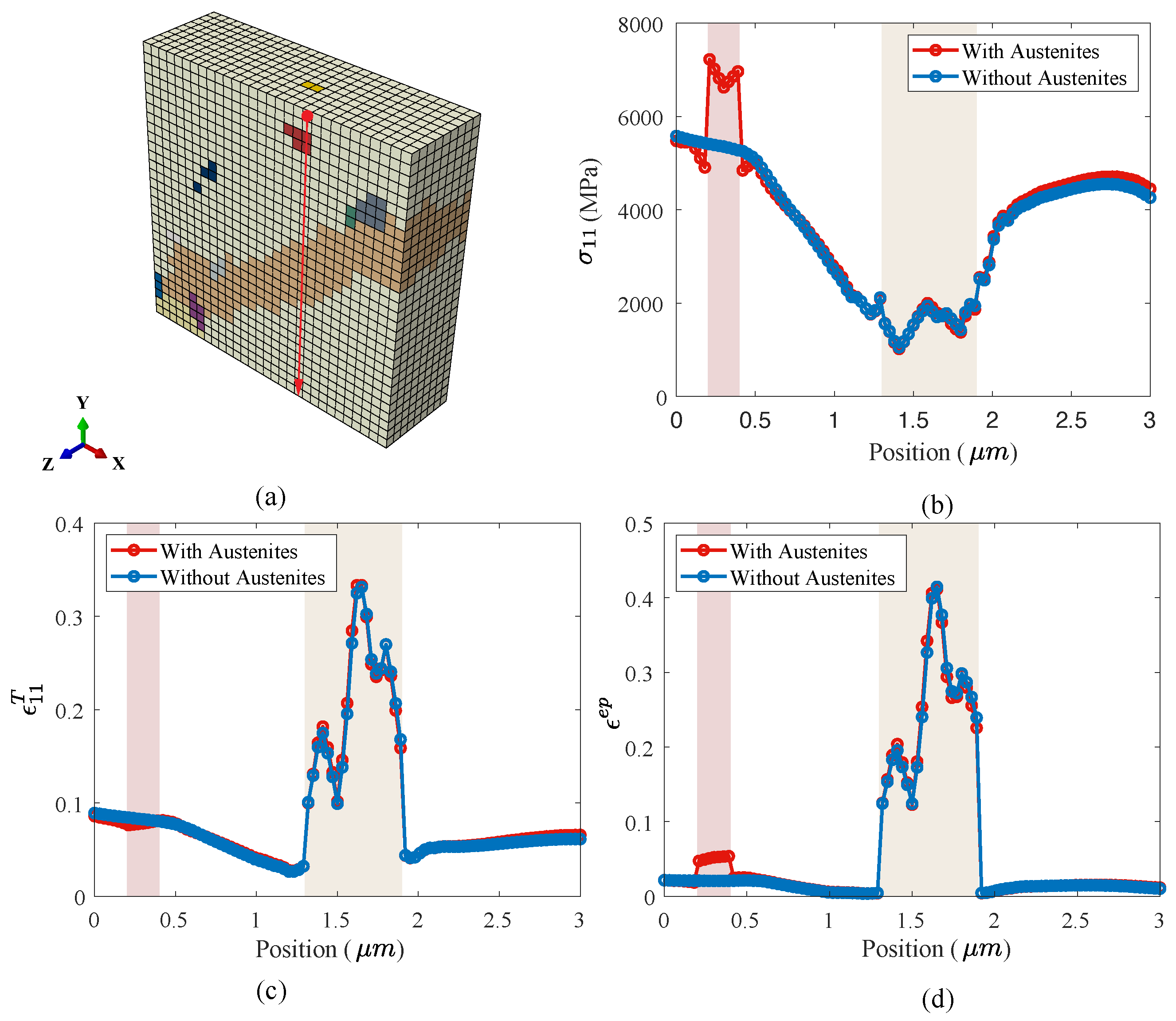
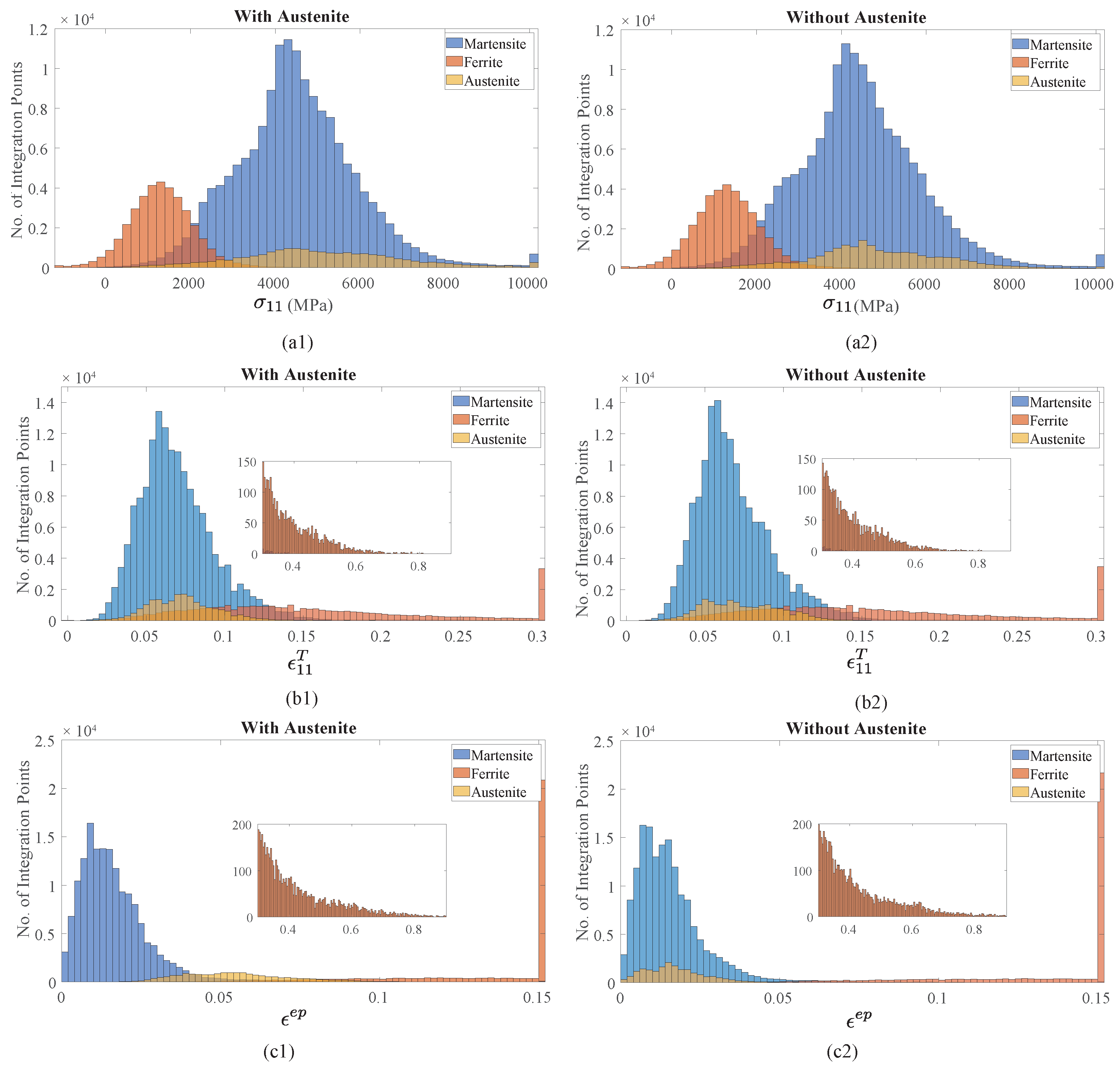

| Recon. resolution (μm) | 1 | 0.5 | 0.25 | 0.1 | 0.08 | 0.05 |
| Mesh size (μm) | 1.0 | 0.5 | 0.25 | 0.1 | 0.08 | 0.05 |
| No. of grains | 26 | 184 | 491 | 1170 | 1248 | 1473 |
| No. of C3D8 elements | 270 | 2160 | 18,900 | 311,040 | 609,280 | 2,530,980 |
| No. of nodes | 601 | 4067 | 29,131 | 381,803 | 696,857 | 2,482,194 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, P.; Liu, Y.; Zhang, X. Crystal Plasticity Finite Element Modeling of the Influences of Ultrafine-Grained Austenite on the Mechanical Response of a Medium-Mn Steel. Crystals 2024, 14, 405. https://doi.org/10.3390/cryst14050405
Shen P, Liu Y, Zhang X. Crystal Plasticity Finite Element Modeling of the Influences of Ultrafine-Grained Austenite on the Mechanical Response of a Medium-Mn Steel. Crystals. 2024; 14(5):405. https://doi.org/10.3390/cryst14050405
Chicago/Turabian StyleShen, Pengfei, Yang Liu, and Xiang Zhang. 2024. "Crystal Plasticity Finite Element Modeling of the Influences of Ultrafine-Grained Austenite on the Mechanical Response of a Medium-Mn Steel" Crystals 14, no. 5: 405. https://doi.org/10.3390/cryst14050405
APA StyleShen, P., Liu, Y., & Zhang, X. (2024). Crystal Plasticity Finite Element Modeling of the Influences of Ultrafine-Grained Austenite on the Mechanical Response of a Medium-Mn Steel. Crystals, 14(5), 405. https://doi.org/10.3390/cryst14050405






