Highly Efficient Terahertz Waveguide Using Two-Dimensional Tellurium Photonic Crystals with Complete Photonic Bandgaps
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
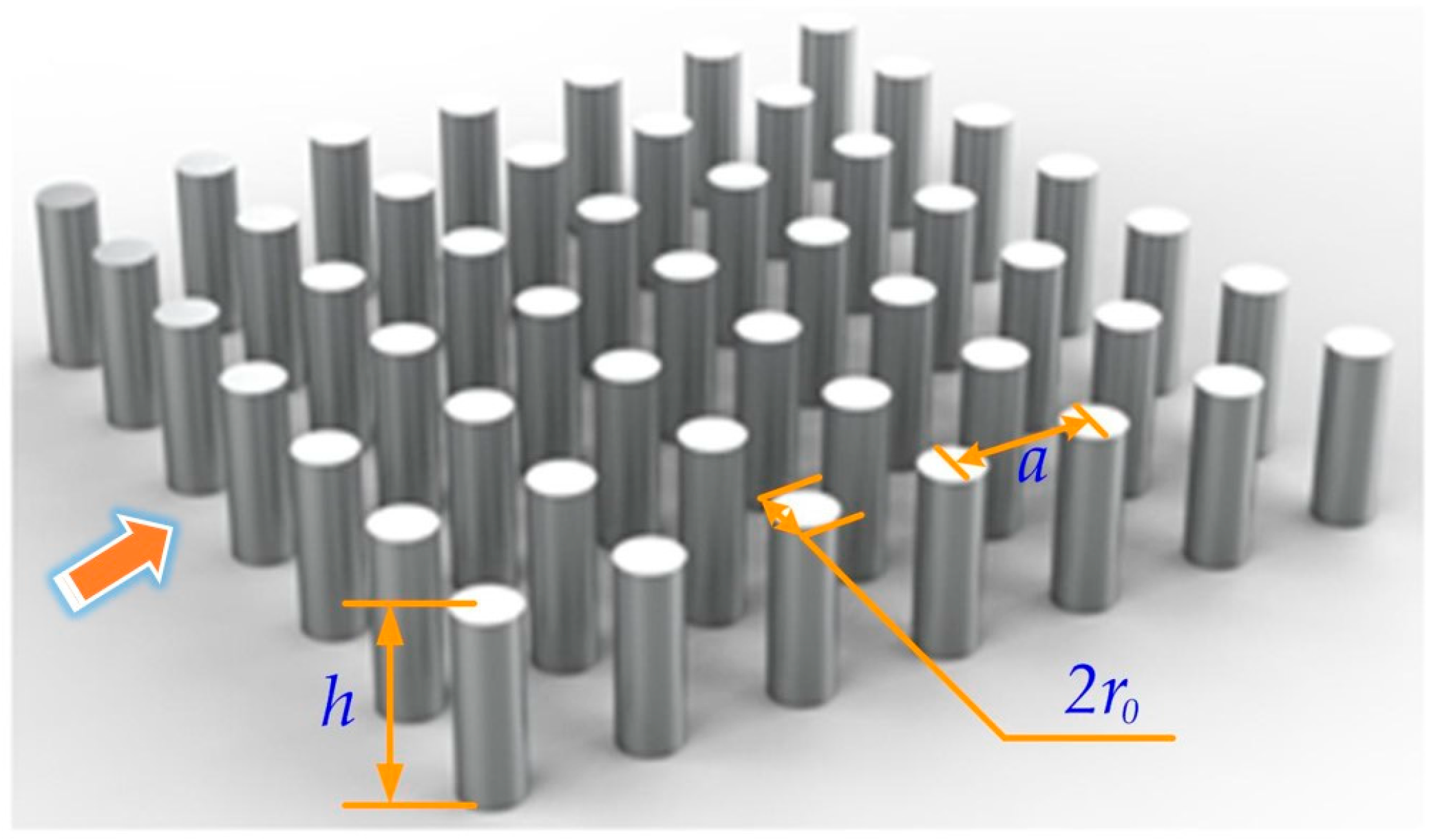
2.2. Complete PBGs of Tellurium PhCs
3. Numerical Results for the Designed THz PhCs Full-Polarized Transmission Line
3.1. Design of PhCs Full-Polarized Transmission Line
3.2. The Functions of PhCs Waveguide
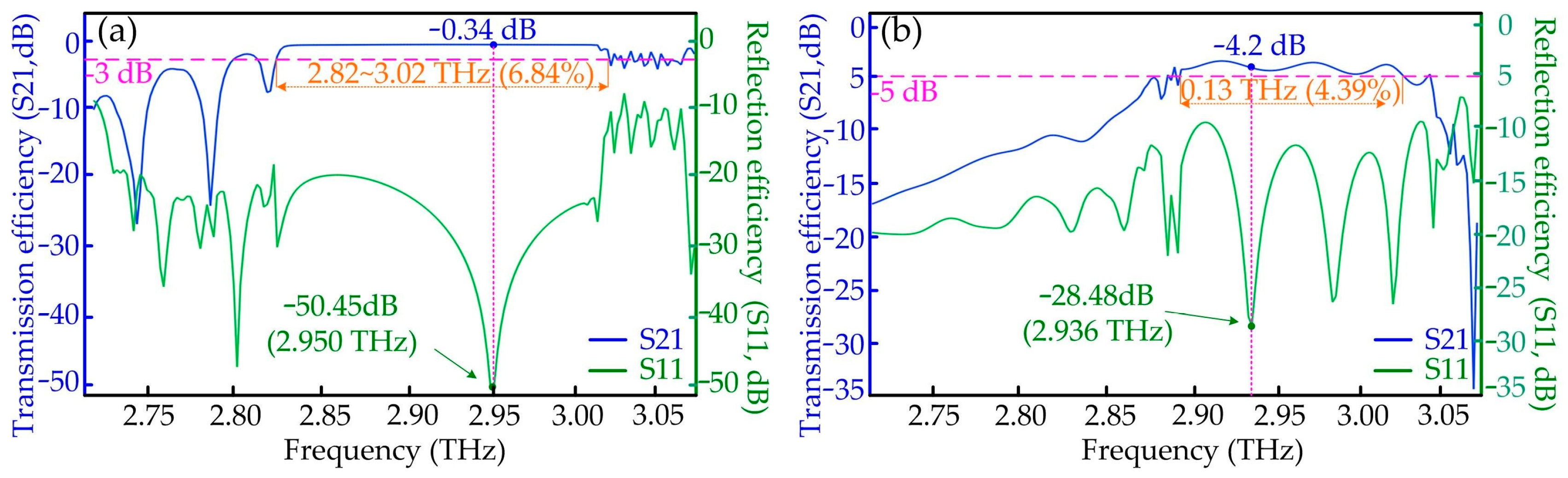
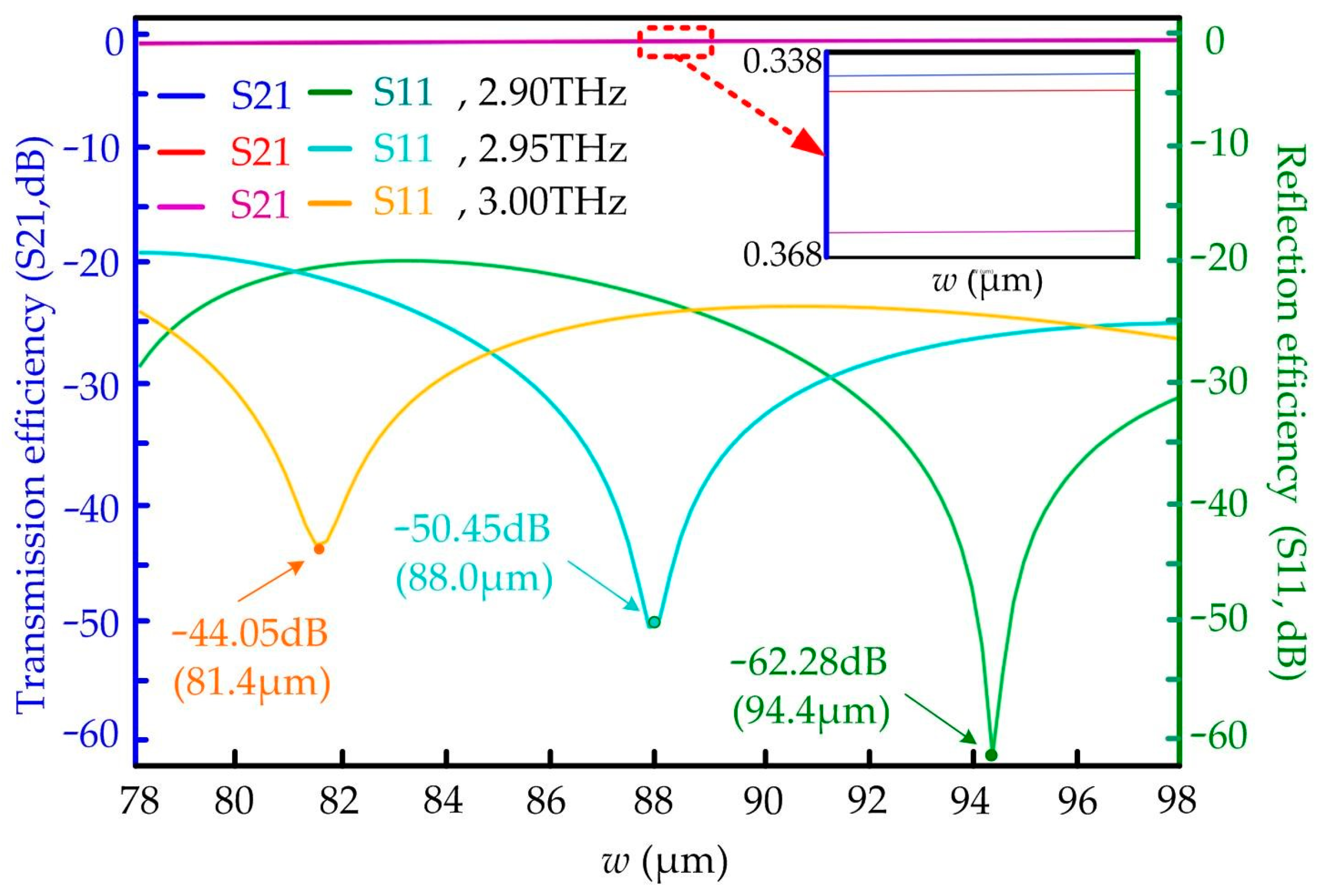
3.3. The Transmission Characteristics of the PhCs Waveguide
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Vision for the 6G Network Ecosystem. Available online: https://5g-ppp.eu/wp-content/uploads/2021/06/WhitePaper-6G-Europe.pdf (accessed on 7 June 2021).
- Chang, L.; Xie, W.; Shu, H.; Yang, Q.F.; Shen, B.; Boes, A.; Perters, D.; Jin, W.; Xiang, C.; Liu, S.; et al. Ultra-Efficient Frequency Comb Generation in AlGaAs-on-Insulator Microresonators. Nat. Commun. 2020, 11, 1331. [Google Scholar] [CrossRef]
- Shih, Y.; Silalahi, H.; Tsai, T.; Chen, Y.C.; Su, J.Y.; Lee, C.R.; Huang, C.Y. Optically Tunable and Thermally Erasable Terahertz Intensity Modulators Using Dye-Doped Liquid Crystal Cells with Metasurfaces. Crystals 2021, 11, 1580. [Google Scholar] [CrossRef]
- Jin, G.; Ren, Y.; Tang, B. Numerical Simulations of Circular Dichroism and Polarization Conversion in VO2-Based Terahertz Metamaterials. Crystals 2023, 13, 437. [Google Scholar] [CrossRef]
- Campion, J.; Xenidis, N.; Smirnov, S.; Ivanov, R.; Oberhammer, J.; Hussainova, I. Ultra-wideband integrated graphene-based absorbers for terahertz waveguide systems. Adv. Electron. Mater. 2022, 9, 8. [Google Scholar] [CrossRef]
- Ohlinger, K.; Lin, Y.; Qualls, J. Maximum and overlapped photonic band gaps in both transverse electric and transverse magnetic polarizations in two-dimensional photonic crystals with low symmetry. J. Appl. Phys. 2009, 106, 063520. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, K.; Liu, H.; Li, R.; Li, L. Dual-band metasurface generating multiple OAM beams independently in full polarizations. Opt. Express 2023, 31, 32637–32651. [Google Scholar] [CrossRef] [PubMed]
- Wen, F.; David, S.; Checoury, X.; Kurdi, M.E.; Boucaud, P. Two-dimensional photonic crystals with large complete photonic band gaps in both TE and TM polarizations. Opt. Express 2008, 16, 12278–12289. [Google Scholar] [CrossRef]
- Ma, B.; Hao, R.; Yan, H.; Jiang, H.; Chen, J.; Tang, K. Deep learning-based inverse design of the complete photonic band gap in two-dimensional photonic crystals. Curr. Nanosci. 2023, 19, 423–431. [Google Scholar]
- Katyba, G.M.; Kurlov, V.N.; Zaytsev, K.I. Terahertz Photonic Crystal Waveguides Based on Sapphire Shaped Crystals. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 576–582. [Google Scholar]
- Soltanian, M.; Amiri, I.S.; Alavi, S.E.; Ahmad, H. Dual-wavelength erbium-doped fiber laser to generate terahertz radiation using photonic crystal fiber. J. Light. Technol. 2015, 3, 5038–5046. [Google Scholar] [CrossRef]
- Liu, L.; Hesler, J.L.; Xu, H.; Lichtenberger, A.W.; Weikle, R.M. A broadband quasi-optical terahertz detector utilizing a zero bias schottky diode. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 504–506. [Google Scholar] [CrossRef]
- Srinivasan, K.; Stadler, B.J.H. Review of integrated magneto-optical isolators with rare-earth iron garnets for polarization diverse and magnet-free isolation in silicon photonic. Opt. Mater. Express 2022, 12, 697–716. [Google Scholar] [CrossRef]
- Wei, Z.; Yan, W.; Qin, J.; Deng, L.; Bi, L. Dysprosium substituted Ce: YIG thin films for temperature insensitive integrated optical isolator applications. Materials 2022, 15, 1691. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Keyvaninia, S.; Shirato, Y.; Mizumoto, T.; Roclkens, G.; Baets, R. Optical isolator for TE Polarized light realized by adhesive bonding of Ce:YIG on silicon-on-insulator waveguide circuits. IEEE Photonic J. 2013, 5, 6601108. [Google Scholar] [CrossRef]
- Tian, H.; Liu, J.; Siddharth, A.; Wang, R.; Blesin, T.; He, J.; Kippenberg, T.; Bhave, S.A. Magnetic-free silicon nitride integrated optical isolator. Nat. Photonics 2021, 15, 828–836. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, B.G.; Zhang, D.G.; Xu, S.X.; Dong, Z.; Zeng, X.K.; Lu, X.W.; Pei, J.H. Magneto-optical isolator based on ultra-wideband photonic crystals waveguide for 5G communication. Crystals 2019, 9, 570. [Google Scholar] [CrossRef]
- Liu, W.; Liu, H.; Sun, X.; Zhang, F. The design of large curved waveguide based on sunflower graded photonic crystal. Photonics 2023, 10, 781. [Google Scholar] [CrossRef]
- Maleki, M.J.; Soroosh, M. A low-loss subwavelength plasmonic waveguide for surface plasmon polariton transmission in optical circuits. Opt. Quantum Electron. 2023, 55, 1266. [Google Scholar] [CrossRef]
- Noori, M.; Soroosh, M. A comprehensive comparison of photonic band gap and self-collimation based 2D square array waveguides. Optik 2015, 126, 4775–4781. [Google Scholar] [CrossRef]
- Lin, Y.; Che, D.; Hao, W.; Dong, Y.; Guo, H.; Wang, J.; Zhang, X. Controllable patterning of metallic photonic crystals for waveguide-plasmon interaction. Nanomaterials 2023, 13, 629. [Google Scholar] [CrossRef]
- Oliver, S.; Smith, C.; Rattier, M.; Benisty, H.; Weisbuch, C.; Krauss, T.; Hondre, R.; Oesterle, U. Miniband transmission in a hotonic crystal coupled-resonator optical waveguide. Opt. Lett. 2001, 26, 1019–1021. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.Y.; Gu, B.Y.; Yang, G.Z. Large absolute band gap in 2D anisotropic photonic crystals. Phys. Rev. Lett. 1998, 81, 2574. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Liu, V.; Fan, S. Ultracompact nonreciprocal optical isolator based on guided resonance in a magneto-optical photonic crystal slab. Opt. Lett. 2011, 36, 4254–4256. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.Y.; Lai, Y.C.; Cheng, Y.C. Spatial beam filtering with auto-cloned photonic crystals. Crystals 2019, 9, 585. [Google Scholar] [CrossRef]
- Jao, R.F.; Lin, M.C. Quantitative analysis of photon density of states for one-dimensional photonic crystals in a rectangular waveguide. Crystals 2019, 9, 576. [Google Scholar] [CrossRef]
- Duan, S.Q.; Chen, Y.P.; Li, G.Z.; Zhu, C.Y.; Chen, X.F. Broadband polarization beam splitter based on a negative refractive lithium niobate photonic crystal slab. Chin. Opt. Lett. 2016, 14, 042301–042304. [Google Scholar] [CrossRef]
- Pligovka, A.; Poznyak, A.; Norek, M. Optical Properties of Porous Alumina Assisted Niobia Nanostructured Films–Designing 2-D Photonic Crystals Based on Hexagonally Arranged Nanocolumns. Micromachines 2021, 12, 589. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Zhang, D.; Wang, Y.; Hong, B.; Shu, G.; He, W. A Terahertz Circulator Based on Magneto Photonic Crystal Slab. Photonics 2023, 10, 360. [Google Scholar] [CrossRef]
- Hasanuzzaman, G.; Rana, S.; Habib, M.S. A novel low loss, highly birefringent photonic crystal fiber in THz regime. IEEE Photonics Technol. Lett. 2016, 28, 899–902. [Google Scholar] [CrossRef]
- Fan, F.; Chang, S.J.; Niu, C.; Hou, Y.; Wang, X.H. Magnetically tunable silicon ferrite photonic crystals for terahertz circulator. Opt. Commun. 2012, 285, 3763–3769. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.G.; Xu, B.G.; He, W.L.; Ian, H. Ultra-wideband terahertz circulator with a ferrite-sphere filled triangle photonic crystal. Mater. Sci. Eng. B 2022, 277, 115603. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.G.; Xu, B.G.; Dong, Z.; Zeng, X.K.; Pei, J.H.; Xu, S.X.; Xue, Q. Four ports double Y-shaped ultra-wideband magneto-photonic crystals circulator for 5G communication system. IEEE Access 2019, 7, 120463–120474. [Google Scholar] [CrossRef]
- Dmitriev, V.; Portela, G.; Martins, L. Photonic crystal-based circulators with three and four ports for sub-terahertz region. Photonic Netw. Commun. 2017, 33, 303–312. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, B.G.; Chang, K.; Huang, H.; Xu, Z.; He, W.; Wang, W. Band Broadening of Terahertz Photonic Crystals Circulator Using Two Symmetrical Hexagonal Aluminum Sheets. Crystals 2023, 13, 779. [Google Scholar] [CrossRef]





| Literature | Wavelength | Transmission | Insertion Loss |
|---|---|---|---|
| [18] | 0.85, 1.31, 1.55 μm | above 90 percent | Less than 10 percent |
| [19] | 6 to 9.4 μm | above 93.5 percent | 0.029 dB/μm |
| [20] | 1.55 μm | above 90 percent | Less than 10 percent |
| Our data | 101.7 μm | above 92.5 percent | 0.34 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Feng, L.; Huang, H.; Zeng, Z.; Liu, Y.; Liu, X.; Li, X.; Yang, K.; Zheng, Z.; Xu, B.; et al. Highly Efficient Terahertz Waveguide Using Two-Dimensional Tellurium Photonic Crystals with Complete Photonic Bandgaps. Crystals 2024, 14, 518. https://doi.org/10.3390/cryst14060518
Wang Y, Feng L, Huang H, Zeng Z, Liu Y, Liu X, Li X, Yang K, Zheng Z, Xu B, et al. Highly Efficient Terahertz Waveguide Using Two-Dimensional Tellurium Photonic Crystals with Complete Photonic Bandgaps. Crystals. 2024; 14(6):518. https://doi.org/10.3390/cryst14060518
Chicago/Turabian StyleWang, Yong, Luyao Feng, Hongwei Huang, Zhifeng Zeng, Yuhan Liu, Xiaotong Liu, Xingquan Li, Kaiming Yang, Zhijian Zheng, Biaogang Xu, and et al. 2024. "Highly Efficient Terahertz Waveguide Using Two-Dimensional Tellurium Photonic Crystals with Complete Photonic Bandgaps" Crystals 14, no. 6: 518. https://doi.org/10.3390/cryst14060518
APA StyleWang, Y., Feng, L., Huang, H., Zeng, Z., Liu, Y., Liu, X., Li, X., Yang, K., Zheng, Z., Xu, B., He, W., Zhan, S., & Wang, W. (2024). Highly Efficient Terahertz Waveguide Using Two-Dimensional Tellurium Photonic Crystals with Complete Photonic Bandgaps. Crystals, 14(6), 518. https://doi.org/10.3390/cryst14060518






