Abstract
We present an analysis of α-helix folding in the coarse-grained coordinate of number of formed helical hydrogen bonds (NHBs) for four alanine peptides (ALA)n, with n = 5, 8, 15, and 21 residues. Starting with multi-microsecond all-atom molecular dynamics trajectories in aqueous solution, we represent the system dynamics in a space of between four (for ALA5) and twenty (for ALA21) hydrogen-bonding microstates. In all cases, transitions changing the hydrogen bond count by 1–2 dominate and the coil formation, NHB 1 → 0, is the fastest process. The calculation of global maximum weight paths shows that, when analyzed at a sufficiently long lag time, folding in the NHB coordinate is consecutive, with direct folding, 0 → 3, for ALA5 and bottlenecks at transitions 4 → 6 for ALA8, 0 → 5 for ALA15, and 0 → 9 for ALA21. Further coarse-graining to 2–4 dimensions was performed with the optimal dimensionality reduction method, allowing the identification of crucial folding intermediates and time scales of their formation in ALA8, ALA15, and ALA21. The detailed analysis of hydrogen bonding patterns revealed that folding is initiated preferentially at both peptide termini. The kinetic model was also used to estimate diffusion and friction coefficients for helix propagation. The description of the helix formation process in the hydrogen bonding coordinate NHB was in good general agreement with the experimental data and qualitatively similar to previous kinetic models of higher dimensions based on structural clustering. Use of the low-dimensional hydrogen bonding picture thus provides a different, complementary way of describing the complex and fascinating mechanism of helix formation.
1. Introduction
Hydrogen bonds are the outstanding features of protein secondary structures, with specific patterns defining helices and sheets [1]. It is thus natural to model the properties of these elements through hydrogen bond analysis. In an analogy with the description of protein folding through native contacts [2] and earlier studies using helix folding statistical thermodynamics through helix nucleation and propagation [3], we propose here an approach to describing helix kinetics in terms of hydrogen bond breaking and formation in a coarse-grained representation.
Due to the importance of helical structures in biology, helix folding has been the subject of much experimental and computational work. Experimentally, folding times from tens to hundreds of nanoseconds have been observed for peptides of various sizes [4,5,6]. A time scale of 50 ns for helix elongation has been estimated [7]. Higher melting temperatures and slower relaxation in the center relative to termini [8,9,10] and directional folding from the N- towards the C-terminus [11] have been observed.
Atomistic computer simulations have contributed significant microscopic insights into helix dynamics in general and folding in particular [12]. Among applied methods are molecular dynamics (MD), replica exchange, milestoning [13,14,15] and Markov state modeling [11]. We have previously undertaken joint experimental and computational studies for model peptides, following the structure, dynamics, and pathways of their folding. This included studying the influence of force field, peptide length, and pH on the energy landscape [16,17]. Recently, we performed extensive MD simulations of a series of alanine homopeptides with lengths of 5, 8, 15, and 21 residues: ALA5, ALA8, ALA15, and ALA21 [18]. We found an increase in helix content from 6% to 60% and a slowing of relaxation from 2 to 500 ns with peptide length. The shorter peptides had different folding landscapes than the longer ones and specific folding intermediates were detected in the longer systems [18].
In this work, we employ the multi-microsecond atomistic MD trajectories of ALA5, ALA8, ALA15, and ALA21 at 300 K, as described previously [18], with some new extended simulations for the largest ALA21 system (see Section 2—Methods). Rather than structurally clustering the trajectories, as was undertaken previously, we use the natural variable of the number of formed helical hydrogen bonds (NHBs) to define the basic structural microstates. An appropriate lag time is applied when analyzing transitions to smooth out fast fluctuations and focus on the slowest processes. This allows a simplified analysis of hydrogen bond dynamics in helical systems, with several interesting features. We find that a majority of transitions occur for NHB changes of and . We calculate global maximum weight paths in the hydrogen bond space, finding consecutive folding, a direct coil-to-helix transition in ALA5, and specific bottleneck transitions for the longer peptides. An additional level of coarse-graining is then applied through the optimal dimensionality reduction method to generate even more simplified kinetic models of the folding process. These models reflect the main features from the previous structural clustering analysis and also provide new structural insights. Finally, we map the hydrogen bond kinetics on a diffusion model to provide alternative estimates of conformational diffusion rates and internal friction for helix propagation. Our investigation presents an alternative picture of helix folding, using the natural coordinate of hydrogen bond number to uncover new microscopic details of this crucial biological process.
2. Methods
The simulated peptides were Ac-Ala5-NH2 (ALA5), Ac-Ala8-NH2 (ALA8), Ac-Ala15-NH2 (ALA15), and Ac-Ala21-NH2 (ALA21). The molecular dynamics (MD) trajectories were generated at 300 K in TIP3P water and Na+ and Cl− ions at 0.15 M concentration, as described previously [18]. For each system, there were two trajectories starting from the helical (trajectory h) and extended (trajectory e) structures, each being 5 in length for ALA5, 10 for ALA 8, 10 for ALA15, and 20 for ALA21 [18]. To improve sampling for ALA21, three additional 20 trajectories were created, starting from the structures selected from a 1 simulation at 500 K, denoted as b, c and d. The system details are presented in the Supplementary Materials. The MD simulations were performed with GROMACS 5.1.4 [19,20] using the CHARMM36m force field [21] and TIP3P water model [22]. A time step of 2 fs was employed under conditions of constant number of particles, volume and temperature (NVT), the temperature of 300 K was maintained by velocity scaling. Nonbonded cutoffs were 1.2 nm, and the Particle–Mesh Ewald (PME) method [23] was used to account for long-range electrostatic interactions.
Alpha helical hydrogen bonds’ distance time series were calculated for all peptides C=O of residue i and the peptide NH of residue i + 4. In order to smooth out the data, each hydrogen bond was counted as fully formed for O…N distance below 3.2 Å (weight of 1) and fully broken for distances above 4.0 Å (weight of 0). At intermediate distances, the bond was partially formed, with an intermediate weight obtained from a cubic interpolation. The weights for all helical hydrogen bonds were then added up in order to obtain the value of our reaction coordinate, NHB (the total number of present alpha helical hydrogen bonds). Our blocked peptides had maximum numbers of helical hydrogen bonds (MAXHB) of 3, 6, 13, and 19 for ALA5, ALA8, ALA15, and ALA21, respectively. The helix fraction f for each trajectory was calculated as the average of the ratio NHB(t)/MAXHB, where NHB(t) is the number of formed helical h-bonds at time t. The structures of the helical conformations of the peptides are shown in Figure 1, which also illustrates the hydrogen bonds present.

Figure 1.
Three-dimensional structures of helical conformations of the studied peptides, with the backbone depicted by ribbons, and terminal blocking groups and sidechains as sticks. Colors are gold for C, red for O, blue for N, and white for H atoms. Standard helical hydrogen bonds are shown as blue-dashed lines; additional hydrogen bonds due to blocking groups are shown as orange-dashed lines. (A) ALA5. (B) ALA8. (C) ALA15. (D) ALA21. Figures created by USCF ChimeraX [8].
The kinetic model analysis started in the space defined by the variable NHB, the total number of helical hydrogen bonds. Thus, the space was of 4 dimensions for ALA5 (NHB from 0 to 3), 7 for ALA8 (NHB from 0 to 6), 14 for ALA15 (NHB from 0 to 13), and 20 for ALA21 (NHB from 0 to 19). Initial kinetic matrices and transition matrices were calculated from the transitions and residence times in the NHB space using the moving window count method based on the data processing used in MSM [24]. The lag time was chosen so that the slowest relaxation agreed with the slow correlation time of the global properties of MD [25] (see Supplementary Materials for details). Finally, kinetic coarse-graining was performed using PCCA+ [26] to lower dimensionality further to 2–4 dimensions, and effective rates were determined with optimal dimensionality reduction (ODR) [27]. Committor values were calculated with the EMMA package transition path theory tool [28].
Global maximum weight paths (GMWPs) for the kinetic networks defined by hydrogen bond transitions were calculated using the recursive Dijkstra algorithm described by Elber et al. [29]. The initial state was NHB = 0 and the final state was NHB = MAXHB for each peptide. The total number of transitions between microstates, proportional to the reactive flux and symmetrized to ensure detailed balance [30], were used as edge weights (see Supplementary Materials).
To analyze diffusion and friction for helix formation, we converted the kinetic equation to a diffusion equation, as described by Bicout and Szabo [31]. We used our data for rate constants and populations to estimate local diffusion coefficients for the consecutive transitions along the helix folding path. Diffusion coefficients were converted to friction coefficients through the Einstein relation [32] , with representing the Boltzmann constant and T the absolute temperature. Equations and method details are described in more detail in the Supplementary Materials.
3. Results and Discussion
The basic trajectory properties, including helix content, relaxation times, and times for folding and unfolding, are presented in the Supplementary Materials. These results are the same as previously reported for ALA5, ALA8, and ALA15, and are updated here to incorporate the extended simulations for ALA21 [18]. Briefly, the helix fraction based on hydrogen bonding was about 3% for ALA5, 6% for ALA8, 25% for ALA15, and 53% for ALA21.
The slow relaxation times found in the autocorrelation functions of the global variables in the MD trajectories were 2.4, 13.2, 110, and 340 ns, for ALA5, ALA8, ALA15, and ALA21, respectively, and were assigned to global peptide folding. Faster relaxations, assigned to individual hydrogen bond fluctuations, were estimated at 0.2, 0.8, 2, and 10 ns, respectively. Combining helix fractions with the slow relaxations yielded the folding and unfolding times and rates (see Supplementary Materials). The peptide folding times were 40, 145, 390, and 610 ns, while the unfolding times were 2.6, 14, 140, and 770 ns for ALA5, ALA8, ALA15, and ALA21, respectively. Peptide trajectories exhibit multiple folding and unfolding events, which have been discussed in more detail previously [18]. As expected, the time scales of the global folding transition increased with peptide length. The rates for ALA21 are comparable to those found for the WH21 peptide, which has a similar length and a more diverse amino acid composition [25]. The rates for ALA5 are comparable to measurements for the helical pentapeptide WH5 [33,34].
Table 1 shows a comparison of the basic peptide kinetic parameters obtained with different methods. The slow relaxation times can be well determined from MD data, and are reproduced in the RMSD clustering by the adjustment of the cluster radius [18] and in HB kinetics by the adjustment of lag-time (Section 2—Methods). Thus, these results agree well for all methods. Notably, the average folding relaxation is 340 ns for ALA21 from five 20 MD trajectories, lower than the 500 ns previously reported based on two trajectories. A single fast relaxation time is difficult to determine from the MD data due to presence of processes at multiple time scales [35], which is denoted by prefacing the MD values with the ‘~’ symbol. While MD relaxations are based on the analysis of millions of structures with picosecond time resolution, kinetic models involve significant coarse-graining, based on 10–200 structures for RMSD clustering with an adjustable core radius and 4–20 for hydrogen bond count with an adjustable lag-time. As a result, the fast motions are filtered out in the last two approaches, and estimates for each peptide increase (from 0.2 to 1.6 ns for ALA5, from ~1 to ~5 ns for ALA8, from 2 to 18 ns for ALA15, and from 10 ns to 100 ns for ALA21) between the direct MD method and the models. Interestingly, the estimates of from the trajectory discretization by RMSD and NHB are comparable.

Table 1.
Relaxation times and in alanine homopeptides. Molecular dynamics results in MD C(t) column are obtained from two exponential fits of autocorrelation functions C(t) of global variables in MD trajectories, such as distance from helix state and number of hydrogen bonds (NHBs) (details in Supplementary Materials). RMSD column shows slowest time scales from kinetic modeling, obtained by discretizing MD trajectories based on C atom RMSD clustering with selected cluster radius, as described in [18]. NHB column shows slowest relaxations from kinetic modeling obtained from hydrogen bond count discretization with selected lag-time in this work, as described in Methods and below. Units: ns.
3.1. Folding Kinetics in Hydrogen Bond Space
The populations of the states with different helical hydrogen bond counts are shown in Figure 2. Interestingly, the coil state (NHB = 0) is the most highly populated for all peptides. This is true even for ALA21, which has a helix fraction of 53%. At equilibrium, the microstate populations and transition rates are related by detailed balance: [27,30]. Thus, the population ratios from Figure 2 may be used to explain the ratios of the microscopic rate constants provided in Table 2 and Table 3 and the Supplementary Materials.
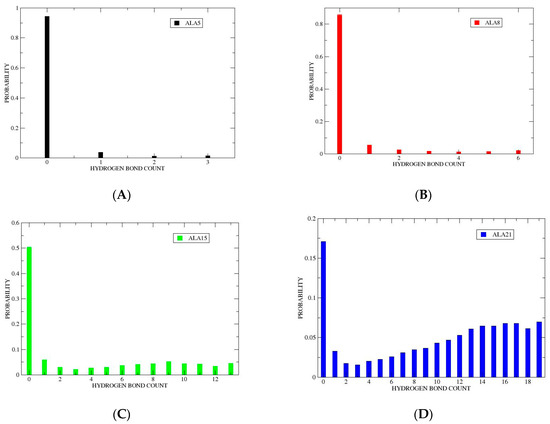
Figure 2.
Microstate populations in alpha-helical hydrogen bond space. (A) ALA5 from 2 × 5 s MD trajectories. (B) ALA8 from 2 × 10 s MD trajectories. (C) ALA15 from 2 × 10 s MD trajectories. (D) ALA21 from 5 × 20 s MD trajectories.

Table 2.
Rate constants for transitions in hydrogen bond space of ALA5 in units of . The value of describes the rate of transition for microstates The diagonal elements are . State 0 corresponds to the fully unfolded form, NHB = 0, and state 3 to the fully folded form, NHB = 3.

Table 3.
Rate constants for transitions in hydrogen bond space of ALA8 in units of . Details are listed in Table 2. State 0 corresponds to the fully unfolded form, NHB = 0, and state 6 to the fully folded, NHB = 6.
Table 2 shows the full kinetic matrix of ALA5 in the hydrogen bond space. The main characteristic of this matrix is the much faster rate of hydrogen bond breaking/unfolding (upper triangle) relative to forming/folding (lower triangle). This may be explained by the very high population of the fully unfolded form of this peptide (94% for i = 0). The second interesting feature is the fall of the transition rate with the hydrogen bond difference between states: Thus, the highest rate is , describing transition NHB = 1, i.e., the unfolding of the state with a single h-bond to form the coil with NHB = 0. The unfolding processes NHB = 2 and NHB = 3 are also fast, with rates of about This picture is in accord with our previous study, where an important contribution of direct helix coil transitions was found in ALA5 dynamics [18]. For folding, the rate of the 0 transition is the slowest, with rates increasing to for 1 3 and for 2 3. Thus, generally, the fastest transitions are between NHB = and . Only for states 2 and 3, which have comparable populations (both ca. 1%), do we find similar folding and unfolding rates: and For comparison, the global unfolding and folding rates for ALA5 are 390 and ca 26 (see above).
Table 3 shows the full kinetic matrix of ALA8 in the hydrogen bond space. This matrix exhibits somewhat different features than ALA5. Overall, there tend to be higher rates for unfolding relative to folding and higher rates for smaller changes in the NHB count. For ALA8, the fastest process is also NHB = 1, with a rate of , and NHB = 2 and 3 are also among the fastest. However, the transitions among the states with the highest h-bond count (i = 4–6, NHB = 4–6) occur at similar rates in the forward and reverse directions, e.g., and . This may be explained by the similarity of their populations (all ca. 1.5%, see Figure 2). The full direct unfolding of NHB = 6 is present, but with a much lower rate of The slowest process is the full direct folding of NHB = 0, with , which is not statistically different from zero, given the trajectory length. The global folding and unfolding rates for ALA8 are 69 and 7 (see above).
The kinetic matrices for ALA15 () and ALA21 () are shown in the Supplementary Materials. These display some new features compared to ALA8. The fastest rates are still for NHB = 1, with for ALA15 and for ALA21, as the fully unfolded state remains the most highly populated (53% for ALA15 and 17% for ALA21). However, the transition rates become more symmetric within the set of more structured states (i > 4), with i rates becoming comparable, as these states exhibit comparable low populations. Corresponding to the dip in the populations in the intermediate range (i = 4–6 for ALA15 and i = 3–10 for ALA21, see Figure 2), there is also a decrease in transition rates between states.
Thus, there is an overall trend for the fastest process being the formation of the coil state, i = 0, from states with a relatively small number of h-bonds (i = 1–2 for ALA5, i = 1–9 for ALA21). The unfolding rates are faster than folding for the states close to the coil, while the folding and unfolding transition speeds become comparable for states close to the full helix. A general trend is that rates become slower with an increasing difference in h-bond count k. This is in accord with our previous analysis of correlations of individual h-bond fluctuations in helical peptides, where significant correlations were found only for the 2–3 nearest neighbor hydrogen bonds [18]. Finally, all rates decrease with peptide length.
3.2. Global Maximum Weight Paths
The global maximum weight path (GMWP) is an insightful way of analyzing discrete kinetic networks [29]. Briefly, kinetic networks may be represented by directed graphs, with edges assigned weights equal to the reactive flux passing between the two vertices forming the edge. Any path between an initial state s and final state f may be assigned a weight equal to the minimal edge weight along the path. This edge is called a bottleneck or edge of minimum weight (EMW) along the path. The maximum weight path (MWP) between s and f is then defined as the path with the highest weight of its EMW. Finally, the global maximum weight path GMWP is introduced as a path in which each sub-path is also an MWP. Here, we use the total transition counts as edge weights (see Section 2—Methods, and Supplementary Materials).
The GMWPs for helix folding in the hydrogen bond space are presented in Figure 3. For the smallest ALA5 peptide, we find a direct folding GMWP from coil to full helix, which may be denoted by in the NHB space. This transition/edge is also the bottleneck for ALA5 folding. For ALA8, the GMWP is , passing through the intermediate with NHB = 4. Here, the bottleneck is . In the case of ALA15, the GMWP is , i.e., the state with NHB = 5 forms directly from the coil, followed by the sequential addition of further hydrogen bonds, and the bottleneck is . The GMWP for ALA21 is the most complex, following the path of , with the coil first forming the NHB = 9 intermediate, after which hydrogen bonds are added in groups of one, two or three. In this case, the bottleneck is .

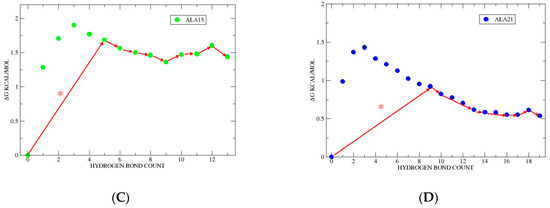
Figure 3.
Global maximum weight paths (GMWPs), shown with arrows, overlaid on potentials of mean force (PMFs), shown with circles. PMFs in hydrogen bond space are given by , with R representing the gas constant, T = 300 K the temperature, the population of state i, and the population of the most stable state. Bottleneck edges are marked with asterisks ‘*’. (A) ALA5 GMWP is , same as bottleneck. (B) ALA8 GMWP is and bottleneck is . (C) ALA15 GMWP is and bottleneck is . (D) ALA21 GMWP is and bottleneck is .
All paths represent monotonic increases in the number of hydrogen bonds. As expected, the path complexity increases with peptide length, with ALA5 folding directly, ALA8 exhibiting a single intermediate, and ALA15 and ALA21 passing through multiple partly folded states. Except for the case of ALA5, the first intermediates on the GMWPs correspond to the state with about half of the hydrogen bonds formed: NHB = 4 for ALA8, NHB = 5 for ALA15, and NHB = 9 for ALA21.
3.3. Kinetic Models
To gain further insight into the hydrogen bond dynamics, we performed kinetic coarse-graining with optimal dimensionality reduction (ODR [25]) for the four studied alanine homopeptides. The starting points were the discretized MD trajectories in the hydrogen bond count space (NHB), obtained as described in the Methods. Lower dimensional models with N = 2–4 aggregate states were then generated with ODR. Details of the procedure and results are in the Supplementary Materials. The assignment of helix and coil states is easy with NHB discretization—the helix aggregate state is the one containing the microstate with NHB = MAXHB, i.e., the maximum possible number of helical h-bonds, while the coil aggregate state contains microstate NHB = 0. The relaxation times obtained from the ODR models are in very good agreement with the times obtained with the full NHB kinetic matrix (Table 1), typically differing by less than 10% in the two slowest relaxations (details in Supplementary Materials).
Two-state models (N = 2). Summaries of the lowest levels of coarse-graining, found with the two-state models, are given in Table 4 and Figure 4. These models are in good accord with the results extracted directly from the MD trajectories (above and Supplementary Materials). The rates agree quite well, while the free energies are within 0.1–0.4 kcal/mol. Thus, most of our two-state models capture the system structure and dynamics main features, with the additional insight of the partition of microstates into the helix and coil aggregate sets. There are two noteworthy features of the aggregate sets: heterogeneity and contiguity. The helix set covers the fully helical structure and neighboring partly folded forms: 1–2 h-bonds for ALA5, 4–6 for ALA8, 6–13 for ALA15, and 7–19 for ALA21. The coil set includes microstates with the lowest numbers of hydrogen bonds: 0–1, 0–3, 0–5, and 0–6 for ALA5, ALA8, ALA15, and ALA21, respectively.

Table 4.
Time constants for folding are inverses of the reduced-dimension effective rate matrix R [27] off-diagonal elements in ns. The folding free energy = G(helix) − G(coil) is calculated from the populations of the aggregate states (ODR) and compared to the corresponding microstate populations obtained directly from trajectories (MD) at 300 K kcal/mol (details in Supplementary Materials).
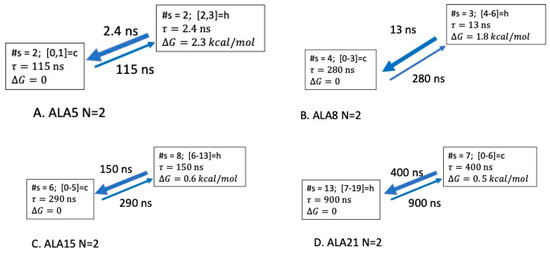
Figure 4.
Optimal dimensionality reduction (ODR) coarse-grained kinetic models of dimension N = 2 for the ALAn peptides. (A) ALA5 model based on discretization with lag time . (B) ALA8 model with . (C) ALA15 model with . (D) ALA21 model with .
Properties of coarse-grained models of the four peptides with N = 3–4 aggregate states are shown in Figure 5, Figure 6, Figure 7 and Figure 8 and described below.
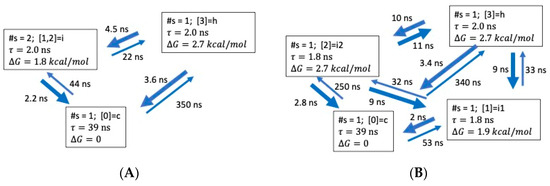
Figure 5.
Optimal dimensionality reduction (ODR) coarse-grained kinetic models for ALA5 with lag time . (A) N = 3 aggregate states. (B) N = 4 aggregate states.
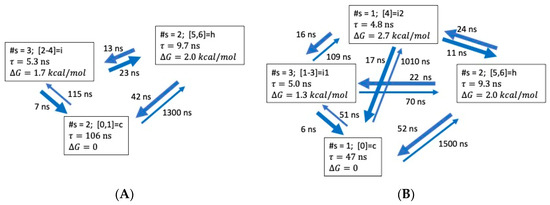
Figure 6.
Optimal dimensionality reduction (ODR) coarse-grained kinetic models for ALA8 with lag time . (A) N = 3 aggregate states. (B) N = 4 aggregate states.
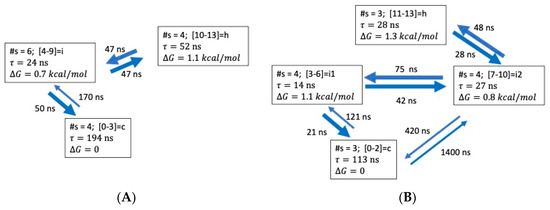
Figure 7.
Optimal dimensionality reduction (ODR) coarse-grained kinetic models for ALA15 with lag time . (A) N = 3 aggregate states. (B) N = 4 aggregate states.
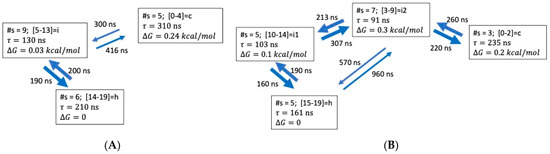
Figure 8.
Optimal dimensionality reduction (ODR) coarse-grained kinetic models for ALA21 with lag time . (A) N = 3 aggregate states. (B) N = 4 aggregate states.
ALA5. Here, the unfolded or coil state is the most highly populated, and the helix is a minor conformer (3%). In the N = 3 state model (Figure 5A), the helix and coil are represented as single microstates; NHB = 0 for the coil and NHB = 3 for the helix, while the intermediate state has 1–2 h-bonds. In the N = 4 state model (Figure 5B), which for ALA5 describes the full kinetics, there are two intermediate states, with 1 and 2 h-bonds, respectively. The intermediates have lifetimes of ca. 2 ns and of 2–3 kcal/mol, comparable to the helix. The unfolding rates are significantly faster than the folding rates. All states are connected by transitions. The direct folding/unfolding path from coil to helix is present at all levels of detail (N = 2–4).
ALA8. Here, the helix is also a minor conformer (7%). In the N = 3 model (Figure 6A), the helix is represented by microstates with NHB = 5, 6, the coil with NHB = 0, 1, and the intermediate by NHB = 2–4. In the N = 4 case (Figure 6B), the coil involves only NHB = 0, while the two intermediates contain NHB = 1–3 and NHB = 4. The helix aggregate state is thus heterogenous. The intermediates have lifetimes of ca. 5 ns, shorter than the helix (9–10 ns) or coil (50–100 ns). The intermediate free energies are about 1–2 kcal/mol above the coil. The unfolding rates are faster than the folding rates. All states are connected by transitions and a direct folding/unfolding path from coil to helix is possible, but with a low flux.
ALA15. The population of the helix is quite high for this peptide (25% helix fraction). In the N = 3 model (Figure 7A), the helix involves microstates with NHB = 10–13, the coil NHB = 0–3, and the intermediate NHB = 4–9. There emerges a simple consecutive folding pathway from the coil through the intermediate and then to the helix. For the N = 4 model (Figure 7B), the helix corresponds to NHB = 11–13 and the coil to NHB = 0–2. A consecutive pathway emerges from the coil to i1 (NHB = 3–6), then to i2 (NHB = 7–9) to the helix. Only in the initial states, coil to i1, is folding significantly faster than unfolding. The intermediate lifetimes are 14–27 ns, comparable to the helix, and their free energies are ca. 1 kcal/mol above the coil.
ALA21. For this longer peptide, the helix is the major conformer, with 53% helix fraction. For the N = 3 model (Figure 8A), the helix consists of microstates NHB = 14–19, the coil of NHB = 0–4, and the intermediate of NHB = 5–13. A consecutive folding path from the coil through the intermediate to the helix can be seen. In the N = 4 model (Figure 8B), the helix has NHB = 15–19, the coil NHB = 0–2, the intermediate i1 NHB = 10–14, and i2 NHB = 3–9. Here, a consecutive folding path is also found from the coil through i1, then to i2, and finally to the helix. The intermediate lifetimes are about 100 ns, somewhat shorter than the helix or coil (200–300 ns). The free energies of the intermediate states are about 0.1–0.3 kcal/mol above the helix.
3.4. Helix Folding Pathways from GMWPs and ODR
Both the GMWPs (Figure 3) and ODR modeling (Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8) showed progressive increases in hydrogen bond formation along the folding paths, with similar but somewhat differing patterns. The GMWP of ALA5, based on reactive flux, represents the single-step direct folding of as the main reaction path, while the ODR models, based on the reaction rates, show several possible paths in ALA5, with some preference for passing through intermediates and no resolved transition state. For ALA8, the GMWP has two stages, , and the bottleneck is the later stage, i.e., the transition. In the kinetic models, the peptide forms through intermediates, including the NHB = 4 state involved in the bottleneck. For N = 4, the NHB = 4 state has a committor value of q = 0.52. Thus, this is essentially a transition state for folding, as q = 0.5 is expected at the transition state [36,37]. In the case of ALA15, the GMWP bottleneck is , followed by the consecutive addition of further hydrogen bonds. The ODR models indicate folding through intermediates with a range of formed h-bonds close to NHB = 5. TPT analysis indicates that the aggregate state with NHB = 6–7, found in the N = 5 state model (data in Supplementary Materials), is close to the transition state, with q = 0.53. In ALA21, the GMWP bottleneck is followed by addition of small batches of hydrogen bonds. The ODR models indicate folding through a range of intermediates with about one half of the possible hydrogen bonds formed. The microstate close to a transition state is NHB = 3–8 (N = 3), with q = 0.504. Thus, while details differ, there is good qualitative agreement between the ODR model transition state and the GMWP bottleneck predictions. As has been discussed, kinetic paths based on reactive flux are considered more reliable than those based on rates [29].
3.5. Structures of the Intermediates: Hydrogen Bond Patterns
In general, a peptide with a total of n possible hydrogen bonds can have a total of states corresponding to individual formed/broken bonds, and a state with k hydrogen bonds formed out of n possible includes different hydrogen bond patterns. The sampled patterns are described in more detail in the Supplementary Materials, and some examples are shown in Table 5 and Table 6. The patterns are encoded as ordered strings of 0/1 values, with 1 denoting a formed and 0 a broken hydrogen bond at a given position. The main feature of the most highly populated patterns in the ALAn peptides is the prevalence of contiguous helix segments formed at the N- and C-terminal. Thus, for ALA5, ‘001′ and ‘100′ have higher populations than ‘010′, while ‘011′ and ‘110′ are more populated than ‘101′. For a high enough NHB value, single helices at the N- and C-terminal are strongly favored: at for ALA8, for ALA15, and for ALA21 (Table 5 and Table 6 and Supplementary Materials).

Table 5.
Populations of all sampled hydrogen bond patterns for ALA5. Patterns given as character strings with ‘0′ for broken and ‘1′ for formed helical hydrogen bonds. Thus, ‘110′ denotes a state with formed h-bonds at positions 1 and 2, and a broken h-bond at 3. Populations are given as fractions of total time spent in a given state. More details in Supplementary Materials.

Table 6.
Populations of selected sampled hydrogen bond patterns for ALA15. Data as described in Table 5. Details in Supplementary Materials. Data sorted by population for each NHB value.
It is interesting to look at the hydrogen bond patterns of the important folding intermediates found in the analysis above. In ALA8, the most populated intermediates with NHB = 4 are ‘111100′ and ‘001111′, followed by ‘011110′. For ALA15 and NHB = 5, the top patterns are ‘1111100000000′, ‘0000111110000′, and ‘0000000011111′. Analogously, in the case of ALA21 and NHB = 9, the most populated patterns are ‘0000000000111111111′, ‘1111111110000000000′, and ‘0000000011111111100′.
Folding intermediates identified previously in kinetic models based on 3D structural clustering also included partly formed N- and C-terminal helices, as well as other forms such as structured turns and compact coils [18]. Thus, there is an overlap between the folding intermediates found in both approaches, but differences in the details are also present.
3.6. Self-Diffusion Constants and Friction Coefficients Associated with Helix Propagation
The rate constants and populations obtained for the hydrogen bonding microstates were used to define a diffusion model based on the Smoluchowski equation [31]. The results are presented in Figure 9 and in the Supplementary Materials. The average diffusion coefficients D were and for the four peptides, ALA5, ALA8, ALA15, and ALA21, respectively. There is a clear trend of slowing diffusion with peptide length. This may be rationalized by the decreasing helix propagation rates with peptide length (see above). Due to the Einstein relationship [32], friction coefficients follow the opposite trend, with average f values of and for the four peptides, respectively. As shown in the Supplementary Materials, there is some variation in and with helix content —diffusion tends to be fastest at the start and end of the folding process, and slowest at the early intermediate stages, with friction exhibiting the inverse trend. Again, this may mostly be explained by the pattern of rate constants.
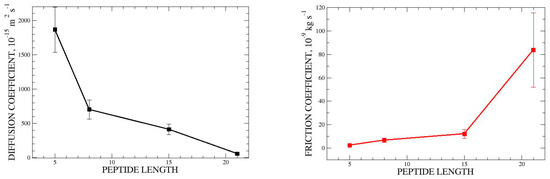
Figure 9.
Average diffusion and friction coefficients of helix propagation for the four simulated alanine peptides. Diffusion coefficients are calculated using the method of Bicout and Szabo [31] and friction coefficients are calculated through Einstein relation [32]. Estimated peptide length change upon helix propagation is d = 0.15 nm (see Supplementary Materials).
It must be noted that the results of D and f are crucially dependent on the value of the parameter d for peptide elongation due to helix propagation. In the Supplementary Materials, we present an expanded discussion and comparison of several strategies for obtaining this parameter, which lead to d being estimated between 0.05 and 0.34 nm [35]. Here, we employ an intermediate value of d = 0.15 nm, which is also consistent with our earlier works. Then, the results obtained here are not only qualitatively, but also quantitatively similar to previously obtained estimates of helical friction coefficients in water and not so far off the corresponding internal friction obtained in the limit of vanishing viscosity. Namely, the averaged values of f in water from Ref. [31] were as follows: and for the four peptides ALA5, ALA8, ALA15, and ALA21, respectively. It must be mentioned, however, that herein these results are obtained from the diffusion models based on the Smoluchowski equation, while in the other works [35] they were obtained from overall folding/unfolding reaction rate constants. The agreement is striking and shows indeed that such theoretically calculated friction coefficients serve as good discriminatory parameters between helical peptides. Their actual values, however, have yet to be experimentally measured.
3.7. Comparison with Experiment
A detailed comparison between alanine-based peptide simulations and experimental data has been presented previously [18]. Here, we reiterate the main findings, focusing on hydrogen-bond-based behavior and including data from the additional ALA21 trajectories. Briefly, the hydrogen-bond-based helix content at room temperature for ALA5 was lower (~3% vs. 20–46%) and that for ALA21 (53% vs. 60%), and was in excellent agreement with the observed values for peptides of a similar size. The global relaxation times were comparable for ALA5 (~2 ns with MD vs. ~10 ns observed) and in excellent agreement for ALA21 (340 with MD vs. 300 ns observed). Faster relaxation components were also in reasonable agreement: ~1.6 vs. ~1 ns for pentapeptides [34] and 10–87 vs. ~20 ns in a 21-residue system [25,38]. A helix propagation rate of ~50 ns measured for a 20-residue alanine-based peptide [7] agrees quite well with our faster ALA21 component. Further, temperature-jump experiments with isotopically edited peptides have shown that the central region of a helix tends to be more stable, with higher melting temperatures and slower relaxations than the termini [8,9,10]. This is in accord with our pattern analysis in Section 3.5, although our results indicate that this might be a result of the overlap of nascent helices forming independently at the N- and C-terminal.
Overall, comparing direct molecular dynamics data, 3D structural clustering models, and experiments, it appears that the simple one-dimensional kinetic analysis of hydrogen bond space is able to realistically represent the helix folding landscape in a low-resolution way. Structural coarse-graining and a focus on the slowest time scale leads to the loss of some details, but the main features of structure and dynamics are reproduced.
4. Conclusions
In this work, we present an approach to a description of alpha-helix folding using hydrogen bonding analysis. Based on multi-microsecond atomistic MD trajectories of model alanine-based peptides ALA5, ALA8, ALA15, and ALA21 at room temperature, we find that a simple picture of helix formation appears at sufficiently long time scales when viewed in terms of the natural variable of the number of formed helical hydrogen bonds (NHBs).
Following native contacts has been found to be a good reaction coordinate for protein folding [2], as well as the basis of successful protein folding models [39,40,41,42] and experimental analyses of folding [43]. However, there are several problems with using this coordinate for -helices. At short time scales of 100 ps to 10 ns, depending on peptide length, helix hydrogen bonds undergo fast formation/breaking fluctuations [18] and folding is non-monotonic in the hydrogen bond count variable [38]. Further, states for which only the hydrogen bond count is specified are highly heterogenous. A peptide with k out of n possible hydrogen bonds formed exhibits sub-states. As shown in our analysis, the picture of helix folding along the hydrogen bonding coordinate becomes significantly simplified when analyzed at time scales long enough to average out the fast fluctuations.
Kinetic matrices in hydrogen bond space indicate that the fastest processes involve the unfolding of the last hydrogen bond and that transitions with small changes in NHBs are dominant. To further characterize the folding pathways, we calculated global maximum weight paths (GMWPs), performed optimal dimensionality reduction (ODR) coarse-graining, and identified transition states. GMWPs indicate a direct folding mechanism for the smallest peptide, ALA5. In the case of ALA8, able to form six helical hydrogen bonds, the folding bottleneck is the transition, corresponding to the formation of the full helix from an NHB = 4 intermediate. For the longer peptides, the bottlenecks are the transition for ALA15 and for ALA21, involving forming intermediates with about half the possible hydrogen bonds present from the coil state. These are followed by the consecutive addition of small batches of hydrogen bonds till the full helix is reached.
An additional level of coarse-graining is applied through optimal dimensionality reduction, generating even more simplified kinetic models of the folding process. These models reflect the main features from the previous structural clustering analysis [18] and also provide new structural insights. Here, direct folding is also detected for ALA5, and important intermediates are identified with 4 hydrogen bonds for ALA8, 6–7 for ALA15, and 3–9 for ALA21. As in previous studies, the helix, coil, and intermediate states exhibit heterogeneity, mostly consisting of multiple basic microstates. A deeper look at sampled structures allows the decomposition of states with a defined total number of hydrogen bonds into separate individual patterns, showing the preferred helix formation at the termini.
Finally, we map the hydrogen kinetics on a diffusion model to provide alternative estimates of conformational diffusion rates and the internal friction of helical peptides, yielding results comparable to previous nanomechanical calculations.
Due to the nature of the coarse-graining procedure, our models mostly represent only the 2–3 slowest modes of motion in the studied peptides. Faster time scales represent the formation of individual hydrogen bonds for shorter systems and folding intermediates for longer ones. These times are also comparable to the faster time constants found directly in molecular dynamics trajectories and previous structure-based kinetic models involving much larger numbers of microstates.
Our findings on helix content, folding times, and helix propagation time scales agree with the available experimental data. The inclusion of more trajectories for the largest ALA21 system led to the improved agreement of models with observations, indicating the excellent performance of the CHARMM36m protein force field with TIP3P water [21].
Our investigation presents an alternative picture of helix folding using the natural coordinate of hydrogen bonding. This presents a different, complementary view of the microscopic details of this crucial biological process. The observed features—folding paths, intermediates, heterogenous ‘helix’ states, and timescales—were similar to those found in previous models. New insights involved the identification of GMWPs and bottlenecks, and the observation of folding initiation at both peptide termini. Finally, we provide a mapping of hydrogen bond kinetics on helix diffusion. These discoveries show that helix folding remains an interesting object of scientific inquiry.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst14060532/s1, Additional details about the simulations and their analysis are provided in the Supplementary Materials.
Author Contributions
Conceptualization, K.K., G.S.J. and R.S.; methodology, K.K., G.S.J. and R.S.; software, K.K.; validation, K.K., G.S.J. and R.S.; formal analysis, K.K.; investigation, K.K., G.S.J. and R.S.; resources, K.K. and R.S.; data curation, K.K.; writing—original draft preparation, K.K.; writing—review and editing, K.K., G.S.J. and R.S.; visualization, K.K. and G.S.J.; supervision, K.K.; project administration, K.K. and R.S.; funding acquisition, R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Science Center, Poland, grant no. 2018/30/M/ST4/00005 for Robert Szoszkiewicz.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
Molecular dynamics simulations were carried out on the bigjay cluster at the Center for Research Computing at the University of Kansas, supported by the NSF grant MRI-2117449, and a computer cluster at the Warsaw University Center for Biological and Chemical Research. The work of RS was supported by the National Science Center, Poland, grant no. 2018/30/M/ST4/00005. We wish to thank Ron Elber from the University of Texas at Austin, for providing the computer codes for the GMWP calculations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kuriyan, J.; Konforti, B.; Wemmer, D. The Molecules of Life; Garland Science: New York, NY, USA, 2013. [Google Scholar]
- Best, R.B.; Hummer, G.; Eaton, W.A. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA 2013, 110, 17874–17879. [Google Scholar] [CrossRef] [PubMed]
- Qian, H.; Schellman, J.A. Helix-Coil Theories—A Comparative-Study for Finite Length Polypeptides. J. Phys. Chem. 1992, 96, 3987–3994. [Google Scholar] [CrossRef]
- Williams, S.; Causgrove, T.P.; Gilmanshin, R.; Fang, K.S.; Callender, R.H.; Woodruff, W.H.; Dyer, R.B. Fast events in protein folding: Helix melting and formation in a small peptide. Biochemistry 1996, 35, 691–697. [Google Scholar] [CrossRef] [PubMed]
- Thompson, P.A.; Munoz, V.; Jas, G.S.; Henry, E.R.; Eaton, W.A.; Hofrichter, J. The helix-coil kinetics of a heteropeptide. J. Phys. Chem. B 2000, 104, 378–389. [Google Scholar] [CrossRef]
- Ianoul, A.; Mikhonin, A.; Lednev, I.K.; Asher, S.A. UV resonance Raman study of the spatial dependence of alpha-helix unfolding. J. Phys. Chem. A 2002, 106, 3621–3624. [Google Scholar] [CrossRef]
- Fierz, B.; Reiner, A.; Kiefhaber, T. Local conformational dynamics in alpha-helices measured by fast triplet transfer. Proc. Natl. Acad. Sci. USA 2009, 106, 1057–1062. [Google Scholar] [CrossRef] [PubMed]
- Dyer, R.B.; Gai, F.; Woodruff, W.H. Infrared studies of fast events in protein folding. Acc. Chem. Res. 1998, 31, 709–716. [Google Scholar] [CrossRef]
- Woodruff, W.H.; Dyer, R.B.; Callender, R.H.; Paige, K.; Causgrove, T. Fast Events in Protein-Folding-Laser T-Jump-Time-Resolved Infrared Study of the Ribonuclease-a S-Peptide. Biophys. J. 1994, 66, A397. [Google Scholar]
- Woodruff, W.H.; Dyer, R.B.; Williams, S.; Callender, R.H.; Gilmanshin, R. Laser-induced temperature jump/time-resolved infrared study of the fast events in protein folding. Abstr. Pap. Am. Chem. S 1996, 211, 57-Inor. [Google Scholar]
- Acharyya, A.; Ge, Y.H.; Wu, H.F.; DeGrado, W.F.; Voelz, V.A.; Gai, F. Exposing the Nucleation Site in alpha-Helix Folding: A Joint Experimental and Simulation Study. J. Phys. Chem. B 2019, 123, 1797–1807. [Google Scholar] [CrossRef]
- Jas, G.S.; Kuczera, K. Computer simulations of helix folding in homo- and heteropeptides. Mol. Simulat. 2012, 38, 682–694. [Google Scholar] [CrossRef]
- Kuczera, K.; Jas, G.S.; Elber, R. Kinetics of Helix Unfolding: Molecular Dynamics Simulations with Milestoning. J. Phys. Chem. A 2009, 113, 7461–7473. [Google Scholar] [CrossRef] [PubMed]
- Kreuzer, S.M.; Elber, R.; Moon, T.J. Early Events in Helix Unfolding under External Forces: A Milestoning Analysis. J. Phys. Chem. B 2012, 116, 8662–8691. [Google Scholar] [CrossRef] [PubMed]
- Elber, R.; Kreuzer, S. Coiled-Coil Response to Mechanical Force: Global Stability and Local Cracking. Biophys. J. 2013, 105, 951–961. [Google Scholar]
- Jas, G.S.; Childs, E.W.; Kuczera, K. Kinetic pathway analysis of an alpha-helix in two protonation states: Direct observation and optimal dimensionality reduction. J. Chem. Phys. 2019, 150, 074902. [Google Scholar] [CrossRef] [PubMed]
- Jas, G.S.; Kuczera, K. Deprotonation of a Single Amino Acid Residue Induces Significant Stability in an alpha-Helical Heteropeptide. J. Phys. Chem. B 2018, 122, 11508–11518. [Google Scholar] [CrossRef] [PubMed]
- Kuczera, K.; Szoszkiewicz, R.; He, J.Y.; Jas, G.S. Length Dependent Folding Kinetics of Alanine-Based Helical Peptides from Optimal Dimensionality Reduction. Life 2021, 11, 385. [Google Scholar] [CrossRef] [PubMed]
- Kutzner, C.; Pall, S.; Fechner, M.; Esztermann, A.; de Groot, B.L.; Grubmuller, H. Best bang for your buck: GPU nodes for GROMACS biomolecular simulations. J. Comput. Chem. 2015, 36, 1990–2008. [Google Scholar] [CrossRef] [PubMed]
- Pronk, S.; Pall, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmuller, H.; MacKerell, A.D. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Darden, T.; Perera, L.; Li, L.P.; Pedersen, L. New tricks for modelers from the crystallography toolkit: The particle mesh Ewald algorithm and its use in nucleic acid simulations. Struct. Fold Des. 1999, 7, R55–R60. [Google Scholar] [CrossRef] [PubMed]
- Bowman, G.R.; Noé, F.; Pande, V.S. An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation. In Advances in Experimental Medicine and Biology, 1st ed.; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Jas, G.S.; Kuczera, K. Helix-Coil Transition Courses Through Multiple Pathways and Intermediates: Fast Kinetic Measurements and Dimensionality Reduction. J. Phys. Chem. B 2018, 122, 10806–10816. [Google Scholar] [CrossRef] [PubMed]
- Kube, S.; Weber, M. A coarse graining method for the identification of transition rates between molecular conformations. J. Chem. Phys. 2007, 126, 024103. [Google Scholar] [CrossRef] [PubMed]
- Hummer, G.; Szabo, A. Optimal Dimensionality Reduction of Multistate Kinetic and Markov-State Models. J. Phys. Chem. B 2015, 119, 9029–9037. [Google Scholar] [CrossRef] [PubMed]
- Senne, M.; Trendelkamp-Schroer, B.; Mey, A.S.J.S.; Schutte, C.; Noe, F. EMMA: A Software Package for Markov Model Building and Analysis. J. Chem. Theory Comput. 2012, 8, 2223–2238. [Google Scholar] [CrossRef] [PubMed]
- Viswanath, S.; Kreuzer, S.M.; Cardenas, A.E.; Elber, R. Analyzing milestoning networks for molecular kinetics: Definitions, algorithms, and examples. J. Chem. Phys. 2013, 139, 174105. [Google Scholar] [CrossRef] [PubMed]
- Buchete, N.V.; Hummer, G. Coarse master equations for peptide folding dynamics. J. Phys. Chem. B 2008, 112, 6057–6069. [Google Scholar] [CrossRef] [PubMed]
- Bicout, D.J.; Szabo, A. Electron transfer reaction dynamics in non-Debye solvents. J. Chem. Phys. 1998, 109, 2325–2338. [Google Scholar] [CrossRef]
- Kubo, R. Fluctuation-Dissipation Theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Hegefeld, W.A.; Chen, S.E.; DeLeon, K.Y.; Kuczera, K.; Jas, G.S. Helix Formation in a Pentapeptide Experiment and Force-field Dependent Dynamics. J. Phys. Chem. A 2010, 114, 12391–12402. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.M.; Mohammed, O.F.; Jas, G.S.; Zewail, A.H. Speed limit of protein folding evidenced in secondary structure dynamics. Proc. Natl. Acad. Sci. USA 2011, 108, 16622–16627. [Google Scholar] [CrossRef] [PubMed]
- Swiatek, A.; Kuczera, K.; Szoszkiewicz, R. Effects of Proline on Internal Friction in Simulated Folding Dynamics of Several Alanine-Based α-Helical Peptides. J. Phys. Chem. B 2024, 128, 3856–3869. [Google Scholar] [CrossRef]
- Vanden-Eijnden, E. Transition Path Theory. Adv. Exp. Med. Biol. 2014, 797, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Weinan, E.; Vanden-Eijnden, E. Transition-Path Theory and Path-Finding Algorithms for the Study of Rare Events. Annu. Rev. Phys. Chem. 2010, 61, 391–420. [Google Scholar] [CrossRef] [PubMed]
- Jas, G.S.; Hegefeld, W.A.; Middaugh, C.R.; Johnson, C.K.; Kuczera, K. Detailed microscopic unfolding pathways of an alpha-helix and a beta-hairpin: Direct observation and molecular dynamics. J. Phys. Chem. B 2014, 118, 7233–7246. [Google Scholar] [CrossRef] [PubMed]
- Taketomi, H.; Ueda, Y.; Go, N. Studies on Protein Folding, Unfolding and Fluctuations by Computer-Simulation.1. Effect of Specific Amino-Acid Sequence Represented by Specific Inter-Unit Interactions. Int. J. Pept. Prot. Res. 1975, 7, 445–459. [Google Scholar] [CrossRef]
- Onuchic, J.N.; LutheySchulten, Z.; Wolynes, P.G. Theory of protein folding: The energy landscape perspective. Annu. Rev. Phys. Chem. 1997, 48, 545–600. [Google Scholar] [CrossRef] [PubMed]
- Ohkubo, Y.Z.; Brooks, C.L. Exploring Flory's isolated-pair hypothesis: Statistical mechanics of helix-coil transitions in polyalanine and the C-peptide from RNase A. Proc. Natl. Acad. Sci. USA 2003, 100, 13916–13921. [Google Scholar] [CrossRef]
- Scholtz, J.M.; Qian, H.; York, E.J.; Stewart, J.M.; Baldwin, R.L. Parameters of helix-coil transition theory for alanine-based peptides of varying chain lengths in water. Biopolymers 1991, 31, 1463–1470. [Google Scholar] [CrossRef]
- Matouschek, A.; Kellis, J.T.; Serrano, L.; Fersht, A.R. Mapping the Transition-State and Pathway of Protein Folding by Protein Engineering. Nature 1989, 340, 122–126. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).