The Microstructure Characterization of a Titanium Alloy Based on a Laser Ultrasonic Random Forest Regression
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Materials and Microstructure Inspection
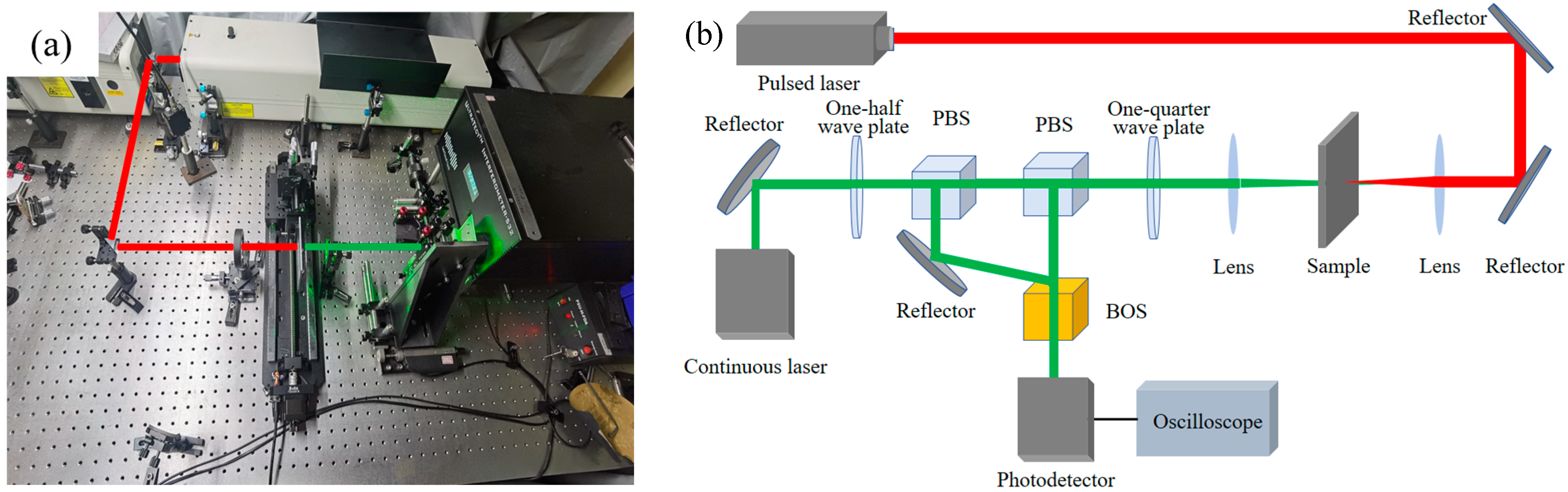
2.2. Experimental Scheme of Laser Ultrasonic Inspection
2.3. SEM Sample Preparation and Testing
3. Experimental Results
3.1. Microstructure Experimental Results
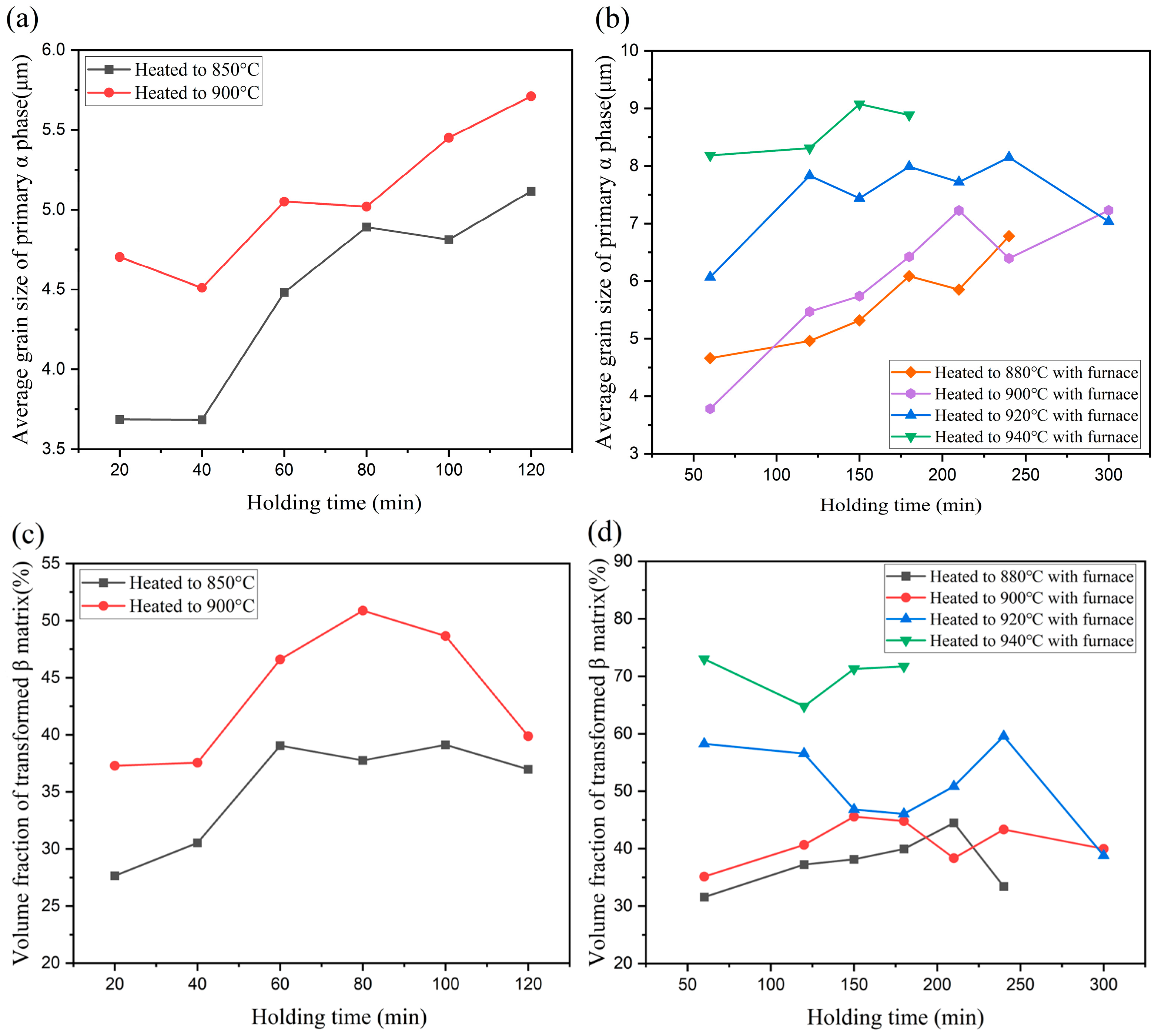
3.2. Calculation of the Average Grain Size of the Primary α Phase and the Volume Fraction of the Transformed β Matrix
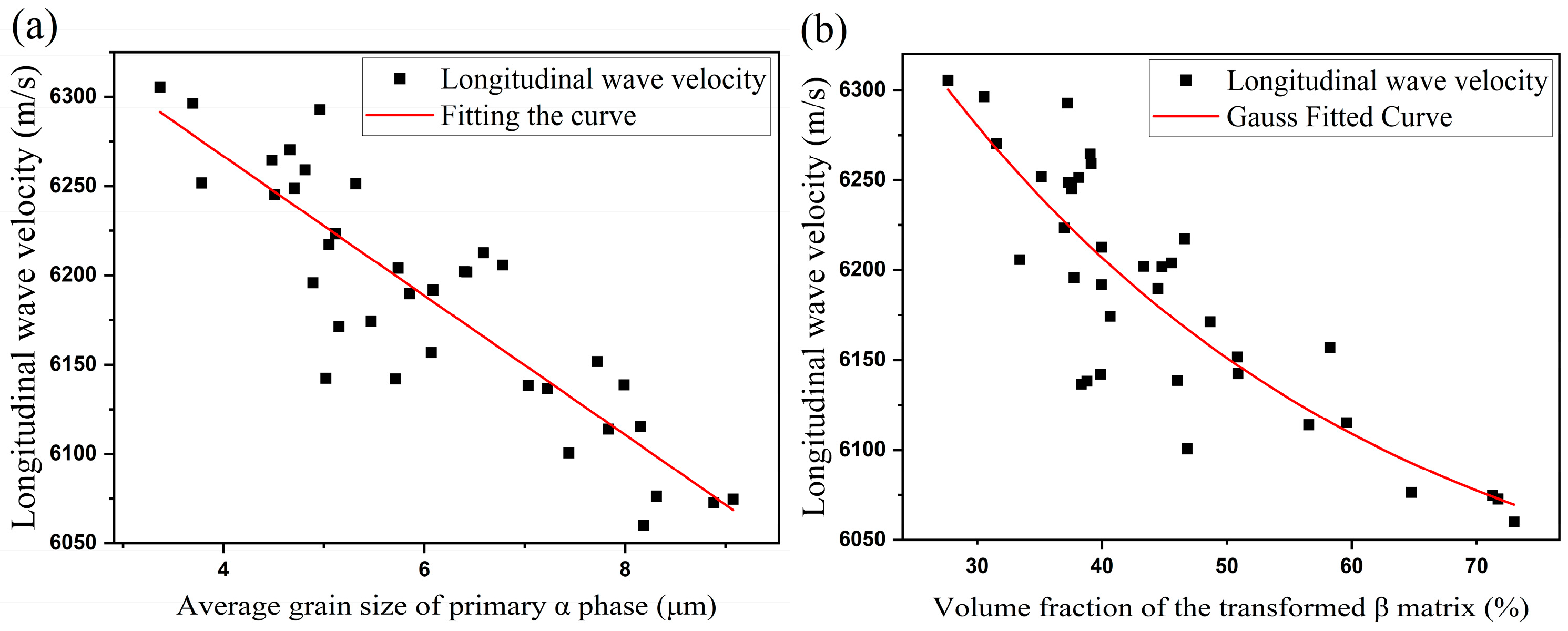
3.3. Signal Processing and Longitudinal Wave Velocity Extraction
4. Analysis and Discussion
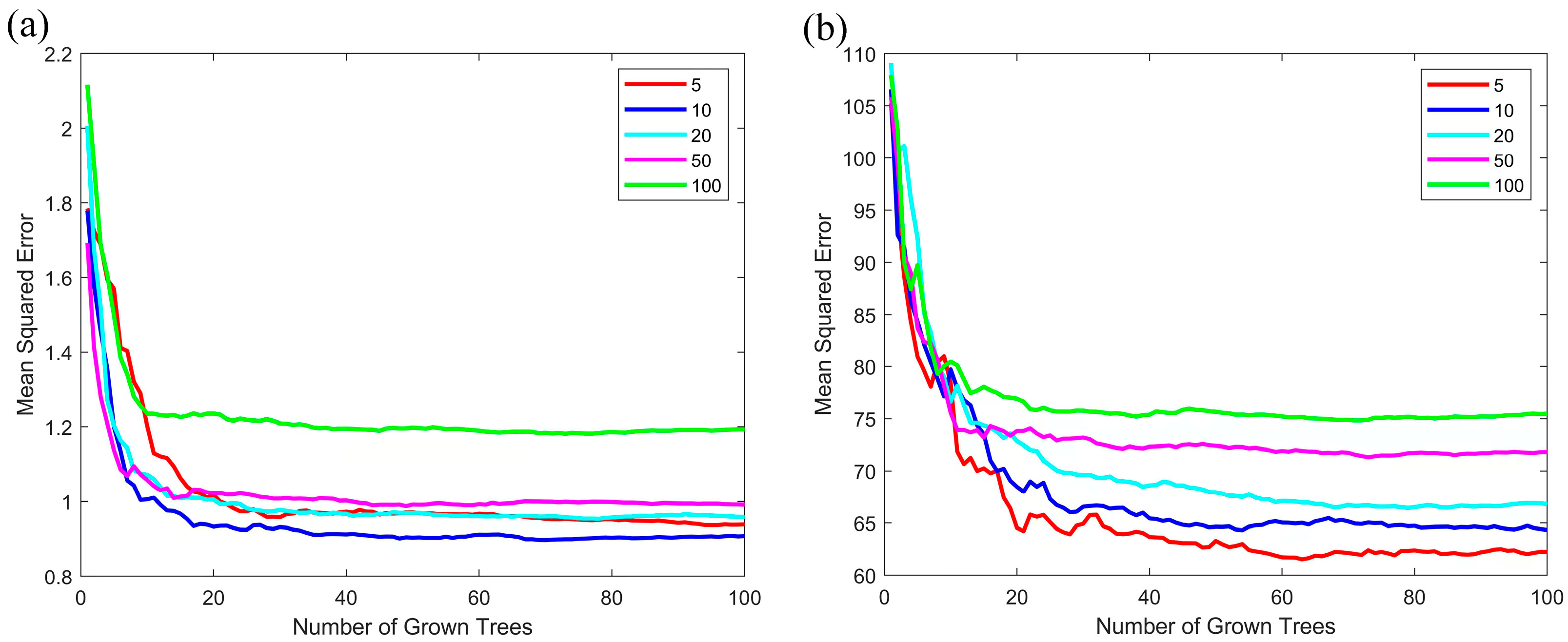
4.1. RFR Model Building
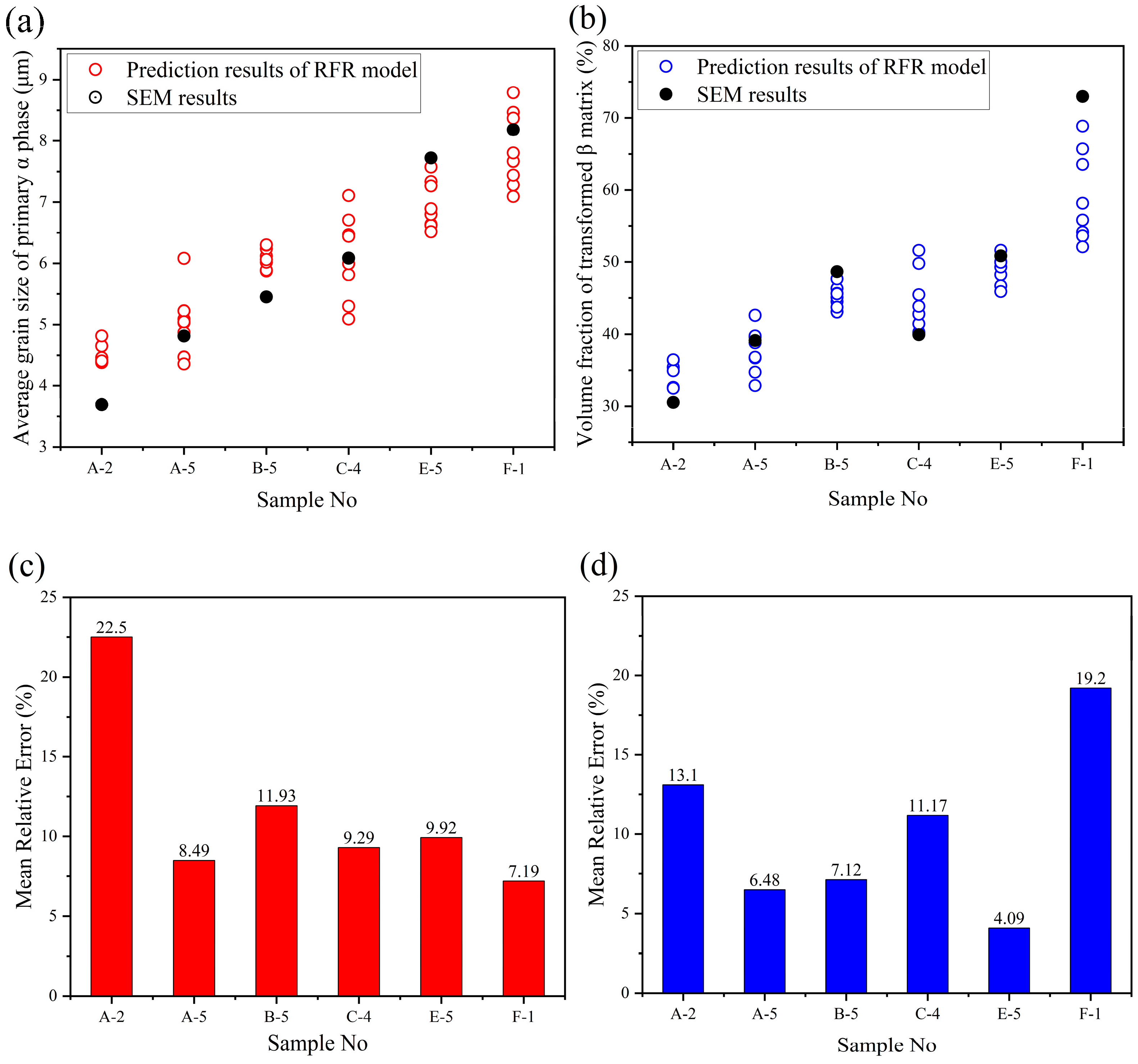
4.2. Construction and Validation Results of RFR Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cui, C.; Hu, B.; Zhao, L.; Liu, S. Titanium alloy production technology, market prospects and industry development. Mater. Design 2011, 32, 1684–1691. [Google Scholar] [CrossRef]
- Sun, L.; Li, M.; Li, H. Dynamic Recrystallization-Related Interface Phase Boundary Migration of TC17/TC4 Bond with Initial Equiaxed Microstructure. J. Nutr. 2019, 71, 2253–2261. [Google Scholar] [CrossRef]
- Yu, Z.; Yu, S.; Cheng, J.; Ma, X. Development and Application of Novel Biomedical Titanium Alloy Materials. Acta Metall. Sin. 2017, 53, 1238–1264. [Google Scholar]
- Chong, Y.; Bhattacharjee, T.; Tsuji, N. Bi-lamellar microstructure in Ti–6Al–4V: Microstructure evolution and mechanical properties. Mat. Sci. Eng. A 2019, 762, 138077. [Google Scholar] [CrossRef]
- Long, W.; Zhang, S.; Liang, Y.-L.; Ou, M.-G. Influence of multi-stage heat treatment on the microstructure and mechanical properties of TC21 titanium alloy. Int. J. Min. Met. Mater. 2021, 28, 296–304. [Google Scholar] [CrossRef]
- Mandal, P.K.; Mathews, M.S.; A Daniel, B.; Devasia, J. Effect of ageing treatment on microstructure and mechanical properties of α + β type titanium alloy used for biomaterials. IOP Conf. Ser. Mater. Sci. Eng. 2019, 561, 012060. [Google Scholar] [CrossRef]
- Zhao, P.; Wei, C.; Li, Y.; Tao, J.; Zhang, C.; Xiao, X.; Zhang, M. Effect of heat treatment on the microstructure, microhardness and impact toughness of TC11 and TC17 linear friction welded joint. Mat. Sci. Eng. A 2021, 803, 140496. [Google Scholar] [CrossRef]
- Roman, I.; Ward, C.H. Acoustic-Emission Characterization of the Deformation and Fracture of A Ti3Al Alloy. Scripta Mater. 1992, 27, 413–418. [Google Scholar] [CrossRef]
- Chen, G.; Liu, C. Cyclic Plastic Deformation Behavior of TC4 Titanium Alloy Under Different Microstructures and Load Conditions Using Finite Element Method. J. Fail. Anal. Prev. 2021, 21, 678–688. [Google Scholar] [CrossRef]
- Maalekian, M.; Radis, R.; Militzer, M.; Moreau, A.; Poole, W. In situ measurement and modelling of austenite grain growth in a Ti/Nb microalloyed steel. Acta Mater. 2012, 60, 1015–1026. [Google Scholar] [CrossRef]
- Rodrigues, M.C.; Garcin, T.; Militzer, M. In-situ measurement of α formation kinetics in a metastable β Ti-5553 alloy using laser ultrasonics. J. Alloys Compd. 2021, 866, 158954. [Google Scholar] [CrossRef]
- Li, Y.; Hou, S.; Chai, Y.; Zhou, Y.; Zou, Y. Nondestructive measurement of the grain size of laser cladding coatings using a laser ultrasonic method. Appl. Opt. 2022, 61, 1885–1891. [Google Scholar] [CrossRef] [PubMed]
- Keyvani, M.; Garcin, T.; Militzer, M.; Fabregue, D. Laser ultrasonic measurement of recrystallization and grain growth in an L605 cobalt superalloy. Mater. Charact. 2020, 167, 110465. [Google Scholar] [CrossRef]
- Falkenström, M.; Engman, M.; Lindh-Ulmgren, E.; Hutchinson, B. Laser ultrasonics for process control in the metal industry. Nondestruct. Test. Eval. 2011, 26, 237–252. [Google Scholar] [CrossRef]
- Du, H.; Turner, J.A. Ultrasonic attenuation in pearlitic steel. Ultrasonics 2014, 54, 882–887. [Google Scholar] [CrossRef] [PubMed]
- Dong, F.; Wang, X.; Yang, Q.; Liu, H.; Xu, D.; Sun, Y.; Zhang, Y.; Xue, R.; Krishnaswamy, S. In-situ measurement of Ti-6Al-4V grain size distribution using laser-ultrasonic technique. Scr. Mater. 2018, 154, 40–44. [Google Scholar] [CrossRef]
- White, R.M. Generation of elastic waves by transient surface heating. J. Appl. Phys. 1963, 34, 3559–3567. [Google Scholar] [CrossRef]
- Moreau, A.; Lévesque, D.; Lord, M.; Dubois, M.; Monchalin, J.-P.; Padioleau, C.; Bussière, J. On-line measurement of texture, thickness and plastic strain ratio using laser-ultrasound resonance spectroscopy. Ultrasonics 2002, 40, 1047–1056. [Google Scholar] [CrossRef]
- Kruger, S.E.; Damm, E.B. Monitoring austenite decomposition by ultrasonic velocity. Mat. Sci. Eng. A 2006, 425, 238–243. [Google Scholar] [CrossRef]
- Shinbine, A.; Garcin, T.; Sinclair, C. In-situ laser ultrasonic measurement of the hcp to bcc transformation in commercially pure titanium. Mater. Charact. 2016, 117, 57–64. [Google Scholar] [CrossRef]
- Sarpun, I.H.; Selami, K.M.; Tuncel, S. Mean grain size determination in marbles by ultrasonic velocity techniques. NDT&E Int. 2005, 38, 21–25. [Google Scholar]
- Li, P.; Chu, S.; Chou, C.; Chen, F. Use of ultrasonic velocity for nondestructive evaluation of ferrite content in duplex Fe-Mn-Al alloy steels. Scr. Metall. Mater. 1992, 26, 127–132. [Google Scholar] [CrossRef]
- Palanichamy, P.; Joseph, A.; Jayakumar, T.; Raj, B. Ultrasonic velocity measurements for estimation of grain size in austenitic stainless steel. NDT&E Int. 1995, 28, 179–185. [Google Scholar]
- Gronau, O.; Regener, D. Ultrasonic testing of extruded and rolled green compacts from TiAl. NDT&E Int. 1997, 30, 351–357. [Google Scholar]
- Senkov, O.N.; Dubois, M.; Jonas, J.J. Elastic moduli of titanium-hydrogen alloys in the temperature range 20 degrees C to 1100 degrees C. Metall. Mater. Trans. B 1996, 27, 3963–3970. [Google Scholar] [CrossRef]
- Ünal, R.; Sarpün, I.H.; Yalım, H.A.; Erol, A.; Özdemir, T.; Tuncel, S. The mean grain size determination of boron carbide (B4C)-aluminium (Al) and boron carbide (B4C)-nickel (Ni) composites by ultrasonic velocity technique. Mater. Charact. 2006, 56, 241–244. [Google Scholar] [CrossRef]
- Yin, A.; Yang, Q.; He, F.; Wang, X.; Dong, F.; Wang, Y.; Shu, X. Laser ultrasound-based nondestructive inspection method for average grain size of mild steel. Chin. J. Mech. Eng-En. 2017, 53, 9. (In Chinese) [Google Scholar]
- Bate, P.; Lundin, P.; Lindh-Ulmgren, E.; Hutchinson, B. Application of laser-ultrasonics to texture measurements in metal processing. Acta Mater. 2017, 123, 329–336. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Xu, D.; Yang, Q.; Zhao, J.; Xue, R. Prediction of volume fraction of primary α phase in dual-phase titanium alloy based on laser ultrasonic. Measurement 2022, 195, 111115. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, X. Research on laser ultrasonic surface defect identification based on a support vector machine. Sci. Prog.-Uk 2021, 104, 00368504211059038. [Google Scholar] [CrossRef]
- Taylor, P.L.; Conduit, G. Machine learning predictions of superalloy microstructure. Comp. Mater. Sci. 2022, 201, 110916. [Google Scholar] [CrossRef]
- Jin, Y.; Zhao, J.; Zhang, C.; Luo, J.; Wang, S. Research on Neural Network Prediction of Multidirectional Forging Microstructure Evolution of GH4169 Superalloy. J. Mater. Eng. Perform. 2021, 30, 2708–2719. [Google Scholar] [CrossRef]
- Luo, J.H.; Liu, X.F.; Shi, Z.Z.; Liu, Y.F. Microstructure quantification of Cu–4.7 Sn alloys prepared by two-phase zone continuous casting and a BP artificial neural network model for microstructure prediction. Rare Metals 2019, 38, 1124–1130. [Google Scholar] [CrossRef]
- Xue, R.; Wang, X.; Yang, Q.; Xu, D.; Sun, Y.; Zhang, J.; Krishnaswamy, S. Grain size distribution characterization of aluminum with a particle swarm optimization neural network using laser ultrasonics. Appl. Acoust. 2021, 180, 108125. [Google Scholar] [CrossRef]
- Zhang, J.; Yin, A.; Tao, C.; Wang, Y.; Zhu, Z.; Peng, H.; Shu, X. Rapid measurement of the fourth-order texture coefficient by laser ultrasonic surface acoustic waves based on a neural network expert system. Appl. Opt. 2019, 58, 626–634. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE T Signal Proces. 2013, 62, 531–544. [Google Scholar] [CrossRef]




| Element | Ti | Fe | Al | V | H | C | O | N |
|---|---|---|---|---|---|---|---|---|
| Content/% | Remaining | 0.0495 | 6.0764 | 4.0920 | 0.0042 | 0.0113 | 0.1248 | 0.0192 |
| Group Number | Holding Temperature/°C | Holding Time/min | Cooling Method |
|---|---|---|---|
| A | Heated to 850 °C | 20/40/60/80/100/120 | Air cooling |
| B | Heated to 900 °C | 20/40/60/80/100/120 | |
| C | Heated to 880 °C with furnace | 60/120/150/180/210/240 | |
| D | Heated to 900 °C with furnace | 60/120/150/180/210/240/300 | |
| E | Heated to 920 °C with furnace | 60/120/150/180/210/240/300 | |
| F | Heated to 940 °C with furnace | 60/120/150/180 |
| Ultrasonic Parameters |
|---|
| Model | Test Set | ||
|---|---|---|---|
| R2 | RMSE | MAE | |
| Average grain size prediction model | 0.82 | 0.7140 | 0.6414 |
| Volume fraction prediction model | 0.77 | 7.6064 | 5.2933 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Yuan, S.; Wang, X.; Chen, H.; Huang, F.; Yu, C.; He, Y.; Yin, A. The Microstructure Characterization of a Titanium Alloy Based on a Laser Ultrasonic Random Forest Regression. Crystals 2024, 14, 607. https://doi.org/10.3390/cryst14070607
Wu J, Yuan S, Wang X, Chen H, Huang F, Yu C, He Y, Yin A. The Microstructure Characterization of a Titanium Alloy Based on a Laser Ultrasonic Random Forest Regression. Crystals. 2024; 14(7):607. https://doi.org/10.3390/cryst14070607
Chicago/Turabian StyleWu, Jinfeng, Shuxian Yuan, Xiaogang Wang, Huaidong Chen, Fei Huang, Chang Yu, Yeqing He, and Anmin Yin. 2024. "The Microstructure Characterization of a Titanium Alloy Based on a Laser Ultrasonic Random Forest Regression" Crystals 14, no. 7: 607. https://doi.org/10.3390/cryst14070607
APA StyleWu, J., Yuan, S., Wang, X., Chen, H., Huang, F., Yu, C., He, Y., & Yin, A. (2024). The Microstructure Characterization of a Titanium Alloy Based on a Laser Ultrasonic Random Forest Regression. Crystals, 14(7), 607. https://doi.org/10.3390/cryst14070607






