Magnon Confinement on the Two-Dimensional Penrose Lattice: Perpendicular-Space Analysis of the Dynamic Structure Factor
Abstract
:1. Introduction
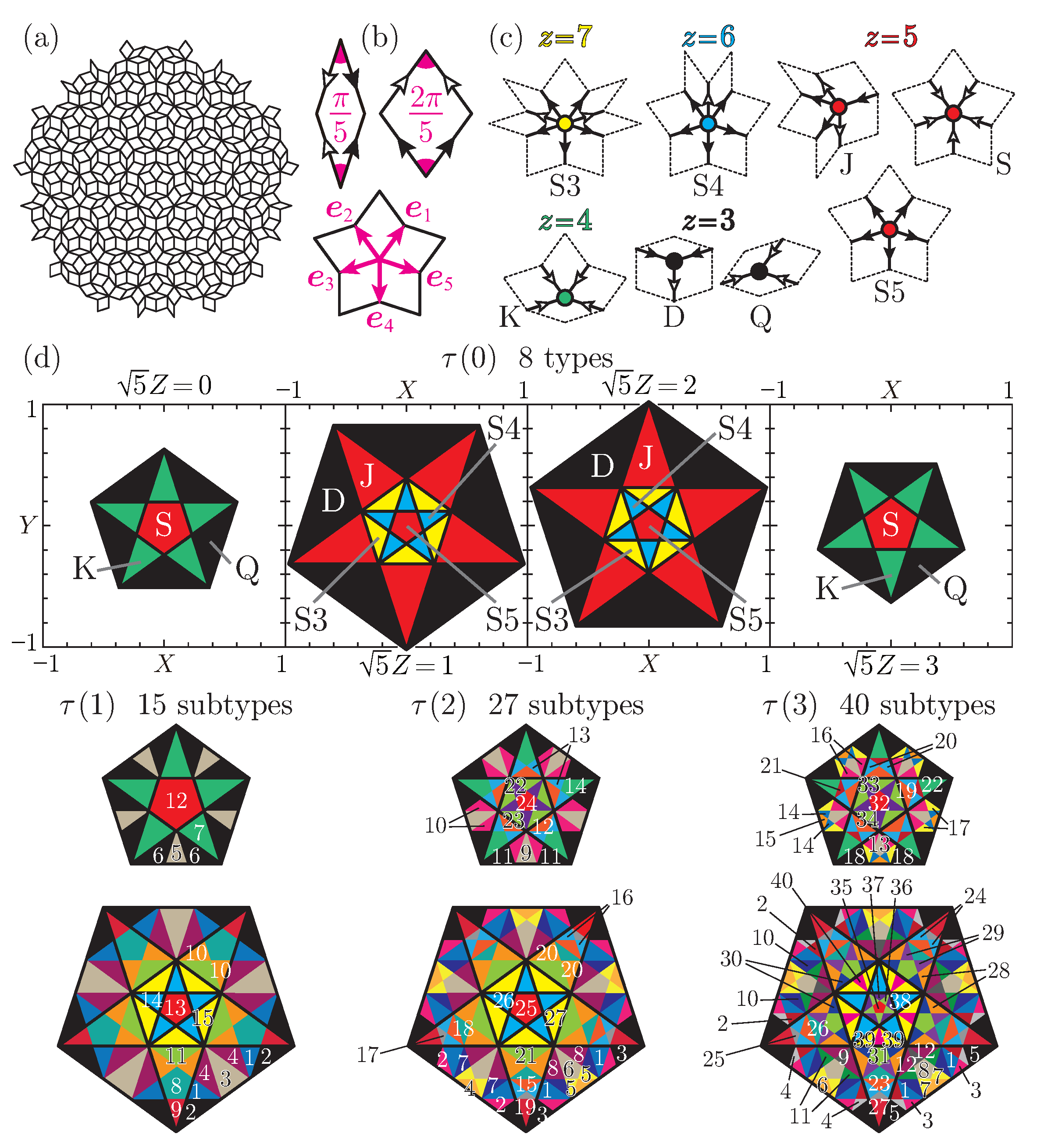
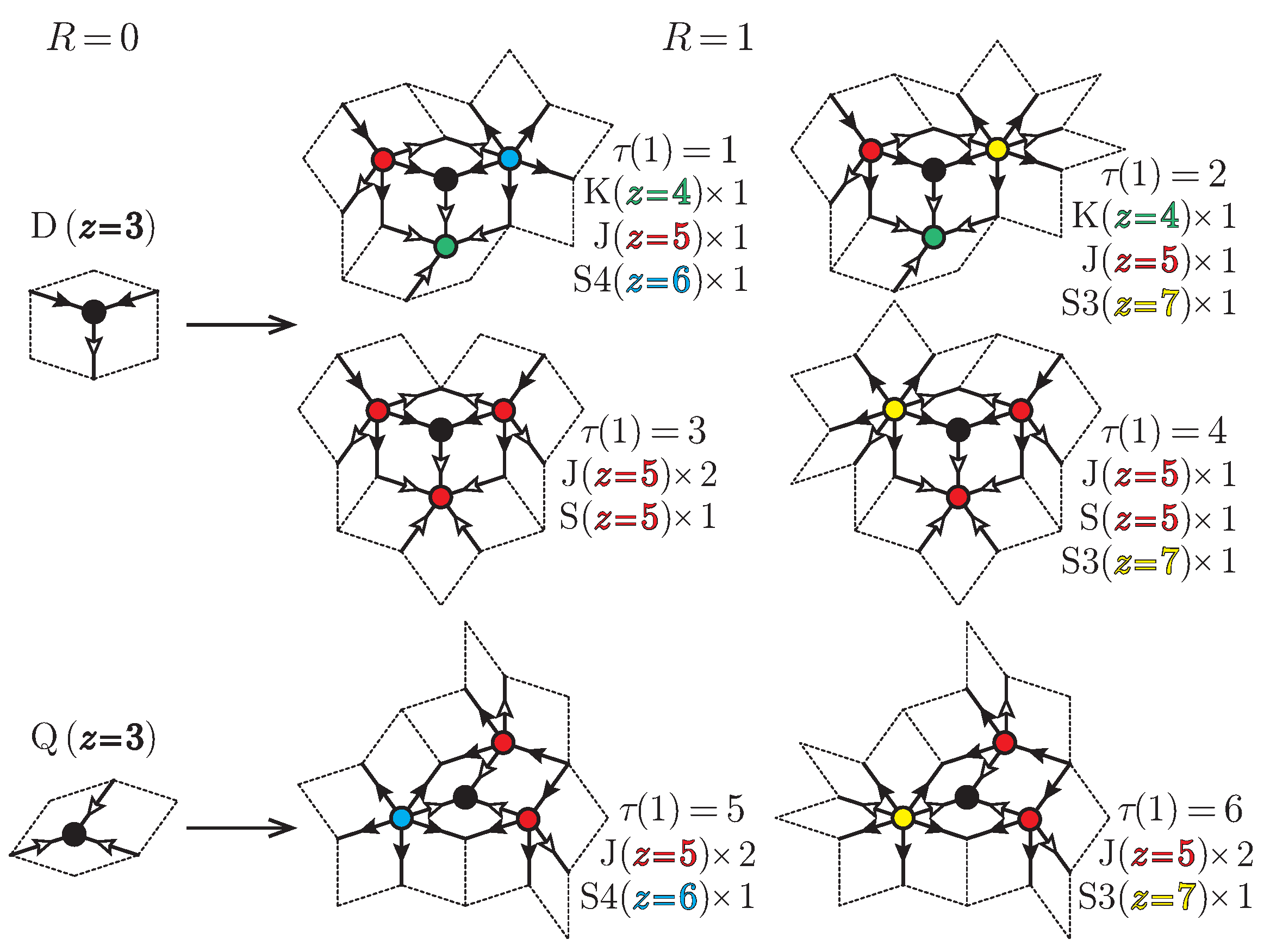
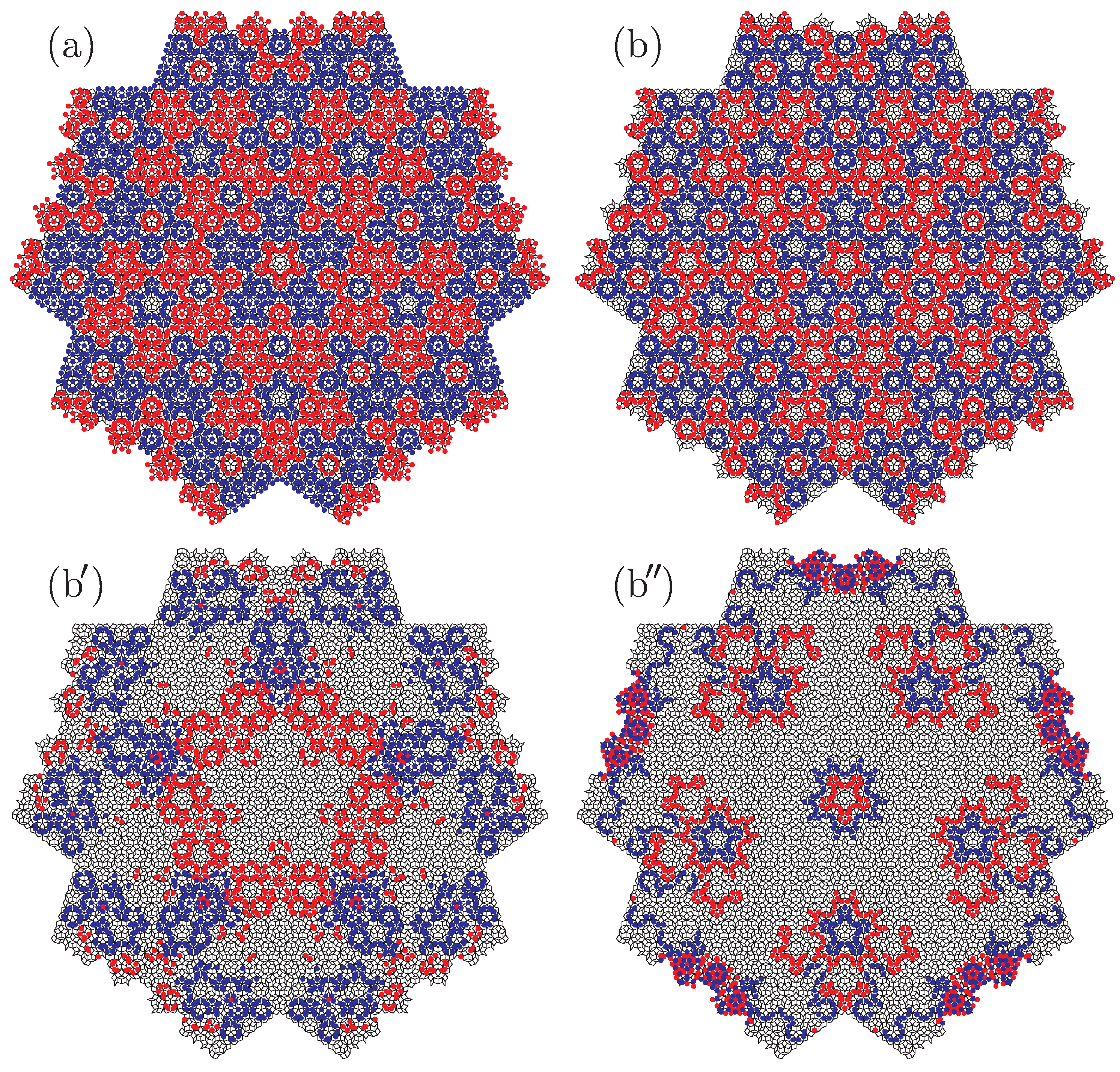
2. Quasiperiodic Tilings in Two Dimensions
3. Spin-Wave Formalism
4. Spin-Wave Dynamics
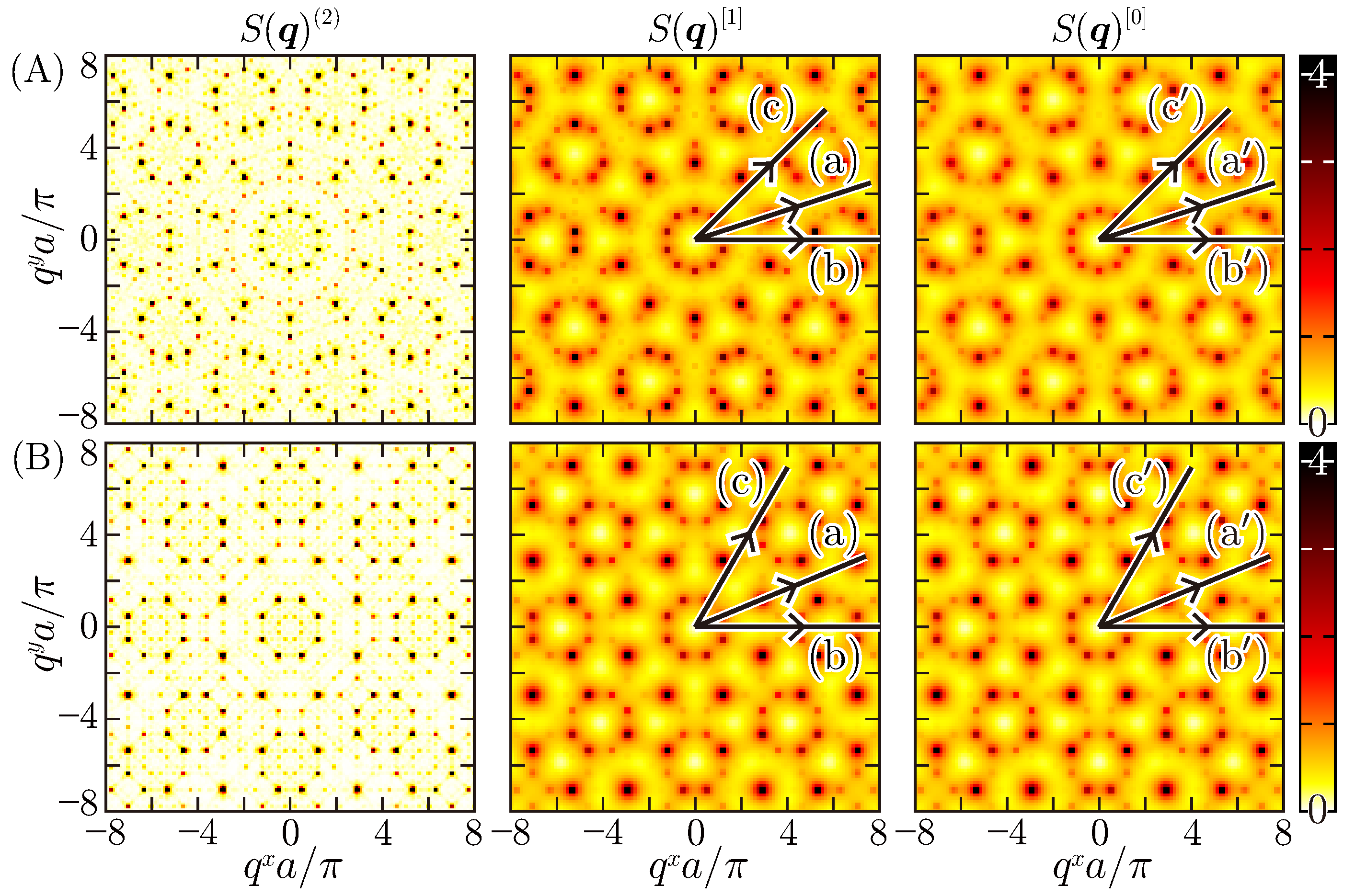
4.1. Static Structure Factors
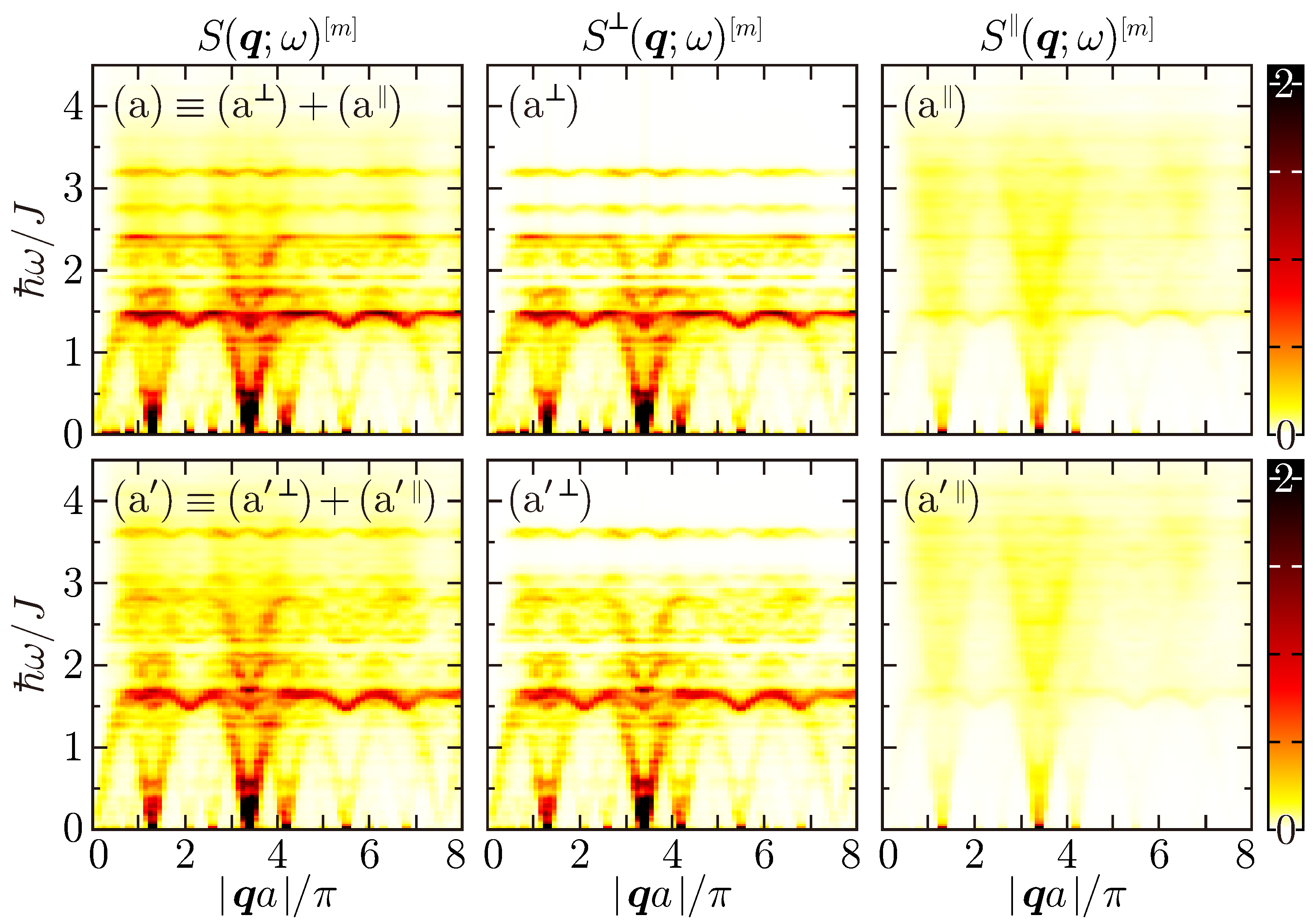
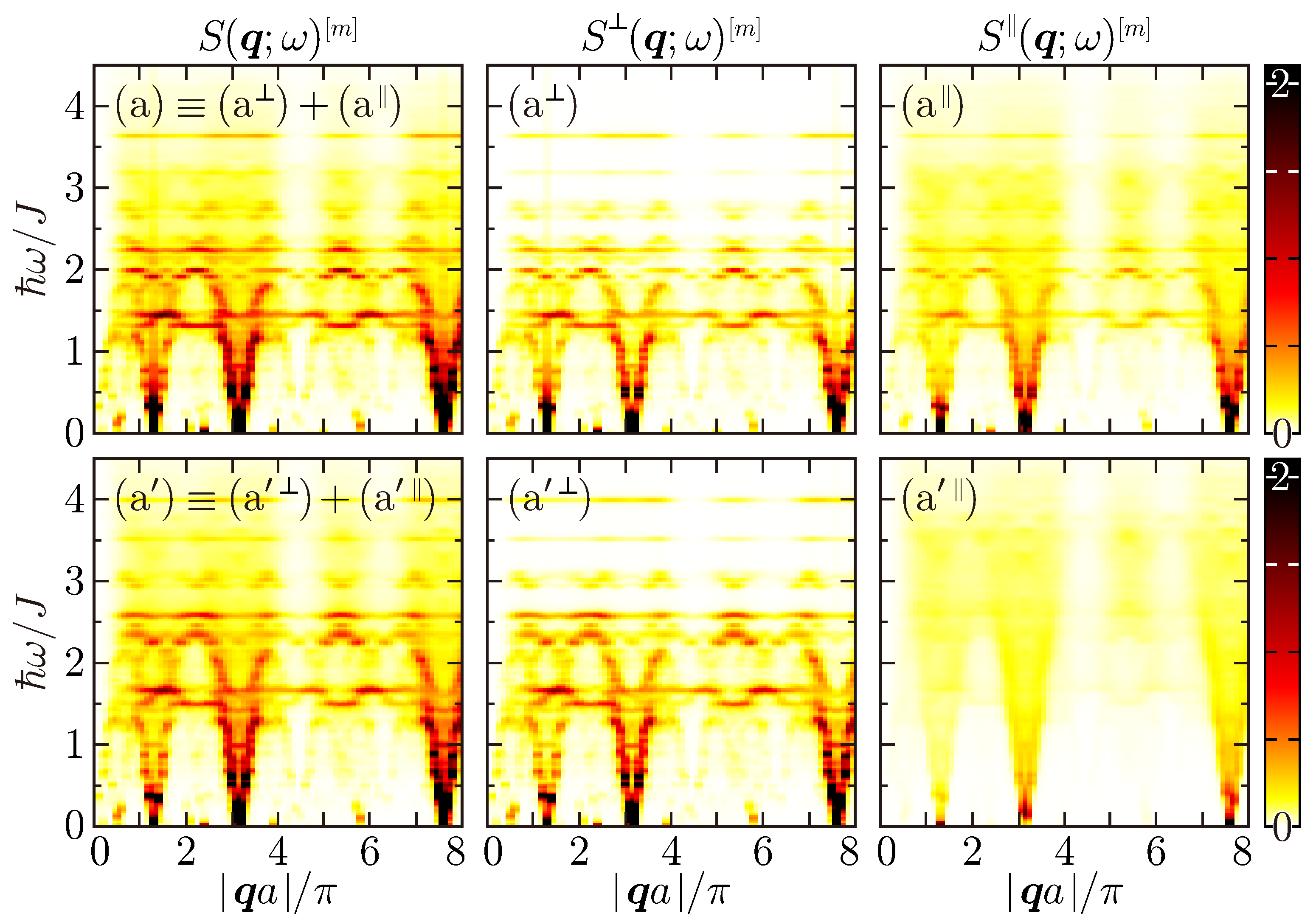
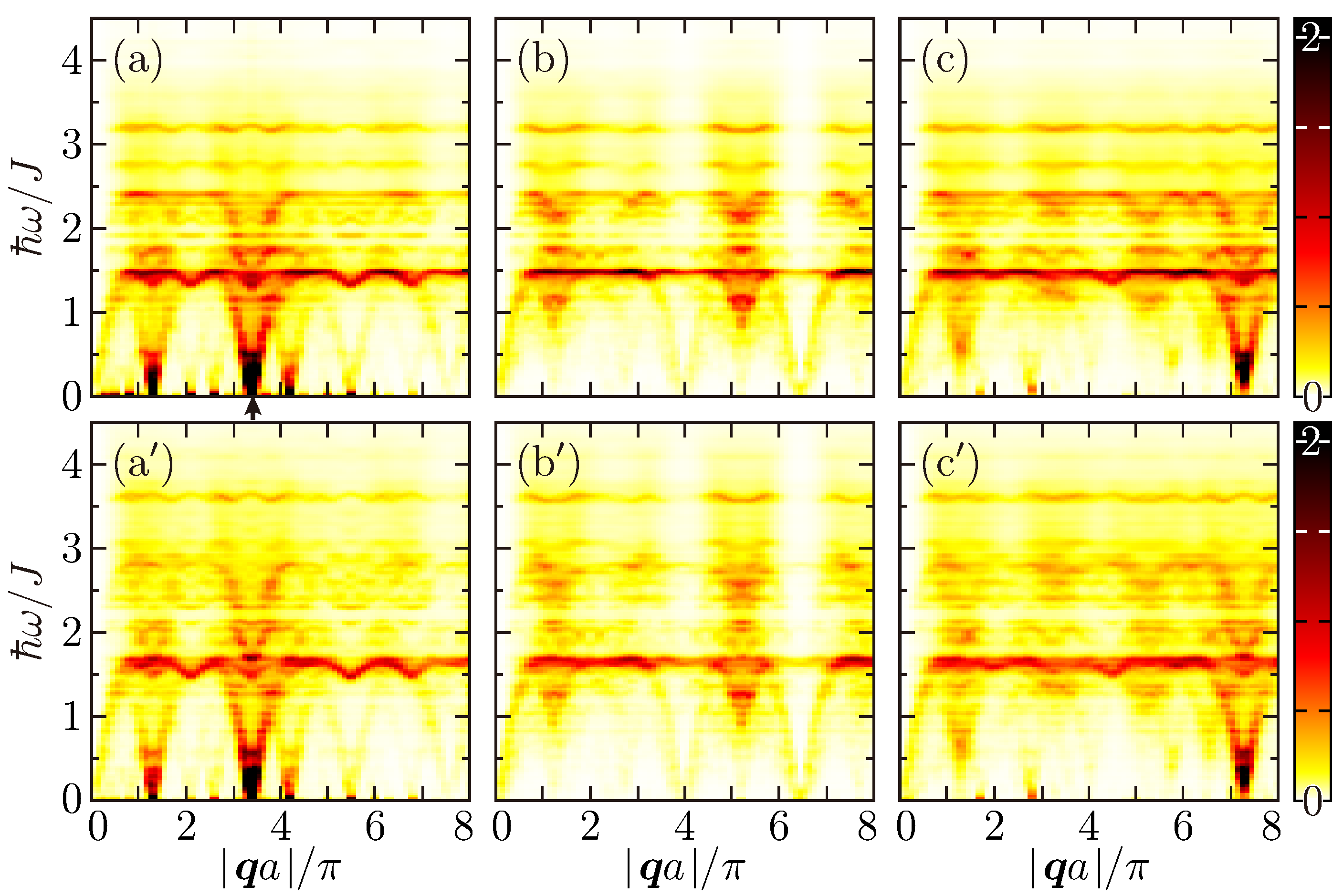
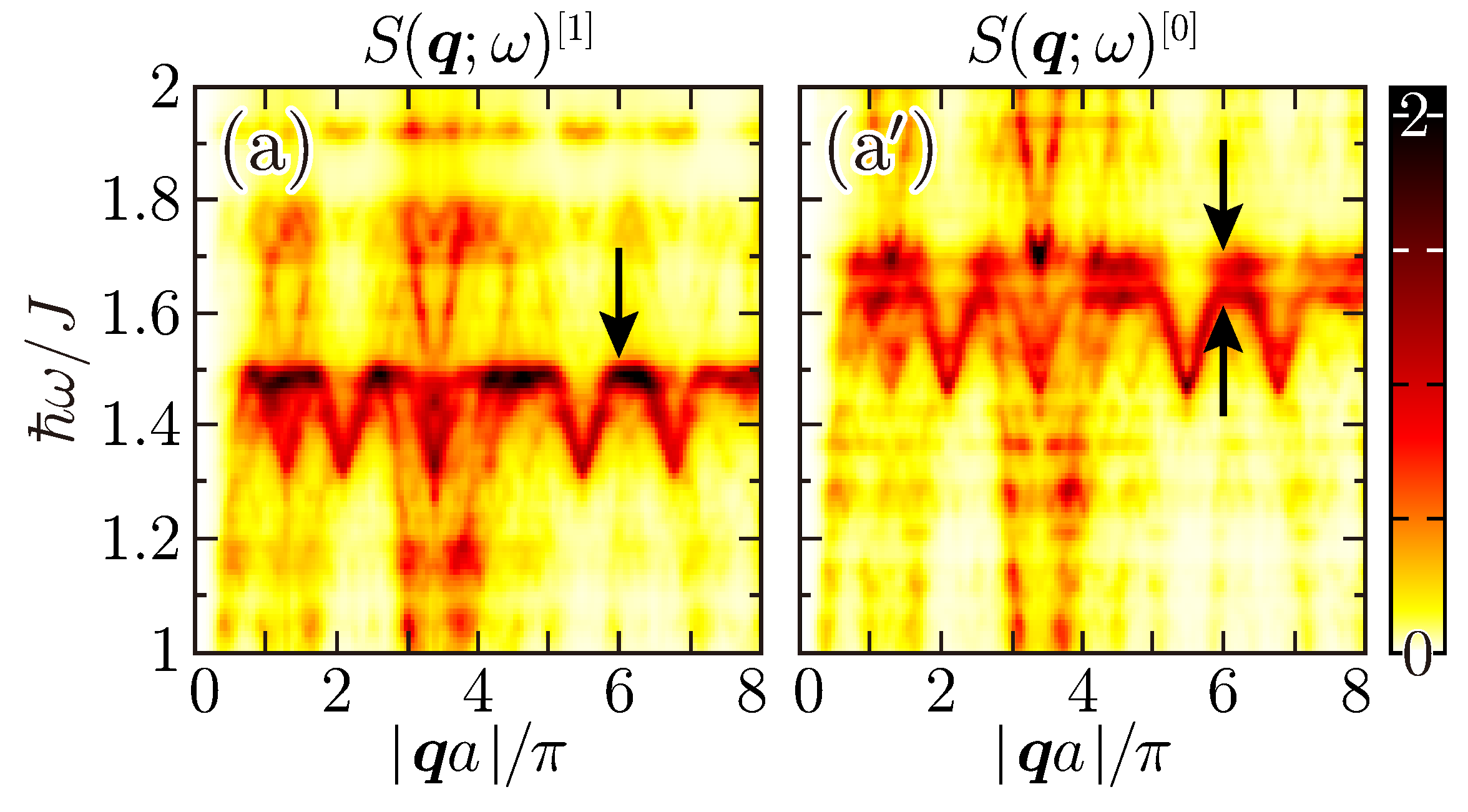
4.2. Dynamic Structure Factors
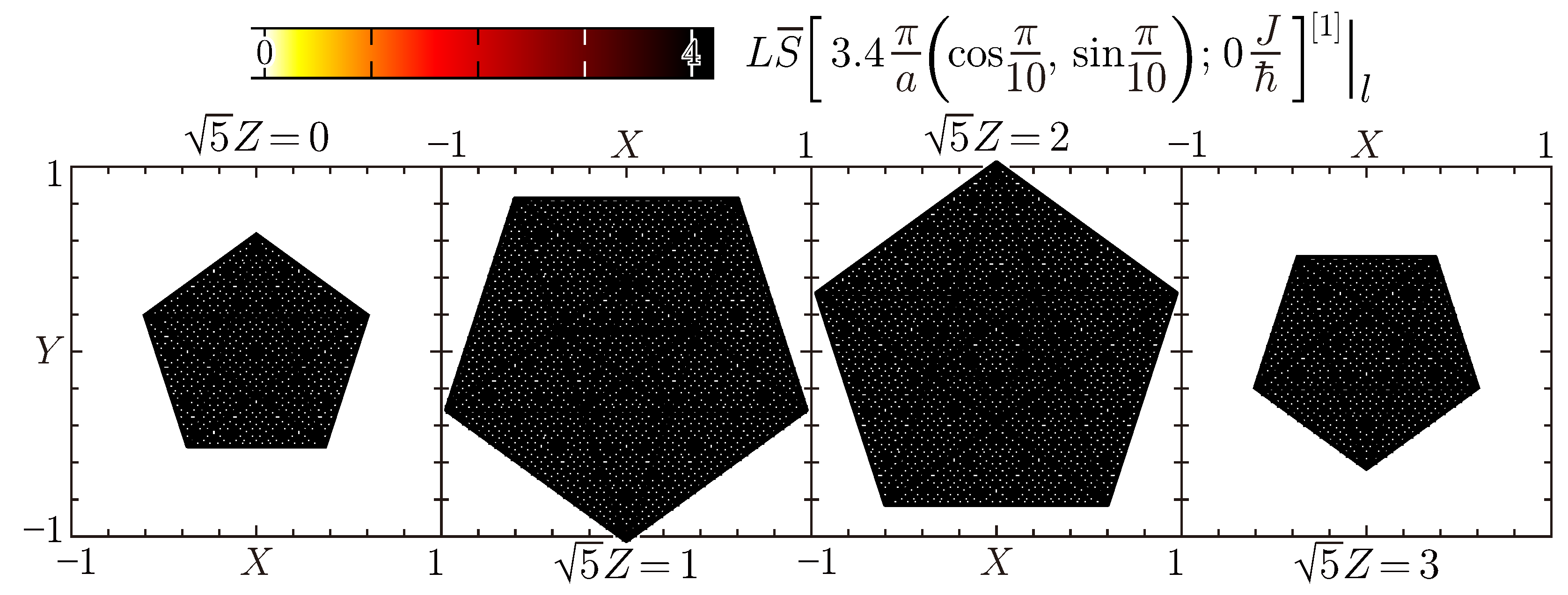
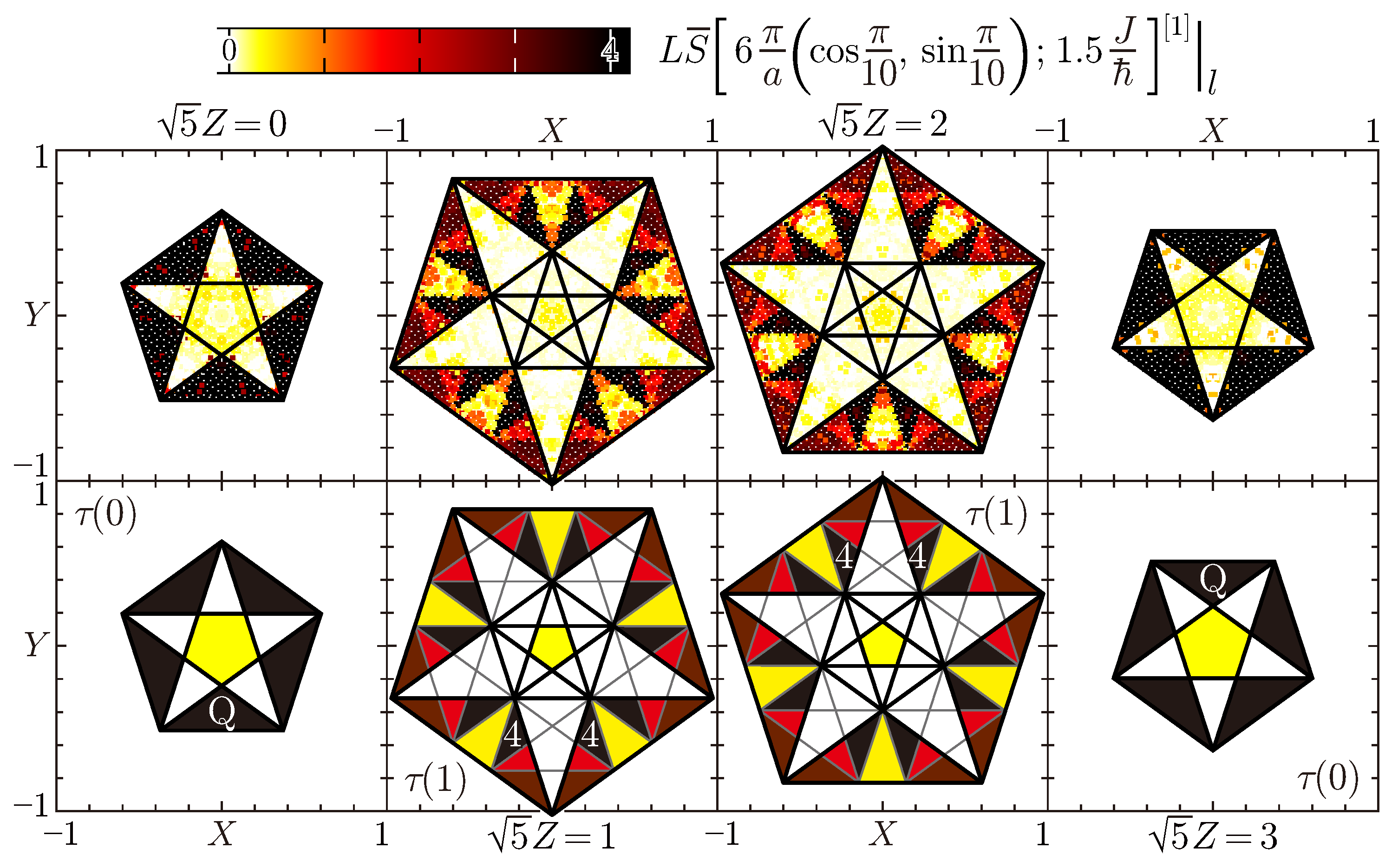
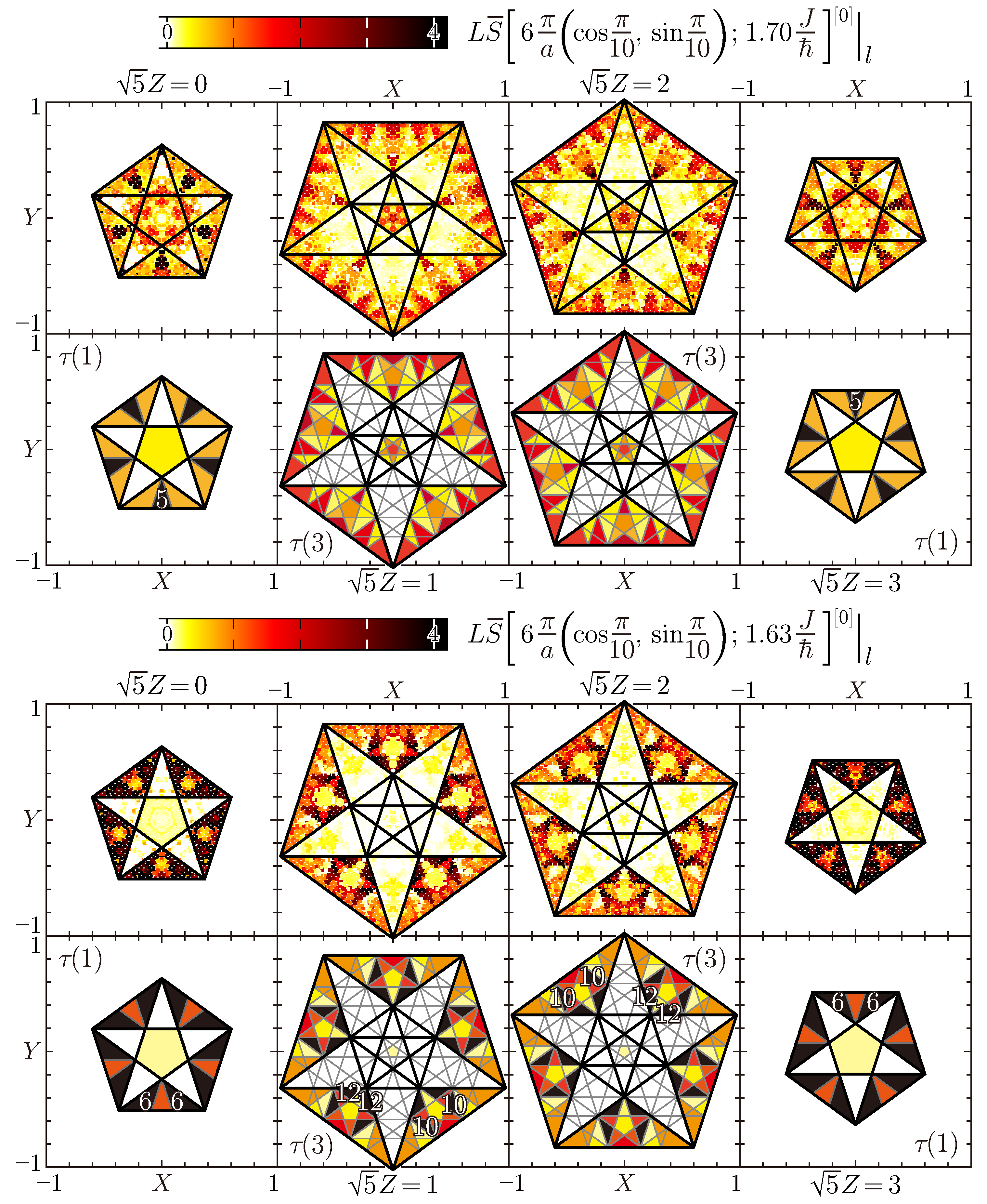
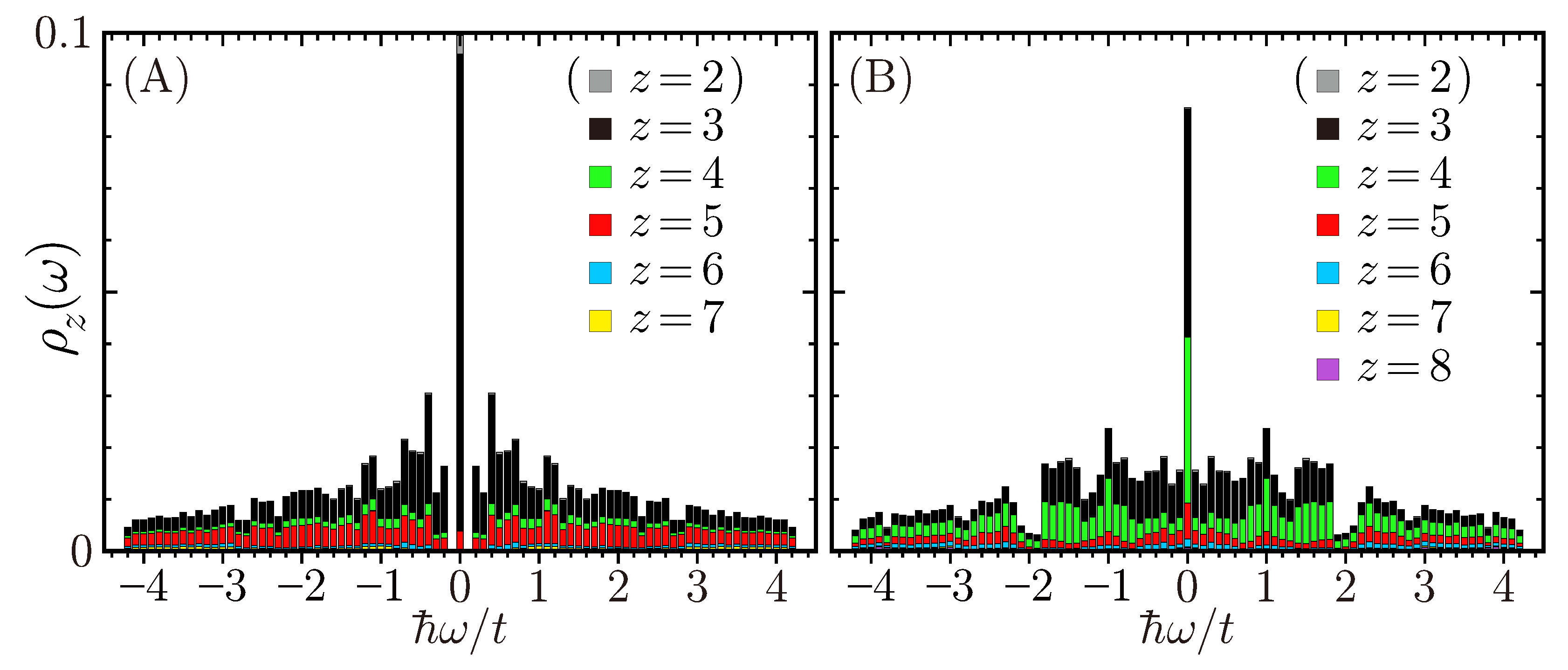
4.3. Perpendicular-Space Analysis
5. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Dynamic Transverse and Longitudinal Structure Factors
References
- Penrose, R. The role of aesthetics in pure and applied mathematical research. Bull. Inst. Math. Appl. 1974, 10, 266. [Google Scholar]
- Gardner, M. Extraordinary nonperiodic tiling that enriches the theory of tiles. Sci. Am. 1977, 236, 110. [Google Scholar] [CrossRef]
- Mackay, A.L. Crystallography and the penrose pattern. Physica A 1982, 114, 609. [Google Scholar] [CrossRef]
- Beenker, F.P.M. Algebraic Theory of Non-Periodic Tilings of the Plane by Two Simple Building Blocks: A Suqare and a Rhombus; T.H.-Report, 82-WSK-04; Eindhoven University of Technology: Eindhoven, The Netherlands, 1982. [Google Scholar]
- Niizeki, K.; Mitani, H. Two-dimensional dodecagonal quasilattices. J. Phys. A Math. Gen. 1987, 20, L405. [Google Scholar] [CrossRef]
- Choy, T.C. Density of States for a Two-Dimensional Penrose Lattice: Evidence of a Strong Van Hove Singularity. Phys. Rev. Lett. 1985, 55, 2915. [Google Scholar] [CrossRef] [PubMed]
- Odagaki, T.; Nguyen, D. Electronic and vibrational spectra of two-dimensional quasicrystals. Phys. Rev. B 1986, 33, 2184. [Google Scholar] [CrossRef] [PubMed]
- Tsunetsugu, H.; Fujiwara, T.; Ueda, K.; Tokihiro, T. Eigenstates in 2-Dimensional Penrose Tiling. J. Phys. Soc. Jpn. 1986, 55, 1420. [Google Scholar] [CrossRef]
- Tsunetsugu, H.; Fujiwara, T.; Ueda, K.; Tokihiro, T. Electronic properties of the Penrose lattice. I. Energy spectrum and wave functions. Phys. Rev. B 1991, 43, 8879. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sutherland, B. Electronic States on a Penrose Lattice. Phys. Rev. Lett. 1986, 56, 2740. [Google Scholar] [CrossRef]
- Arai, M.; Tokihiro, T.; Fujiwara, T.; Kohmoto, M. Strictly localized states on a two-dimensional Penrose lattice. Phys. Rev. B 1988, 38, 1621. [Google Scholar] [CrossRef]
- Zijlstra, E.S.; Janssen, T. Density of states and localization of electrons in a tight-binding model on the Penrose tiling. Phys. Rev. B 2000, 61, 3377. [Google Scholar] [CrossRef]
- de Bruijn, N.G. Algebraic theory of Penrose’s non-periodic tilings of the plane. I. Indag. Math. Proc. Ser. A 1981, 84, 39. Available online: https://www.sciencedirect.com/science/article/pii/1385725881900160 (accessed on 7 July 2024). [CrossRef]
- de Bruijn, N.G. Algebraic theory of Penrose’s non-periodic tilings of the plane. II. Indag. Math. Proc. Ser. A 1981, 84, 53. Available online: https://www.sciencedirect.com/science/article/pii/1385725881900172 (accessed on 7 July 2024). [CrossRef]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic Phase with Long-Range Orientational Order and No Translational Symmetry. Phys. Rev. Lett. 1984, 53, 1951. [Google Scholar] [CrossRef]
- Tsai, A.P.; Inoue, A.; Masumoto, T. A Stable Quasicrystal in Al-Cu-Fe System. Jpn. J. Appl. Phys. 1987, 26, L1505. [Google Scholar] [CrossRef]
- Tsai, A.P.; Inoue, A.; Masumoto, T. New Stable Icosahedral Al-Cu-Ru and Al-Cu-Os Alloys. Jpn. J. Appl. Phys. 1988, 27, L1587. [Google Scholar] [CrossRef]
- Levine, D.; Steinhardt, P.J. Quasicrystals: A New Class of Ordered Structures. Phys. Rev. Lett. 1984, 53, 2477. [Google Scholar] [CrossRef]
- Levine, D.; Steinhardt, P.J. Quasicrystals. I. Definition and structure. Phys. Rev. B 1986, 34, 596. [Google Scholar] [CrossRef] [PubMed]
- Koga, A.; Tsunetsugu, H. Antiferromagnetic order in the Hubbard model on the Penrose lattice. Phys. Rev. B 2017, 96, 214402. [Google Scholar] [CrossRef]
- Sakai, S.; Arita, R.; Ohtsuki, T. Hyperuniform electron distributions controlled by electron interactions in quasicrystals. Phys. Rev. B 2022, 105, 054202. [Google Scholar] [CrossRef]
- Wessel, S.; Milat, I. Quantum fluctuations and excitations in antiferromagnetic quasicrystals. Phys. Rev. B 2005, 71, 104427. [Google Scholar] [CrossRef]
- Jagannathan, A.; Szallas, A.; Wessel, S.; Duneau, M. Penrose quantum antiferromagnet. Phys. Rev. B 2007, 75, 212407. [Google Scholar] [CrossRef]
- Wessel, S.; Jagannathan, A.; Haas, S. Quantum Antiferromagnetism in Quasicrystals. Phys. Rev. Lett. 2003, 90, 177205. [Google Scholar] [CrossRef] [PubMed]
- Sandvik, A.W. Finite-size scaling of the ground-state parameters of the two-dimensional Heisenberg model. Phys. Rev. B 1997, 56, 11678. [Google Scholar] [CrossRef]
- Szallas, A.; Jagannathan, A. Spin waves and local magnetizations on the Penrose tiling. Phys. Rev. B 2008, 77, 104427. [Google Scholar] [CrossRef]
- Inoue, T.; Yamamoto, S. Optical Observation of Quasiperiodic Heisenberg Antiferromagnets in Two Dimensions. Phys. Status Solidi B 2020, 257, 2000118. [Google Scholar] [CrossRef]
- Inoue, T.; Yamamoto, S. Polarized Raman Response of Two-Dimensional Quasiperiodic Antiferromagnets: Configuration-Interaction versus Green’s Function Approaches. J. Phys. Soc. Jpn. 2022, 91, 053701. [Google Scholar] [CrossRef]
- Sato, T.J.; Takakura, H.; Tsai, A.P.; Shibata, K.; Ohoyama, K.; Andersen, K.H. Antiferromagnetic spin correlations in the Zn-Mg-Ho icosahedral quasicrystal. Phys. Rev. B 2000, 61, 476. [Google Scholar] [CrossRef]
- Sato, T.J.; Takakura, H.; Tsai, A.P.; Shibata, K. Magnetic excitations in the Zn-Mg-Tb icosahedral quasicrystal: An inelastic neutron scattering study. Phys. Rev. B 2006, 73, 054417. [Google Scholar] [CrossRef]
- Sato, T.J.; Kashimoto, S.; Masuda, C.; Onimaru, T.; Nakanowatari, I.; Iida, K.; Morinaga, R.; Ishimasa, T. Neutron scattering study on spin correlations and fluctuations in the transition-metal-based magnetic quasicrystal Zn-Fe-Sc. Phys. Rev. B 2008, 77, 014437. [Google Scholar] [CrossRef]
- Guidoni, L.; Triché, C.; Verkerk, P.; Grynberg, G. Quasiperiodic Optical Lattices. Phys. Rev. Lett. 1997, 79, 3363. [Google Scholar] [CrossRef]
- Viebahn, K.; Sbroscia, M.; Carter, E.; Yu, J.-C.; Schneider, U. Matter-Wave Diffraction from a Quasicrystalline Optical Lattice. Phys. Rev. Lett. 2019, 122, 110404. [Google Scholar] [CrossRef] [PubMed]
- Sbroscia, M.; Viebahn, K.; Carter, E.; Yu, J.-C.; Gaunt, A.; Schneider, U. Observing Localization in a 2D Quasicrystalline Optical Lattice. Phys. Rev. Lett. 2020, 125, 200604. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Palencia, L.; Santos, L. Bose-Einstein condensates in optical quasicrystal lattices. Phys. Rev. A 2005, 72, 053607. [Google Scholar] [CrossRef]
- Jagannathan, A.; Duneau, M. An eightfold optical quasicrystal with cold atoms. Europhys. Lett. 2013, 104, 66003. [Google Scholar] [CrossRef]
- Jagannathan, A.; Duneau, M. The eight-fold way for optical quasicrystals. Eur. Phys. J. B 2014, 87, 149. [Google Scholar] [CrossRef]
- Duan, L.-M.; Demler, E.; Lukin, M.D. Controlling Spin Exchange Interactions of Ultracold Atoms in Optical Lattices. Phys. Rev. Lett. 2003, 91, 090402. [Google Scholar] [CrossRef] [PubMed]
- Lifshitz, R. What is a crystal? Z. Kristallogr. 2007, 222, 313. [Google Scholar] [CrossRef]
- Ghadimi, R.; Sugimoto, T.; Tohyama, T. Mean-field study of the Bose-Hubbard model in the Penrose lattice. Phys. Rev. B 2020, 102, 224201. [Google Scholar] [CrossRef]
- Koga, A. Superlattice structure in the antiferromagnetically ordered state in the Hubbard model on the Ammann-Beenker tiling. Phys. Rev. B 2020, 102, 115125. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field Dependence of the Intrinsic Domain Magnetization of a Ferromagnet. Phys. Rev. 1940, 58, 1098. [Google Scholar] [CrossRef]
- Yamamoto, S.; Fukui, T.; Maisinger, K.; Schollwöck, U. Combination of ferromagnetic and antiferromagnetic features in Heisenberg ferrimagnets. J. Phys. Condens. Matter 1998, 10, 11033. [Google Scholar] [CrossRef]
- Noriki, Y.; Yamamoto, S. Modified Spin-Wave Theory on Low-Dimensional Heisenberg Ferrimagnets: A New Robust Formulation. J. Phys. Soc. Jpn. 2017, 86, 034714. [Google Scholar] [CrossRef]
- Yamamoto, S.; Noriki, Y. Spin-wave thermodynamics of square-lattice antiferromagnets revisited. Phys. Rev. B 2019, 99, 094412. [Google Scholar] [CrossRef]
- Yamamoto, S. Bosonic representation on one-dimensional Heisenberg ferrimagnets. Phys. Rev. B 2004, 69, 064426. [Google Scholar] [CrossRef]
- Brehmer, S.; Mikeska, H.-J.; Yamamoto, S. Low-temperature properties of quantum antiferromagnetic chains with alternating spins S=1 and S=1/2. J. Phys. Condens. Matter 1997, 9, 3921. [Google Scholar] [CrossRef]
- Yamamoto, S.; Fukui, T. Thermodynamic properties of Heisenberg ferrimagnetic spin chains: Ferromagnetic-antiferromagnetic crossover. Phys. Rev. B 1998, 57, R14008(R). [Google Scholar] [CrossRef]
- Louisell, W.H. Radiation and Noise in Quantum Electronics; McGraw-Hill: New York, NY, USA, 1964; p. 101. [Google Scholar]
- Messio, L.; Cépas, O.; Lhuillier, C. Schwinger-boson approach to the kagome antiferromagnet with Dzyaloshinskii-Moriya interactions: Phase diagram and dynamical structure factors. Phys. Rev. B 2010, 81, 064428. [Google Scholar] [CrossRef]
- Chernyshev, A.L.; Zhitomirsky, M.E. Order and excitations in large-S kagome-lattice antiferromagnets. Phys. Rev. B 2015, 92, 144415. [Google Scholar] [CrossRef]
- Yamamoto, S.; Ohara, J. Thermal features of Heisenberg antiferromagnets on edge- versus corner-sharing triangular-based lattices: A message from spin waves. J. Phys. Commun. 2023, 7, 065004. [Google Scholar] [CrossRef]
- Harris, A.B.; Kallin, C.; Berlinsky, A.J. Possible Néel orderings of the Kagomé antiferromagnet. Phys. Rev. B 1992, 45, 2899. [Google Scholar] [CrossRef] [PubMed]
- Syromyatnikov, A.V. Spectrum of short-wavelength magnons in a two-dimensional quantum Heisenberg antiferromagnet on a square lattice: Third-order expansion in 1/S. J. Phys. Condens. Matter 2010, 22, 216003. [Google Scholar] [CrossRef] [PubMed]
- Auerbach, A.; Arovas, D.P. Spin dynamics in the square-lattice antiferromagnet. Phys. Rev. Lett. 1988, 61, 617. [Google Scholar] [CrossRef] [PubMed]
- Jagannathan, A. Self-similarity under inflation and level statistics: A study in two dimensions. Phys. Rev. B 2000, 61, R834. [Google Scholar] [CrossRef]
- Fazekas, P. Lecture Notes on Electron Correlations and Magnetism; World Scientific: Singapore, 1999. [Google Scholar]
- Noda, K.; Koga, A.; Kawakami, N.; Pruschke, T. Ferromagnetism of cold fermions loaded into a decorated square lattice. Phys. Rev. A 2009, 80, 063622. [Google Scholar] [CrossRef]



| D () | Q () | K () | J () | S () | S5 () | S4 () | S3 () | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | (1;0) | (0;0) | (0;1) | (0;1) | (0;0) | (0;0) | (0;1) | (0;0) | 15 |
| 2 | (1;0) | (0;0) | (0;1) | (0;1) | (0;0) | (0;0) | (0;0) | (0;1) | 16 |
| 3 | (1;0) | (0;0) | (0;0) | (0;2) | (0;1) | (0;0) | (0;0) | (0;0) | 15 |
| 4 | (1;0) | (0;0) | (0;0) | (0;1) | (0;1) | (0;0) | (0;0) | (0;1) | 17 |
| 5 | (0;0) | (1;0) | (0;0) | (0;2) | (0;0) | (0;0) | (0;1) | (0;0) | 16 |
| 6 | (0;0) | (1;0) | (0;0) | (0;2) | (0;0) | (0;0) | (0;0) | (0;1) | 17 |
| 7 | (0;2) | (0;0) | (1;0) | (0;2) | (0;0) | (0;0) | (0;0) | (0;0) | 16 |
| 8 | (0;2) | (0;2) | (0;0) | (1;0) | (0;0) | (0;1) | (0;0) | (0;0) | 17 |
| 9 | (0;2) | (0;2) | (0;0) | (1;0) | (0;0) | (0;0) | (0;1) | (0;0) | 18 |
| 10 | (0;2) | (0;1) | (0;1) | (1;0) | (0;0) | (0;0) | (0;1) | (0;0) | 19 |
| 11 | (0;2) | (0;0) | (0;2) | (1;0) | (0;0) | (0;0) | (0;0) | (0;1) | 21 |
| 12 | (0;5) | (0;0) | (0;0) | (0;0) | (1;0) | (0;0) | (0;0) | (0;0) | 15 |
| 13 | (0;0) | (0;0) | (0;0) | (0;5) | (0;0) | (1;0) | (0;0) | (0;0) | 25 |
| 14 | (0;2) | (0;1) | (0;0) | (0;3) | (0;0) | (0;0) | (1;0) | (0;0) | 24 |
| 15 | (0;4) | (0;2) | (0;0) | (0;1) | (0;0) | (0;0) | (0;0) | (1;0) | 23 |
| D () | Q () | K () | J () | S () | S5 () | S4 () | S3 () | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | (1;0,2) | (0;0,2) | (0;1,0) | (0;1,4) | (0;0,0) | (0;0,1) | (0;1,0) | (0;0,0) | 15 |
| 2 | (1;0,4) | (0;0,3) | (0;1,0) | (0;1,2) | (0;0,0) | (0;0,1) | (0;0,0) | (0;1,0) | 16 |
| 3 | (1;0,4) | (0;0,3) | (0;1,0) | (0;1,2) | (0;0,0) | (0;0,0) | (0;0,1) | (0;1,0) | 16 |
| 4 | (1;0,4) | (0;0,2) | (0;0,1) | (0;2,0) | (0;1,0) | (0;0,0) | (0;0,2) | (0;0,0) | 15 |
| 5 | (1;0,4) | (0;0,1) | (0;0,2) | (0;2,0) | (0;1,0) | (0;0,0) | (0;0,1) | (0;0,1) | 15 |
| 6 | (1;0,4) | (0;0,0) | (0;0,3) | (0;2,0) | (0;1,0) | (0;0,0) | (0;0,0) | (0;0,2) | 15 |
| 7 | (1;0,6) | (0;0,3) | (0;0,0) | (0;1,1) | (0;1,0) | (0;0,1) | (0;0,0) | (0;1,0) | 17 |
| 8 | (1;0,6) | (0;0,2) | (0;0,1) | (0;1,1) | (0;1,0) | (0;0,0) | (0;0,1) | (0;1,0) | 17 |
| 9 | (0;0,4) | (1;0,2) | (0;0,0) | (0;2,3) | (0;0,0) | (0;0,1) | (0;1,0) | (0;0,0) | 16 |
| 10 | (0;0,6) | (1;0,3) | (0;0,0) | (0;2,1) | (0;0,0) | (0;0,1) | (0;0,0) | (0;1,0) | 17 |
| 11 | (0;0,6) | (1;0,2) | (0;0,1) | (0;2,1) | (0;0,0) | (0;0,0) | (0;0,1) | (0;1,0) | 17 |
| 12 | (0;2,3) | (0;0,2) | (1;0,0) | (0;2,1) | (0;0,0) | (0;0,0) | (0;0,2) | (0;0,0) | 16 |
| 13 | (0;2,3) | (0;0,1) | (1;0,1) | (0;2,1) | (0;0,0) | (0;0,0) | (0;0,1) | (0;0,1) | 16 |
| 14 | (0;2,3) | (0;0,0) | (1;0,2) | (0;2,1) | (0;0,0) | (0;0,0) | (0;0,0) | (0;0,2) | 16 |
| 15 | (0;2,0) | (0;2,0) | (0;0,1) | (1;0,4) | (0;0,0) | (0;1,0) | (0;0,2) | (0;0,0) | 17 |
| 16 | (0;2,0) | (0;2,0) | (0;0,1) | (1;0,4) | (0;0,0) | (0;1,0) | (0;0,1) | (0;0,1) | 17 |
| 17 | (0;2,0) | (0;2,0) | (0;0,1) | (1;0,4) | (0;0,0) | (0;1,0) | (0;0,0) | (0;0,2) | 17 |
| 18 | (0;2,0) | (0;2,0) | (0;0,0) | (1;0,4) | (0;0,1) | (0;1,0) | (0;0,0) | (0;0,2) | 17 |
| 19 | (0;2,2) | (0;2,1) | (0;0,1) | (1;0,2) | (0;0,0) | (0;0,0) | (0;1,0) | (0;0,2) | 18 |
| 20 | (0;2,3) | (0;1,1) | (0;1,0) | (1;0,3) | (0;0,1) | (0;0,0) | (0;1,0) | (0;0,1) | 19 |
| 21 | (0;2,6) | (0;0,2) | (0;2,0) | (1;0,2) | (0;0,1) | (0;0,0) | (0;0,0) | (0;1,0) | 21 |
| 22 | (0;5,0) | (0;0,0) | (0;0,0) | (0;0,5) | (1;0,0) | (0;0,0) | (0;0,0) | (0;0,0) | 15 |
| 23 | (0;5,0) | (0;0,0) | (0;0,0) | (0;0,4) | (1;0,0) | (0;0,0) | (0;0,0) | (0;0,1) | 15 |
| 24 | (0;5,0) | (0;0,0) | (0;0,0) | (0;0,3) | (1;0,0) | (0;0,0) | (0;0,0) | (0;0,2) | 15 |
| 25 | (0;0,10) | (0;0,5) | (0;0,0) | (0;5,0) | (0;0,0) | (1;0,0) | (0;0,0) | (0;0,0) | 25 |
| 26 | (0;2,6) | (0;1,2) | (0;0,2) | (0;3,2) | (0;0,0) | (0;0,0) | (1;0,0) | (0;0,0) | 24 |
| 27 | (0;4,2) | (0;2,0) | (0;0,2) | (0;1,4) | (0;0,1) | (0;0,0) | (0;0,0) | (1;0,0) | 23 |
| D () | Q () | K () | J () | S () | S5 () | S4 () | S3 () | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | (1;0,2,7) | (0;0,2,3) | (0;1,0,1) | (0;1,4,4) | (0;0,0,0) | (0;0,1,0) | (0;1,0,1) | (0;0,0,0) | 15 |
| 2 | (1;0,2,7) | (0;0,2,2) | (0;1,0,2) | (0;1,4,4) | (0;0,0,0) | (0;0,1,0) | (0;1,0,0) | (0;0,0,1) | 15 |
| 3 | (1;0,4,3) | (0;0,3,1) | (0;1,0,1) | (0;1,2,6) | (0;0,0,1) | (0;0,1,0) | (0;0,0,1) | (0;1,0,0) | 16 |
| 4 | (1;0,4,3) | (0;0,3,0) | (0;1,0,2) | (0;1,2,6) | (0;0,0,1) | (0;0,1,0) | (0;0,0,0) | (0;1,0,1) | 16 |
| 5 | (1;0,4,5) | (0;0,3,1) | (0;1,0,2) | (0;1,2,4) | (0;0,0,1) | (0;0,0,0) | (0;0,1,0) | (0;1,0,1) | 16 |
| 6 | (1;0,4,4) | (0;0,2,2) | (0;0,1,0) | (0;2,0,5) | (0;1,0,0) | (0;0,0,0) | (0;0,2,0) | (0;0,0,2) | 15 |
| 7 | (1;0,4,7) | (0;0,1,3) | (0;0,2,0) | (0;2,0,4) | (0;1,0,0) | (0;0,0,0) | (0;0,1,0) | (0;0,1,1) | 15 |
| 8 | (1;0,4,10) | (0;0,0,4) | (0;0,3,0) | (0;2,0,3) | (0;1,0,0) | (0;0,0,0) | (0;0,0,0) | (0;0,2,0) | 15 |
| 9 | (1;0,4,10) | (0;0,0,4) | (0;0,3,0) | (0;2,0,2) | (0;1,0,0) | (0;0,0,0) | (0;0,0,0) | (0;0,2,1) | 15 |
| 10 | (1;0,6,2) | (0;0,3,0) | (0;0,0,2) | (0;1,1,7) | (0;1,0,0) | (0;0,1,0) | (0;0,0,0) | (0;1,0,1) | 17 |
| 11 | (1;0,6,5) | (0;0,2,1) | (0;0,1,2) | (0;1,1,6) | (0;1,0,0) | (0;0,0,0) | (0;0,1,0) | (0;1,0,0) | 17 |
| 12 | (1;0,6,5) | (0;0,2,1) | (0;0,1,2) | (0;1,1,5) | (0;1,0,0) | (0;0,0,0) | (0;0,1,0) | (0;1,0,1) | 17 |
| 13 | (0;0,4,6) | (1;0,2,2) | (0;0,0,2) | (0;2,3,3) | (0;0,0,0) | (0;0,1,0) | (0;1,0,2) | (0;0,0,0) | 16 |
| 14 | (0;0,4,6) | (1;0,2,2) | (0;0,0,2) | (0;2,3,3) | (0;0,0,0) | (0;0,1,0) | (0;1,0,1) | (0;0,0,1) | 16 |
| 15 | (0;0,4,6) | (1;0,2,2) | (0;0,0,2) | (0;2,3,3) | (0;0,0,0) | (0;0,1,0) | (0;1,0,0) | (0;0,0,2) | 16 |
| 16 | (0;0,6,2) | (1;0,3,0) | (0;0,0,2) | (0;2,1,5) | (0;0,0,1) | (0;0,1,0) | (0;0,0,1) | (0;1,0,1) | 17 |
| 17 | (0;0,6,2) | (1;0,3,0) | (0;0,0,2) | (0;2,1,5) | (0;0,0,1) | (0;0,1,0) | (0;0,0,0) | (0;1,0,2) | 17 |
| 18 | (0;0,6,5) | (1;0,2,1) | (0;0,1,2) | (0;2,1,4) | (0;0,0,1) | (0;0,0,0) | (0;0,1,0) | (0;1,0,1) | 17 |
| 19 | (0;2,3,2) | (0;0,2,2) | (1;0,0,0) | (0;2,1,4) | (0;0,0,1) | (0;0,0,1) | (0;0,2,0) | (0;0,0,2) | 16 |
| 20 | (0;2,3,5) | (0;0,1,3) | (1;0,1,0) | (0;2,1,3) | (0;0,0,1) | (0;0,0,1) | (0;0,1,0) | (0;0,1,1) | 16 |
| 21 | (0;2,3,8) | (0;0,0,4) | (1;0,2,0) | (0;2,1,2) | (0;0,0,1) | (0;0,0,1) | (0;0,0,0) | (0;0,2,0) | 16 |
| 22 | (0;2,3,8) | (0;0,0,4) | (1;0,2,0) | (0;2,1,2) | (0;0,0,1) | (0;0,0,0) | (0;0,0,1) | (0;0,2,0) | 16 |
| 23 | (0;2,0,8) | (0;2,0,3) | (0;0,1,0) | (1;0,4,6) | (0;0,0,0) | (0;1,0,0) | (0;0,2,0) | (0;0,0,0) | 17 |
| 24 | (0;2,0,10) | (0;2,0,4) | (0;0,1,0) | (1;0,4,4) | (0;0,0,0) | (0;1,0,0) | (0;0,1,0) | (0;0,1,0) | 17 |
| 25 | (0;2,0,12) | (0;2,0,5) | (0;0,1,0) | (1;0,4,2) | (0;0,0,0) | (0;1,0,0) | (0;0,0,0) | (0;0,2,0) | 17 |
| 26 | (0;2,0,13) | (0;2,0,5) | (0;0,0,0) | (1;0,4,2) | (0;0,1,0) | (0;1,0,0) | (0;0,0,0) | (0;0,2,0) | 17 |
| 27 | (0;2,2,8) | (0;2,1,2) | (0;0,1,2) | (1;0,2,4) | (0;0,0,0) | (0;0,0,0) | (0;1,0,0) | (0;0,2,0) | 18 |
| 28 | (0;2,3,8) | (0;1,1,3) | (0;1,0,1) | (1;0,3,3) | (0;0,1,0) | (0;0,0,0) | (0;1,0,1) | (0;0,1,0) | 19 |
| 29 | (0;2,3,8) | (0;1,1,2) | (0;1,0,2) | (1;0,3,3) | (0;0,1,0) | (0;0,0,0) | (0;1,0,0) | (0;0,1,1) | 19 |
| 30 | (0;2,6,3) | (0;0,2,1) | (0;2,0,1) | (1;0,2,4) | (0;0,1,1) | (0;0,0,0) | (0;0,0,1) | (0;1,0,1) | 21 |
| 31 | (0;2,6,3) | (0;0,2,0) | (0;2,0,2) | (1;0,2,4) | (0;0,1,1) | (0;0,0,0) | (0;0,0,0) | (0;1,0,2) | 21 |
| 32 | (0;5,0,0) | (0;0,0,0) | (0;0,0,5) | (0;0,5,0) | (1;0,0,0) | (0;0,0,0) | (0;0,0,0) | (0;0,0,5) | 15 |
| 33 | (0;5,0,2) | (0;0,0,2) | (0;0,0,3) | (0;0,4,1) | (1;0,0,0) | (0;0,0,0) | (0;0,0,2) | (0;0,1,2) | 15 |
| 34 | (0;5,0,4) | (0;0,0,4) | (0;0,0,1) | (0;0,3,2) | (1;0,0,0) | (0;0,0,1) | (0;0,0,2) | (0;0,2,0) | 15 |
| 35 | (0;0,10,0) | (0;0,5,0) | (0;0,0,5) | (0;5,0,0) | (0;0,0,0) | (1;0,0,0) | (0;0,0,5) | (0;0,0,0) | 25 |
| 36 | (0;0,10,0) | (0;0,5,0) | (0;0,0,4) | (0;5,0,0) | (0;0,0,1) | (1;0,0,0) | (0;0,0,3) | (0;0,0,2) | 25 |
| 37 | (0;0,10,0) | (0;0,5,0) | (0;0,0,3) | (0;5,0,0) | (0;0,0,2) | (1;0,0,0) | (0;0,0,1) | (0;0,0,4) | 25 |
| 38 | (0;2,6,2) | (0;1,2,2) | (0;0,2,1) | (0;3,2,2) | (0;0,0,2) | (0;0,0,1) | (1;0,0,0) | (0;0,0,2) | 24 |
| 39 | (0;4,2,5) | (0;2,0,3) | (0;0,2,1) | (0;1,4,2) | (0;0,1,1) | (0;0,0,1) | (0;0,0,1) | (1;0,0,0) | 23 |
| 40 | (0;4,2,5) | (0;2,0,2) | (0;0,2,2) | (0;1,4,2) | (0;0,1,1) | (0;0,0,0) | (0;0,0,2) | (1;0,0,0) | 23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamamoto, S.; Inoue, T. Magnon Confinement on the Two-Dimensional Penrose Lattice: Perpendicular-Space Analysis of the Dynamic Structure Factor. Crystals 2024, 14, 702. https://doi.org/10.3390/cryst14080702
Yamamoto S, Inoue T. Magnon Confinement on the Two-Dimensional Penrose Lattice: Perpendicular-Space Analysis of the Dynamic Structure Factor. Crystals. 2024; 14(8):702. https://doi.org/10.3390/cryst14080702
Chicago/Turabian StyleYamamoto, Shoji, and Takashi Inoue. 2024. "Magnon Confinement on the Two-Dimensional Penrose Lattice: Perpendicular-Space Analysis of the Dynamic Structure Factor" Crystals 14, no. 8: 702. https://doi.org/10.3390/cryst14080702
APA StyleYamamoto, S., & Inoue, T. (2024). Magnon Confinement on the Two-Dimensional Penrose Lattice: Perpendicular-Space Analysis of the Dynamic Structure Factor. Crystals, 14(8), 702. https://doi.org/10.3390/cryst14080702






