General Properties of Conventional and High-Temperature Superconductors
Abstract
:1. Introduction
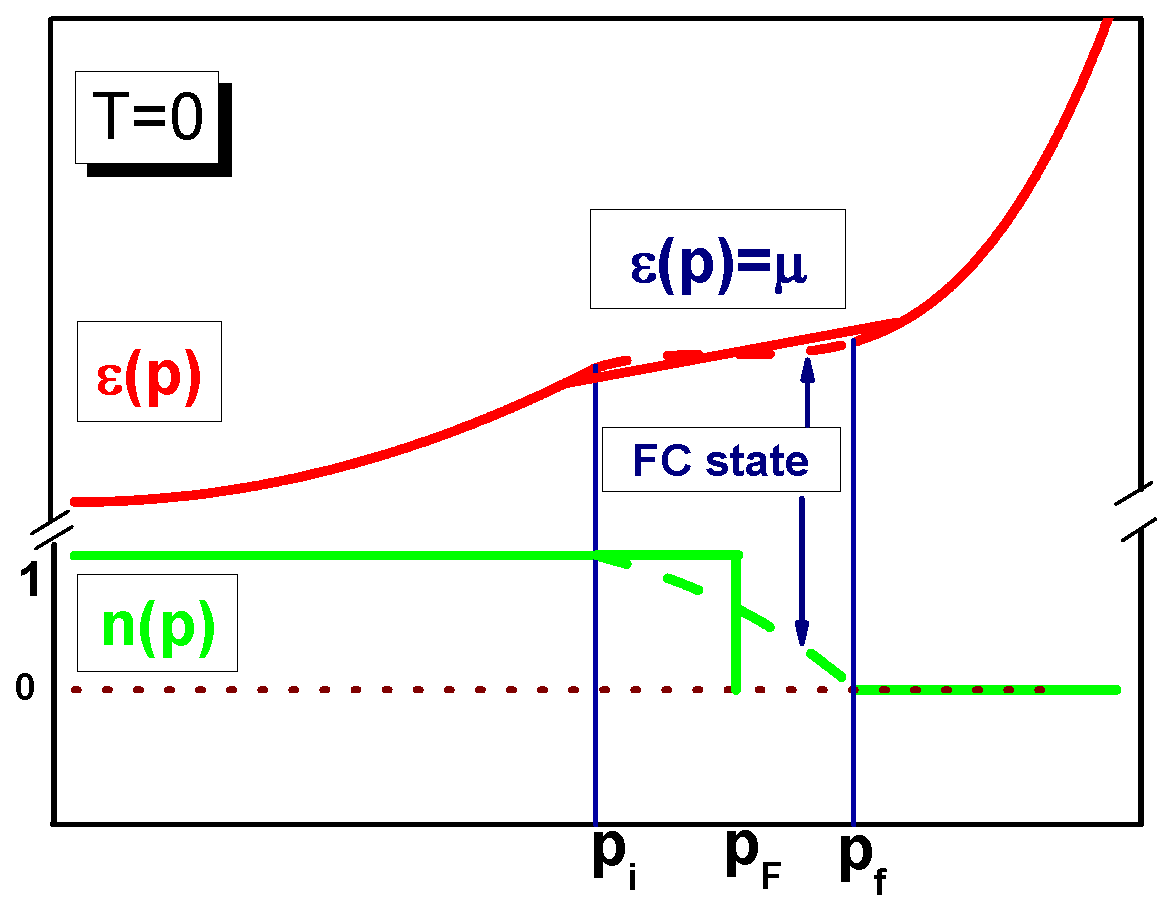
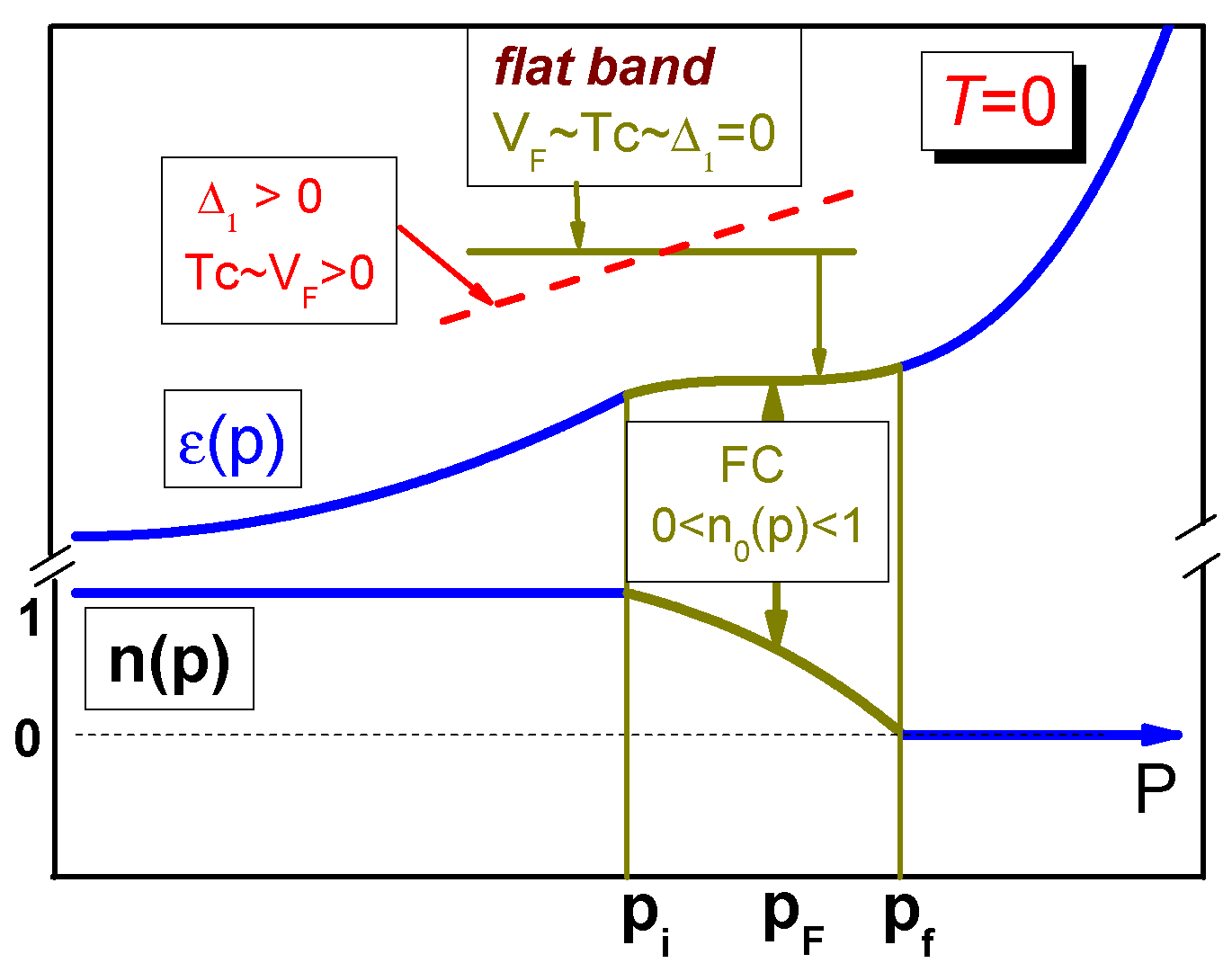
2. Superconducting Systems with the FC State at
3. Validity of the Quasiparticle Pattern
3.1. Finite Systems
3.2. Macroscopic Systems
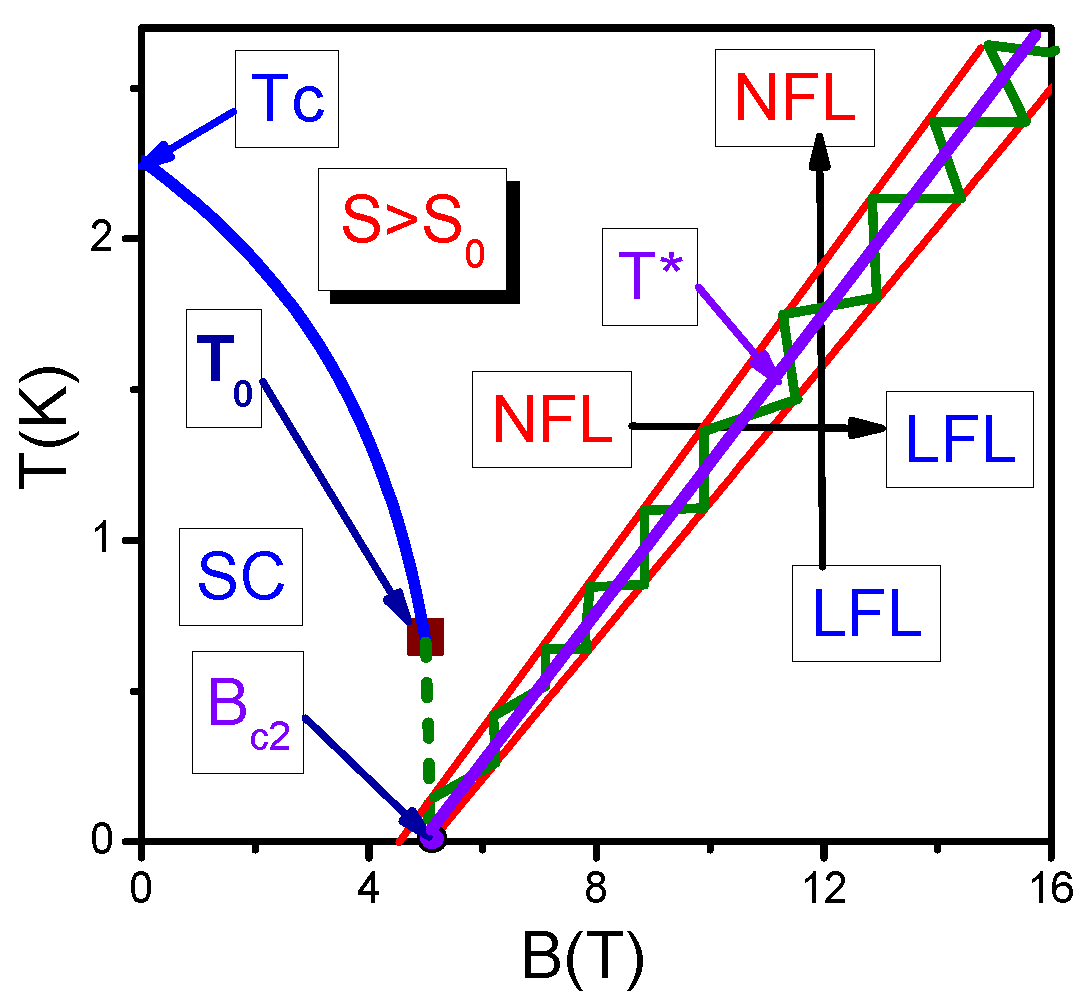
4. Superconducting State with FC at Finite Temperatures
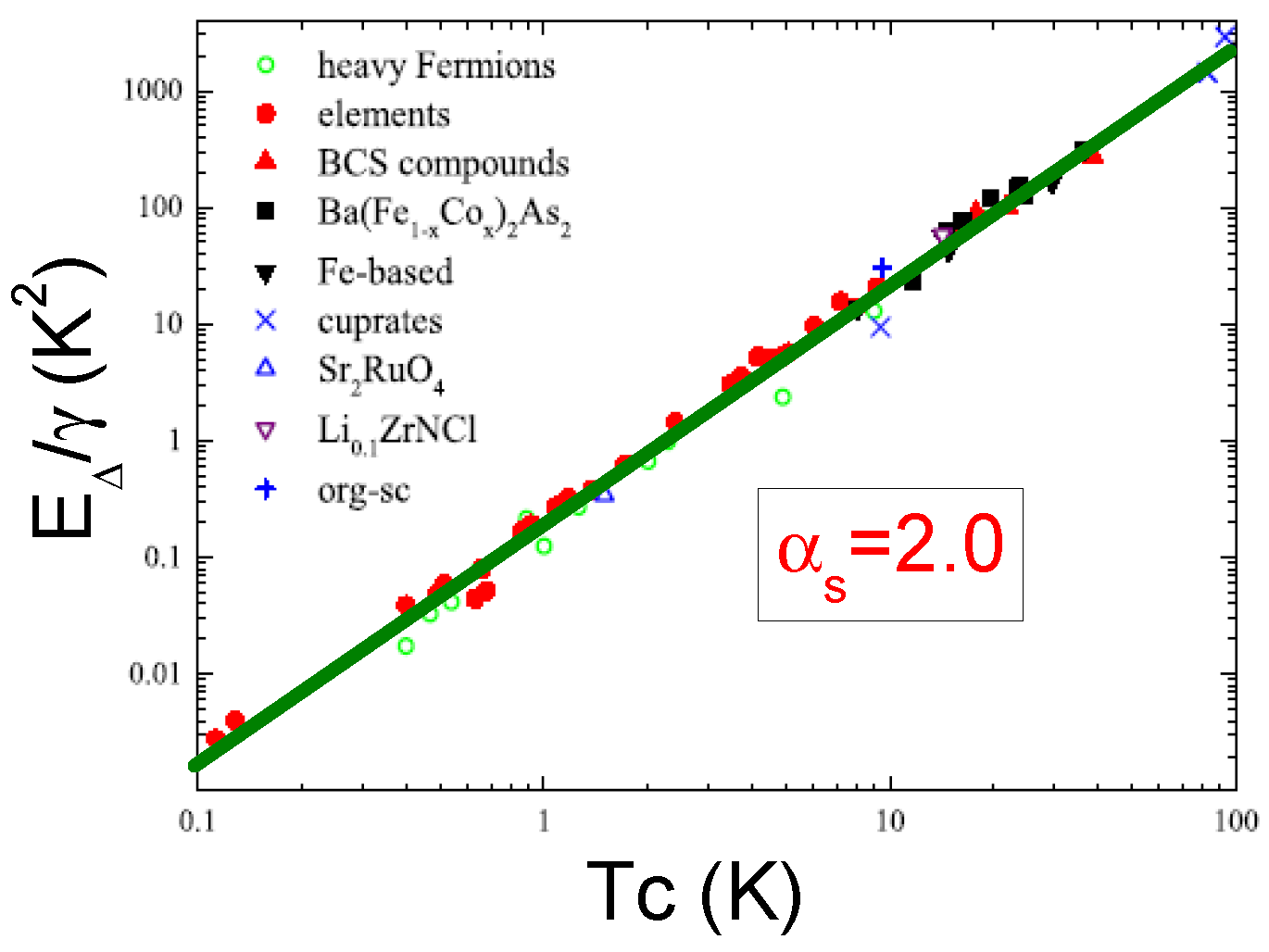
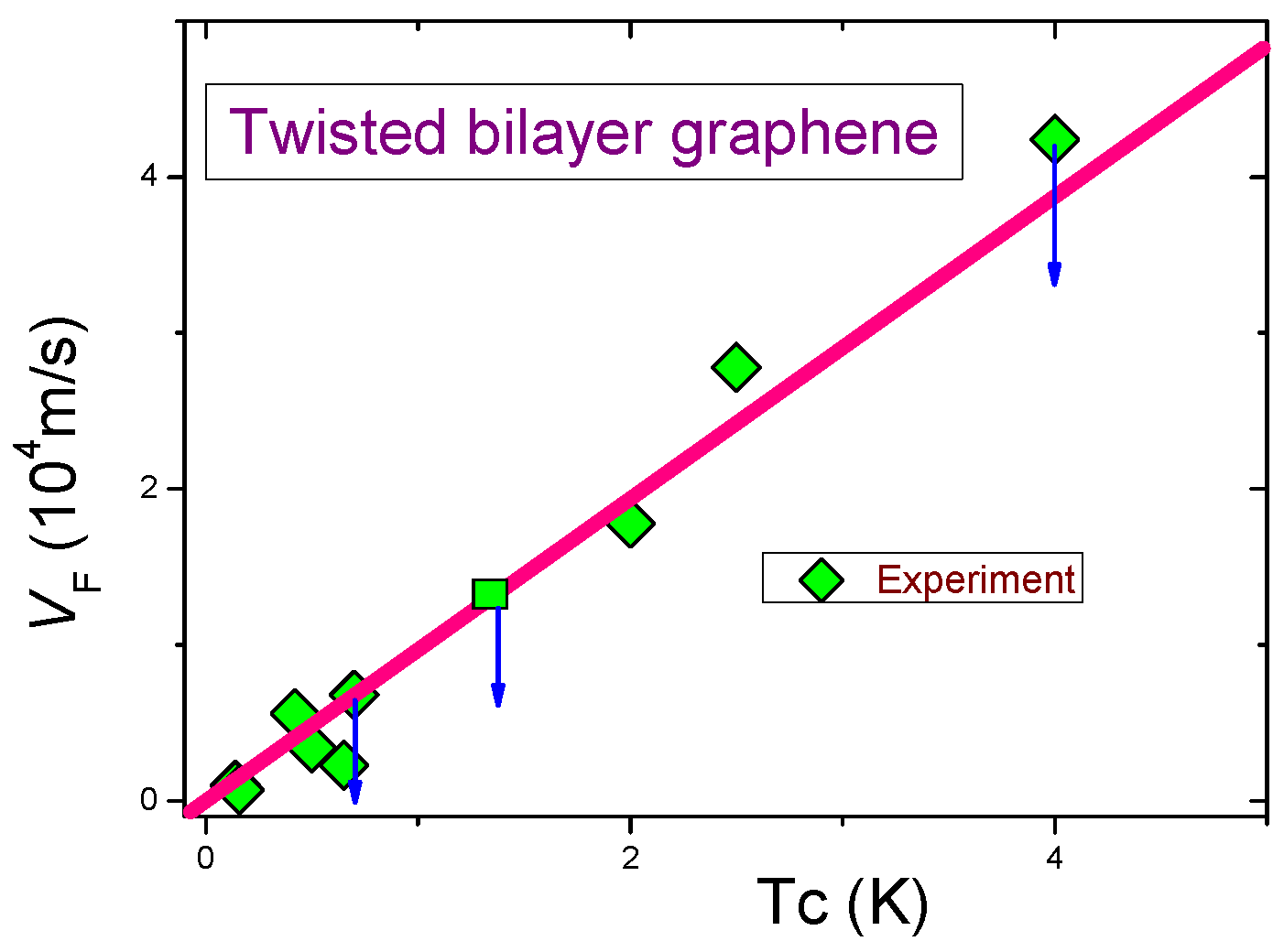
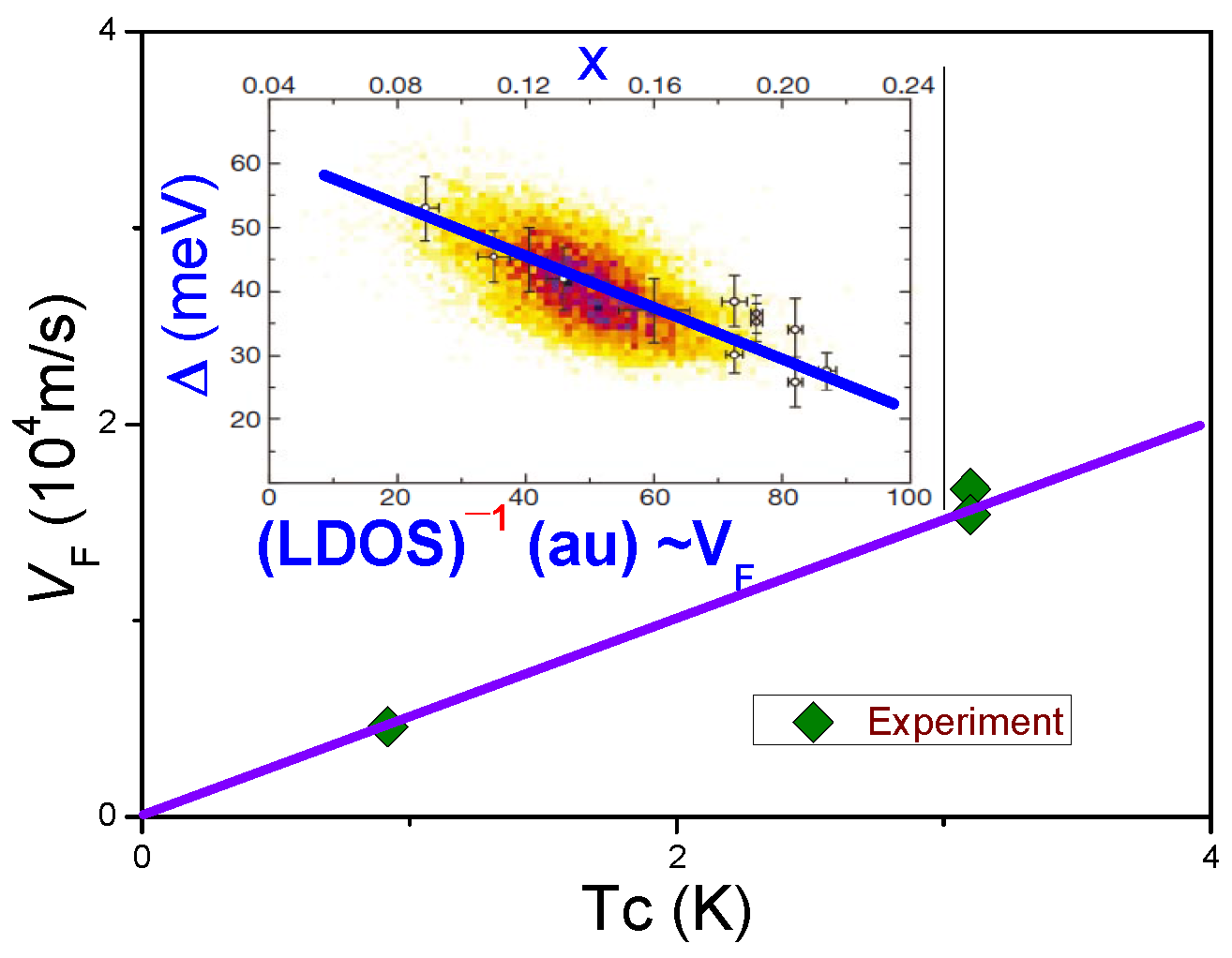
5. General Behavior of the Scaled Condensation Energy of Conventional and Unconventional Superconductors
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Regnault, N.; Xu, Y.; Li, M.-R.; Ma, D.-S.; Jovanovic, M.; Bernevig, B.A.; Yazdani, A.; Cava, R.J.; Ong, N.P.; Schoop, L.M.; et al. Catalogue of flat-band stoichiometric materials. Nature 2022, 603, 824. [Google Scholar] [CrossRef] [PubMed]
- Coleman, P.; Pèpin, C.; Si, Q.; Ramazashvili, R. How do Fermi liquids get heavy and die? J. Phys. Condens. Matt. 2001, 13, R723. [Google Scholar] [CrossRef]
- Chen, L.; Lowder, D.T.; Bakali, E.; Andrews, A.M.; Schrenk, W.; Waas, M.; Natelson, D.; Setty, C.; Si, Q.; Sur, S.; et al. Shot noise in a strange metal. Science 2023, 382, 907. [Google Scholar] [CrossRef] [PubMed]
- Matsui, H.; Sato, T.; Takahashi, T.; Wang, S.-C.; Yang, H.-B.; Ding, H.; Fujii, T.; Watanabe, T.; Matsuda, A. BCS-like Bogoliubov Quasiparticles in High-Tc Superconductors Observed by Angle-Resolved Photoemission Spectroscopy. Phys. Rev. Lett. 2003, 90, 217002. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.S.; Tam, G.N.; Stewart, G.R. Universal scaling law for the condensation energy across a broad range of superconductor classes. Phys. Rev. B 2015, 92, 224509. [Google Scholar] [CrossRef]
- Hunter, A.; Beck, S.; Cappelli, E.; Margot, F.; Straub, M.; Alexanian, Y.; Tamai, A.; Zingl, M.; Mravlje, J.; Georges, A.; et al. Fate of Quasiparticles at High Temperature in the Correlated Metal Sr2RuO4. Phys. Rev. Lett. 2023, 131, 236502. [Google Scholar] [CrossRef]
- Xu, K.-J.; Guo, Q.; Hashimoto, M.; Li, Z.-X.; Chen, S.-D.; He, J.; Shen, Z.X.; Tjernberg, O.; Lee, D.-H.; Lu, D.-H.; et al. Bogoliubov quasiparticle on the gossamer Fermi surface in electron-doped cuprates. Nat. Phys. 2023, 19, 1834. [Google Scholar] [CrossRef]
- Qin, W.; Zou, B.; MacDonald, A.H. Critical magnetic fields and electron pairing in magic-angle twisted bilayer graphene. Phys. Rev. B 2023, 107, 024509. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Msezane, A.Z.; Amusia, M.Y.; Japaridze, G.S. Effect of superconductivity on the shape of flat bands. Europhys. Lett. 2022, 138, 16004. [Google Scholar] [CrossRef]
- Volovik, G.E. From standard model of particle physics to room-temperature superconductivity. Phys. Scr. 2015, T164, 014014. [Google Scholar] [CrossRef]
- Khodel, V.A.; Clark, J.W.; Zverev, M.V. Topological disorder triggered by interaction-induced flattening of electron spectra in solids. Phys. Rev. B 2020, 102, 201108. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Shaginyan, V.R. Strongly Correlated Fermi Systems: A New State of Matter; Springer Tracts in Modern Physics; Springer Nature: Cham, Switzerland, 2020; Volume 283. [Google Scholar]
- Törmä, P.; Peotta, S.; Bernevig, B.A. Superconductivity, superfluidity and quantum geometry in twisted multilayer systems. Nat. Rev. Phys. 2022, 4, 528. [Google Scholar] [CrossRef]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Pitaevskii, L. Statistical Physics, Part 2; Butterworth-Heinemann: Oxford, UK, 2002. [Google Scholar]
- Khodel, V.A.; Shaginyan, V.R. Superfluidity in system with fermion condensate. JETP Lett. 1990, 51, 553. [Google Scholar]
- Volovik, G.E. A new class of normal Fermi liquids. JETP Lett. 1991, 53, 222. [Google Scholar]
- Shaginyan, V.R.; Amusia, M.Y.; Msezane, A.Z.; Popov, K.G. Scaling behavior of heavy fermion metals. Phys. Rep. 2010, 492, 31. [Google Scholar] [CrossRef]
- Heikkila, T.T.; Volovik, G.E. Flat Bands as a Route to High-Temperature Superconductivity in Graphite; Springer Series in Materials Science; Springer Nature: Cham, Switzerland, 2016; Volume 244. [Google Scholar]
- Rosenzweig, P.; Karakachian, H.; Marchenko, D.; Küster, K.; Starke, U. Overdoping Graphene beyond the van Hove Singularity. Phys. Rev. Lett. 2020, 125, 176403. [Google Scholar] [CrossRef]
- Peri, V.; Song, Z.D.; Bernevig, B.A.; Huber, S.D. Fragile Topology and Flat-Band Superconductivity in the Strong-Coupling Regime. Phys. Rev. Lett. 2021, 126, 027002. [Google Scholar] [CrossRef] [PubMed]
- Peotta, S.; Törmä, P. Superfluidity in topologically nontrivial flat bands. Nat. Commun. 2015, 6, 8944. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175. [Google Scholar] [CrossRef]
- Bennemann, K.H.; Ketterson, J.B. Superconductivity; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Amusia, M.Y.; Shaginyan, V.R. Quasiparticle picture of high-temperature superconductors in the frame of a Fermi liquid with the fermion condensate. Phys. Rev. B 2001, 63, 224507. [Google Scholar] [CrossRef]
- Shaginyan, V.R. Quasiparticles in a strongly correlated liquid with the fermion condensate: Applications to high-temperature superconductors. Phys. Lett. 1998, A249, 237. [Google Scholar] [CrossRef]
- Nozières, P. Properties of Fermi liquids with a finite range interaction. J. Phys. Fr. I 1992, 2, 443. [Google Scholar] [CrossRef]
- Dukelsky, J.; Khodel, V.A.; Schuck, P.; Shaginyan, V.R. Fermion condensation and non Fermi liquid behavior in a model with long range forces. Z. Phys. B 1997, 102, 245. [Google Scholar] [CrossRef]
- Takatsuka, T. Proton mixing in π0-condensed phase of neutron star matter. Prog. Theor. Phys. 1984, 71, 1432. [Google Scholar] [CrossRef]
- Yang, S.; Gu, Z.-C.; Sun, K.; Sarma, S.D. Topological flat band models with arbitrary Chern numbers. Phys. Rev. 2012, B86, 241112. [Google Scholar] [CrossRef]
- Yang, M. Flat bands and high Chern numbers in twisted multilayer graphene. J. Math. Phys. 2023, 64, 111901. [Google Scholar] [CrossRef]
- Efros, A.L.; Shklovskii, B.I. Coulomb gap and low temperature conductivity of disordered systems. J. Phys. 1975, C8, L49. [Google Scholar] [CrossRef]
- Pines, D.; Nozières, P. Theory of Quantum Liquids; W.A. Benjamin: New York, NY, USA, 1966. [Google Scholar]
- Shaginyan, V.R.; Mezane, A.Z.; Zverev, M.V. Transport properties of strongly correlated Fermi systems. Symmetry 2023, 15, 2055. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Msezane, A.Z.; Popov, K.G.; Clark, J.W.; Zverev, M.V.; Khodel, V.A. Magnetic field dependence of the residual resistivity of the heavy-fermion metal CeCoIn5. Phys. Rev. B 2012, 86, 085147. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Stephanovich, V.A.; Msezane, A.Z.; Japaridze, G.S.; Popov, K.G. The influence of topological phase transition on the superfluid density of overdoped copper oxides. Phys. Chem. Chem. Phys. 2017, 19, 21964. [Google Scholar] [CrossRef] [PubMed]
- Boẑović, J.I.; He, X.; Wu, J.; Bollinger, A.T. Dependence of the critical temperature in overdoped copper oxides on superfluid density. Nature 2016, 536, 309. [Google Scholar] [CrossRef] [PubMed]
- Zaanen, J. Superconducting electrons go missing. Nature 2016, 536, 282. [Google Scholar] [CrossRef]
- Shaginyan, V.R.; Msezane, A.Z.; Stephanovich, V.A.; Kirichenko, E.V. Quasiparticles and quantum phase transition in universal low-temperature properties of heavy-fermion metals. Europhys. Lett. 2006, 76, 898. [Google Scholar] [CrossRef]
- Bianchi, A.; Movshovich, R.; Oeschler, N.; Gegenwart, P.; Steglich, F.; Thompson, J.D.; Sarrao, J.L.; Pagliuso, P.G. First-Order Superconducting Phase Transition in CeCoIn5. Phys. Rev. Lett. 2002, 89, 137002. [Google Scholar] [CrossRef] [PubMed]
- Izawa, K.; Yamaguchi, H.; Matsuda, Y.; Shishido, H.; Settai, R.; Onuki, Y. Angular position of nodes in the superconducting gap of quasi-2D heavy-fermion superconductor CeCoIn5. Phys. Rev. Lett. 2001, 87, 057002. [Google Scholar] [CrossRef]
- Pan, S.H.; O’Neal, J.P.; Badzey, R.L.; Chamon, C.; Ding, H.; Engelbrecht, J.R.; Davis, J.C.; Ng, K.-W.; Hudson, E.W.; Lang, K.M.; et al. Microscopic electronic inhomogeneity in the high-Tc superconductor Bi2Sr2CaCu2O8+x. Nature 2001, 413, 282. [Google Scholar] [CrossRef]
- Yankowitz, M.; Chen, S.; Polshyn, H.; Zhang, Y.; Watanabe, K.; Taniguchi, T.; Graf, D.; Young, A.F.; Dean, C.R. Tuning superconductivity in twisted bilayer graphene. Science 2019, 363, 1059. [Google Scholar] [CrossRef]
- Lu, X.; Stepanov, P.; Yang, W.; Xie, M.; Aamir, M.A.; Das, I.; Urgell, C.; Watanabe, K.; Taniguchi, T.; Zhang, G.; et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 2019, 574, 653. [Google Scholar] [CrossRef]
- Stepanov, P.; Das, I.; Lu, X.; Fahimniya, A.; Watanabe, K.; Taniguchi, T.; Koppens, F.H.L.; Lischner, J.; Levitov, L.; Efetov, D.K. Untying the insulating and superconducting orders in magic-angle graphene. Nature 2020, 583, 375. [Google Scholar] [CrossRef]
- Nakamae, S.; Behnia, K.; Mangkorntong, N.; Nohara, M.; Takagi, H.; Yates, S.J.C.; Hussey, N.E. Electronic ground state of heavily overdoped nonsuperconducting La2-xSrxCuO4. Phys. Rev. B 2003, 68, 100502. [Google Scholar] [CrossRef]
- Laughlin, R.B.; Pines, D. The middle way. Proc. Natl. Acad. Sci. USA 2000, 97, 28. [Google Scholar] [CrossRef] [PubMed]
- Loram, J.W.; Mirza, K.A.; Wade, J.M.; Cooper, J.R.; Liang, W.Y. The electronic specific heat of cuprate superconductors. Phys. C 1994, 235–240, 134. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaginyan, V.R.; Msezane, A.Z.; Artamonov, S.A. General Properties of Conventional and High-Temperature Superconductors. Crystals 2024, 14, 826. https://doi.org/10.3390/cryst14090826
Shaginyan VR, Msezane AZ, Artamonov SA. General Properties of Conventional and High-Temperature Superconductors. Crystals. 2024; 14(9):826. https://doi.org/10.3390/cryst14090826
Chicago/Turabian StyleShaginyan, Vasily R., Alfred Z. Msezane, and Stanislav A. Artamonov. 2024. "General Properties of Conventional and High-Temperature Superconductors" Crystals 14, no. 9: 826. https://doi.org/10.3390/cryst14090826
APA StyleShaginyan, V. R., Msezane, A. Z., & Artamonov, S. A. (2024). General Properties of Conventional and High-Temperature Superconductors. Crystals, 14(9), 826. https://doi.org/10.3390/cryst14090826