Constitutive Equation and Heat Distortion Behavior of TA4 Titanium Alloy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Materials
2.2. High-Temperature Thermal Compression Test
2.3. Microstructural Characterization
3. Results
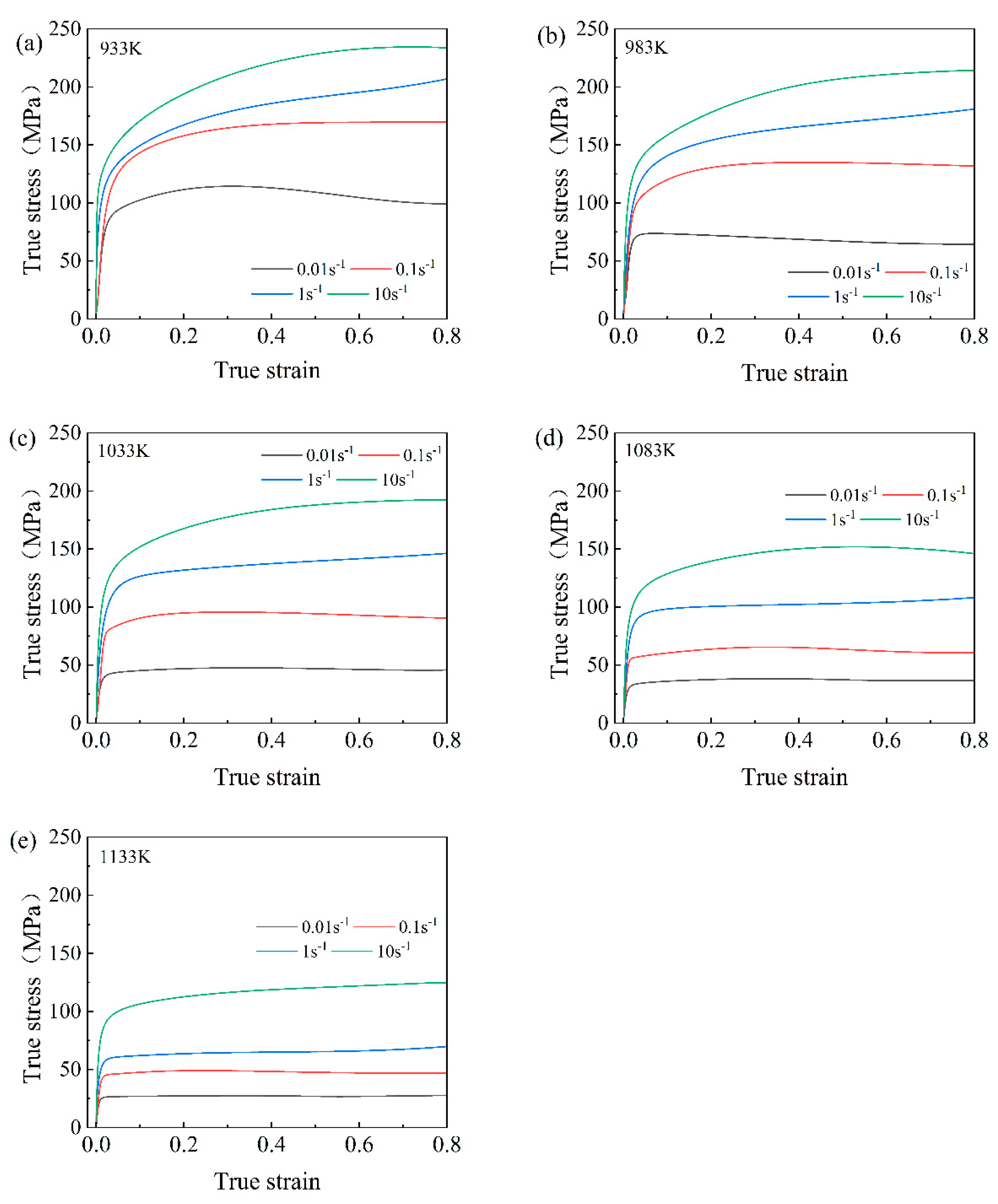
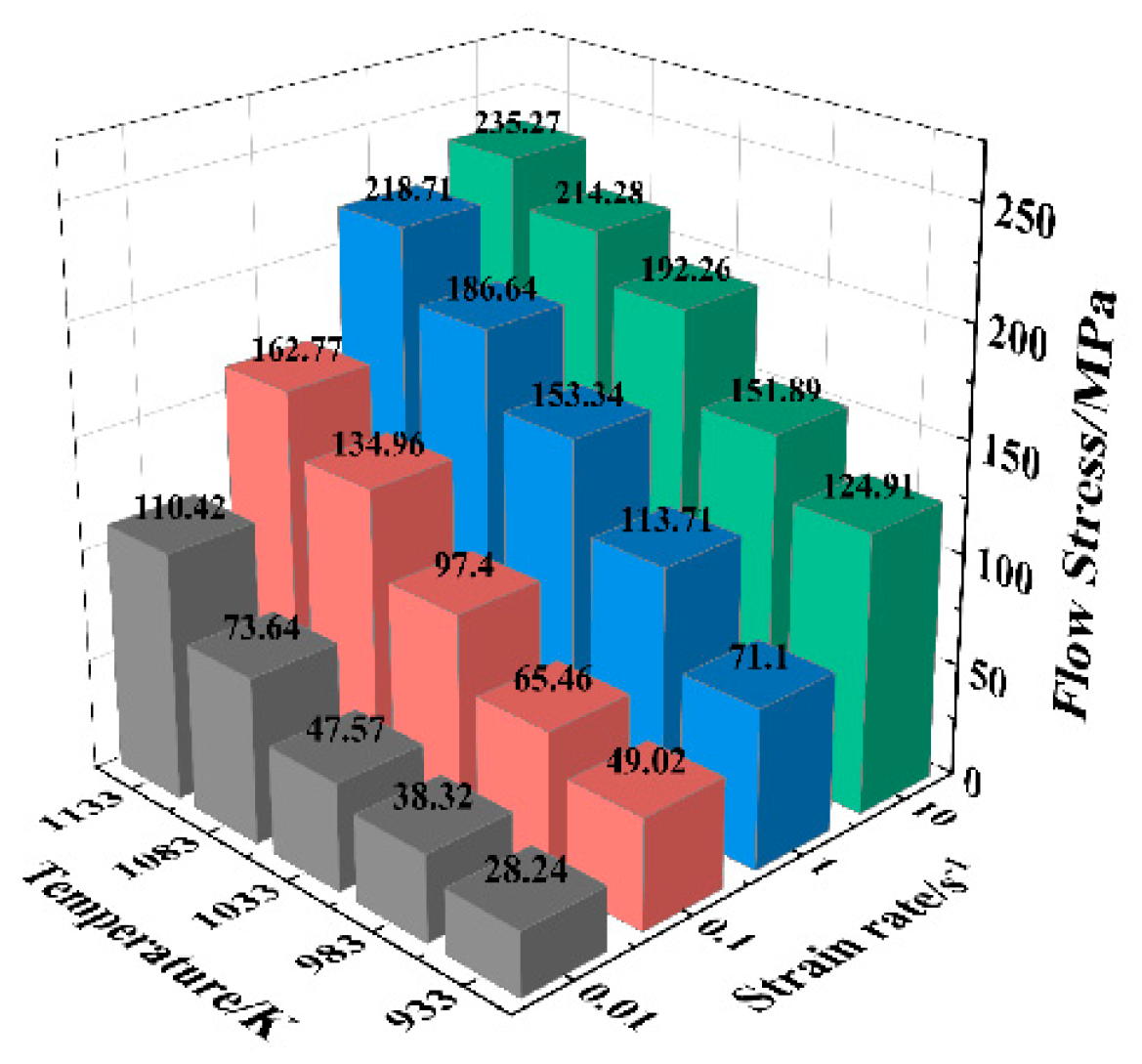
3.1. Flow Stress Behavior
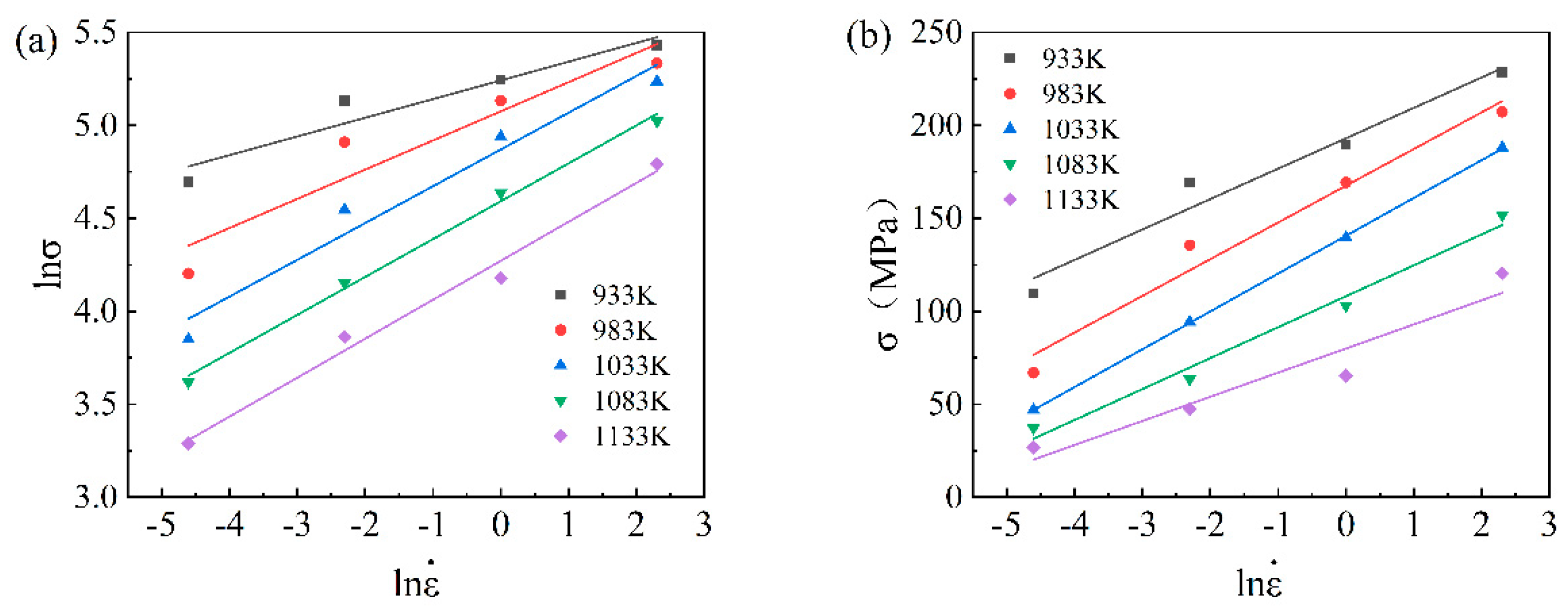
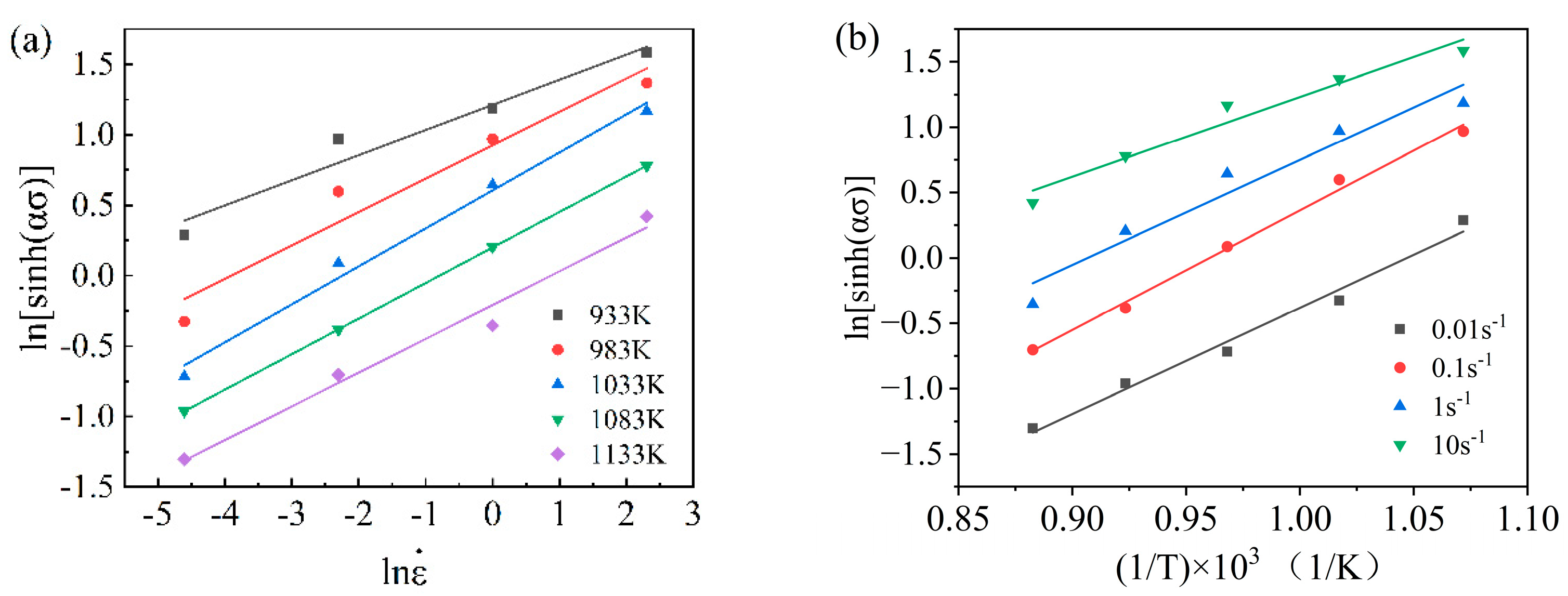
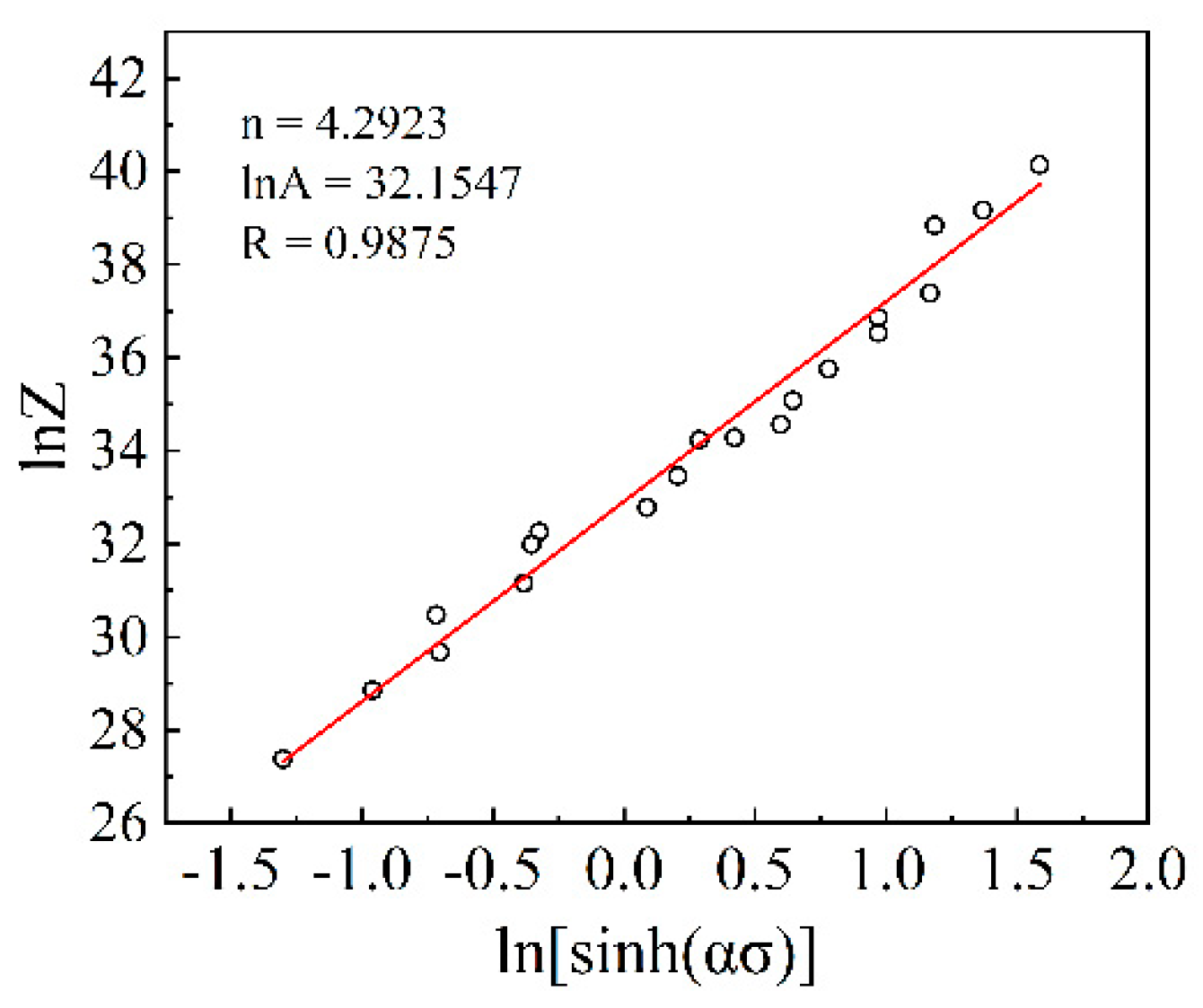
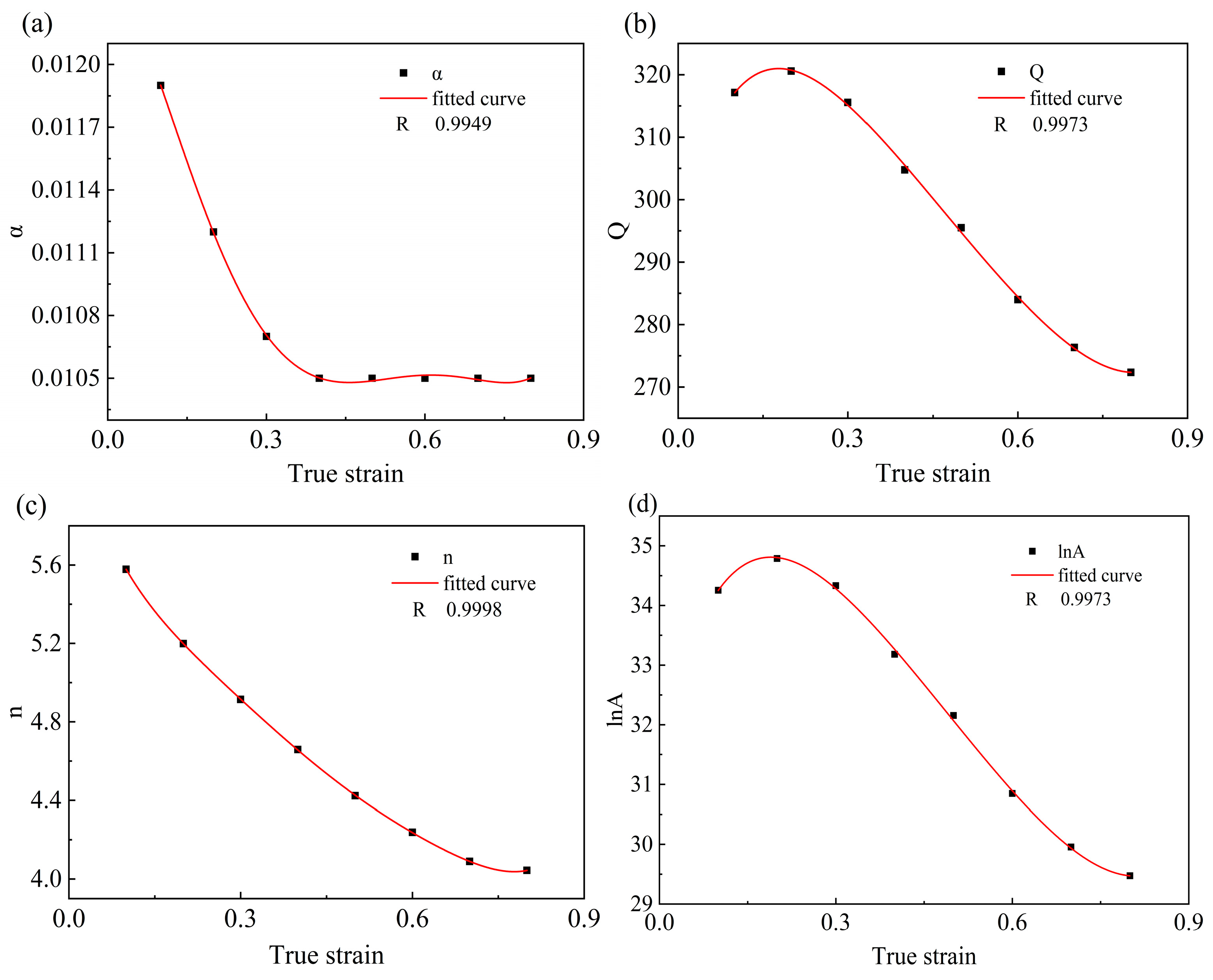
3.2. Derivation of the Constitutive Equation
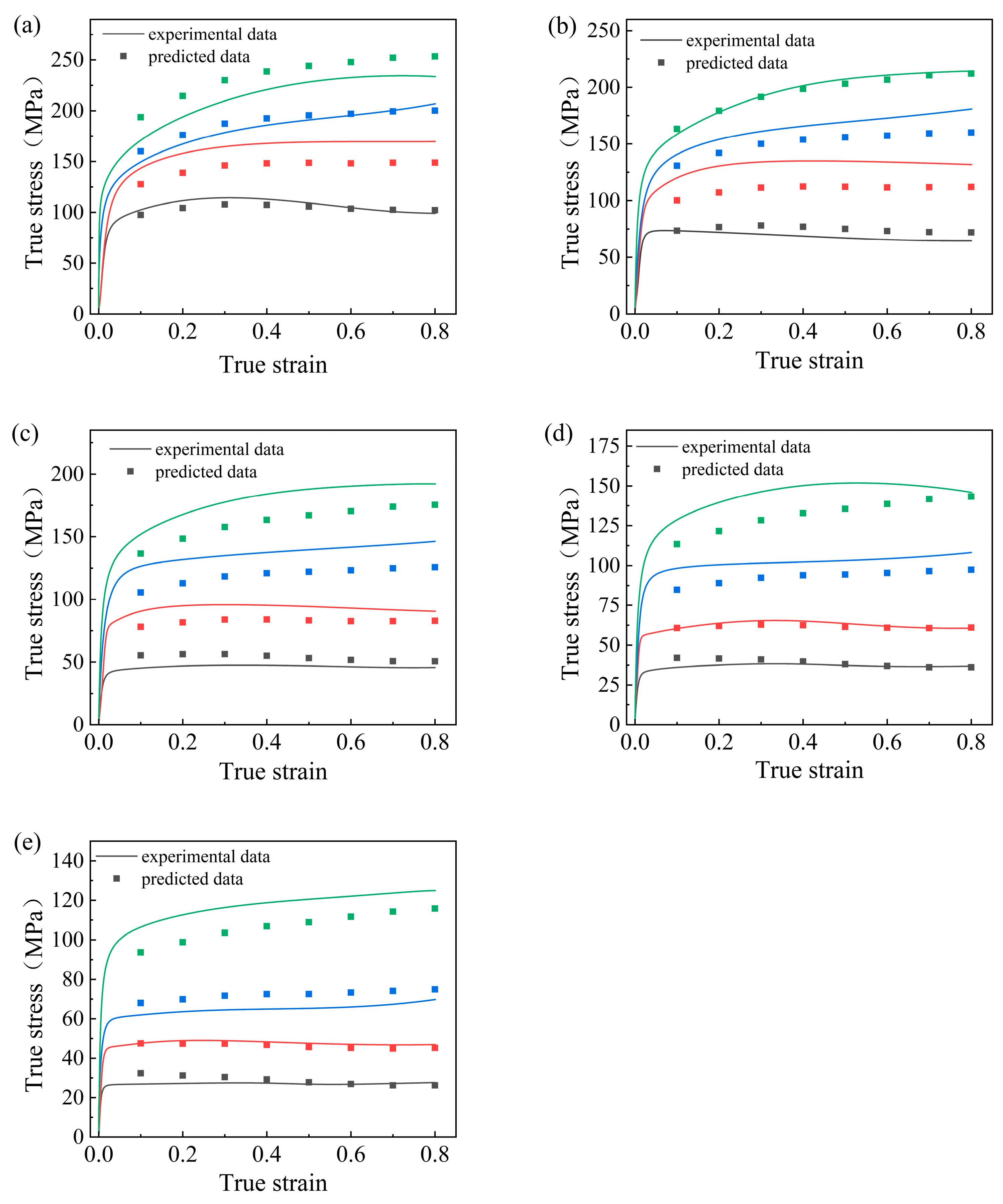
3.3. Evaluation of the Ontological Model
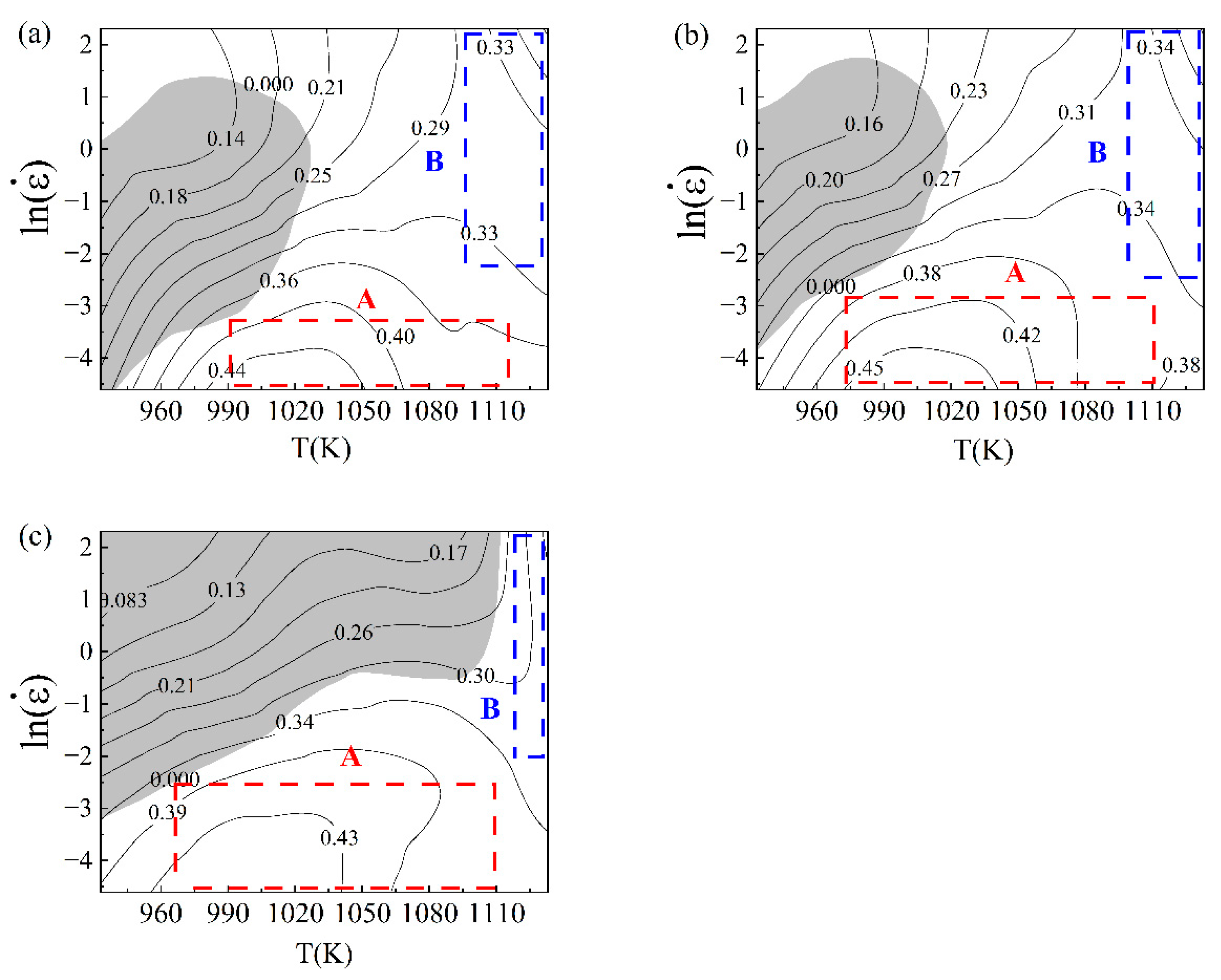
3.4. Creation and Analysis of Thermal Processing Diagrams
3.5. EBSD Analyses
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.B.; Hu, H.X.; Zheng, Y.G.; Ke, W.; Qiao, Y.X. Comparison of the corrosion behavior of pure titanium and its alloys in fluoride-containing sulfuric acid. Corros. Sci. 2016, 103, 50–65. [Google Scholar] [CrossRef]
- Shahmir, H.; Pereira, P.H.R.; Huang, Y.; Langdon, T.G. Mechanical properties and microstructural evolution of nanocrystalline titanium at elevated temperatures. Mater. Sci. Eng. A 2016, 669, 358–366. [Google Scholar] [CrossRef]
- Yuan, B.; Zheng, Y.; Wang, Y.; Chen, Q.; Gong, L.; Lv, M. Effect of temperature on hydrogen absorption characteristic and microstructural evolution of TC21 alloy. J. Alloys Compd. Interdiscip. J. Mater. Sci. Solid-State Chem. Phys. 2015, 648, 794–802. [Google Scholar]
- Zhao, H.; Shan, X.; Tang, Y.; Wang, B.; Tian, Y. Hot deformation behavior and dynamic recrystallization mechanism of Ti2ZrTa0.75 refractory complex concentrated alloy. Mater. Charact. 2023, 203, 113061. [Google Scholar]
- Després, A.; Mithieux, J.D.; Sinclair, C.W. Modelling the relationship between deformed microstructures and static recrystallization textures: Application to ferritic stainless steels. Acta Mater. 2021, 219, 117226. [Google Scholar]
- Fan, X.G.; Yang, H.; Gao, P.F. Prediction of constitutive behavior and microstructure evolution in hot deformation of TA15 titanium alloy. Mater. Des. 2013, 51, 34–42. [Google Scholar] [CrossRef]
- Momeni, A.; Abbasi, S.M. Effect of hot working on flow behavior of Ti–6Al–4V alloy in single phase and two phase regions. Mater. Des. 2010, 31, 3599–3604. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, D.; Cao, S.; Wu, S.; Zhu, Z.; Wang, H.; Li, L.; Xin, S.; Qu, L.; Huang, A. Effect of strain rate and temperature on the deformation behavior in a Ti-23.1Nb-2.0Zr-1.0O titanium alloy. J. Mater. Sci. Technol. 2021, 73, 52–60. [Google Scholar] [CrossRef]
- Hao, F.; Xiao, J.; Feng, Y.; Wang, Y.; Ju, J.; Du, Y.; Wang, K.; Nie, Z.; Tan, C. Tensile deformation behavior of a near-α titanium alloy Ti-6Al-2Zr-1Mo-1V under a wide temperature range. J. Mater. Res. Technol. 2020, 9, 2818–2831. [Google Scholar]
- Wang, X.; Liu, P.; Liang, C.; Lu, T.; Feng, T.; Niu, H.; Dong, Y.; Liu, X. Investigation on the thermal deformation mechanisms and constitutive model of Ti-55511 titanium alloy. J. Mater. Res. Technol. 2024, 33, 6780–6797. [Google Scholar] [CrossRef]
- Li, L.; Ma, G.; Huang, H.; Xiao, H.; Yuan, Z.; Li, Y.; Zhou, R. Flow behavior analysis and prediction of flow instability of a lamellar TA10 titanium alloy. Mater. Charact. 2022, 194, 112403. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, T.; Zhou, Z.; Li, M.; Tan, L.; Gan, B.; Jie, Z.; Qin, L.; Zhang, J.; Liu, L. Variation of Homogenization Pores during Homogenization for Nickel-Based Single-Crystal Superalloys. Adv. Eng. Mater. 2021, 23, 2001547. [Google Scholar] [CrossRef]
- Ji, R.; Zhu, K.; Zhang, H.; Luo, H.; Mao, J. Microstructure evolution, mechanical response and strengthening models for TA15 titanium alloy during thermal processes: A brief review. J. Mater. Res. Technol. 2024, 28, 1644–1656. [Google Scholar] [CrossRef]
- Abbasi, S.M.; Momeni, A.; Lin, Y.C.; Jafarian, H.R. Dynamic softening mechanism in Ti-13V-11Cr-3Al beta Ti alloy during hot compressive deformation. Mater. Sci. Eng. A 2016, 665, 154–160. [Google Scholar] [CrossRef]
- Xiang, Y.; Xiang, W.; Yuan, W. Flow softening and microstructural evolution of near β titanium alloy Ti-55531 during hot compression deformation in the α + β region. J. Alloys Compd. 2023, 955, 170165. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, G.; Zhang, S.; Xiu, S. Effect of crystal orientation on micro-stress distribution in a damage-tolerant titanium alloy TC21. J. Alloys Compd. Interdiscip. J. Mater. Sci. Solid-State Chem. Phys. 2022, 924, 166637. [Google Scholar]
- Si-Wei, D.; Xiang-Long, D. Interpretation of the Latest Edition of ⟪GB/T 3620.1-2016 Titanium and Titanium Alloy Grades and Chemical Compositions⟫. Science & Technology Vision 2019.
- Xie, H.; Wang, J.; Li, Y.; Song, J.; Hu, H.; Qin, L.; Zhao, H.; Li, C.; Cui, Y.; Tan, Z. Fast shot speed induced microstructure and mechanical property evolution of high pressure die casting Mg-Al-Zn-RE alloys. J. Mater. Process. Technol. 2024, 331, 118523. [Google Scholar] [CrossRef]
- Han, L.; Zhang, H.; Cheng, J.; Zhou, G.; Wang, C.; Chen, L. Thermal Deformation Behavior of Ti-6Mo-5V-3Al-2Fe Alloy. Crystals 2021, 11, 1245. [Google Scholar] [CrossRef]
- Chai, Y.; Zhu, Y.; Qin, L.; Luo, Y.; Niu, Y.; Shao, Z. High-temperature hot deformation behavior and processing map of Ti-22Al-25Nb alloy. Mater. Today Commun. 2024, 41, 110599. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15, 1883–1892. [Google Scholar]
- Shokry, A.; Gowid, S.; Kharmanda, G. An improved generic Johnson-Cook model for the flow prediction of different categories of alloys at elevated temperatures and dynamic loading conditions. Mater. Today Commun. 2021, 27, 102296. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, J.; Li, J.; Yan, Y.; Wang, P. A comparative study on Johnson-Cook and modified Johnson-Cook constitutive material model to predict the dynamic behavior laser additive manufacturing FeCr alloy. J. Alloys Compd. 2017, 723, 179–187. [Google Scholar] [CrossRef]
- Chen, W.; Guan, Y.; Wang, Z. Modeling of Flow Stress of High Titanium Content 6061 Aluminum Alloy Under Hot Compression. J. Mater. Eng. Perform. 2016, 25, 4081–4088. [Google Scholar] [CrossRef]
- Liao, H.; Wu, Y.; Zhou, K.; Yang, J. Hot deformation behavior and processing map of Al–Si–Mg alloys containing different amount of silicon based on Gleebe-3500 hot compression simulation. Mater. Des. 2015, 65, 1091–1099. [Google Scholar] [CrossRef]
- Abbasi-Bani, A.; Zarei-Hanzaki, A.; Pishbin, M.H.; Haghdadi, N. A comparative study on the capability of Johnson–Cook and Arrhenius-type constitutive equations to describe the flow behavior of Mg–6Al–1Zn alloy. Mech. Mater. 2014, 71, 52–61. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhong, L.; Pan, F. Modeling and application of constitutive model considering the compensation of strain during hot deformation. J. Alloys Compd. 2016, 681, 455–470. [Google Scholar] [CrossRef]
- Zhou, Z.; Fan, Q.; Xia, Z.; Hao, A.; Yang, W.; Ji, W.; Cao, H. Constitutive Relationship and Hot Processing Maps of Mg-Gd-Y-Nb-Zr Alloy. J. Mater. Sci. Technol. 2017, 33, 637–644. [Google Scholar] [CrossRef]
- Mandal, S.; Rakesh, V.; Sivaprasad, P.V.; Venugopal, S.; Kasiviswanathan, K.V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel. Mater. Sci. Eng. A 2009, 500, 114–121. [Google Scholar] [CrossRef]
- Robi, P.S.; Dixit, U.S. Application of neural networks in generating processing map for hot working. J. Mater. Process. Technol. 2003, 142, 289–294. [Google Scholar] [CrossRef]
- Long, F.-W.; Jiang, Q.-W.; Xiao, L.; Li, X.-W. Compressive Deformation Behaviors of Coarse- and Ultrafine-Grained Pure Titanium at Different Temperatures: A Comparative Study. Mater. Trans. 2011, 52, 1617–1622. [Google Scholar] [CrossRef]
- Li, L.; Li, M.Q.; Luo, J. Flow softening mechanism of Ti–5Al–2Sn–2Zr–4Mo–4Cr with different initial microstructures at elevated temperature deformation. Mater. Sci. Eng. A 2015, 628, 11–20. [Google Scholar] [CrossRef]
- Hou, Z.; Liu, H.; Lu, L.; Li, W.; Zhang, Z.; Lu, W.; Feng, Q.; Jia, B.; Song, K. Effect of rare earth yttrium and the deformation process on the thermal deformation behavior and microstructure of pure titanium for cathode rolls. J. Mater. Res. Technol. 2024, 33, 4192–4205. [Google Scholar] [CrossRef]
- Xu, G.; Tao, J.; Deng, Y.; Zheng, B.; Zhang, Y.; Jiang, Y. Multi-stage hot deformation and dynamic recrystallization behavior of low-cost Ti–Al–V–Fe alloy via electron beam cold hearth melting. J. Mater. Res. Technol. 2022, 20, 1186–1203. [Google Scholar] [CrossRef]
- Al-Samman, T. Modification of texture and microstructure of magnesium alloy extrusions by particle-stimulated recrystallization. Mater. Sci. Eng. A 2013, 560, 561–566. [Google Scholar] [CrossRef]
- Qu, F.S.; Zhou, Y.H.; Zhang, L.Y.; Wang, Z.H.; Zhou, J. Research on hot deformation behavior of Ti-5Al-5Mo-5V-1Cr-1Fe alloy. Mater. Des. 2015, 69, 153–162. [Google Scholar] [CrossRef]
- Xu, J.; Zeng, W.; Zhang, X.; Zhou, D. Analysis of globularization modeling and mechanisms of alpha/beta titanium alloy. J. Alloys Compd. 2019, 788, 110–117. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, H.; Feng, Z.; Shi, Q.; Yang, B.; Chen, M.; Qi, H.; Wang, X. Study on the warm deformation behavior and microstructure evolution of the MDIFed Ti–6Al–4V titanium alloy. J. Mater. Res. Technol. 2024, 33, 8929–8943. [Google Scholar] [CrossRef]
- Ma, L.; Wan, M.; Li, W.; Shao, J.; Bai, X.; Zhang, J. Superplastic deformation mechanical behavior and constitutive modelling of a near-α titanium alloy TNW700 sheet. Mater. Sci. Eng. A 2021, 817, 141419. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Wang, H.; Hou, M.; Yu, K.; Xu, Y.; Xiao, H. Flow behavior and dynamic recrystallization mechanism of a new near-alpha titanium alloy Ti-0.3 Mo-0.8 Ni-2Al-1.5 Zr. J. Mater. Res. Technol. 2024, 30, 3863–3876. [Google Scholar] [CrossRef]
- Yu, J.; Li, Z.; Qian, C.; Huang, S.; Xiao, H. Investigation of deformation behavior, microstructure evolution, and hot processing map of a new near-α Ti alloy. J. Mater. Res. Technol. 2023, 23, 2275–2287. [Google Scholar]





| Fe | C | N | H | O | Ti |
|---|---|---|---|---|---|
| 0.1500 | 0.0500 | 0.0070 | 0.0021 | 0.3600 | Bal. |
| Material Constant | True Strain | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | |
| α | 0.0119 | 0.0112 | 0.0107 | 0.0105 | 0.0105 | 0.0105 | 0.0105 | 0.0105 |
| Q | 317.1401 | 320.5820 | 315.5531 | 304.7553 | 295.4912 | 283.9743 | 276.3184 | 272.3312 |
| n | 5.5782 | 5.1983 | 4.9145 | 4.6582 | 4.4234 | 4.2371 | 4.0892 | 4.0433 |
| lnA | 34.2532 | 34.7864 | 34.3312 | 33.1813 | 32.1540 | 30.8460 | 29.9552 | 29.4720 |
| Polynomial Coefficient | |||||||
|---|---|---|---|---|---|---|---|
| C0 | C1 | C2 | C3 | C4 | C5 | ||
| α = f() | 0.0124 | −0.0017 | −0.0493 | 0.1819 | −0.2362 | 0.1058 | |
| D0 | D1 | D2 | D3 | D4 | D5 | D6 | |
| Q = f() | 303.546 | 168.836 | −132.412 | −2689.08 | 8011.976 | −9079.71 | 3772.389 |
| E0 | E1 | E2 | E3 | E4 | E5 | E6 | |
| n = f() | 6.1858 | −7.9749 | 23.8815 | −56.1106 | 73.0744 | −48.186 | 13.5021 |
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | |
| lnA = f() | 32.5454 | 21.0176 | −17.966 | −292.158 | 869.1344 | −981.078 | 406.9907 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Liu, W.; Zhu, Y.; Qin, L.; Zou, J. Constitutive Equation and Heat Distortion Behavior of TA4 Titanium Alloy. Crystals 2025, 15, 290. https://doi.org/10.3390/cryst15040290
Ma L, Liu W, Zhu Y, Qin L, Zou J. Constitutive Equation and Heat Distortion Behavior of TA4 Titanium Alloy. Crystals. 2025; 15(4):290. https://doi.org/10.3390/cryst15040290
Chicago/Turabian StyleMa, Lifeng, Wenshuai Liu, Yanchun Zhu, Ling Qin, and Jingfeng Zou. 2025. "Constitutive Equation and Heat Distortion Behavior of TA4 Titanium Alloy" Crystals 15, no. 4: 290. https://doi.org/10.3390/cryst15040290
APA StyleMa, L., Liu, W., Zhu, Y., Qin, L., & Zou, J. (2025). Constitutive Equation and Heat Distortion Behavior of TA4 Titanium Alloy. Crystals, 15(4), 290. https://doi.org/10.3390/cryst15040290









