Next Article in Journal
Plasma Spraying of W Coatings for Nuclear Fusion Applications: Advancements and Challenges
Previous Article in Journal
Polyvinyl Alcohol–Polyethylene Glycol Embedded Reduced Graphene Oxide Electronic Nose Sensor for Seafood Monitoring
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 15
Issue 5
10.3390/cryst15050406
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Hydrogen-Bonded Ladder Motifs in Naphthalene Dicarboxamides: Influence of Linear vs. Angular Amide Orientation

by
Abdulrahman Mohabbat
,
István Boldog
,
Takin Haj Hassani Sohi
,
Nils Reistel
,
Philipp Seiffert
and
Christoph Janiak
*
Institut für Anorganische Chemie und Strukturchemie, Heinrich-Heine-Universität, 40204 Düsseldorf, Germany
*
Author to whom correspondence should be addressed.
Crystals 2025, 15(5), 406; https://doi.org/10.3390/cryst15050406 (registering DOI)
Submission received: 22 March 2025 / Revised: 22 April 2025 / Accepted: 23 April 2025 / Published: 26 April 2025
(This article belongs to the Section Crystal Engineering)
Browse Figures
Versions Notes

Abstract

:
The crystal structures of naphthalene dicarboxamides, namely 1,4-naphthalene dicarboxamide (1,4-NDA), 2,6-naphthalene dicarboxamide (2,6-NDA), and 2,7-naphthalene dicarboxamide (2,7-NDA), are presented for the first time, along with an analysis of their supramolecular organization. The compounds, obtained in single-crystalline form via solvothermal crystallization from methanol, are stable in air to near 350 °C and have melting points above 300 °C. In their densely packed structures (ρ = 1.43–1.47 cm3g−1) the combination of C 1 1 (4) chains and R 2 2 (8) rings generates one-dimensional hydrogen-bonded ladders, with an additional R 4 2 (8) pattern. The amide groups and the naphthalene rings form dihedral angles between 22° and 40°. Neighboring H-bond ladders run parallel in 1,4-NDA and 2,6-NDA and are connected by means of the naphthalenedyil cores so that two-dimensional (2D) H-bonded sheets are obtained. Except for a weak intra-sheet π–π stacking in 1,4-NDA, there are no π–π stacking and C–H⋯π interactions. The R 2 2 (8) rings act as four-connected nodes, leading to the formation of two-dimensional H-bonded planar sheets with sql topology for the nearly linear dicarboxamides 1,4-NDA and 2,6-NDA and cds topology for the angular 2,7-NDA. Hirshfeld surface analysis and NCI plots provide additional insight into the H-bonding interactions.

Graphical Abstract

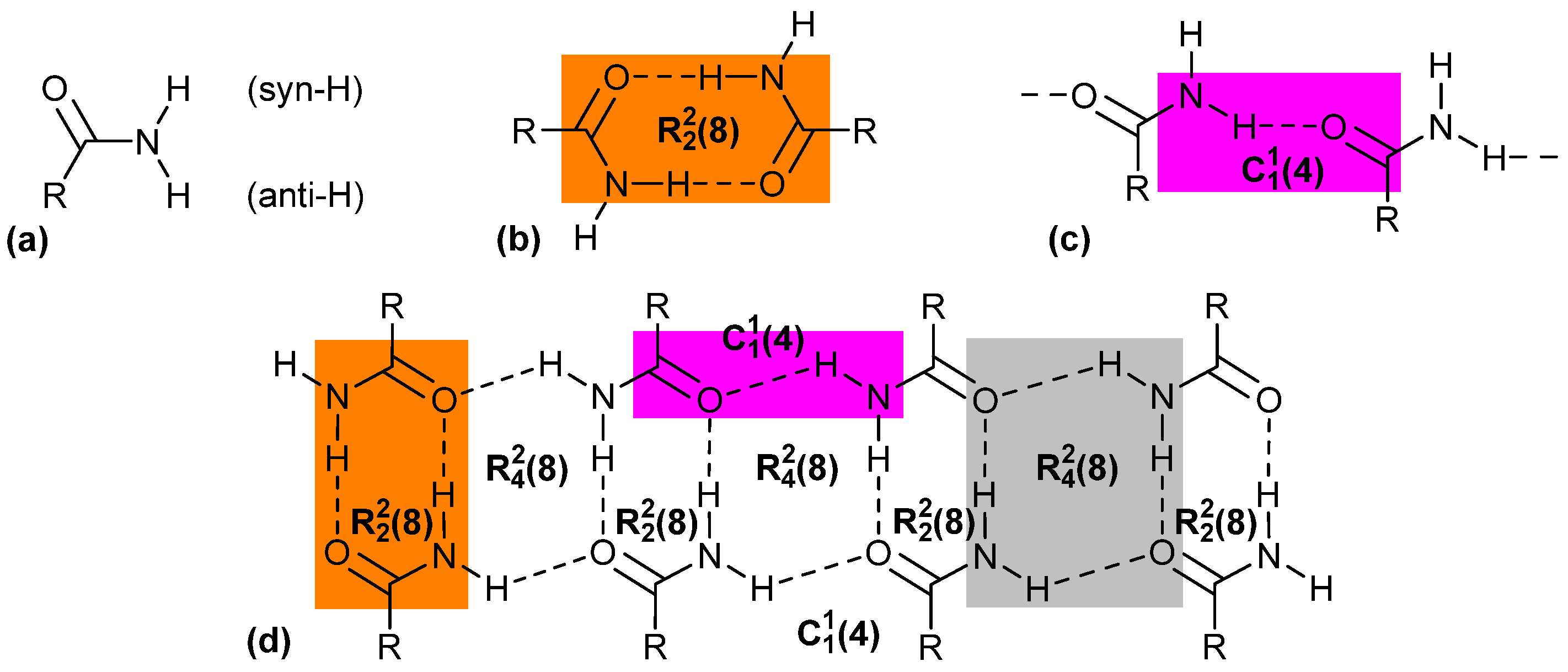
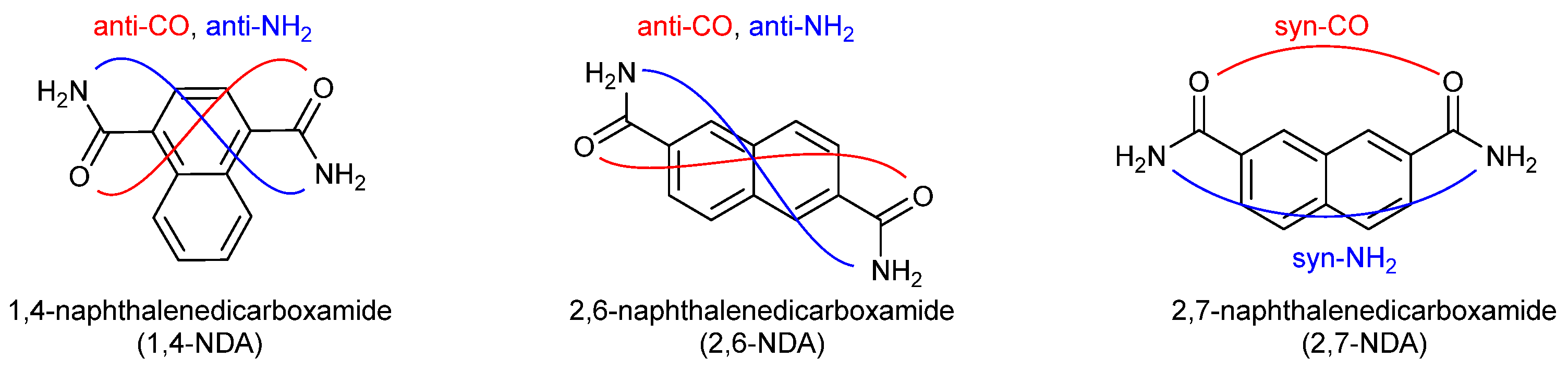
1. Introduction

The important role of hydrogen bonding to sustain the functioning of complex biological systems first inspired the Fischer’s lock-and-key model [1] and eventually, led to the establishment of supramolecular chemistry as a core field for the rational design of self-assembled materials [2,3]. Over the years, perspectives on self-assembly have evolved significantly. Initially, researchers assumed its principles could be universally applied across disciplines, from biology and engineering to materials science [4,5,6]. Now, however, machine learning could be effective in identifying patterns and correlations within complex datasets, making it a valuable tool for targeted structure prediction in self-assembly [7,8,9,10].
The amide group (RCO-NR′R″) is fundamental in the context of hydrogen-bonded solids due to its high frequency in biological systems, its synthetic affordability, and its proven practical utility in material science, with polyamide materials, e.g., Kevlar®, being one of the most recognizable examples [10,11,12,13,14]. Additionally, the hydrogen-bonding properties of amides have found extensive application in pharmaceuticals, where they are used to enhance drug efficacy [15,16,17,18,19,20,21].
The self-assembly patterns of secondary, N-monosubstituted amides (RCO-NHR′), having one NH hydrogen bond donor and one CO hydrogen bond acceptor (1:1 ratio), are relatively predictable. These usually lead to the formation of R 2 2 (8) homodimeric rings (Figure 1), as described by Etter’s notation, which is widely used in many publications [22,23,24]. In the Etter notation G d a n the letter G describes the motif (R = ring, C = chain, D = dimer or other finite set, S = intramolecular interaction), the subscript d stands for the number of hydrogen-bond donors, the superscript a for represents the number of hydrogen-bond acceptors, and the number n in parentheses for equals the number of atoms involved in the motif. The hydrogen-bonded R 2 2 (8) bis-amide synthon, with syn-NH involved, is similar to the R 2 2 (8) ring for carboxylic acids. When the other packing constraints are not favorable, C 1 1 (4) chains with H-bonds from anti-NH to the O atoms are formed (Figure 1) [25,26,27,28]. The primary amides (RCO-NH2) demonstrate a more complex and less predictable self-assembly due to two NH2 hydrogen-bond donors over only one CO acceptor (2:1 ratio). This leads to a larger number of assembly variants, which can include branched hydrogen bonding or involvement of terminating hydrogen-bond acceptor molecules, typically solvents. Unlike cyclic dicarboxylic acids, which consistently form predictable hydrogen-bonded structures (e.g., R 2 2 (8)), primary amides behave less predictably. Therefore, their use in rational design requires a precise understanding of the structural context [29].
Successful supramolecular design using amide groups requires accounting for steric effects and secondary interactions that also influence the resulting network [30,31]. In this context, our previous study demonstrated how heteroatoms, such as nitrogen, sulfur, and oxygen, present in pyridine, thiophene, and furan rings, significantly affected the hydrogen-bonding motifs in dicarboxamides. The results indicated that both the position and basicity of the heteroatom are crucial in determining the hydrogen-bonded packing arrangement [32].
This study investigates the effect of the relative (linear vs. angular) orientation of two carboxamide groups with a naphthalene linker (Figure 2) on the hydrogen-bonding motifs and crystal packing. The naphthalene core would have the additional possibility to engage in π–π stacking and C–H⋯π interactions, which are important interactions in the supramolecular chemistry of aromatic ring structures [33,34,35,36,37,38,39,40]. The π-π stacking interactions are typically in the energy range of 2 kJ mol⁻1, whereas hydrogen bonds range from weak (4 kJ mol⁻1) to strong (45 kJ mol⁻1) [41]. Both influence molecular packing and conformational dynamics in various systems, from biological macromolecules, such as protein folding and nucleobase stacking [42,43,44,45,46], to applications in materials science and drug design [47,48,49,50,51]. Hydrogen-bonded organic frameworks can display functionality in the form of improved conductivity and magnetism, making such materials interesting in the context of organic electronics, molecular magnetism, and spintronics [52,53,54,55,56,57,58].

2. Materials and Methods

All chemicals were obtained from commercial suppliers and used as received, without additional purification steps (for details, see Supplementary Section S1). Deionized water was used in all cases where water is mentioned. Single-crystal X-ray diffraction measurements were performed on a Rigaku XtaLAB Synergy S system (Rigaku, Tokyo, Japan) utilizing a PhotonJet Cu Kα radiation source (λ = 1.54184 Å) and a hybrid pixel array detector. Suitable crystals were selected under a Leica M80 polarized-light microscope (Leica, Wetzlar, Germany) and mounted on a cryo-loop in oil. Data processing, including cell refinement, reduction, and absorption correction were carried out using CrysAlisPro, while structure solution and refinement were performed in Olex2 with SHELXT and SHELXL, respectively [59,60,61]. The molecular graphics were created using Diamond 5 software [62]. The powder X-ray diffraction (PXRD) patterns were recorded on a Rigaku Mini-Flex600 diffractometer (Rigaku, Tokyo, Japan) (600 W, 40 kV, 15 mA) at room temperature using Cu-Kα radiation (λ = 1.54184 Å). The PXRD patterns were normalized based on the intensity of the highest peak. The simulation of the PXRD data, as well as the graph set analysis, were performed using MERCURY 2020.3.0 software based on the single-crystal XRD data [63]. The Hirshfeld surface analysis was carried out using CrystalExplorer 21.5 software [64], while the Atoms in Molecules (AIM) and scatterplot analyses were performed using MultiWFN 3.8 with .wfn files generated from crystal structure data via DFT (B3LYP/6-31G**) in Gaussian16 [65] (note the precision limitations due to reasonable, but somewhat limited, accounting of electron correlation, important for weaker interactions, by the LYP correlation functional). AIM analysis was performed on molecular coordinates obtained from single-crystal structures, with interaction energies computed individually for each distinct hydrogen bond between crystallographically independent molecules. The NCI figures and scatterplots were prepared in VMD 1.9.4 and gnuplot 5.4, respectively. Gnuplot is a graph visualization program for plotting scientific data and mathematical functions [66,67].
Fourier-transform infrared (FT-IR) spectra were recorded in the range of 500 and 4000 cm−1 using a Bruker TENSOR 37 spectrometer (Bruker, Billerica, MA, USA) in ATR mode (Platinum ATR-QL, Diamond). Nuclear magnetic resonance (NMR) spectra were ac-quired on a Bruker Avance III—300 spectrometer (Bruker, Billerica, MA, USA), with the operating frequency of 300 MHz for 1H-NMR and 150 MHz for 13C-NMR. Electron impact (EI) mass spectra were recorded on a Thermo Finnigan Trace DSQ spectrometer (Thermo Fisher Scientific).
Thermogravimetric analysis (TGA) was performed under air using a Netzsch TG209 F3 Tarsus (Netzsch, Selb, Germany), with a heating rate of 10 K min−1 up to 1000 °C. Melting points were determined using a Büchi Melting Point B-540 apparatus in an open capillary (Büchi Labortechnik AG, Flawil, Switzerland).

2.1. Synthesis of Dicarboxamides

The synthesis was performed in analogy with a procedure reported in the literature [68]. A total of 2.16 g (10.00 mmol) of the respective naphthalenedicarboxylic acid was dissolved in 25 mL (345 mmol) of thionyl chloride and subjected to reflux at 90 °C for a duration of 12 h in the presence of a catalytic amount (1 mmol) of dimethylformamide (DMF). After this time, the excess thionyl chloride was distilled off, and the resulting residue washed with hexane (3 × 15 mL), followed by drying under vacuum (~10−2 Torr, room temperature). Subsequently, 5 mL of a 25% aqueous ammonia solution was added dropwise under stirring in an ice bath. The reaction mixture was maintained under stirring in an ice bath for one hour, after which the solvents were removed under reduced pressure. The obtained solid was thoroughly washed with water and ethanol (3×15 mL) before being dried under vacuum.
1,4-naphthalenedicarboxamide (1,4-NDA), 1.88 g yield (88%): 1H NMR (DMSO-d6, 300 MHz) δ (ppm) = 8.30 (dd, J1 = 6 Hz and J2 = 3 Hz), 7.69 (s, 2H), 7.61 (dd, J = 9 and 6 Hz, 2H), 7.62 (s, 2H); 13C NMR (DMSO-d6, 600 MHz), δ (ppm) = 170.2, 136.3, 129.8, 126.7, 123.9. EI-MS: m/z = 214 [M]⁺•.
2,6-naphthalenedicarboxamide (2,6-NDA) 1.92 g yield (90%): 1H NMR (DMSO-d6, 300 MHz), δ (ppm) = 8.51 (d, J = 3 Hz, 2H), 8.81 (s, 2H), 8.04 (s, 2H) 8.02 (dd, J = 18 and 9 Hz, 2H); 13C NMR (DMSO-d6, 150 MHz), δ (ppm) = 168.1, 133.4, 133.3, 129.2, 127.8, 125.3. EI-MS: m/z = 214 [M]⁺•.
2,7-naphthalenedicarboxamide (2,7-NDA) 1.96 g yield (91%): 1H NMR (DMSO-d6, 300 MHz), δ (ppm) = 8.53 (s, 2H), 8.16 (s, 2H), 8.06 (s, 2H), 7.53 (s, 2H); 13C NMR (DMSO-d6, 150 MHz), δ (ppm) = 167.7, 135.3, 132.3, 131.4, 128.8, 127.7, 125.9. EI-MS: m/z = 214 [M]⁺•.

2.2. Crystallization of Dicarboxamides

The crystals, suitable for SCXRD studies, were grown by slow cooling of a methanolic solution. A clear solution, nearly saturated at ~100 °C, in a sealed culture tube was cooled to room temperature at a rate of 0.8 °C h−1 to yield colorless single crystals.

3. Results and Discussion

The 1,4-naphthalenedicarboxamide (1,4-NDA), 2,6-naphthalenedicarboxamide (2.6-NDA), and 2,7-naphthalenedicarboxamide (2,7-NDA) dicarboxamides were synthesized from the corresponding dicarboxylic acids via conversion to acyl chloride by thionyl chloride, followed by reaction with aqueous ammonia under Shotten–Baumann reaction conditions (Section 2.1). The crystallization was performed solvothermally from methanol (Section 2.2). The latter was chosen due to its sufficient solubilizing capability at elevated temperatures, combined with the moderate-to-low probability of its non-desirable incorporation to the structure as a solvent of crystallization. The experimental powder X-ray diffraction patterns of the bulk crystallized amides matched well with the simulated patterns derived from the crystal structures, confirming their phase purity (see Supplementary Materials, Section S5).

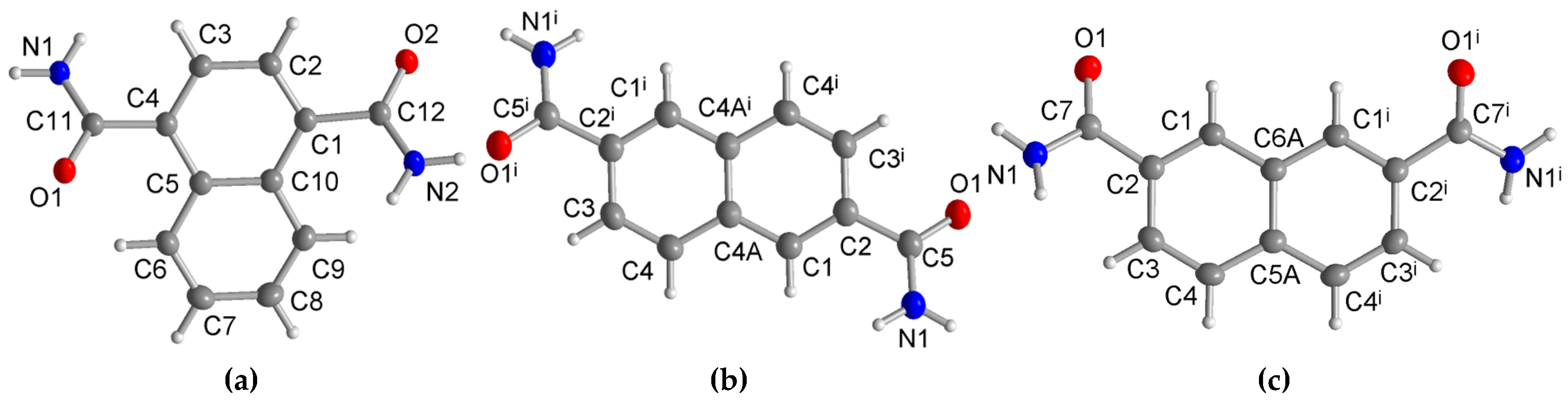
3.1. Crystal Structures of the Dicarboxamides 1,4-NDA, 2,6-NDA, and 2,7-NDA

The molecular structures within the asymmetric unit are illustrated in Figure 3 and Table 1 summarizes the crystallographic data for the dicarboxamide structures. Compounds 1,4-NDA and 2,6-NDA crystallize in the triclinic system and 2,7-NDA in the monoclinic system. While both 1,4-NDA and 2,6-NDA are assigned to the space group P 1 - , their asymmetric units feature different content. The asymmetric unit of 1,4-NDA contains a single molecule (Z = 2, Z′ = 1), while that of 2,6-NDA consists of half a molecule in the asymmetric unit (Z = 4, Z′ = 0.5). In contrast, 2,7-NDA crystallizes in the C2/c space group, with a quarter of the molecule representing the asymmetric unit. Notably, only the basic hydrogen-bond motifs forming the shortest rings and chains are depicted in the graph-set analysis shown in Figure 1d, as determined using the Mercury software [63].
In 1,4-NDA the Cnaph–Camide bond vectors are close to parallel to each other (acute angle of 10.6°), the dihedral angle between the amide planes, where each plane is defined by the three N-C-O atoms, is 14.2°, not far from coplanarity. In 2,6 NDA the Cnaph–Camide bond vectors are exactly parallel, and the amide planes exactly coplanar by the centrosymmetry of the molecule. In 2,7 NDA, the Cnaph–Camide bond vectors form an angle of 64.8°, and the amide N-C-O planes form a dihedral angle of 43.6°.

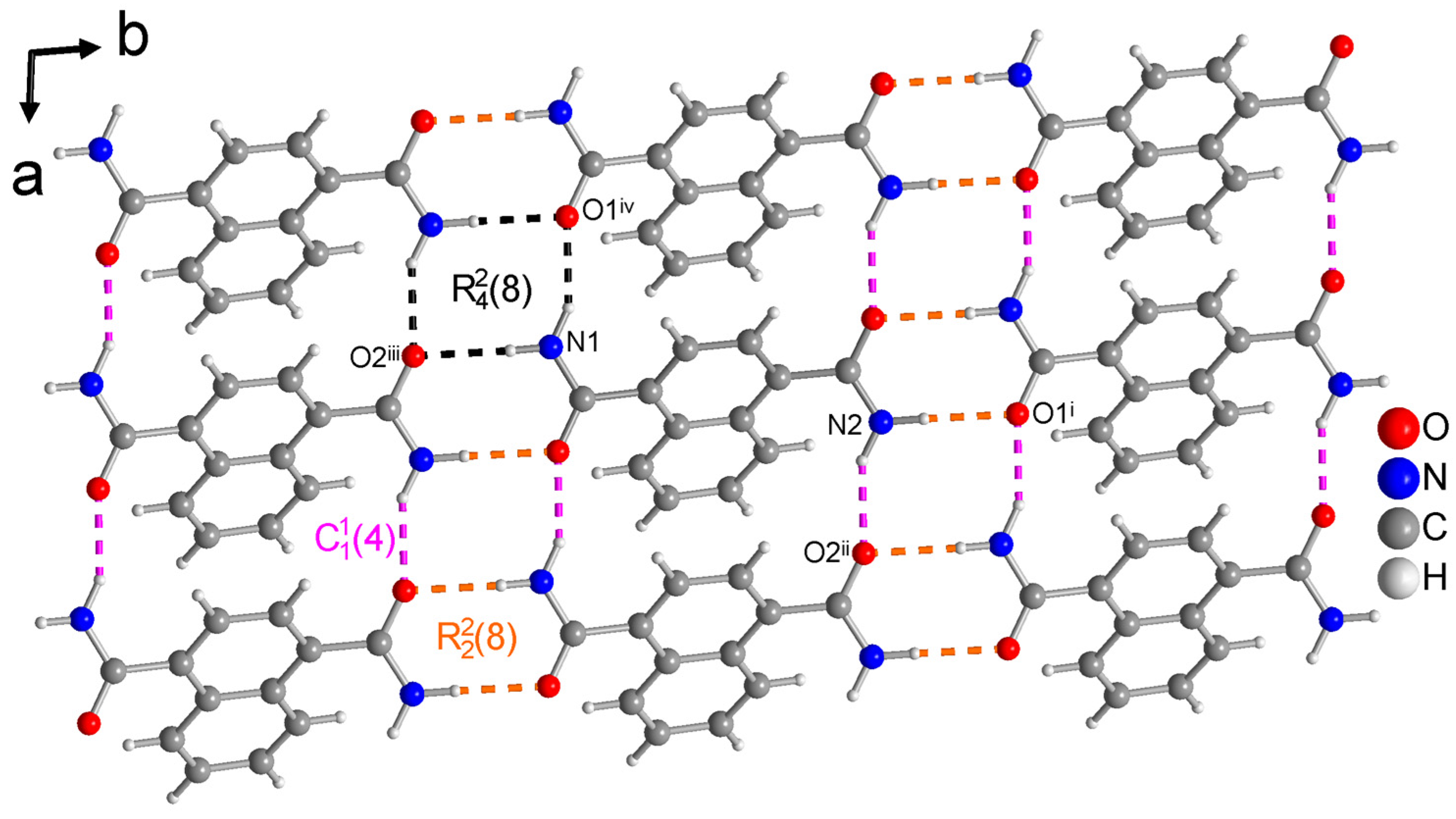
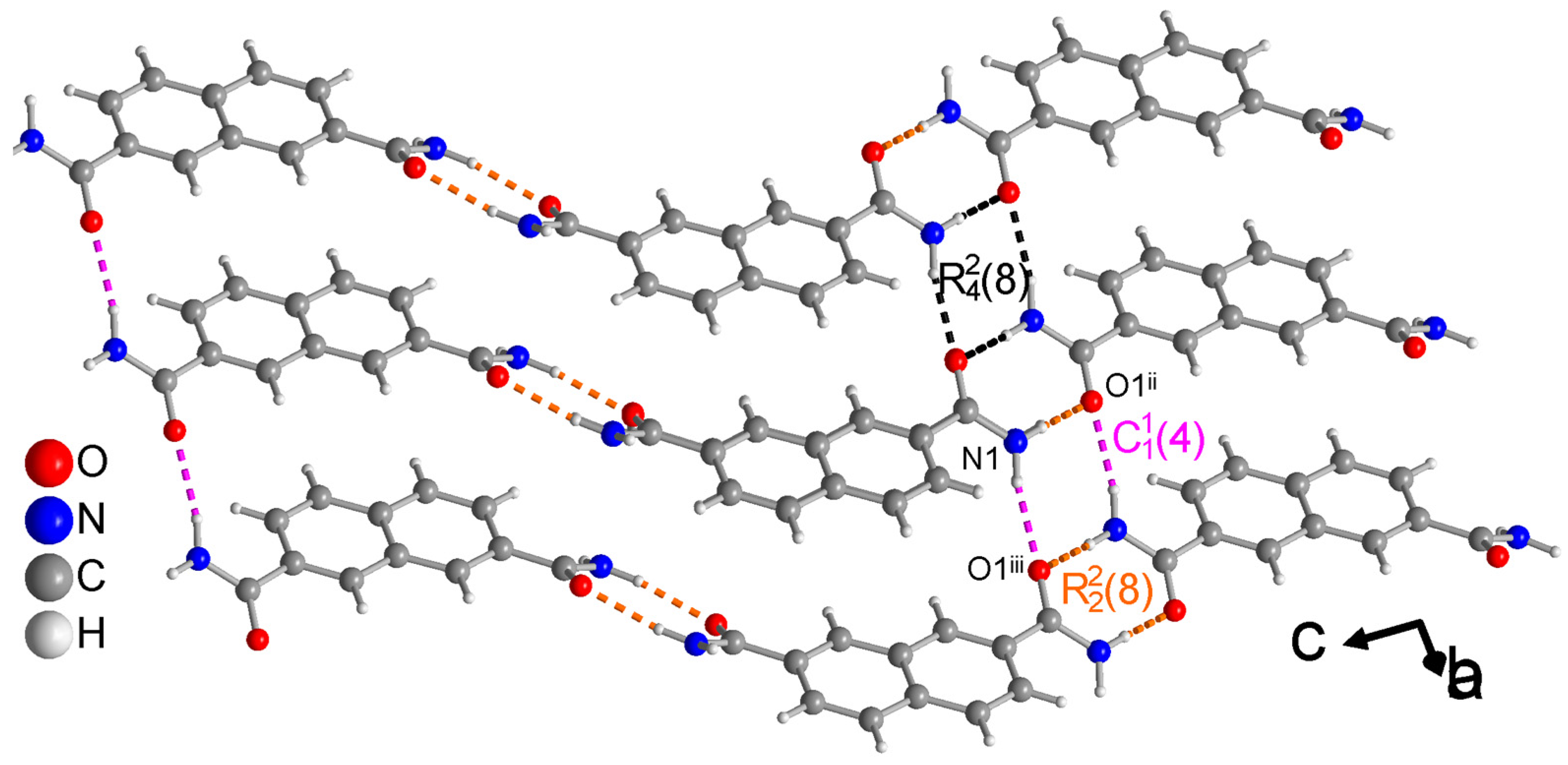
3.1.1. Hydrogen Bonding in 1,4-NDA

The basic H-bonded self-assembly of the structure of 1,4-NDA is a combination of C 1 1 (4) chains and R 2 2 (8) rings, generating a one-dimensional (1D), nearly straight ladder parallel to the a axis with its additional R 4 2 (8) pattern (Figure 4, cf. Figure 1, Table 2). This 1D H-bond ladder is common for all structures reported here. Neighboring ladders run parallel and are connected by means of the naphthalene-1,4-dyil molecular cores along the b axis, so that two-dimensional H bonded sheets in the ab plane are obtained (Figure 4). If the H-bonded bis-amide R 2 2 (8) rings are viewed as four-connected nodes—with two opposite edges defined by the naphthalene connectors and the other two by the side-connections via the R 4 2 (8) ring to the neighboring R 2 2 (8) rings—then the topology of the sheets corresponds to a square planar net, sql (see Section 3.1.4).
The amide group rotates out of the aromatic plane, with a dihedral angle ϕ between the planes of the naphthalene core and the amide moiety close to 40° (Figure 5, Table 3). The two amide groups in a 1,4-NDA molecule are close to coplanar, which leads to the parallel orientation of their respective 1D H-bond ladders. The deplanarization of the naphthalenedicarboxamide molecules is a prerequisite for the 1D-ladder structure; otherwise, the C 1 1 (4) edge of the R 4 2 (8) ring (Figure 4) would be shorter than the length of naphthalene moiety, making such a ladder impossible.
Simultaneously, the naphthalene cores participate in a weak π–π interaction (dintc ≈ 3.8 Å inter-centroid distance) along the chains and within the 2D layer. The optimization of the π–π interaction also influences the ϕ rotation angle. Accordingly, the annulated C6 rings of the 1,4-NDA molecules are oriented to one side of the 2D sheet. There are no inter-sheet π–π stacking and C–H⋯π interactions.

3.1.2. Hydrogen Bonding in 2,6-NDA

As in 1,4-NDA, from the combination of C 1 1 (4) chains and R 2 2 (8) rings, 1D H-bonded ladders, albeit now kinked, are generated with the additional R 4 2 (8) pattern. Again, the 1D ladders run parallel to each other and parallel to the a axis. The bridging action of the naphthalene-2,6-diyl core takes place along the bc diagonal, so that two-dimensional H-bonded sheets parallel to the {0 1 −1} planes are obtained (Figure 6, Table 4). As for 1,4-NDA, the topology of the sheets corresponds to a square planar net, sql (see Section 3.1.4). The 2,6-NDA molecule shows a dihedral angle ϕ = 29° between the naphthalene core and the amide group (Figure 5, Table 3). The two amide groups in a 2,6-NDA molecule are coplanar via the centrosymmetry of the molecule, which leads to the parallel orientation of their respective 1D H-bond ladders. There are no inter-sheet π–π stacking or C–H⋯π interactions between the naphthalene rings in 2,6-NDA.

3.1.3. Hydrogen Bonding in 2,7-NDA

The combination of C 1 1 (4) chains and R 2 2 (8) rings again lead to 1D H-bonded ladders with the additional R 4 2 (8) pattern. The ladders are kinked as in 2,6-NDA. Each amide group of 2,7-NDA is part of a 1D ladder, but different from 1,4-NDA and 2,6-NDA, the ladders of the two amide groups from a 2,7-NDA molecule neither run parallel to each other nor parallel to a crystallographic axis (Figure 7, Table 5). This non-parallel and almost perpendicular orientation of the H-bond ladders at an angle of 88.2° is due to the angular disposition of the amide groups in 2,7-NDA. Both the angle of 64.8° between the Cnaph–Camide bond vectors and the dihedral angle of 43.6° between the amide N-C-O planes are far from co-linearity and co-planarity, respectively, as in 1,4-NDA and 2,6-NDA.
While the colinear and coplanar amide arrangement in 1,4-NDA and 2,6-NDA yielded parallel 1D H-bond ladders arranged in 2D sheets, the angular disposition of the amide groups in 2,7-NDA yields 1D-ladders close to perpendicular to each other and thereby, arranged in a 3D H-bond network. On the level of the four-connected (4-c) bis-amide R 2 2 (8) node, the topology is then a CdSO4 (cds) net. The latter is the primary alternative to the square planar net (sql), when two out of the four neighboring nodes in a 4-c net are situated off-plane (see Section 3.1.4). Again, there are no π–π stacking or C–H⋯π interactions between the naphthalene rings in 2,7-NDA.

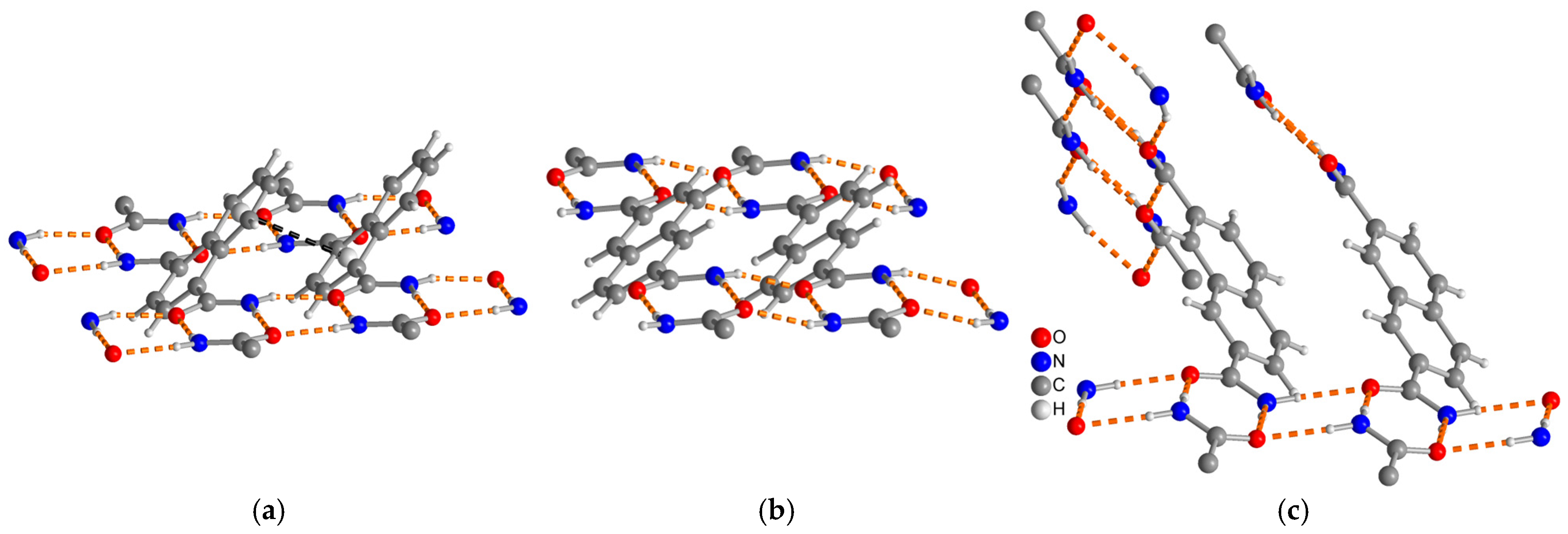
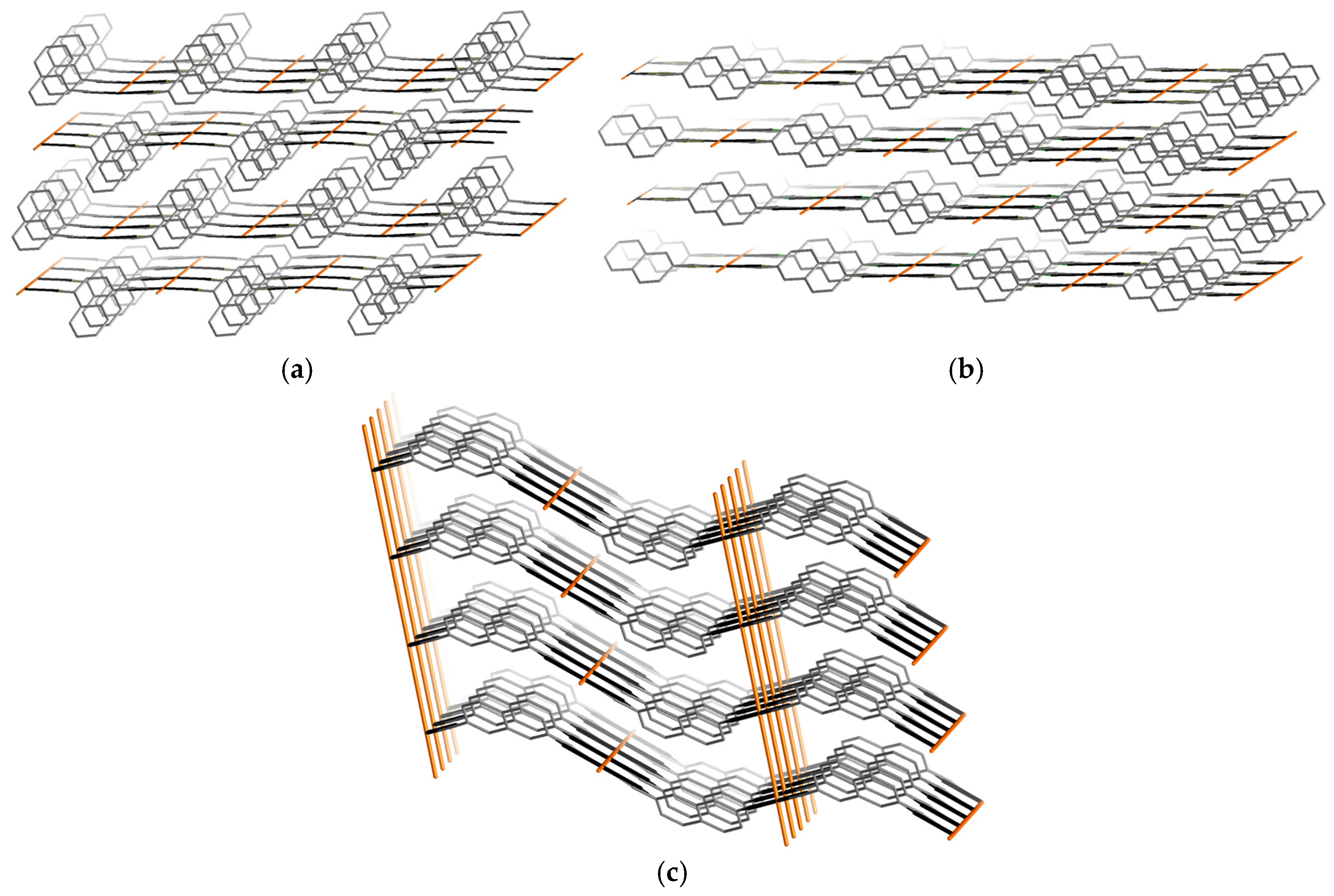
3.1.4. Comparative Topological Presentation

A direct comparison of the linear 1D H-bond ladders and their relative parallel orientation in 2D sheets in 1,4-NDA and 2,6-NDA vs. an almost perpendicular orientation in a 3D net is given in Figure 8.
As for the topology analysis of the structures, in all of them, the bis-amide R 2 2 (8) rings are taken as four-connected nodes. The H-bonds connect these bis-amide rings in one direction in 1D ladders, while the naphthalene cores then connect these 1D ladders.
In the structure of 1,4-NDA and 2,6-NDA, sheets with sql topology are then formed, with an inter-sheet distance of 4.1 Å and 4.2 Å, respectively. Adjacent, neighboring sheets are arranged in a staggered fashion, with the naphthalene units of one sheet positioned above the 1D H-bond ladders of the next sheet (Figure 9a,b).
The topology in 2,7-NDA differs from the previous cases of 2D structures because of the nearly perpendicular directions of the 1D H-bond ladder propagation. Thus, 2,7-NDA features a 3D network structure (Figure 9c). The resulting 3D CdSO4 (cds) topology is typical for this case, when the connectivity of the neighboring square-planar nodes no longer proceeds close to parallel but off-plane or more perpendicular to each other. It is worth recalling that there are no H-bonds, no π–π stacking or C–H⋯π interactions between the naphthalene rings between the sheets in both 1,4-NDA and 2,6-NDA, or within the network of 2,7-NDA. Relevant π–π stacking interactions require centroid–centroid contacts of less than 3.8 Å, near parallel ring planes, small slip angles, and small vertical displacements (slippage < 1.5 Å), which would translate into a sizable overlap of the aryl-plane areas [40]. Significant intermolecular C–H···π contacts are below 2.7 Å for the (C-)H···ring centroid distances, while C–H·· centroid > 145° [69,70].

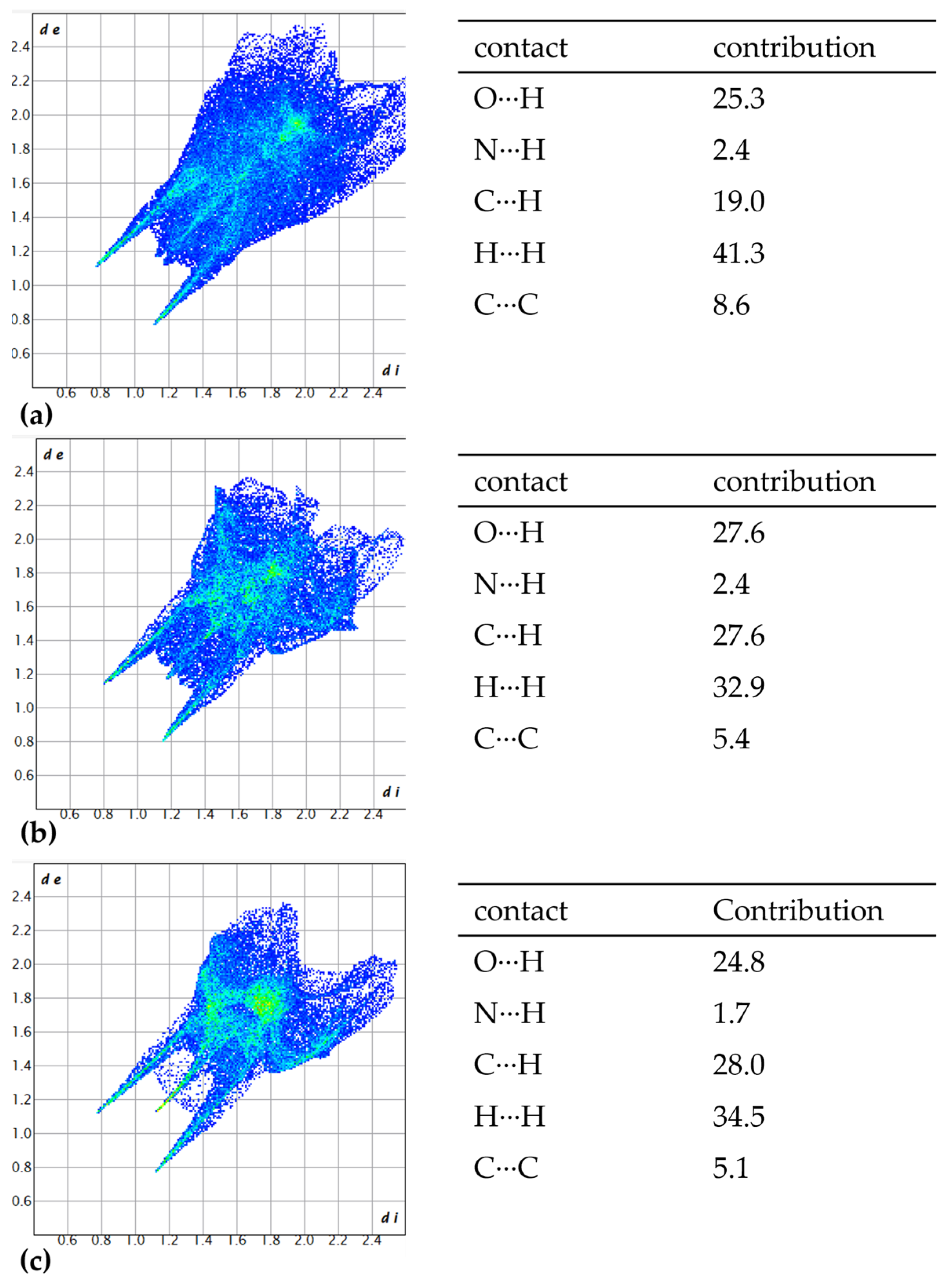
3.2. Hirshfeld Analysis

The analysis of the Hirshfeld surface, which defines the boundaries of each molecular entity based on the electron density distribution and is widely used in crystallographic studies [71,72,73,74], is used here as a practical visualization tool to reveal the strength of the intermolecular interactions with di and de, the distances from the point on the Hirshfeld surface to the nearest atom in the neighbor and in the same molecule, respectively, as the measures of the interaction strengths via their comparison with the typical van der Waals radii by means of a normalized distance function. The latter, dnorm, is equal to (di−dvdwi)/dvdwi + (de−dvdwe)/dvdwe—where dvdwi and dvdwe are the van der Waals radii of the closest atoms of the inner and outer molecules—and describes the deflection from the average van der Waals distances.
The Hirshfeld surfaces, derived from electron density distributions, enable a depiction of intermolecular contacts (Figure 10). In the two-dimensional de and di contact distance fingerprint plots (Figure 11), a visualization of the N–O···O intermolecular interactions is depicted by the spikes directed towards the lower left corner. The individual O···H, N···H, C···H, C···C, and H···H interaction sub-plots distinguish between the respective interactions and are provided in the Supplementary Materials, Section S6.
All examined dicarboxamides display characteristic spikes in the Hirshfeld 2D plots, indicating the formation of N–O···O hydrogen bonds (Figures S16, S21 and S26). These spikes extend for 1,4-NDA and 2,7-NDA to (di, de) ≈ (<0.8, 1.1) and correspond to H···O distances of 1.9–2.0 Å. For 2,6-NDA, the spikes are slightly shorter (di, de) ≈ (0.8, 1.2), consistent with slightly longer hydrogen bonds (Table 2, Table 4 and Table 5). The O···H contacts for the classic strong N–O···O hydrogen bonds have nearly the same share of 25–28% of all intermolecular contacts for the three NDA structures. Broad wings at di + de ≈ 2.8 Å represent C···H interactions (Figure S23), while H···H interactions dominate the remaining interactions (Figure S24). The distinctly green colored zones around di = de ≈ 1.9 Å are associated primarily with C···C contacts (Figure S25). The majority of the intermolecular interactions are represented by the combined weak C···H, H···H, and C···C van der Waals contacts, with a total of 66–69%, which is typical for organic structures [75,76,77,78]).
The contribution of the C···C contacts is slightly higher in the 1,4-NDA structure (8.6% compared to 5.4% and 5.1%), because of the weak intra-ladder π–π interactions, as seen in this structure.
An interesting small detail on the 2D fingerprint plot for 2,7-NDA is the presence of an additional green spike (in between the characteristic hydrogen bond spikes for the strong hydrogen bonds) extending to di = de ≈ 1.7 Å. This spike corresponds to the somewhat stronger H···H interactions.

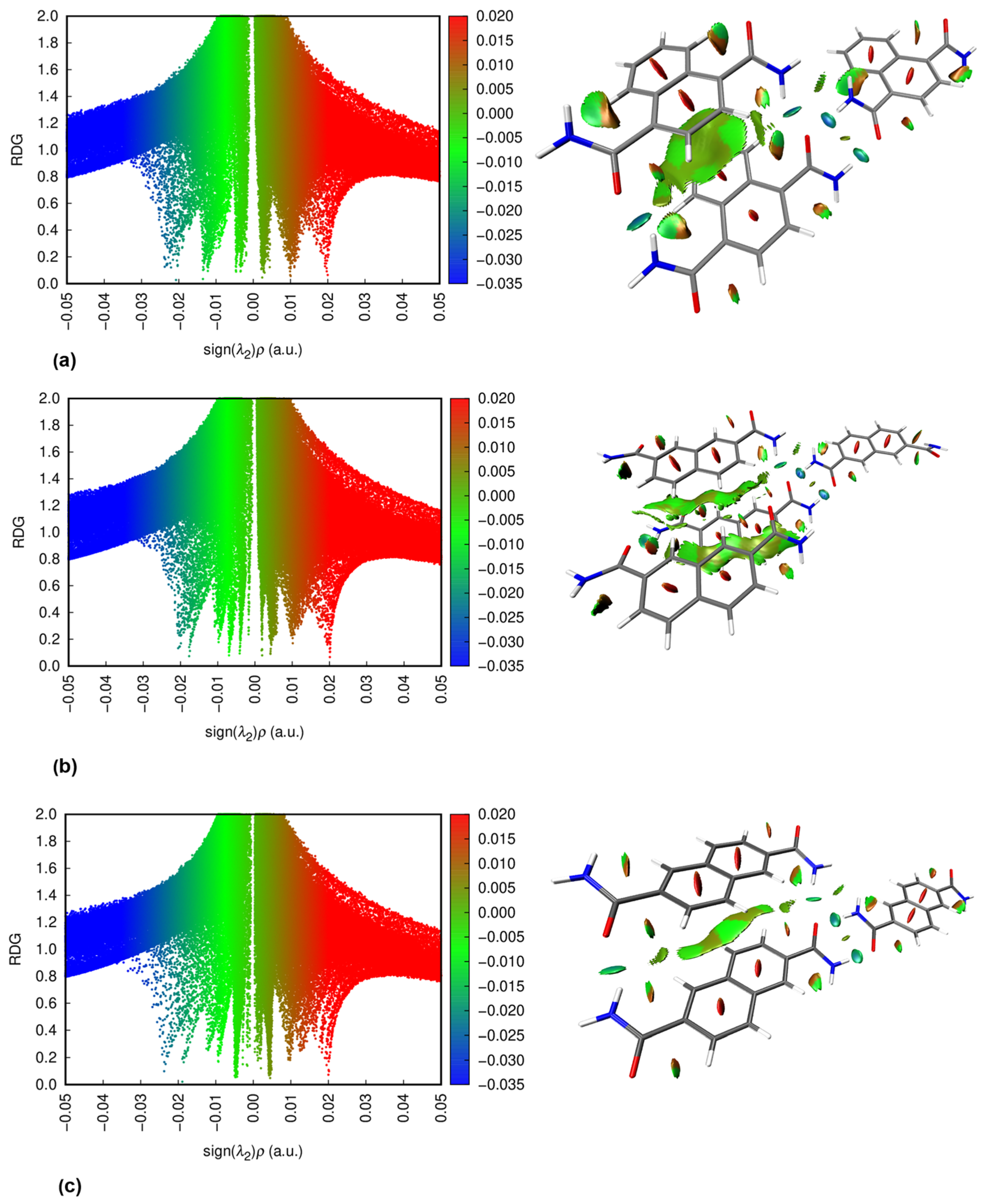
3.3. NCI Plots

The Non-Covalent Interaction (NCI) plot method graphically represents non-covalent interactions in real space using color-coded 3D isosurfaces: blue for attractive, green for van der Waals interactions, and red for steric repulsions, highlighting their spatial distribution within molecular systems (Figure 12). These 3D isosurfaces can also be visualized in NCI scattering plots, which use the Reduced Density Gradient (RDG) and (sign (λ2)ρ) to characterize the interactions. Similar to the 3D plot, scattering plots of RDG vs. (sign (λ2)ρ) show strong attractions (blue) at lower density (ρ < 0.01 a.u.), repulsive interactions (red) at higher density (ρ > 0.01 a.u.), and weak van der Waals interactions (green) in the intermediate range [79,80,81]. The position and intensity of the spikes provide insights into non-covalent interactions. However, NCI analysis remains qualitative and does not quantify individual energy contributions from Coulombic and dispersive interactions. While the Hirshfeld analysis provides a global and semi-quantitative assessment of intermolecular contacts, the NCI plot offers a local and rather qualitative analysis of individual non-covalent interactions; together, they complement each other to provide a comprehensive interaction profile.
For the NDA structures, strong non-covalent interactions appear as pronounced downward blue spikes in the scattering plot, corresponding to small blue isosurfaces of N–O···O hydrogen bonds. Additionally, intense green spikes with a significant fraction are observed in the attractive interaction region, representing the weak C···H, H···H, and C···C van der Waals contacts. A deeper look into the green spike region in the scattering plots reveals subtle structural differences. Notably, in 1,4-NDA, the most intense green spike splits downward, with its largest contribution occurring at a lower ρ critical value sign (λ2)ρ < −0.01 a.u., indicating stronger π···π interactions (vide supra). In contrast, for the other structures, the green spike is divided into three components, with the most prominent part of the peaks appearing at a higher ρ critical value sign (λ2)ρ > −0.01 a.u., suggesting no π···π interactions compared to the results for 1,4-NDA.

3.4. Thermogravimetric Analysis and Melting Points

The temperature stability of the compounds was assessed via thermogravimetric analysis (TGA) (Figure 13).
TGA reveals that all investigated dicarboxamides exhibit very similar thermal behavior. Both 1,4-NDA and 2,6-NDA show an oxidative degradation starting at around 305 °C, with the oxidation completed at approximately 360 °C. Notably, any type of local degradation, e.g., conversion of the amide to carboxylic acid with further decarboxylation, would induce a sublimation of the residual part. Naphthalene already sublimes at room temperature. For 2,7-NDA, a comparable degradation pattern is observed, but the oxidation starts slightly earlier at 290 °C and is nearly complete at around 345 °C, leaving a small amount of residue, which only completely burns off at ~480°. A possible hypothesis is that those are residues rich in triazine, which are the condensation products of the amides. They form at elevated temperatures and oxidize less easily.
The melting points were measured using the open capillary method (1.15 mm diameter), where the temperature gradually increased during visual monitoring of the samples. Notably, all NDA compounds melt within a specific temperature range before undergoing decomposition. The recorded melting intervals were 325–330 °C for 1,4-NDA, 322–330 °C for 2,6-NDA, and 300–312 °C for 2,7-NDA, aligning with the onset of decomposition observed in the TGA analysis. Additionally, all samples changed color to brown and shrank before reaching their melting points, indicating partial decomposition before complete melting.

4. Conclusions

The structural investigation of three primary naphthalenedicarboxamides opens up an interesting uncharted territory comprising supramolecular periodic structures of dicarboxamides with a non-heterocyclic annulated aromatic core. While primary amides are among the most important functionalities regarding the supramolecular chemistry of both molecular and periodic H-bonded solids, the structural chemistry of annulated aromatic amides of is nearly uncharted. The structures of the unsubstituted 1-naphthaleneamide and 2-naphthaleneamide are unknown; the only related reported structure is that of 9-anthraceneamide [82], in addition to 6-bromo-2-naphthaleneamide [83] and 5,6,7,8-tetrafluoro-2-naphthaleneamide [84]. The structures of primary bis- or polyamides of naphthalenes or larger non-heterocyclic annulated aromatic derivatives are not reported at all.
In this study, it was shown that in all three investigated naphthalenedicarboxamide structures, a highly favorable one-dimensional (1D) H-bonded amide ladder motif is formed from the combination of C 1 1 (4) chains and the R 2 2 (8), as well as the R 4 2 (8), pattern. In 1,4-NDA and in 2,6-NDA, where the amide groups are arranged close to linearly, the parallel 1D hydrogen-bonded ladders assemble into two-dimensional (2D) sheets exhibiting sql topology. In 2,7-NDA, the bend or angular amide disposition results in an almost perpendicular arrangement of the amide ladders. Consequently, the hydrogen-bonded network extends into a three-dimensional (3D) cds topology. There are no π–π stacking or C–H···π interactions of the naphthalene rings between the 2D sheets in 1,4-NDA and 2,6-NDA or in the 3D network of 2,7-NDA.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst15050406/s1, Section S1: Chemicals used; Section S2: NMR spectra of the dicarboxamides; Section S3: IR spectra of the dicarboxamides; Section S4: Mass spectra of the dicarboxamides; Section S5: PXRD of the dicarboxamides; Section S6: 2D Hirshfeld plots of the dicarboxamides.

Author Contributions

Conceptualization, A.M. and C.J.; methodology, A.M.; software, A.M. and T.H.H.S.; validation, A.M. and I.B.; formal analysis, A.M., I.B., N.R., P.S., T.H.H.S., and C.J.; investigation, A.M. and N.R.; resources, C.J.; data curation, A.M., P.S., T.H.H.S., and N.R.; writing—original draft preparation, A.M. and I.B.; writing—review and editing, C.J.; visualization, A.M., I.B., and C.J.; supervision, I.B. and C.J.; project administration, C.J.; funding acquisition, C.J. All authors have read and agreed to the published version of the manuscript.

Funding

Funding was provided by Deutsche Forschungsgemeinschaft (DFG), under grant 440366605 (for the Rigaku diffractometer).

Data Availability Statement

The data presented in this study are available upon request from the corresponding author. The CCDC numbers 2431506-2431508 for compounds 2,6-NDA, 1,4-NDA and 2,7-NDA, respectively, contain the supplementary crystallographic data reported in this paper. These data can be obtained free of charge from the Cambridge Crystallographic Data Center via www.ccdc.cam.ac.uk/data_request/cif (accessed on 15 March 2025).

Acknowledgments

The authors would like to thank Birgit Tommes for providing the IR measurements. We also thank the Center for Molecular and Structural Analytics at Heinrich Heine University (CeMSA@HHU) for recording the mass spectrometric and NMR spectrometric data.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Fischer, E. Einfluss der Configuration auf die Wirkung der Enzyme (Influence of configuration on the action of enzymes). Ber. Dtsch. Chem. Ges. 1894, 27, 2985–2993. [Google Scholar] [CrossRef]
  2. Pauling, L. The nature of the chemical bond. II. The one-electron bond and the three-electron bond. J. Am. Chem. Soc. 1931, 53, 3225–3237. [Google Scholar] [CrossRef]
  3. Lugger, S.J.D.; Houben, S.J.A.; Foelen, Y.; Debije, M.G.; Schenning, A.P.; Mulder, D.J. Hydrogen-bonded supramolecular liquid crystal polymers: Smart materials with stimuli-responsive, self-healing, and recyclable properties. Chem. Rev. 2021, 122, 4946–4975. [Google Scholar] [CrossRef] [PubMed]
  4. Stang, P.J.; Olenyuk, B. Self-assembly, symmetry, and molecular architecture: Coordination as the motif in the rational design of supramolecular metallacyclic polygons and polyhedra. Acc. Chem. Res. 1997, 30, 502–518. [Google Scholar] [CrossRef]
  5. Keller, E.F. Self-organization, self-assembly, and the origin of life. In Mapping the Future of Biology: Evolving Concepts and Theories; Barberousse, A., Morange, M., Pradeu, T., Eds.; Springer: Dordrecht, The Netherlands, 2009; Volume 266, pp. 131–140. [Google Scholar] [CrossRef]
  6. Palma, C.-A.; Cecchini, M.; Samorì, P. Predicting self-assembly: From empirism to determinism. Chem. Soc. Rev. 2012, 41, 3713–3730. [Google Scholar] [CrossRef]
  7. Dijkstra, M.; Luijten, E. From predictive modelling to machine learning and reverse engineering of colloidal self-assembly. Nat. Mater. 2021, 20, 762–773. [Google Scholar] [CrossRef]
  8. Li, F.; Han, J.; Cao, T.; Lam, W.; Fan, B.; Tang, W.; Chen, S.; Fok, K.L.; Li, L. Design of self-assembly dipeptide hydrogels and machine learning via their chemical features. Proc. Natl. Acad. Sci. USA 2019, 116, 11259–11264. [Google Scholar] [CrossRef]
  9. Li, Y.; Zhang, R.; Yan, X.; Fan, K. Machine learning facilitating the rational design of nanozymes. J. Mater. Chem. B 2023, 11, 6466–6477. [Google Scholar] [CrossRef]
  10. Gardin, A.; Perego, C.; Doni, G.; Pavan, G.M. Classifying soft self-assembled materials via unsupervised machine learning of defects. Commun. Chem. 2022, 5, 82. [Google Scholar] [CrossRef]
  11. Zhao, Y.; Li, X.; Shen, J.; Gao, C.; van der Bruggen, B. The potential of Kevlar aramid nanofiber composite membranes. J. Mater. Chem. A 2020, 8, 7548–7568. [Google Scholar] [CrossRef]
  12. Prasad, V.V.; Talupula, S. A review on reinforcement of basalt and aramid (Kevlar 129) fibers. Mater. Today Proc. 2018, 5, 5993–5998. [Google Scholar] [CrossRef]
  13. Majed, A.A.; Al-Duhaidahawi, D.; Omran, H.A.; Abbas, S.; Abid, D.S.; Hmood, A.Y. Synthesis, molecular docking of new amide thiazolidine derived from isoniazid and studying their biological activity against cancer cells. J. Biomol. Struct. Dyn. 2024, 42, 13485–13496. [Google Scholar] [CrossRef] [PubMed]
  14. Xu, Y.; Tang, H.; Xu, Y.; Guo, J.; Zhao, X.; Meng, Q.; Xiao, J. Design, synthesis, bioactivity evaluation, crystal structures, and in silico studies of new α-amino amide derivatives as potential histone deacetylase 6 inhibitors. Molecules 2022, 27, 3335. [Google Scholar] [CrossRef]
  15. Hubbard, R.E.; Haider, M.K. Hydrogen bonds in proteins: Role and strength. Encycl. Life Sci. 2010, 1, 1–6. [Google Scholar] [CrossRef]
  16. Dong, Y.; Yao, C.; Zhu, Y.; Yang, L.; Luo, D.; Yang, D. DNA functional materials assembled from branched DNA: Design, synthesis, and applications. Chem. Rev. 2020, 120, 9420–9481. [Google Scholar] [CrossRef]
  17. Hutchins, K.M. Functional materials based on molecules with hydrogen-bonding ability: Applications to drug co-crystals and polymer complexes. R. Soc. Open Sci. 2018, 5, 180564. [Google Scholar] [CrossRef]
  18. Deng, L.; Deng, S.-S.; Pan, S.-Y.; Wu, Z.-Y.; Hu, Y.-Y.; Li, K.; Zhou, Y.; Li, J.-T.; Huang, L.; Sun, S.-G. Multivalent amide-hydrogen-bond supramolecular binder enhances the cyclic stability of silicon-based anodes for lithium-ion batteries. ACS Appl. Mater. Interfaces 2021, 13, 22567–22576. [Google Scholar] [CrossRef] [PubMed]
  19. Zhang, Q.; Huang, J.; Wang, K.; Huang, W. Recent structural engineering of polymer semiconductors incorporating hydrogen bonds. Adv. Mater. 2022, 34, 2110639. [Google Scholar] [CrossRef]
  20. Galuska, L.A.; Ocheje, M.U.; Ahmad, Z.C.; Rondeau-Gagné, S.; Gu, X. Elucidating the role of hydrogen bonds for improved mechanical properties in a high-performance semiconducting polymer. Chem. Mat. 2022, 34, 2259–2267. [Google Scholar] [CrossRef]
  21. Yu, X.; Li, C.; Gao, C.; Zhang, X.; Zhang, G.; Zhang, D. Incorporation of hydrogen-bonding units into polymeric semiconductors toward boosting charge mobility, intrinsic stretchability, and self-healing ability. SmartMat 2021, 2, 347–366. [Google Scholar] [CrossRef]
  22. Bojarska, J.; Łyczko, K.; Breza, M.; Mieczkowski, A. Recurrent Supramolecular Patterns in a Series of Salts of Heterocyclic Polyamines and Heterocyclic Dicarboxylic Acids: Synthesis, Single-Crystal X-ray Structure, Hirshfeld Surface Analysis, Energy Framework, and Quantum Chemical Calculations. Crystals 2024, 14, 733. [Google Scholar] [CrossRef]
  23. Boeré, R.T. Hydrogen Bonds Stabilize Chloroselenite Anions: Crystal Structure of a New Salt and Donor-Acceptor Bonding to SeO2. Molecules 2023, 28, 7489. [Google Scholar] [CrossRef] [PubMed]
  24. Haro-Saltos, L.A.; Bonilla-Valladares, P.M.; Alcívar-León, C.D. Theoretical Study of Intermolecular Interactions in Benzopyrans Substituted with Polyhaloalkyl Groups. Chem. Proc. 2024, 16, 32. [Google Scholar] [CrossRef]
  25. Leiserowitz, L.; Schmidt, G.M. Molecular packing modes. Part III. Primary amides. J. Chem. Soc. A 1969, 2372–2382. [Google Scholar] [CrossRef]
  26. Etter, M.C. Encoding and decoding hydrogen-bond patterns of organic compounds. Acc. Chem. Res. 1990, 23, 120–126. [Google Scholar] [CrossRef]
  27. Etter, M.C. Aggregate structures of carboxylic acids and amides. Isr. J. Chem. 1985, 25, 312–319. [Google Scholar] [CrossRef]
  28. Etter, M.C. Hydrogen bonds as design elements in organic chemistry. J. Phys. Chem. 1991, 95, 4601–4610. [Google Scholar] [CrossRef]
  29. Leiserowitz, L. Molecular packing modes. Carboxylic acids. Acta Crystallogr. B Struct. Crystallogr. Cryst. Chem. 1976, 32, 775–802. [Google Scholar] [CrossRef]
  30. Lima, P.S.V.; Weimer, G.H.; Oliveira, L.P.; Souza, H.D.S.; Fiss, G.F.; Bonacorso, H.G.; Martins, M.A.P. Mesoionic compounds: The role of intermolecular interactions in their crystalline design. CrystEngComm 2023, 25, 4976–4991. [Google Scholar] [CrossRef]
  31. Pagliari, A.B.; Meyer, A.R.; Solner, V.B.; Rosa, J.M.L.; Hörner, M.; Bonacorso, H.G.; Zanatta, N.; Martins, M.A.P. Effect of hydrogen bonds and π⋯π interactions on the crystallization of phenyl-perfluorophenyl amides: Understanding the self-organization of a cocrystal. CrystEngComm 2022, 24, 5348–5363. [Google Scholar] [CrossRef]
  32. Mohabbat, A.; Salama, J.; Seiffert, P.; Boldog, I.; Janiak, C. Single-Crystal Structure Analysis of Dicarboxamides: Impact of Heteroatoms on Hydrogen Bonding of Carboxamide Groups. Crystals 2024, 14, 811. [Google Scholar] [CrossRef]
  33. Shishkina, S.V.; Konovalova, I.S.; Kovalenko, S.M.; Trostianko, P.V.; Geleverya, A.O.; Bunyatyan, N.D. Hydrogen bonding vs. stacking interaction in the crystals of the simplest coumarin derivatives: A study from the energetic viewpoint. CrystEngComm 2019, 21, 6945–6957. [Google Scholar] [CrossRef]
  34. Niu, D.; Jiang, Y.; Ji, L.; Ouyang, G.; Liu, M. Self-assembly through coordination and π-stacking: Controlled switching of circularly polarized luminescence. Angew. Chem. 2019, 131, 6007–6011. [Google Scholar] [CrossRef]
  35. Li, G.-L.; Zhuo, Z.; Wang, B.; Cao, X.-L.; Su, H.-F.; Wang, W.; Huang, Y.-G.; Hong, M. Constructing π-stacked supramolecular cage based hierarchical self-assemblies via π⋯π stacking and hydrogen bonding. J. Am. Chem. Soc. 2021, 143, 10920–10929. [Google Scholar] [CrossRef] [PubMed]
  36. Zhuang, W.-R.; Wang, Y.; Cui, P.-F.; Xing, L.; Lee, J.; Kim, D.; Jiang, H.-L.; Oh, Y.-K. Applications of π-π stacking interactions in the design of drug-delivery systems. J. Control. Release 2019, 294, 311–326. [Google Scholar] [CrossRef] [PubMed]
  37. Huang, C.-W.; Mohamed, M.G.; Zhu, C.-Y.; Kuo, S.-W. Functional supramolecular polypeptides involving π–π stacking and strong hydrogen-bonding interactions: A conformation study toward carbon nanotubes (CNTs) dispersion. Macromolecules 2016, 49, 5374–5385. [Google Scholar] [CrossRef]
  38. Yagai, S. Supramolecularly engineered functional π-assemblies based on complementary hydrogen-bonding interactions. Bull. Chem. Soc. Jpn. 2015, 88, 28–58. [Google Scholar] [CrossRef]
  39. Burattini, S.; Greenland, B.W.; Merino, D.H.; Weng, W.; Seppala, J.; Colquhoun, H.M.; Hayes, W.; Mackay, M.E.; Hamley, I.W.; Rowan, S.J. A healable supramolecular polymer blend based on aromatic π−π stacking and hydrogen-bonding interactions. J. Am. Chem. Soc. 2010, 132, 12051–12058. [Google Scholar] [CrossRef]
  40. Janiak, C. A critical account on π–π stacking in metal complexes with aromatic nitrogen-containing ligands. J. Chem. Soc. Dalton Trans. 2000, 3885–3896. [Google Scholar] [CrossRef]
  41. Calhorda, M.J. Weak hydrogen bonds: Theoretical studies. Chem. Commun. 2000, 801–809. [Google Scholar] [CrossRef]
  42. Kaur, S.; Grover, P.; Wetmore, S.D.; Sharma, P. Role of stacking interactions in the stability of primitive genetics: A quantum chemical view. J. Chem. Inf. Model. 2021, 61, 4321–4330. [Google Scholar] [CrossRef] [PubMed]
  43. Bogdanov, A.M.; Acharya, A.; Titelmayer, A.V.; Mamontova, A.V.; Bravaya, K.B.; Kolomeisky, A.B.; Lukyanov, K.A.; Krylov, A.I. Turning on and off photoinduced electron transfer in fluorescent proteins by π-stacking, halide binding, and Tyr145 mutations. J. Am. Chem. Soc. 2016, 138, 4807–4817. [Google Scholar] [CrossRef] [PubMed]
  44. Ardejani, M.S.; Powers, E.T.; Kelly, J.W. Using cooperatively folded peptides to measure interaction energies and conformational propensities. Acc. Chem. Res. 2017, 50, 1875–1882. [Google Scholar] [CrossRef]
  45. Beall, E.; Ulku, S.; Liu, C.; Wierzbinski, E.; Zhang, Y.; Bae, Y.; Zhang, P.; Achim, C.; Beratan, D.N.; Waldeck, D.H. Effects of the backbone and chemical linker on the molecular conductance of nucleic acid duplexes. J. Am. Chem. Soc. 2017, 139, 6726–6735. [Google Scholar] [CrossRef]
  46. Heller, B.A.; Gindt, Y.M. A biochemical study of noncovalent forces in proteins using phycocyanin from Spirulina. J. Chem. Educ. 2000, 77, 1458. [Google Scholar] [CrossRef]
  47. Wang, S.; Guo, G.; Lu, X.; Ji, S.; Tan, G.; Gao, L. Facile soaking strategy toward simultaneously enhanced conductivity and toughness of self-healing composite hydrogels through constructing multiple noncovalent interactions. ACS Appl. Mater. Interfaces. 2018, 10, 19133–19142. [Google Scholar] [CrossRef]
  48. Meli, M.; Engel, H.; Laor, D.; Gazit, E.; Colombo, G. Mechanisms of metabolite amyloid formation: Computational studies for drug design against metabolic disorders. ACS Med. Chem. Lett. 2019, 10, 666–670. [Google Scholar] [CrossRef]
  49. Yang, D.; Gao, S.; Fang, Y.; Lin, X.; Jin, X.; Wang, X.; Ke, L.; Shi, K. The π–π stacking-guided supramolecular self-assembly of nanomedicine for effective delivery of antineoplastic therapies. Nanomed. 2018, 13, 3159–3177. [Google Scholar] [CrossRef]
  50. Wei, X.; Wang, Y.; Xiong, X.; Guo, X.; Zhang, L.; Zhang, X.; Zhou, S. Codelivery of a π–π stacked dual anticancer drug combination with nanocarriers for overcoming multidrug resistance and tumor metastasis. Adv. Funct. Mater. 2016, 26, 8266–8280. [Google Scholar] [CrossRef]
  51. Li, P.; Ryder, M.R.; Stoddart, J.F. Hydrogen-bonded organic frameworks: A rising class of porous molecular materials. Acc. Mater. 2020, 1, 77–87. [Google Scholar] [CrossRef]
  52. Zhang, Z.; Ye, Y.; Xiang, S.; Chen, B. Exploring multifunctional hydrogen-bonded organic framework materials. Acc. Chem. Res. 2022, 55, 3752–3766. [Google Scholar] [CrossRef] [PubMed]
  53. Zhang, C.; Wang, C.; Li, C.; Zhang, T.; Jiang, Y.; Cheng, X.; Wang, K.; Ma, C.; Li, Y. Topological hydrogen-bonded organic frameworks (HOFs) and their electronic applications in sensor, memristor, and neuromorphic computing. Appl. Phys. Rev. 2024, 11, 031303. [Google Scholar] [CrossRef]
  54. Xiong, Z.; Xiang, S.; Lv, Y.; Chen, B.; Zhang, Z. Hydrogen-Bonded Organic Frameworks as an Appealing Platform for Luminescent Sensing. Adv. Funct. Mater. 2024, 34, 2403635. [Google Scholar] [CrossRef]
  55. Chen, L.; Zhang, B.; Chen, L.; Liu, H.; Hu, Y.; Qiao, S. Hydrogen-bonded organic frameworks: Design, applications, and prospects. Mater. Adv. 2022, 3, 3680–3708. [Google Scholar] [CrossRef]
  56. Ueda, A.; Hatakeyama, A.; Enomoto, M.; Kumai, R.; Murakami, Y.; Mori, H. Modulation of a molecular π-electron system in a purely organic conductor that shows hydrogen-bond-dynamics-based switching of conductivity and magnetism. Chem. Eur. J. 2015, 21, 15020–15028. [Google Scholar] [CrossRef] [PubMed]
  57. Ren, X.M.; Nishihara, S.; Akutagawa, T.; Noro, S.; Nakamura, T. Design of a Magnetic Bistability Molecular System Constructed by H-Bonding and π···π-Stacking Interactions. Inorg. Chem. 2006, 45, 2229–2234. [Google Scholar] [CrossRef]
  58. Ueda, A.; Yamada, S.; Isono, T.; Kamo, H.; Nakao, A.; Kumai, R.; Nakao, H.; Murakami, Y.; Yamamoto, K.; Nishio, Y. Hydrogen-bond-dynamics-based switching of conductivity and magnetism: A phase transition caused by deuterium and electron transfer in a hydrogen-bonded purely organic conductor crystal. J. Am. Chem. Soc. 2014, 136, 12184–12192. [Google Scholar] [CrossRef]
  59. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  60. Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
  61. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
  62. Brandenburg, K. Diamond, Version 5.0.0. Crystal and Molecular Structure Visualization, Crystal Impact. K. Brandenburg & H. Putz Gbr: Bonn, Germany, 1997–2023.
  63. Macrae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From visualization to analysis, design and prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef] [PubMed]
  64. Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef] [PubMed]
  65. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision, C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. Available online: https://gaussian.com/citation/ (accessed on 17 March 2025).
  66. Lu, T.; Chen, Q. Interaction region indicator: A simple real space function clearly revealing both chemical bonds and weak interactions. Chem.-Methods 2021, 1, 231–239. [Google Scholar] [CrossRef]
  67. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
  68. Wu, Y.Y.; Meng, M.; Wang, G.Y.; Feng, P.; Liu, C.Y. Optically probing the localized to delocalized transition in Mo2–Mo2 mixed-valence systems. Chem. Commun. 2017, 53, 3030–3033. [Google Scholar] [CrossRef]
  69. Nishio, M. The CH/π Hydrogen Bond in Chemistry. Conformation, Supramolecules, Optical Resolution and Interactions Involving Carbohydrates. Phys. Chem. Chem. Phys. 2011, 13, 13873. [Google Scholar] [CrossRef]
  70. Nishio, M.; Umezawa, Y.; Honda, K.; Tsuboyama, S.; Suezawa, H. CH/π Hydrogen Bonds in Organic and Organometallic Chemistry. CrystEngComm 2009, 11, 1757. [Google Scholar] [CrossRef]
  71. Popa, M.M.; Răducă, M.; Man, I.C.; Dumitrascu, F. The Role of Hydrogen Bond Interactions in Crystal Formation of Pyrrolo-Azines Alcohols. Crystals 2025, 15, 78. [Google Scholar] [CrossRef]
  72. Castro, J.; Ferraro, V.; Bortoluzzi, M. Single-crystal X-ray structure determination of tris (pyrazol-1-yl) methane triphenylphosphine copper (I) tetrafluoroborate, Hirshfeld surface analysis and DFT calculations. Crystals 2024, 14, 162. [Google Scholar] [CrossRef]
  73. Gomes, L.R.; Low, J.N.; Pinheiro, A.C.; Wardell, J.L. Structural Study of N-(1, 3-Benzothiazol-2-yl)-4-Halobenzenesulfonylhydrazides: Hirshfeld Surface Analysis and PIXEL Calculations. Crystals 2024, 14, 330. [Google Scholar] [CrossRef]
  74. El Hafi, M.; Anouar, E.H.; Lahmidi, S.; Boulhaoua, M.; Loubidi, M.; Alanazi, A.S.; Filali, I.; Hefnawy, M.; El Ghayati, L.; Mague, J.T. Synthesis of New Pyrazolo [3, 4-d] pyrimidine Derivatives: NMR Spectroscopic Characterization, X-Ray, Hirshfeld Surface Analysis, DFT, Molecular Docking, and Antiproliferative Activity Investigations. Molecules 2024, 29, 5020. [Google Scholar] [CrossRef] [PubMed]
  75. Al-Resayes, S.I.; Azam, M.; Trzesowska-Kruszynska, A.; Kruszynski, R.; Soliman, S.M.; Mohapatra, R.K.; Khan, Z. Structural and theoretical investigations, Hirshfeld surface analyses, and cytotoxicity of a naphthalene-based chiral compound. ACS Omega 2020, 5, 27227–27234. [Google Scholar] [CrossRef] [PubMed]
  76. Karmakar, A.; Oliver, C.L.; Platero-Prats, A.E.; Laurila, E.; Öhrström, L. Crystal structures and hydrogen bond analysis of five amino acid conjugates of terephthalic and benzene-1, 2, 3-tricarboxylic acids. CrystEngComm 2014, 16, 8243–8251. [Google Scholar] [CrossRef]
  77. Hachuła, B.; Polasz, A.; Książek, M.; Kusz, J.; Kozik, V.; Matussek, M.; Pisarski, W. Insight into hydrogen bonding of terephthalamides with amino acids: Synthesis, structural and spectroscopic investigations. Tetrahedron 2017, 73, 2901–2912. [Google Scholar] [CrossRef]
  78. Martin, A.D.; Hartlieb, K.J.; Sobolev, A.N.; Raston, C.L. Hirshfeld surface analysis of substituted phenols. Cryst. Growth Des. 2010, 10, 5302–5306. [Google Scholar] [CrossRef]
  79. Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
  80. Contreras-García, J.; Boto, R.A.; Izquierdo-Ruiz, F.; Reva, I.; Woller, T.; Alonso, M. A benchmark for the non-covalent interaction (NCI) index or… is it really all in the geometry? Theor. Chem. Acc. 2016, 135, 242. [Google Scholar] [CrossRef]
  81. Venkataramanan, N.S.; Suvitha, A. Nature of bonding and cooperativity in linear DMSO clusters: A DFT, AIM and NCI analysis. J. Mol. Graph. 2018, 81, 50–59. [Google Scholar] [CrossRef]
  82. Heller, E.; Schmidt, G.M. Topochemistry. Part XXXIII. The Solid-State Photochemistry of Some Anthracene Derivatives. Isr. J. Chem. 1971, 9, 449–462. [Google Scholar] [CrossRef]
  83. Ossowski, J.; Wächter, T.; Silies, L.; Kind, M.; Noworolska, A.; Blobner, F.; Gnatek, D.; Rysz, J.; Bolte, M.; Feulner, P. Thiolate versus selenolate: Structure, stability, and charge transfer properties. ACS Nano 2015, 9, 4508–4526. [Google Scholar] [CrossRef]
  84. Cozzi, F.; Bacchi, S.; Filippini, G.; Pilati, T.; Gavezzotti, A. Competition between hydrogen bonding and arene–perfluoroarene stacking. X-Ray diffraction and molecular simulation on 5,6,7,8-tetrafluoro-2-naphthoic acid and 5,6,7,8-tetrafluoro-2-naphthamide crystals. CrystEngComm 2009, 11, 1122–1127. [Google Scholar] [CrossRef]
Crystals 15 00406 g001
Figure 1. (a) Syn-/anti-designation of the amide H-atoms. The illustrations (b) to (d) highlight characteristic hydrogen-bond motifs formed between amide groups, labeled according to the Etter classification scheme for the motif of chains (C), rings (R), discrete finite patterns (D), or intramolecular interactions (S). Each pattern is described using the graph-set notation G d a ( n ) , where G indicates the motif, the superscript a denotes the number of H-bond acceptors, the subscript d represents the number of H-bond donors, and the number n in parentheses stands for the number of atoms involved in the motif. (b) R 2 2 (8) ring, (c) C 1 1 (4) chain motif, and (d) the combination of C 1 1 (4) and R 2 2 (8) in a ladder, which generates a new R 4 2 (8) pattern. The patterns are highlighted by the same colors which are later used in the figures to show the respective hydrogen bonds [25,26,27,28].
Figure 1. (a) Syn-/anti-designation of the amide H-atoms. The illustrations (b) to (d) highlight characteristic hydrogen-bond motifs formed between amide groups, labeled according to the Etter classification scheme for the motif of chains (C), rings (R), discrete finite patterns (D), or intramolecular interactions (S). Each pattern is described using the graph-set notation G d a ( n ) , where G indicates the motif, the superscript a denotes the number of H-bond acceptors, the subscript d represents the number of H-bond donors, and the number n in parentheses stands for the number of atoms involved in the motif. (b) R 2 2 (8) ring, (c) C 1 1 (4) chain motif, and (d) the combination of C 1 1 (4) and R 2 2 (8) in a ladder, which generates a new R 4 2 (8) pattern. The patterns are highlighted by the same colors which are later used in the figures to show the respective hydrogen bonds [25,26,27,28].
Crystals 15 00406 g001
Crystals 15 00406 g002
Figure 2. The dicarboxamides studied in this work: 1,4-naphthalene dicarboxamide (1,4-NDA), 2,6-naphthalene dicarboxamide (2,6-NDA), and 2,7-naphthalene dicarboxamide (2,7-NDA), as well as the syn/anti amide–CO (in red) and amide–NH2 (in blue) orientations observed in the crystal structures (see below).
Figure 2. The dicarboxamides studied in this work: 1,4-naphthalene dicarboxamide (1,4-NDA), 2,6-naphthalene dicarboxamide (2,6-NDA), and 2,7-naphthalene dicarboxamide (2,7-NDA), as well as the syn/anti amide–CO (in red) and amide–NH2 (in blue) orientations observed in the crystal structures (see below).
Crystals 15 00406 g002
Crystals 15 00406 g003
Figure 3. Expanded asymmetric units for (a) 1,4-NDA; (b) 2,6 NDA, symmetry code: (i) 1 − x, 1 − y, 1 − z; (c) 2,7-NDA, symmetry code: (i) 1 − x, y, 3/2 − z.
Figure 3. Expanded asymmetric units for (a) 1,4-NDA; (b) 2,6 NDA, symmetry code: (i) 1 − x, 1 − y, 1 − z; (c) 2,7-NDA, symmetry code: (i) 1 − x, y, 3/2 − z.
Crystals 15 00406 g003
Crystals 15 00406 g004
Figure 4. Section of the 2D H-bonded sheet of 1,4-NDA with graph-set patterns. Dashed lines represent hydrogen bonds. Symmetry codes: (i) x, y + 1, z; (ii) x + 1, y, z; (iii) x, y − 1, z; (iv) x − 1, y, z.
Figure 4. Section of the 2D H-bonded sheet of 1,4-NDA with graph-set patterns. Dashed lines represent hydrogen bonds. Symmetry codes: (i) x, y + 1, z; (ii) x + 1, y, z; (iii) x, y − 1, z; (iv) x − 1, y, z.
Crystals 15 00406 g004
Crystals 15 00406 g005
Figure 5. Non-planar conformation of the dicarboxamides molecules exemplified by 1,4-NDA, with the dihedral angle ϕ between the naphthalene core and the amide group.
Figure 5. Non-planar conformation of the dicarboxamides molecules exemplified by 1,4-NDA, with the dihedral angle ϕ between the naphthalene core and the amide group.
Crystals 15 00406 g005
Crystals 15 00406 g006
Figure 6. Section of the 2D H-bonded sheet of 2,6-NDA with graph-set patterns. Dashed lines represent hydrogen bonds. Symmetry codes: (ii) −x + 1, −y, −z; (iii) x + 1, y, z.
Figure 6. Section of the 2D H-bonded sheet of 2,6-NDA with graph-set patterns. Dashed lines represent hydrogen bonds. Symmetry codes: (ii) −x + 1, −y, −z; (iii) x + 1, y, z.
Crystals 15 00406 g006
Crystals 15 00406 g007
Figure 7. Section of 3D H-bonded network of 2,7-NDA with graph-set pattern. Dashed lines represent hydrogen bonds. Symmetry codes: (ii) -x + 3/2, −y + 1/2, −z + 1; (iii) x + 1/2, y + 1/2, z.
Figure 7. Section of 3D H-bonded network of 2,7-NDA with graph-set pattern. Dashed lines represent hydrogen bonds. Symmetry codes: (ii) -x + 3/2, −y + 1/2, −z + 1; (iii) x + 1/2, y + 1/2, z.
Crystals 15 00406 g007
Crystals 15 00406 g008
Figure 8. H-bonded ladder arrangements in (a) 1,4 NDA, (b) 2,6-NDA molecules bonded into 2D networks, (c) 2,7-NDA bonded into a 3D network. Dashed orange lines represent hydrogen bonds. For the structure of 1,4-NDA, the weak intra-ladder π–π stacking with a centroid–centroid distance of 3.80 Å is also indicated (black dashed line).
Figure 8. H-bonded ladder arrangements in (a) 1,4 NDA, (b) 2,6-NDA molecules bonded into 2D networks, (c) 2,7-NDA bonded into a 3D network. Dashed orange lines represent hydrogen bonds. For the structure of 1,4-NDA, the weak intra-ladder π–π stacking with a centroid–centroid distance of 3.80 Å is also indicated (black dashed line).
Crystals 15 00406 g008
Crystals 15 00406 g009
Figure 9. Topological representation of the propagation of the R 2 2 (8) bis-amide rings in 1D ladders (orange lines), which are arranged into 2D staggered planar sheets of sql topology for (a) 1,4-NDA and (b) 2,6-NDA and into a 3D network of cds topology for (c) 2,7-NDA. For clarity, only the naphthalene carbon framework is shown, with propagating bis-amides represented by orange lines passing through the center of the dimeric R 2 2 (8) bis-amide rings.
Figure 9. Topological representation of the propagation of the R 2 2 (8) bis-amide rings in 1D ladders (orange lines), which are arranged into 2D staggered planar sheets of sql topology for (a) 1,4-NDA and (b) 2,6-NDA and into a 3D network of cds topology for (c) 2,7-NDA. For clarity, only the naphthalene carbon framework is shown, with propagating bis-amides represented by orange lines passing through the center of the dimeric R 2 2 (8) bis-amide rings.
Crystals 15 00406 g009
Crystals 15 00406 g010
Figure 10. 3D Hirshfeld surface representation of the dicarboxamides plotted over dnorm for (a) 1,4-NDA, (b) 2,6-NDA, and (c) 2,7-NDA. (dnorm < 0, red regions, indicate strong attractive interactions to an adjacent molecule; dnorm > 0, blue regions, indicate interactions weaker than the van der Waals interactions).
Figure 10. 3D Hirshfeld surface representation of the dicarboxamides plotted over dnorm for (a) 1,4-NDA, (b) 2,6-NDA, and (c) 2,7-NDA. (dnorm < 0, red regions, indicate strong attractive interactions to an adjacent molecule; dnorm > 0, blue regions, indicate interactions weaker than the van der Waals interactions).
Crystals 15 00406 g010
Crystals 15 00406 g011
Figure 11. The 2D fingerprint plots and the percentage contribution of specific non-covalently bound atomic contacts to the Hirshfeld surface for (a) 1,4-NDA, (b) 2,6-NDA, and (c) 2,7-NDA. The spikes, representing the shortest intermolecular distances, directed towards the lower left corner correspond to the N–O···O hydrogen bonds.
Figure 11. The 2D fingerprint plots and the percentage contribution of specific non-covalently bound atomic contacts to the Hirshfeld surface for (a) 1,4-NDA, (b) 2,6-NDA, and (c) 2,7-NDA. The spikes, representing the shortest intermolecular distances, directed towards the lower left corner correspond to the N–O···O hydrogen bonds.
Crystals 15 00406 g011
Crystals 15 00406 g012
Figure 12. NCI-based two-dimensional scatterplot (left) and 3D isosurface (right) for (a) 1,4-NDA, (b) 2,6-NDA, and (c) 2,7-NDA.
Figure 12. NCI-based two-dimensional scatterplot (left) and 3D isosurface (right) for (a) 1,4-NDA, (b) 2,6-NDA, and (c) 2,7-NDA.
Crystals 15 00406 g012
Crystals 15 00406 g013
Figure 13. TGA curves for the reported dicarboxamides (synthetic air; heating rate 10 K min–1).
Figure 13. TGA curves for the reported dicarboxamides (synthetic air; heating rate 10 K min–1).
Crystals 15 00406 g013
Table 1. Crystal data for 1,4-NDA, 2,6-NDA, and 2,7-NDA.
Table 1. Crystal data for 1,4-NDA, 2,6-NDA, and 2,7-NDA.
1,4-NDA2,6-NDA2,7-NDA
empirical formulaC12H10N2O2C12H10N2O2C12H10N2O2
mol wt (g mol–1)214.22214.22214.22
temperature (K)150150150
crystal systemtriclinictriclinicmonoclinic
space group P 1 - P 1 - C2/c
a (Å)5.0306 (1)5.0058 (3)6.9974 (2)
b (Å)9.9799 (3)7.2347 (7)7.2089 (2)
c (Å)10.0706 (3)7.4349 (7)19.4417 (5)
α (deg)98.620 (2)68.216 (9)90.00
β (deg)92.433 (2)82.306 (7)98.110 (2)
γ (deg)96.459 (2)80.076 (7)90.00
Volume, V (Å3)495.80 (2)245.57 (4)970.90 (5)
Z, Z′Z = 2, Z′ = 1Z = 1, Z′ = 0.5Z = 4, Z′ = 0.5
Dcalc (g/cm3)1.4351.4491.466
μ (mm−1)0.8230.8300.840
F(000)224112448
crystal size [mm3]0.65 × 0.05 × 0.020.13 × 0.07 × 0.040.13 × 0.07 × 0.05
wavelength (Å)1.541841.541841.54184
No. of unique reflections21129381042
No. of total reflections19,08021805554
No. of parameters1617382
Rint0.05090.03040.0245
R1[F2 > 2σ(F2)] (a)0.04860.05390.0358
wR1[F2 > 2σ(F2)] (a)0.14380.15470.1006
R2, wR2(F2) [all data] (a)0.0535, 0.14920.0609, 0.16040.0414, 0.1059
S [all data] (a)1.0451.1341.095
Δρmax, Δρmin (e·Å−3) (b)0.320, −0.2150.279, −0.2070.158, −0.193
CCDC no.243150724315062431508
(a) R1 = [Σ(||Fo| − |Fc||)/Σ|Fo|]; wR2 = [Σ[w(Fo2 − Fc2)2]/Σ[w(Fo2)2]]1/2. Goodness-of-fit S = [Σ[w(Fo2 − Fc2)2]/(n − p)]1/2. (b) Largest difference peak and hole.
Table 2. The parameters of the H-bonded interactions in the crystal structure of 1,4-NDA.
Table 2. The parameters of the H-bonded interactions in the crystal structure of 1,4-NDA.
D—H···A(a) (a)D—H [ Å]H···A [ Å]D···A [ Å]D—H···A [deg]Bond Energy [kcal/mol]
N1—H1A···O2 iii0.90 (2)2.07 (2)2.9601 (16)170.8 (17)−16
N1—H1B···O1 iv0.93 (2)1.96 (2)2.8105 (16)152.4 (18)−17
N2—H2A···O1 i0.92 (2)2.01 (2)2.9255 (16)177.5 (16)−16
N2—H2B···O2 ii0.92 (2)1.98 (2)2.8386 (16)153.2 (19)−19
(a) Symmetry codes: (i) x, y + 1, z; (ii) x + 1, y, z; (iii) x, y − 1, z; (iv) x − 1, y, z.
Table 3. Dihedral angles ϕ between the naphthalene core and the amide group for 1,4-NDA, 2,6-NDA and 2,7-NDA.
Table 3. Dihedral angles ϕ between the naphthalene core and the amide group for 1,4-NDA, 2,6-NDA and 2,7-NDA.
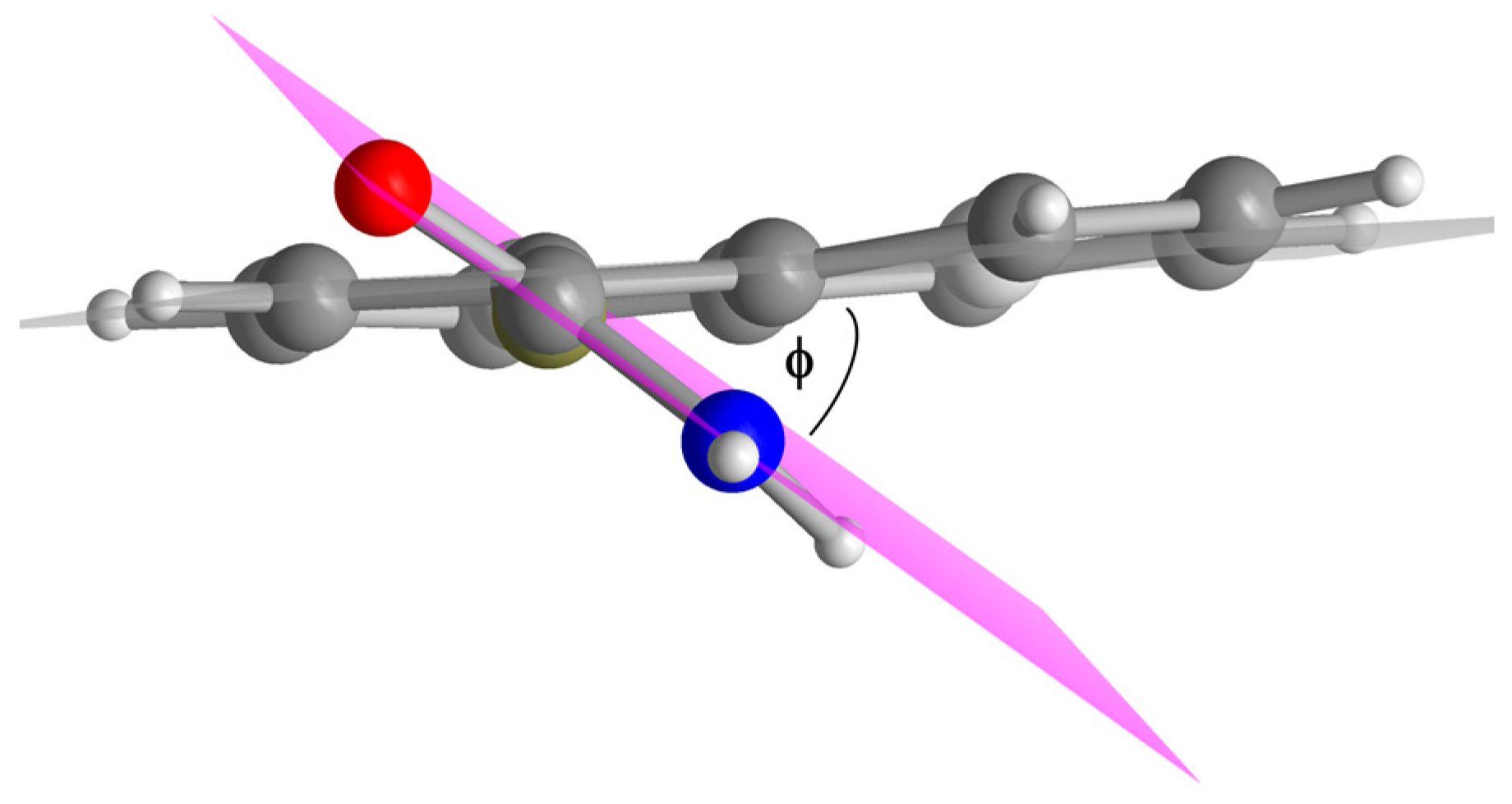
CompoundDihedral Angle ϕ [°]
1,4-NDA40
2,6-NDA29
2,7-NDA22
Table 4. The parameters of the H-bonded interactions in the structure of 2,6-NDA.
Table 4. The parameters of the H-bonded interactions in the structure of 2,6-NDA.
D—H···A(a) (a)D—H [Å]H···A [Å]D···A [Å]D—H···A [°]Bond Energy [kcal/mol]
N1—H1A···O1 ii0.89 (3)2.04 (3)2.864 (2)154 (2)−16
N1—H1B···O1 iii0.88 (3)2.07 (3)2.942 (2)173 (2)−16
(a) Symmetry codes: (ii) −x + 1, −y, −z; (iii) x + 1, y, z.
Table 5. The parameters of the H-bonded interactions in the crystal structure 2,7-NDA.
Table 5. The parameters of the H-bonded interactions in the crystal structure 2,7-NDA.
D—H···A (a)D—H [ Å]H···A [ Å]D···A [ Å]D—H···A [deg]Bond Energy [kcal/mol]
N1—H1A···O1 ii0.906 (18)1.998 (19)2.8983 (14)171.9 (15)−19
N1—H1B···O1 iii0.924 (18)2.074 (18)2.9133 (13)150.4 (14)−14
(a) Symmetry codes: (ii) −x + 3/2, −y + 1/2, −z + 1; (iii) x + 1/2, y + 1/2, z.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Mohabbat, A.; Boldog, I.; Sohi, T.H.H.; Reistel, N.; Seiffert, P.; Janiak, C. Hydrogen-Bonded Ladder Motifs in Naphthalene Dicarboxamides: Influence of Linear vs. Angular Amide Orientation. Crystals 2025, 15, 406. https://doi.org/10.3390/cryst15050406

AMA Style

Mohabbat A, Boldog I, Sohi THH, Reistel N, Seiffert P, Janiak C. Hydrogen-Bonded Ladder Motifs in Naphthalene Dicarboxamides: Influence of Linear vs. Angular Amide Orientation. Crystals. 2025; 15(5):406. https://doi.org/10.3390/cryst15050406

Chicago/Turabian Style

Mohabbat, Abdulrahman, István Boldog, Takin Haj Hassani Sohi, Nils Reistel, Philipp Seiffert, and Christoph Janiak. 2025. "Hydrogen-Bonded Ladder Motifs in Naphthalene Dicarboxamides: Influence of Linear vs. Angular Amide Orientation" Crystals 15, no. 5: 406. https://doi.org/10.3390/cryst15050406

APA Style

Mohabbat, A., Boldog, I., Sohi, T. H. H., Reistel, N., Seiffert, P., & Janiak, C. (2025). Hydrogen-Bonded Ladder Motifs in Naphthalene Dicarboxamides: Influence of Linear vs. Angular Amide Orientation. Crystals, 15(5), 406. https://doi.org/10.3390/cryst15050406

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop