Next Article in Journal
On the Derivation of Boundary Conditions for Continuum Dislocation Dynamics
Next Article in Special Issue
Binuclear Copper(I) Borohydride Complex Containing Bridging Bis(diphenylphosphino) Methane Ligands: Polymorphic Structures of [(µ2-dppm)2Cu2(η2-BH4)2] Dichloromethane Solvate
Previous Article in Journal
Non-Destructive In Situ Study of Plastic Deformations in Diamonds: X-ray Diffraction Topography and µFTIR Mapping of Two Super Deep Diamond Crystals from São Luiz (Juina, Brazil)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 7
Issue 8
10.3390/cryst7080234
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

What Can We Learn from the Crystal Structures of Metallacarboranes?

by
Alan J. Welch
Institute of Chemical Sciences, School of Engineering & Physical Sciences, Heriot-Watt University, Edinburgh EH14 4AS, UK
Crystals 2017, 7(8), 234; https://doi.org/10.3390/cryst7080234
Submission received: 26 June 2017 / Revised: 25 July 2017 / Accepted: 25 July 2017 / Published: 29 July 2017
(This article belongs to the Special Issue Crystal Structures of Boron Compounds)
Browse Figures
Versions Notes

Abstract

:
The determination of the molecular structures of metallacarboranes by X-ray diffraction remains critical to the development of the field, in some cases being the only viable way in which the overall architecture and the isomeric form of the molecule can be established. In such studies one problem frequently met is how to distinguish correctly {BH} and {CH} vertices, and this review begins by describing two relatively new methods, the Vertex-Centroid Distance (VCD) and Boron-Hydrogen Distance (BHD) methods, that have been developed to overcome the problem. Once the cage C atoms are located correctly, the resulting metallacarborane structure can frequently be analysed on the basis that cage B has a greater Structural Trans Effect (STE) than does cage C. In the absence of significant competing effects this gives rise to unequal M–L distances for a homogeneous ligand set and to a preferred Exopolyhedral Ligand Orientation (ELO) for a heterogeneous ligand set. ELO considerations can be used, amongst other things, to rank order the STEs of ligands and to identify suspect (in terms of cage C atom positions) metallacarborane structures.

Graphical Abstract

1. Introduction

The first metallacarboranes, the sandwich complexes [3-Fe(1,2-C2B9H11)2]2−, [3-Fe(1,2-C2B9H11)2]− and their C-methyl derivatives, were reported in 1965 [1] and the first crystallographic study of a metallacarborane, [3-Cp-closo-3,1,2-FeC2B9H11], appeared later that year [2]. Ever since those early days single-crystal X-ray diffraction studies have been a vital component of research into metallacarborane chemistry. As an illustration of the importance of crystallographic studies to the field, of 735 entries in a recent listing of selected 12-vertex transition-element metallacarboranes [3], 449 were characterised by single-crystal diffraction studies. Metallacarboranes are 3-dimensional cluster compounds that in general can exist in a number of isomeric forms which cannot always be distinguished spectroscopically, in which case crystallographic study is the essential experimental technique [4]. A good example concerns the icosahedral metallacarboranes MC2B9 for which there are nine possible isomers (Figure 1), eight of which have been reported for the ubiquitous [CpCoC2B9H11] [5,6,7,8,9,10,11]. Identification of any one of these isomers by NMR spectroscopy alone would be impossible: Four isomers (3,1,2; 2,1,7; 9,1,7; and 8,1,2; Cs molecular symmetry) have equivalent cage {CH} fragments and a 1:1:1:2:2:2 pattern in the 11B NMR spectrum, three further isomers (2,1,12; 2,1,9; and 9,1,2; also Cs symmetry) have inequivalent cage {CH} fragments and a 1:2:2:2:2 pattern of resonances in the 11B spectrum, whilst the final two isomers (4,1,2 and 2,1,8) are completely asymmetric. Since the 3,1,2, the 2,1,7 and the 2,1,12 isomers are synthesised by straightforward metalation of deboronated carborane dianions prepared from the three commercially-available [C2B10H12] isomers [closo-1,2-C2B10H12], [closo-1,7-C2B10H12] and [closo-1,12-C2B10H12], respectively, one could confidently predict the correct isomer for each of these. In contrast, the remaining known isomers are prepared from the 3,1,2 isomer, either by thermolysis or a redox reaction, or by deboronation and oxidative closure of a 13-vertex precursor. This makes it impossible to predict with confidence the correct isomeric form of the 12-vertex cobaltacarborane by either chemical intuition or NMR spectroscopy and means that recourse to crystallographic study is necessary. At the time of writing, six of the eight known isomers of [CpCoC2B9H11] have been characterised crystallographically [9,10,11,12,13,14].

2. Distinguishing B and C Vertices

The structural studies we have performed on the isomers of [CpCoC2B9H11] highlight an important point—since the isomers are distinguished only by the positions of the {BH} and {CH} fragments, in a crystallographic study can one be completely confident which non-metal vertices are boron and which are carbon? This is a relevant and long-standing question in structural studies of carboranes and heterocarboranes because the atomic scattering factors for X-rays, f, of B and C are similar due to the adjacency of these elements in the Periodic Table. Consistent with it being an established problem, two early methods were developed to locate the C atoms in carboranes and heterocarboranes in cases where the C atom does not carry a non-H substituent (typically alkyl or aryl group):
  • Make use of the conventional wisdom that the lengths of cage connectivities are C–C < C–B < B–B. The basis of this is simply that C has a smaller atomic radius than B since the valence electrons experience a greater effective nuclear charge (Zeff) through imperfect shielding.
  • Refine all the potential cage C and cage B atoms as B (the Prostructure) and identify the C atoms by their relatively small Ueq values, since if insufficient electron density has been assigned to an atom, the process of least-squares refinement compensates by condensing the available electron density, shrinking Ueq.
Both these approaches to cage C atom identification have merit but they also have limitations. Everything else being equal, the paradigm C–C < C–B < B–B is perfectly sound. Thus, unambiguous crystallographic studies of the three icosahedral carborane isomers [closo-1,2-C2B10H12], [closo-1,7-C2B10H12] and [closo-1,12-C2B10H12], in which the cage C atoms were clearly identified by H-bonding interactions [15], afforded C–C 1.630(8) Å, C–B 1.705(14) Å and B–B 1.772(11) Å. Therefore, in an icosahedral metallacarborane derived from [closo-1,2-C2B10H12] in which the cage C atoms retain their adjacency, and whose crystal structure is free from disorder [16], it should be fairly obvious which vertices are C from inspection of the lengths of the cage connectivities. It necessarily becomes less clear when the cage C atoms are not adjacent, but in such cases cage C should still be distinguishable.
Problems arise, however, in species in which the degree of each vertex (the number of cage connectivities it makes), is not equal. In an icosahedral cluster, all vertices are degree-5, but in sub-icosahedral clusters some vertices are degree-4, whilst in supraicosahedral clusters some are degree-6, and since the lengths of the connectivities increase with the degree of a vertex the simple pattern C–C < C–B < B–B can be overturned. Thus, for example, in the 7-vertex anion [3-Cl-closo-2-CB6H6]−, shown in Figure 2a, the C2–B1 and C2–B7 distances (between degree-4 C and degree-5 B) are significantly longer than the B4–B5 and B5–B6 distances (between two degree-4 B atoms) [17], and in the 10-vertex carborane [8-Br-closo-1,6-C2B8H9], Figure 2b, all the connectivities from degree-5 C6 to degree-5 B atoms are longer than those from degree-4 B10 to the degree-5 atoms B7 and B9 [18]. In the 14-vertex cobaltacarborane [1,13-Cp2-closo-1,13,2,9-Co2C2B10H12], Figure 3a, the C9–B14 distance is actually longer than the B11–B14 distance, even though C9 and B11 are both degree-5 and B14 is degree-6 [19]. Clearly it would be challenging to predict with confidence the cage C atom positions in cases like these on the basis of connectivity lengths alone.
Using Ueq values to identify cage C atoms can also be problematic, simply because the Ueq of an atom is influenced by its local environment. In particular, heavy atoms frequently suppress the Ueq of atoms directly bonded to them, meaning that this approach to discriminating between B and C atoms can be particularly unreliable for metallacarboranes. As an example, consider the cobaltacarborane [1,13-Cp2-closo-1,13,2,10-Co2C2B10H12] [19]. Figure 3b shows the Prostructure and Table 1 lists the Ueq values of vertices 2–12 and 14 in this Prostructure. Vertices 2 and 10 correspond to C atoms (Ueq underlined) but whilst vertex 2 has the smallest Ueq of all the vertices, the Ueq of vertex 10 is larger than that of seven B atoms (Ueq italicised). Vertex 2 is directly connected to both Co atoms and all B atoms with Ueq values smaller than that of vertex 10 are bound to at least one Co, whilst vertex 10 is directly connected to neither, clearly illustrating the influence of an adjacent metal on the magnitude of Ueq.
In summary, both of the established methods (connectivity lengths and Ueq values) for distinguishing between {BH} and {CH} fragments in (hetero)carboranes generally, and metalla(hetero)carboranes specifically, have deficiencies and should be used with caution. Because of this we have developed two further approaches to the problem which we term the Vertex-Centroid Distance (VCD) method and the Boron-Hydrogen Distance (BHD) method.

2.1. The VCD Method

The basis of the Vertex-Centroid Distance method, similar to that of the connectivity length approach, is that carbon has a smaller atomic radius than boron. In the VCD method the centroid of the cluster is calculated and the distances from each vertex to the centroid are measured. Since carbon is smaller than boron, the C atoms will lie closer to the centroid and are therefore identified by the VCDs. The advantage of this method over the connectivity length approach is that (i) a single parameter is associated with each vertex (greatly simplifying analysis), and (ii) it is independent of the isomer, working just as well for species in which two C atoms are separated as those in which the C atoms are adjacent.
We first described the VCD method in 2013, carefully validating it against a large number of carborane and metallacarborane structures in the literature in which the cage C atoms were located unambiguously [19]. The method is independent of whether a particular vertex has been refined as B or C (this only affects Ueq of the vertex not its position), so we were able to use the VCD approach to identify literature cases in which cage C had been wrongly positioned, to suggest B/C disorder that had been overlooked and to refute erroneously assigned disorder.
In the VCD method some care needs to be taken in calculating the position of the polyhedral centroid and in interpreting the VCDs. In the case of the 11-vertex nido polyhedron in Figure 4a only vertices 2–11 should be used to define the centroid, since to include vertex 1 would bias the centroid towards it. Equally, in the 10-vertex closo metallacarborane in Figure 4b, the metal vertex 1 should be excluded from the centroid calculation (since metal atoms generally lie further from the centroid than do B or C atoms) and, for balance, the antipodal vertex 10 should also be excluded. Note, however, that even if a vertex is excluded from the set from which the centroid is calculated, the VCD from that vertex can still be used. When using VCD it is important that only VCDs from equivalent vertices (as defined by symmetry-equivalence with respect to the parent closed polyhedron) are compared. Thus, in the polyhedron shown in Figure 4b only VCDs from the degree-5 vertices 2–9 should be compared (the VCD from the degree-4 vertex 10 will be considerably longer), and in the dodecahedral cluster of Figure 4c VCDs from the degree-4 vertices 1, 2, 7, and 8 should be compared as one group and those from the degree-5 vertices 3–6 compared as a separate group.
Centroids and VCDs are easily calculated using standard software such as Mercury [20] or Olex2 [21]. Roughly speaking, within a set of equivalent vertices a VCD to carbon will be typically 0.1–0.15 Å shorter than a VCD to boron, as demonstrated by the entries in Table 2 for the carborane [closo-1,7-C2B10H12] in which the positions of the cage C atoms are unambiguously known by their involvement in intermolecular H-bonding [15].
One caveat to the VCD approach to identifying cage C positions that we have recently identified concerns carborane cages in which a cage C atom is σ-bonded to a metal atom. These C atoms have longer VCDs than equivalent C atoms not involved in M–C bonding, making the distinction between B and C less obvious (the VCD to this C atom may even exceed that to B), and Table 3 demonstrates this effect in the case of [1-{CpRu(PMe2Ph)2}-2-Me-closo-1,2-C2B10H10] [22]. In such cases, however, the presence of M–C bonding should be clearly inferred from NMR spectroscopy.
This notwithstanding, we have found that the VCD method is a quick and effective addition to the techniques available to distinguish B and C atoms in carboranes and heterocarboranes. One useful benefit is that because VCD uses only atomic coordinates the method can be used to check published carborane and heterocarborane structures, useful in analysis of literature compounds [23].

2.2. The BHD Method

The basis of the Boron-Hydrogen Distance method is that crystallographic refinement of an atom at which insufficient electron density has been assigned will compensate for this by moving a bound H atom artificially close to that atom. Thus, in the Prostructure, if a vertex which is really C has been refined as B, not only will Ueq be relatively small but an unusually short vertex–H distance will be observed. In a carborane or heterocarborane, a typical B–H bond length is ca. 1.1 Å and a typical C–H distance ca. 1.0 Å. But if a C atom has been refined as B, the vertex–H distance will usually be shortened to between 0.2 and 0.5 Å, clearly identifying the vertex as a C atom. Short bonds to H are clearly visible at vertices 2 and 10 of Figure 3b, and Table 4 summarises all the vertex–H bonds in this Prostructure. On correctly assigning the vertices as C, further refinement subsequently affords perfectly sensible vertex–H bond lengths.
We first described the BHD method in 2002 [24] and reported on it more comprehensively in 2014 [25]. It relies on crystallographic data of reasonable precision (and certainly the ability to refine H atoms positionally) but given that a standard crystallographic experiment typically now involves data collected at low temperature on a CCD-equipped diffractometer precise diffraction data should be routinely achieved. Moreover, the practice of including F2 data in CIFs means that the BHD method can now be used to check recent literature structures.
It is now standard operating procedure in our laboratory to use both the VCD and BHD methods to help distinguish between {BH} and {CH} fragments using the Prostructures of carboranes and heterocarboranes, in conjunction with the established practices of inspection of the lengths of cage connectivities and the values of Ueq. When all four methods lead to the same conclusion, we can have a high level of confidence that the C atoms are correctly located. Being confident about C atom positions is a vital prerequisite for an analysis of metallacarborane structures, discussed below.

3. Structural Trans Effects in Metallacarboranes

By far the most common carborane ligand is [nido-7,8-C2B9H11]2−, easily derived from [closo-1,2-C2B10H12] by a straightforward deboronation reaction. When this anion is bound η5 to a metal atom the resultant metallacarborane is the 3,1,2-MC2B9 isomer. There are hundreds of examples of such metallacarboranes [3], very many of which have been subject to crystallographic study (a search for the {3,1,2-MC2B9H11} fragment in the Cambridge Structural Database (CSD) [26] affords nearly 400 hits). What useful information can we glean from these many structural studies?
A fundamental issue is that, although the carborane is bound η5, the C and B atoms in the upper pentagonal face do not bind equally strongly to the metal atom. Since Zeff C > Zeff B, the C atoms contribute disproportionately more to the core molecular orbitals and the facial B atoms contribute more to the frontier molecular orbitals (FMOs) of the carborane ligand, leading to relatively weak M–C bonding [27]. However, this relatively weak M–C bonding is not directly obvious from crystallographic studies due to the smaller radius of C compared to B (see above). Thus, for example, in [3-Cp-closo-3,1,2-CoC2B9H11] [13], Figure 5a, the Co–Ccage connectivities are actually significantly shorter that the three Co–B distances even though the former are the weaker bonds [27]. On the other hand, clear, albeit indirect, evidence for weaker Co–Ccage bonding relative to Co–B bonding is evident in the Co–CCp distances, those trans to cage C being significantly shorter than those trans to B. This arises because, in a metallacarborane, the more strongly bound B atoms exert a greater Structural Trans Effect (STE, trans influence) than do the relatively weakly bound C atoms, leading to weaker M–ligand bonds trans to B and stronger M–ligand bonds trans to C. There are many examples of the STE in metallacarboranes. As well as marked asymmetry in the bonding of η-bonded ligands as in [3-Cp-closo-3,1,2-CoC2B9H11] and the related [3-(C6H6)-closo-3,1,2-RuC2B9H11] [28], unequal M–L distances which can be rationalised in STE terms are observed in [L3MC2B9H11] species such as [3,3,3-(CO)3-closo-3,1,2-FeC2B9H11] [29] and [3,3,3-Cl3-closo-3,1,2-TaC2B9H11] [30], Figure 5b,c. In considering [L3MC2B9H11] species it is convenient to define the orientation of an individual ligand L by the torsion angle θ (Figure 6). Ligands with large |θ| sit trans to cage C (and are relatively strongly bound) whilst those with small |θ| sit cis to cage C (and are relatively weakly bound). We recently summarised data for literature [3,3,3-(CO)3-closo-3,1,2-MC2B9H11]x− structures [31], showing a general inverse relationship between |θ| and the M−CO distance.

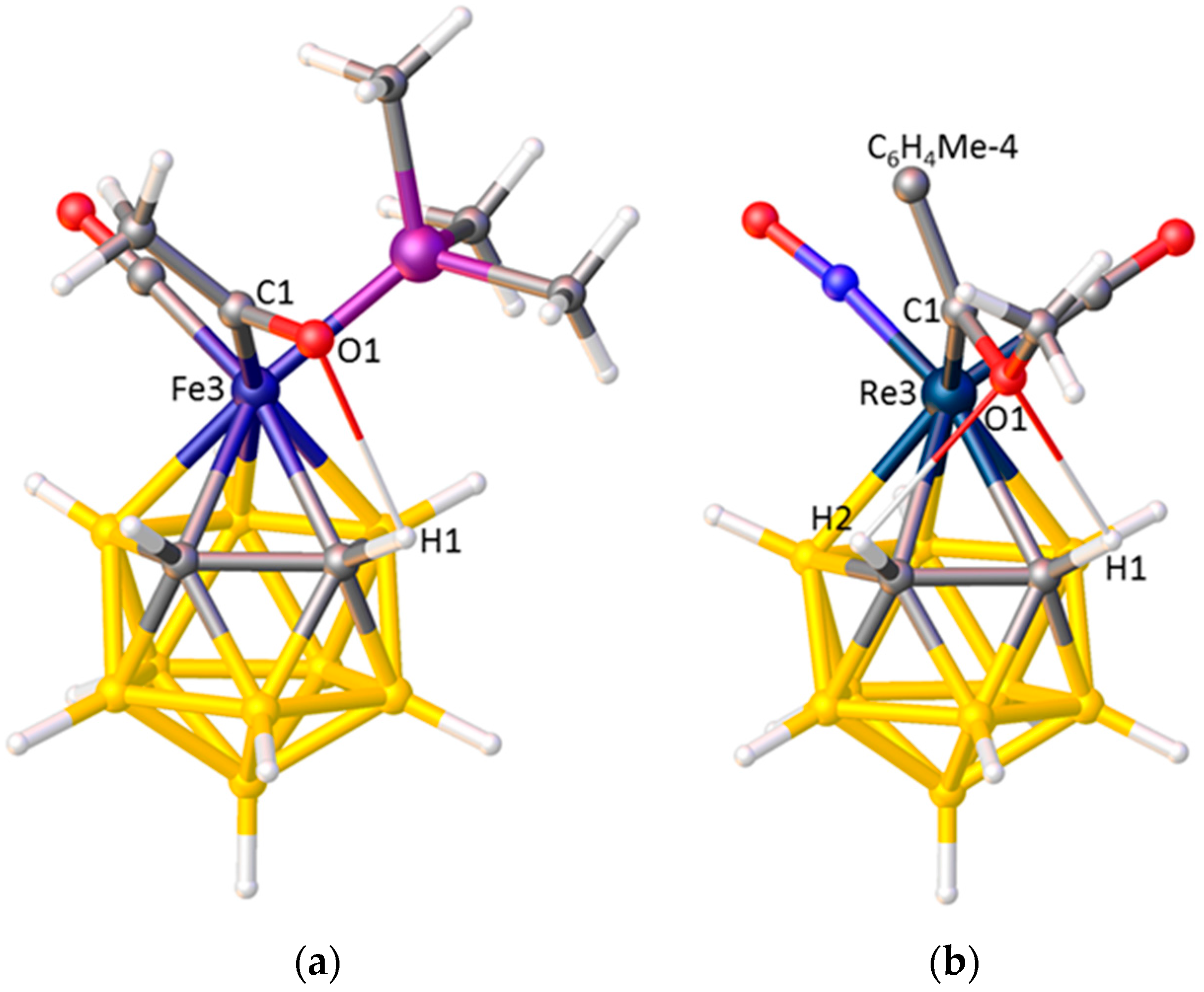
3.1. Exopolyhedral Ligand Orientation

In cases where the non-carborane ligand is η-bonded but asymmetric or in cases where the κ1-bound ligand set is heterogeneous, the STE in metallacarboranes gives rise to a preferred Exopolyhedral Ligand Orientation (ELO) of the non-carborane ligand(s). In the absence of significant competing effects, the preferred ELO will be that in which the exopolyhedral ligand (or part of ligand) with the greater or greatest STE lies approximately trans to cage C, whilst that with smaller or smallest STE lies approximately trans to cage B. Thus, the differing STEs of the cage C and cage B atoms control the orientation of the exopolyhedral ligand(s).

3.1.1. ELO of η-Bound Ligands

A striking example of preferred exopolyhedral ligand orientation comes from comparison of the structures of metallacarboranes with pyrrolyl and boratabenzene as exopolyhedral ligands. In [3-(C4H4N)-closo-3,1,2-CoC2B9H11], Figure 7a, the orientation of the pyrrolyl ring is such that the N heteroatom lies above the C1–C2 connectivity of the carborane ligand [32], whilst in [3-(C5H5BMe)-closo-3,1,2-RhC2B9H11], Figure 7b, the boratabenzene ligand is oriented such that its B heteroatom is positioned trans to C1–C2 [33]. Given that Zeff N > Zeff C > Zeff B, in the pyrrolyl ligand the N atom will contribute least to the π-FMOs and have the smallest STE, whilst in the boratabenzene ligand the B atom will contribute most to the π-FMOs and have the greatest STE. Hence the observed, very different, exopolyhedral ligand orientations are rationalised.
In indenyl, naphthalene, and related η-bonded ligands the π-atomic orbitals of the ring-junction C atoms are simultaneously involved in two aromatic systems and consequently are relatively weakly bound to the metal atom (small STE) compared to the non-ring-junction C atoms. In metallacarborane complexes of these ligands this gives rise to a preferred ELO. Thus in [3-(C9H7)-closo-3,1,2-CoC2B9H11], Figure 8a, the η5-indenyl ligand is oriented such that the ring-junction atoms are cisoid to the cage C atoms (cisoid describes the orientation in which atoms are as close to each other as possible given the overall staggered conformation of η5-indenyl and η5-carborane rings) [12]. In the analogous iron species [3-(C9H7)-closo-3,1,2-FeC2B9H11] the two rings are eclipsed and the ring-junction C atoms sit directly above the cage C atoms [34], rationalised by a significantly greater distance between the rings in the iron complex (3.23 Å) compared to that in the cobalt complex (3.09 Å). One η5-fluorenyl metallacarborane is known [35]. In the fluorenyl ligand are two pairs of ring-junction C atoms, and the observed orientation in [3-(C13H9)-closo-3,1,2-CoC2B9H11], Figure 8b, is that which maximises the adjacency of ring-junction and carborane C atoms, as predicted by STE arguments. A conformation very close to cisoid is also observed in the naphthalene ruthenacarborane [3-(C10H8)-closo-3,1,2-RuC2B9H11] [36].
A final example of the preferred orientation of an η-bonded ligand in a metallacarborane is when that η-bonded ligand is another carborane. Without doubt the single most studied metallacarborane is [3-Co(1,2-C2B9H11)2]− (trivial name CoSAN) because its stability and tailorability has led to a vast number of applications. Like the very first metallacarboranes, CoSAN is a sandwich complex, formally composed of two [nido-7,8-C2B9H11]2− anions and a Co3+ metal centre. There are 73 crystallographic determinations of the [3-Co(1,2-C2B9H11)2]− anion in the CSD and in the vast majority of these the conformation is cisoid. This cisoid conformation, Figure 9, has been shown to be the most thermodynamically stable by DFT calculations performed on the isoelectronic complex [3-Ni(1,2-C2B9H11)2] [37], but it can be very easily rationalised by STE/ELO arguments with the large STE B atoms of one cage lying trans to the small STE C atoms of the other.

3.1.2. ELO of κ1 Ligands

A significant number of [L3MC2B9H11] metallacarboranes (where the metallacarborane is the 3,1,2-MC2B9 isomer) are known in which the three ligands L are not all the same, and within examples which have been studied crystallographically, a well-represented sub-group is that with two phosphine ligands and one chloride ligand. When M = Co or Rh these are neutral, 18-e species. For M = Ru an 18-e monoanion is known, but there is also a series of 17-e neutral species for both Fe and Ru. All these compounds, together with their CSD refcodes and the torsion angles (θ) for each of the exopolyhedral ligands, are listed in Table 5. Entries in italics refer to 17-e compounds.
It is immediately apparent that in all cases the ligand with the lowest |θ| (ca. 0–20°) is always Cl, whilst one P atom has |θ| ca. 95–115° and the other P has |θ| ca. 125–145°. There is therefore a clear orientational preference for a {MClP2} fragment in a 3,1,2-MC2B9 metallacarborane in which the Cl ligand is located cis to the cage C atoms, fully consistent with the STE of Cl being smaller than that of phosphine.
How strong is this orientational preference? Using DFT calculations we have computed the energy of the model compound [3,3-(PH3)2-3-Cl-closo-3,1,2-RhC2B9H11] as a function of |θCl| [49], and the results are plotted in Figure 10. The global minimum is the conformation with |θCl| = 0°, ca. 15 kcal mol−1 more stable than the conformation with |θCl| = 180°. The strength of this orientational preference is therefore of the order of strong H-bonding implying that, in the absence of significant inter- or intramolecular forces (which could be either attractive or repulsive), the exopolyhedral ligand orientation should be controlled by the relative structural trans effects of the ligands. The |θCl| values of the 12 compounds in Table 5 all fall within the small circle superimposed on Figure 10. Further examples of [L3MC2B9H11] metallacarboranes in which one ligand has a smaller STE than the other two include (stronger ligands given first) [3,3-(CO)2-3-Cl-closo-3,1,2-RuC2B9H11]− [50], [3,3-(PPh2Me)2-3-NCMe-closo-3,1,2-RhC2B9H11]+ [42] and [3,3-(CO)2-3-(η-MeC≡CPh)-closo-3,1,2-RuC2B9H11] [51], and in all cases the ligand with the smallest |θ| is the unique weaker one.
In all the above cases the 3,1,2-MC2B9 metallacarborane contains two exopolyhedral ligands with relatively large STEs and one with a relatively small STE. Fewer examples exist of the reverse situation; two ligands with relatively small STEs and one with a relatively large STE. In [3,3-(PPh3)2-3-H-closo-3,1,2-RuC2B9H11]−, shown in Figure 11a, the ligand with the smallest |θ| is one of the relatively weak PPh3 ligands [44], whilst the other PPh3 ligand at greater |θ| has a significantly shorter Ru–P bond length, consistent with it lying less trans to boron. The ligand with the greatest |θ| is the relatively strong H. A similar situation pertains in [3,3-(κ2-tmeda)-3-CO-closo-3,1,2-RuC2B9H11], Figure 11b [52]. Here the relatively weakly-bound atoms are the N atoms of the tmeda ligand and the strong ligand is CO. One N has the smallest |θ| whilst the other N is significantly closer to the metal atom. The CO ligand is oriented with the greatest |θ|. A secondary feature of both these structures is that since the single ligand with the greater STE (H and CO, respectively) is positioned essentially directly trans to C1, the Ru–C1 connectivity is significantly longer than Ru–C2.

3.1.3. Applications of ELO

There are a number of ways in which the recognition of exopolyhedral ligand orientation can be useful in metallacarborane chemistry. In the following sections, we discuss only a few selected examples to illustrate the potential value of ELO considerations in this area.

Rank Ordering the STEs of Exopolyhedral Ligands

We have noted that the preferred orientation of exopolyhedral ligands in mixed-ligand 3,1,2-MC2B9 metallacarboranes is consistent with STEs in the relative order H > PR3 > Cl. This is as expected since there is general agreement in the literature that H is a strong STE ligand, phosphines have a moderate STE, and Cl is invariably weak [53,54]. Rankings of the STEs of ligands are usually made on the basis of extensive compilations of M–X distances, where X is a probe ligand trans to the ligand in question. In contrast, analysis of metallacarborane structures allows the STEs of ligands to be compared very quickly, based on a simple orientational preference.
CO and PPh3 are both considered as moderate STE ligands. Coe and Glenwright order their STEs as CO > PPh3 on the basis of analysis of [M(CO)5PPh3] structures [53], whilst See and Kozina conclude the reverse ordering, PPh3 > CO, from analysis of the structures of complexes in which these ligands are trans to Cl [54]. We recently surveyed the preferred ELO in mixed carbonyl-phosphine 3,1,2-MC2B9 metallacarboranes (of both types, [3,3-(PPh3)2-3-CO-closo-3,1,2-MC2B9H11] and [3,3-(CO)2-3-PPh3-closo-3,1,2-MC2B9H11]) and concluded that, at least in this class of compound, the STE of CO is greater than that of PPh3 [55].
A small number of 3,1,2-MC2B9 metallacarboranes are known having three different exopolyhedral ligands (Table 6). In KISBOD and LOBSUQ the exopolyhedral ligands are oriented in accord with their accepted STEs, with |θ|CO > |θ|PPh3 > |θ|NCMe for KISBOD and |θ|CO > |θ|PPh3 > |θ|I for LOBSUQ. However, the ELOs in TAKCUD, [3-CO-3-PMe3-3-C(O)Me-closo-3,1,2-FeC2B9H11]−, and LICDOQ, [3-NO-3-CO-3-{C(OMe)C6H4Me-4)-closo-3,1,2-ReC2B9H11], appear to be at variance with the accepted ligand STEs. In TAKCUD the ligand with the lowest |θ| is acetyl, but there is substantial literature evidence that, in terms of STE, acetyl > CO [56]. Equally, the observation in LICDOQ that the alkylidene ligand has the lowest |θ| (implying it has the smallest STE) is anomalous in terms or literature precedence [57].
An understanding of the unexpected ELOs in TAKCUD and LICDOQ is afforded by a detailed examination of their structures, revealing intramolecular H-bonding between the O atom of the acetyl or methoxyalkylidene ligand and the protonic H atom(s) on cage carbon. In TAKCUD, Figure 12a, the H-bond is between O1 and H2 whilst in LICDOQ, Figure 12b, bifurcated H-bonding exists involving O1···H1 and O1···H2. These H-bonds lock the acetyl and alkylidene ligands into a low |θ| orientation and presumably override the preferred ELO based only on STE considerations.
Preferred ELO can also be overruled by intramolecular steric crowding. A recent demonstration of this involves the molybdacarboranes [3,3,3-(CO)3-3-PPh3-closo-3,1,2-MoC2B9H11], Figure 13a, and its C,C-dimethyl analogue [1,2-Me2-3,3,3-(CO)3-3-PPh3-closo-3,1,2-MoC2B9H9], Figure 13b. In the former, the lower STE PPh3 ligand has the smallest |θ|, 25.0°, as expected, whilst in the latter species steric congestion between PPh3 and the cage Me substituents pushes the phosphine round to the largest |θ|, 170.9° [55]. For this reason, all discussion of preferred exopolyhedral ligand orientation in terms of structural trans effects is best restricted to cases of unsubstituted carborane cages.

Rapid Identification of Suspect Structures

Since, in the absence of intramolecular H-bonding or steric crowding, the ELO is a direct consequence of the cage C positions, literature structures with an unexpected ELO may signify that the cage C atoms are wrongly placed. One such example concerns the rhodacarborane [3,3-(κ2-NO3)-3-PPh3-closo-3,1,2-RhC2B9H11], the original structure of which was published in 1979 [61]. It was clear from the high e.s.d.s that this was a relatively imprecise structure (room temperature data collection on a serial diffractometer), but what was particularly striking was the orientation of the nitrato and phosphine ligands, with the latter apparently cis to the cage C atoms, Figure 14a. Nitrate is a very weak ligand compared to PPh3, so this orientation was certainly suspicious.
VCD analysis supported the possibility that the cage C atoms were misplaced. Consequently, we resynthesised the compound and redetermined the structure (at low temperature using a CCD-equipped diffractometer), locating the cage C atoms unambiguously and at different vertices to those of the original structure [19]. The new structure, Figure 14b, is fully consistent with ELO expectations since in both crystallographically-independent molecules the PPh3 ligand now lies at large |θ| values, 168.9 and 174.3°.

Exploring the STEs of Cage Heteroatoms

Since the ELOs of a heterogeneous set of ligands of differing STEs are a consequence of the differing STEs of boron and cage heteroatoms, it should be possible to use the ELOs to comment on the STEs of those cage heteroatoms, relative to boron. Figure 15 shows the structures of three icosahedral metallaheteroboranes in which a metal-ligand fragment is bonded to a {B10X} cage. From the orientation of the hydride ligands in [2,2-(PPh3)2-2-H-closo-2,1-RhNB10H11] [62], Figure 15a, and [2,2-(PEt3)2-2-H-closo-2,1-PtCB10H11] [63], Figure 15b, we conclude that both N and C have smaller STEs than boron. Recall that in Section 3.1.1 the STE ranking B > C > N was deduced from the orientations of pyrrolyl and boratabenzene ligands in metallacarboranes. Also note that, in principle, the orientation of the {PtHP2} fragment in the platinacarborane could be used to identify the position of the cage C atom, as an interesting complement to the established methods previously discussed. From the structure of the rhodathiaborane [2,2-(PMe2Ph)2-2-Cl-closo-2,1-RhSB10H10] [64], Figure 15c, it is clear that S also has a smaller STE than boron since the ligand with the largest |θ|, P1, makes a significantly shorter Rh–P bond than does P2.
Finally, there is some evidence that consideration of ELO can allow comment on the relative STEs of cage vertices of differing degrees. In the 13-vertex stannacarborane [1,10-Me2-4,4-(κ2-Me2bipy)-closo-4,1,10-SnC2B10H10], shown in Figure 16a, the Sn4 centre has a κ2-dimethylbipyridine ligand and a stereochemically-active lone pair of electrons. The orientation of the dimethylbipyridine, lying cis to the degree-4 atom C1 and trans to the degree-5 atom C10, implies that degree-4 C has a larger STE than degree-5 C, which is intuitively reasonable [65]. On thermolysis of the analogous bipyridine species the cage undergoes isomerisation from 4,1,10-SnC2B10 to 4,1,12-SnC2B10, affording [1,12-Me2-4,4-(κ2-bipy)-closo-4,1,12-SnC2B10H10], Figure 16b, and the bipyridine ligand “flips” so that it now lies trans to C1 and cis to B10. This suggests that, in terms of STE, degree-5 B > degree-4 C, which is not intuitively obvious. Note that even though in these stannacarborane molecules the cage C atoms carry Me substituents, space-filling models suggest that intramolecular steric crowding is minimal and consequently that the exopolyhedral ligand orientation is electronically-controlled.

4. Conclusions

What can we learn from the crystal structures of metallacarboranes? It goes without saying that, in common with such studies generally, crystallographic structure determination provides absolute proof of the identity and isomeric nature of the metallacarborane that, in the vast majority of cases, can be correlated with the synthetic procedure used, the spectroscopic properties, and chemical reactivity of the compound and, increasingly, the structure optimised by computational means. In addition, however, this review has demonstrated that the heterogeneity of a carborane ligand, manifest in the differing structural trans effects (STEs) of carbon and boron, leads to heterogeneity in the bonding of exopolyhedral ligands and preferred orientations of these ligands. Recognition of this can be used, amongst other things, to establish quickly and simply the relative STEs of exopolyhedral ligands and to identify literature structures which are suspicious. All of this, however, is predicated on the cage C atoms being correctly identified in the crystallographic study. This sometimes remains a challenge, but new approaches such as the VCD and BHD methods have been developed to overcome that challenge, and have proven to be useful in many cases. Unfortunately, most papers which report (hetero)carborane crystal structures give no indication as to how the cage C and cage B atoms were distinguished, whether it be by one of the newer methods or by the more established approaches of analysis of the lengths of the cage connectivities and/or Ueq values of the vertex atoms. Such detail, although minor, would be a welcome addition to published work.

Acknowledgments

I thank past and present members of the HWU Heteroborane Research Group for their contributions to many of the results described here, especially Greig Scott for his particular interest in ELO. Many of the metallacarborane structures discussed were determined at HWU by my colleague Georgina M. Rosair, whose fruitful collaboration over many years I gratefully acknowledge.

Conflicts of Interest

The author declares no conflict of interest.

References and Notes

  1. Hawthorne, M.F.; Young, D.C.; Wegner, P.A. Carbametallic Boron Hydride Derivatives. I. Apparent Analogs of Ferrocene and Ferricinium Ion. J. Am. Chem. Soc. 1965, 87, 1818–1819. [Google Scholar] [CrossRef]
  2. Zalkin, A.; Templeton, D.H.; Hopkins, T.E. The Crystal and Molecular Structure of C5H5FeB9C2H11. J. Am. Chem. Soc. 1965, 87, 3988–3990. [Google Scholar] [CrossRef]
  3. Grimes, R.N. Carboranes, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 831–863. [Google Scholar]
  4. Robertson, A.P.M.; Beattie, N.A.; Scott, G.; Man, W.Y.; Jones, J.J.; Macgregor, S.A.; Rosair, G.M.; Welch, A.J. 14-Vertex Heteroboranes with 14 Skeletal Electron Pairs: An Experimental and Computational Study. Angew. Chem. Int. Ed. 2016, 55, 8706–8710. [Google Scholar] [CrossRef] [PubMed]
  5. Hawthorne, M.F.; Young, D.C.; Andrews, T.D.; Howe, D.V.; Pilling, R.L.; Pitts, A.D.; Reintjes, M.; Warren, L.F.; Wegner, P.A. π-Dicarbollyl derivatives of the transition metals. Metallocene analogs. J. Am. Chem. Soc. 1968, 90, 879–896. [Google Scholar] [CrossRef]
  6. Kaloustian, M.K.; Wiersema, R.J.; Hawthorne, M.F. Thermal rearrangement of π-cyclopentadienyl-π-dicarbollyl derivatives of cobalt. J. Am. Chem. Soc. 1972, 94, 6679–6686. [Google Scholar] [CrossRef]
  7. Busby, D.C.; Hawthorne, M.F. The crown ether promoted base degradation of p-carborane. Inorg. Chem. 1982, 21, 4101–4103. [Google Scholar] [CrossRef]
  8. Hanusa, T.P.; Todd, L.J. Reductive Isomerization of Icosahedral Metallocarbaboranes. Polyhedron 1985, 4, 2063–2066. [Google Scholar] [CrossRef]
  9. Lopez, M.E.; Ellis, D.; Murray, P.R.; Rosair, G.M.; Welch, A.J.; Yellowlees, L.J. Synthesis and/or Molecular Structures of Some Simple 2,1,7- and 2,1,12-Ruthena and Cobaltacarboranes. Collect. Czech. Chem. Commun. 2010, 75, 853–869. [Google Scholar] [CrossRef]
  10. Man, W.Y.; Zlatogorsky, S.; Tricas, H.; Ellis, D.; Rosair, G.M.; Welch, A.J. How to Make 8,1,2-closo-MC2B9 Metallacarboranes. Angew. Chem. Int. Ed. 2014, 53, 12222–12225. [Google Scholar] [CrossRef] [PubMed]
  11. Man, W.Y.; Rosair, G.M.; Welch, A.J. Reduction-induced facile isomerisation of metallacarboranes: Synthesis and crystallographic characterisation of [4-Cp-4,1,2-closo-CoC2B9H11]. Dalton Trans. 2015, 44, 15417–15419. [Google Scholar] [CrossRef] [PubMed]
  12. Smith, D.E.; Welch, A.J. Indenylmetallacarboranes. 1. The 18-Valence-Electron Complex [3-(η5-C9H7)-3,1,2-CoC2B9H11] and Comparative Molecular Structures of This Complex and [3-(η5-C5H5)-3,1,2-CoC2B9H11]. Organometallics 1986, 5, 760–766. [Google Scholar] [CrossRef]
  13. Planas, J.G.; Viñas, C.; Teixidor, F.; Light, M.E.; Hursthouse, M.B. Polymorphism and phase transformations in cobaltacarborane molecular crystals. CrystEngComm 2007, 9, 888–894. [Google Scholar] [CrossRef]
  14. Man, W.Y.; Rosair, G.M.; Welch, A.J. Crystal structure of a second polymorph of 2-cyclopentadienyl-1,7-dicarba-2-cobalta-closo-dodecaborane(11). Acta Crystallogr. Sect. E Struct. Rep. Online 2015, 71, m141. [Google Scholar] [CrossRef] [PubMed]
  15. Davidson, M.G.; Hibbert, T.G.; Howard, J.A.K.; Mackinnon, A.; Wade, K. Definitive crystal structures of ortho, meta- and para-carboranes: Supramolecular structures directed solely by C–H···O hydrogen bonding to hmpa (hmpa = hexamethylphosphoramide). Chem. Commun. 1996, 2285–2286. [Google Scholar] [CrossRef]
  16. Disorder between {BH} and {CH} vertices is relatively commonplace in crystallographic studies of carboranes and heterocarboranes, complicating all approaches to discriminating between B and C vertices. Although in principle such disorder could be extensive, in our experience most examples appear to involve 50:50 disorder over two vertices which is fairly easily identified and simply modelled.
  17. Schlüter, F.; Bernhardt, E. Synthesis of 3-DBU-closo-2-C2B6H6 and [3-Cl-closo-2-CB6H6]−—A First Straightforward Synthesis of [CB6]-closo-Clusters. Z. Anorg. Allg. Chem. 2010, 636, 2462–2466. [Google Scholar] Note that some of the distances given in the legend to Figure 5 in this paper do not agree with those calculated from the deposited CIF.
  18. Bakardjiev, M.; Štíbr, B.; Holub, J.; Padělková, Z.; Růžička, A. Simple Synthesis, Halogenation and Rearrangement of closo-1,6-C2B8H10. Organometallics 2015, 34, 450–454. [Google Scholar] [CrossRef]
  19. McAnaw, A.; Scott, G.; Elrick, L.; Rosair, G.M.; Welch, A.J. The VCD method—A simple and reliable way to distinguish cage C and B atoms in (hetero)carborane structures determined crystallographically. Dalton Trans. 2013, 42, 645–664. [Google Scholar] [CrossRef] [PubMed]
  20. Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0—New features for the visualization and investigation of crystal structures. J. Appl. Cryst. 2008, 41, 466–470. [Google Scholar] [CrossRef]
  21. Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
  22. Basato, M.; Biffis, A.; Buscemi, G.; Callegaro, E.; Polo, M.; Tubaro, C.; Venzo, A.; Vianini, C.; Graiff, C.; Tiripicchio, A.; Benetollo, F. Reaction of Cyclopentadienyl Ruthenium Complexes with a Carborane Anion: Effect of the Spectator Ligands on the Substitution Site. Organometallics 2007, 26, 4265–4270. [Google Scholar] [CrossRef]
  23. Note that in all cases in this review where we have analysed literature structures we have confirmed the cage C atom positions ex-post by the VCD method.
  24. Burke, A.; McIntosh, R.; Ellis, D.; Rosair, G.M.; Welch, A.J. 13-Vertex carbacobaltaboranes: Synthesis and molecular structures of the 4,1,6-, 4,1,8- and 4,1,12-isomers of Cp*CoC2B10H12. Collect. Czech. Chem. Commun. 2002, 67, 991–1006. [Google Scholar] [CrossRef]
  25. McAnaw, A.; Lopez, M.E.; Ellis, D.; Rosair, G.M.; Welch, A.J. Asymmetric 1,8/13,2,x-M2C2B10 14-vertex metallacarboranes by direct electrophilic insertion reactions; the VCD and BHD methods in critical analysis of cage C positions. Dalton Trans. 2014, 43, 5095–5105. [Google Scholar] [CrossRef] [PubMed]
  26. Groom, C.R.; Allen, F.H. The Cambridge Structural Database in Retrospect and Prospect. Angew. Chem. Int. Ed. 2015, 53, 662–671, For this search we used ConQuest version 1.19, 2016. [Google Scholar] [CrossRef] [PubMed]
  27. Mingos, D.M.P.; Forsyth, M.I.; Welch, A.J. Molecular and Crystal Structure of 3,3-Bis(triethylphosphine)-1,2-dicarba-3-platinadodecaborane(11) and Molecular-orbital Analysis of the “Slip” Distortion in Carbametallaboranes. J. Chem. Soc. Dalton Trans. 1978, 1363–1374. [Google Scholar] [CrossRef]
  28. Garcia, M.P.; Green, M.; Stone, F.G.A.; Somerville, R.G.; Welch, A.J.; Briant, C.E.; Cox, D.N.; Mingos, D.M.P. Metallaborane Chemistry. Part 14. Icosahedral η6-Arene Carbametallaboranes of Iron and Ruthenium; Molecular Structures of closo-[1-(η6-C6H5Me)-2,4-Me2-1,2,4-FeC2B9H9] and closo-[3-(η6-C6H6)-3,1,2-RuC2B9H11]. J. Chem. Soc. Dalton Trans. 1985, 2343–2348. [Google Scholar] [CrossRef]
  29. Lee, S.S.; Knobler, C.B.; Hawthorne, M.F. Synthesis and structural characterization of mononuclear iron(II) ferracarboranes. Organometallics 1991, 10, 670–677. [Google Scholar] [CrossRef]
  30. Uhrhammer, R.; Crowther, D.J.; Olson, J.D.; Swenson, D.C.; Jordan, R.F. Synthesis and characterization of tantalum(V) dicarbollide complexes. Organometallics 1992, 11, 3098–3104. [Google Scholar] [CrossRef]
  31. Powley, S.L.; Rosair, G.M.; Welch, A.J. Further studies of the Enhanced Structural Carborane Effect: Tricarbonylruthenium and related derivatives of benzocarborane, dihydrobenzocarborane and biphenylcarborane. Dalton Trans. 2016, 45, 11742–11752. [Google Scholar] [CrossRef] [PubMed]
  32. Lamrani, M.; Gómez, S.; Viñas, C.; Teixidor, F.; Sillanpää, R.; Kivekäs, R. First examples of mixed (h5-pyrrolyl)(dicarbollide) sandwich cobalt-carboranes. New J. Chem. 1996, 20, 909–912. [Google Scholar]
  33. Loginov, D.A.; Starikova, Z.A.; Petrovskii, P.V.; Kudinov, A.R. Synthesis and structure of (boratabenzene)rhodacarborane (η-7,8-C2B9H11)Rh(η-C5H5BMe). Russ. Chem. Bull. Int. Ed. 2010, 59, 654–656. [Google Scholar] [CrossRef]
  34. Shirokii, V.L.; Knizhnikov, V.A.; Konovalov, T.P.; Zubreichuk, Z.P.; Erdman, A.A.; Nefedov, S.E.; Eremenko, I.L.; Yanovskii, A.I.; Struchkov, Y.T.; Mayer, N.A. Electrochemical synthesis of π-indenyl-π-(3)-1,2-dicarbollyliron(III). Russ. Chem. Bull. Int. Ed. 1993, 42, 732–733. [Google Scholar] [CrossRef]
  35. Lewis, Z.G.; Welch, A.J. Synthesis and Structure of 3-Fluorenyl-3-cobalta-1,2-dicarba-closo-dodecaborane(11), 3-(η5-C13H9)-3,1,2-closo-CoC2B9H11. Acta Cryst. 1992, C48, 53–57. [Google Scholar]
  36. Scott, G.; Ellis, D.; Rosair, G.M.; Welch, A.J. Icosahedral and supraicosahedral naphthalene ruthenacarboranes. J. Organomet. Chem. 2012, 721–722, 78–84. [Google Scholar] [CrossRef]
  37. Hawthorne, M.F.; Zink, J.I.; Skelton, J.M.; Bayer, M.J.; Liu, C.; Livshits, E.; Baer, R.; Neuhauser, D. Electrical or Photocontrol of the Rotary Motion of a Metallacarborane. Science 2004, 303, 1849–1851. [Google Scholar] [CrossRef] [PubMed]
  38. Hendershot, S.L.; Jeffrey, J.C.; Jelliss, P.A.; Mullica, D.F.; Sappenfield, E.L.; Stone, F.G.A. Reaction of nido-7,8-C2B9H13 with Dicobalt Octacarbonyl: Crystal Structures of the Complexes [Co2(CO)2(η5-7,8-C2B9H11)2], [Co2(CO)(PMe2Ph)(η5-7,8-C2B9H11)2], and [CoCl(PMe2Ph)2(η5-7,8-C2B9H11)]. Inorg. Chem. 1996, 35, 6561–6570. [Google Scholar] [CrossRef] [PubMed]
  39. Tyurin, A.P.; Smol’yakov, A.F.; Dolgushin, F.M.; Godovikov, A.A.; Chizhevsky, I.T. Synthesis of 12-vertex mixed ligand closo-cobaltcarborane complexes and molecular structure of [3,3-(Ph2P(CH2)2PPh2)-3-Cl-closo-3,1,2-CoC2B9H11]. Russ. Chem. Bull. Int. Ed. 2013, 62, 1938–1940. [Google Scholar] [CrossRef]
  40. Ferguson, G.; McEneaney, P.A.; Spalding, T.R. 3-Chloro-3,3-bis(triphenylphosphine-P)1,2-dicarba-3-rhoda-closo-dodecaborane-Dichloromethane (1/1.1). Acta Cryst. 1996, C52, 2710–2713. [Google Scholar] [CrossRef]
  41. Chizhevsky, I.T.; Pisareva, I.V.; Vorontzov, E.V.; Bregadze, V.I.; Dolgushin, F.M.; Yanovsky, A.I.; Struchkov, Y.T.; Knobler, C.B.; Hawthorne, M.F. Synthesis, structure and reactivity of a novel monocarbon hydridorhodacarborane closo-2,2-(Ph3P)2-2-H-1-(Me3N)-2,1-RhCB10H10 molecular structure of 16-electron closo-2-(Ph3P)-2-Cl-1-(Me3N)-2,1-RhCB10H10 and closely related 18-electron closo-3,3-(Ph3P)2-3-Cl-3,1,2-RhC2B9H11. J. Organomet. Chem. 1997, 536–537, 223–231. [Google Scholar]
  42. Ferguson, G.; Pollock, J.; McEneaney, P.A.; O’Connell, D.P.; Spalding, T.R.; Gallagher, J.F.; Maciás, R.; Kennedy, J.D. An air-stable, cationic metallacarborane without a charge-compensated carborane ligand. Chem. Commun. 1996, 679–681. [Google Scholar] [CrossRef]
  43. Tyurin, A.P.; Dolgushin, F.M.; Smol’yakov, A.F.; Grishin, I.D.; D’yachihin, D.I.; Turmina, E.S.; Grishin, D.F.; Chizhevsky, I.T. Synthesis and characterization of mixed-ligand ferracarboranes. Direct metalation of the nido-carborane [nido-7,8-C2B9H12]− mono-anion with 14-e [Ph2P(CH2)nPPh2]FeCl2 (n = 2, 3). J. Organomet. Chem. 2013, 747, 148–154. [Google Scholar] [CrossRef]
  44. Chizhevsky, I.T.; Lobanova, I.A.; Petrovskii, P.V.; Bregadze, V.I.; Dolgushin, F.M.; Yanovsky, A.I.; Struchkov, Y.T.; Chistyakov, A.L.; Stankevich, I.V.; Knobler, C.B.; Hawthorne, M.F. Synthesis of Mixed-Metal (Ru–Rh) Bimetallacarboranes via exo-nido- and closo-Ruthenacarboranes. Molecular Structures of (η4-C8H12)Rh(μ-H)Ru(PPh3)2(η5-C2B9H11) and (CO)(PPh3)Rh(μ-H)Ru(PPh3)2(η5-C2B9H11) and Their Anionic closo-Ruthenacarborane Precursors. Organometallics 1999, 18, 726–735. [Google Scholar] [CrossRef]
  45. Cheredilin, D.N.; Kadyrov, R.; Dolgushin, F.M.; Balagurova, E.V.; Godovikov, I.A.; Solodovnikov, S.P.; Chizhevsky, I.T. Chiral paramagnetic closo-ruthenacarboranes via phosphine–diphosphine displacement reaction of “three-bridge” exo-nido-ruthenacarboranes: Molecular Structure of (−)-[closo-3-Cl-3,3-{(Ph2PCHCH3)2CH2}-3,1,2-RuC2B9H11] and its ortho-cycloboronated derivative. Inorg. Chem. Commun. 2005, 8, 614–618. [Google Scholar] [CrossRef]
  46. Cheredilin, D.N.; Dolgushin, F.M.; Grishin, I.D.; Kolyakina, E.V.; Nikiforov, A.S.; Solodovnikov, S.P.; Il’in, M.M.; Davankov, V.A.; Chizhevsky, I.T.; Grishin, D.F. Facile method for the synthesis of ruthenacarboranes, diamagnetic 3,3-[Ph2P(CH2)nPPh2]-3-H-3-Cl-closo-3,1,2-RuC2B9H11 (n = 3 or 4) and paramagnetic 3,3-[Ph2P(CH2)nPPh2]-3-Cl-closo-3,1,2-RuC2B9H11 (n = 2 or 3), as efficient initiators of controlled radical polymerization of vinyl monomers. Russ Chem. Bull. 2006, 55, 1163–1170. [Google Scholar]
  47. Grishin, I.D.; D’yachihin, D.I.; Piskunov, A.V.; Dolgushin, F.M.; Smol’yakov, A.F.; Il’in, M.M.; Davankov, V.A.; Chizhevsky, I.T.; Grishin, D.F. Carborane Complexes of Ruthenium(III): Studies on Thermal Reaction Chemistry and the Catalyst Design for Atom Transfer Radical Polymerization of Methyl Methacrylate. Inorg. Chem. 2011, 50, 7574–7585. [Google Scholar] [CrossRef] [PubMed]
  48. Grishin, I.D.; D’yachihin, D.I.; Turmina, E.S.; Dolgushin, F.M.; Smol’yakov, A.F.; Piskunov, A.V.; Chizhevsky, I.T.; Grishin, D.F. Mononuclear closo-ruthenacarborane complexes containing a rare eight-membered metal-diphosphine ring. J. Organomet. Chem. 2012, 721–722, 113–118. [Google Scholar] [CrossRef]
  49. McKay, D.; Welch, A.J. Unpublished results.
  50. Anderson, S.; Mullica, D.F.; Sappenfield, E.L.; Stone, F.G.A. Carborane Complexes of Ruthenium: A Convenient Synthesis of [Ru(CO)3(η5-7,8-C2B9H11)] and a Study of Reactions of This Complex. Organometallics 1995, 14, 3516–3526. [Google Scholar] [CrossRef]
  51. Jeffery, J.C.; Jelliss, P.A.; Psillakis, E.; Rudd, G.E.A.; Stone, F.G.A. Synthesis, crystal structure and some reactions of the ruthenacarborane complex [Ru(CO)2(MeC≡CPh)(η5-7,8-C2B9H11)]. J. Organomet. Chem. 1998, 562, 17–27. [Google Scholar] [CrossRef]
  52. Jelliss, P.A.; Mason, J.; Nazzoli, J.M.; Orlando, J.H.; Vinson, A.; Rath, N.P.; Shaw, M.J. Synthesis and Characterisation of Ruthenacarborane Complexes Incorporating Chelating N-Donor Ligands: Unexpected Luminescence from the Complex [3-CO-3,3-{κ2-Me2N(CH2)2NMe2}-closo-3,1,2-RuC2B9H11]. Inorg. Chem. 2006, 45, 370–385. [Google Scholar] [CrossRef] [PubMed]
  53. Coe, B.J.; Glenwright, S.J. Trans-effects in octahedral transition metal complexes. Coord. Chem. Rev. 2000, 203, 5–80. [Google Scholar] [CrossRef]
  54. See, R.F.; Kozina, D. Quantification of the trans influence in d8 square planar and d6 octahedral complexes: A database study. J. Coord. Chem. 2013, 66, 490–500. [Google Scholar] [CrossRef]
  55. Robertson, A.P.M.; Reckziegel, A.; Jones, J.J.; Rosair, G.M.; Welch, A.J. Balancing Steric and Electronic Effects in Carbonyl-Phosphine Molybdacarboranes. Eur. J. Inorg. Chem. 2017. [Google Scholar] [CrossRef]
  56. Vickers, P.W.; Pearson, J.M.; Ghaffar, T.; Adams, H.; Haynes, A. Kinetics and thermodynamics of C–Cl bond activation by [Ir(CO)2Cl2]−. J. Phys. Org. Chem. 2004, 17, 1007–1016. [Google Scholar] [CrossRef]
  57. Gunnoe, T.B.; White, P.S.; Templeton, J.L. Synthesis and Deprotonation/Alkylation Reactions of the Chiral Carben Complex Tp′(CO)(NO)Mo=C(OMe)(Me). Organometallics 1997, 16, 370–377. [Google Scholar] [CrossRef]
  58. Du, S.; Ellis, D.D.; Jelliss, P.A.; Kautz, J.A.; Malget, J.M.; Stone, F.G.A. Studies with the Ruthenacarborane Complex [Ru(CO)(PPh3)(THF)(η5-7,8-C2B9H11)]: Reactions with Terminal Alkynes. Organometallics 2000, 19, 1983–1992. [Google Scholar] [CrossRef]
  59. Lee, S.S.; Knobler, C.B.; Hawthorne, M.F. A Ferracarborane Analogue to [Fp]−. Synthesis and Reactions of [closo-3,3-(CO)2-3,1,2-FeC2B9H11]2−. Organometallics 1991, 10, 1054–1063. [Google Scholar] [CrossRef]
  60. Ellis, D.D.; Jelliss, P.A.; Stone, F.G.A. Rhenacarborane complexes with nitrosyl and alkylidene ligands. Structures of the complexes [[Re{=C(OMe)C6H4Me-4}(NO)(η5-7,8-C2B9H11)] and [Re(NO)(CNBut){η5,σ-7-C=N(H)But-7,8-C2B9H10}]. Chem. Commun. 1999, 2385–2386. [Google Scholar] [CrossRef]
  61. Demidowicz, Z.; Teller, R.G.; Hawthorne, M.F. Synthesis and Molecular Structure of [3-(PPh3)-3,3-(NO3)-3,1,2-RhC2B9H11], a Versatile Metallocarbaborane Reagent. J. Chem. Soc. Chem. Comm. 1979, 831–832. [Google Scholar] [CrossRef]
  62. Hansen, H.-P.; Müller, J.; Englert, U.; Paetzold, P. Azarhoda-closo-dodecaborane. Angew. Chem. Int. Ed. 1991, 30, 1377–1379. [Google Scholar] [CrossRef]
  63. Batten, S.A.; Jeffery, J.C.; Jones, P.L.; Mullica, D.F.; Rudd, M.D.; Sappenfield, E.L.; Stone, F.G.A.; Wolf, A. Synthesis of the Reagent [Na][Pt(PEt3)2(η5-7-CB10H11)] and Preparation of the Platinacarborane Complexes [PtX(PEt3)2(η5-7-CB10H11)] (X = H, Au(PPh3), Cu(PPh3), HgPh). Inorg. Chem. 1997, 36, 2570–2577. [Google Scholar] [CrossRef]
  64. Macías, R.; Thornton-Pett, M.; Holub, J.; Spalding, T.R.; Faridoon, Y.; Štíbr, B.; Kennedy, J.D. Polyhedral metallathiaborane chemistry: Synthesis and characterisation of metallathiaboranes based on the twelve-vertex icosahedral closo-{MSB10H10} unit, where M is Rh or Ir. J. Organomet. Chem. 2008, 693, 435–445. [Google Scholar] Note that the Rh–P distances given in Table 4 in this paper do not correspond to the atom labelling in Figure 2.
  65. Abram, P.D.; Ellis, D.; Rosair, G.M.; Welch, A.J. Exopolyhedral ligand flipping on isomerisation of novel supraicosahedral stannacarboranes. Chem. Commun. 2009, 5403–5405. [Google Scholar] [CrossRef] [PubMed]
Crystals 07 00234 g001 550
Figure 1. The nine isomers of an icosahedral MC2B9 metallacarborane.
Figure 1. The nine isomers of an icosahedral MC2B9 metallacarborane.
Crystals 07 00234 g001
Crystals 07 00234 g002 550
Figure 2. (a) The structure of [3-Cl-closo-2-CB6H6]−. C2–B1 1.741(3), C2–B7 1.746(3), B4–B5 1.665(3), B5–B6 1.640(4) Å; (b) The structure of [8-Br-closo-1,6-C2B8H9]. C6–B2 1.736(5), C6–B3 1.745(5), C6–B7 1.760(5), C6–B9 1.765(5), B10–B7 1.707(5), B10–B9 1.702(5) Å.
Figure 2. (a) The structure of [3-Cl-closo-2-CB6H6]−. C2–B1 1.741(3), C2–B7 1.746(3), B4–B5 1.665(3), B5–B6 1.640(4) Å; (b) The structure of [8-Br-closo-1,6-C2B8H9]. C6–B2 1.736(5), C6–B3 1.745(5), C6–B7 1.760(5), C6–B9 1.765(5), B10–B7 1.707(5), B10–B9 1.702(5) Å.
Crystals 07 00234 g002
Crystals 07 00234 g003 550
Figure 3. (a) The structure of [1,13-Cp2-closo-1,13,2,9-Co2C2B10H12]. C9–B14 1.904(3), B11–B14 1.858(3) Å; (b) The Prostructure of [1,13-Cp2-closo-1,13,2,10-Co2C2B10H12] with non-metal vertices numbered.
Figure 3. (a) The structure of [1,13-Cp2-closo-1,13,2,9-Co2C2B10H12]. C9–B14 1.904(3), B11–B14 1.858(3) Å; (b) The Prostructure of [1,13-Cp2-closo-1,13,2,10-Co2C2B10H12] with non-metal vertices numbered.
Crystals 07 00234 g003
Crystals 07 00234 g004 550
Figure 4. Choosing the correct vertices to define the polyhedral centroid and comparing vertex-centroid distances (VCDs) within an appropriate group: (a) A nido 11-vertex polyhedron—the centroid is defined by only vertices 2–11 but all VCDs can be compared as a single group; (b) A closo 10-vertex polyhedron with a metal atom at vertex 1—the centroid should be defined by vertices 2–9 only, and only VCDs from these vertices should be compared; (c) A closo 8-vertex polyhedron—all vertices are used to calculate the centroid but the VCDs from vertices 1, 2, 7, and 8 and from vertices 3–6 should be considered separately.
Figure 4. Choosing the correct vertices to define the polyhedral centroid and comparing vertex-centroid distances (VCDs) within an appropriate group: (a) A nido 11-vertex polyhedron—the centroid is defined by only vertices 2–11 but all VCDs can be compared as a single group; (b) A closo 10-vertex polyhedron with a metal atom at vertex 1—the centroid should be defined by vertices 2–9 only, and only VCDs from these vertices should be compared; (c) A closo 8-vertex polyhedron—all vertices are used to calculate the centroid but the VCDs from vertices 1, 2, 7, and 8 and from vertices 3–6 should be considered separately.
Crystals 07 00234 g004
Crystals 07 00234 g005 550
Figure 5. (a) The structure of [3-Cp-closo-3,1,2-CoC2B9H11]. Co3–C1 2.009(2), Co3–C2 2.005(2), Co3–B7 2.069(2), Co3–B8 2.106(2), Co3–B4 2.076(2), Co3–C4 2.036(2), Co3–C5 2.035(2), Co3–C6 2.046(2), Co3–C7 2.069(2), Co3–C8 2.056(2) Å; (b) The structure of [3,3,3-(CO)3-closo-3,1,2-FeC2B9H11]. Fe3–C3(|θ| = 113.2°) 1.792(9), Fe3–C4(|θ| = 135.9°) 1.777(9), Fe3–C5(|θ| = 12.9°) 1.804(11) Å; (c) The structure of [3,3,3-Cl3-closo-3,1,2-TaC2B9H11]. Ta3–Cl(|θ| = 50.9°) 2.259(5), Ta3–Cl2(|θ| = 63.1°) 2.233(5), Ta3–Cl3(|θ| = 172.1°) 2.205(5) Å.
Figure 5. (a) The structure of [3-Cp-closo-3,1,2-CoC2B9H11]. Co3–C1 2.009(2), Co3–C2 2.005(2), Co3–B7 2.069(2), Co3–B8 2.106(2), Co3–B4 2.076(2), Co3–C4 2.036(2), Co3–C5 2.035(2), Co3–C6 2.046(2), Co3–C7 2.069(2), Co3–C8 2.056(2) Å; (b) The structure of [3,3,3-(CO)3-closo-3,1,2-FeC2B9H11]. Fe3–C3(|θ| = 113.2°) 1.792(9), Fe3–C4(|θ| = 135.9°) 1.777(9), Fe3–C5(|θ| = 12.9°) 1.804(11) Å; (c) The structure of [3,3,3-Cl3-closo-3,1,2-TaC2B9H11]. Ta3–Cl(|θ| = 50.9°) 2.259(5), Ta3–Cl2(|θ| = 63.1°) 2.233(5), Ta3–Cl3(|θ| = 172.1°) 2.205(5) Å.
Crystals 07 00234 g005
Crystals 07 00234 g006 550
Figure 6. The orientation of the ligand L is defined by the modulus of the torsion angle θ where θ = L–M3–A–B; A is the centroid of the metal-bound C2B3 face (green dot) and B is the centroid of the C1–C2 bond (purple dot).
Figure 6. The orientation of the ligand L is defined by the modulus of the torsion angle θ where θ = L–M3–A–B; A is the centroid of the metal-bound C2B3 face (green dot) and B is the centroid of the C1–C2 bond (purple dot).
Crystals 07 00234 g006
Crystals 07 00234 g007 550
Figure 7. (a) The structure of [3-(C4H4N)-closo-3,1,2-CoC2B9H11]. Note the N atom of the pyrrolyl ligand lies above the cage C atoms; (b) The structure of [3-(C5H5BMe)-closo-3,1,2-RhC2B9H11] in which the B atom of the boratabenzene ligand is trans to the cage C atoms.
Figure 7. (a) The structure of [3-(C4H4N)-closo-3,1,2-CoC2B9H11]. Note the N atom of the pyrrolyl ligand lies above the cage C atoms; (b) The structure of [3-(C5H5BMe)-closo-3,1,2-RhC2B9H11] in which the B atom of the boratabenzene ligand is trans to the cage C atoms.
Crystals 07 00234 g007
Crystals 07 00234 g008 550
Figure 8. (a) The structure of [3-(C9H7)-closo-3,1,2-CoC2B9H11] in plan view; (b) The structure of [3-(C13H9)-closo-3,1,2-CoC2B9H11] in similar view. In both structures note the cisoid arrangements of ring-junction and carborane C atoms.
Figure 8. (a) The structure of [3-(C9H7)-closo-3,1,2-CoC2B9H11] in plan view; (b) The structure of [3-(C13H9)-closo-3,1,2-CoC2B9H11] in similar view. In both structures note the cisoid arrangements of ring-junction and carborane C atoms.
Crystals 07 00234 g008
Crystals 07 00234 g009 550
Figure 9. The cisoid structure of the [3-Co(1,2-C2B9H11)2]− anion.
Figure 9. The cisoid structure of the [3-Co(1,2-C2B9H11)2]− anion.
Crystals 07 00234 g009
Crystals 07 00234 g010 550
Figure 10. Plot of energy vs. |θCl| for [3,3-(PH3)2-3-Cl-closo-3,1,2-RhC2B9H11] by DFT calculation. The |θCl| values of the compounds in Table 5 all fall within the pink circle.
Figure 10. Plot of energy vs. |θCl| for [3,3-(PH3)2-3-Cl-closo-3,1,2-RhC2B9H11] by DFT calculation. The |θCl| values of the compounds in Table 5 all fall within the pink circle.
Crystals 07 00234 g010
Crystals 07 00234 g011 550
Figure 11. (a) The structure of the [3,3-(PPh3)2-3-H-closo-3,1,2-RuC2B9H11]− anion (phenyl rings omitted for clarity). Ru3–P1(|θ| = 24.7°) 2.322(3), Ru3–P2(|θ| = 116.7°) 2.294(3) Å, |θ|H = 136.4°, Ru3–C1 2.301(12), Ru3–C2 2.250(11) Å; (b) The structure of [3,3-(κ2-tmeda)-3-CO-closo-3,1,2-RuC2B9H11] (Me groups and H atoms of tmeda ligand omitted for clarity). Ru3–N1(|θ| = 21.7°) 2.270(3), Ru3–P2(|θ| = 98.1°) 2.232(4) Å, |θ|CO = 142.8°, Ru3–C1 2.224(5), Ru3–C2 2.190(5) Å.
Figure 11. (a) The structure of the [3,3-(PPh3)2-3-H-closo-3,1,2-RuC2B9H11]− anion (phenyl rings omitted for clarity). Ru3–P1(|θ| = 24.7°) 2.322(3), Ru3–P2(|θ| = 116.7°) 2.294(3) Å, |θ|H = 136.4°, Ru3–C1 2.301(12), Ru3–C2 2.250(11) Å; (b) The structure of [3,3-(κ2-tmeda)-3-CO-closo-3,1,2-RuC2B9H11] (Me groups and H atoms of tmeda ligand omitted for clarity). Ru3–N1(|θ| = 21.7°) 2.270(3), Ru3–P2(|θ| = 98.1°) 2.232(4) Å, |θ|CO = 142.8°, Ru3–C1 2.224(5), Ru3–C2 2.190(5) Å.
Crystals 07 00234 g011
Crystals 07 00234 g012 550
Figure 12. (a) The structure of the [3-CO-3-PMe3-3-C(O)Me-closo-3,1,2-FeC2B9H11]−, anion. O1···H1 2.43 Å; (b) The structure of [3-NO-3-CO-3-{C(OMe)C6H4Me-4)-closo-3,1,2-ReC2B9H11] (C6H4Me-4 omitted for clarity). O1···H1 2.46, O1···H2 2.49 Å.
Figure 12. (a) The structure of the [3-CO-3-PMe3-3-C(O)Me-closo-3,1,2-FeC2B9H11]−, anion. O1···H1 2.43 Å; (b) The structure of [3-NO-3-CO-3-{C(OMe)C6H4Me-4)-closo-3,1,2-ReC2B9H11] (C6H4Me-4 omitted for clarity). O1···H1 2.46, O1···H2 2.49 Å.
Crystals 07 00234 g012
Crystals 07 00234 g013 550
Figure 13. (a) The structure of [3,3,3-(CO)3-3-PPh3-closo-3,1,2-MoC2B9H11] (Ph groups omitted for clarity) showing the phosphine at low |θ|; (b) The structure of [1,2-Me2-3,3,3-(CO)3-3-PPh3-closo-3,1,2-MoC2B9H9] (Ph groups omitted for clarity) in which the phosphine is displaced to a high |θ| value by steric crowding between it and the cage Me substituents.
Figure 13. (a) The structure of [3,3,3-(CO)3-3-PPh3-closo-3,1,2-MoC2B9H11] (Ph groups omitted for clarity) showing the phosphine at low |θ|; (b) The structure of [1,2-Me2-3,3,3-(CO)3-3-PPh3-closo-3,1,2-MoC2B9H9] (Ph groups omitted for clarity) in which the phosphine is displaced to a high |θ| value by steric crowding between it and the cage Me substituents.
Crystals 07 00234 g013
Crystals 07 00234 g014 550
Figure 14. (a) Original structure of [3,3-(κ2-NO3)-3-PPh3-closo-3,1,2-RhC2B9H11] (no coordinates for cage H atoms or phenyl rings deposited) suggesting the cage C atoms are cis to PPh3; (b) Redetermined structure (Ph groups omitted for clarity).
Figure 14. (a) Original structure of [3,3-(κ2-NO3)-3-PPh3-closo-3,1,2-RhC2B9H11] (no coordinates for cage H atoms or phenyl rings deposited) suggesting the cage C atoms are cis to PPh3; (b) Redetermined structure (Ph groups omitted for clarity).
Crystals 07 00234 g014
Crystals 07 00234 g015 550
Figure 15. (a) The structure of [2,2-(PPh3)2-2-H-closo-2,1-RhNB10H11]. Ph groups omitted for clarity; (b) The structure of [2,2-(PEt3)2-2-H-closo-2,1-PtCB10H11]. Et groups omitted for clarity; (c) The structure of [2,2-(PMe2Ph)2-2-Cl-closo-2,1-RhSB10H10]. Ph and Me groups omitted for clarity. Rh2–P1(|θ| = 165.7°) 2.3286(5), Rh2–P2(|θ| = 62.6°) 2.3992(5) Å. Here θ is defined by the torsion angle P–Rh2–A–S1 where A is the centroid of the metal-bound SB4 face.
Figure 15. (a) The structure of [2,2-(PPh3)2-2-H-closo-2,1-RhNB10H11]. Ph groups omitted for clarity; (b) The structure of [2,2-(PEt3)2-2-H-closo-2,1-PtCB10H11]. Et groups omitted for clarity; (c) The structure of [2,2-(PMe2Ph)2-2-Cl-closo-2,1-RhSB10H10]. Ph and Me groups omitted for clarity. Rh2–P1(|θ| = 165.7°) 2.3286(5), Rh2–P2(|θ| = 62.6°) 2.3992(5) Å. Here θ is defined by the torsion angle P–Rh2–A–S1 where A is the centroid of the metal-bound SB4 face.
Crystals 07 00234 g015
Crystals 07 00234 g016 550
Figure 16. (a) The structure of [1,10-Me2-4,4-(κ2-Me2bipy)-closo-4,1,10-SnC2B10H10] with most of the Me2bipy ligand omitted for clarity; (b) The structure of [1,12-Me2-4,4-(κ2-bipy)-closo-4,1,12-SnC2B10H10] with most of the bipy ligand omitted. From (a) to (b) the bipy ligand has “flipped” from cis to C1 to trans to C1.
Figure 16. (a) The structure of [1,10-Me2-4,4-(κ2-Me2bipy)-closo-4,1,10-SnC2B10H10] with most of the Me2bipy ligand omitted for clarity; (b) The structure of [1,12-Me2-4,4-(κ2-bipy)-closo-4,1,12-SnC2B10H10] with most of the bipy ligand omitted. From (a) to (b) the bipy ligand has “flipped” from cis to C1 to trans to C1.
Crystals 07 00234 g016
Table
Table 1. Ueq values (/Å2) for non-metal vertices in Prostructure of [1,13-Cp2-closo-1,13,2,10-Co2C2B10H12].
Table 1. Ueq values (/Å2) for non-metal vertices in Prostructure of [1,13-Cp2-closo-1,13,2,10-Co2C2B10H12].
VertexUeqVertexUeq
20.0089(9)80.0163(10)
30.0209(12)90.0269(14)
40.0311(16)10 0.0308(18)
50.0308(15)110.0340(17)
60.0237(13)120.0231(12)
70.0178(11)140.0210(12)
Table
Table 2. Vertex–centroid distances (/Å) in [closo-1,7-C2B10H12] 1.
Table 2. Vertex–centroid distances (/Å) in [closo-1,7-C2B10H12] 1.
VertexVCDVertexVCDVertexVCD
11.546(5)51.668(6)91.672(7)
21.696(7)61.668(7)101.680(9)
31.698(7)71.546(4)111.690(6)
41.694(6)81.679(7)121.656(6)
1 The C atoms are at vertices 1 and 7.
Table
Table 3. Vertex–centroid distances (/Å) in [1-{CpRu(PMe2Ph)2}-2-Me-closo-1,2-C2B10H10] 1.
Table 3. Vertex–centroid distances (/Å) in [1-{CpRu(PMe2Ph)2}-2-Me-closo-1,2-C2B10H10] 1.
VertexVCDVertexVCDVertexVCD
11.702(2)51.668(3)91.678(3)
21.577(2)61.672(3)101.680(3)
31.671(3)71.690(3)111.691(3)
41.674(2)81.687(3)121.697(3)
1 The C atoms are at vertices 1 and 2, but C1 is σ-bonded to the Ru centre.
Table
Table 4. Vertex–H distances (/Å) for non-metal vertices in Prostructure of [1,13-Cp2-closo-1,13,2,10-Co2C2B10H12].
Table 4. Vertex–H distances (/Å) for non-metal vertices in Prostructure of [1,13-Cp2-closo-1,13,2,10-Co2C2B10H12].
VertexVertex–H 1VertexVertex–H 1
20.46(7)0.99(6)81.08(6)1.08(6)
31.06(7)1.05(5)91.07(7)1.04(7)
41.06(7)1.05(7)100.34(9)0.86(8)
51.07(7)1.08(6)111.05(7)1.05(7)
61.18(6)1.19(6)121.09(7)1.09(7)
71.14(6)1.13(5)141.13(7)1.13(7)
1 For each vertex the left entry is for the Prostructure, the right entry for the final, correctly assigned, structure.
Table
Table 5. ELO data (θ, /°) in [3,3-P2-3-Cl-closo-3,1,2-MC2B9H11] species (P = phosphine or P2 = diphosphine).
Table 5. ELO data (θ, /°) in [3,3-P2-3-Cl-closo-3,1,2-MC2B9H11] species (P = phosphine or P2 = diphosphine).
RefcodeMPhosphineθClθP1θP2Ref.
TUBLUXCoPMe2Ph−15.599.3−128.9[38]
HIPQIICodppe/211.4−102.9131.6[39]
TELCIW 1RhPPh312.6−98.3127.6[40]
NITWOC 1RhPPh3−12.498.5−127.2[41]
ZOTVOTRhPPh2Me9.1−107.5127.9[42]
HIMRUSFedppe/29.4−113.8131.6[43]
HIMROMFedppp3/2 2−10.7102.3−134.1[43]
CEHCEXRu−PPh3−12.999.5−127.2[44]
QAQQABRu2,4-dppp5/2 3−15.899.6−137.5[45]
QEXWEWRudppe/215.6−114.4132.9[46]
UZUYEURudppb/2−14.6101.0−138.5[47]
SEMZIVRu1,5-dppp5/2 418.7−95.2143.2[48]
1 These structures differ in that NITWOC contains solvate; 2 dppp3 = diphenylphosphinopropane; 3 2,4-dppp5 = 2,4-diphenylphosphinopentane; 4 1,5-dppp5 = 1,5-diphenylphosphinopentane.
Table
Table 6. ELO data (θ, /°) in [3-L-3-L′-3-L′′-closo-3,1,2-MC2B9H11] species.
Table 6. ELO data (θ, /°) in [3-L-3-L′-3-L′′-closo-3,1,2-MC2B9H11] species.
RefcodeML|θ|LL′|θ|L′L′′|θ|L′′Ref.
KISBODFeCO148.9PPh391.9NCMe28.0[29]
LOBSUQRuCO149.4PPh389.3I30.5[58]
TAKCUDFe−CO134.2PMe3102.8C(O)Me12.6[59]
LICDOQReNO 1134.7CO103.4C(OMe)C6H4Me-47.8[60]
1 Linear nitrosyl ligand.

Share and Cite

MDPI and ACS Style

Welch, A.J. What Can We Learn from the Crystal Structures of Metallacarboranes? Crystals 2017, 7, 234. https://doi.org/10.3390/cryst7080234

AMA Style

Welch AJ. What Can We Learn from the Crystal Structures of Metallacarboranes? Crystals. 2017; 7(8):234. https://doi.org/10.3390/cryst7080234

Chicago/Turabian Style

Welch, Alan J. 2017. "What Can We Learn from the Crystal Structures of Metallacarboranes?" Crystals 7, no. 8: 234. https://doi.org/10.3390/cryst7080234

APA Style

Welch, A. J. (2017). What Can We Learn from the Crystal Structures of Metallacarboranes? Crystals, 7(8), 234. https://doi.org/10.3390/cryst7080234

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop