Effects of Alloying Atoms on Antiphase Boundary Energy and Yield Stress Anomaly of L1₂ Intermetallics: First-Principles Study ^†

Abstract

The antiphase boundary energies of {111} and {010} planes in L1${}_2$ intermetallics (Ni${}_3$Ge, Ni${}_3$Si, Al${}_3$Sc, Ni${}_3$Al, Ni${}_3$Ga and Al${}_3$Ti) under different pressure are presented using first-principle methods. The yield stress anomaly is predicted by the energy criterion p-factor based on the anisotropy of antiphase boundary energies and elasticity. These L1${}_2$ intermetallics exhibit anomalous yield stress behavior except Al${}_3$Sc. It is found that pressure cannot introduce the transition between anomalous and normal behavior. In order to investigate the transition, Al${}_3$Sc, Ni${}_3$Si and Ni${}_3$Ge with substituting atoms are investigated in detail due to p-factors of them are close to the critical value ${\mathrm{p}}_{\mathrm{c}}=\sqrt{3}$. Al${}_3$Sc can change to anomalous when Sc atoms in {010} planes are substituted by Ti with plane concentration 25%. When Li substitutes Al in {111} planes, anomalous Al${}_3$Sc will change to normal. Ni${}_3$Si and Ni${}_3$Ge can exhibit normal yield stress behavior when Ge and Si in {111} planes are substituted by alloying atoms with plane concentrations 12.5% and 25%. When Ga and Al substitute in {010} planes, normal Ni${}_3$Si and Ni${}_3$Ge will revert to anomalous behavior. Therefore, transparent transition between normal and anomalous yield stress behavior in L1${}_2$ intermetallics can be introduced by alloying atoms.

1. Introduction

In materials science, the yield stress anomaly (YSA) means the yield stress of the unusual materials has a positive dependence with the increasing temperature, in contrast to the usual materials which the yield stress decreases with temperature [1,2,3,4]. L1${}_2$ structure intermetallics are one kind of those materials. This property has attracted much attention for high temperature applications. For example, due to this property, L1${}_2$${\gamma }^{\prime }$ Ni-base superalloys are widely used for blades and vanes in gas turbine engines for aircrafts and power generations [5,6,7].

Most models explain that the YSA in L1${}_2$ intermetallics is caused by the exhaustion of the mobile dislocations on {010} planes by the Kear-Wilsdorf (K-W) locking mechanism [8,9,10,11,12,13,14]. The K-W locks are mainly caused by the cross-slip of the screw superdislocations [11,15,16]. With the temperature increasing, the mobile superdislocations are thermally activated to cross-slip from the {111} hexagonal planes onto the {010} cubic planes. This process is more frequent at higher temperature. Then, it leads to the formation of K-W locks that decrease the velocity and density of the mobile dislocations. Finally the K-W locks exhaust the mobile dislocations and make the yield strength increase. Therefore, whether the materials satisfy the requirements to occur the cross-slip can be the criterion of whether they have the property of YSA. The differences of the antiphase boundary (APB) energies between {111} and {010} planes provides the driving force to form the cross-slip [17,18]. The dissociation of ⟨110⟩ superdislocation is shown as follow:

$$⟨110⟩\to \frac{1}{2}⟨110⟩+\mathrm{APB}+\frac{1}{2}⟨110⟩$$

(1)

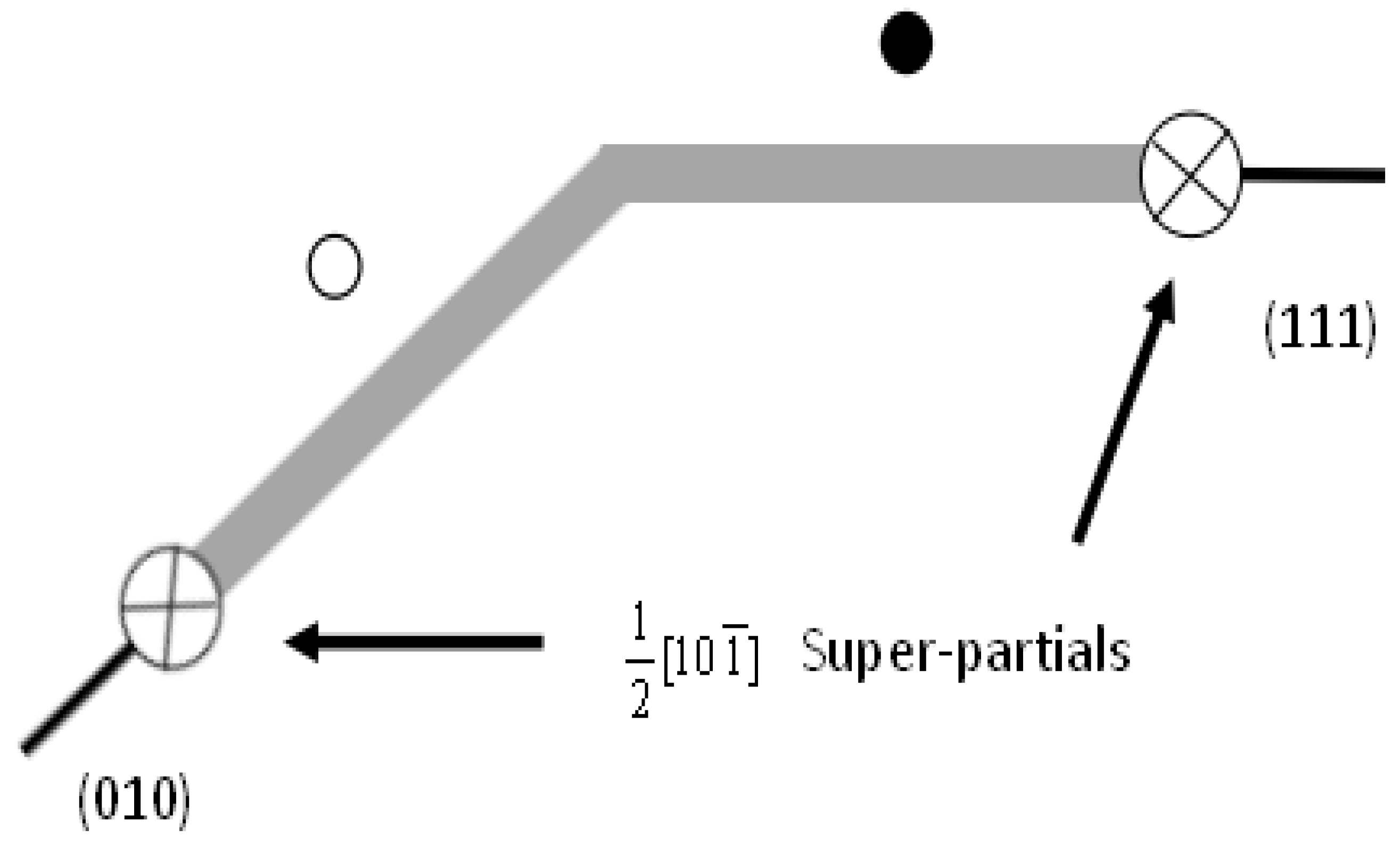
where ⟨110⟩ is the Burgers vector of superdislocations in {111} and {010} planes which will be dissociated into two ⟨110⟩/2 partials with an APB between them [19,20,21,22,23]. There may be other dissociation types like CSF (complex stacking fault) and SISF (superlattice intrinsic stacking fault). However, according to Schoeck et al. [24], the cross-slip can be achieved only by the recombination of two Shockley partials. Therefore here we only consider the APB energy. When the p-factor is larger than the critical value, the slip on the {111} planes will cross-slip onto the {010} planes and be divided into two 1/2[10$\overline{1}$] superpartials as shown in Figure 1. Then with the temperature increasing, the intermetallics will display anomalous behavior of yield stress. This transition from superdislocations to fully dissociated partials is examined to be related to the APB anisotropy. Therefore, the APB anisotropy ratio $\lambda$ = ${\gamma }_{\{111\}}$/${\gamma }_{\{010\}}$ is used to predict the existence of the cross-slip of L1${}_2$ materials. However, Yoo considers the effect of elastic anisotropy of anisotropy materials is also important [25]. Therefore the improved energy based criterion is shown below:

$$\mathrm{p}=\frac{3\mathrm{A}}{\mathrm{A}+2}\frac{{\gamma }_{\mathrm{APB}}^{\{111\}}}{{\gamma }_{\mathrm{APB}}^{\{010\}}}>\sqrt{3}$$

(2)

where ${\mathrm{c}}_{11}$, ${\mathrm{c}}_{12}$ and ${\mathrm{c}}_{44}$ are elastic constants of L1${}_2$ materials, A = 2c${}_{44}$/(c${}_{11}$− c${}_{12}$) is the elastic anisotropy, ${\gamma }_{\mathrm{APB}}^{\{111\}}$ is the APB energy on {111} planes and ${\gamma }_{\mathrm{APB}}^{\{010\}}$ is the APB energy on {010} planes. This means when the p exceeds $\sqrt{3}$, the material will have enough energy to occur cross-slip with the increasing of temperature. The material displays the behavior of YSA.

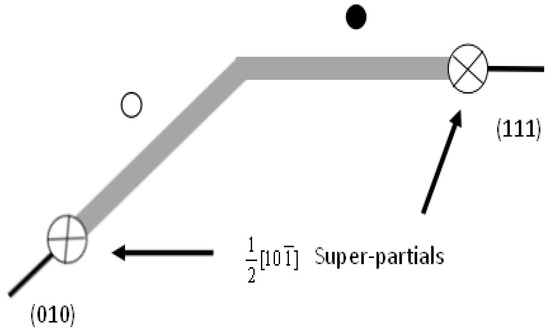
Figure 1. Structure of cross-slip from {111} onto the {010} plane. The white and black circles are substitutions on the {010} and {111} planes.

L1${}_2$ structure Ni${}_3$Al is the first material reported to have this property [11,26,27,28,29]. L1${}_2$ structure Ni${}_3$Ge [30,31,32], Ni${}_3$Si [33,34,35] Ni${}_3$Ga [36,37,38] and Al${}_3$Ti [39] are also found to have this property. Geng et al. [40] provided a quantitative method to confirm the increase of yield strength of Ni-base superalloys at elevated temperature which is in agreement with the results of experiments. Liu et al. [41] studied the origin of the loss of the YSA of Ni${}_3$Ge with Fe substitution. Besides L1${}_2$ structure materials, many other materials are found to have this behavior. Hagihara et al. [42,43] studied Ni${}_3$(Ti,Nb) which is identified as long-period-stacking ordered (LPSO) compound in the Ni-Ti-Nb ternary system. They found the behavior of YSA is caused by basal slip in Ni-based LPSO phase and the mobility of dislocations on the non-basal plane have negligible effects. The work of Nishino et al. [44] shows that the occurrence of the YSA of D0${}_3$ Fe${}_3$Al is related to the D0${}_3$-B2 phase transition. Also they studied the effects of substitutions on the phase stability and high-temperature strength. George et al. [45] explained the YSA of B2 FeAl with the vacancy-hardening model and dislocation creep at high temperatures. They also found up-quenching and down-quenching may corroborate this vacancy-hardening model through experiments. Mitchell et al. [46] studied that the YSA of C11${}_b$ MoSi${}_2$ is related to various slip systems and calculated the stacking fault energies with modified embedded atom method (MEAM). The work of Takayoshi et al. [47] shows the behavior of C40 NbSi${}_2$ is controlled by the phase stability and the YSA is caused by the formation of a dragging atmosphere around dislocations.

In the previous work of Liu et al. [48], p-factors increasing with temperature are investigated by using first principles calculations and quasiharmonic approach. This can give a more accurate description of the anomalous yield stress than predictions at 0 K. Pressure also has important effects on elastic constants and stacking fault energy. Therefore, it is interesting to study the pressure dependent p-factor for typical L1${}_2$ intermetallics, such as Ni${}_3$Al [27,28,29], Ni${}_3$Ge [30,31,32], Ni${}_3$Si [33,34,35], Ni${}_3$Ga [36] and Al${}_3$Ti [39] which have the YSA properties. To make comparisons, we also choose Al${}_3$Sc which has the normal behavior.

Beside pressure, alloying elements in materials also have effects on the APB energy and yield stress [44,49]. In this paper, Ni${}_3$Ge, Ni${}_3$Si and Al${}_3$Sc are investigated since the p-factors of these materials are close to the critical value p${}_{\mathrm{c}}=\sqrt{3}$. Based on the work of Golovin et al. [50] and Balk et al. [51], the Ni${}_3$Ge losses the property of YSA with Fe substitution. Therefore, Ni${}_3$Ge is alloyed with Fe. Since p-factors of Ni${}_3$Ge, Ni${}_3$Si and Al${}_3$Sc are close to $\sqrt{3}$, while the p-factors of Ni${}_3$Al, Ni${}_3$Ga and Al${}_3$Ti are much larger than $\sqrt{3}$, Ni${}_3$Ge is alloyed with Al and Ga, Ni${}_3$Si is alloyed with Al, Ga and Ti, Al${}_3$Sc is alloyed with Ti. On the other hand, since Al${}_3$Sc is the only material that displays the normal behavior, Ni${}_3$Ge and Ni${}_3$Si are alloyed with Sc to investigate whether their property can be changed. Since Sc and Y, Ti and Zr are in same groups, Al${}_3$Sc is alloyed with Y and Zr. The addition of Li in Al-Sc alloys can result in greater peak hardness from the L1${}_2$ Al-Li-Sc [52]. After determining the alloying atoms, in order to confirm the alloying sites, formation energies are calculated in detail. Then, APB energies with and without alloying are calculated to obtain the p-factors.

This paper is organized as follows. The next section contains the technical details of the calculations we performed. In Section 3, we discuss our results for p-factors under different pressure. Our main results for p-factors effected by different substitutional atoms and concentrations are described in Section 4. Finally, in Section 5 we summarize the main conclusions and results.

2. Computational Methodology and Models

Calculations are performed by using the Vienna Ab-initio Simulation Package (VASP), which is based on the density functional theory (DFT). Generalized gradient approximation (GGA) with The Perdew–Burke–Ernzerhof (PBE) functional is employed as the exchange-correlation functional. All the materials calculated are L1${}_2$ structures.

In cubic crystals, there are three independent elastic constants c${}_{11}$, c${}_{12}$ and c${}_{44}$. A 1 × 1 × 1 supercell is constructed to calculate the lattice constants and the elastic constants. The cut-off energy of plane wave is set to 450 eV due to convergence test, and the Brillouin zones are performed by using Monkhorst and Pack special k points generated with a 15 × 15 × 15 mesh parameters grid.

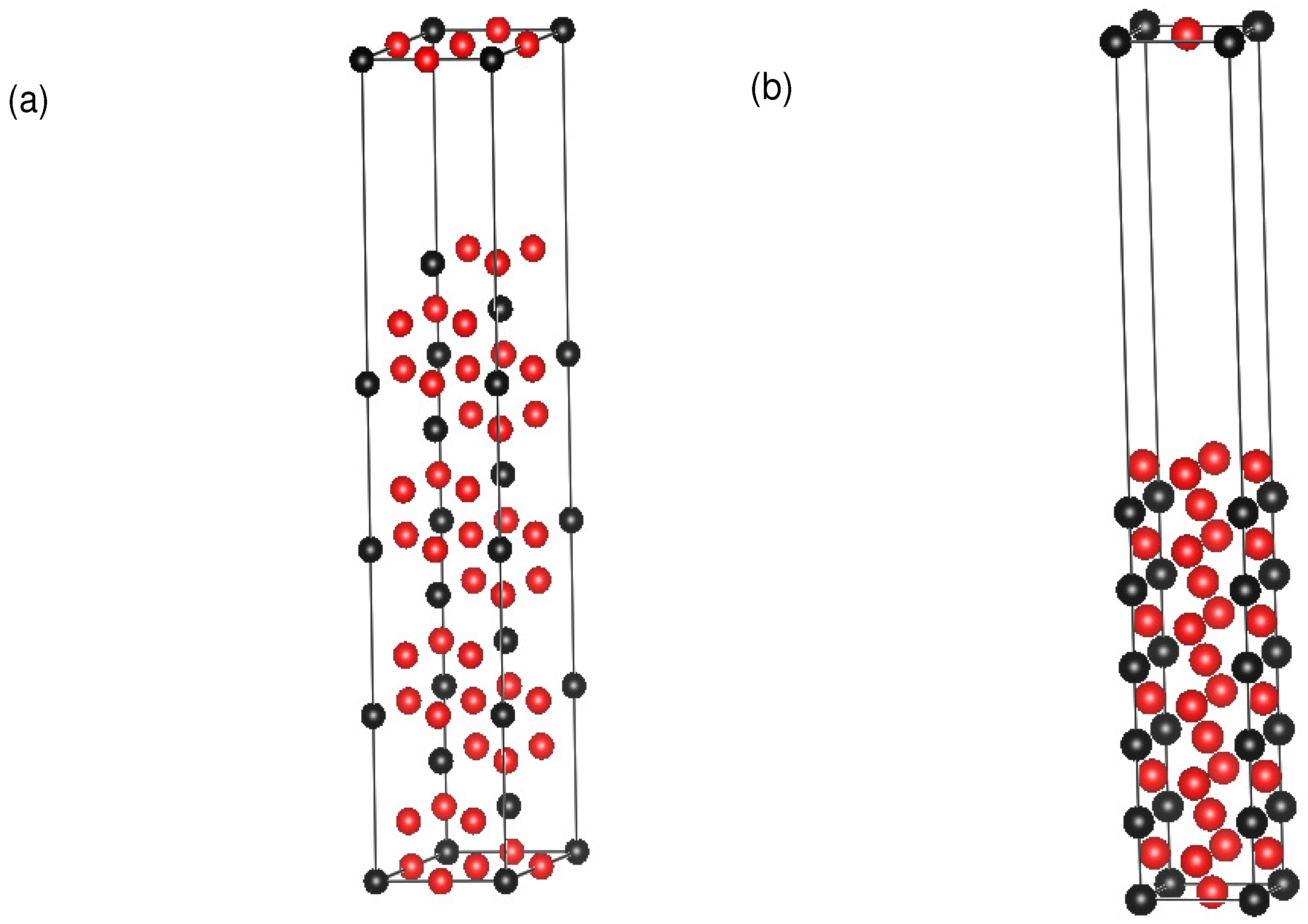
A supercell model of 12 layers perpendicular to the APB and four atoms per layer with vacuum layers is constructed to calculate APB energies in both {111} and {010} planes under the pressures of 0, 20 and 40 GPa [53]. We add vacuum layers since the vacuum layers can reduce the effects from the neighbor supercell [54]. The k points are set as 15 × 15 × 1. The structures of the {111} and {010} planes are shown in Figure 2.

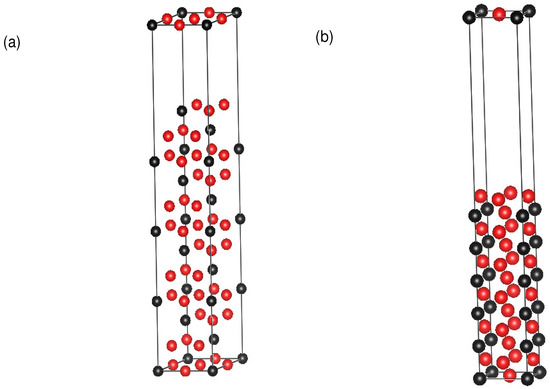
Figure 2. Supercells for antiphase boundary (APB) energy calculations in (a) {111} planes and (b) {010} planes with a concentration of 25%. Red spheres represent A atoms and black spheres represent B atoms in A${}_3$B L1${}_2$ materials.

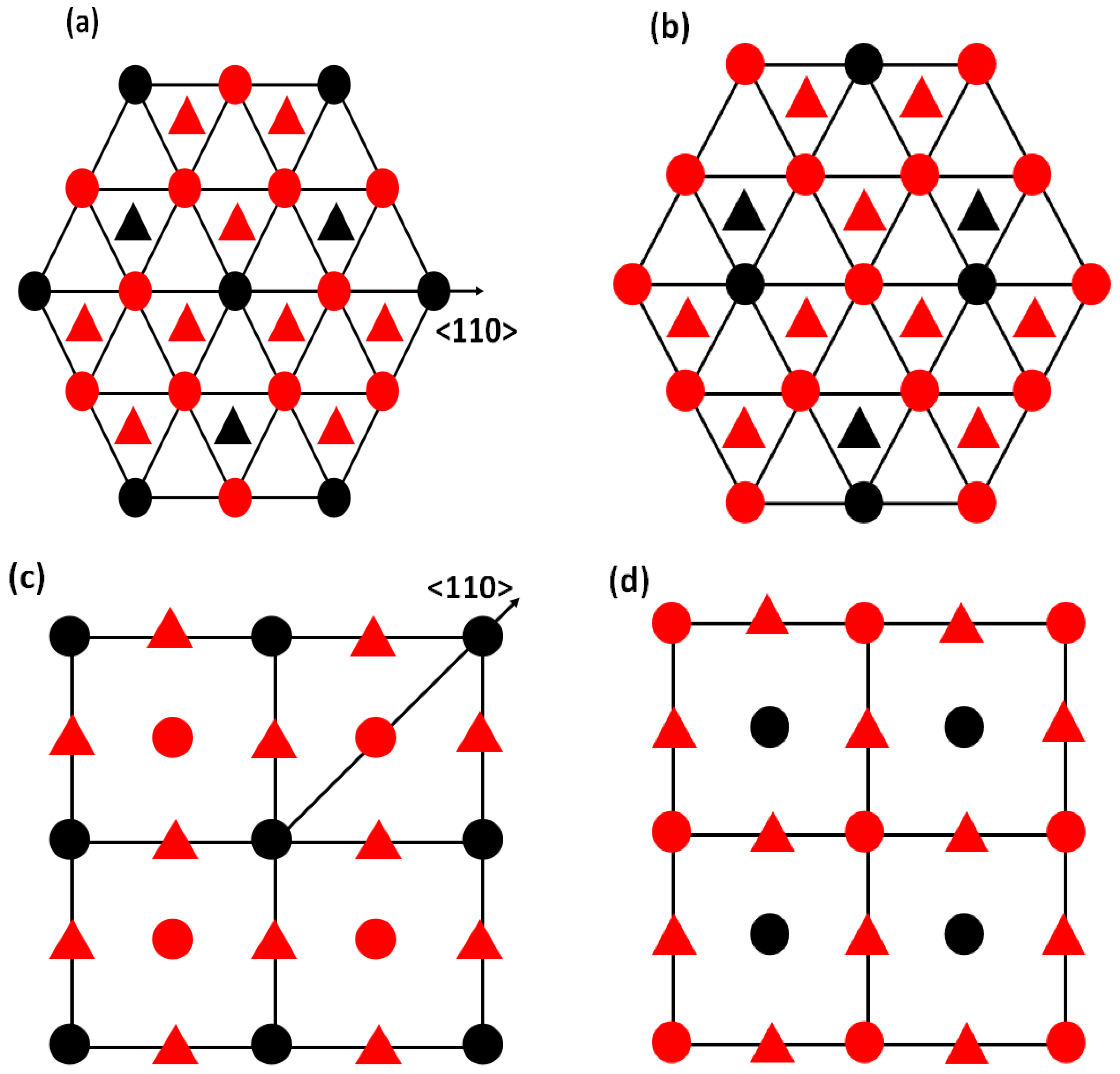
The {111} and {010} planes with and without APB are shown in Figure 3. They are created by applying 1/2⟨110⟩ shift vectors on the {111} and {010} planes or not. The APB energy $\gamma$ is given by:

$$\gamma =({\mathrm{E}}_{\mathrm{APB}}-{\mathrm{E}}_0)/{\mathrm{A}}_{\mathrm{APB}}$$

(3)

where $\gamma$ is the APB energy, ${\mathrm{E}}_{\mathrm{APB}}$ and ${\mathrm{E}}_0$ are the total energies of the supercell with and without APB, respectively. A${}_{\mathrm{APB}}$ is the cross-section area of the APB. They can be calculated accurately by using first-principle methods.

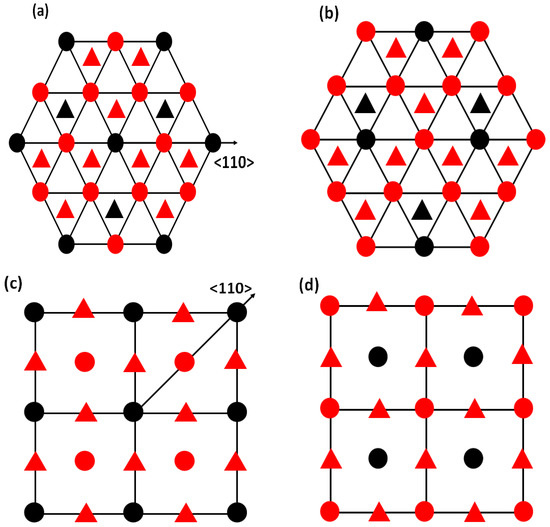
Figure 3. The atomic projection of L1${}_2$ A${}_3$B (a) without and (b) with APB on the {111} planes; (c) without and (d) with APB on the {010} planes. Red spheres represent A atoms and black spheres represent B atoms in A${}_3$B L1${}_2$ materials.

When calculating the APB energies with substituting atoms, different supercells are used for different concentrations in the slip planes: 2 × 2 × 12 for a plane concentration 6.25%, 2 × 1 × 12 for a plane concentration of 12.5% and 1 × 1 × 12 for a plane concentration of 25%. All the supercells have vacuum layers. As for the Brillouin zone k-point grids, 7 × 7 × 1, 7 × 15 × 1 and 15 × 15 × 1 k-point meshes are used for different bulks.

Before calculating the APB energies, formation energies to confirm the preference of the substitutions are calculated first. Since there are different concentrations, only the supercell with the plane concentration 25% is chosen. The formation energies is given by:

$${\mathrm{E}}_{\mathrm{f}}={\mathrm{E}}_{{\mathrm{A}}_3\mathrm{B}-\mathrm{X}}-({\mathrm{E}}_{\mathrm{A}}+{\mathrm{E}}_{\mathrm{B}}+{\mathrm{E}}_{\mathrm{X}})$$

(4)

where E${}_{\mathrm{f}}$ is the formation energy, A and B are the two kinds atoms of A${}_3$B materials, X is the substituted atom, E${}_{{\mathrm{A}}_3\mathrm{B}-\mathrm{X}}$ is the total energy of A${}_3$B material with substitution, E${}_{\mathrm{A}}$, E${}_{\mathrm{B}}$ and E${}_{\mathrm{X}}$ are the energies of single atom of atoms A, B and substitutional atom X. By comparing the results, the most preference substitutional site can be confirmed, thus to optimize the calculations of the APB energies.

3. Effects of Pressure on Stacking Fault Energy and p-Factor

Lattice constants and elastic constants under different pressures are presented in Table 1. In general, results are in good agreement with experiments and previous theoretical calculations [55,56]. The elastic constants and anisotropy A increase with pressure. Results of A of Ni${}_3$Al and Ni${}_3$Ga are the larger ones, which indicate that these two materials much easily form cross-slip to have the property of YSA according to Equation (2). Specifically, it is found that the structures of Al${}_3$Ti and Al${}_3$Sc are not stable when P = 40 GPa. Therefore, the lattice constants and elastic constants of Al${}_3$Ti and Al${}_3$Sc at 40 GPa are not presented.

Table 1. Lattice constants a (in units of Å), elastic constants ${\mathrm{c}}_{11}$, ${\mathrm{c}}_{12}$ and ${\mathrm{c}}_{44}$ (in units of GPa) and the elastic anisotropy ratio A of Ni${}_3$X (X = Al, Ge, Si and Ga), Al${}_3$X’ (X’ = Ti and Sc) under different pressures P (in units of GPa).

$\mathbf{Materials}$	P	a	${\mathbf{c}}_{11}$	${\mathbf{c}}_{12}$	${\mathbf{c}}_{44}$	A
Ni${}_3$Al	0	3.569	228.42	151.76	116.89	3.05
	1.4 [55]	-	223.50	149.00	122.90	3.30
	20	3.463	330.25	231.54	161.43	3.27
	40	3.389	415.88	302.55	197.93	3.49
Ni${}_3$Ge	0	3.585	253.81	149.28	98.83	1.89
	0 [41]	3.500	263.00	143.00	103.00	1.72
	20	3.484	367.87	231.14	141.99	2.08
	40	3.413	474.76	310.69	183.49	2.24
Ni${}_3$Si	0	3.511	298.15	166.93	129.24	1.97
	20	3.420	410.44	247.02	174.86	2.14
	40	3.354	514.69	322.28	216.06	2.25
Ni${}_3$Ga	0	3.588	226.66	154.68	105.40	2.93
	0 [57]	3.521	288.86	192.53	127.74	2.65
	0 [57]	3.570	264.14	169.99	116.39	2.47
	0 [58]	3.580	191.00	123.00	108.00	3.17
	20	3.482	329.99	240.69	147.18	3.30
	40	3.408	424.04	320.88	184.82	3.58
Al${}_3$Ti	0	3.980	190.74	64.27	75.41	1.19
	0 [59]	3.985	184.40	64.21	74.61	1.24
	0 [59]	3.984	184.32	62.41	72.89	1.20
	0 [59]	3.900	207.54	69.05	87.29	1.26
	20	3.797	299.66	122.13	127.42	1.44
	20 [59]	3.799	292.10	120.50	126.80	1.48
Al${}_3$Sc	0	4.106	182.21	39.39	71.37	1.00
	0 [60]	-	180.67	40.62	72.00	1.03
	0 [56]	4.101	187.84	35.14	73.32	0.96
	20	3.887	293.69	94.29	124.15	1.25
	20 [56]	-	312.83	88.19	128.13	1.14

The APB energies in both {111} and {010} planes of Ni${}_3$Al, Ni${}_3$Ge, Ni${}_3$Si, Ni${}_3$Ga, Al${}_3$Ti and Al${}_3$Sc under 0, 20 and 40 GPa are shown in Table 2. Obviously, the APB energies in {010} planes are much smaller than those in {111} planes. Larger APB energy in {111} planes results in smaller dissociation distance between partial dislocations. The possibility of construction is high for dissociated dislocation in {111} planes. Therefore, the cross-slip from {111} to {010} may be generated.

Table 2. APB energies (in units of J/m${}^2$) on {111} and {010} planes of Ni${}_3$X (X = Al, Ge, Si and Ga), Al${}_3$X’ (X’ = Ti and Sc) under different pressures P (in units of GPa). $\lambda$ (ratio of APB${}_{111}$/APB${}_{010}$) and p-factors are also presented.

$\mathbf{Materials}$	P	0	20	40
Ni${}_3$Al	{111}	0.344	0.406	0.459
	{010}	0.117	0.173	0.205
	$\lambda$	2.940	2.346	2.239
	p	5.352	4.626	4.282
Ni${}_3$Ge	{111}	0.509	0.587	0.651
	{010}	0.381	0.415	0.442
	$\lambda$	1.336	1.414	1.473
	p	1.950	2.163	2.331
Ni${}_3$Si	{111}	0.455	0.515	0.565
	{010}	0.395	0.453	0.506
	$\lambda$	1.152	1.137	1.117
	p	1.718	1.766	1.777
Ni${}_3$Ga	{111}	0.272	0.308	0.337
	{010}	0.016	0.024	0.029
	$\lambda$	17.000	12.833	11.621
	p	31.396	24.485	22.320
Al${}_3$Ti	{111}	0.258	0.643	-
	{010}	0.094	0.173	-
	$\lambda$	2.745	3.717	-
	p	5.615	4.748	-
Al${}_3$Sc	{111}	0.741	1.025	-
	{010}	0.575	0.851	-
	$\lambda$	1.289	1.204	-
	p	1.280	1.394	-

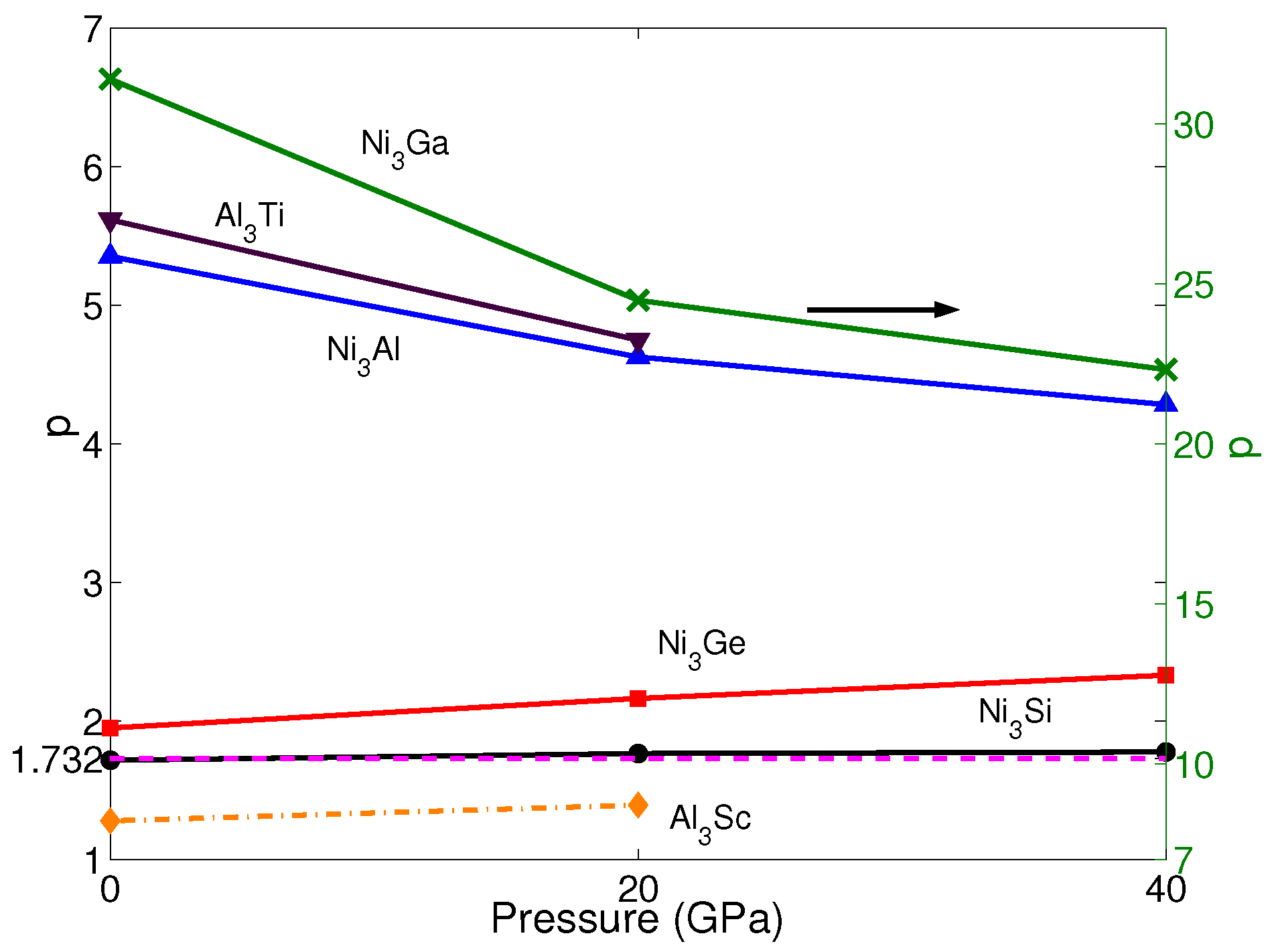
Based on the calculated APB energies and elastic constants, the anomalous yield stress phenomenon is predicted by the energy-based criterion Equation (2). The p-factors of Ni${}_3$Al, Ni${}_3$Ge, Ni${}_3$Si, Ni${}_3$Ga, Al${}_3$Ti and Al${}_3$Sc under the different pressures are shown in Figure 4. Noticeably, the calculated p-factor of Ni${}_3$Si at 0 GPa is lower than $\sqrt{3}$, which is in agreement with Yoo [61]. However, based on the observed behavior of YSA for Ni${}_3$Si, Yoo still considers Ni${}_3$Si to have a positive temperature dependence of yield stress, and by calculating with other supercells, the p-factor of Ni${}_3$Si satisfies the criterion. Therefore, here, Ni${}_3$Si is regarded to have the property of YSA at 0 GPa, as well. According to Equation (2), although the A of Al${}_3$Ti, Ni${}_3$Al and Ni${}_3$Ga increases with pressure (see Table 1), due to the APB energy in {010} planes having a faster growth than the one in {111} planes, p-factors of Al${}_3$Ti, Ni${}_3$Al and Ni${}_3$Ga keep decreasing with pressure, and they are still much larger than $\sqrt{3}$ among all pressures. The values of p-factors of Al${}_3$Sc, Ni${}_3$Ge and Ni${}_3$Si increase with pressure, and the A of them has the same trend of increase. This indicates that APB energy in {010} planes does not have many effects on the changes of the p-factor with pressure. The changes of the p-factors of Ni${}_3$Ge and Ni${}_3$Si are not obvious, and the values are still slightly larger than $\sqrt{3}$. These results mean they all exhibit the YSA under all pressures investigated here. On the other hand, only the p-factor of Al${}_3$Sc is smaller than $\sqrt{3}$ under all pressures, which means this material does not have YSA; although it increases slightly with pressure. All these results are in good agreement with the properties achieved from experiments. This means pressure has negligible influence on the property of yield stress.

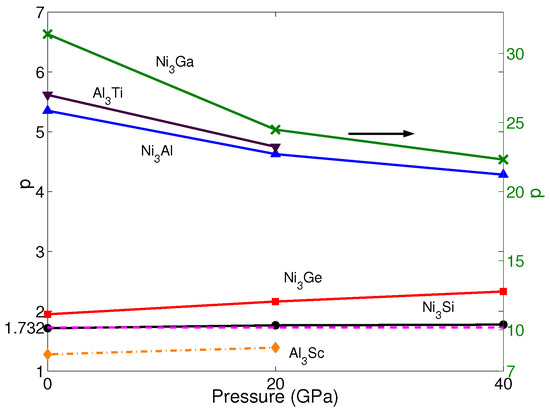
Figure 4. p of Ni${}_3$X (X = Al, Ge, Si and Ga) and Al${}_3$X’ (X’ = Ti and Sc) under different pressures p = 0, 20 and 40 GPa. The blue solid line with up-triangles shows the results of Ni${}_3$Al. The red solid line with squares shows the results of Ni${}_3$Ge. The black solid line with circles shows the results of Ni${}_3$Si. The green solid line with crosses shows the results of Ni${}_3$Ga, which is shown by the right axis. The brown solid line with down-triangles shows the results of Al${}_3$Ti. The yellow dashed-dotted line with diamonds shows the results of Al${}_3$Sc. The magenta dash line represents the critical value of p${}_{\mathrm{c}}$ = $\sqrt{3}$.

4. Effects of Substituting Atoms on Stacking Fault Energy and p-Factor

4.1. Substituted by a Single Atom

Based on the above results, the pressure will not introduce the transition between anomalous and normal behavior. In this section, the effects of substitutional atoms on p-factor will be investigated. p-factors of Ni${}_3$Ge, Ni${}_3$Si and Al${}_3$Sc are studied since they are close to $\sqrt{3}$. In Figure 1, there are substitutions (black circle and white circle) on either {111} and {010} planes, which affect the ${\gamma }_{\mathrm{APB}}^{\{111\}}$ and ${\gamma }_{\mathrm{APB}}^{\{010\}}$. Therefore, as discussed above, Ni${}_3$Ge is substituted with Fe, Sc, Al or Ga, Ni${}_3$Si is substituted with Al, Ga, Ti or Sc and Al${}_3$Sc is substituted with Ti, Y, Zr or Li.

To determine the substitutional sites, the formation energies of Ni${}_3$Ge, Ni${}_3$Si and Al${}_3$Sc with alloying atoms are presented. All possible substitutional sites are taken into consideration. Results of the formation energies of different substitution sites are shown in Table 3. It is easy to see that: (1) the formation energies of Sc${}_{\mathrm{Ge}}$, Al${}_{\mathrm{Ge}}$ Ga${}_{\mathrm{Ge}}$ and Fe${}_{\mathrm{Ni}}$ are lower to make the structure more stable; (2) the formation energies of Sc${}_{\mathrm{Si}}$, Ti${}_{\mathrm{Si}}$ Ga${}_{\mathrm{Si}}$ and Al${}_{\mathrm{Si}}$ are lower to make the structure more stable; (3) the formation energies of Ti${}_{\mathrm{Sc}}$, Y${}_{\mathrm{Sc}}$ and Zr${}_{\mathrm{Sc}}$ and Li${}_{\mathrm{Al}}$ are lower to make the structure more stable. Fe${}_{\mathrm{Ni}}$ means that the Ni site is substituted by Fe, and so forth. Therefore, Sc, Al and Ga tend to occupy the site of Ge, while Fe tends to occupy the site of Ni in Ni${}_3$Ge. Al, Ga, Ti and Sc all tend to occupy the site of Si in Ni${}_3$Si. Ti, Y and Zr tend to occupy the site of Sc, while Li tends to occupy the site of Al in Al${}_3$Sc.

Table 3. Formation energies (in units of eV) of Ni${}_3$Ge substituted with Fe on Ni sublattice and Sc, Al, Ga on the Ge sublattice. Energies of substituted Ni${}_3$Si and Al${}_3$Sc are presented, as well.

Ni${}_3$Ge	Fe	Sc	Al	Ga
Ni	−36.21	−32.22	−32.89	−32.25
Ge	−34.69	−33.02	−33.52	−33.01
Ni${}_3$Si	Al	Ga	Ti	Sc
Ni	−53.90	−53.23	−53.58	−52.64
Si	−54.02	−53.43	−53.87	−52.98
Al${}_3$Sc	Ti	Y	Li	Zr
Al	−50.86	−49.45	−50.86	−50.41
Sc	−51.15	−51.15	−49.46	−51.63

Three different plane concentrations of 6.25%, 12.5%, and 25% are used to calculate the APB energies. APB energies in {111} and {010} planes are shown in Table 4. It is interesting to find that substitutional atoms decrease APB energies in {111} planes except Zr${}_{\mathrm{Sc}}$ in Al${}_3$Sc. The APB energies in {010} planes are also decreased by substitutional atoms except Fe${}_{\mathrm{Ni}}$, Sc${}_{\mathrm{Si}}$, Y${}_{\mathrm{Sc}}$ and Li${}_{\mathrm{Al}}$.

Table 4. The APB energies (in units of J/m${}^2$) of {111} and {010} planes in Ni${}_3$Ge, Ni${}_3$Si and Al${}_3$Sc with different substitutional concentrations (0%, 6.25%, 12.5% and 25%). p-factors of atoms substituted in or both planes are also presented. Fe${}_{\mathrm{Ni}}$ means that the Ni site is substituted by Fe, and so forth.

$\mathbf{Materials}$	$\mathbf{Substitutions}$	APB${}_{\{111\}}$				APB${}_{\{010\}}$				${\mathbf{p}}_{\{111\}\&\{010\}}$
		0%	6.25%	12.5%	25%	0%	6.25%	12.5%	25%	0%	6.25%	12.5%	25%
$\mathrm{N}{\mathrm{i}}_3\mathrm{Ge}$	Fe${}_{\mathrm{Ni}}$	0.691	0.665	0.643	0.621	0.515	0.434	0.412	0.478	1.955	2.235	2.278	1.895
	Sc${}_{\mathrm{Ge}}$	0.691	0.628	0.566	0.442	0.515	0.477	0.465	0.431	1.955	1.919	1.774	1.497
	Al${}_{\mathrm{Ge}}$	0.691	0.648	0.600	0.494	0.515	0.469	0.424	0.295	1.955	2.014	2.064	2.443
	Ga${}_{\mathrm{Ge}}$	0.691	0.655	0.613	0.519	0.515	0.467	0.417	0.277	1.955	2.044	2.143	2.732
Ni${}_3$Si	Al${}_{\mathrm{Si}}$	0.666	0.635	0.602	0.523	0.520	0.507	0.464	0.351	1.831	1.866	1.931	2.219
	Ga${}_{\mathrm{Si}}$	0.666	0.641	0.614	0.548	0.520	0.500	0.450	0.317	1.831	1.907	2.031	2.575
	Ti${}_{\mathrm{Si}}$	0.666	0.631	0.609	0.577	0.520	0.506	0.505	0.480	1.831	1.855	1.796	1.792
	Sc${}_{\mathrm{Si}}$	0.666	0.629	0.596	0.530	0.520	0.518	0.521	0.545	1.831	1.806	1.704	1.449
Al${}_3$Sc	Ti${}_{\mathrm{Sc}}$	0.698	0.666	0.637	0.562	0.558	0.527	0.472	0.343	1.251	1.262	1.349	1.637
	Y${}_{\mathrm{Sc}}$	0.698	0.738	0.775	0.697	0.558	0.600	0.630	0.696	1.251	1.229	1.228	1.001
	Li${}_{\mathrm{Al}}$	0.698	0.669	0.630	0.558	0.558	0.568	0.582	0.604	1.251	1.177	1.083	0.924
	Zr${}_{\mathrm{Sc}}$	0.698	0.704	0.708	0.718	0.558	0.557	0.529	0.454	1.251	1.239	1.337	1.581

Based on APB energies, p-factors of Ni${}_3$Ge, Ni${}_3$Si and Al${}_3$Sc at different concentrations are obtained (see Table 4 and Table 5). Table 4 shows the p-factor of atoms substituted in both {111} and {010} planes, and Table 5 shows the p-factor of atoms substituted only in {111} or {010} planes, respectively.

Table 5. p-factors for Ni${}_3$Ge, Ni${}_3$Si and Al${}_3$Sc with atoms only substituted in the {111} or {010} planes.

Materials	Substitutions		${\mathbf{p}}_{\{111\}}$			${\mathbf{p}}_{\{010\}}$
		0	6.25%	12.5%	25%	6.25%	12.5%	25%
Ni${}_3$Ge	$\mathrm{F}{\mathrm{e}}_{\mathrm{Ni}}$	1.955	1.883	1.820	1.758	2.320	2.447	2.108
	Sc${}_{\mathrm{Ge}}$	1.955	1.789	1.609	1.253	2.110	2.168	2.337
	Al${}_{\mathrm{Ge}}$	1.955	1.845	1.708	1.399	2.147	2.376	3.415
	Ga${}_{\mathrm{Ge}}$	1.955	1.865	1.743	1.470	2.155	2.419	3.635
Ni${}_3$Si	Al${}_{\mathrm{Si}}$	1.831	1.746	1.657	1.499	1.951	2.139	2.826
	Ga${}_{\mathrm{Si}}$	1.831	1.763	1.670	1.569	1.975	2.207	3.133
	Ti${}_{\mathrm{Si}}$	1.831	1.736	1.677	1.654	1.952	1.966	2.068
	Sc${}_{\mathrm{Si}}$	1.831	1.729	1.641	1.518	1.907	1.907	1.822
Al${}_3$Sc	Ti${}_{\mathrm{Sc}}$	1.251	1.175	1.134	1.007	1.327	1.487	2.035
	Y${}_{\mathrm{Sc}}$	1.251	1.304	1.379	1.250	1.166	1.113	1.002
	Li${}_{\mathrm{Al}}$	1.251	1.182	1.122	1.001	1.232	1.206	1.155
	Zr${}_{\mathrm{Sc}}$	1.251	1.244	1.261	1.288	1.257	1.325	1.536

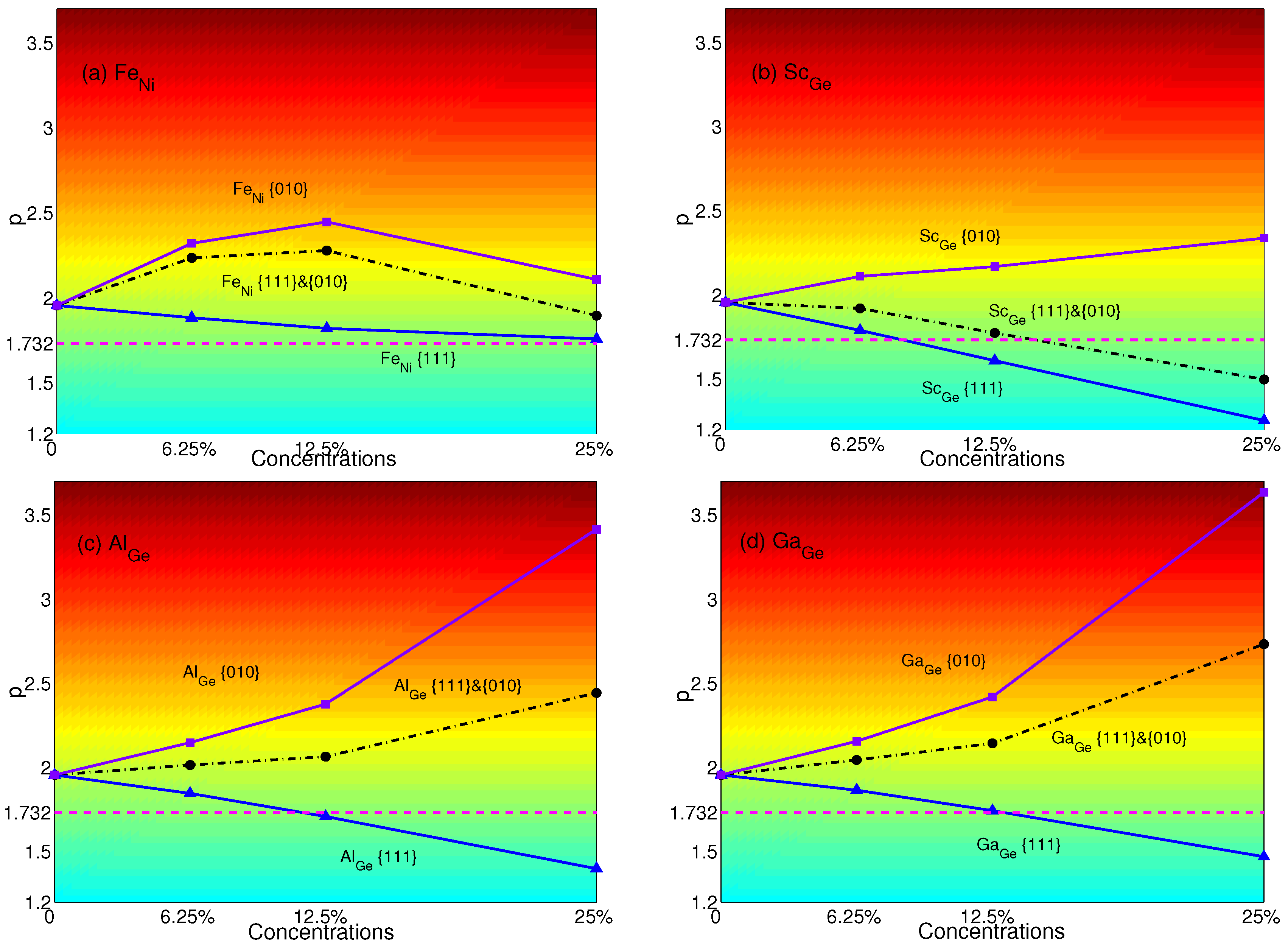
The p-factors of YSA for Ni${}_3$Ge with substitutional atoms are shown in Figure 5. Fe${}_{\mathrm{Ni}}^{\{111\}}$ means Ni substituted by Fe only in {111} planes; Fe${}_{\mathrm{Ni}}^{\{010\}}$ means Ni substituted by Fe only in {010} planes; and Fe${}_{\mathrm{Ni}}^{\{111\}\&\{010\}}$ means Ni substituted by Fe both in {111} and {010} planes, and so forth. It is transparent that when only substituting atoms in {111} planes, the p-factors of Fe${}_{\mathrm{Ni}}^{\{111\}}$, Sc${}_{\mathrm{Ge}}^{\{111\}}$, Al${}_{\mathrm{Ge}}^{\{111\}}$ and Ga${}_{\mathrm{Ge}}^{\{111\}}$ decrease with the concentrations. These are originated from the decrease of APB energies of Ni${}_3$Ge with substitutional atoms in {111} planes (see Table 4). When the concentration is 12.5%, Ni${}_3$Ge will display the normal behavior with Sc${}_{\mathrm{Ge}}^{\{111\}}$ or Al${}_{\mathrm{Ge}}^{\{111\}}$. With the concentration increasing to 25%, Ga${}_{\mathrm{Ge}}^{\{111\}}$ can change the property of YSA for Ni${}_3$Ge, as well. When only substituting atoms in {010} planes, the p-factors of Sc${}_{\mathrm{Ge}}^{\{010\}}$, Al${}_{\mathrm{Ge}}^{\{010\}}$ and Ga${}_{\mathrm{Ge}}^{\{010\}}$ increase, and the properties of YSA for Ni${}_3$Ge are enhanced due to the decrease of APB energies in {010} planes with substitutions; except that Fe${}_{\mathrm{Ni}}^{\{010\}}$ weakens the properties of YSA with the plane concentration increasing from 12.5%–25% due to the APB energy increasing from 0.412 J/m${}^2$–0.478 J/m${}^2$. When substituting atoms in both {111} and {010} planes, p-factors lie between those that only substitute in {111} or {010} planes. Due to the lower decrease of the APB energies of Sc${}_{\mathrm{Ge}}^{\{010\}}$ compared to the APB energies in {111} planes than those of Al${}_{\mathrm{Ge}}$ and Ga${}_{\mathrm{Ge}}$, the p-factor of Sc${}_{\mathrm{Ge}}^{\{111\}\&\{010\}}$ at a concentration of 25% is the only one less than the critical value to make Ni${}_3$Ge show the normal behavior.

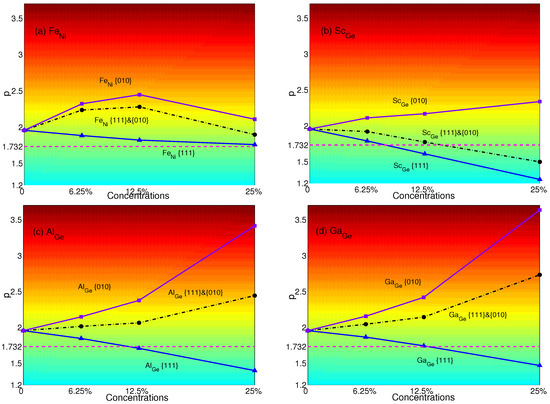
Figure 5. p-factors of Ni${}_3\mathrm{Ge}$ substituted with (a) Fe; (b) Sc; (c) Al; and (d) Ga. Black dashed-dotted lines with circles represent the results of atoms substituted in both {111} and {010} planes; blue solid lines with triangles represent the results of atoms substituted only in {111} planes; purple solid lines with squares represent the results of atoms substituted only in {010} planes. Magenta dashed lines represent the critical value of p${}_{\mathrm{c}}$ = $\sqrt{3}$.

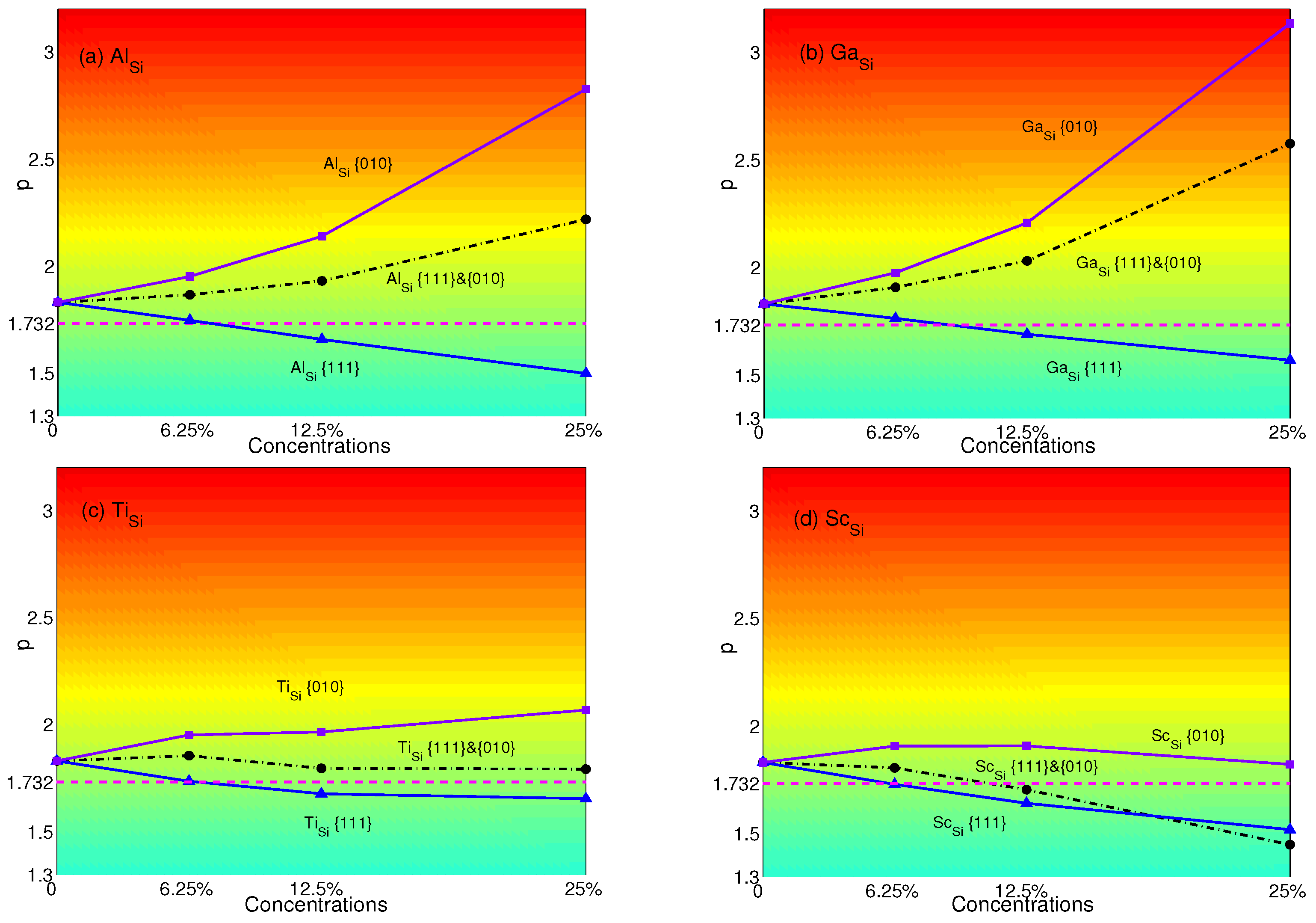
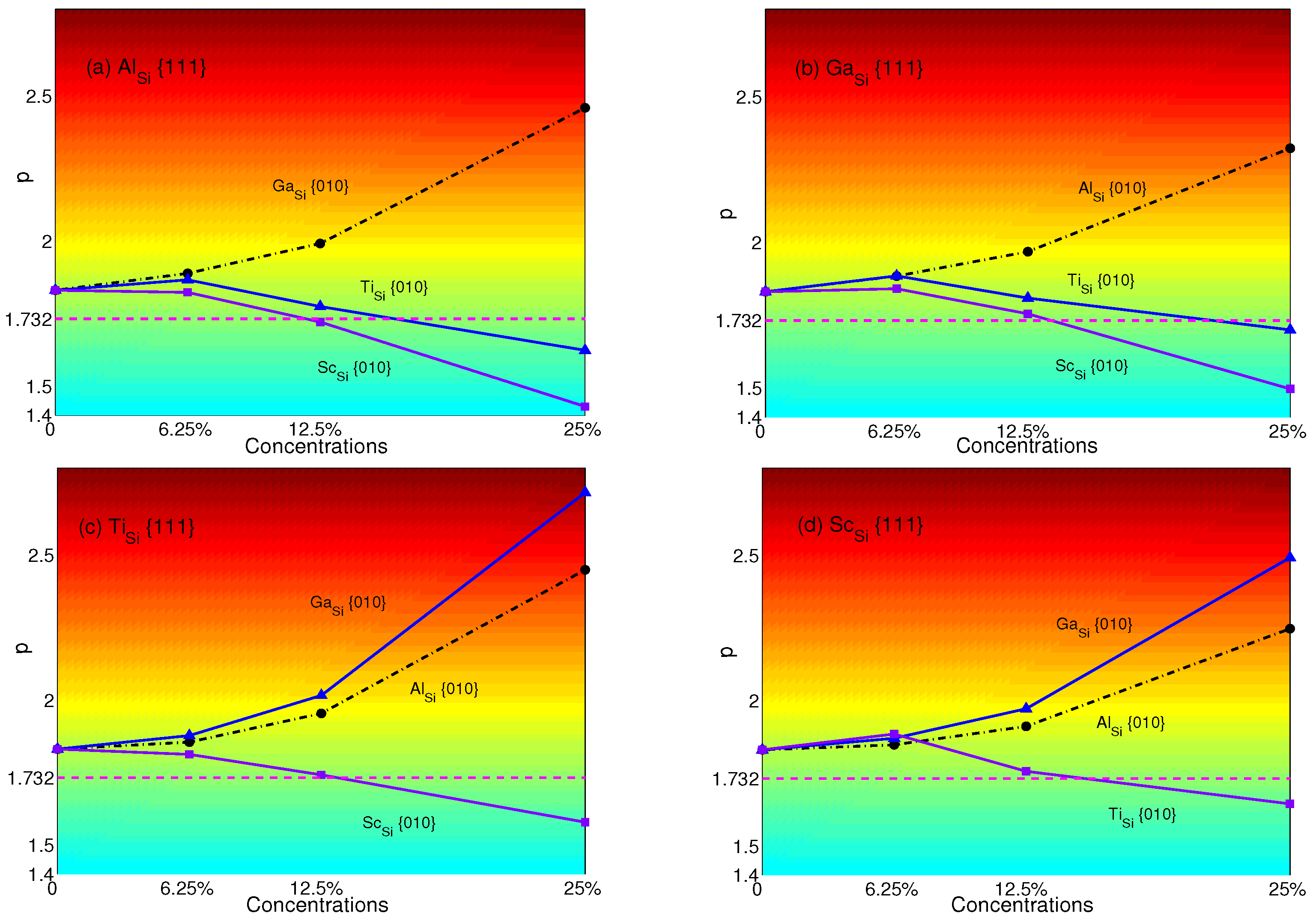
The p-factors of YSA for Ni${}_3$Si with substitutional atoms are shown in Figure 6. It is transparent that p-factors of substituting atoms only in {111} planes decrease with concentrations of Al${}_{\mathrm{Si}}^{\{111\}}$, Ga${}_{\mathrm{Si}}^{\{111\}}$, Ti${}_{\mathrm{Si}}^{\{111\}}$ and Sc${}_{\mathrm{Si}}^{\{111\}}$. These are originated from the decrease of APB energies of Ni${}_3$Si with the substitutional atoms in {111} planes (see Table 4). Ni${}_3$Si starts to display the normal behavior when the plane concentrations are 12.5%. However, when substituting atoms only in {010} planes, the properties of YSA for Ni${}_3$Si are enhanced by Al${}_{\mathrm{Si}}^{\{010\}}$, Ga${}_{\mathrm{Si}}^{\{010\}}$ or Ti${}_{\mathrm{Si}}^{\{010\}}$ due to the decreasing of APB energies in {010} planes with substitutions. Only when Sc is substituted in {010} planes, since the APB energy increases from 0.521 J/m${}^2$–0.545 J/m${}^2$, while plane concentration increases from 12.5%–25%, the p-factor decreases. Due to the decrease of APB energies of Al${}_{\mathrm{Si}}$, Ga${}_{\mathrm{Si}}$, Ti${}_{\mathrm{Si}}$ in both planes, p-factors of atoms substituted in both planes lie between those of substituting in a single plane. Only the p-factor of Sc${}_{\mathrm{Si}}^{\{111\}\&\{010\}}$ stays lower than Sc${}_{\mathrm{Si}}$ in {010} planes to display the normal behavior when the concentration is larger than 12.5%. This is caused by the increase of APB energies in {010} planes and the decrease of APB energies in {111} planes.

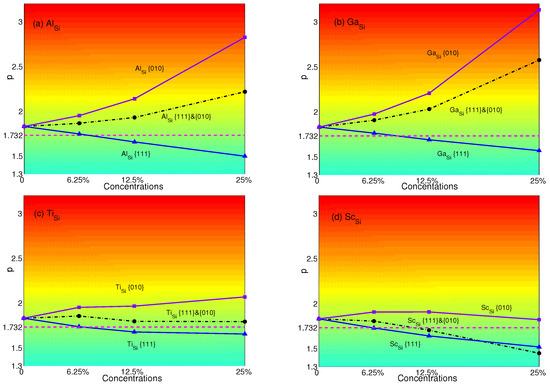
Figure 6. p-factors of Ni${}_3\mathrm{Si}$ substituted by (a) Al; (b) Ga; (c) Ti; and (d) Sc. Black dashed-dotted lines with circles represent the results of atoms substituted in both {111} and {010} planes; blue solid lines with triangles represent the results of atoms substituted only in {111} planes; purple solid lines with squares represent the results of atoms substituted only in {010} planes. Magenta dash lines represent the critical value of p${}_{\mathrm{c}}$ = $\sqrt{3}$.

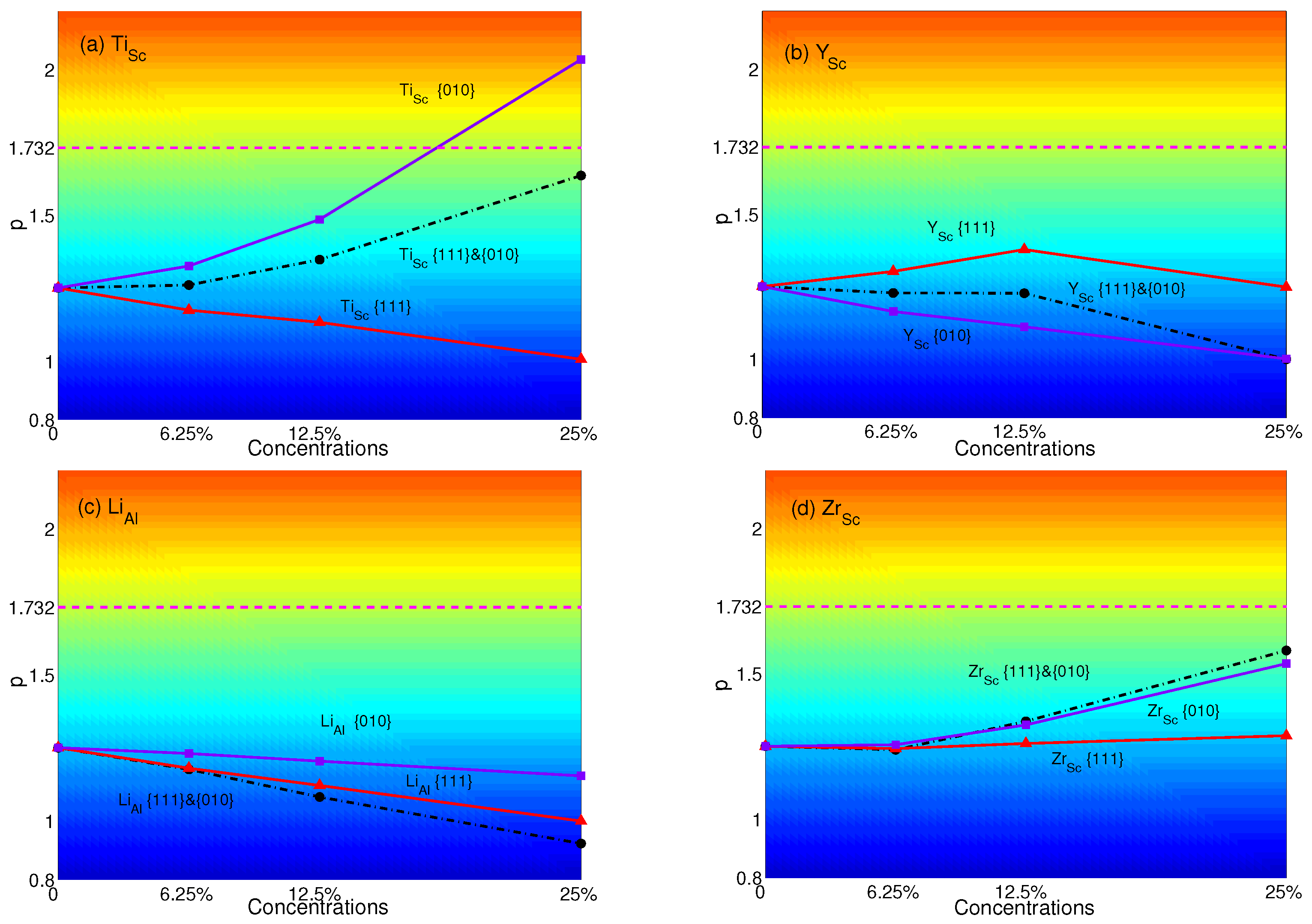
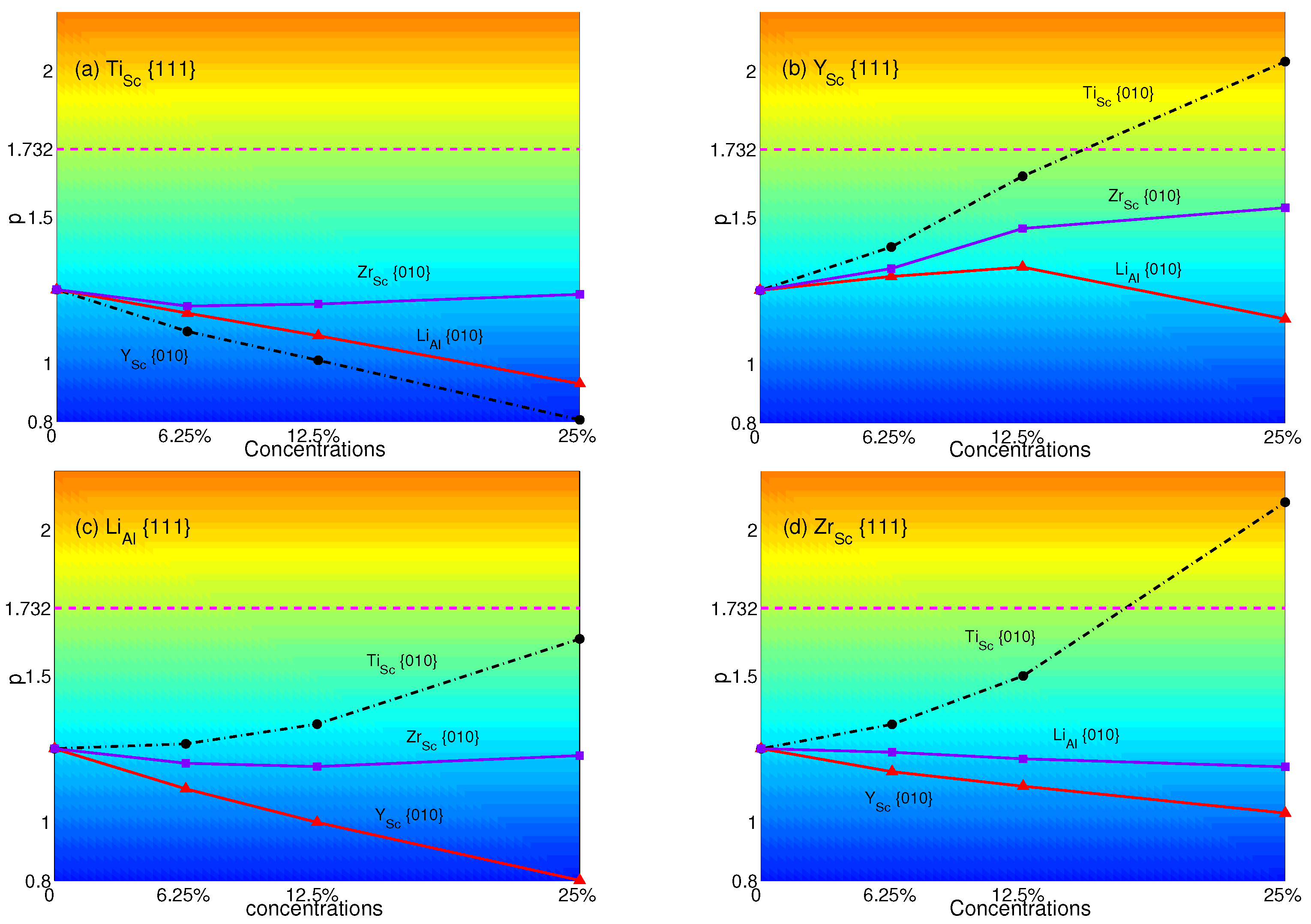
The p-factors of YSA for Al${}_3$Sc with substitutional atoms are shown in Figure 7. It is transparent that the p-factors of substituting atoms only in {111} planes decrease with increasing concentrations of Ti${}_{\mathrm{Sc}}^{\{111\}}$ or Li${}_{\mathrm{Al}}^{\{111\}}$. These are due to the decrease of APB energies of Al${}_3$Sc with substituting Li or Ti in {111} planes (see Table 4). The p-factor of Zr${}_{\mathrm{Sc}}^{\{111\}}$ has few changes. Besides, the p-factor of Y${}_{\mathrm{Sc}}^{\{111\}}$ increases since the APB energy of Y${}_{\mathrm{Sc}}^{\{111\}}$ increases from 0.698 J/m${}^2$–0.775 J/m${}^2$ while the plane concentration increases from 0–12.5%. Then, it decreases with the APB energy decreasing to 0.697 J/m${}^2$ when the plane concentration reaches 25%. When atoms are substituted only in {010} planes, the p-factors of Ti${}_{\mathrm{Sc}}^{\{010\}}$ and Zr${}_{\mathrm{Sc}}^{\{010\}}$ increase with concentrations, while Li${}_{\mathrm{Al}}^{\{010\}}$ and Y${}_{\mathrm{Sc}}^{\{010\}}$ have different trends. Al${}_3$Sc displays the anomalous behavior only when substituting Ti in {010} planes with the plane concentration of 25%. Due to the APB energies of Ti${}_{\mathrm{Sc}}$ in both planes increasing with concentrations, p-factors of Ti${}_{\mathrm{Sc}}^{\{111\}\&\{010\}}$ lie between those of substituting in single plane. p-factors of Y${}_{\mathrm{Sc}}^{\{111\}\&\{010\}}$ are similar to those of Ti${}_{\mathrm{Sc}}^{\{111\}\&\{010\}}$ at the plane concentration of 12.5%. Due to the APB energies of Li${}_{\mathrm{Al}}$ increasing in {010} planes and decreasing in {111} planes, the p-factors of Li${}_{\mathrm{Al}}^{\{111\}\&\{010\}}$ keep decreasing with concentrations. From Figure 7c, the p-factor of Li${}_{\mathrm{Al}}^{\{111\}\&\{010\}}$ lies below the other two and is the lowest at all concentrations. On the other hand, the increase of APB energies of Zr${}_{\mathrm{Sc}}^{\{111\}}$ and the decrease of APB energies of Zr${}_{\mathrm{Sc}}^{\{010\}}$ lead to the p-factor of Zr${}_{\mathrm{Sc}}^{\{111\}\&\{010\}}$ to become the highest. However, none of these p-factors with atoms substituted in both planes can reach the critical value at all concentrations.

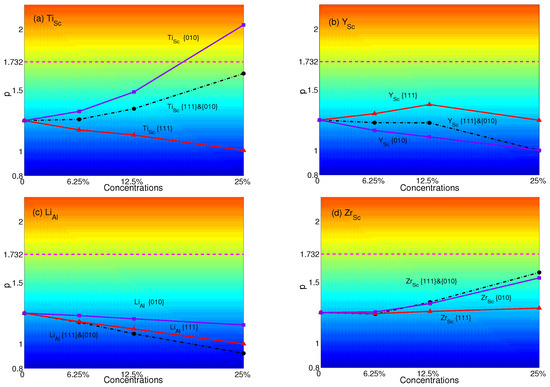
Figure 7. p-factors of Al${}_3\mathrm{Sc}$: substituted with (a) Ti; (b) Y; (c) Li; and (d) Zr. Black dashed-dotted lines with circles represent the results of atoms substituted in both {111} and {010} planes; red solid lines with triangles represent the results of atoms substituted only in {111} planes; purple solid lines with squares represent the results of atoms substituted only in {010} planes. Magenta dashed lines represent the critical value of p${}_{\mathrm{c}}$ = $\sqrt{3}$.

Comparing the different concentrations, the effects of substitutional atoms are enhanced with increasing concentrations. When the concentration is 12.5%, it makes the effects of atom substituted in {111} planes great enough to change the behavior from anomalous to normal obvious, such as Sc${}_{\mathrm{Ge}}^{\{111\}}$, Al${}_{\mathrm{Si}}^{\{111\}}$, Ga${}_{\mathrm{Si}}^{\{111\}}$, Ti${}_{\mathrm{Si}}^{\{111\}}$ and Sc${}_{\mathrm{Si}}^{\{111\}}$. When the concentration is 25%, Ti${}_{\mathrm{Sc}}^{\{010\}}$ can be effective enough to make Al${}_3$Sc have the property of YSA.

4.2. Substituted by Two Different Atoms

In this section, different alloying atoms are substituted in the {111} and {010} planes of Ni${}_3$Ge, Ni${}_3$Si and Al${}_3$Sc with the same concentrations. The p-factors are plotted in Figure 8, Figure 9 and Figure 10.

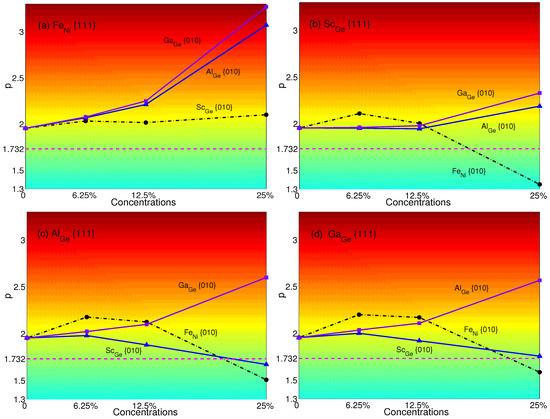
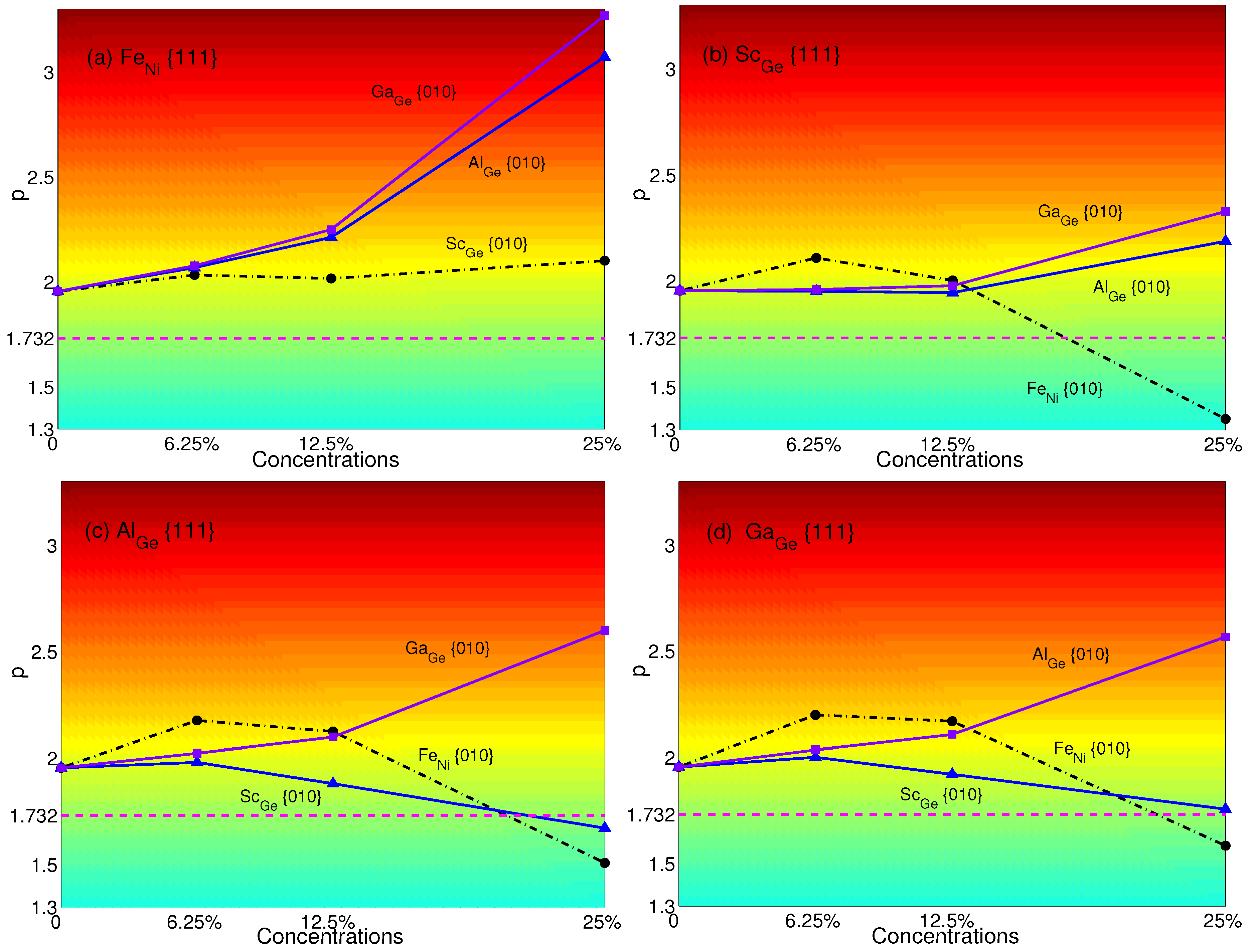
Figure 8. p-factors of Ni${}_3\mathrm{Ge}$: (a) Fe${}_{\mathrm{Ni}}$ in {111} planes with Sc${}_{\mathrm{Ge}}$, Al${}_{\mathrm{Ge}}$ and Ga${}_{\mathrm{Ge}}$ in {010} planes; (b) Sc${}_{\mathrm{Ge}}$ in {111} planes with Fe${}_{\mathrm{Ni}}$, Al${}_{\mathrm{Ge}}$ and Ga${}_{\mathrm{Ge}}$ in {010} planes; (c)Al${}_{\mathrm{Ge}}$ in {111} planes with Fe${}_{\mathrm{Ni}}$, Sc${}_{\mathrm{Ge}}$ and Ga${}_{\mathrm{Ge}}$ in {010} planes; (d) Ga${}_{\mathrm{Ge}}$ in {111} planes with Fe${}_{\mathrm{Ni}}$, Sc${}_{\mathrm{Ge}}$ and Al${}_{\mathrm{Ge}}$ in {010} planes. Magenta dash lines represent the critical value of p${}_{\mathrm{c}}$ = $\sqrt{3}$.

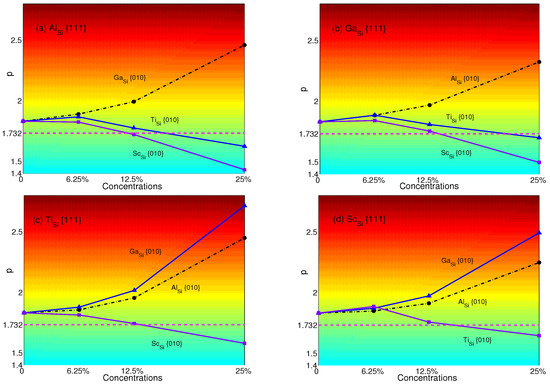
Figure 9. p-factors of Ni${}_3\mathrm{Si}$: (a) Al${}_{\mathrm{Ge}}$ in {111} planes with Ga${}_{\mathrm{Si}}$, Ti${}_{\mathrm{Si}}$ and Sc${}_{\mathrm{Si}}$ in {010} planes; (b) Ga${}_{\mathrm{Si}}$ in {111} planes with Al${}_{\mathrm{Si}}$, Ti${}_{\mathrm{Si}}$ and Sc${}_{\mathrm{Si}}$ in {010} planes; (c) Ti${}_{\mathrm{Si}}$ in {111} planes with Al${}_{\mathrm{Si}}$, Sc${}_{\mathrm{Si}}$ and Sc${}_{\mathrm{Si}}$ in {010} planes; (d) Sc${}_{\mathrm{Si}}$ in {111} planes with Al${}_{\mathrm{Si}}$, Ga${}_{\mathrm{Si}}$ and Ti${}_{\mathrm{Si}}$ in {010} planes. Magenta dash lines represent the critical value of p${}_{\mathrm{c}}$ = $\sqrt{3}$.

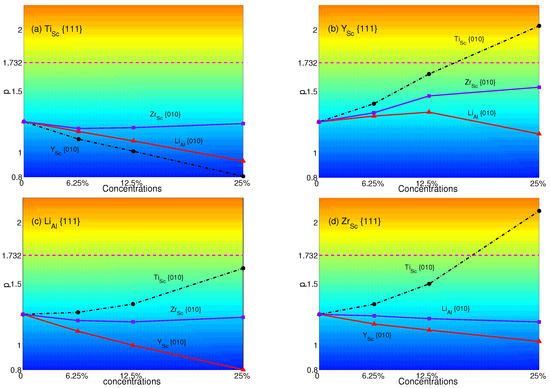
Figure 10. p-factors of Al${}_3\mathrm{Sc}$: (a) Ti${}_{\mathrm{Sc}}$ in {111} planes with Y${}_{\mathrm{Sc}}$, Li${}_{\mathrm{Al}}$ and Zr${}_{\mathrm{Sc}}$ in {010} planes; (b) Y${}_{\mathrm{Sc}}$ in {111} planes with Ti${}_{\mathrm{Sc}}$, Li${}_{\mathrm{Al}}$ and Zr${}_{\mathrm{Sc}}$ in {010} planes; (c) Li${}_{\mathrm{Al}}$ in {111} planes with Ti${}_{\mathrm{Sc}}$, Y${}_{\mathrm{Sc}}$ and Zr${}_{\mathrm{Sc}}$ in {010} planes; (d) Zr${}_{\mathrm{Sc}}$ in {111} planes with Ti${}_{\mathrm{Sc}}$, Y${}_{\mathrm{Sc}}$ and Li${}_{\mathrm{Al}}$ in {010} planes. Magenta dash lines represent the critical value of p${}_{\mathrm{c}}$ = $\sqrt{3}$.

The p-factors of Ni${}_3$Ge are plotted in Figure 8: (a) Fe${}_{\mathrm{Ni}}^{\{111\}}$ with Sc${}_{\mathrm{Ge}}^{\{010\}}$ (black dashed-dotted line with circles), Al${}_{\mathrm{Ge}}^{\{010\}}$ (blue solid line with triangles) and Ga${}_{\mathrm{Ge}}^{\{010\}}$ (purple solid line with squares); (b) Sc${}_{\mathrm{Ge}}^{\{111\}}$ with Al${}_{\mathrm{Ge}}^{\{010\}}$ (blue solid line with triangles), Ga${}_{\mathrm{Ge}}^{\{010\}}$ (purple solid line with squares) and Fe${}_{\mathrm{Ni}}^{\{010\}}$ (black dashed-dotted line with circles); (c) Al${}_{\mathrm{Ge}}^{\{111\}}$ with Sc${}_{\mathrm{Ge}}^{\{010\}}$ (blue solid line with triangles), Ga${}_{\mathrm{Ge}}^{\{010\}}$ (purple solid line with squares) and Fe${}_{\mathrm{Ni}}^{\{010\}}$ (black dashed-dotted line with circles); (d) Ga${}_{\mathrm{Ge}}^{\{111\}}$ with Sc${}_{\mathrm{Ge}}^{\{010\}}$(blue solid line with triangles), Al${}_{\mathrm{Ge}}^{\{010\}}$ (purple solid line with squares) and Fe${}_{\mathrm{Ni}}^{\{010\}}$ (black dashed-dotted line with circles), respectively.

From Figure 8, it is easy to see that the transition of Ni${}_3$Ge does not exist when Fe${}_{\mathrm{Ni}}^{\{111\}}$ with Ga${}_{\mathrm{Ge}}^{\{010\}}$, Al${}_{\mathrm{Ge}}^{\{010\}}$ or Sc${}_{\mathrm{Ge}}^{\{010\}}$. p-factors of Sc${}_{\mathrm{Ge}}^{\{111\}}$ with Ga${}_{\mathrm{Ge}}^{\{010\}}$ or Al${}_{\mathrm{Ge}}^{\{010\}}$, Al${}_{\mathrm{Ge}}^{\{111\}}$ with Ga${}_{\mathrm{Ge}}^{\{010\}}$ and Ga${}_{\mathrm{Ge}}^{\{111\}}$ with Al${}_{\mathrm{Ge}}^{\{010\}}$ have the same trend of increase, which means their properties of YSA will not be changed. Besides, the p-factor of Ga${}_{\mathrm{Ge}}^{\{111\}}$ with Sc${}_{\mathrm{Ge}}^{\{010\}}$ decreases with concentrations. Though the p-factor of it is very close to $\sqrt{3}$ at a plane concentration of 25%, it is still slightly higher than $\sqrt{3}$, which means that there is no transition from anomalous to normal. Sc${}_{\mathrm{Ge}}^{\{111\}}$ with Fe${}_{\mathrm{Ni}}^{\{010\}}$, Al${}_{\mathrm{Ge}}^{\{111\}}$ with Fe${}_{\mathrm{Ni}}^{\{010\}}$ or Sc${}_{\mathrm{Ge}}^{\{010\}}$ and Ga${}_{\mathrm{Ge}}^{\{111\}}$ with Fe${}_{\mathrm{Ni}}^{\{010\}}$ will result in transition with a plane concentration of 25%. It can be found that Fe${}_{\mathrm{Ni}}^{\{010\}}$ will decrease the p-factors with the concentration varying from 6.25%–25% no matter whether there are atoms substituted in {111} planes; only Fe${}_{\mathrm{Ni}}^{\{111\}}$ can lead to a small increase of p-factor with the concentration varying from 6.25%–12.5% (see Figure 5a). Additionally, it will be small enough to change the property of yield stress from anomalous to normal at the concentration of 25%. Comparing with Figure 5 and Figure 8, it can be seen that substituting Al or Ga in {010} planes with a concentration of 25% can be effective to revert the normalized Ni${}_3$Ge with Sc${}_{\mathrm{Ge}}^{\{111\}}$, Al${}_{\mathrm{Ge}}^{\{111\}}$ or Ga${}_{\mathrm{Ge}}^{\{111\}}$ to anomalous.

The p-factors of Ni${}_3$Si are plotted in Figure 9: (a) Al${}_{\mathrm{Si}}^{\{111\}}$ with Ga${}_{\mathrm{Si}}^{\{010\}}$ (black dashed-dotted line with circles), Ti${}_{\mathrm{Si}}^{\{010\}}$(blue solid line with triangles) and Sc${}_{\mathrm{Si}}^{\{010\}}$ (purple solid line with squares); (b) Ga${}_{\mathrm{Si}}^{\{111\}}$ with Al${}_{\mathrm{Si}}^{\{010\}}$ (black dashed-dotted line with circles), Ti${}_{\mathrm{Si}}^{\{010\}}$ (blue solid line with triangles) and Sc${}_{\mathrm{Si}}^{\{010\}}$ (purple solid line with squares); (c) Ti${}_{\mathrm{Si}}^{\{111\}}$ with Al${}_{\mathrm{Si}}^{\{010\}}$ (black dashed-dotted line with circles), Ga${}_{\mathrm{Si}}^{\{010\}}$ (blue solid line with triangles) and Sc${}_{\mathrm{Si}}^{\{010\}}$ (purple solid line with squares); (d) Sc${}_{\mathrm{Si}}^{\{111\}}$ with Al${}_{\mathrm{Si}}^{\{010\}}$ (black dashed-dotted line with circles), Ga${}_{\mathrm{Si}}^{\{010\}}$ (blue solid line with triangles) and Ti${}_{\mathrm{Si}}^{\{010\}}$ (purple solid line with squares), respectively.

From Figure 9, it is easy to see that Al${}_{\mathrm{Si}}^{\{111\}}$ with Ga${}_{\mathrm{Si}}^{\{010\}}$, Ga${}_{\mathrm{Si}}^{\{111\}}$ with Al${}_{\mathrm{Si}}^{\{010\}}$, Ti${}_{\mathrm{Si}}^{\{111\}}$ with Ga${}_{\mathrm{Si}}^{\{010\}}$ or Al${}_{\mathrm{Si}}^{\{010\}}$ and Sc${}_{\mathrm{Si}}^{\{111\}}$ with Ga${}_{\mathrm{Si}}^{\{010\}}$ or Al${}_{\mathrm{Si}}^{\{010\}}$ will not have the transition from anomalous to normal since the p-factors increase with plane concentrations. Although there are temporary increases of Ga${}_{\mathrm{Si}}^{\{111\}}$ with Ti${}_{\mathrm{Si}}^{\{010\}}$ or Sc${}_{\mathrm{Si}}^{\{010\}}$ and Sc${}_{\mathrm{Si}}^{\{111\}}$ with Ti${}_{\mathrm{Si}}^{\{010\}}$ at a concentration of 6.25%, overall, the p-factors of Al${}_{\mathrm{Si}}^{\{111\}}$ with Ti${}_{\mathrm{Si}}^{\{010\}}$ or Sc${}_{\mathrm{Si}}^{\{010\}}$, Ga${}_{\mathrm{Si}}^{\{111\}}$ with Ti${}_{\mathrm{Si}}^{\{010\}}$ or Sc${}_{\mathrm{Si}}^{\{010\}}$, Ti${}_{\mathrm{Si}}^{\{111\}}$ with Sc${}_{\mathrm{Si}}^{\{010\}}$ and Sc${}_{\mathrm{Si}}^{\{111\}}$ with Ti${}_{\mathrm{Si}}^{\{010\}}$ decrease with concentrations and decline low enough to be smaller than $\sqrt{3}$ at the concentration of 25%, which means the transition will occur. In other words, when substituting atoms in both planes, Ti${}_{\mathrm{Si}}^{\{010\}}$ and Sc${}_{\mathrm{Si}}^{\{010\}}$ will change the anomalous behavior of yield stress to normal at the concentration of 25% no matter what atom is substituted in {111} planes, except Ti${}_{\mathrm{Si}}^{\{111\}}$, which makes the p -factor of Ti${}_{\mathrm{Si}}^{\{111\}\&\{010\}}$ be larger than $\sqrt{3}$. (see Figure 6). In contrast, to make the normalized Ni${}_3$Si (see Figure 6) revert to anomalous, it is effective to substitute Al and Ga in {010} planes.

The p-factors of Al${}_3$Sc are plotted in Figure 10: (a) Ti${}_{\mathrm{Sc}}^{\{111\}}$ with Y${}_{\mathrm{Sc}}^{\{010\}}$(black dashed-dotted line with circles), Zr${}_{\mathrm{Sc}}^{\{010\}}$ (purple solid line with triangles) and Li${}_{\mathrm{Al}}^{\{010\}}$ (red solid line with squares); (b) Y${}_{\mathrm{Sc}}^{\{111\}}$ with Ti${}_{\mathrm{Sc}}^{\{010\}}$ (black dashed-dotted line with circles), Zr${}_{\mathrm{Sc}}^{\{010\}}$ (purple solid line with squares) and Li${}_{\mathrm{Al}}^{\{010\}}$ (red solid line with triangles); (c) Li${}_{\mathrm{Al}}^{\{111\}}$ with Ti${}_{\mathrm{Sc}}^{\{010\}}$ (black dashed-dotted line with circles), Y${}_{\mathrm{Sc}}^{\{010\}}$ (red solid line with triangles) and Zr${}_{\mathrm{Sc}}^{\{010\}}$ (purple solid line with squares); (d) Zr${}_{\mathrm{Sc}}^{\{111\}}$ with Ti${}_{\mathrm{Sc}}^{\{010\}}$ (black dashed-dotted line with circles), Y${}_{\mathrm{Sc}}^{\{010\}}$ (red solid line with triangles) and Li${}_{\mathrm{Sc}}^{\{010\}}$ (purple solid line with squares), respectively.

From Figure 10, it is easy to see that only Y${}_{\mathrm{Sc}}^{\{111\}}$ with Ti${}_{\mathrm{Sc}}^{\{010\}}$ and Zr${}_{\mathrm{Sc}}^{\{111\}}$ with Ti${}_{\mathrm{Sc}}^{\{010\}}$ will have the transition from normal to anomalous at a concentration of 25%. p-factors of Ti${}_{\mathrm{Sc}}^{\{111\}}$ with Zr${}_{\mathrm{Sc}}^{\{010\}}$, Li${}_{\mathrm{Al}}^{\{010\}}$ or Y${}_{\mathrm{Sc}}^{\{010\}}$, Y${}_{\mathrm{Sc}}^{\{111\}}$ with Zr${}_{\mathrm{Sc}}^{\{010\}}$ or Li${}_{\mathrm{Al}}^{\{010\}}$, Li${}_{\mathrm{Al}}^{\{111\}}$ with Ti${}_{\mathrm{Sc}}^{\{010\}}$, Zr${}_{\mathrm{Sc}}^{\{010\}}$ or Y${}_{\mathrm{Sc}}^{\{010\}}$ and Zr${}_{\mathrm{Sc}}^{\{111\}}$ with Li${}_{\mathrm{Al}}^{\{010\}}$ or Y${}_{\mathrm{Sc}}^{\{010\}}$ stay lower than $\sqrt{3}$, though some of them increase with concentrations. Among them, the p-factor of Li${}_{\mathrm{Al}}^{\{111\}}$ with Ti${}_{\mathrm{Sc}}^{\{010\}}$ is close to $\sqrt{3}$ at the concentration of 25%. However, it still failed to overcome the critical value. Comparing to Figure 7, only Ti${}_{\mathrm{Sc}}^{\{010\}}$ at the concentration of 25% with Zr, Y or no atoms substituted in {111} planes may have the opportunity to change the property of yield stress from normal to anomalous. This shows that Ti${}_{\mathrm{Sc}}^{\{010\}}$ has a great influence and makes the APB energies in {010} planes small enough to obtain a larger p-factor than $\sqrt{3}$. The only way to maintain the normal behavior is substituting Li or Ti (see Figure 7) in {111} planes.

Comparing to different concentrations, although it has influences on the p- factors, there are no obvious changes of the property of YSA varying from 6.25–12.5%. Only when the concentration is 25%, substitutional atoms can obviously change the property of yield stress between normal and anomalous such as Sc${}_{\mathrm{Ge}}^{\{111\}}$ with Fe${}_{\mathrm{Ni}}^{\{010\}}$, Ga${}_{\mathrm{Si}}^{\{111\}}$ with Sc${}_{\mathrm{Si}}^{\{010\}}$ and Y${}_{\mathrm{Sc}}^{\{111\}}$ with Ti${}_{\mathrm{Sc}}^{\{010\}}$.

5. Conclusions

The pressure-dependent elastic constants and APB energies of L1${}_2$ intermetallics (Ni${}_3$Ge, Ni${}_3$Si, Al${}_3$Sc, Ni${}_3$Al, Ni${}_3$Ga and Al${}_3$Ti) are calculated using first-principles methods. Based on the energy criterion p-factor considering anisotropy, the properties of YSA under different pressures are predicted. Pressure will not introduce transition between anomalous and normal yield stress behavior. All these intermetallics are anomalous, except Al${}_3$Sc. In order to obtain the transition in these intermetallics, the alloying elements are only substituted in Ni${}_3$Ge, Ni${}_3$Si, Al${}_3$Sc due to their p-factors being close to $\sqrt{3}$. When Sc, Al or Ga is substituted in {111} planes in Ni${}_3$Ge and Ni${}_3$Si with the concentration of 25%, the anomalous Ni${}_3$Ge and Ni${}_3$Si will become normal. Based on the obtained normal Ni${}_3$Ge and Ni${}_3$Si, substituting Al or Ga in {010} planes with the concentration of 25%, the normal Ni${}_3$Ge and Ni${}_3$Si will revert to anomalous. Ti${}_{\mathrm{Si}}^{\{111\}}$ may have the same effect as Al and Ga. However, normal Al${}_3$Sc will become anomalous when the concentration of Ti${}_{\mathrm{Sc}}^{\{010\}}$ is 25%. When Al in {111} planes is substituted by Li, the obtained anomalous Al${}_3$Sc will become normal. Therefore, transition between normal and anomalous yield stress behavior can be introduced by alloying atoms in L1${}_2$ intermetallics. Furthermore, when the plane concentration is lower than 6.25%, the transition will not occur. Until the concentration is larger or equal to 12.5%, the property may have the opportunity to be changed such as Sc${}_{\mathrm{Ge}}^{\{111\}}$, Al${}_{\mathrm{Si}}^{\{111\}}$ and Ga${}_{\mathrm{Si}}^{\{111\}}$. When the concentration is 25%, substitutional atoms will have much greater influences on the APB energies to change the property of yield stress between normal and anomalous more obviously, such as Sc${}_{\mathrm{Si}}^{\{111\}}$, Ti${}_{\mathrm{Sc}}^{\{010\}}$, Ga${}_{\mathrm{Si}}^{\{111\}}$ with Sc${}_{\mathrm{Si}}^{\{010\}}$ and Y${}_{\mathrm{Sc}}^{\{111\}}$ with Ti${}_{\mathrm{Sc}}^{\{010\}}$.