Layered Indium Selenide under High Pressure: A Review
Abstract
:1. Introduction
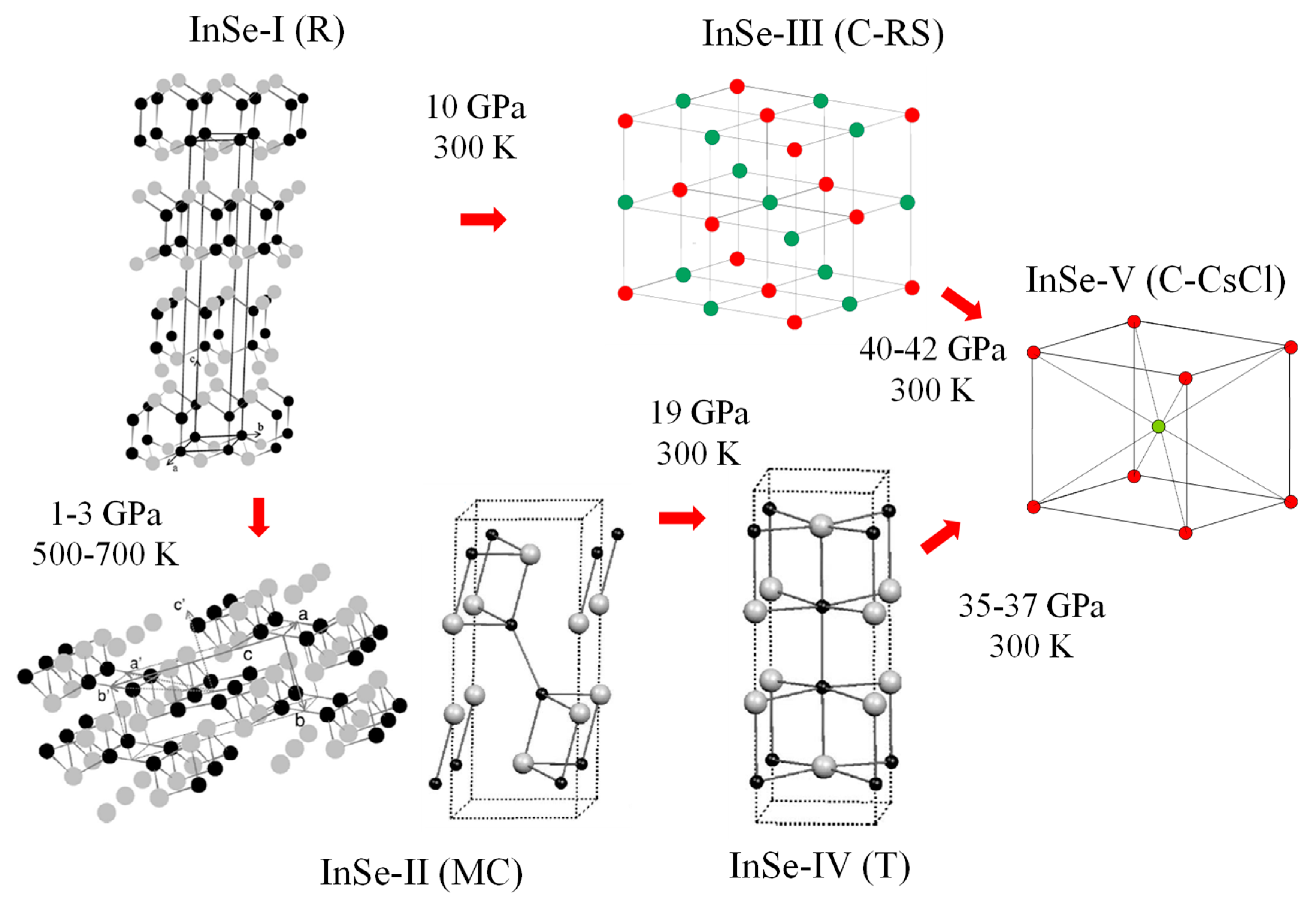
2. Crystal Structure, EOS, and Pressure-Temperature Phase Diagram of InSe
3. Electronic Structure under High Pressure
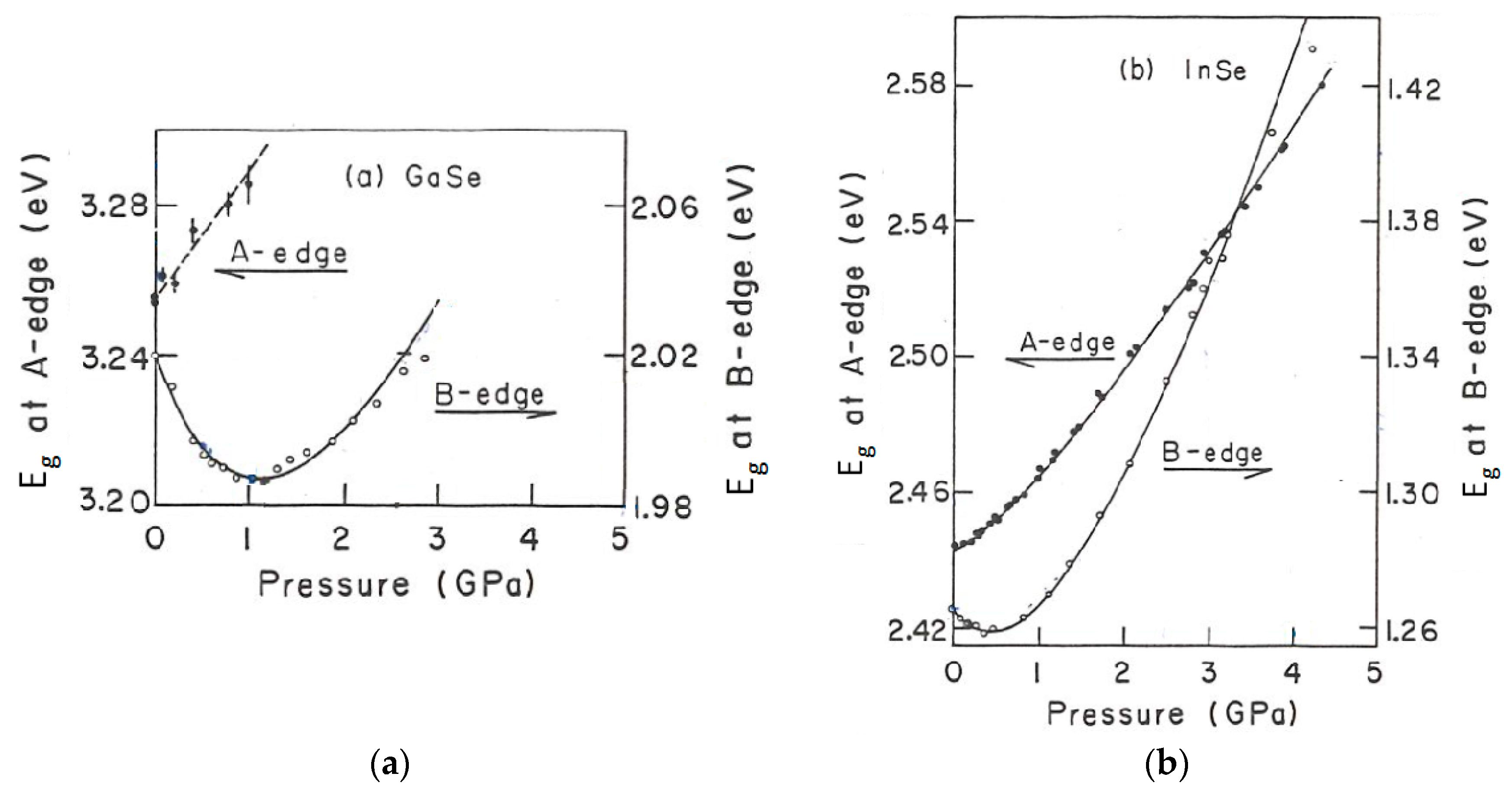
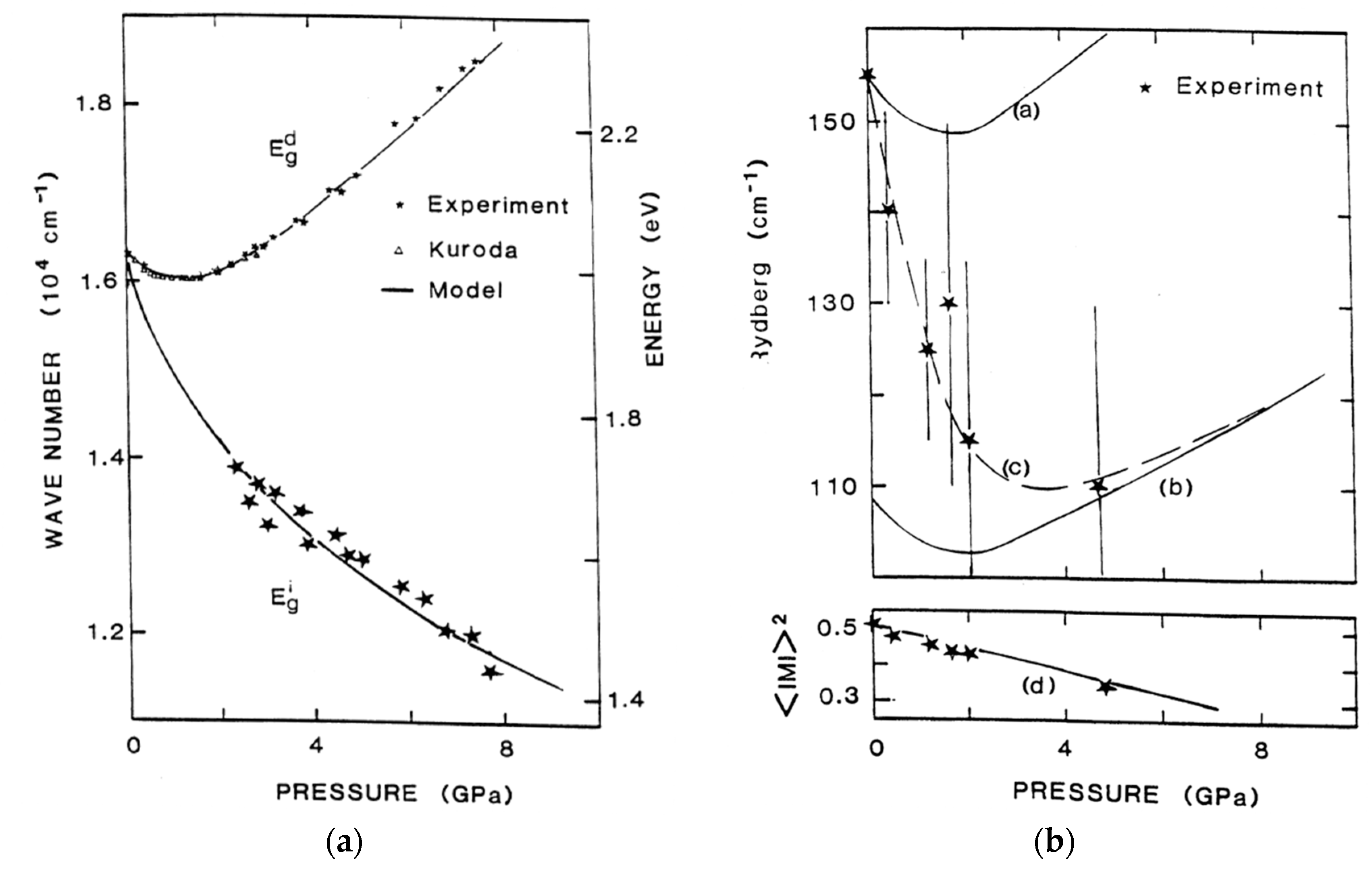
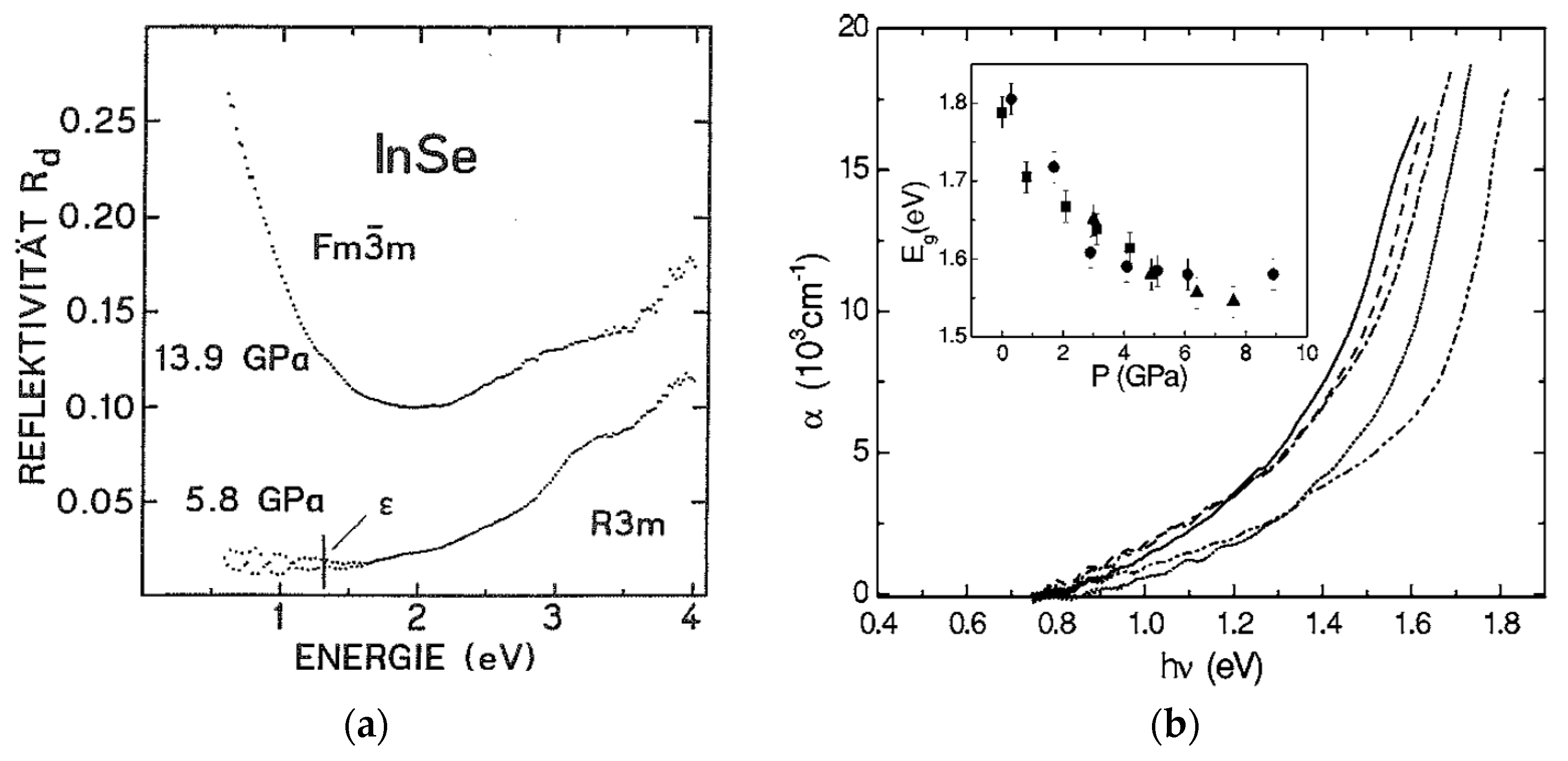
3.1. Optical Measurements and ab-Initio Band Structure Calculations
3.2. Electronic Structure of High Pressure Phases
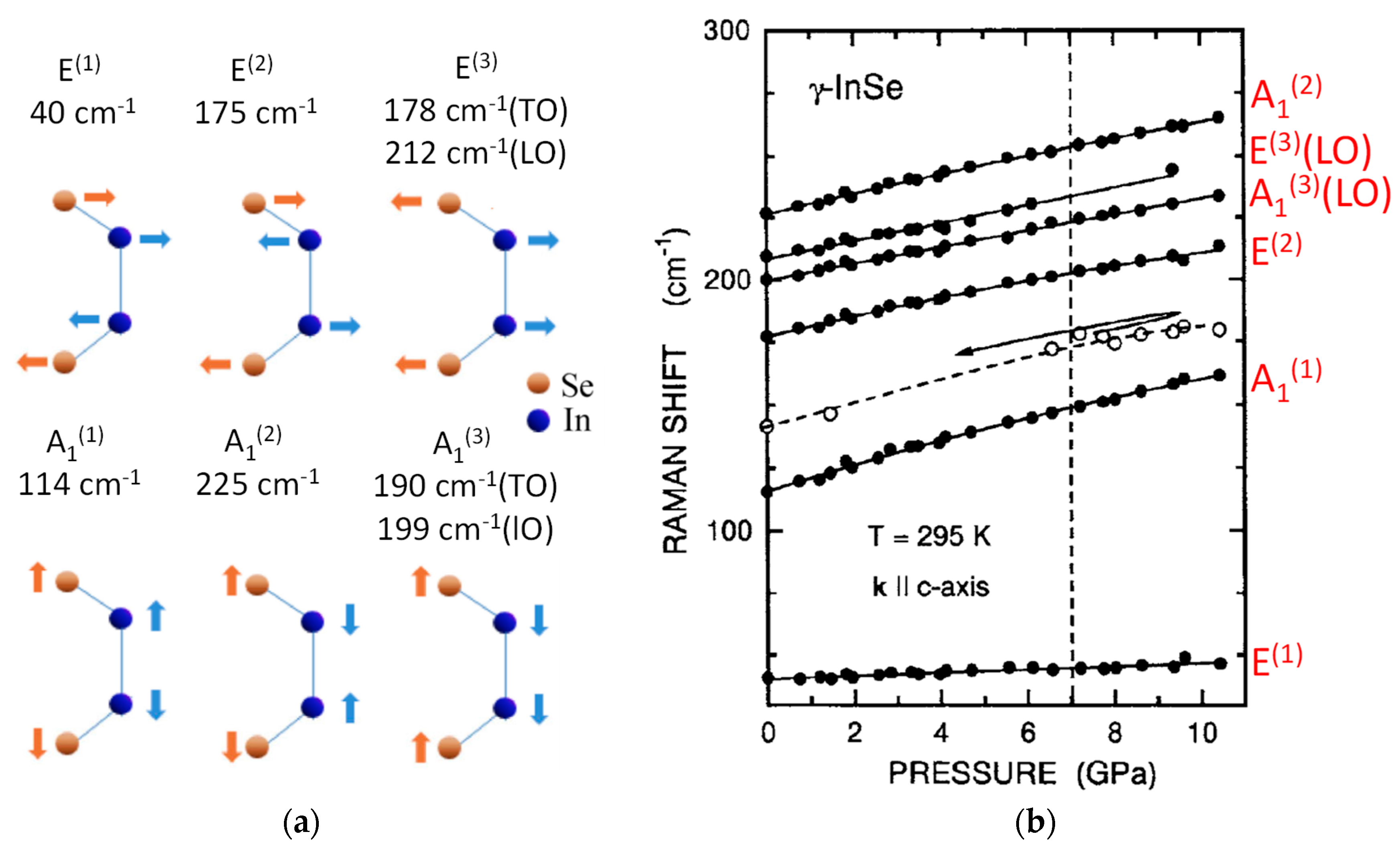
4. Lattice Dynamics under High Pressure
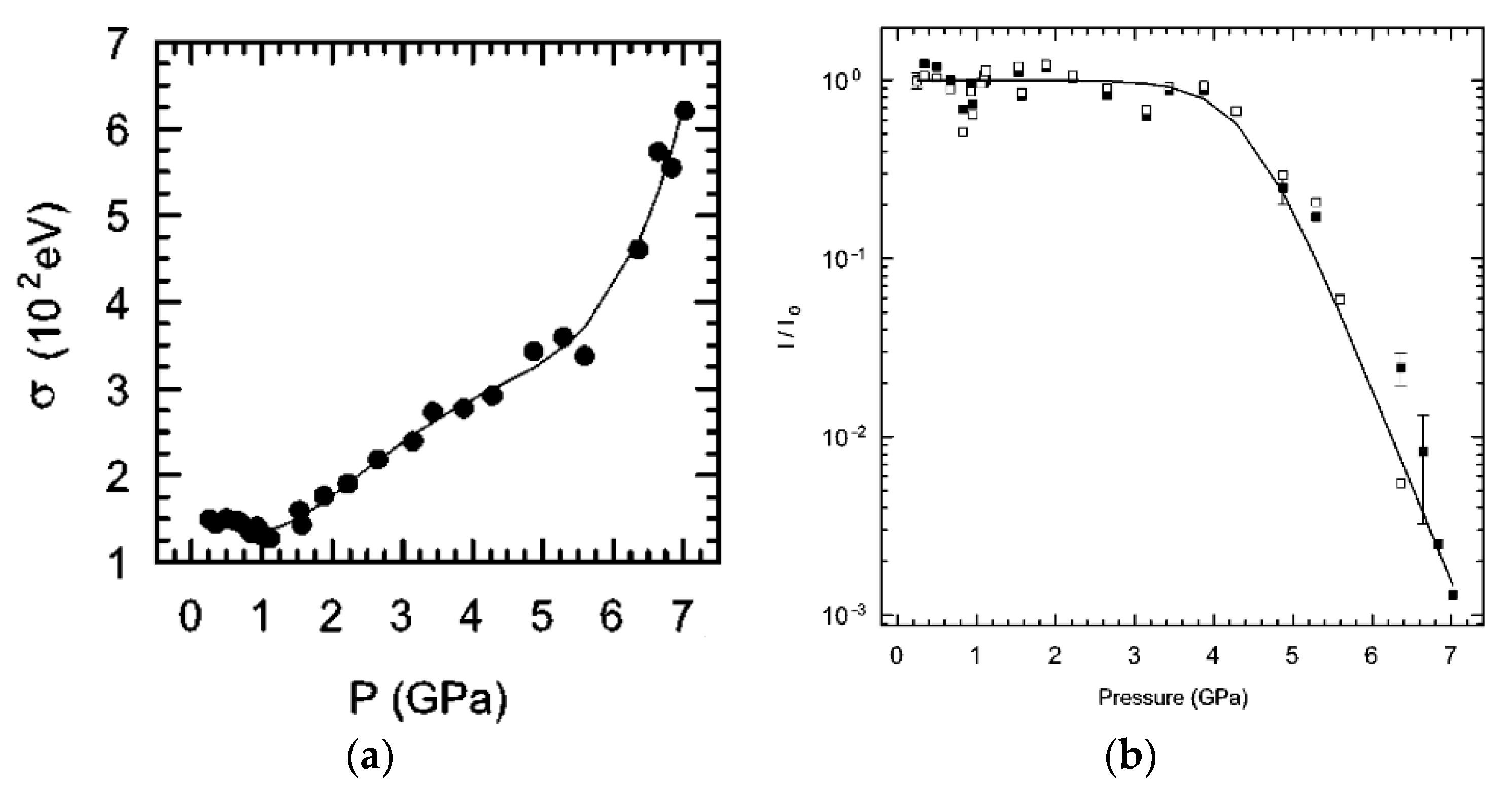
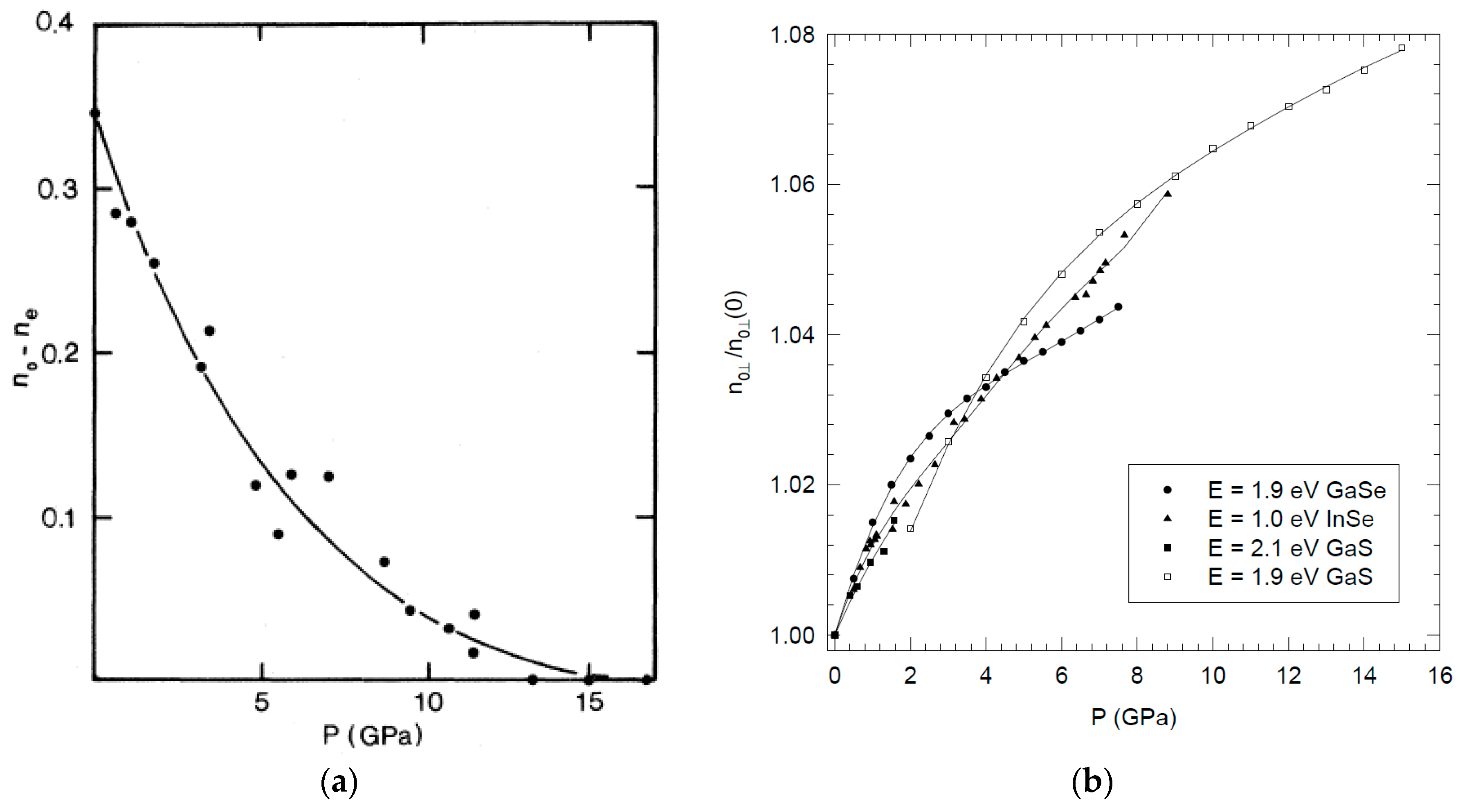
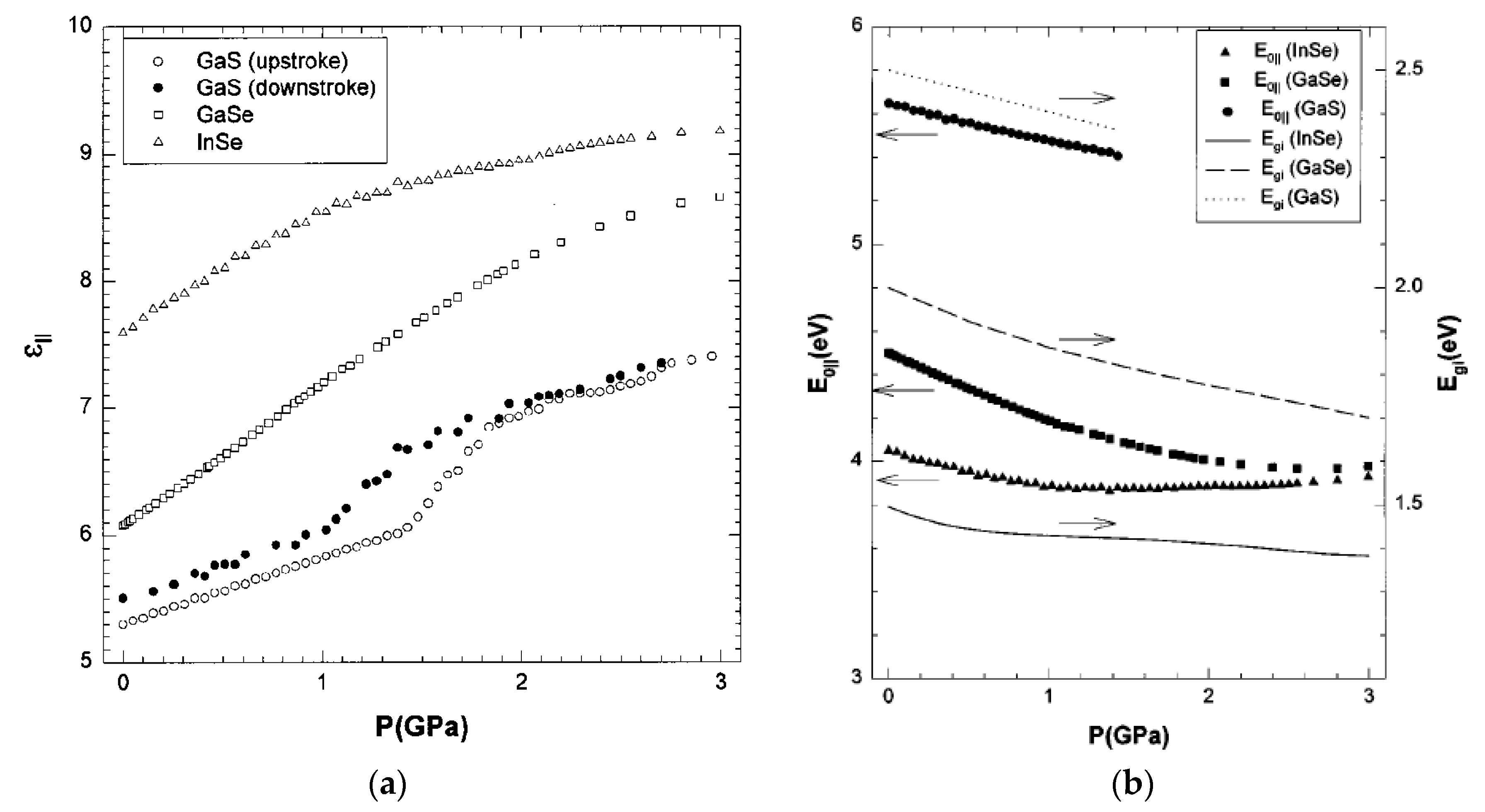
5. Dielectric Properties under High Pressure
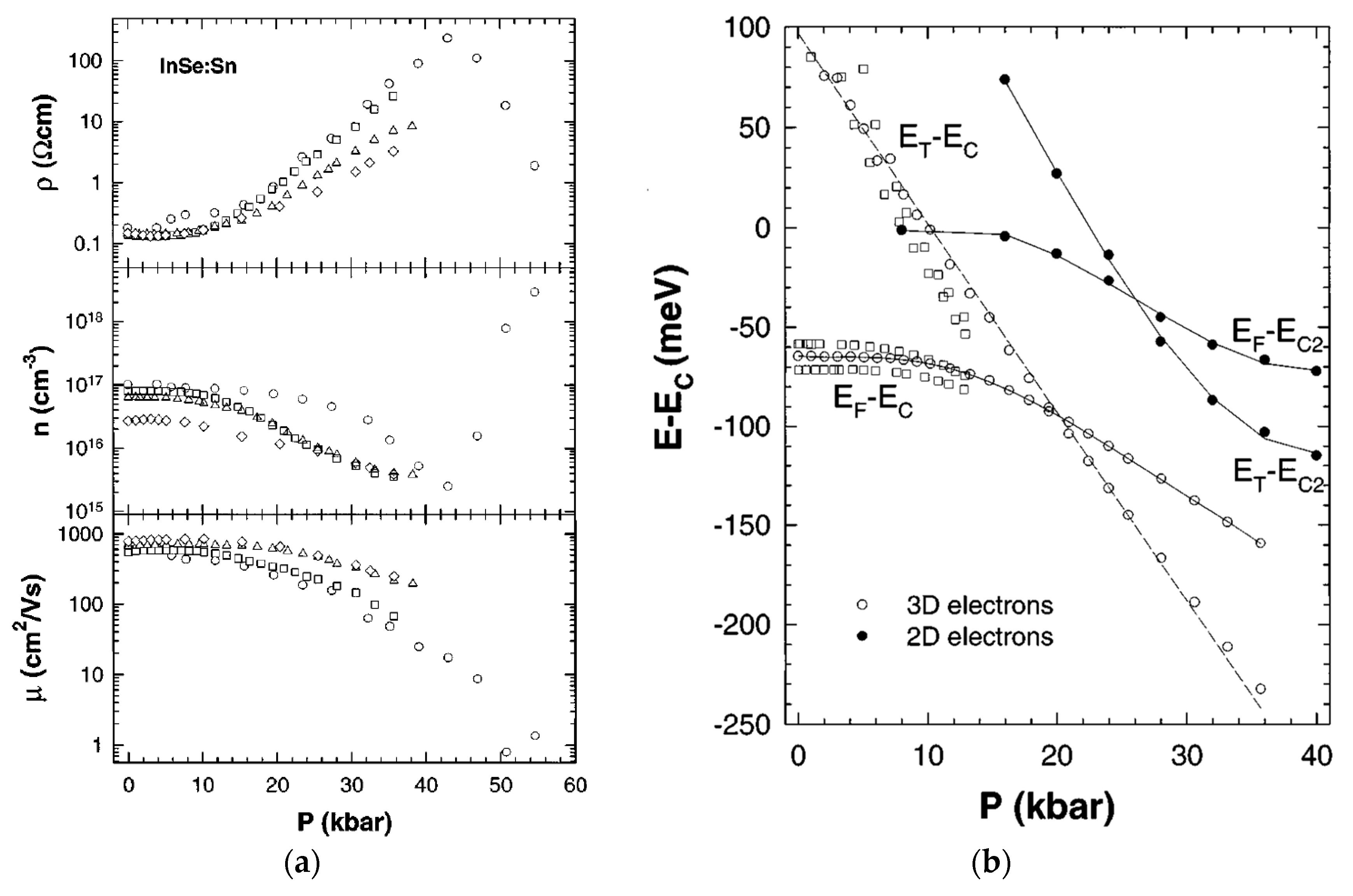
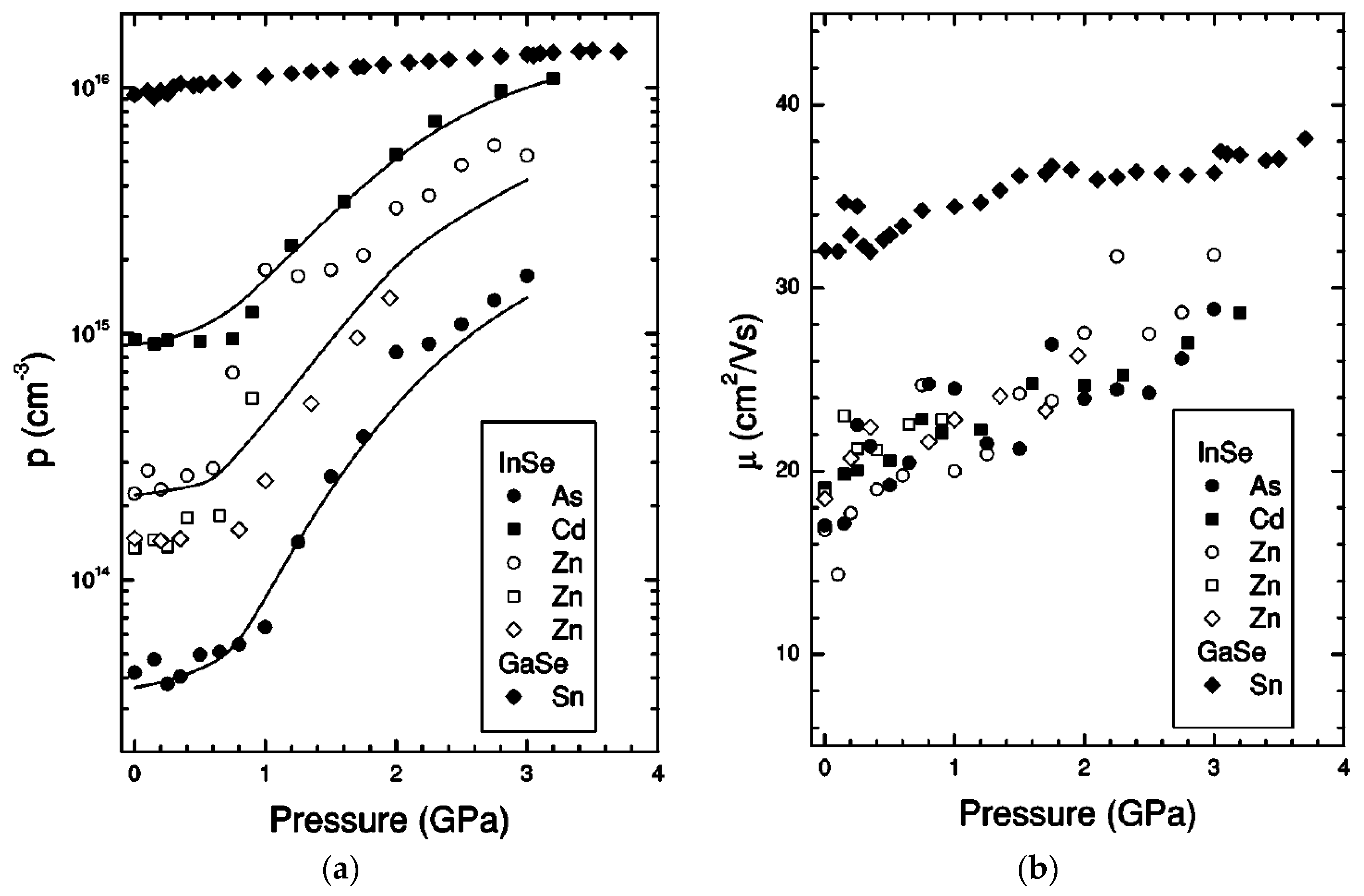
6. Electronic Transport Properties under High Pressure
7. Conclusions and Perspectives
Acknowledgments
Conflicts of Interest
References
- Damon, R.W.; Redington, R.W. Electrical and optical properties of indium selenide. Phys. Rev. 1954, 96, 1498–1500. [Google Scholar] [CrossRef]
- Andriyashik, M.V.; Sakhnovskit, M.Y.; Timofeev, V.B.; Yakimova, A.S. Optical transitions in the spectra of the fundamental absorption and reflection of InSe single crystals. Phys. Status Solidi (B) 1968, 28, 277–285. [Google Scholar] [CrossRef]
- Chevy, A.; Kuhn, A.; Martin, M.S. Large InSe monocrystals grown from a nonstoichiometric melt. J. Cryst. Growth 1977, 38, 118–122. [Google Scholar] [CrossRef]
- Chevy, A. Segregation of dopants in melt-grown indium selenide crystals. J. Appl. Phys. 1984, 56, 978–982. [Google Scholar] [CrossRef]
- Segura, A.; Guesdon, J.P.; Besson, J.M.; Chevy, A. Photoconductivity and photo-voltaic effect in indium selenide. J. Appl. Phys. 1983, 54, 876–888. [Google Scholar] [CrossRef]
- Martinez-Pastor, J.; Segura, A.; Valdes, J.L.; Chevy, A. Electrical and photovoltaic properties of indium-tin-oxide/p-InSe/Au solar cells. J. Appl. Phys. 1987, 62, 1477–1483. [Google Scholar] [CrossRef]
- Bringuier, E.; Bourdon, A.; Piccioli, N.; Chevy, A. Optical 2nd-harmonic generation in lossy media-application to GaSe and InSe. Phys. Rev. B 1994, 49, 16971–16982. [Google Scholar] [CrossRef]
- Koma, A. Van der Waals epitaxy: A new epitaxial-growth method for a highly lattice-mismatched system. Thin Solid Films 1992, 216, 72–76. [Google Scholar] [CrossRef]
- Sanchez-Royo, J.F.; Segura, A.; Lang, O.; Schaar, E.; Pettenkofer, C.; Jaegermann, W.; Roa, L.; Chevy, A. Optical and photovoltaic properties of indium selenide thin films prepared by van der Waals epitaxy. J. Appl. Phys. 2001, 90, 2818–2823. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Mudd, G.W.; Svatek, S.A.; Ren, T.; Patanè, A.; Makarovsky, O.; Eaves, L.; Beton, P.H.; Kovalyuk, Z.D.; Lashkarev, G.V.; Kudrynskyi, Z.R.; et al. Tuning the bandgap of exfoliated InSe nanosheets by quantum confinement. Adv. Mater. 2013, 25, 5714–5718. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Royo, J.F.; Muñoz-Matutano, G.; Brotons-Gisbert, M.; Martínez-Pastor, J.P.; Segura, A.; Cantarero, A.; Mata, R.; Canet-Ferrer, J.; Tobias, G.; Canadell, E.; et al. Gerardot, Electronic structure, optical properties, and lattice dynamics in atomically thin indium selenide flakes. Nano Res. 2014, 7, 1556–1568. [Google Scholar] [CrossRef]
- Sucharitakul, S.; Goble, N.J.; Kumar, U.R.; Sankar, R.; Bogorad, Z.A.; Chou, F.C.; Chen, Y.T.; Gao, X.P.A. Intrinsic Electron Mobility Exceeding 10 cm2/(V s) in Multilayer InSe FETs. Nano Lett. 2015, 15, 3815–3819. [Google Scholar] [CrossRef] [PubMed]
- Bandurin, D.A.; Tyurnina, A.V.; Yu, G.L.; Mishchenko, A.; Zolyomi, V.; Morozov, S.V.; Kumar, R.K.; Gorbachev, R.V.; Kudrynskyi, Z.R.; Pezzini, S.; et al. High electron mobility, quantum Hall effect and anomalous optical response in atomically thin InSe. Nat. Nanotechnol. 2017, 12, 223–227. [Google Scholar] [CrossRef] [PubMed]
- Paul, W. Band structure of intermetallic semiconductors from pressure experiments. J. Appl. Phys. Suppl. 1961, 32, 2092–2095. [Google Scholar] [CrossRef]
- Jayaraman, A. Diamond anvil cell and high-pressure physical investigations. Rev. Mod. Phys. 1983, 55, 65–108. [Google Scholar] [CrossRef]
- Forman, R.A.; Piermarini, G.J.; Barnett, J.D.; Block, S. Pressure Measurement Made by the Utilization of Ruby Sharp-Line Luminescence. Science 1972, 176, 284–285. [Google Scholar] [CrossRef] [PubMed]
- Barnett, J.D.; Block, S.; Piermarini, G.J. An Optical Fluorescence System for Quantitative Pressure Measurement in the Diamond-Anvil Cell. Rev. Sci. Instrum. 1973, 44, 1–9. [Google Scholar] [CrossRef]
- Goñi, A.R.; Syassen, K. Optical Properties of Semiconductors under pressure. In Semiconductors and Semimetals; Suskiy, T., Paul, W., Eds.; Academic Press: New York, NY, USA, 1998; Volume 54, pp. 247–425. [Google Scholar]
- Nelmes, R.J.; McMahon, M.I. Structural transitions in the group IV, III_V and II-VI semiconsuctors under pressure. In Semiconductors and Semimetals; Suskiy, T., Paul, W., Eds.; Academic Press: New York, NY, USA, 1998; Volume 54, pp. 145–246. [Google Scholar]
- Mujica, A.; Rubio, A.; Munoz, A.; Needs, R.J. High-pressure phases of group-IV, III–V, and II–VI compounds. Rev. Mod. Phys. 2003, 75, 863–912. [Google Scholar] [CrossRef]
- Likforman, A.; Carre, D.; Etienne, J.; Bachet, B. Crystal-structure of indium monoselenide (InSe). Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1975, 31, 1252–1254. [Google Scholar] [CrossRef]
- Polian, A.; Kunc, K.; Kuhn, A. Low-frequency lattice-vibrations of δ-GaSe compared to epsilon-polytypes and gamma-polytypes. Solid State Commun. 1976, 19, 1079–1082. [Google Scholar] [CrossRef]
- Gatulle, M.; Fischer, M.; Chevy, A. Elastic-constants of the layered compounds GaS, GaSe, InSe, and their pressure-dependence. 1. Experimental part. Phys. Status Solidi (B) 1983, 119, 327–336. [Google Scholar] [CrossRef]
- Kuroda, N.; Ueno, O.; Nishina, Y. Supernonlinear shifts of optical-energy gaps in InSe and GaSe under hydrostatic-pressure. J. Phys. Soc. Jpn. 1986, 55, 581–589. [Google Scholar] [CrossRef]
- Murnaghan, F.D. The compressibility of media under extreme pressures. Proc. Natl. Acad. Sci. USA 1944, 30, 244–247. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, U. Zustandgleichungen unf Phasenumwaldungen von Halbleitenden Verbindungen unter Hohem Druck: Rötgenpulveruntersuchungen und Optische Spektroskopie, Ph.D. Thesis, Technishen Hochschule Darmstadt, Darmstadt, Germany, 1992. [Google Scholar]
- Schwarz, U.; Goñi, A.R.; Syassen, K.; Cantarero, A.; Chevy, A. Structural and optical properties of InSe under pressure. High Press. Res. 1991, 8, 396–398. [Google Scholar] [CrossRef]
- Pellicer-Porres, J.; Machado-Charry, E.; Segura, A.; Gilliland, S.; Canadell, E.; Ordejon, P.; Polian, A.; Munsch, P.; Chevy, A.; Guignot, N. GaS and InSe equations of state from single crystal diffraction. Phys. Status Solidi (B) 2007, 244, 169–173. [Google Scholar] [CrossRef]
- Errandonea, D.; Martínez-García, D.; Segura, A.; Haines, J.; Machado-Charry, E.; Canadell, E.; Chervin, J.C.; Chevy, A. High-pressure electronic structure and phase transitions in monoclinic InSe: X-ray diffraction, Raman spectroscopy, and density functional theory. Phys. Rev. B 2008, 77, 045208. [Google Scholar] [CrossRef]
- Pellicer-Porres, J.; Segura, A.; Muñoz, V.; San Miguel, A. High-pressure x-ray absorption study of InSe. Phys. Rev. B. 1999, 50, 3757–5763. [Google Scholar] [CrossRef]
- Schwarz, U.; Olguin, D.; Cantarero, A.; Hanfland, M.; Syassen, K. Effect of pressure on the structural properties and electronic band structure of GaSe. Phys. Status Solidi (B) 2007, 244, 244–255. [Google Scholar] [CrossRef]
- Schwarz, U.; Syassen, K.; Kniep, R. Structural phase-transition of GaTe at high-pressure. J. Alloy. Compd. 1995, 224, 212–216. [Google Scholar] [CrossRef]
- Takumi, M.; Hirata, A.; Ueda, T.; Koshio, Y.; Nishimura, H.; Nagata, K. Structural Phase Transitions of Ga2Se3 and GaSe under High Pressure. Phys. Status Solidi (B) 2001, 223, 423–426. [Google Scholar] [CrossRef]
- Pellicer-Porres, J.; Segura, A.; Munoz, V.; San Miguel, A. High-pressure X-ray absorption study of GaTe including polarization. Phys. Rev. B 2000, 61, 125–131. [Google Scholar] [CrossRef]
- Pellicer-Porres, J.; Segura, A.; Ferrer, C.; Munoz, V.; San Miguel, A.; Polian, A.; Itie, J.P.; Gauthier, M.; Pascarelli, S. High-pressure X-ray-absorption study of GaSe. Phys. Rev. B 2002, 65, 174103. [Google Scholar] [CrossRef]
- Segura, A.; Manjón, F.J.; Errandonea, D.; Pellicer-Porres, J.; Muñoz, V.; Tobias, G.; Ordejón, P.; Canadell, E.; San Miguel, A.; Sánchez-Portal, D. Specific features of the electronic structure of III−VI layered semiconductors: Recent results on structural and optical measurements under pressure and electronic structure calculations. Phys. Status Solidi (B) 2003, 235, 267–276. [Google Scholar] [CrossRef]
- Vezzoli, G.C. Synthesis and properties of a pressure-induced and temperature-induced phase of indium selenide. Mater. Res. Bull. 1971, 6, 1201–1204. [Google Scholar] [CrossRef]
- Iwasaki, H.; Watanabe, Y.; Kuroda, N.; Nishina, Y. Pressure-induced layer-nonlayer transformation in InSe. Physica B C 1981, 105B, 314–318. [Google Scholar] [CrossRef]
- Kuroda, N.; Nishina, Y.; Iwasaki, H.; Watanabe, Y. Raman scatterings of layered and non-layered phases of InSe. Solid State Commun. 1981, 38, 139–142. [Google Scholar] [CrossRef]
- Errandonea, D.; Martínez-García, D.; Segura, A.; Chevy, A.; Tobias, G.; Canadell, E.; Ordejon, P. High-pressure, high-temperature phase diagram of InSe: A comprehensive study of the electronic and structural properties of the monoclinic phase of InSe under high pressure. Phys. Rev. B. 2006, 73, 235202. [Google Scholar] [CrossRef]
- Ferlat, G.; Martinez-Garcia, D.; San Miguel, A.; Aouizerat, A.; Muñoz-Sanjosé, V. High pressure-high temperature phase diagram of InSe. High Press. Res. 2004, 4, 111–116. [Google Scholar] [CrossRef]
- Besson, J.M.; Nelmes, R.J.; Hamel, G.; Loveday, J.S.; Weill, G.; Hull, S. Neutron Powder Diffraction above 10-GPa. Physica B 1992, 180, 907–910. [Google Scholar] [CrossRef]
- Segura, A.; Pellicer-Porres, J.; Martinez-García, D.; Rodríguez-Hernández, P.; Muñoz, A.; Itié, J.P. CsCl-InSe as End-Phase of Metastable Rock-Salt and Tetragonal InSe, Book of Abstracts of the Joint AIRAPT-25 and EHPRG-53 (Abstract P2-67). In Proceedings of the Joint AIRAPT-25 and EHPRG-53, Madrid, Spain, 30 August–4 September 2015. [Google Scholar]
- Camassel, J.; Merle, P.; Mathieu, H.; Chevy, A. Excitonic absorption-edge of indium selenide. Phys. Rev. B 1978, 17, 4718–4725. [Google Scholar] [CrossRef]
- Le Toullec, R.; Piccioli, N.; Chervin, J.C. Optical properties of the band-edge exciton in GaSe crystals at 10 K. Phys. Rev. B 1980, 22, 6162–6170. [Google Scholar] [CrossRef]
- Mejatty, M.; Segura, A.; Letoullec, R.; Besson, J.M.; Chevy, A.; Fair, H. Optical absorption edge of GaS under hydrostatic pressure. J. Phys. Chem. Solids 1978, 39, 25–28. [Google Scholar] [CrossRef]
- Besson, J.M.; Jain, K.P.; Kuhn, A. Optical-absorption edge in GaSe under hydrostatic-pressure. Phys. Rev. Lett. 1974, 32, 936–939. [Google Scholar] [CrossRef]
- Segura, A. Phototransport Dans InSe: Application à La Conversion Photovoltaique de L’énergie Solaire. Thèse de Trosième Cycle, Univerité Pierre et Marie Curie, Paris, France, 1977. [Google Scholar]
- Panfilov, V.V.; Subbotin, S.I.; Vereshchagin, L.F.; Ivanov, I.I.; Molchanova, R.T. Exciton absorption, band-structure, and phase-transformation of GaSe under pressure. Phys. Status Solidi (B) 1975, 72, 823–831. [Google Scholar] [CrossRef]
- Bourdon, A.; Chevy, A.; Besson, L. Band Structure of Indium Selenide: Physics of Semiconductors 1978. In Proceedings of the 14th International Conference on the Physics of Semiconductors, Edinburgh, Scotland, 4–8 September 1978; Wilson, H., Ed.; Institute of Physics and Physical Society: London, UK, 1979; pp. 1371–1374. [Google Scholar]
- Gomes da Costa, P.; Dandrea, R.G.; Wallis, R.F.; Balkanski, M. First principles of the electronic structure study of γ-InSe and β-InSe. Phys. Rev. B 1993, 48, 14135–14141. [Google Scholar] [CrossRef]
- Kress-Rogers, E.; Nicholas, R.J.; Portal, J.C.; Chevy, A. Cyclotron-resonance studies on bulk and two-dimensional conduction electrons in InSe. Solid State Commun. 1982, 44, 379–383. [Google Scholar] [CrossRef]
- Ferrer-Roca, C.; Segura, A.; Andres, M.V.; Pellicer, J.; Munoz, V. Investigation of nitrogen-related acceptor centers in indium selenide by means of photoluminescence: Determination of the hole effective mass. Phys. Rev. B 1997, 55, 6981–6987. [Google Scholar] [CrossRef]
- Kane, E.O. Band structure of indium antimonide. J. Phys. Chem. Solids 1957, 1, 249–261. [Google Scholar] [CrossRef]
- Piccioli, N.; Le Toullec, R.; Piccioli, N.; Chervin, J.C. Constantes optiques de InSe entre 10,500 cm−1 (1.30 eV) et 22,500 cm−1 (2.78 eV). J. Physique 1981, 42, 1129–1135. [Google Scholar] [CrossRef]
- Gauthier, M.; Polian, A.; Besson, J.M.; Chevy, A. Optical-properties of gallium selenide under high-pressure. Phys. Rev. B 1989, 40, 3837–3854. [Google Scholar] [CrossRef]
- Elliott, R.J. Intensity of optical absorption by excitons. Phys. Rev. 1957, 108. [Google Scholar] [CrossRef]
- Toyozawa, Y. Theory of line-shapes of the exciton absorption bands. Prog. Theor. Phys. 1958, 20, 53–81. [Google Scholar] [CrossRef]
- Piccioli, N.; Letoullec, R. Exciton-phonon interaction in GaDe. J. Phys. 1989, 50, 3395–3406. [Google Scholar] [CrossRef]
- Goi, A.R.; Cantarero, A.; Schwarz, U.; Syassen, K.; Chevy, A. Low temperature exciton absorption in InSe under pressure. Phys. Rev. B 1992, 45, 4221–4226. [Google Scholar] [CrossRef]
- Ulrich, C.; Olguin, D.; Cantarero, A.; Goñi, A.R.; Syassen, K.; Chevy, A. Effect of pressure on direct optical transitions of gamma-InSe. Phys. Status Solidi (B) 2000, 221, 777–787. [Google Scholar] [CrossRef]
- Errandonea, D.; Manjon, F.J.; Pellicer, J.; Segura, A.; Munoz, V. Direct to indirect crossover in III–VI layered compounds and alloys under pressure. Phys. Status Solidi (B) 1999, 211, 33–38. [Google Scholar] [CrossRef]
- Manjón, F.J.; Errandonea, D.; Segura, A.; Muñoz, V.; Tobías, G.; Ordejón, P.; Canadell, E. Experimental and theoretical study of band structure of InSe and In1−xGaxSe (x < 0.2) under high pressure: Direct to indirect crossovers. Phys. Rev. B 2001, 63, 125330. [Google Scholar] [CrossRef]
- Ferlat, G.; Xu, H.; Timoshevskii, V.; Blasé, X. Ab initio studies of structural and electronic properties of solid indium selenide under pressure. Phys. Rev. B 2002, 66, 085210. [Google Scholar] [CrossRef]
- Olguín, D.; Cantarero, A.; Ulrich, C.; Syassen, K. Effect of pressure on structural properties and energy band gaps of γ-InSe. Phys. Status Solidi (B) 2003, 235, 456–463. [Google Scholar] [CrossRef]
- Manjón, F.J.; Segura, A.; Muñoz-Sanjosé, V.; Tobías, G.; Ordejón, P.; Canadell, E. Band structure of indium selenide investigated by intrinsic photoluminescence under high pressure. Phys. Rev. B 2004, 70, 125201. [Google Scholar] [CrossRef]
- Millot, M.; Broto, J.M.; George, S.; Gonzalez, J.; Segura, A. High pressure and high magnetic field behavior of free and donor-bound-exciton photoluminescence in InSe. Phys. Status Solidi (B) 2009, 246, 532–535. [Google Scholar] [CrossRef]
- Millot, M.; Broto, J.M.; George, S.; Gonzalez, J.; Segura, A. Electronic structure of indium selenide probed by magneto-absorption spectroscopy under high pressure. Phys. Rev. B 2010, 81, 205211. [Google Scholar] [CrossRef]
- Ghalouci, L.; Taibi, F.; Ghalouci, F.; Bensaid, M.O. Ab initio investigation into structural, mechanical and electronic properties of low pressure, high pressure and high pressure-high temperature phases of Indium Selenide. Comput. Mater. Sci. 2016, 124, 62–77. [Google Scholar] [CrossRef]
- Polian, A.; Chervin, J.C.; Besson, J.M. Phonon modes and stability of GaS up to 200 kilobars. Phys. Rev. B 1980, 22, 3049–3058. [Google Scholar] [CrossRef]
- Kuroda, N.; Ueno, O.; Nishina, Y. Lattice-dynamic and photoelastic properties of GaSe under high-pressures studied by raman-scattering and electronic susceptibility. Phys. Rev. B 1987, 35, 3860–3870. [Google Scholar] [CrossRef]
- Allahverdi, K.; Babaev, S.; Ellialtioǧlu, Ş.; Ismailov, A. Raman scattering in layer indium selenide under pressure. Solid State Commun. 1993, 87, 675–678. [Google Scholar] [CrossRef]
- Allakhverdiev, K.; Ellialtioglu, S.; Ismailov, Z. Raman scattering and Hall effect in layer InSe under pressure. High Press. Res. 1994, 13, 121–125. [Google Scholar] [CrossRef]
- Ulrich, C.; Mroginski, M.A.; Goñi, A.; Cantarero, A.; Schwarz, U.; Muñoz, V.; Syassen, K. Vibrational Properties of InSe under Pressure: Experiment and Theory. Phys. Status Solidi (B) 1996, 198, 121–127. [Google Scholar] [CrossRef]
- Choi, I.H.; Yu, P.Y. Pressure dependence of phonons and excitons in InSe films prepared by metal-organic chemical vapor deposition. Phys. Rev. B. 2003, 68, 165339. [Google Scholar] [CrossRef]
- Gauthier, M. Pressure-induced charge transfer. High Press. Res. 1992, 9330–9342. [Google Scholar] [CrossRef]
- Rushchanskii, K.Z. The influence of hydrostatic pressure on the static and dynamic properties of an InSe crystal: A first-principles study. Phys. Solid State 2006, 46, 179–187. [Google Scholar] [CrossRef]
- Polian, A.; Besson, J.M.; Grimsditch, M.; Vogt, H. Elastic properties of GaS under high-pressure by brillouin-scattering. Phys. Rev. B 1982, 25, 2767–2775. [Google Scholar] [CrossRef]
- Manjón, F.J. Estudio de la estructura de bandas del seleniuro de indio mediante medidas ópticas bajo presión hidrostática. Tesis Doctoral, Universitat de València, Valencia, Spain, 1999. [Google Scholar]
- Manjon, F.J.; Van der Vijver, Y.; Segura, A.; Muñoz, V. Pressure dependence of the refractive index in InSe. Semicond. Sci. Technol. 2000, 15, 806–812. [Google Scholar] [CrossRef]
- Van Vechten, J.A. Quantum dielectric theory of electronegativity in covalent systems. I. electronic dielectric constant Phys. Rev. 1969, 182, 891–905. [Google Scholar] [CrossRef]
- Phillips, J.C. Ionicity of chemical bond in crystals. Rev. Mod. Phys. 1970, 42, 317–356. [Google Scholar] [CrossRef]
- Penn, D.R. Wave-number-dependent dielectric function of semiconductors. Phys. Rev. 1962, 128, 2093–2097. [Google Scholar] [CrossRef]
- Segura, A.; Chevy, A. Large increase of the low-frequency dielectric-constant of gallium sulfide under hydrostatic-pressure. Phys. Rev. 1994, 49, 4601–4604. [Google Scholar] [CrossRef]
- Errandonea, D.; Segura, A.; Munoz, V.; Chevy, A. Pressure dependence of the low-frequency dielectric constant in III-VI semiconductors. Phys. Status Solidi (B) 1999, 211, 201–206. [Google Scholar] [CrossRef]
- Errandonea, D.; Segura, A.; Muñoz, V.; Chevy, A. Effects of pressure and temperature on the dielectric constant of GaS, GaSe, and InSe: Role of the electronic contribution. Phys. Rev. B 1999, 60, 15866–15874. [Google Scholar] [CrossRef]
- D’Amour, H.; Holzapfel, W.B.; Polian, A.; Chevy, A. Crystal-structure of a new high-pressure polymorph of gas. Solid State Commun. 1982, 44, 853–855. [Google Scholar] [CrossRef]
- Errandonea, D.; Segura, A.; Sanchez-Royo, J.F.; Muñoz, V.; Ulrich, C.; Grima, P.; Chevy, A. Effects of Conduction Band Structure and Dimensionality of the Electron Gas on Transport Properties of InSe under Pressure. Phys. Status Solidi (B) 1996, 198, 129–134. [Google Scholar] [CrossRef]
- Errandonea, D.; Segura, A.; Sanchez-Royo, J.F.; Muñoz, V.; Grima, P.; Chevy, A.; Ulrich, C. Investigation of conduction-band structure, electron-scattering mechanisms, and phase transitions in indium selenide by means of transport measurements under pressure. Phys. Rev. B 1997, 55, 16217–16225. [Google Scholar] [CrossRef]
- Errandonea, D.; Segura, A.; Manjón, F.J.; Chevy, A. Transport measurements in InSe under high pressure and high temperature: Shallow-to-deep donor transformation of Sn related donor impurities. Semicond. Sci. Technol. 2003, 18, 241–246. [Google Scholar] [CrossRef]
- Manjon, F.J.; Errandonea, D.; Segura, A.; Chervin, J.C.; Muñoz, V. Precursor effects of the rhombohedral-to-cubic phase transition in indium selenide. High Press. Res. 2002, 22, 261. [Google Scholar] [CrossRef]
- Errandonea, D.; Sanchez-Royo, J.F.; Segura, A.; Chevy, A.; Roa, L. Investigation of acceptor levels and hole scattering mechanisms in p-gallium selenide by means of transport measurement under pressure. High Press. Res. 1998, 16, 13–26. [Google Scholar] [CrossRef]
- Errandonea, D.; Segura, A.; Manjón, F.J.; Chevy, A.; Machado, E.; Tobias, G.; Ordejón, P.; Canadell, E. Crystal symmetry and pressure effects on the valence band structure of γ-InSe and γ-GaSe: Transport measurements and electronic structure calculations. Phys. Rev. B 2005, 71, 125206. [Google Scholar] [CrossRef]
- Errandonea, D.; Martínez-García, D.; Segura, A.; Ruiz-Fuertes, J.; Lacomba-Perales, R.; Fages, V.; Chevy, A.; Roa, L.; Muñoz-San José, V. High-pressure electrical transport measurements on p-type GaSe and InSe. High Press. Res. 2006, 26, 513–518. [Google Scholar] [CrossRef]
- Segura, A.; Errandonea, D.; Martínez-García, D.; Manjón, F.J.; Chevy, A.; Tobias, G.; Ordejón, P.; Canadell, E. Transport measurements under pressure in III–IV layered semiconductors. Phys. Status Solidi (B) 2007, 244, 162–168. [Google Scholar] [CrossRef]
- Rydberg, H.; Dion, M.; Jacobson, N.; Schroder, E.; Hyldgaard, P.; Simak, S.I.; Langreth, D.C.; Lundqvist, B.I. Van der Waals density functional for layered structures. Phys. Rev. Lett. 2003, 91, 126402. [Google Scholar] [CrossRef] [PubMed]
- Cazorla, C.; Boronat, J. Simulation and understanding of atomic and molecular quantum crystals. Rev. Mod. Phys. 2017, 89, 035003. [Google Scholar] [CrossRef]
- Tawfik, S.A.; Gould, T.; Stampfl, C.; Ford, M.J. Evaluation of van der Waals density functionals for layered materials. Phys. Rev. Mater. 2018, 2, 034005. [Google Scholar] [CrossRef]
- Martinez-Pastor, J.; Segura, A.; Julien, C.; Chevy, A. Shallow-donor impurities in indium selenide investigated by means of far-infrared spectroscopy. Phys. Rev. B 1992, 46, 4607–4616. [Google Scholar] [CrossRef]











| Crystal | V0 (Å3) | B0 (GPa) | B0′ | (GPa−1) | (GPa−1) | |
|---|---|---|---|---|---|---|
| γ-InSe 1 | - | 35(10) | - | 0.0033(19) | 0.022(7) | 6.7 |
| γ-InSe 2 | - | - | 10.8(8) | 0.0033(19) 3 | - | - |
| γ-InSe 4 | 350.8 | 36(10) | 4.05(30) | 0.005(1) 5 | 0.014(2) 5 | 2.8 |
| γ-InSe 6 | 350.4 | 24(3) | 8.6(8) | 0.0063(6) | 0.016(2) | 2.5 |
| RS-InSe 4 | 190.5 | 51.2 | 4 | - | - | - |
| MC(T)-InSe 7 | 207 | 44 | 5.4 | - | - | - |
| Title | ||||
|---|---|---|---|---|
| Theory 1 | 0.18 | 0.11 | 5 | 0.11 |
| Theory 2 | 0.12 | 0.03 | 3.1 | 0.03 |
| Experiment 3,4 | 0.141(2) | 0.081(9) | 0.73(9) | 0.17(3) |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Segura, A. Layered Indium Selenide under High Pressure: A Review. Crystals 2018, 8, 206. https://doi.org/10.3390/cryst8050206
Segura A. Layered Indium Selenide under High Pressure: A Review. Crystals. 2018; 8(5):206. https://doi.org/10.3390/cryst8050206
Chicago/Turabian StyleSegura, Alfredo. 2018. "Layered Indium Selenide under High Pressure: A Review" Crystals 8, no. 5: 206. https://doi.org/10.3390/cryst8050206
APA StyleSegura, A. (2018). Layered Indium Selenide under High Pressure: A Review. Crystals, 8(5), 206. https://doi.org/10.3390/cryst8050206





