Lu5Pd4Ge8 and Lu3Pd4Ge4: Two More Germanides among Polar Intermetallics
Abstract
:1. Introduction
2. Experimental
2.1. Synthesis and SEM-EDXS Characterization
- (1)
- 25 °C → (10 °C/min) → 950 °C (1 h) → (−0.2 °C/min) → 600 °C (168 h) → (−0.5 °C/min) → 300 °C → furnace switched off
- (2)
- 25 °C → (10 °C/min) → 1150 °C (1 h) → (−0.2 °C/min) → 300 °C → furnace switched off
2.2. X-ray Diffraction (XRD) Measurements on Single Crystals and Powder Samples
2.3. Computational Details
3. Results and Discussion
3.1. Results of SEM-EDXS Characterization
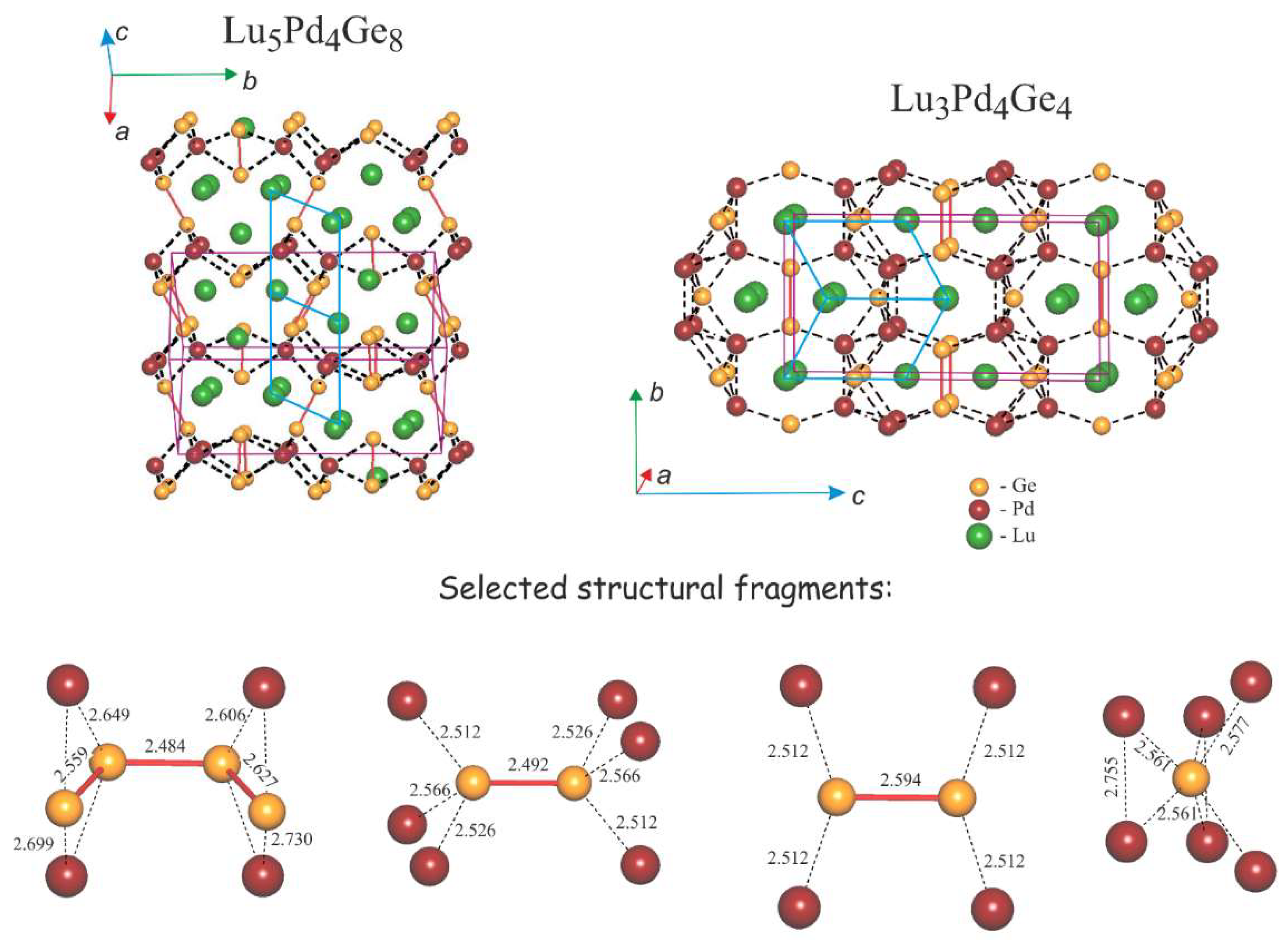
3.2. Crystal Structures of Lu5Pd4Ge8 and Lu3Pd4Ge4
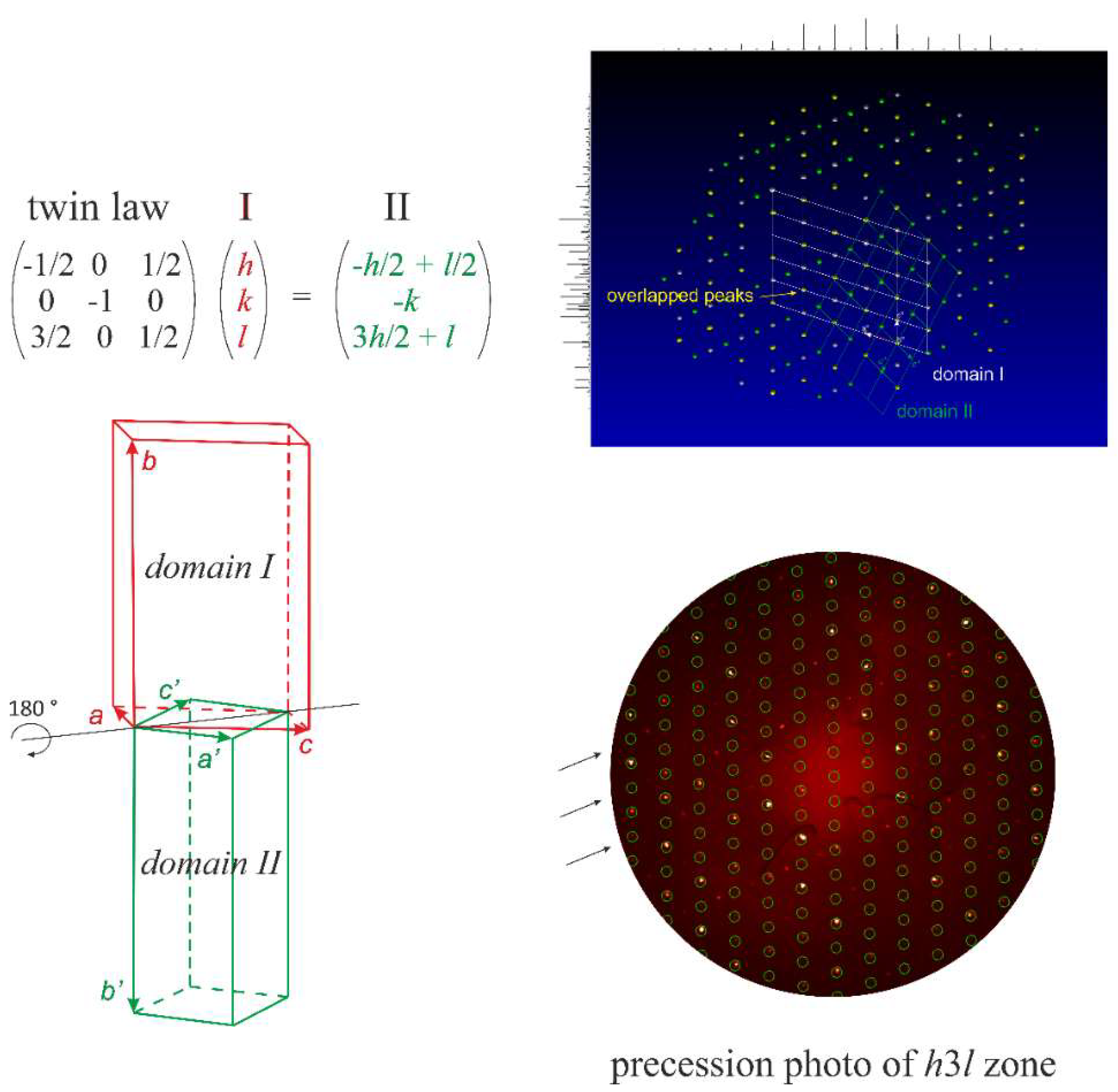
3.2.1. Structural Determination
3.2.2. Lu5Pd4Ge8: Structural Relationships
- -
- a traslationengleiche (t2) decentering leading to a monoclinic Niggli cell (mP16-P21/m).
- -
- a klassengleiche transformation (k2) giving a monoclinic model with doubled cell volume (mP32-P21/m). As a result, all the independent sites split in two (see Figure 4).
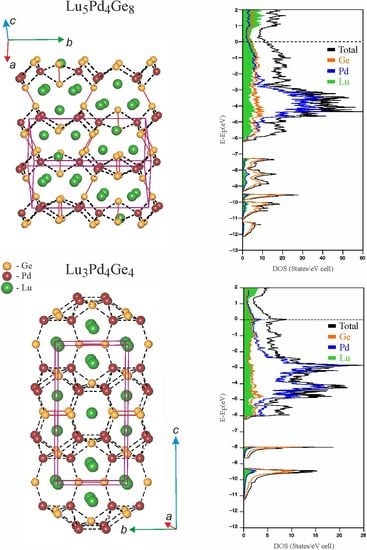
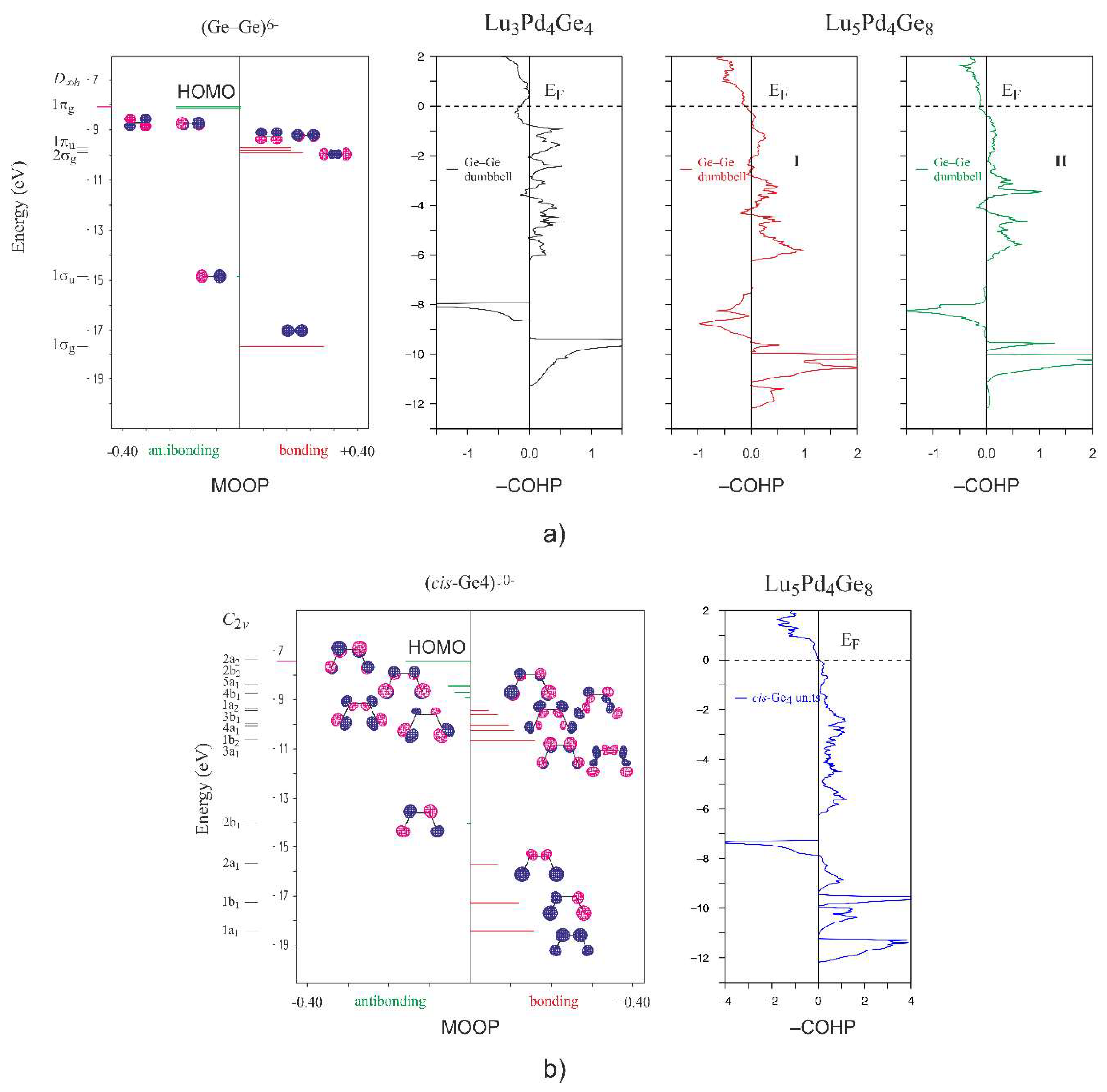
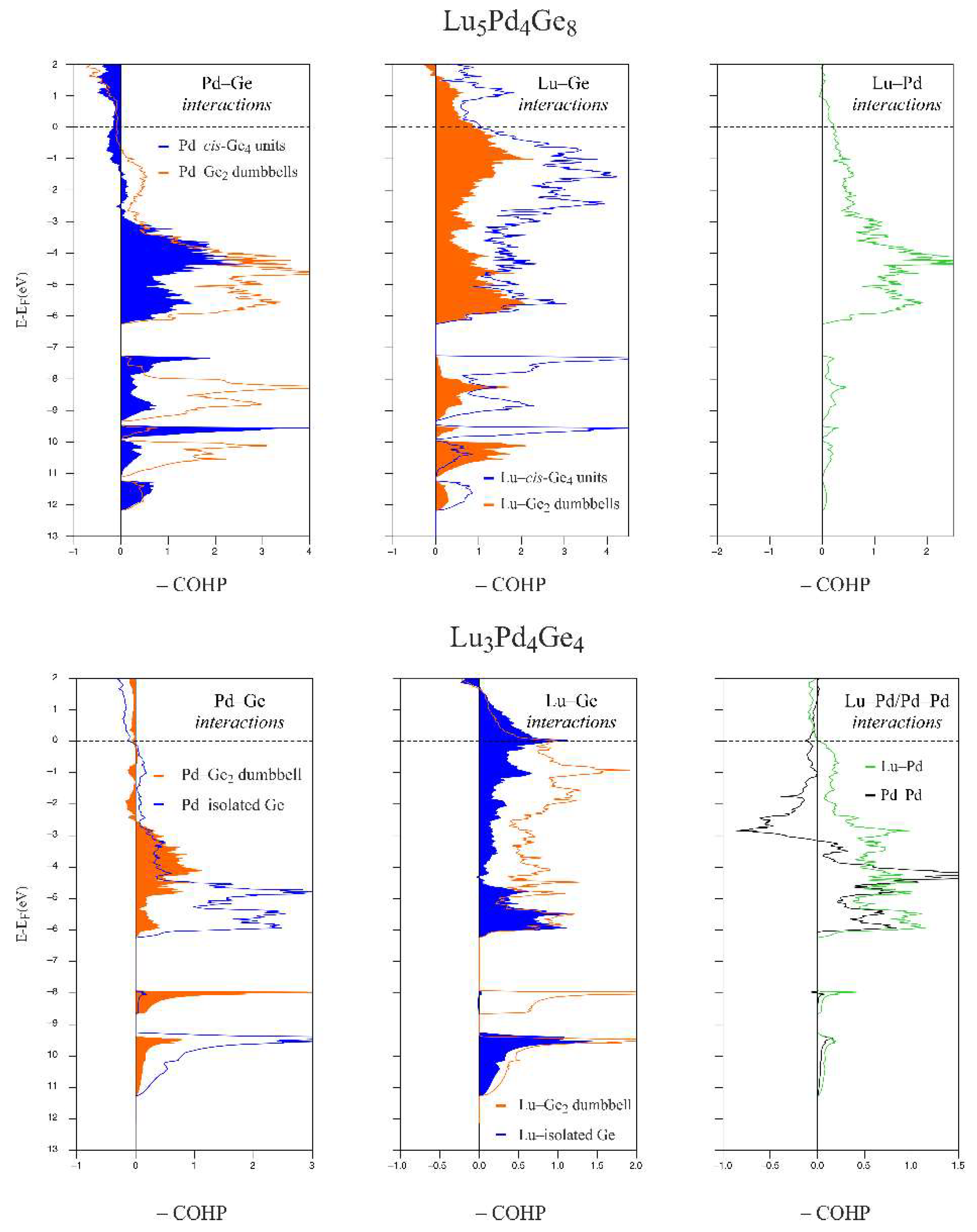
3.3. Chemical Bonding Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Villars, P.; Cenzual, K. Pearson’s Crystal Data; ASM International: Metals Park, OH, USA, 2018. [Google Scholar]
- Freccero, R.; Solokha, P.; Proserpio, D.M.; Saccone, A.; De Negri, S. A new glance on R2MGe6 (R = rare earth metal, M = another metal) compounds. An experimental and theoretical study of R2PdGe6 germanides. Dalton Trans. 2017, 46, 14021–14033. [Google Scholar] [CrossRef] [PubMed]
- Niepman, D.; Prots, Y.M.; Pöttgen, R.; Jeitschko, W. The order of the palladium and germanium atoms in the germanides LnPdGe (Ln = La–Nd, Sm, Gd, Tb) and the new compound Yb3Pd4Ge4. J. Solid State Chem. 2000, 154, 329–337. [Google Scholar] [CrossRef]
- Heying, B.; Rodewald, U.C.; Pöttgen, R. The germanides Er5Pd4Ge8 and Tm5Pd4Ge8—3D [Pd4Ge8] polyanions with Ge2 dumb-bells and Ge4 chains in cis-conformation. Z. Kristallogr. 2017, 232, 435–440. [Google Scholar] [CrossRef]
- Feyerherm, R.; Becker, B.; Collins, M.F.; Mydosh, J.; Nieuwenhuys, G.J.; Ramakrishnan, S. The magnetic structure of CePd2Ge2 and Ce2Pd3Ge5. Phys. B 1998, 241–243, 643–645. [Google Scholar] [CrossRef]
- Anand, V.K.; Thamizhavel, A.; Ramakrishnan, S.; Hossain, Z. Complex magnetic order in Pr2Pd3Ge5: A single crystal study. J. Phys. 2012, 24. [Google Scholar] [CrossRef] [PubMed]
- Solokha, P.; Freccero, R.; De Negri, S.; Proserpio, D.M.; Saccone, A. The R2Pd3Ge5 (R = La–Nd, Sm) germanides: Synthesis, crystal structure and symmetry reduction. Struct. Chem. 2016, 27, 1693–1701. [Google Scholar] [CrossRef]
- Rodewald, U.C.; Heying, B.; Hoffmann, R.-D.; Niepmann, D. Polymorphism in the germanides REPdGe with the heavy rare earth elements. Z. Naturforsch. 2009, 64b, 595–602. [Google Scholar] [CrossRef]
- Chabot, B.; Parthé, E. Dy2Co3Si5, Lu2Co3Si5, Y2Co3Si5 and Sc2Co3Si5 with a monoclinic structural deformation variant of the orthorhombic U2Co3Si5 structure type. J. Less-Common Met. 1985, 106, 53–59. [Google Scholar] [CrossRef]
- Bruker. APEX2, SAINT-Plus, XPREP, SADABS, CELL_NOW and TWINABS. Bruker AXS Inc.: Madison, WI, USA, 2014. [Google Scholar]
- Kraus, W.; Nolze, G. POWDER CELL-A program for the representation and manipulation of crystal structure and calculation of the resulting X-ray powder pattern. J. Appl. Crystallogr. 1996, 29. [Google Scholar] [CrossRef]
- Bader, R.F. Atoms in Molecules: A Quantum Theory; Clarendon Press and Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. J. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Krier, G.; Jepsen, O.; Burkhardt, A.; Andersen, O.K. The TB-LMTO-ASA Program; Version 4.7; Max-Planck-Institut Für Festkörperforschung: Stuttgart, Germany, 2000. [Google Scholar]
- Barth, U.; Hedin, L.A. Local exchange-correlation potential for the spin polarized case: I. J. Phys. Chem. 1972, C5, 1629–1642. [Google Scholar] [CrossRef]
- Dronskowski, R.; Blöchl, P.E. Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Eck, B. Wxdragon, Aachen, Germany, 1994–2018. Available online: http://wxdragon.de/ (accessed on 2 May 2018).
- Mealli, C.; Proserpio, D.M. MO Theory made visible. J. Chem. Educ. 1990, 67, 399–403. [Google Scholar] [CrossRef]
- Mealli, C.; Ienco, A.; Proserpio, D.M. Book of Abstracts of the XXXIII. ICCC; ICCC: Florence, Italy, 1998. [Google Scholar]
- Lowe, J.; Peterson, K. Quantum Chemistry, 3rd ed.; Academic Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Hoffmann, R. Solids and Surfaces: A Chemist’s View of Bonding in Extended Structures; VCH: New York, NY, USA, 1988. [Google Scholar]
- Solokha, P.; De Negri, S.; Saccone, A.; Proserpio, D.M. On a non-merohedrally twinned Tb3Ge5 crystal. In Proceedings of the XII International Conference on Crystal Chemistry of Intermetallic Compounds, Lviv, Ukraine, 22–26 September 2012. [Google Scholar]
- Budnyk, S.L.; Weitzer, F.; Kubata, C.; Prots, Y.; Akselrud, L.G.; Schnelle, W.; Hiebl, K.; Nesper, R.; Wagner, F.R.; Grin, Yu. Barrelane-like germanium clusters in Eu3Ge5: Crystal structure, chemical bonding and physical properties. J. Solid State Chem. 2006, 179, 2329–2338. [Google Scholar] [CrossRef]
- Shcherban, O.; Savysyuk, I.; Semuso, N.; Gladyshevskii, R.; Cenzual, K. Crystal structure of the compound Pr4Ge7. Chem. Met. Alloys 2009, 2, 115–122. [Google Scholar]
- Müller, P. Crystal Structure Refinement: A Crystallographer’s Guide to SHELXL; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Clegg, W. Crystal Structure Analysis: Principle and Practice, 2nd ed.; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic computing system JANA2006: General features. Z. Kristallogr. 2014, 229, 345–352. [Google Scholar]
- Cooper, R.I.; Gould, R.O.; Parsons, S.; Watkin, D.J. The derivation of non-merohedral twin laws during refinement by analysis of poorly fitting intensity data and the refinement of non-merohedrally twinned crystal structures in the program crystals. J. Appl. Crystallogr. 2002, 35, 168–174. [Google Scholar] [CrossRef]
- Farrugia, L.J. WinGX and ORTEP for windows: An update. J. Appl. Cryst. 2012, 45, 849–854. [Google Scholar] [CrossRef]
- Gelato, L.; Parthé, E. Structure tidy—A computer program to standardize crystal structure data. J. Appl. Crystallogr. 1987, 20, 139–143. [Google Scholar] [CrossRef]
- Parthé, E.; Gelato, L.; Chabot, B.; Penzo, M.; Cenzual, K.; Gladyshevskii, R. TYPIX Standardized Data and Crystal Chemical Characterization of Inorganic Structure Types; Springer-Verlag: Heidelberg, Germany, 1993. [Google Scholar]
- Prots, Y.; Demchyna, R.; Burkhardt, U.; Schwarz, U. Crystal structure and twinning of HfPdGe. Z. Kristallogr. 2007, 222, 513–520. [Google Scholar] [CrossRef]
- Wondratschek, H.; Müller, U. International Tables for Crystallography, Symmetry Relations between Space Groups; Vol. A1; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Müller, U. Symmetry Relationships between Crystal Structures. Applications of Crystallographic Group Theory in Crystal Chemistry; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Pöttgen, R. Coloring, distortions, and puckering in selected intermetallic structures from the perspective of group—Subgroup relations. Z. Anorg. Allg. Chem. 2014, 640, 869–891. [Google Scholar] [CrossRef]
- Landrum, G.A.; Dronskowski, R. The orbital origins of magnetism: from atoms to molecules to ferromagnetic alloys. Angew. Chem. Int. Ed. 2000, 39, 1560–1585. [Google Scholar] [CrossRef]
- Lin, Q.; Corbett, J.D. Centric and non-centric Ca3Au~7.5Ge~3.5: Electron-poor derivatives of La3Al11. syntheses, structures, and bonding analyses. Inorg. Chem. 2009, 48, 5403–5411. [Google Scholar] [CrossRef] [PubMed]
- Mudring, A.-V.; Corbett, J.D. Unusual electronic and bonding properties of the zintl phase Ca5Ge3 and related compounds. A theoretical analysis. J. Am. Chem. Soc. 2004, 126, 5277–5281. [Google Scholar] [CrossRef] [PubMed]
- Siggelkow, L.; Hlukhyy, V.; Fässler, T.F. Sr7Ge6, Ba7Ge6 and Ba3Sn2—Three new binary compounds containing dumbbells and four-membered chains of tetrel atoms with considerable Ge-Ge π-bonding character. J. Solid State Chem. 2012, 191, 76–89. [Google Scholar] [CrossRef]
- Eisenmann, B.; Schäfer, H. Zur Strukturchemie der Verbindungsreihe BaMg2X2 (X = Si, Ge, Sn, Pb). Z. Anorg. Allg. Chem. 1974, 403, 163–172. [Google Scholar] [CrossRef]
- Doverbratt, I.; Ponou, S.; Lidin, S. Ca2Pd3Ge, a new fully ordered ternary Laves phase structure. J. Solid State Chem. 2013, 197, 312–316. [Google Scholar] [CrossRef]
- Kurylyshyn, I.M.; Fässler, T.F.; Fischer, A.; Hauf, C.; Eickerling, G.; Presnitz, M.; Scherer, W. Probing the Zintl-Klemm concept: A combined experimental and theoretical charge density study of the Zintl phase CaSi. Angew. Chem. Int. Ed. 2014, 53, 3029–3032. [Google Scholar] [CrossRef] [PubMed]



| Empirical Formula | Lu5Pd4Ge8 | Lu3Pd4Ge4 |
|---|---|---|
| EDXS data | Lu28.6Pd24.9Ge46.5 | Lu25.7Pd35.0Ge39.5 |
| Space group (No.) | P21/m (11) | Immm (71) |
| Pearson symbol-prototype, Z | mP34-Tm5Pd4Ge8, 2 | oI22-Gd3Cu4Ge4, 2 |
| а [Å] | 5.7406(3) | 4.1368(3) |
| b [Å] | 13.7087(7) | 6.9192(5) |
| c [Å] | 8.3423(4) | 13.8229(9) |
| β (°) | 107.8(1) | – |
| V [Å3] | 625.20(5) | 395.66(5) |
| Abs. coeff. (μ), mm−1 | 63.5 | 60.7 |
| Twin law | [] | – |
| k (BASF) | 0.49(1) | – |
| Unique reflections | 2105 | 404 |
| Reflections I > 2σ(I)/parameters | 1877/87 | 398/23 |
| GOF on F2 (S) | 1.17 | 1.17 |
| R indices [I > 2σ(I)] | R1 = 0.0190;wR2 = 0.0371 | R1 = 0.0238;wR2 = 0.0869 |
| R indices [all data] | R1 = 0.0247;wR2 = 0.0384 | R1 = 0.0242;wR2 = 0.0871 |
| Δρfin (max/min), [e/Å3] | 2.00/−2.83 | 2.87/−3.33 |
| No. Overall Composition [at %] Synthesis/Thermal Treatment | Phases | Phase Composition [at %] Lu; Pd; Ge | Crystal Structure |
|---|---|---|---|
| 1 Lu21.4Pd11.2Ge67.4 Arc melting followed by thermal treatment (1) | Lu2PdGe6 Lu5Pd4Ge8 LuPd0.16Ge2 Ge | 21.5; 12.1; 66.4 28.6; 25.1; 46.3 31.1; 5.4; 63.5 –; –; –; | oS72–Ce2(Ga0.1Ge0.9)7 mP34-Tm5Pd4Ge8 oS16-CeNiSi2 cF8-C |
| 2 Lu28.9Pd24.1Ge47.0 Arc melting | Lu5Pd4Ge8 new phase Lu2PdGe6 LuPd0.16Ge2 | 28.8; 24.8; 46.4 32.4; 28.5; 39.1 21.7; 11.8; 66.5 30.1; 6.9; 63.0 | mP34-Tm5Pd4Ge8 AlB2 related oS72–Ce2(Ga0.1Ge0.9)7 oS16-CeNiSi2 |
| 3 * Lu30.8Pd25.5Ge43.7 Direct synthesis with thermal treatment (2) | Lu5Pd4Ge8 new phase Ge | 28.6; 24.9; 46.5 33.0; 26.8; 40.2 –; –; –; | mP34-Tm5Pd4Ge8 AlB2 related cF8-C |
| 4 * Lu33.0Pd26.0Ge41.0 Arc melting followed by thermal treatment (2) | Lu3Pd4Ge4 Lu5Pd4Ge8 LuPdGe PdGe Ge | 25.7; 35.0; 39.5 28.4; 25.1; 46.5 31.9; 34.5; 33.6 0.0; 53.4; 47.6 0.0; 0.0; 100.0 | oI22-Gd3Cu4Ge4 mP34-Tm5Pd4Ge8 oI36-AuYbSn oP8-FeAs cF8-C |
| 5 Lu17.9Pd29.0Ge53.1 Arc melting | Lu3Pd4Ge4 LuPdGe PdGe Ge | 26.1; 34.2; 39.7 32.0; 33.5; 34.5 0.0; 52.4; 47.8 0.0; 0.0; 100.0 | oI22-Gd3Cu4Ge4 oI36-AuYbSn oP8-FeAs cF8-C |
| Atom | Site | x/a | y/b | z/c | Ueq (Å2) |
|---|---|---|---|---|---|
| Lu5Pd4Ge8 | |||||
| Lu1 | 2e | 0.71858(8) | 1/4 | 0.93028(6) | 0.0047(1) |
| Lu2 | 4f | 0.13606(7) | 0.11370(2) | 0.78913(7) | 0.0051(1) |
| Lu3 | 4f | 0.62176(8) | 0.11902(2) | 0.28943(7) | 0.0056(1) |
| Pd1 | 4f | 0.07436(13) | 0.08476(3) | 0.14089(12) | 0.0072(1) |
| Pd2 | 4f | 0.42601(13) | 0.58211(3) | 0.35985(12) | 0.0075(1) |
| Ge1 | 2e | 0.0515(2) | 1/4 | 0.28977(15) | 0.0081(2) |
| Ge2 | 2e | 0.3343(2) | 1/4 | 0.58221(15) | 0.0078(2) |
| Ge3 | 2e | 0.7797(2) | 1/4 | 0.5814(2) | 0.0063(2) |
| Ge4 | 4f | 0.15453(17) | 0.04252(5) | 0.44776(16) | 0.0071(1) |
| Ge5 | 2e | 0.2797(2) | 1/4 | 0.0606(2) | 0.0048(2) |
| Ge6 | 4f | 0.34622(17) | 0.54443(4) | 0.05049(16) | 0.0060(1) |
| Lu3Pd4Ge4 | |||||
| Lu1 | 2a | 0 | 0 | 0 | 0.0110(2) |
| Lu2 | 4j | 1/2 | 0 | 0.37347(4) | 0.0081(2) |
| Pd | 8l | 0 | 0.30094(10) | 0.32738(5) | 0.0155(3) |
| Ge1 | 4h | 0 | 0.18745(17) | 1/2 | 0.0084(3) |
| Ge2 | 4i | 0 | 0 | 0.21754(10) | 0.0132(3) |
| Central Atom | Adjacent Atoms | d (Å) | -iCOHP | Central Atom | Adjacent Atoms | d (Å) | -iCOHP | Central Atom | Adjacent Atoms | d (Å) | -iCOHP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lu1 | Ge6 (×2) | 2.853 | 1.26 | Lu3 | Ge5 | 2.904 | 1.25 | (1b)Ge6 | Ge6 | 2.494 | 2.39 |
| Ge1 | 3.025 | 0.81 | Ge3 | 2.938 | 1.25 | Pd1 | 2.516 | 2.16 | |||
| Ge5 | 3.033 | 1.02 | Pd1 | 3.042 | 0.71 | Pd2 | 2.533 | 2.12 | |||
| Ge3 | 3.036 | 0.85 | Ge1 | 3.051 | 0.92 | Pd1 | 2.619 | 1.80 | |||
| Ge2 | 3.064 | 0.79 | Pd2 | 3.063 | 0.68 | Lu1 | 2.853 | 1.26 | |||
| Ge5 | 3.069 | 0.81 | Ge6 | 3.072 | 0.90 | Lu2 | 3.016 | 0.96 | |||
| Pd1 (×2) | 3.194 | 0.52 | Ge6 | 3.094 | 0.75 | Lu2 | 3.050 | 0.80 | |||
| Pd2 (×2) | 3.258 | 0.46 | Pd2 | 3.100 | 0.63 | Lu3 | 3.072 | 0.90 | |||
| Lu2 | Ge5 | 2.857 | 1.29 | Ge4 | 3.105 | 0.71 | Lu3 | 3.094 | 0.75 | ||
| Ge3 | 2.918 | 1.20 | Ge4 | 3.120 | 0.84 | Pd1 | Ge6 | 2.516 | 2.16 | ||
| Ge2 | 2.994 | 0.99 | Pd1 | 3.236 | 0.52 | Ge4 | 2.526 | 2.11 | |||
| Ge6 | 3.016 | 0.95 | Ge4 | 3.493 | 0.27 | Ge1 | 2.606 | 1.66 | |||
| Ge4 | 3.043 | 0.91 | (1b)Ge3 | Ge2 | 2.559 | 1.92 | Ge6 | 2.619 | 1.80 | ||
| Ge4 | 3.043 | 0.79 | Pd2 (×2) | 2.699 | 1.46 | Ge5 | 2.730 | 1.35 | |||
| Ge6 | 3.050 | 0.80 | Lu2 (×2) | 2.918 | 1.20 | Lu3 | 3.042 | 0.71 | |||
| Pd1 | 3.087 | 0.68 | Lu3 (×2) | 2.938 | 1.25 | Lu2 | 3.087 | 0.68 | |||
| Pd1 | 3.104 | 0.63 | Lu1 | 3.036 | 0.86 | Lu2 | 3.104 | 0.63 | |||
| Pd2 | 3.114 | 0.64 | (1b)Ge4 | Ge4 | 2.492 | 2.48 | Lu1 | 3.194 | 0.52 | ||
| Pd2 | 3.156 | 0.57 | Pd2 | 2.512 | 2.14 | Pd2 | Ge4 | 2.512 | 2.14 | ||
| (2b)Ge1 | Ge2 | 2.484 | 2.98 | Pd1 | 2.526 | 2.11 | Ge6 | 2.533 | 2.12 | ||
| Pd1 (×2) | 2.606 | 1.66 | Pd2 | 2.566 | 1.94 | Ge4 | 2.566 | 1.94 | |||
| Ge5 | 2.627 | 1.69 | Lu2 | 3.043 | 0.91 | Ge2 | 2.649 | 1.53 | |||
| Lu1 | 3.025 | 0.81 | Lu2 | 3.043 | 0.79 | Ge3 | 2.699 | 1.46 | |||
| Lu3 (×2) | 3.051 | 0.92 | Lu3 | 3.105 | 0.71 | Lu3 | 3.063 | 0.68 | |||
| (2b)Ge2 | Ge1 | 2.484 | 2.98 | (1b)Ge5 | Ge1 | 2.627 | 1.69 | Lu3 | 3.100 | 0.63 | |
| Ge3 | 2.559 | 1.92 | Pd1 (×2) | 2.730 | 1.35 | Lu2 | 3.114 | 0.65 | |||
| Pd2 (×2) | 2.649 | 1.53 | Lu2 (×2) | 2.857 | 1.29 | Lu2 | 3.156 | 0.58 | |||
| Lu2 (×2) | 2.994 | 1.00 | Lu3 (×2) | 2.904 | 1.26 | ||||||
| Lu1 | 3.064 | 0.79 | Lu1 | 3.033 | 1.02 | ||||||
| Lu1 | 3.069 | 0.81 |
| Central Atom | Adjacent Atoms | d (Å) | -iCOHP | Central Atom | Adjacent Atoms | d (Å) | -iCOHP |
|---|---|---|---|---|---|---|---|
| Lu1 | Ge4 (×4) | 2.992 | 1.21 | (0b)Ge2 | Pd (×4) | 2.562 | 1.88 |
| Ge5 (×2) | 3.006 | 1.05 | Pd (×2) | 2.577 | 1.86 | ||
| Pd (×8) | 3.445 | 0.41 | Lu2 (×2) | 2.988 | 0.83 | ||
| Lu2 | Ge5 (×2) | 2.988 | 0.83 | Lu1 | 3.006 | 1.05 | |
| Ge4 (×4) | 3.003 | 0.99 | Pd | Ge4 | 2.512 | 2.23 | |
| Pd (×4) | 3.003 | 0.79 | Ge5 (×2) | 2.562 | 1.88 | ||
| Pd (×2) | 3.100 | 0.58 | Pd | 2.755 | 0.97 | ||
| (1b)Ge1 | Pd (×2) | 2.512 | 2.23 | Lu2 (×2) | 3.003 | 0.79 | |
| Ge1 | 2.595 | 1.82 | Pd (×2) | 3.058 | 0.46 | ||
| Lu1 (×2) | 2.992 | 1.22 | Lu2 | 3.100 | 0.58 | ||
| Lu2 (×4) | 3.003 | 0.99 | Lu1 (×2) | 3.445 | 0.41 |
| Element/Compound | Atom/Site | Volume, [Å3] | QTAIM Charge, Qeff | Compound | Atom/Site | Volume, [Å3] | QTAIM Charge, Qeff |
|---|---|---|---|---|---|---|---|
| Lu (hP2) | Lu/2c | 29.74 # | 0 | Lu5Pd4Ge8 | Lu1/2e | 15.88 | +1.45 |
| Pd (cF4) | Pd/4a | 14.71 # | 0 | (mP34) | Lu2/4f | 15.48 | +1.48 |
| Ge (cF8) | Ge/8a | 22.66 # | 0 | Lu3/4f | 15.85 | +1.51 | |
| Pd1/4f | 19.91 | −0.79 | |||||
| Lu3Pd4Ge4 | Lu1/2a | 16.90 | +1.57 | Pd2/4f | 19.77 | −0.76 | |
| (oI22) | Lu2/4j | 15.05 | +1.53 | (2b)Ge1/2e | 19.39 | −0.23 | |
| Pd/8l | 19.43 | −0.67 | (2b)Ge2/2e | 19.51 | −0.30 | ||
| (1b)Ge1/4h | 22.35 | −0.89 | (1b)Ge3/2e | 22.66 | −0.87 | ||
| (0b)Ge2/4i | 16.42 | −0.09 | (1b)Ge4/4f | 18.73 | −0.30 | ||
| (1b)Ge5/2e | 23.96 | −1.14 | |||||
| (1b)Ge6/4f | 19.67 | −0.59 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freccero, R.; Solokha, P.; Proserpio, D.M.; Saccone, A.; De Negri, S. Lu5Pd4Ge8 and Lu3Pd4Ge4: Two More Germanides among Polar Intermetallics. Crystals 2018, 8, 205. https://doi.org/10.3390/cryst8050205
Freccero R, Solokha P, Proserpio DM, Saccone A, De Negri S. Lu5Pd4Ge8 and Lu3Pd4Ge4: Two More Germanides among Polar Intermetallics. Crystals. 2018; 8(5):205. https://doi.org/10.3390/cryst8050205
Chicago/Turabian StyleFreccero, Riccardo, Pavlo Solokha, Davide Maria Proserpio, Adriana Saccone, and Serena De Negri. 2018. "Lu5Pd4Ge8 and Lu3Pd4Ge4: Two More Germanides among Polar Intermetallics" Crystals 8, no. 5: 205. https://doi.org/10.3390/cryst8050205
APA StyleFreccero, R., Solokha, P., Proserpio, D. M., Saccone, A., & De Negri, S. (2018). Lu5Pd4Ge8 and Lu3Pd4Ge4: Two More Germanides among Polar Intermetallics. Crystals, 8(5), 205. https://doi.org/10.3390/cryst8050205