The Crystal Orbital Hamilton Population (COHP) Method as a Tool to Visualize and Analyze Chemical Bonding in Intermetallic Compounds
Abstract
1. Introduction
2. The COHP Method—An Introduction
3. Applications of the COHP Method to Intermetallic Compounds
3.1. Rare-Earth Transition-Metal Halides as Anti-Werner-Fashioned Complexes
3.2. The Bonding Situations in Electron-Poorer Polar Intermetallics Containing Gold
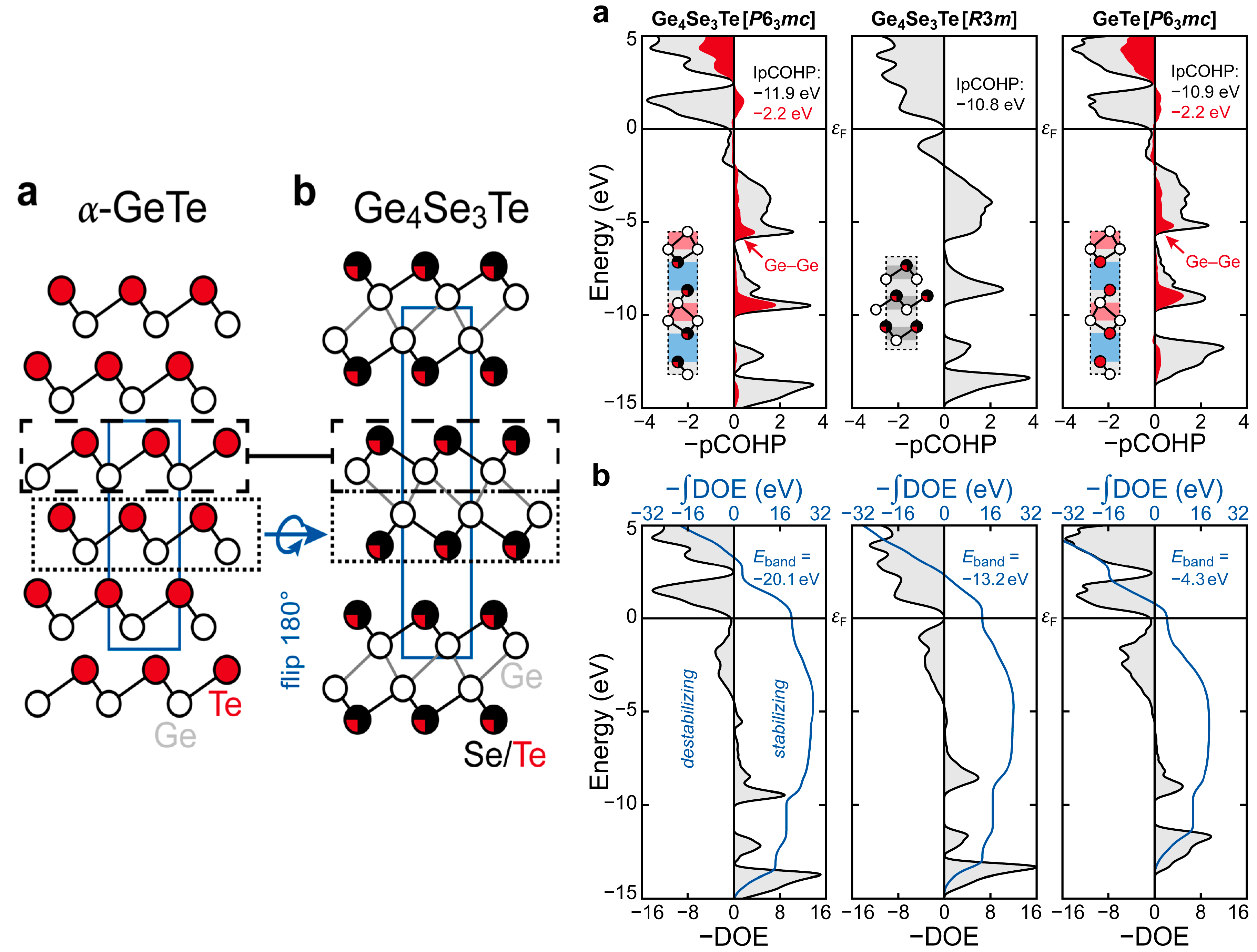
3.3. The Role of Vacancies and Structural Preferences in Phase-Change Materials
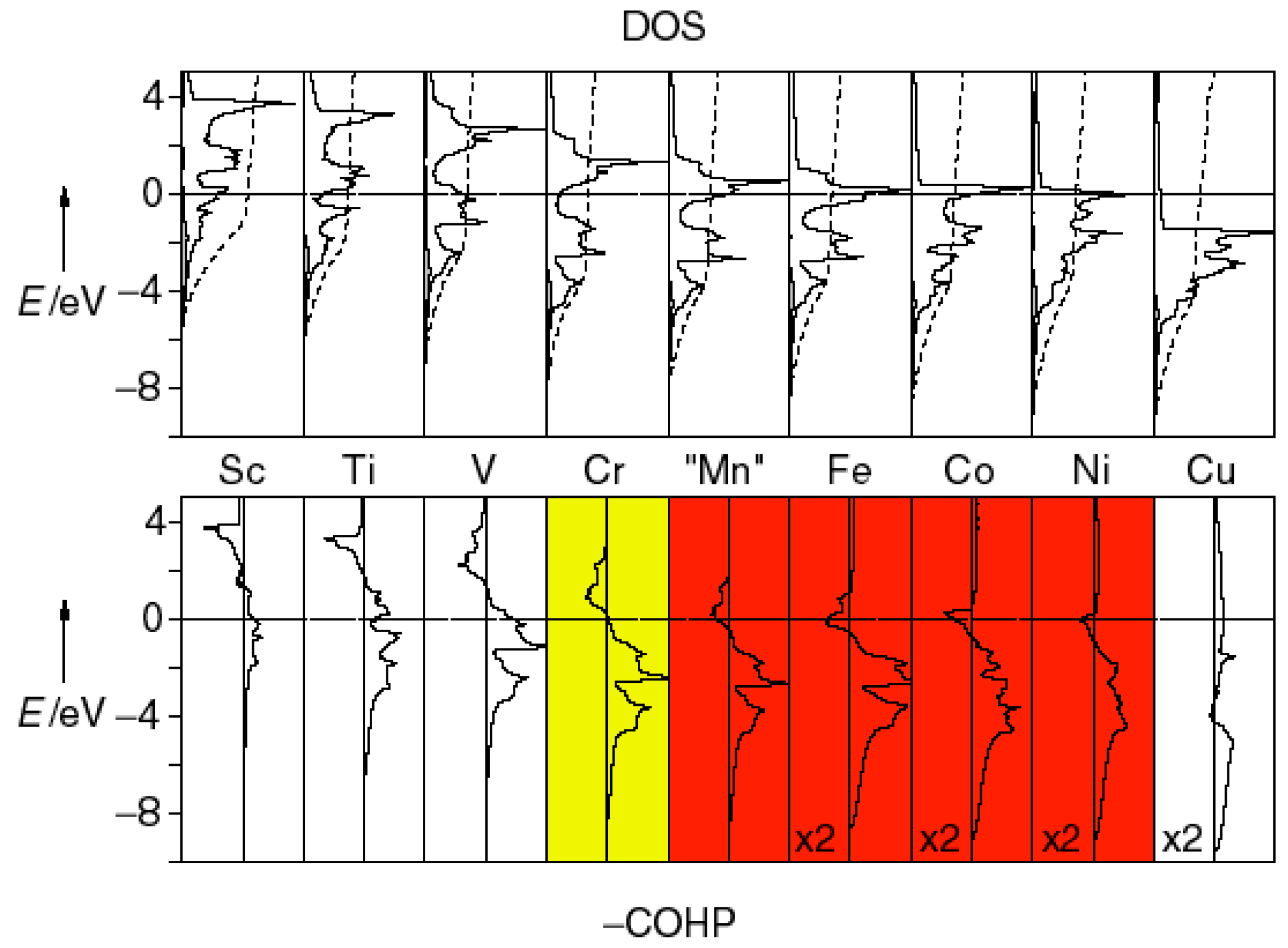
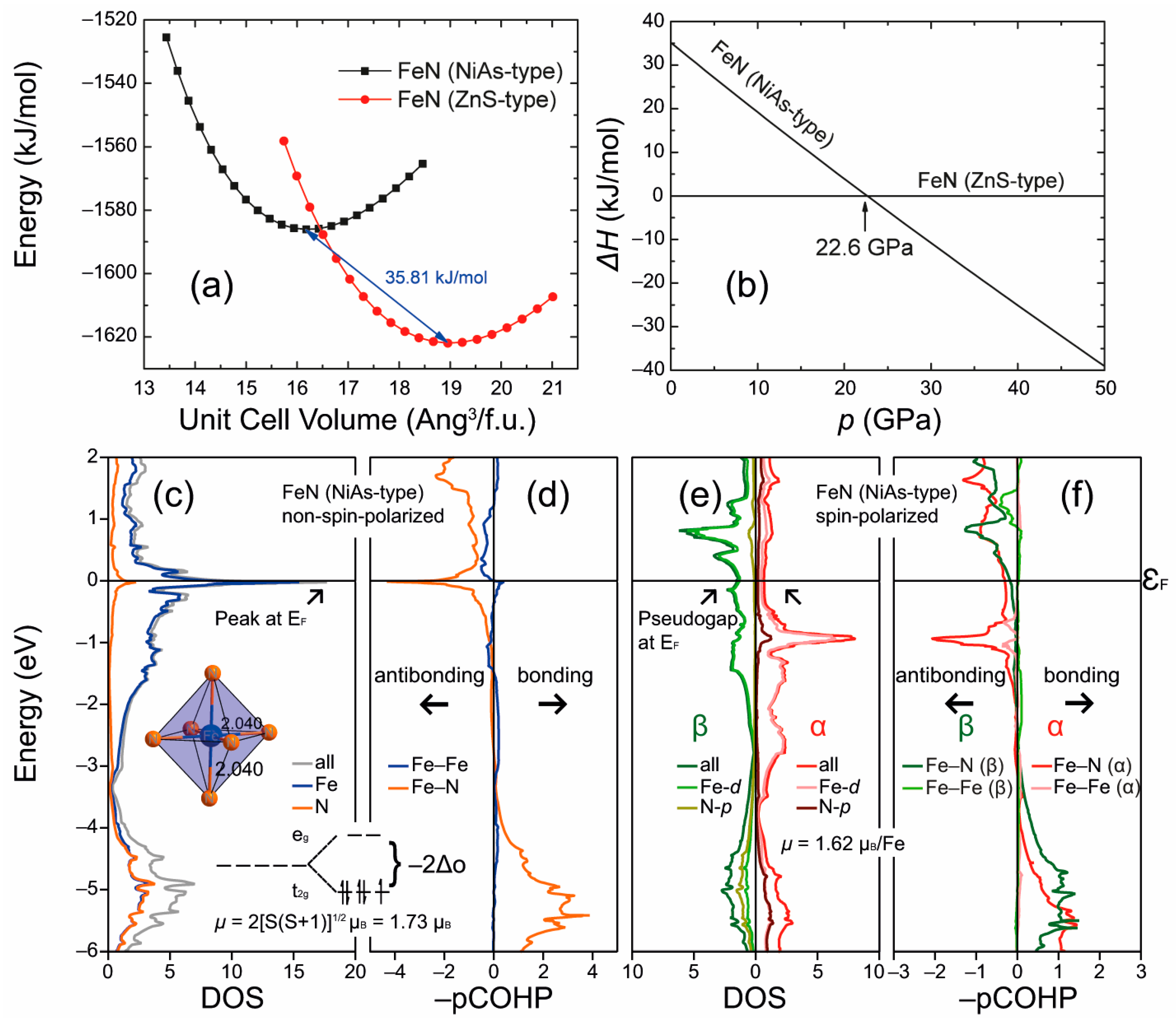
3.4. Itinerant Antiferromagnetism and Ferromagnetism from the Viewpoint of Chemical Bonding in Intermetallic Compounds
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Goethe, J.W. Faust—Der Tragödie Erster Teil; Reclam Publishers: Stuttgart, Germany, 1957. [Google Scholar]
- Pauling, L. The Modern Theory of Valency. J. Chem. Soc. 1948, 1461–1467. [Google Scholar] [CrossRef]
- Lewis, G.N. The atom and the molecule. J. Am. Chem. Soc. 1916, 38, 762–785. [Google Scholar] [CrossRef]
- Pauling, L. The principles determining the structure of complex ionic crystals. J. Am. Chem. Soc. 1929, 51, 1010–1026. [Google Scholar] [CrossRef]
- Zintl, E. Intermetallische Verbindungen. Angew. Chem. 1939, 52, 1–6. [Google Scholar] [CrossRef]
- Klemm, W.; Busmann, E. Volumeninkremente und Radien einiger einfach negativ geladener Ionen. Z. Anorg. Allg. Chem. 1963, 319, 297–311. [Google Scholar] [CrossRef]
- Papoian, G.A.; Hoffmann, R. Hypervalent Bonding in One, Two, and Three Dimensions: Extending the Zintl-Klemm Concept to Nonclassical Electron-Rich Networks. Angew. Chem. Int. Ed. 2000, 39, 2408–2448. [Google Scholar] [CrossRef]
- Köhler, J.; Whangbo, M.-H. Late transition metal anions acting as p-metal elements. Solid State Sci. 2008, 10, 444–449. [Google Scholar] [CrossRef]
- Miller, G.J.; Schmidt, M.W.; Wang, F.; You, T.-S. Quantitative Advances in the Zintl-Klemm Formalism. In Structure and Bonding; Fässler, T., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 139, pp. 1–55. ISBN 978-3-642-21150-8. [Google Scholar]
- Nesper, R. The Zintl-Klemm Concept—A Historical Survey. Z. Anorg. Allg. Chem. 2014, 640, 2639–2648. [Google Scholar] [CrossRef]
- Jones, H. The phase boundaries in binary alloys, Part 2: The theory of the α, β phase boundaries. Proc. Phys. Soc. 1937, 49, 250–257. [Google Scholar] [CrossRef]
- Massalski, T.B.; Mizutani, U. Electronic Structure of Hume-Rothery Phases. Prog. Mater. Sci. 1978, 22, 151–262. [Google Scholar] [CrossRef]
- Mizutani, U.; Sato, H. The Physics of the Hume-Rothery Electron Concentration Rule. Crystals 2017, 7, 9. [Google Scholar] [CrossRef]
- Corbett, J.D. Exploratory Synthesis in the Solid State. Endless Wonders. Inorg. Chem. 2000, 39, 5178–5191. [Google Scholar] [CrossRef] [PubMed]
- Corbett, J.D. Exploratory Synthesis: The Fascinating and Diverse Chemistry of Polar Intermetallic Phases. Inorg. Chem. 2010, 49, 13–28. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 384, 361–376. [Google Scholar] [CrossRef]
- Bloch, F. Über die Quantenmechanik der Elektronen in Kristallgittern. Z. Physik 1929, 52, 555–600. [Google Scholar] [CrossRef]
- Dronskowski, R. Computational Chemistry of Solid State Materials; WILEY-VCH Publishers: Weinheim, Germany, 2005; ISBN 978–3-527-31410-2. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Jones, R.O.; Gunnarsson, O. The density functional formalism, its applications and prospects. Rev. Mod. Phys. 1989, 61, 689–746. [Google Scholar] [CrossRef]
- Dronskowski, R.; Blöchl, P.E. Crystal Orbital Hamilton Populations (COHP). Energy-Resolved Visualization of Chemical Bonding in Solids Based on Density-Functional Calculations J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Crystal Orbital Hamilton Population (COHP) Analysis As Projected from Plane-Wave Basis Sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef] [PubMed]
- Roothaan, C.C.J. New Developments in Molecular Orbital Theory. Rev. Mod. Phys. 1951, 23, 69–89. [Google Scholar] [CrossRef]
- Hughbanks, T.; Hoffmann, R. Chains of Trans-Edge-Sharing Molybdenum Octahedra: Metal-Metal Bonding in Extended Systems. J. Am. Chem. Soc. 1983, 105, 3528–3537. [Google Scholar] [CrossRef]
- Hoffmann, R. How Chemistry and Physics Meet in the Solid State. Angew. Chem. Int. Ed. Engl. 1987, 26, 846–878. [Google Scholar] [CrossRef]
- Wolfsberg, M.; Helmholz, L. The Spectra and Electronic Structure of the Tetrahedral Ions MnO4−, CrO4−, and ClO4−. J. Chem. Phys. 1952, 20, 837–843. [Google Scholar] [CrossRef]
- Slater, J.C. Wave Functions in a Periodic Potential. Phys. Rev. 1937, 51, 846–851. [Google Scholar] [CrossRef]
- Andersen, O.K. Linear methods in band theory. Phys. Rev. B Condens. Matter Mater. Phys. 1975, 12, 3060–3083. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Küpers, M.; Konze, P.M.; Maintz, S.; Steinberg, S.; Mio, A.M.; Cojocaru-Mirédin, O.; Zhu, M.; Müller, M.; Luysberg, M.; Mayer, J.; et al. Unexpected Ge–Ge Contacts in the Two-Dimensional Ge4Se3Te Phase and Analysis of Their Chemical Cause with the Density of Energy (DOE) Function. Angew. Chem. Int. Ed. 2017, 56, 10204–10208. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Marsman, M.; Furthmüller, J. Vienna Ab Initio Simulation Package (VASP); The Guide Computational Materials Physics, Faculty of Physics, Universität Wien: Vienna, Austria, 2014. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B Condens. Matter Mater. Phys. 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Gonze, X.; Jollet, F.; Abreu Araujo, F.; Adams, D.; Amadon, B.; Applencourt, T.; Audouze, C.; Beuken, J.-M.; Bieder, J.; Bokhanchuk, A.; et al. Recent developments in the ABINIT software package. Comput. Phys. Commun. 2016, 205, 106–131. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Anglade, P.-M.; Beuken, J.-M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M.; et al. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Gonze, X.; Rignanese, G.-M.; Verstraete, M.; Beuken, J.-M.; Pouillon, Y.; Caracas, R.; Jollet, F.; Torrent, M.; Zerah, G.; Mikami, M.; et al. A brief introduction to the ABINIT software package. Z. Kristallog. Cryst. Mater. 2005, 220, 558–562. [Google Scholar] [CrossRef]
- Gonze, X.; Beuken, J.-M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.-M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-principles computation of material properties: The ABINIT software projec. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Maintz, S.; Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Analytic Projection From Plane-Wave and PAW Wavefunctions and Application to Chemical-Bonding Analysis in Solids. J. Comput. Chem. 2013, 34, 2557–2567. [Google Scholar] [CrossRef] [PubMed]
- Maintz, S.; Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. LOBSTER: A Tool to Extract Chemical Bonding from Plane-Wave Based DFT. J. Comput. Chem. 2016, 37, 1030–1035. [Google Scholar] [CrossRef] [PubMed]
- Gladisch, F.C.; Steinberg, S. Revealing Tendencies in the Electronic Structures of Polar Intermetallic Compounds. Crystals 2018, 8, 80. [Google Scholar] [CrossRef]
- Schäfer, H.; Schnering, H.G. Metall-Metall-Bindungen bei niederen Halogeniden, Oxyden und Oxydhalogeniden schwerer Übergangsmetalle. Angew. Chem. 1964, 76, 833–849. [Google Scholar] [CrossRef]
- Cotton, F.A. Strong Homonuclear Metal-Metal Bonds. Acc. Chem. Res. 1969, 2, 240–247. [Google Scholar] [CrossRef]
- Simon, A. Cluster of Valence Electron Poor Metals—Structure, Bonding, and Properties. Angew. Chem. Int. Ed. Engl. 1988, 27, 159–183. [Google Scholar] [CrossRef]
- Hughbanks, T. Bonding in clusters and condensed cluster compounds that extend in one, two and three dimension. Prog. Solid St. Chem. 1989, 19, 329–372. [Google Scholar] [CrossRef]
- Corbett, J.D. Exploratory synthesis of reduced rare-earth-metal halides, chalcogenides, intermetallics: New compounds, structures, and properties. J. Alloys Compds. 2006, 418, 1–20. [Google Scholar] [CrossRef]
- Corbett, J.D. Interstitially-stabilized cluster-based halides of the early transition metals. J. Alloys Compds. 1995, 229, 10–23. [Google Scholar] [CrossRef]
- Simon, A.; Mattausch, H.J.; Ryazanov, M.; Kremer, R.K. Lanthanides as d Metals. Z. Anorg. Allg. Chem. 2006, 632, 919–929. [Google Scholar] [CrossRef]
- Meyer, G. Reduced Halides of the Rare-Earth Elements. Chem. Rev. 1988, 88, 93–107. [Google Scholar] [CrossRef]
- Meyer, G. Cluster Complexes as anti-Werner Complexes. Z. Anorg. Allg. Chem. 2008, 634, 2729–2736. [Google Scholar] [CrossRef]
- Meyer, G. Rare Earth Metal Cluster Complexes. In The Rare Earth Elements; Atwood, D.A., Ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2012; ISBN 978-1-119-95097-4. [Google Scholar]
- Hughbanks, T.; Corbett, J.D. Encapsulation of Heavy Transition Metals in Iodide Clusters. Synthesis, Structure, and Bonding of the Unusual Cluster Phase Y6I10Ru. Inorg. Chem. 1989, 28, 631–635. [Google Scholar] [CrossRef]
- Hughbanks, T.; Corbett, J.D. Rare-Earth-Metal Iodide Clusters Centered by Transition Metals: Synthesis, Structure, and Bonding of R7II2M Compounds (R = Sc, Y, Pr, Gd; M = Mn, Fe, Co, Ni). Inorg. Chem. 1988, 27, 2022–2026. [Google Scholar] [CrossRef]
- Rustige, C.; Brühmann, M.; Steinberg, S.; Meyer, E.; Daub, K.; Zimmermann, S.; Wolberg, M.; Mudring, A.-V.; Meyer, G. The Prolific {ZR6}X12R and {ZR6}X10 Structure Types with Isolated Endohedrally Stabilized (Z) Rare-Earth Metal (R) Cluster Halide (X) Complexes. Z. Anorg. Allg. Chem. 2012, 638, 1922–1931. [Google Scholar] [CrossRef]
- Hughbanks, T.; Rosenthal, G.; Corbett, J.D. Alloy Clusters: The Encapsulation of Transition Metals (Mn, Fe, Co, Ni) within Cluster Halides of Zirconium and the Rare-Earth Metals. J. Am. Chem. Soc. 1986, 108, 8289–8290. [Google Scholar] [CrossRef]
- Sweet, L.E.; Roy, L.E.; Meng, F.; Hughbanks, T. Ferromagnetic Coupling in Hexanuclear Gadolinium Clusters. J. Am. Chem. Soc. 2006, 128, 10193–10201. [Google Scholar] [CrossRef] [PubMed]
- Cotton, F.A.; Haas, T.E. A Molecular Orbital Treatment of the Bonding in Certain Metal Atom Clusters. Inorg. Chem. 1964, 3, 10–17. [Google Scholar] [CrossRef]
- Ebihara, M.; Martin, J.D.; Corbett, J.D. Novel Chain and Oligomeric Condensed Cluster Phases for Gadolinium Iodides with Manganese Interstitials. Inorg. Chem. 1994, 33, 2079–2084. [Google Scholar] [CrossRef]
- Payne, M.W.; Ebihara, M.; Corbett, J.D. A Novel Oligomer of Condensed Metal Atom Clusters in [Y16Ru4I20]. Angew. Chem. Int. Ed. Engl. 1991, 30, 856–858. [Google Scholar] [CrossRef]
- Steinwand, S.J.; Corbett, J.D. Oligomeric Rare-Earth-Metal Halide Clusters. Three Structures Built of (Y16Z4)Br36 Units (Z = Ru, Ir). Inorg. Chem. 1996, 35, 7056–7067. [Google Scholar] [CrossRef] [PubMed]
- Steinberg, S.; Zimmermann, S.; Brühmann, M.; Meyer, E.; Rustige, C.; Wolberg, M.; Daub, K.; Bell, T.; Meyer, G. Oligomeric rare-earth metal cluster complexes with endohedral transition metal atoms. J. Solid State Chem. 2014, 219, 159–167. [Google Scholar] [CrossRef]
- Steinberg, S.; Bell, T.; Meyer, G. Electron Counting Rules and Electronic Structure in Tetrameric Transition-Metal (T)-Centered Rare-Earth (R) Cluster Complex Halides (X). Inorg. Chem. 2015, 54, 1026–1037. [Google Scholar] [CrossRef] [PubMed]
- Dorhout, P.K.; Payne, M.W.; Corbett, J.D. Condensed Metal Cluster Iodides Centered by Noble Metals. Six Examples of Cubic R3I3Z Phases (R = La, Pr; Z = Os, Ir, Pt). Inorg. Chem. 1991, 30, 4960–4962. [Google Scholar] [CrossRef]
- Zheng, C.; Mattausch, H.J.; Hoch, C.; Simon, A. La3Br3Ni: Jahn–Teller Distortion in the Reduced Rare Earth Metal Halide. Z. Anorg. Allg. Chem. 2009, 635, 2429–2433. [Google Scholar] [CrossRef]
- Herzmann, N.; Mudring, A.-V.; Meyer, G. Seven-Coordinate Ruthenium Atoms Sequestered in Praseodymium Clusters in the Chloride {RuPr3}Cl3. Inorg. Chem. 2008, 47, 7954–7956. [Google Scholar] [CrossRef] [PubMed]
- Payne, M.W.; Dorhout, P.K.; Kim, S.-J.; Hughbanks, T.R.; Corbett, J.D. Chains of Centered Metal Clusters with a Novel Range of Distortions: Pr3I3Ru, Y3I3Ru, and Y3I3Ir. Inorg. Chem. 1992, 31, 1389–1394. [Google Scholar] [CrossRef]
- Steinberg, S.; Valldor, M.; Meyer, G. Change of magnetic and electronic features through subtle substitution in cubic, non-centrosymmetric extended rare-earth metal cluster complexes {TR3}X3. J. Solid State Chem. 2013, 206, 176–181. [Google Scholar] [CrossRef]
- Steinberg, S.; Brgoch, J.; Miller, G.J.; Meyer, G. Identifying a Structural Preference in Reduced Rare-Earth Metal Halides by Combining Experimental and Computational Techniques. Inorg. Chem. 2012, 51, 11356–11364. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Meyer, G.; Corbett, J.D. Contrasts in Structural and Bonding Representations among Polar Intermetallic Compounds. Strongly Differentiated Hamilton Populations for Three Related Condensed Cluster Halides of the Rare-Earth Elements. Inorg. Chem. 2010, 49, 9949–9957. [Google Scholar] [CrossRef] [PubMed]
- Köckerling, M.; Martin, J.D. Electronic Fine Tuning of the Structures of Reduced Rare-Earth Metal Halides. Inorg. Chem. 2001, 40, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Bell, T. Seltenerd-Clusterkomplexe mit endohedralen Übergangsmetallatomen und ihre strukturellen sowie elektronischen Beziehungen zu intermetallischen Phasen. Dr. rer. nat. Thesis, University of Cologne, Dr. Hut Publishers, Munich, Germany, 2014. [Google Scholar]
- Nesper, R. Bonding Patterns in Intermetallic Compounds. Angew. Chem. Int. Ed. Engl. 1991, 30, 789–817. [Google Scholar] [CrossRef]
- Wade, K. The Structural Significance of the Number of Skeletal Bonding Electron-pairs in Carboranes, the Higher Boranes and Borane Anions, and Various Transition-metal Carbonyl Cluster Compounds. J. Chem. Soc. D Chem. Commun. 1971, 792–793. [Google Scholar] [CrossRef]
- Wade, K. Skeletal electron counting in cluster species. some generalisations and predictions. Inorg. Nucl. Chem. Lett. 1972, 8, 559–562. [Google Scholar] [CrossRef]
- Lin, Q.; Corbett, J.D. Exploratory Syntheses and Structures of SrAu4.3In1.7 and CaAg3.5In1.9: Electron-Poor Intermetallics with Diversified Polyanionic Frameworks That Are Derived from the CaAu4In2 Approximant. Inorg. Chem. 2011, 50, 11091–11098. [Google Scholar] [CrossRef] [PubMed]
- Pyykkö, P. Strong Closed-Shell Interactions in Inorganic Chemistry. Chem. Rev. 1997, 97, 597–636. [Google Scholar] [CrossRef] [PubMed]
- Pyykkö, P.; Desclaux, J.-P. Relativity and the Periodic System of the Elements. Acc. Chem. Res. 1979, 12, 276–281. [Google Scholar] [CrossRef]
- Pyykkö, P. Relativistic Effects in Structural Chemistry. Chem. Rev. 1988, 88, 563–594. [Google Scholar] [CrossRef]
- Pyykkö, P. Theoretical Chemistry of Gold. Angew. Chem. Int. Ed. 2004, 43, 4412–4456. [Google Scholar] [CrossRef] [PubMed]
- Smetana, V.; Lin, Q.; Pratt, D.K.; Kreyssig, A.; Ramazanoglu, M.; Corbett, J.D.; Goldman, A.I.; Miller, G.J. A Sodium-Containing Quasicrystal: Using Gold To Enhance Sodium´s Covalency in Intermetallic Compounds. Angew. Chem. Int. Ed. 2012, 51, 12699–12702. [Google Scholar] [CrossRef] [PubMed]
- Gautier, R.; Zhang, X.; Hu, L.; Yu, L.; Lin, Y.; Sunde, T.O.L.; Chon, D.; Poeppelmeier, K.R.; Zunger, A. Prediction and accelerated laboratory discovery of previously unknown 18-electron ABX compounds. Nat. Chem. 2015, 7, 308–316. [Google Scholar] [CrossRef] [PubMed]
- Steinberg, S.; Stoffel, R.P.; Dronskowski, R. Search for the Mysterious SiTe—An Examination of the Binary Si-Te System Using First-Principles-Based Methods. Cryst. Growth Des. 2016, 16, 6152–6155. [Google Scholar] [CrossRef]
- Wang, F.; Pearson, K.N.; Miller, G.J. EuAgxAl11-x with the BaCd11-Type Structure: Phase Width, Coloring, and Electronic Structure. Chem. Mater. 2009, 21, 230–236. [Google Scholar] [CrossRef]
- Steinberg, S.; Card, N.; Mudring, A.-V. From the Ternary Eu(Au/In)2 and EuAu4(Au/In)2 with Remarkable Au/In Distributions to a New Structure Type: The Gold-Rich Eu5Au16(Au/In)6 Structure. Inorg. Chem. 2015, 54, 8187–8196. [Google Scholar] [CrossRef] [PubMed]
- Smetana, V.; Corbett, J.D.; Miller, G.J. Four Polyanionic Compounds in the K-Au-Ga System: A Case Study in Exploratory Synthesis and of the Art of Structural Analysis. Inorg. Chem. 2012, 51, 1695–1702. [Google Scholar] [CrossRef] [PubMed]
- Smetana, V.; Miller, G.J.; Corbett, J.D. Three Alkali-Metal-Gold-Gallium Systems. Ternary Tunnel Structures and Some Problems with Poorly Ordered Cations. Inorg. Chem. 2012, 51, 7711–7721. [Google Scholar] [CrossRef] [PubMed]
- Smetana, V.; Miller, G.J.; Corbett, J.D. Polycluster and Substitution Effects in the Na-Au-Ga System: Remarkable Sodium Bonding Characteristics in Polar Intermetallics. Inorg. Chem. 2013, 52, 12502–12510. [Google Scholar] [CrossRef] [PubMed]
- Smetana, V.; Corbett, J.D.; Miller, G.J. Complex Polyanionic Nets in RbAu4.01(2)Ga8.64(5) and CsAu5Ga9: The Role of Cations in the Formation of New Polar Intermetallics. Z. Anorg. Allg. Chem. 2014, 640, 790–796. [Google Scholar] [CrossRef]
- Mishra, T.; Lin, Q.; Corbett, J.D. Gold Network Structures in Rhombohedral and Monoclinic Sr2Au6(Au,T)3 (T = Zn, Ga). A Transition via Relaxation. Inorg. Chem. 2013, 52, 13623–13630. [Google Scholar] [CrossRef] [PubMed]
- Palasyuk, A.; Grin, Y.; Miller, G.J. Turning Gold into “Diamond”: A Family of Hexagonal Diamond-Type Au-Frameworks Interconnected by Triangular Clusters in the Sr-Al-Au System. J. Am. Chem. Soc. 2014, 136, 3108–3117. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Kim, S.-J.; Miller, G.J.; Corbett, J.D. Synthesis, Structure, and Bonding in K12Au21Sn4. A Polar Intermetallic Compound with Dense Au20 and open AuSn4 Layers. Inorg. Chem. 2009, 48, 11108–11113. [Google Scholar] [CrossRef] [PubMed]
- Smetana, V.; Corbett, J.D.; Miller, G.J. Na8Au9.8(4)Ga7.2 and Na17Au5.87(2)Ga46.63: The diversity of pseudo 5-fold symmetries in the Na–Au–Ga system. J. Solid State Chem. 2013, 207, 21–28. [Google Scholar] [CrossRef]
- Celania, C.; Smetana, V.; Provino, A.; Pecharsky, V.; Manfrinetti, P.; Mudring, A.-V. R3Au9Pn (R = Y, Gd-Tm; Pn = Sb, Bi): A Link between Cu10Sn3 and Gd14Ag51. Inorg. Chem. 2017, 56, 7247–7256. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Corbett, J.D. Multiple Nonstoichiometric Phases with Discrete Composition Ranges in the CaAu5-CaAu4Bi-BiAu2 System. A Case Study of the Chemistry of Spinodal Decomposition. J. Am. Chem. Soc. 2010, 132, 5662–5671. [Google Scholar] [CrossRef] [PubMed]
- Smetana, V.; Steinberg, S.; Mudryk, Y.; Pecharsky, V.; Miller, G.J.; Mudring, A.-V. Cation-Poor Complex Metallic Alloys in Ba(Eu)-Au-Al(Ga) Systems: Identifying the Keys that Control Structural Arrangements and Atom Distributions at the Atomic Level. Inorg. Chem. 2015, 54, 10296–10308. [Google Scholar] [CrossRef] [PubMed]
- Provino, A.; Steinberg, S.; Smetana, V.; Kulkarni, R.; Dhar, S.K.; Manfrinetti, P.; Mudring, A.-V. Gold-rich R3Au7Sn3: Establishing the interdependence between electronic features and physical properties. J. Mater. Chem. C 2015, 3, 8311–8321. [Google Scholar] [CrossRef]
- Lin, Q.; Vetter, J.; Corbett, J.D. Disorder-Order Structural Transformation in Electron-Poor Sr3Au8Sn3 Driven by Chemical Bonding Optimization. Inorg. Chem. 2013, 52, 6603–6609. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.; Corbett, J.D. Different Cation Arrangements in Au-In Networks. Syntheses and Structures of Six Intermetallic Compounds in Alkali-Metal-Au-In Systems. Inorg. Chem. 2007, 46, 6022–6028. [Google Scholar] [CrossRef]
- Lin, Q.; Mishra, T.; Corbett, J.D. Hexagonal-Diamond-like Gold Lattices, Ba and (Au,T)3 Interstitials and Delocalized Bonding in a Family of Intermetallic Phases Ba2Au6(Au,T)3 (T = Zn, Cd, Ga, In, or Sr). J. Am. Chem. Soc. 2013, 135, 11023–11031. [Google Scholar] [CrossRef] [PubMed]
- Gerke, B.; Hoffmann, R.-D.; Pöttgen, R. Zn3 and Ga3 Triangles as Building Units in Sr2Au6Zn3 and Sr2Au6Ga3. Z. Anorg. Allg. Chem. 2013, 639, 2444–2449. [Google Scholar] [CrossRef]
- Gerke, B.; Korthaus, A.; Niehaus, O.; Haarmann, F.; Pöttgen, R. Triangular Zn3 and Ga3 units in Sr2Au6Zn3, Eu2Au6Zn3, Sr2Au6Ga3, and Eu2Au6Ga3—Structure, magnetism, 151Eu Mössbauer and 69;71Ga solid state NMR spectroscopy. Z. Naturforsch. B 2016, 71, 567–577. [Google Scholar] [CrossRef]
- Gerke, B.; Pöttgen, R. Sr2Au6Al3 and Eu2Au6Al3—First Representatives of the Sr2Au6Zn3 Type with Aluminium Triangles. Z. Naturforsch. B 2014, 69, 121–124. [Google Scholar] [CrossRef]
- Smetana, V.; Steinberg, S.; Card, N.; Mudring, A.-V.; Miller, G.J. Crystal Structure and Bonding in BaAu5Ga2 and AeAu4+xGa3‒x (Ae = Ba and Eu): Hexagonal Diamond-Type Au Frameworks and Remarkable Cation/Anion Partitioning in the Ae-Au-Ga Systems. Inorg. Chem. 2015, 54, 1010–1018. [Google Scholar] [CrossRef] [PubMed]
- Dubois, J.-M.; Belin-Ferré, E. Complex. Metallic Alloys: Fundamentals and Applications; WILEY-VCH Publishers GmbH & Co. KGaA: Weinheim, Germany, 2011; ISBN 978–3-527-32523-8. [Google Scholar]
- Urban, K.; Feuerbach, M. Structurally complex alloy phases. J. Non. Cryst. Solids 2004, 334–335, 143–150. [Google Scholar] [CrossRef]
- Li, B.; Kim, S.-J.; Miller, G.J.; Corbett, J.D. Gold Tetrahedra as Building Blocks in K3Au5Tr (Tr = In, Tl) and Rb2Au3Tl and in Other Compounds: A Broad Group of Electron-Poor Intermetallic Phases. Inorg. Chem. 2009, 48, 6573–6583. [Google Scholar] [CrossRef] [PubMed]
- Wuttig, M.; Yamada, N. Phase-change materials for rewriteable data storage. Nat. Mater. 2007, 6, 824–832. [Google Scholar] [CrossRef] [PubMed]
- Lencer, D.; Salinga, M.; Wuttig, M. Design Rules for Phase-Change Materials in Data Storage Applications. Adv. Mater. 2011, 23, 2030–2058. [Google Scholar] [CrossRef] [PubMed]
- Wuttig, M.; Raoux, S. The Science and Technology of Phase Change Materials. Z. Anorg. Allg. Chem. 2012, 638, 2455–2465. [Google Scholar] [CrossRef]
- Bensch, W. Phasenwechselverbindungen auf Chalkogenidbasis für die optische und elektrische Datenspeicherung. Z. Anorg. Allg. Chem. 2008, 634, 2009. [Google Scholar] [CrossRef]
- Chen, M.; Rubin, K.A.; Barton, R.W. Compound materials for reversible, phase-change optical data storage. Appl. Phys. Lett. 1986, 49, 502–504. [Google Scholar] [CrossRef]
- Ohno, E.; Yamada, N.; Kurumizawa, T.; Kimura, K.; Takao, M. TeGeSnAu Alloys for Phase Change Type Optical Disk Memories. Jpn. J. Appl. Phys. 1989, 28, 1235–1240. [Google Scholar] [CrossRef]
- Lencer, D.; Salinga, M.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Wuttig, M. A map for phase-change materials. Nat. Mater. 2008, 7, 972–977. [Google Scholar] [CrossRef] [PubMed]
- Shportko, K.; Kremers, S.; Woda, M.; Lencer, D.; Robertson, J.; Wuttig, M. Resonant bonding in crystalline phase-change materials. Nat. Mater. 2008, 7, 653–658. [Google Scholar] [CrossRef] [PubMed]
- Esser, M.; Maintz, S.; Dronskowski, R. Automated first-principles mapping for phase-change materials. J. Comput. Chem. 2017, 38, 620–628. [Google Scholar] [CrossRef] [PubMed]
- Deringer, V.L.; Zhang, W.; Lumeij, M.; Maintz, S.; Wuttig, M.; Mazzarello, R.; Dronskowski, R. Bonding Nature of Local Structural Motifs in Amorphous GeTe. Angew. Chem. Int. Ed. 2014, 53, 10817–10820. [Google Scholar] [CrossRef] [PubMed]
- Wuttig, M.; Lüsebrink, D.; Wamwangi, D.; Welnic, W.; Gilleßen, M.; Dronskowski, R. The role of vacancies and local distortions in the desing of new phase-change materials. Nat. Mater. 2007, 6, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, T.; Yamada, N.; Kubota, Y. Structure of stable and metastable Ge2Sb2Te5, an intermetallic compound in GeTe-Sb2Te3 pseudo-binary systems. Acta Crystallogr. Sect. B 2004, 60, 685–691. [Google Scholar] [CrossRef] [PubMed]
- Chong, T.C.; Shi, L.P.; Zhao, R.; Tan, P.K.; Li, J.M.; Lee, H.K.; Miao, X.S.; Du, A.Y.; Tung, C.H. Phase change random access memory cell with superlattice-like structure. Appl. Phys. Lett. 2006, 88, 122114. [Google Scholar] [CrossRef]
- Simpson, R.E.; Fons, P.; Kolobov, A.V.; Fukaya, T.; Krbal, M.; Yagi, T.; Tominaga, J. Interfacial phase-change memory. Nat. Nanotechnol. 2011, 6, 501–505. [Google Scholar] [CrossRef] [PubMed]
- Buck, M.R.; Sines, I.T.; Schaak, R.E. Liquid-Phase Synthesis of Uniform Cube-Shaped GeTe Microcrystals. Chem. Mater. 2010, 22, 3236–3240. [Google Scholar] [CrossRef]
- Konze, P.M.; Deringer, V.L.; Dronskowski, R. Understanding the Shape of GeTe Nanocrystals from First Principles. Chem. Mater. 2016, 28, 6682–6688. [Google Scholar] [CrossRef]
- Tominaga, J.; Kolobov, A.V.; Fons, P.; Nakano, T.; Murakami, S. Ferroelectric Order Control of the Dirac-Semimetal Phase in GeTe-Sb2Te3 Superlattices. Adv. Mater. Interfaces 2014, 1, 1300027. [Google Scholar] [CrossRef]
- Ohyanagi, T.; Kitamura, M.; Araidai, M.; Kato, S.; Takaura, N.; Shiraishi, K. GeTe sequences in superlattice phase change memories and their electrical characteristics. Appl. Phys. Lett. 2014, 104, 252106. [Google Scholar] [CrossRef]
- Momand, J.; Wang, R.; Boschker, J.E.; Verheijen, M.A.; Calarco, R.; Kooi, B.J. Interface formation of two- and three-dimensionally bonded materials in the case of GeTe-Sb2Te3 superlattices. Nanoscale 2015, 7, 19136–19143. [Google Scholar] [CrossRef] [PubMed]
- Stoner, E.C. Collective electron ferromagnetism. Proc. R. Soc. Lond. A 1938, 165, 372–414. [Google Scholar] [CrossRef]
- Landrum, G.A.; Dronskowski, R. The Orbital Origins of Magnetism: From Atoms to Molecules to Ferromagnetic Alloys. Angew. Chem. Int. Ed. 2000, 39, 1560–1585. [Google Scholar] [CrossRef]
- Dronskowski, R. Itinerant Ferromagnetism and Antiferromagnetism from the Perspective of Chemical Bonding. J. Quantum. Chem. 2004, 96, 89–94. [Google Scholar] [CrossRef]
- Dronskowski, R.; Korczak, K.; Lueken, H.; Jung, W. Chemically Tuning between Ferromagnetnism and Antiferromagnetism by Combining Theory and Synthesis in Iron/Manganese Rhodium Borides. Angew. Chem. Int. Ed. 2002, 41, 2528–2532. [Google Scholar] [CrossRef]
- Fokwa, B.P.T.; Lueken, H.; Dronskowski, R. Rational Synthetic Tuning between Itinerant Antiferromagnetism and Ferromagnetism in the Complex Boride Series Sc2FeRu5–nRhnB2 (0≤n≤5). Chem. Eur. J. 2007, 13, 6040–6046. [Google Scholar] [CrossRef] [PubMed]
- Brgoch, J.; Goerens, C.; Fokwa, B.P.T.; Miller, G.J. Scaffolding, Ladders, Chains, and Rare Ferrimagnetism in Intermetallic Borides: Electronic Structure Calculations and Magnetic Ordering. J. Am. Chem. Soc. 2011, 133, 6832–6840. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Miller, G.J.; Fokwa, B.P.T. Computational Design of Rare-Earth-Free Magnets with the Ti3Co5B2-Type Structure. Chem. Mater. 2017, 29, 2535–2541. [Google Scholar] [CrossRef]
- Fokwa, B.P.T.; Samolyuk, G.D.; Miller, G.J.; Dronskowski, R. Ladders of a Magnetically Active Element in the Structure of the Novel Complex Borid Ti9Fe2Ru18B8: Synthesis, Structure, Bonding, and Magnetism. Inorg. Chem. 2008, 47, 2113–2120. [Google Scholar] [CrossRef]
- Eck, B.; Dronskowski, R.; Takahashi, M.; Kikkawa, S. Theoretical calculations on the structures, electronic and magnetic properties of binary 3d transition metal nitrides. J. Mater. Chem. 1999, 9, 1527–1537. [Google Scholar] [CrossRef]
- Clark, W.P.; Steinberg, S.; Dronskowski, R.; McCammon, C.; Kupenko, I.; Bykov, M.; Dubronvinsky, L.; Akselrud, L.G.; Schwarz, U.; Niewa, R. High-Pressure NiAs-Type Modification of FeN. Angew. Chem. Int. Ed. 2017, 56, 7302–7306. [Google Scholar] [CrossRef] [PubMed]
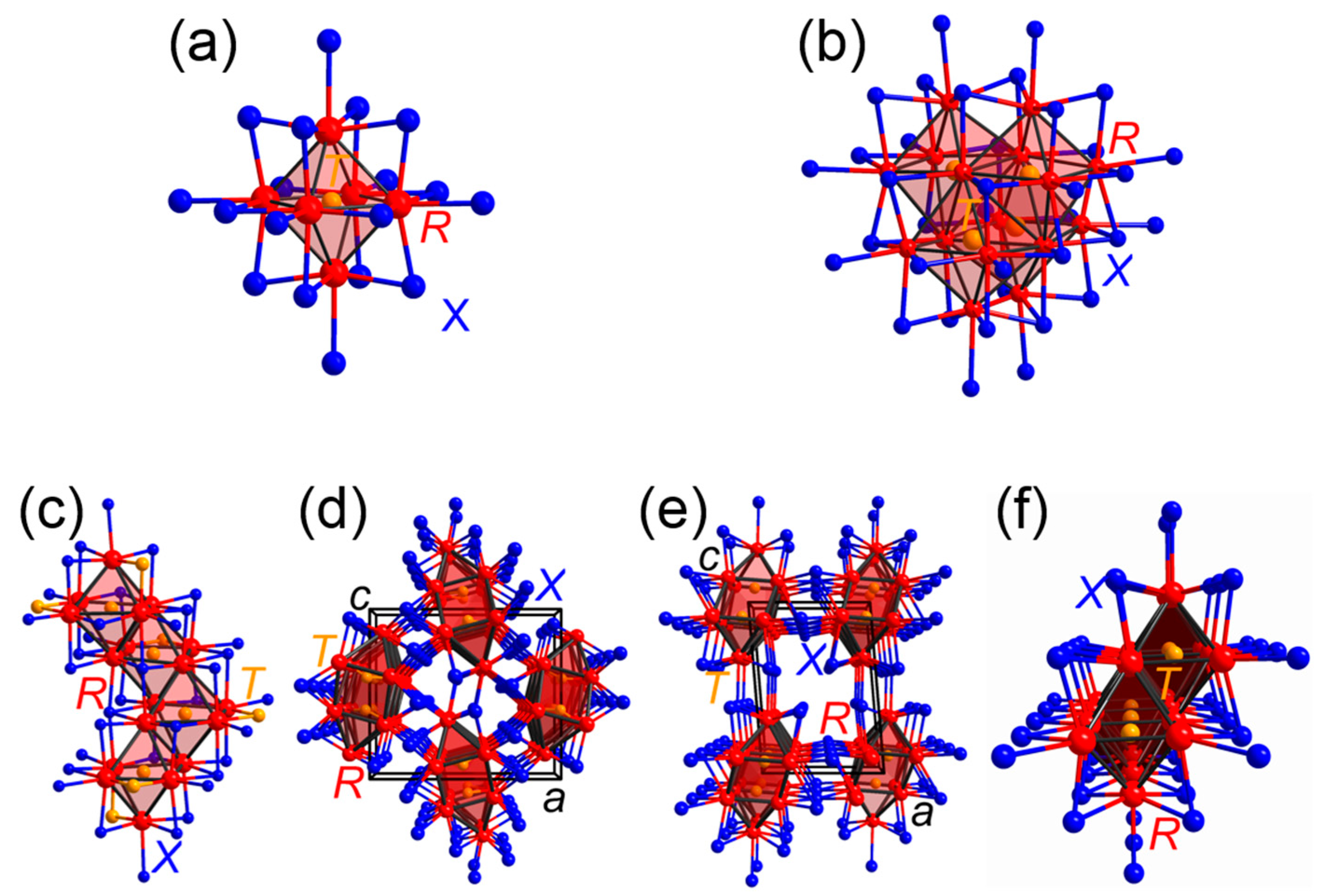
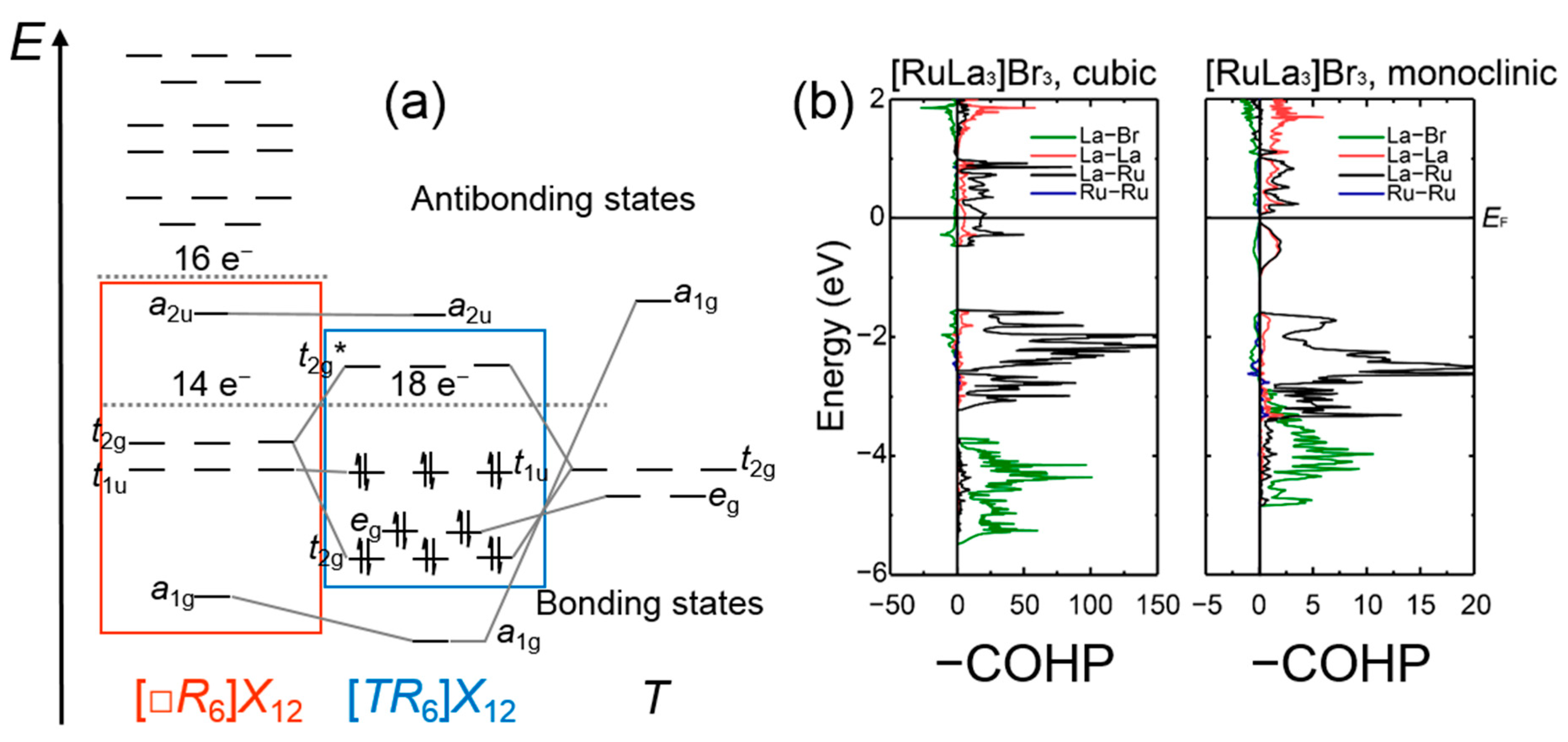

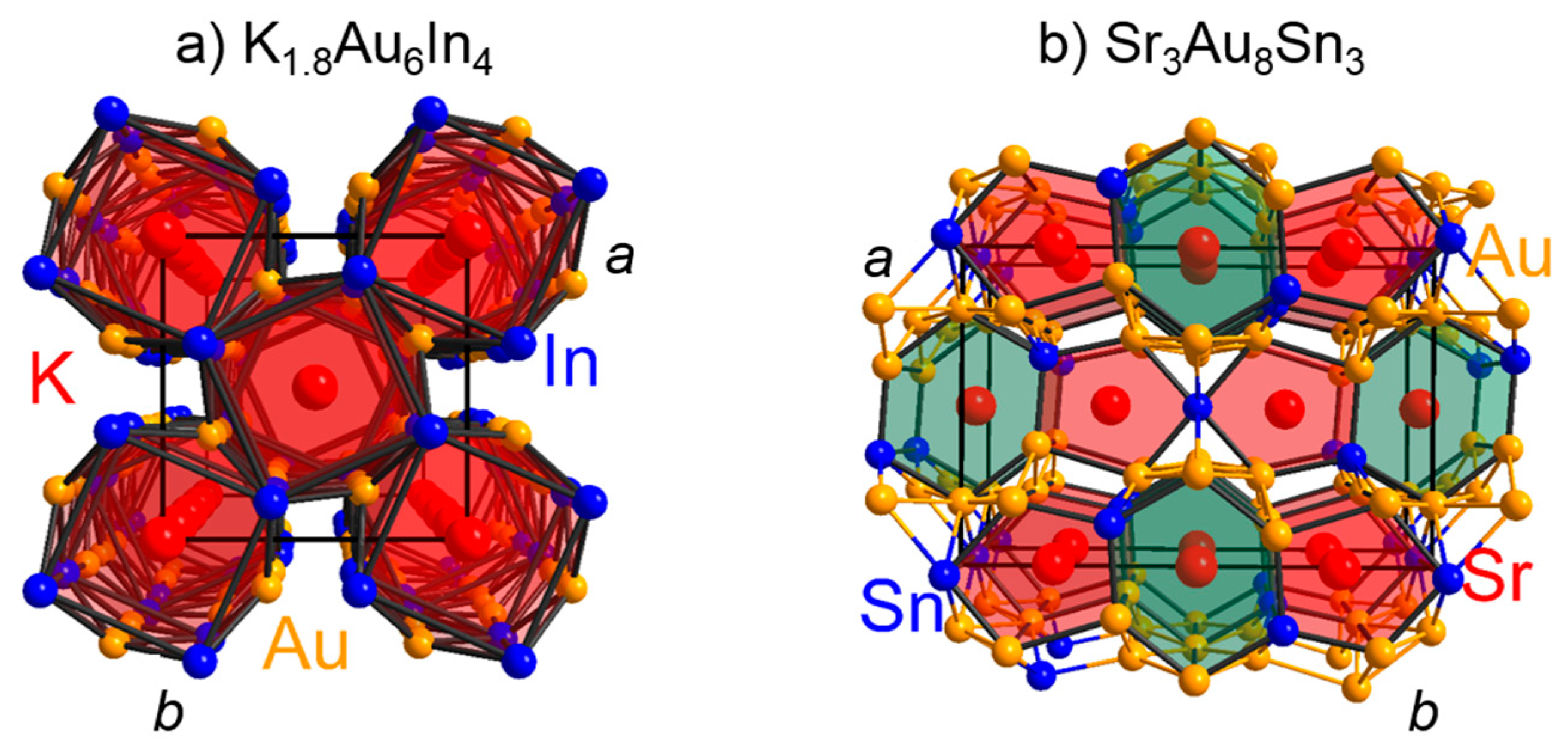

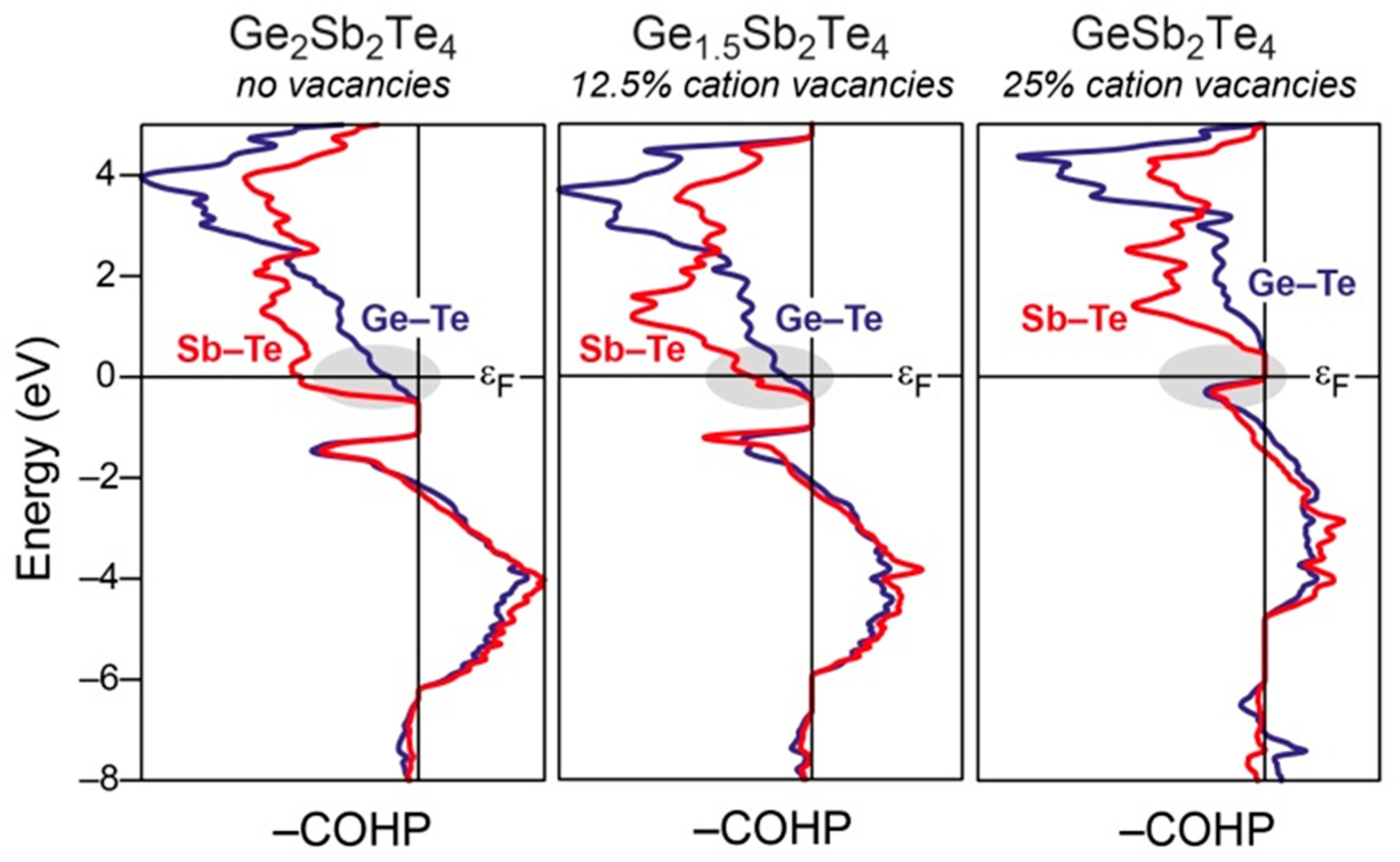
| Compound | R−T | R−R | R−X | T−T | Ref. | ||||
|---|---|---|---|---|---|---|---|---|---|
| Ave. −ICOHP/ Bond (eV/bond) | % | Ave. –ICOHP/ Bond (eV/bond) | % | Ave. –ICOHP/ Bond (eV/bond) | % | Ave. −ICOHP/ Bond (eV/bond) | % | ||
| Rare-earth transition-metal halides comprising tetramers | |||||||||
| [Ru4Y16]Br20 | 2.03 | 48.8 | 0.11 | 5.2 | 0.60 | 43.2 | 0.48 | 2.9 | [66] |
| [Ru4Y16]I20 | 1.89 | 50.1 | 0.08 | 4.5 | 0.56 | 44.2 | 0.18 | 1.2 | [66] |
| [Ir4Y16]Br24 | 2.03 | 41.9 | 0.08 | 3.5 | 0.80 | 51.8 | 0.60 | 2.8 | [66] |
| [Ru4Ho16]I24(Ho4I4) | 2.02 | 39.0 | 0.09 | 4.1 | 0.71 | 54.9 | 0.42 | 2.0 | [66] |
| [Ir4Tb16]Cl24(TbCl3)4 | 2.12 | 35.3 | 0.10 | 3.4 | 0.87 | 57.2 | 0.86 | 3.6 | [66] |
| [Rh4Tb16]Br24(TbBr3)4 | 2.17 | 34.0 | 0.14 | 4.5 | 0.95 | 59.6 | 0.49 | 1.9 | [66] |
| [Ir4Tb16]Br24(TbBr3)4 | 2.41 | 37.4 | 0.11 | 3.7 | 0.90 | 56.0 | 0.77 | 3.0 | [66] |
| [Ir4Sc16]Cl24(ScCl3)4 | 2.16 | 33.6 | 0.08 | 2.7 | 0.95 | 59.1 | 1.25 | 4.9 | [66] |
| [Os4Sc16]Cl24(ScCl3)4 | 2.26 | 33.5 | 0.09 | 2.7 | 0.98 | 58.0 | 1.57 | 5.8 | [66] |
| [Ru4Sc16]Cl24(ScCl3)4 | 2.08 | 31.6 | 0.10 | 3.3 | 1.01 | 61.1 | 1.07 | 4.0 | [66] |
| [Ru4Gd16]Br24(GdBr3)4 | 2.47 | 35.5 | 0.16 | 4.8 | 1.00 | 57.6 | 0.62 | 2.2 | [66] |
| Rare-earth transition-metal halides comprising cluster chains | |||||||||
| c-[RuLa3]Br3 | 1.91 | 65.0 | 0.07 | 4.2 | 0.45 | 30.7 | 0.003 | 0.1 | [72] |
| m-[RuLa3]Br3 a | 2.37 | 64.3 | 0.18 | 9.1 | 0.49 | 26.5 | −0.01 | 0.1 | [72] |
| c-[IrLa3]Br3 | 1.87 | 67.2 | 0.06 | 3.6 | 0.40 | 29.1 | 0.004 | 0.1 | [72] |
| m-[RuLa3]I3 | 2.45 | 60.8 | 0.22 | 9.9 | 0.59 | 29.2 | −0.003 | 0.1 | [72] |
| o-[RuPr3]Cl3 | 1.30 | 52.5 | 0.11 | 4.3 | 0.37 | 30.0 | 1.15 | 13.2 | [73] |
| m-[RuPr3]I3 | 2.14 | 62.7 | 0.20 | 8.7 | 0.48 | 28.4 | 0.03 | 0.26 | [73] |
| m-[MnGd3]I3 | 1.45 | 39.4 | 0.39 | 10.5 | 0.73 | 34.1 | 2.06 | 16.0 | [73] |
| Compound | e/a | Parent Compound Disordered? | Homoatomic Contacts | Heteroatomic Contacts | Ref. | ||
|---|---|---|---|---|---|---|---|
| Ave. −ICOHP/Bond | % | Ave. −ICOHP/Bond | % | ||||
| Compounds with anionic fragments in the forms of 1D tunnels in the crystal structures | |||||||
| EuAu5In | 1.43 | y/EuAu5.0In1.0 | Au−Au: 0.79 | 57.1 | Au−In: 0.81 | 36.5 | [88] |
| KAu3Ga2 | 1.67 | y/KAu3.1Ga1.9 | Au−Au: 0.79 Ga−Ga: 0.55 | 20.1 5.6 | Au−Ga: 1.18 | 72.2 | [89] |
| RbAu3Ga2 | 1.67 | n | Au−Au: 0.66 Ga−Ga: 0.53 | 17.7 5.7 | Au−Ga: 1.17 | 75.4 | [90] |
| Na0.5Au2Ga2 | 1.89 | y/Na0.6Au2Ga2 | Au−Au: 1.00 Ga−Ga: 0.63 | 10.2 6.5 | Au−Ga: 1.31 | 80.9 | [90] |
| K0.5Au2Ga2 | 1.89 | y/K0.6Au2Ga2 | Au−Au: 0.97 Ga−Ga: 0.51 | 8.5 4.4 | Au−Ga: 1.64 | 85.7 | [89] |
| Rb0.5Au2Ga2 | 1.89 | y/Rb0.6Au2Ga2 | Au−Au: 1.02 Ga−Ga: 0.62 | 9.9 5.9 | Au−Ga: 1.43 | 83.1 | [90] |
| NaAu2Ga4 | 2.14 | no | Ga−Ga: 1.04 | 20.0 | Au−Ga: 1.73 | 72.2 | [91] |
| KAu2Ga4 | 2.14 | y/KAu2.2Ga3.8 | Au−Au: 1.04 Ga−Ga: 1.20 | 1.6 22.7 | Au−Ga: 1.88 | 71.3 | [89] |
| CsAu5Ga9 | 2.20 | no | Au−Au: 0.59 Ga−Ga: 0.48 | 2.7 16.2 | Au−Ga: 1.42 | 78.8 | [92] |
| Compds. with hexagonal diamond-type networks as anionic fragments in the crystal structures | |||||||
| Sr2Au7Zn2 | 1.36 | y/Sr2Au6(Au,Zn)3 | Au−Au: 1.21 Zn−Zn: 0.56 | 40.5 1.0 | Au−Zn: 1.02 | 37.7 | [93] |
| Sr2Au7Al2 | 1.55 | y/Sr2Au7.3Al1.7 | Au−Au: 1.07 Al−Al: 1.26 | 32.0 2.4 | Au−Al: 1.65 | 43.0 | [94] |
| SrAu5Al2 | 1.63 | y/SrAu5.05Al1.95 | Au−Au: 1.01 Al−Al: 0.71 | 32.0 1.6 | Au−Al: 1.61 | 54.6 | [94] |
| Sr2Au6Al3 | 1.73 | y/Sr2Au6.2Al2.8 | Au−Au: 1.09 Al−Al: 1.56 | 21.5 7.7 | Au−Al: 1.68 | 50.0 | [94] |
| SrAu4Al3 | 1.88 | y/SrAu4.1Al2.9 | Au−Au: 0.93 Al−Al: 1.48 | 17.0 8.9 | Au−Al: 1.61 | 63.0 | [94] |
| Compounds with diverse (types of) polyhedrons formed by the anions in the crystal structures | |||||||
| K12Au21Sn4 | 1.32 | no | Au−Au: 1.22 | 28.0 | Au−Sn: 2.70 | 43.1 | [95] |
| Na8Au11Ga6 | 1.48 | y/Na8Au10.1Ga6.9 | Au−Au: 1.22 Ga−Ga: 1.49 | 31.9 5.2 | Au−Ga: 1.71 | 44.7 | [96] |
| NaAu4Ga2 | 1.57 | no | Au−Au: 1.20 Ga−Ga: 0.51 | 27.9 1.2 | Au−Ga: 1.61 | 65.0 | [91] |
| Y3Au9Sb | 1.77 | no | Au−Au: 1.17 | 51.7 | Au−Sb: 1.06 | 11.7 | [97] |
| CaAu4Bi | 1.83 | y/CaAu4.1Bi0.9 | Au−Au: 1.40 | 57.5 | Au−Bi: 0.54 | 22.2 | [98] |
| EuAu6Al6 | 2.00 | y/EuAu6.1Al5.9 | Au−Au: 0.88 Al−Al: 0.95 | 11.6 10.8 | Au−Al: 1.58 | 67.8 | [99] |
| EuAu6Ga6 | 2.00 | y/EuAu6.2Ga5.8 | Au−Au: 0.64 Ga−Ga: 0.91 | 11.2 11.1 | Au−Ga: 1.40 | 68.0 | [99] |
| Na5Au10Ga16 | 2.03 | no | Au−Au: 0.42 Ga−Ga: 1.10 | 0.8 22.2 | Au−Ga: 1.67 | 71.2 | [91] |
| Y3Au7Sn3 | 2.15 | no | Au−Au: 0.78 | 22.2 | Au−Sn: 1.33 | 42.1 | [100] |
| Gd3Au7Sn3 | 2.15 | no | Au−Au: 0.78 | 21.9 | Au−Sn: 1.31 | 41.1 | [100] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steinberg, S.; Dronskowski, R. The Crystal Orbital Hamilton Population (COHP) Method as a Tool to Visualize and Analyze Chemical Bonding in Intermetallic Compounds. Crystals 2018, 8, 225. https://doi.org/10.3390/cryst8050225
Steinberg S, Dronskowski R. The Crystal Orbital Hamilton Population (COHP) Method as a Tool to Visualize and Analyze Chemical Bonding in Intermetallic Compounds. Crystals. 2018; 8(5):225. https://doi.org/10.3390/cryst8050225
Chicago/Turabian StyleSteinberg, Simon, and Richard Dronskowski. 2018. "The Crystal Orbital Hamilton Population (COHP) Method as a Tool to Visualize and Analyze Chemical Bonding in Intermetallic Compounds" Crystals 8, no. 5: 225. https://doi.org/10.3390/cryst8050225
APA StyleSteinberg, S., & Dronskowski, R. (2018). The Crystal Orbital Hamilton Population (COHP) Method as a Tool to Visualize and Analyze Chemical Bonding in Intermetallic Compounds. Crystals, 8(5), 225. https://doi.org/10.3390/cryst8050225







