Optimization of Ca14MgSb11 through Chemical Substitutions on Sb Sites: Optimizing Seebeck Coefficient and Resistivity Simultaneously
Abstract
:1. Introduction
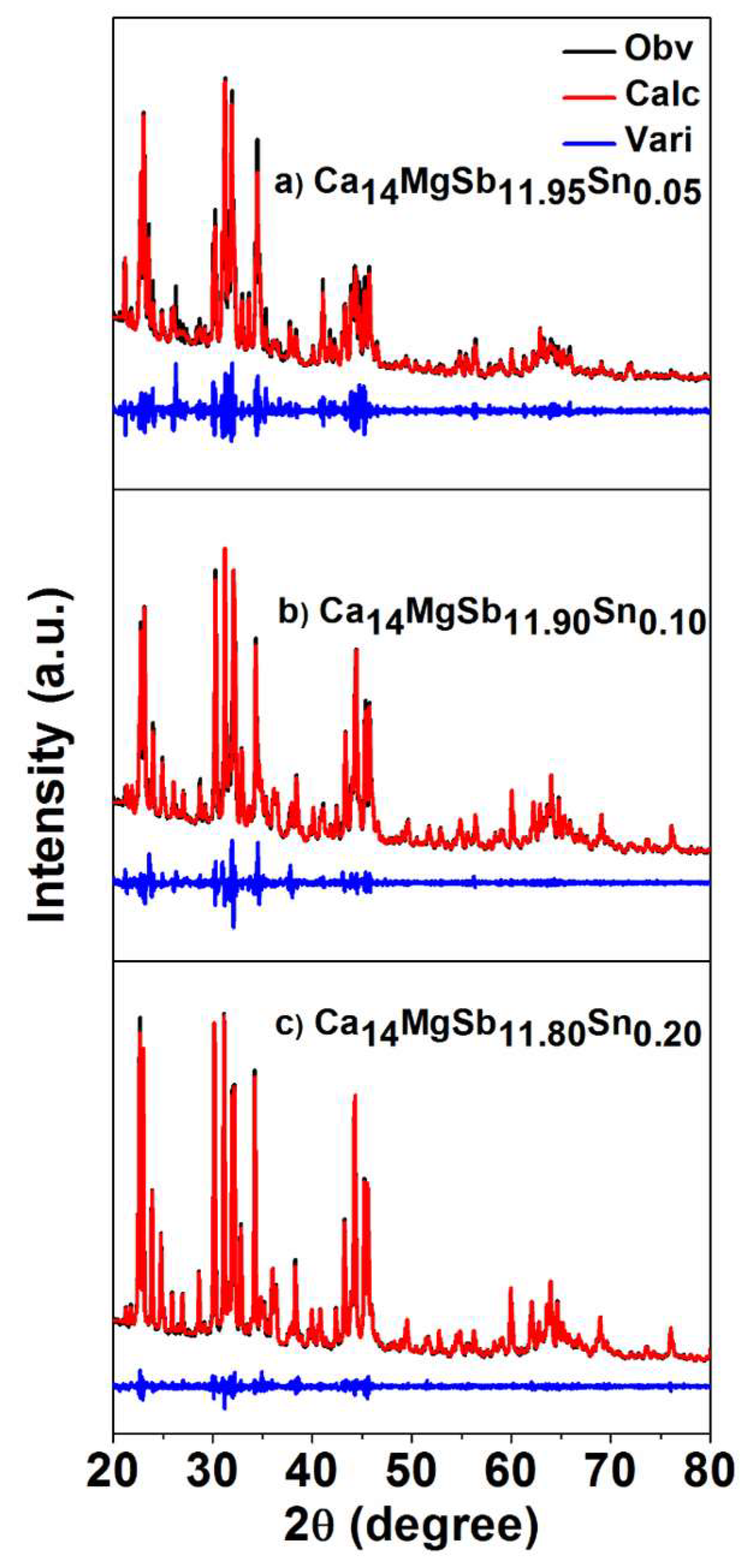
2. Experimental Section
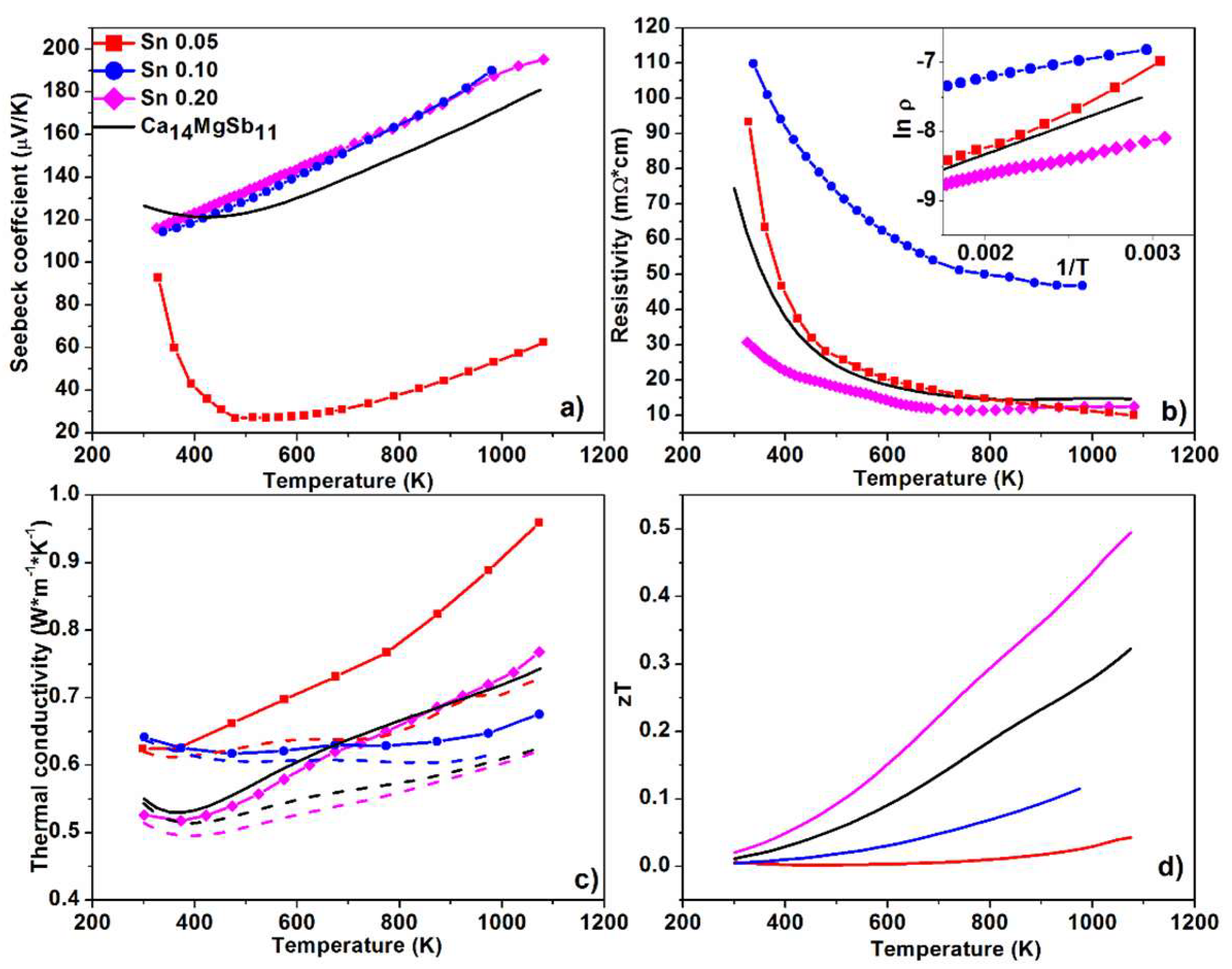
3. Results and Discussion
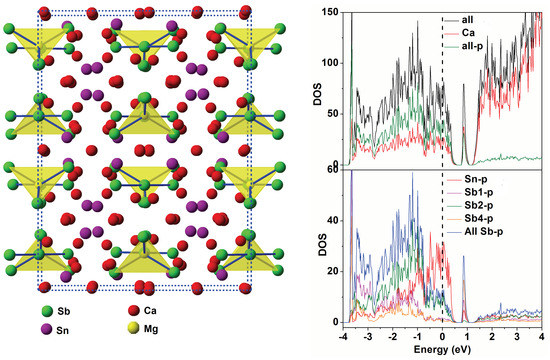
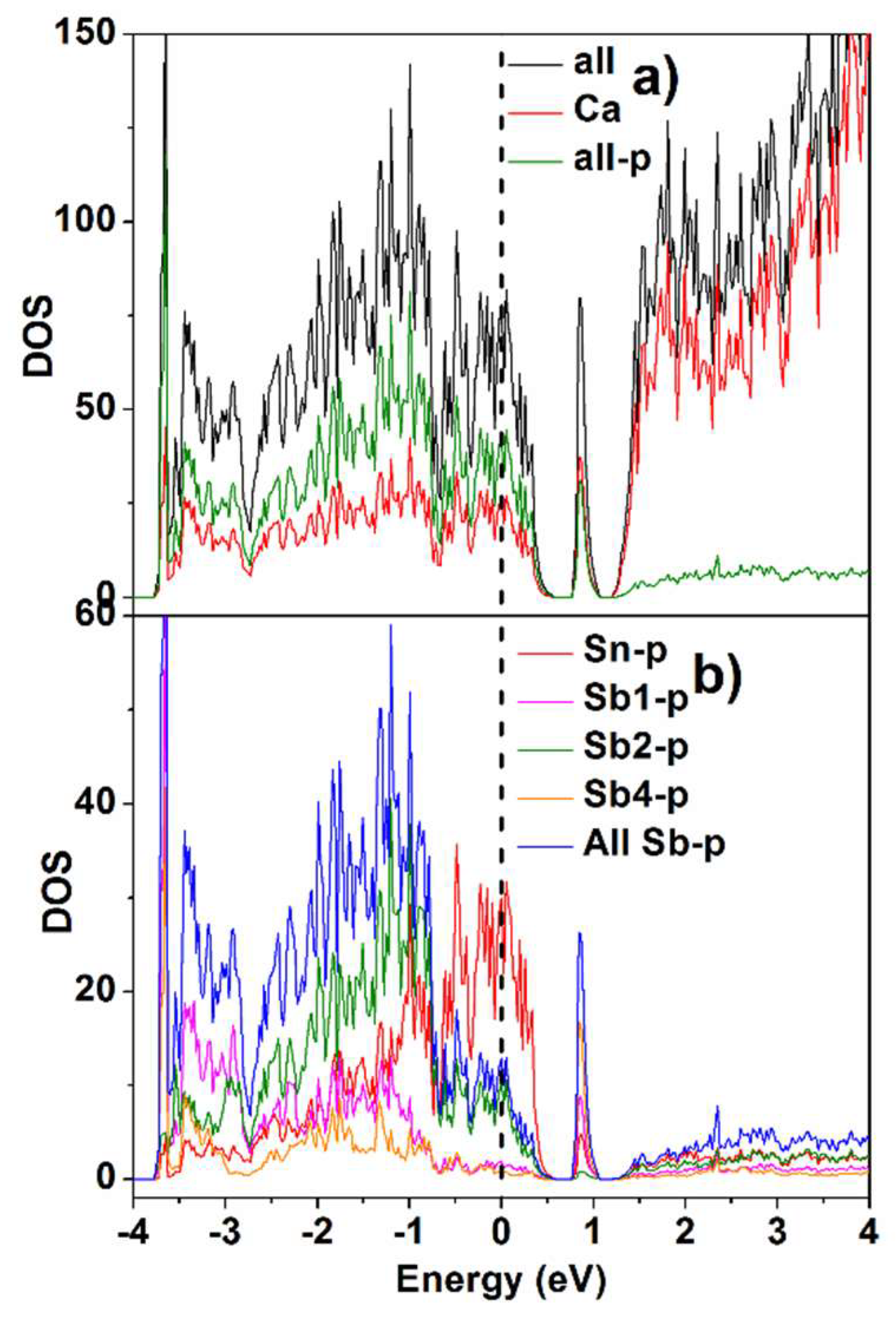
4. DOS Calculation
5. Summary
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Pomrehn, G.S.; Zevalkink, A.; Zeier, W.G.; van de Walle, A.; Snyder, G.J. Defect-Controlled Electronic Properties in AZn2Sb2 Zintl Phases. Angew. Chem. In. Ed. 2014, 53, 3422–3426. [Google Scholar] [CrossRef] [PubMed]
- Grebenkemper, J.H.; Hu, Y.; Barrett, D.; Gogna, P.; Huang, C.-K.; Bux, S.K.; Kauzlarich, S.M. High Temperature Thermoelectric Properties of Yb14MnSb11 Prepared from Reaction of MnSb with the Elements. Chem. Mater. 2015, 27, 5791. [Google Scholar] [CrossRef]
- Zevalkink, A.; Zeier, W.G.; Cheng, E.; Snyder, J.; Fleurial, J.-P.; Bux, S. Nonstoichiometry in the Zintl Phase Yb1−δZn2Sb2 as a Route to Thermoelectric Optimization. Chem. Mater. 2014, 26, 5710. [Google Scholar] [CrossRef]
- Toberer, E.S.; Cox, C.A.; Brown, S.R.; Ikeda, T.; May, A.F.; Kauzlarich, S.M.; Snyder, G.J. Traversing the Metal-Insulator Transition in a Zintl Phase: Rational Enhancement of Thermoelectric Efficiency in Yb14Mn1−xAlxSb11. Adv. Funct. Mater. 2008, 18, 2795. [Google Scholar] [CrossRef]
- Toberer, E.S.; Rauwel, P.; Gariel, S.; Taftø, J.; Jeffrey Snyder, G. Composition and the Thermoelectric Performance of β-Zn4Sb3. J. Mater. Chem. 2010, 20, 9877. [Google Scholar] [CrossRef]
- Snyder, G.J.; Christensen, M.; Nishibori, E.; Caillat, T.; Iversen, B.B. Disordered Zinc in Zn4Sb3 with Phonon-glass and Electron-crystal Thermoelectric Properties. Nat. Mater. 2004, 3, 458. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Zhang, T.; Shi, X.; Wei, S.H.; Chen, L. High Thermoelectric Performance in Copper Telluride. NPG Asia Mater. 2015, 7, e210. [Google Scholar] [CrossRef]
- He, Y.; Day, T.; Zhang, T.; Liu, H.; Shi, X.; Chen, L.; Snyder, G.J. High Thermoelectric Performance in Non-Toxic Earth-abundant Copper Sulfide. Adv. Mater. 2014, 26, 3974. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.H.; Zhang, B.P.; Chen, Y.X.; Yu, Z.X.; Liu, Y.; Li, J.F. Synthesis and Transport Property of Cu1.8S as a Promising Thermoelectric Compound. Chem. Commun. 2011, 47, 12697. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Shi, X.; Xu, F.; Zhang, L.; Zhang, W.; Chen, L.; Li, Q.; Uher, C.; Day, T.; Snyder, G.J. Copper Ion Liquid-like Thermoelectrics. Nat. Mater. 2012, 11, 422. [Google Scholar] [CrossRef] [PubMed]
- Kaltzoglou, A.; Fässler, T.; Christensen, M.; Johnsen, S.; Iversen, B.; Presniakov, I.; Sobolev, A.; Shevelkov, A. Effects of the Order–disorder Phase Transition on the Physical Properties of A8Sn44□2 (A = Rb, Cs). J. Mater. Chem. 2008, 18, 5630. [Google Scholar] [CrossRef]
- Kaltzoglou, A.; Fässler, T.F.; Gold, C.; Scheidt, E.W.; Scherer, W.; Kume, T.; Shimizu, H. Investigation of Substitution Effects and the Phase Transition in Type-I clathrates RbxCs8–xSn44□2 (1.3 ≤ x ≤ 2.1) Using Single-crystal X-ray Diffraction, Raman Spectroscopy, Heat Capacity and Electrical Resistivity Measurements. J. Solid State Chem. 2009, 182, 2924. [Google Scholar] [CrossRef]
- Chung, D.; Hogan, T.; Brazis, P.; Roccilane, M.; Kannewurf, C.; Bastea, M.; Uher, C.; Kanatzidis, M.G. CsBi4Te6: A High-Performance Thermoelectric Material for Low-Temperature Applications. Science 2000, 287, 1024. [Google Scholar] [CrossRef] [PubMed]
- Dolyniuk, J.A.; Owens-Baird, B.; Wang, J.; Zaikina, J.V.; Kovnir, K. Clathrate Thermoelectrics. Mater. Sci. Eng. R 2016, 108, 1. [Google Scholar] [CrossRef]
- Zaikina, J.V.; Kovnir, K.A.; Sobolev, A.V.; Presniakov, I.A.; Prots, Y.; Baitinger, M.; Schnelle, W.; Olenev, A.V.; Lebedev, O.I.; Van Tendeloo, G.; et al. Sn20.5□3.5As22I8: A Largely Disordered Cationic Clathrate with a New Type of Superstructure and Abnormally Low Thermal Conductivity. Chem. Eur. J. 2007, 13, 5090. [Google Scholar] [CrossRef] [PubMed]
- Aydemir, U.; Zevalkink, A.; Ormeci, A.; Gibbs, Z.M.; Bux, S.; Snyder, G.J. Thermoelectric Enhancement in BaGa2Sb2 by Zn Doping. Chem. Mater. 2015, 27, 1622. [Google Scholar] [CrossRef]
- Chanakian, S.; Aydemir, U.; Zevalkink, A.; Gibbs, Z.M.; Fleurial, J.-P.; Bux, S.; Snyder, G.J. High Temperature Thermoelectric Properties of Zn-doped Eu5In2Sb6. J. Mater. Chem. C 2015, 3, 10518. [Google Scholar] [CrossRef]
- Chanakian, S.; Zevalkink, A.; Aydemir, U.; Gibbs, Z.M.; Pomrehn, G.; Fleurial, J.-P.; Bux, S.; Snyder, G.J. Enhanced Thermoelectric Properties of Sr5In2Sb6 via Zn-doping. J. Mater. Chem. A 2015, 3, 10289. [Google Scholar] [CrossRef]
- Heremans, J.P.; Jovovic, V.; Toberer, E.S.; Saramat, A.; Kurosaki, K.; Charoenphakdee, A.; Yamanaka, S.; Snyder, G.J. Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States. Science 2008, 321, 554. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Cao, F.; Liu, W.; Lukas, K.; Yu, B.; Chen, S.; Opeil, C.; Broido, D.; Chen, G.; Ren, Z. Heavy Doping and Band Engineering by Potassium to Improve the Thermoelectric Figure of Merit in p-Type PbTe, PbSe, and PbTe1-ySey. J. Am. Chem. Soc. 2012, 134, 10031. [Google Scholar] [CrossRef] [PubMed]
- Pei, Y.; LaLonde, A.; Iwanaga, S.; Snyder, G.J. High Thermoelectric Figure of Merit in Heavy Hole Dominated PbTe. Energy Environ. Sci. 2011, 4, 2085. [Google Scholar] [CrossRef]
- Girard, S.N.; He, J.; Zhou, X.; Shoemaker, D.; Jaworski, C.M.; Uher, C.; Dravid, V.P.; Heremans, J.P.; Kanatzidis, M.G. High Performance Na-doped PbTe-PbS Thermoelectric Materials: Electronic Density of States Modification and Shape-controlled Nanostructures. J. Am. Chem. Soc. 2011, 133, 16588. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.D.; Tan, G.; Hao, S.; He, J.; Pei, Y.; Chi, H.; Wang, H.; Gong, S.; Xu, H.; Dravid, V.P.; et al. Ultrahigh Power Factor and Thermoelectric Performance in Hole-doped Single-Crystal SnSe. Science 2016, 351, 141. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Zhao, L.D.; Hao, S.; Jiang, Q.; Zheng, F.; Doak, J.W.; Wu, H.; Chi, H.; Gelbstein, Y.; Uher, C.; et al. Origin of the High Performance in GeTe-Based Thermoelectric Materials upon Bi2Te3 Doping. J. Ame. Chem. Soc. 2014, 136, 11412. [Google Scholar] [CrossRef] [PubMed]
- Levin, E.M.; Cook, B.A.; Harringa, J.L.; Bud’ko, S.L.; Venkatasubramanian, R.; Schmidt-Rohr, K. Analysis of Ce- and Yb-Doped TAGS-85 Materials with Enhanced Thermoelectric Figure of Merit. Adv. Funct. Mater. 2011, 21, 441. [Google Scholar] [CrossRef]
- Levin, E.M.; Bud’ko, S.L.; Schmidt-Rohr, K. Enhancement of Thermopower of TAGS-85 High-Performance Thermoelectric Material by Doping with the Rare Earth Dy. Adv. Funct. Mater. 2012, 22, 2766. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Pope, A.L.; Littleton, R.T.; Tritt, T.M.; Ponnambalam, V.; Xia, Y.; Poon, S.J. Effect of Sb Doping on the Thermoelectric Properties of Ti-based half-Heusler Compounds, TiNiSn1−xSbx. Appl. Phys. Lett. 2000, 77, 2476. [Google Scholar] [CrossRef]
- Shen, Q.; Chen, L.; Goto, T.; Hirai, T.; Yang, J.; Meisner, G.P.; Uher, C. Effects of Partial Substitution of Ni by Pd on the Thermoelectric Properties of ZrNiSn-based half-Heusler Compounds. Appl. Phys. Lett. 2001, 79, 4165. [Google Scholar] [CrossRef]
- Appel, O.; Zilber, T.; Kalabukhov, S.; Beeri, O.; Gelbstein, Y. Morphological Effects on the Thermoelectric Properties of Ti0.3Zr0.35Hf0.35Ni1+δSn Alloys Following Phase Separation. J. Mater. Chem. C 2015, 3, 11653. [Google Scholar] [CrossRef]
- Casper, F.; Graf, T.; Chadov, S.; Balke, B.; Felser, C. Half-Heusler Compounds: Novel Materials for Energy and Spintronic Applications. Semicond. Sci. Technol. 2012, 27, 063001. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, J.; Kawamura, A.; Kovnir, K.; Kauzlarich, S.M. Yb14MgSb11 and Ca14MgSb11—New Mg-Containing Zintl Compounds and Their Structures, Bonding, and Thermoelectric Properties. Chem. Mater. 2015, 27, 343. [Google Scholar] [CrossRef]
- Toberer, E.S.; Brown, S.R.; Ikeda, T.; Kauzlarich, S.M.; Jeffrey Snyder, G. High Thermoelectric Efficiency in Lanthanum Doped Yb14MnSb11. Appl. Phys. Lett. 2008, 93, 062110. [Google Scholar] [CrossRef]
- Yi, T.; Abdusalyamova, M.N.; Makhmudov, F.; Kauzlarich, S.M. Magnetic and Transport Properties of Te Doped Yb14MnSb11. J. Mater. Chem. 2012, 22, 14378. [Google Scholar] [CrossRef]
- Rauscher, J.F.; Cox, C.A.; Yi, T.; Beavers, C.M.; Klavins, P.; Toberer, E.S.; Snyder, G.J.; Kauzlarich, S.M. Synthesis, Structure, Magnetism, and High Temperature Thermoelectric Properties of Ge Doped Yb14MnSb11. Dalton Trans. 2010, 39, 1055. [Google Scholar] [CrossRef] [PubMed]
- Rodríquez-Carvajal, J. Recent Advances in Magnetic Structure Determination by Neutron Powder Diffraction. Physica B 1993, 192, 55. [Google Scholar] [CrossRef]
- Ravi, V.; Firdosy, S.; Caillat, T.; Brandon, E.; Van Der Walde, K.; Maricic, L.; Sayir, A. Thermal Expansion Studies of Selected High-Temperature Thermoelectric Materials. J. Electron. Mater. 2009, 38, 1433. [Google Scholar] [CrossRef]
- Mackey, J.; Dynys, F.; Sehirlioglu, A. Uncertainty Analysis for Common Seebeck and Electrical Resistivity Measurement Systems. Rev. Sci. Instrum. 2014, 85, 085119. [Google Scholar] [CrossRef] [PubMed]
- Andersen, O.K. Linear Methods in Band Theory. Phys. Rev. B 1975, 12, 3060. [Google Scholar] [CrossRef] [Green Version]
- Andersen, O.K.; Jepsen, O. Explicit, First-Principles Tight-Binding Theory. Phys. Rev. Lett. 1984, 53, 2571. [Google Scholar] [CrossRef]
- Andersen, O.K.; Pawlowska, Z.; Jepsen, O. Illustration of the Linear-muffin-tin-orbital Tight-binding Representation: Compact Orbitals and Charge Density in Si. Phys. Rev. B 1986, 34, 5253. [Google Scholar] [CrossRef]
- Nowak, H.J.; Andersen, O.K.; Fujiwara, T.; Jepsen, O.; Vargas, P. Electronic-structure Calculations for Amorphous Solids Using the Recursion Method and Linear Muffin-tin Orbitals: Application to Fe80B20. Phys. Rev. B 1991, 44, 3577. [Google Scholar] [CrossRef]
- Lambrecht, W.R.L.; Andersen, O.K. Minimal Basis Sets in the Linear Muffin-tin Orbital Method: Application to the Diamond-structure Crystals C, Si, and Ge. Phys. Rev. B 1986, 34, 2439. [Google Scholar] [CrossRef]
- Brown, S.R.; Kauzlarich, S.M.; Gascoin, F.; Jeffrey Snyder, G. High-temperature Thermoelectric Studies of A11Sb10 (A=Yb, Ca). J. Solid State Chem. 2007, 180, 1414. [Google Scholar] [CrossRef]
- Fistul, V.I. Heavily Doped Semiconductor; Plenum Press: New York, NY, USA, 1969. [Google Scholar]
- Cutler, M.; Mott, N.F. Observation of Anderson Localization in an Electron Gas. Phys. Rev. 1969, 181, 1336. [Google Scholar] [CrossRef]
- Mahan, G.D.; Sofo, J.O. The Best Thermoelectric. Proc. Natl. Acad. Sci. USA 1996, 93, 7436. [Google Scholar] [CrossRef] [PubMed]

| Atom | Wyckoff Positions | x | y | z |
|---|---|---|---|---|
| Ca1 | 32g | 9580(2) | 9274(2) | 8281(1) |
| Ca2 | 32g | 9771(2) | 1264(2) | 79(1) |
| Ca3 | 16e | 3553(2) | 0 | 2500 |
| Ca4 | 32g | 1781(2) | 4030(2) | 8439(1) |
| Mg1 | 8a | 0 | 2500 | 8750 |
| Sb1 | 16f | 1364(1) | 3864(1) | 1250 |
| Sb2 | 32g | 37(1) | 1100(1) | 8059(1) |
| Sb3 * | 32g | 8705(1) | 9751(1) | 9516(1) |
| Sb4 | 8b | 0 | 2500 | 1250 |
| Sn Amount Used in Synthesis | a (Å) | c (Å) | V (Å3) |
|---|---|---|---|
| 0.00 | 16.73(1) | 22.54(1) | 6309(1) |
| 0.05 | 16.72(1) | 22.60(1) | 6318(3) |
| 0.10 | 16.73(1) | 22.59(1) | 6323(3) |
| 0.20 | 16.73(1) | 22.62(1) | 6331(3) |
| Composition | Activation Energy (eV) |
|---|---|
| x = 0.00 | 0.15 |
| x = 0.05 | 0.17 |
| x = 0.10 | 0.08 |
| x = 0.20 | 0.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Lee, K.; Kauzlarich, S.M. Optimization of Ca14MgSb11 through Chemical Substitutions on Sb Sites: Optimizing Seebeck Coefficient and Resistivity Simultaneously. Crystals 2018, 8, 211. https://doi.org/10.3390/cryst8050211
Hu Y, Lee K, Kauzlarich SM. Optimization of Ca14MgSb11 through Chemical Substitutions on Sb Sites: Optimizing Seebeck Coefficient and Resistivity Simultaneously. Crystals. 2018; 8(5):211. https://doi.org/10.3390/cryst8050211
Chicago/Turabian StyleHu, Yufei, Kathleen Lee, and Susan M. Kauzlarich. 2018. "Optimization of Ca14MgSb11 through Chemical Substitutions on Sb Sites: Optimizing Seebeck Coefficient and Resistivity Simultaneously" Crystals 8, no. 5: 211. https://doi.org/10.3390/cryst8050211
APA StyleHu, Y., Lee, K., & Kauzlarich, S. M. (2018). Optimization of Ca14MgSb11 through Chemical Substitutions on Sb Sites: Optimizing Seebeck Coefficient and Resistivity Simultaneously. Crystals, 8(5), 211. https://doi.org/10.3390/cryst8050211