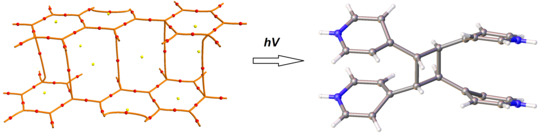
Solid-State Photoinitiated Cycloaddition Reaction of 4,4′-(Ethene-1,2-diyl)bis(pyridinium) Dinitrate: Charge-Density Perspective on Initial Stage of the Reaction
Abstract
:1. Introduction
2. Experimental Part
2.1. Synthesis
2.2. Single-Crystal X-ray Diffraction
3. Results and Discussion
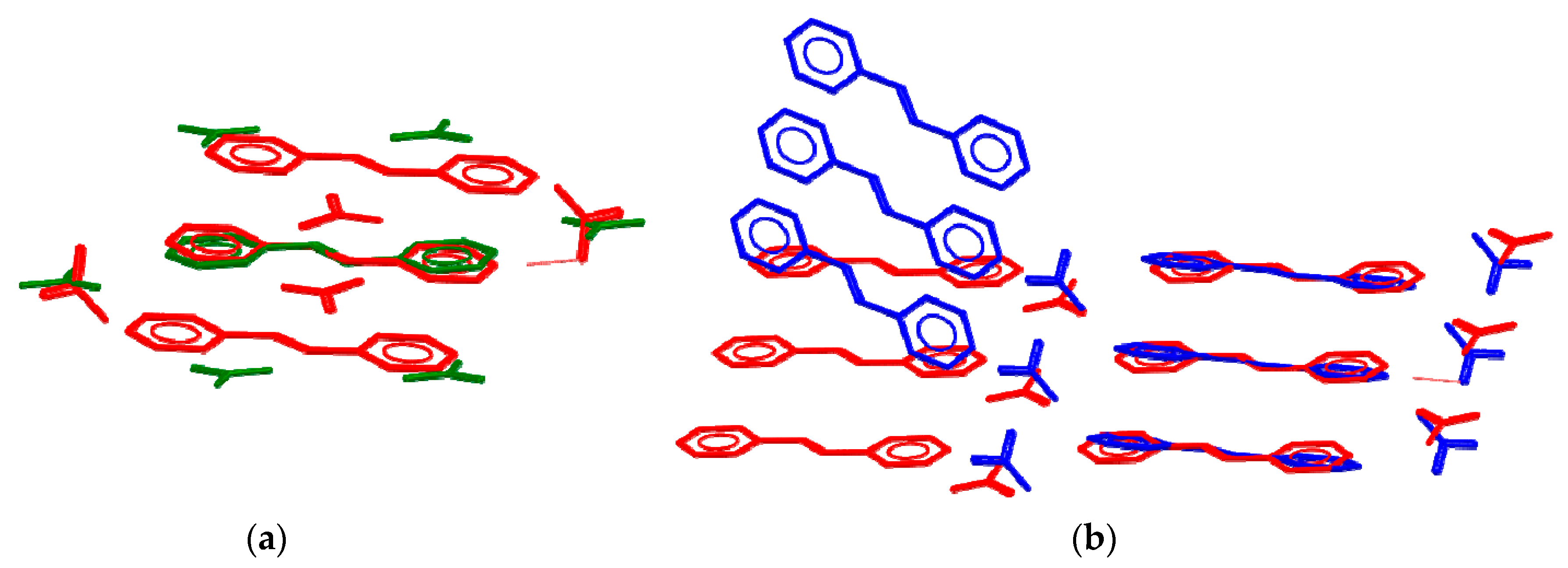
3.1. Solid-State Potocycloaddition Reaction 1 → 2
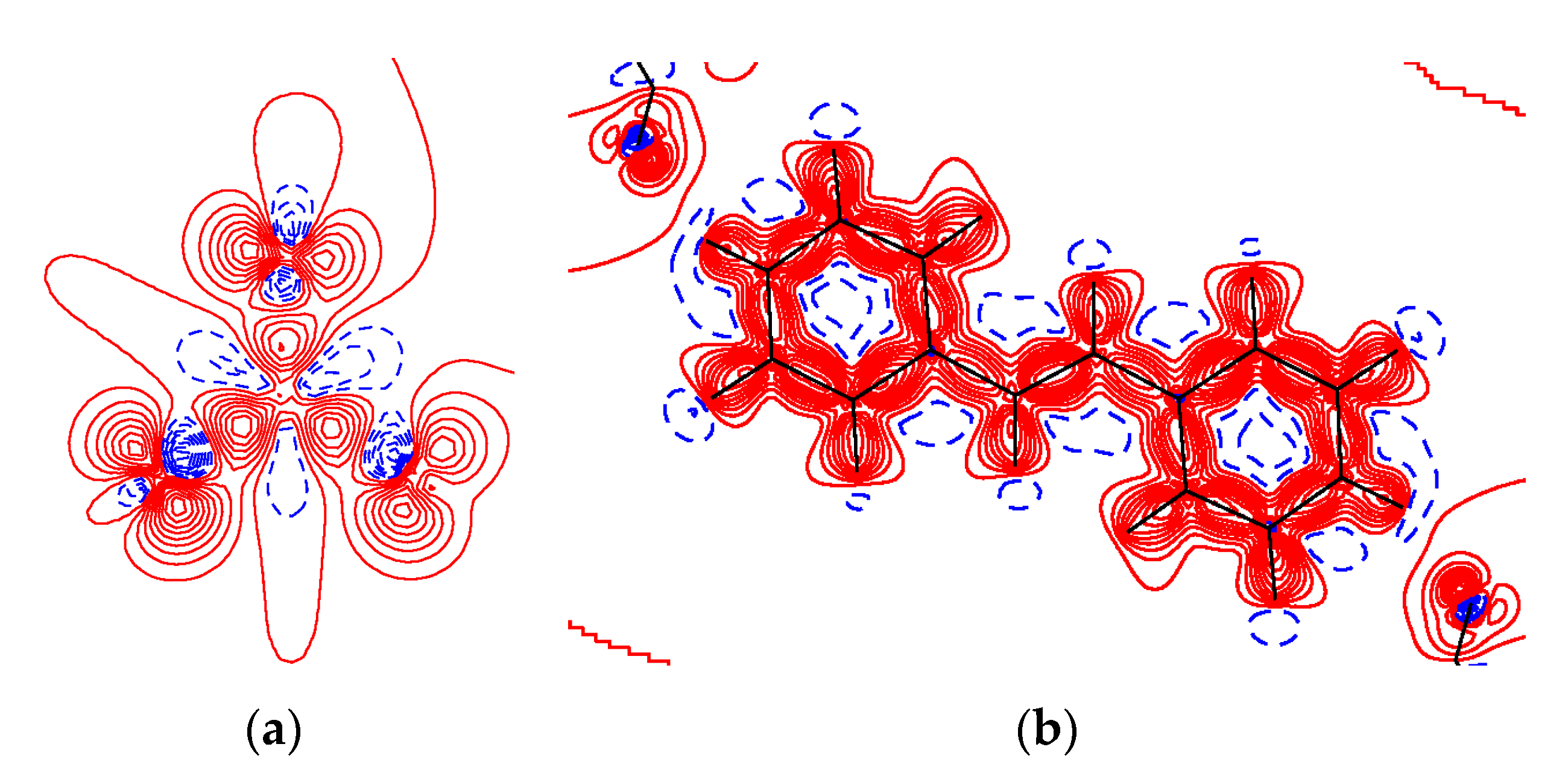
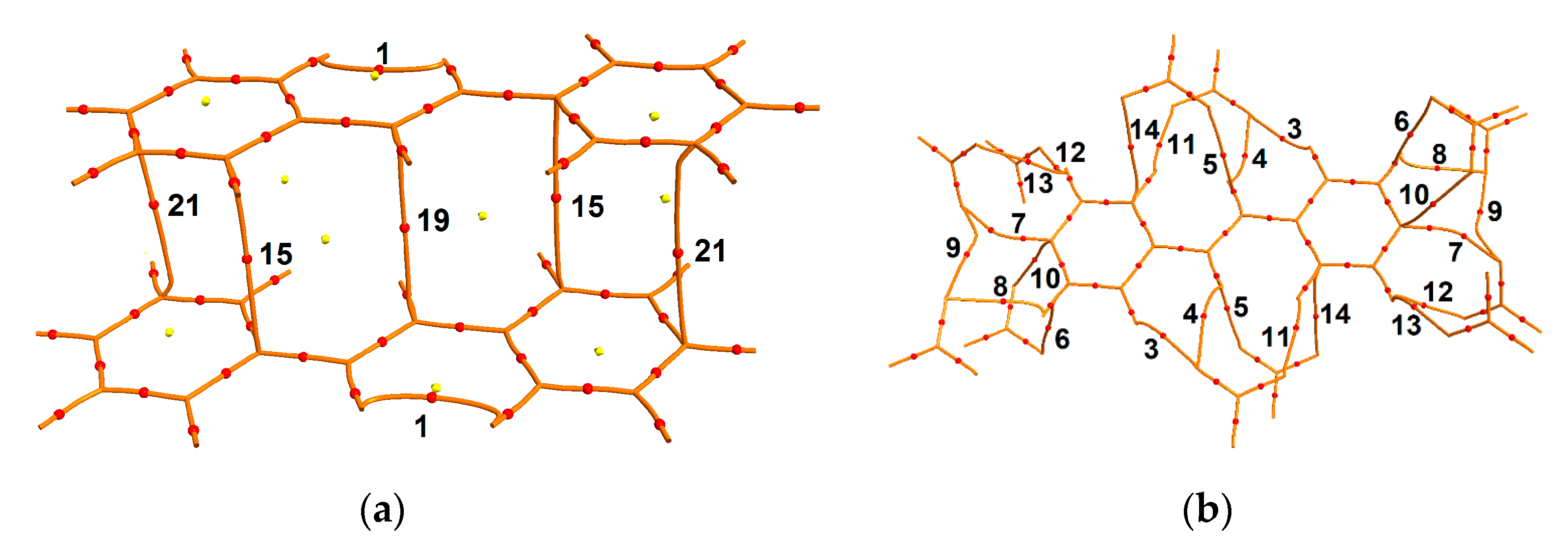
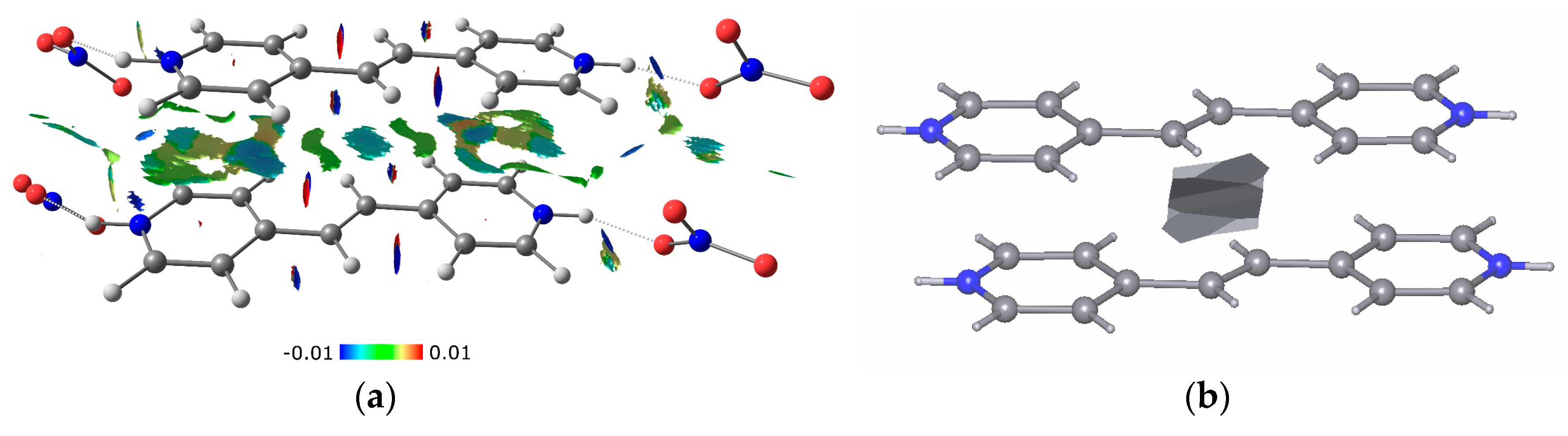
3.2. Charge-Density Analysis of Intermolecular Bonding in 1
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cohen, M.D.; Schmidt, G.M.J. 383. Topochemistry. Part I. A survey. J. Chem. Soc. 1964, 1996–2000. [Google Scholar] [CrossRef]
- Huang, S.-L.; Hor, T.S.A.; Jin, G.-X. Photodriven single-crystal-to-single-crystal transformation. Coord. Chem. Rev. 2017, 346, 112–122. [Google Scholar] [CrossRef]
- Volodin, A.D.; Korlyukov, A.A.; Zorina-Tikhonova, E.N.; Chistyakov, A.S.; Sidorov, A.A.; Eremenko, I.L.; Vologzhanina, A.V. Diastereoselective solid-state crossed photocycloaddition of olefins in a 3D Zn(II) coordination polymer. Chem. Commun. 2018, 54, 13861–13864. [Google Scholar] [CrossRef] [PubMed]
- Hu, F.; Shi, Y.-X.; Chen, H.-H.; Lang, J.-P. A Zn(II) coordination polymer and its photocycloaddition product: Syntheses, structures, selective luminescence sensing of iron(III) ions and selective absorption of dyes. Dalton Trans. 2015, 44, 18795–18803. [Google Scholar] [CrossRef] [PubMed]
- Sato, H.; Matsuda, R.; Mir, M.H.; Kitagawa, S. Photochemical cycloaddition on the pore surface of a porous coordination polymer impacts the sorption behavior. Chem. Commun. 2012, 48, 7919–7921. [Google Scholar] [CrossRef] [PubMed]
- Park, I.-H.; Medishetty, R.; Lee, H.-H.; Mulijanto, C.E.; Quah, H.S.; Lee, S.S.; Vittal, J.J. Formation of a Syndiotactic Organic Polymer Inside a MOF by a [2 + 2] Photo-Polymerization Reaction. Angew. Chem. Int. Ed. Engl. 2015, 54, 7313–7317. [Google Scholar] [CrossRef] [PubMed]
- Park, I.-H.; Chanthapally, A.; Lee, H.-H.; Quah, H.S.; Lee, S.S.; Vittal, J.J. Solid-state conversion of a MOF to a metal-organo polymeric framework (MOPF) via [2 + 2] cycloaddition reaction. Chem. Commun. 2014, 50, 3665–3667. [Google Scholar] [CrossRef] [PubMed]
- Pathigoolla, A.; Sureshan, K.M. Synthesis of Triazole-linked Homonucleoside Polymers through Topochemical Azide–Alkyne Cycloaddition. Angew. Chem. Int. Ed. Engl. 2014, 53, 9522–9525. [Google Scholar] [CrossRef]
- Nagarathinam, M.; Vittal, J.J. A Rational Approach to Crosslinking of Coordination Polymers Using the Photochemical [2 + 2] Cycloaddition Reaction. Macromol. Rap. Commun. 2006, 27, 1091–1099. [Google Scholar] [CrossRef]
- He, W.-W.; Li, S.-L.; Lan, Y.-Q. Liquid-free single-crystal to single-crystal transformations in coordination polymers. Inorg. Chem. Front. 2018, 5, 279–300. [Google Scholar] [CrossRef]
- Nagarathinam, M.; Peedikakkal, A.M.P.; Vittal, J.J. Stacking of double bonds for photochemical [2 + 2] cycloaddition reactions in the solid state. Chem. Commun. 2008, 42, 5277–5288. [Google Scholar] [CrossRef] [PubMed]
- Kuz’mina, L.G.; Vedernikov, A.I.; Gromov, S.P.; Alfimov, M.V. Crystallographic Approach to the [2 + 2] Photocycloaddition Topochemical Reactions of Unsaturated Compounds with Single Crystal Retention. Crystallogr. Rep. 2019, 64, 691–712. [Google Scholar] [CrossRef]
- Schmidt, G.M.J. Photodimerization in the solid state. Pure Appl. Chem. 1971, 27, 647–678. [Google Scholar] [CrossRef]
- Kaupp, G. Photodimerization of Cinnamic Acid in the Solid State: New Insights on Application of Atomic Force Microscopy. Angew. Chem. Int. Ed. Engl. 1992, 31, 592–595. [Google Scholar] [CrossRef]
- Kaupp, G.; Schmeyers, J.; Hangen, U.D. Anisotropic molecular movements in organic crystals by mechanical stress. J. Phys. Org. Chem. 2002, 15, 307–313. [Google Scholar] [CrossRef]
- Mishra, M.K.; Mukherjee, A.; Ramamurty, U.; Desiraju, G.R. Crystal chemistry and photomechanical behavior of 3,4-dimethoxycinnamic acid: Correlation between maximum yield in the solid-state topochemical reaction and cooperative molecular motion. IUCrJ 2015, 2, 653–660. [Google Scholar] [CrossRef]
- Berkovitch-Yellin, Z.; Leiserowitz, L. Electron density distribution in cumulenes: An X-ray study of tetraphenylbutatriene at 20 °C and −160 °C. Acta Crystallogr. B 1977, 33, 3657–3669. [Google Scholar] [CrossRef]
- Howard, J.A.K.; Mahon, M.F.; Raithby, P.R.; Sparkes, H.A. Trans-cinnamic acid and coumarin-3-carboxylic acid: Experimental charge-density studies to shed light on [2 + 2] cycloaddition reactions. Acta Crystallogr. B 2009, 65, 230–237. [Google Scholar] [CrossRef]
- Vologzhanina, A.V.; Zorina-Tikhonova, E.N.; Chistyakov, A.S.; Sidorov, A.A.; Korlyukov, A.A.; Eremenko, I.L. Analysis of intermolecular interactions in crystals of photosensitive zinc(II) coordination compounds. Rus. J. Coord. Chem. 2018, 44, 733–737. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules. A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Felloni, M.; Blake, A.J.; Hubberstey, P.; Wilson, C.; Schröder, M. Hydrogen-bonding interactions between linear bipyridinium cations and nitrate anions. CrystEngComm 2002, 4, 483–495. [Google Scholar] [CrossRef]
- Singh, A.S.; Sun, S.-S. Recyclable nitrate-templated photochemical [2 + 2] cycloaddition reaction promoted by a tripodal receptor. Chem. Commun. 2013, 49, 10070–10072. [Google Scholar] [CrossRef] [PubMed]
- Yan, G.-B. 4,4′-(Ethene-1,2-diyl)dipyridinium dinitrate. Acta Crystallogr. E 2006, 62, o4942–o4943. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. 2015, A71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. 2015, C71, 3–8. [Google Scholar]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Hansen, N.K.; Coppens, P. Testing aspherical atom refinements on small-molecule data sets. Acta Crystallogr. 1978, A34, 909–921. [Google Scholar] [CrossRef]
- Koritsansky, T.S.; Howard, S.T.; Richter, T.; Macchi, P.; Volkov, A.; Gatti, C.; Mallinson, P.R.; Farrugia, L.J.; Su, Z.; Hansen, N.K. XD—A Computer Program Package for Multipole Refinement and Topological Analysis of Charge Densities from Diffraction Data; Buffalo: New York, NY, USA, 2006. [Google Scholar]
- Allen, F.H.; Bruno, I.J. Bond lengths in organic and metal-organic compounds revisited: X–H bond lengths from neutron diffraction data. Acta Crystallogr. Sect. B 2010, 66, 380–386. [Google Scholar] [CrossRef]
- Madsen, A.Ø. SHADE web server for estimation of hydrogen anisotropic displacement parameters. J. Appl. Crystallogr. 2006, 39, 757–758. [Google Scholar] [CrossRef]
- Volkov, A.; Abramov, Y.A.; Coppens, P. Density-optimized radial exponents for X-ray charge-density refinement from ab initio crystal calculations. Acta Crystallogr. Sect. A 2001, 57, 272–282. [Google Scholar] [CrossRef]
- Henn, J.; Meindl, K. More about systematic errors in charge-density studies. Acta Crystallogr. Sect. A 2014, 70, 499–513. [Google Scholar] [CrossRef]
- Zhurov, V.V.; Zhurova, E.A.; Pinkerton, A.A. Optimization and evaluation of data quality for charge density studies. J. Appl. Crystallogr. 2008, 41, 340–349. [Google Scholar] [CrossRef]
- Farrugia, L.J. WinGX and ORTEP for Windows: An update. J. Appl. Crystallogr. 2012, 45, 849–854. [Google Scholar] [CrossRef]
- Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0—New features for the visualization and investigation of crystal structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
- Childs, S.L.; Wood, P.A.; Rodríguez-Hornedo, N.; Reddy, L.S.; Hardcastle, K.I. Analysis of 50 Crystal Structures Containing Carbamazepine Using the Materials Module of Mercury CSD. Cryst. Growth Des. 2009, 9, 1869–1888. [Google Scholar] [CrossRef]
- Vologzhanina, A.V. Intermolecular Interactions in Functional Crystalline Materials: From Data to Knowledge. Crystals 2019, 9, 478. [Google Scholar] [CrossRef] [Green Version]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Gavezzotti, A. Are Crystal Structures Predictable? Acc. Chem. Res. 1994, 27, 309–314. [Google Scholar] [CrossRef]
- Gavezzotti, A.; Filippini, G. Geometry of the Intermolecular X-H…Y (X, Y = N, O) Hydrogen Bond and the Calibration of Empirical Hydrogen-Bond Potentials. J. Phys. Chem. 1994, 98, 4831–4837. [Google Scholar] [CrossRef]
- Dunitz, J.D.; Gavezzotti, A. Molecular Recognition in Organic Crystals: Directed Intermolecular Bonds or Nonlocalized Bonding? Angew. Chem. Int. Ed. 2005, 44, 1766–1787. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [Green Version]
- Saleh, G.; Gatti, C.; Lo Presti, L. Non-covalent interaction via the reduced density gradient: Independent atom model vs experimental multipolar electron densities. Compt. Theor. Chem. 2012, 998, 148–163. [Google Scholar] [CrossRef]
- Baggioli, A.; Cavallotti, C.A.; Famulari, A. Exploring short intramolecular interactions in alkylaromatic substrates. Phys. Chem. Chem. Phys. 2016, 18, 29616–29628. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hey, J.; Leusser, D.; Kratzert, D.; Fliegl, H.; Dieterich, J.M.; Mata, R.A.; Stalke, D. Heteroaromaticity approached by charge density investigations and electronic structure calculations. Phys. Chem. Chem. Phys. 2013, 15, 20600–20610. [Google Scholar] [CrossRef] [PubMed]
- Arkhipov, D.E.; Lyubeshkin, A.V.; Volodin, A.D.; Korlyukov, A.A. Molecular Structures Polymorphism the Role of F…F Interactions in Crystal Packing of Fluorinated Tosylates. Crystals 2019, 9, 242. [Google Scholar] [CrossRef] [Green Version]
- Peresypkina, E.V.; Blatov, V.A. Topology of molecular packings in organic crystals. Acta Crystallogr. Sect. B 2000, 56, 1035–1045. [Google Scholar] [CrossRef] [Green Version]
- Blatova, O.A.; Blatov, V.A.; Serezhkin, V.N. A new set of molecular descriptors. Acta Crystallogr. Sect. B 2002, 58, 219–226. [Google Scholar] [CrossRef] [Green Version]
- Serezhkin, V.N.; Serezhkina, L.B.; Vologzhanina, A.V. Voronoi-Dirichlet tesselation as a tool for investigation of polymorphism in molecular crystals with CwHxNyOz composition and photochromic properties. Acta Crystallogr. Sect. B 2012, 68, 305–312. [Google Scholar] [CrossRef]
- Serezhkin, V.N.; Savchenkov, A.V. Application of the Method of Molecular Voronoi–Dirichlet Polyhedra for Analysis of Noncovalent Interactions in Crystal Structures of Flufenamic Acid—The Current Record-Holder of the Number of Structurally Studied Polymorphs. Cryst. Growth Des. 2015, 15, 2878–2882. [Google Scholar] [CrossRef]
- Vologzhanina, A.V.; Savchenkov, A.V.; Dmitrienko, A.O.; Korlyukov, A.A.; Bushmarinov, I.S.; Pushkin, D.V.; Serezhkina, L.B. Electronic Structure of Cesium Butyratouranylate(VI) as Derived from DFT-assisted Powder X-ray Diffraction Data. J. Phys. Chem. A 2014, 118, 9745–9752. [Google Scholar] [CrossRef]
- Vologzhanina, A.V.; Kats, S.V.; Penkova, L.V.; Pavlenko, V.A.; Efimov, N.N.; Minin, V.V.; Eremenko, I.L. Combined analysis of chemical bonding in a CuII dimer using QTAIM, Voronoi tessellation and Hirshfeld surface approaches. Acta Crystallogr. Sect. B 2015, 71, 543–554. [Google Scholar] [CrossRef]
- Vologzhanina, A.V.; Lyssenko, K.A. Interatomic interactions in the crystal of (C4H11N2)2(C4H12N2)[Mo(CN)8]: Comparison of two approaches. Rus. Chem. Bull. 2013, 62, 1786–1792. [Google Scholar] [CrossRef]
- Lyssenko, K.A.; Vologzhanina, A.V.; Torubaev, Y.V.; Nelyubina, Y.V. A comparatie study of a mixed-ligand copper(II) complex by the theory of atoms in molecules and the Voronoi tessellation. Mendeleev Commun. 2014, 24, 216–218. [Google Scholar] [CrossRef]
- Mahon, M.F.; Raithby, P.R.; Sparkes, H.A. Investigation of the factors favouring solid state [2 + 2] cycloaddition reactions; the [2 + 2] cycloaddition reaction of coumarin-3-carboxylic acid. CrystEngComm 2008, 10, 573–576. [Google Scholar] [CrossRef]



| Identification Code | 1 | 2 |
|---|---|---|
| Formula | C12H12N4O6 | C24H24N8O12 |
| Formula weight | 308.26 | 616.51 |
| Space group | C 2/c | I 2/a |
| a (Å) | 17.4543(4) | 19.143(10) |
| b (Å) | 3.6714(1) | 3.6089(19) |
| c (Å) | 20.0021(5) | 19.428(17) |
| β (°) | 93.832(1) | 93.539(5) |
| V (Å3) | 1278.90(6) | 1339.6(12) |
| Z | 4 | 2 |
| µ (mm−1) | 0.131 | 0.125 |
| dcalc (g cm−1) | 1.600 | 1.528 |
| F(000) | 640 | 640 |
| Crystal size (mm) | 0.35 × 0.19 × 0.16 | 0.35 × 0.19 × 0.16 |
| Tmin, Tmax | 0.931, 0.962 | 0.932, 0.960 |
| No. of measured, independent and observed [I > 2σ(I)] reflections | 182,334, 5992, 5169 | 7208, 2291, 1284 |
| Rint | 0.030 | 0.055 |
| Refinement method IAM/multipole model | ||
| No. of parameters | 100/385 | 117/- |
| Goodness-of-fit (on F2/on F) | 1.05/0.93 | 0.99/- |
| Final R(F) indices (all data) | ||
| Spherical atom model (on F2) | R1 = 0.048, wR2 = 0.100 | R1 = 0.135, wR2 = 0.180 |
| Multipole atom model (on F/F2) | R1 = 0.031/0.033 | |
| Final R(F) indices (I > 2σ(I)) | ||
| IAM model (on F2) | R1 = 0.042, wR2 = 0.098 | R1 = 0.081, wR2 = 0.158 |
| Multipole atom model (on F/F2) | R1 = 0.024/0.031, wR2 = 0.027/0.053 | |
| Δρmax, Δρmin (eÅ−3) | ||
| IAM model (all data) | 0.77, −0.25 | 0.67, −0.34 |
| Multipole atom model (all data) | 0.18, −0.19 | |
| 1 | 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| № | Atom1 | Atom2 | R, Å | ρ(r), e Å−3 | ∇2ρ(r), e Å−5 | V(r), a.u. | Ebond, kJ mol−1 | Ω, % | R, Å | Ω, % |
| Intramolecular | ||||||||||
| 1 | H4 | H6 | 1.980 | 0.865 | 1.2 | −0.008 | 2.56 | 17.9 | 2.114 | 8.9 |
| Intermolecular cation…anion | ||||||||||
| 2 | O1 | H1A a | 2.263 | 0.049 | 1.2 | −0.006 | −1.87 | 14.7 | 2.540 | 12.1 |
| 3 | H2 b | 2.307 | 0.071 | 1.2 | −0.007 | −2.18 | 14.3 | 2.403 | 11.9 | |
| 4 | H6 b | 2.479 | 0.037 | 0.7 | −0.003 | −1.07 | 11.4 | 2.107 | 12.1 | |
| 5 | H6 c | 2.777 | 0.041 | 0.5 | −0.003 | −0.95 | 10.9 | 2.314 | 7.0 | |
| 6 | H1A d | 2.829 | 0.035 | 0.5 | −0.003 | −0.89 | 7.8 | 2.754 | 9.6 | |
| 7 | O2 | H1 | 1.802 | 0.310 | 1.2 | −0.038 | −11.97 | 19.6 | 1.801 | 22.0 |
| 8 | H1A a | 2.477 | 0.066 | 1.0 | −0.006 | −1.91 | 9.4 | 2.502 | 11.7 | |
| 9 | O2 d | 2.565 | 0.056 | 0.6 | −0.004 | −1.32 | 11.2 | 3.135 | 3.7 | |
| 10 | N1 d | 3.059 | 0.035 | 0.7 | −0.003 | −1.03 | 1.6 | #3.252 | #0.2 | |
| 11 | O3 | H4 e | 2.256 | 0.067 | 1.4 | −0.009 | −2.80 | 16.0 | 2.467 | 9.4 |
| 12 | H5 f | 2.473 | 0.048 | 0.8 | −0.004 | −1.33 | 13.9 | 2.752 | 9.7 | |
| 13 | H5 | 2.590 | 0.055 | 0.8 | −0.005 | −1.49 | 11.0 | 2.797 | 12.2 | |
| 14 | C4 g | 2.984 | 0.032 | 0.4 | −0.002 | −0.73 | 6.4 | #3.213 | #0.1 | |
| Intermolecular cation…cation | ||||||||||
| 15 | C2 | C3 f | 3.332 | 0.033 | 0.3 | −0.002 | −0.61 | 3.5 | #3.619 | #0.8 |
| 16 | H2 h | 3.557 | 0.016 | 0.2 | −0.008 | −2.43 | 2.0 | 3.330 | 2.8 | |
| 17 | H1A h | 3.594 | 0.012 | 0.1 | −0.001 | −0.19 | 1.9 | #3.799 | #0.2 | |
| 18 | C4 | H4 f | 3.357 | 0.017 | 0.2 | −0.008 | −2.64 | 3.7 | #3.691 | #0.6 |
| 19 | C6 | C6 i | 3.310 | 0.026 | 0.3 | −0.002 | −0.53 | 2.1 | 1.635 | 15.7 |
| 20 | H6 i | 3.515 | 0.016 | 0.2 | −0.001 | −0.26 | 1.8 | - | - | |
| 21 | N1 | C5 f | 3.320 | 0.022 | 0.2 | −0.001 | −0.39 | 2.9 | - | - |
| 22 | H2 | H2 j | 2.824 | 0.021 | 0.3 | −0.001 | −0.43 | 8.7 | 3.005 | 5.2 |
| 23 | H5 | H5 f | 2.507 | 0.013 | 0.3 | −0.001 | −0.33 | 11.9 | 2.678 | 12.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vologzhanina, A.V.; Aleshin, D.Y.; Volodin, A.D.; Savchenkov, A.V.; Ushakov, I.E.; Korlyukov, A.A. Solid-State Photoinitiated Cycloaddition Reaction of 4,4′-(Ethene-1,2-diyl)bis(pyridinium) Dinitrate: Charge-Density Perspective on Initial Stage of the Reaction. Crystals 2019, 9, 613. https://doi.org/10.3390/cryst9120613
Vologzhanina AV, Aleshin DY, Volodin AD, Savchenkov AV, Ushakov IE, Korlyukov AA. Solid-State Photoinitiated Cycloaddition Reaction of 4,4′-(Ethene-1,2-diyl)bis(pyridinium) Dinitrate: Charge-Density Perspective on Initial Stage of the Reaction. Crystals. 2019; 9(12):613. https://doi.org/10.3390/cryst9120613
Chicago/Turabian StyleVologzhanina, Anna V., Dmitry Yu. Aleshin, Alexander D. Volodin, Anton V. Savchenkov, Ivan E. Ushakov, and Alexander A. Korlyukov. 2019. "Solid-State Photoinitiated Cycloaddition Reaction of 4,4′-(Ethene-1,2-diyl)bis(pyridinium) Dinitrate: Charge-Density Perspective on Initial Stage of the Reaction" Crystals 9, no. 12: 613. https://doi.org/10.3390/cryst9120613
APA StyleVologzhanina, A. V., Aleshin, D. Y., Volodin, A. D., Savchenkov, A. V., Ushakov, I. E., & Korlyukov, A. A. (2019). Solid-State Photoinitiated Cycloaddition Reaction of 4,4′-(Ethene-1,2-diyl)bis(pyridinium) Dinitrate: Charge-Density Perspective on Initial Stage of the Reaction. Crystals, 9(12), 613. https://doi.org/10.3390/cryst9120613