Tunable and Polarization-Independent Plasmon-Induced Transparency in a Fourfold Symmetric Metal-Graphene Terahertz Metamaterial
Abstract
:1. Introduction
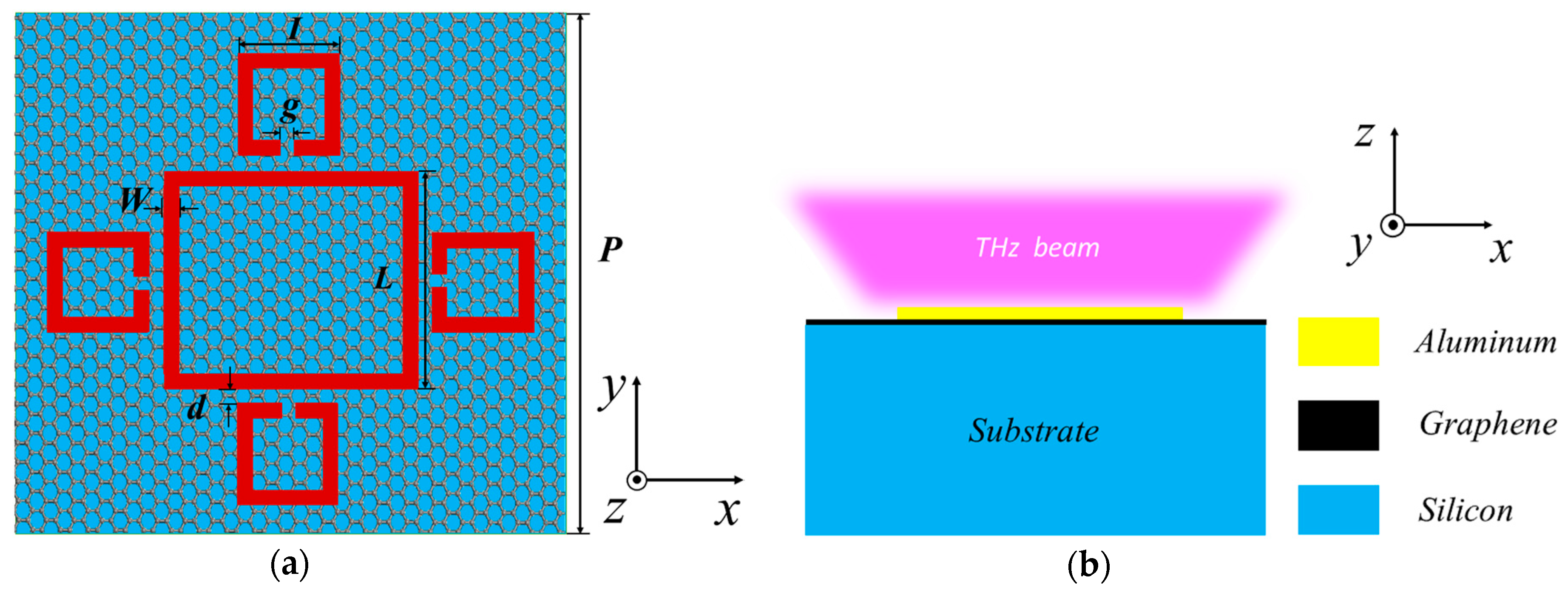
2. Proposed Structure and Methods
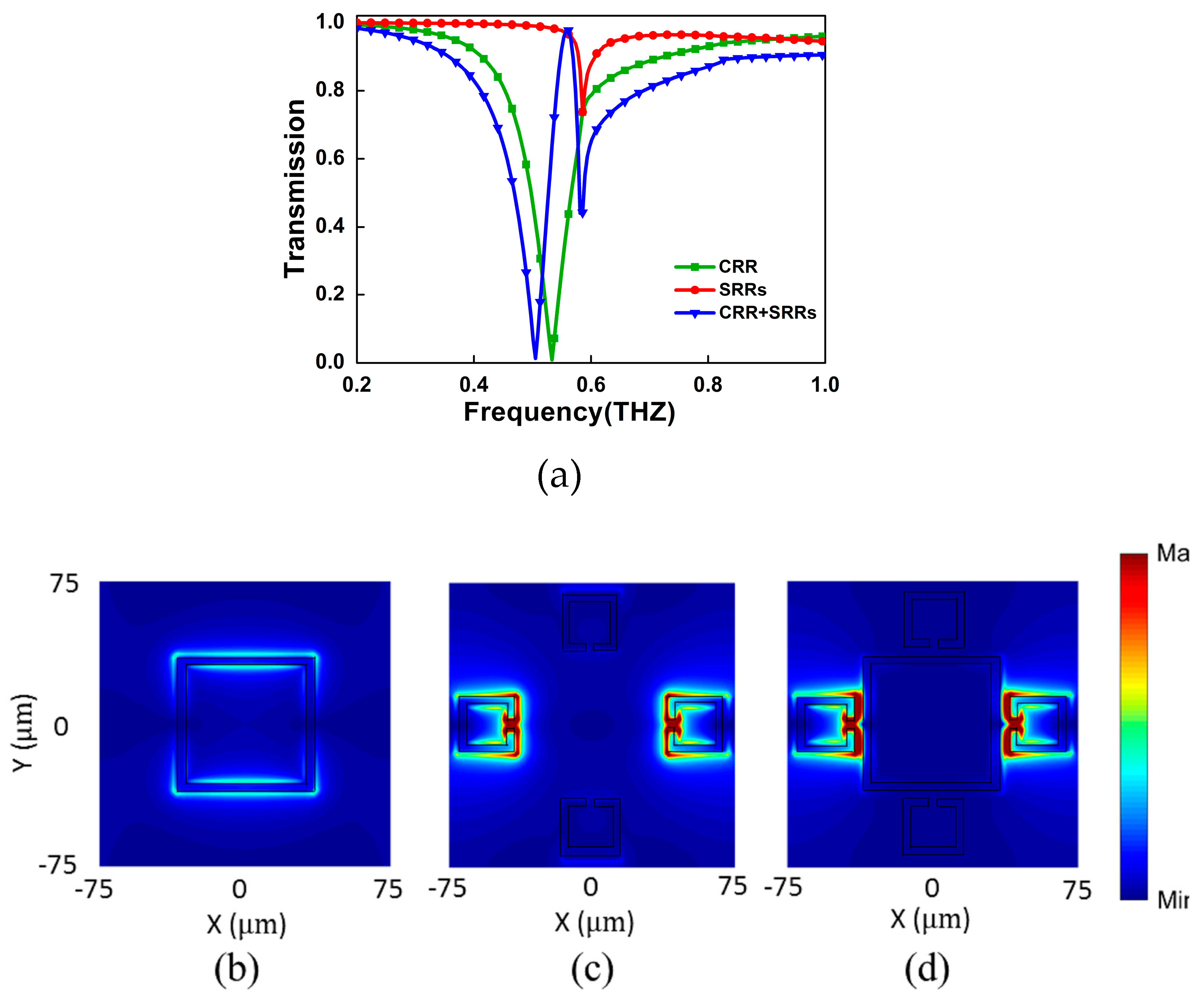
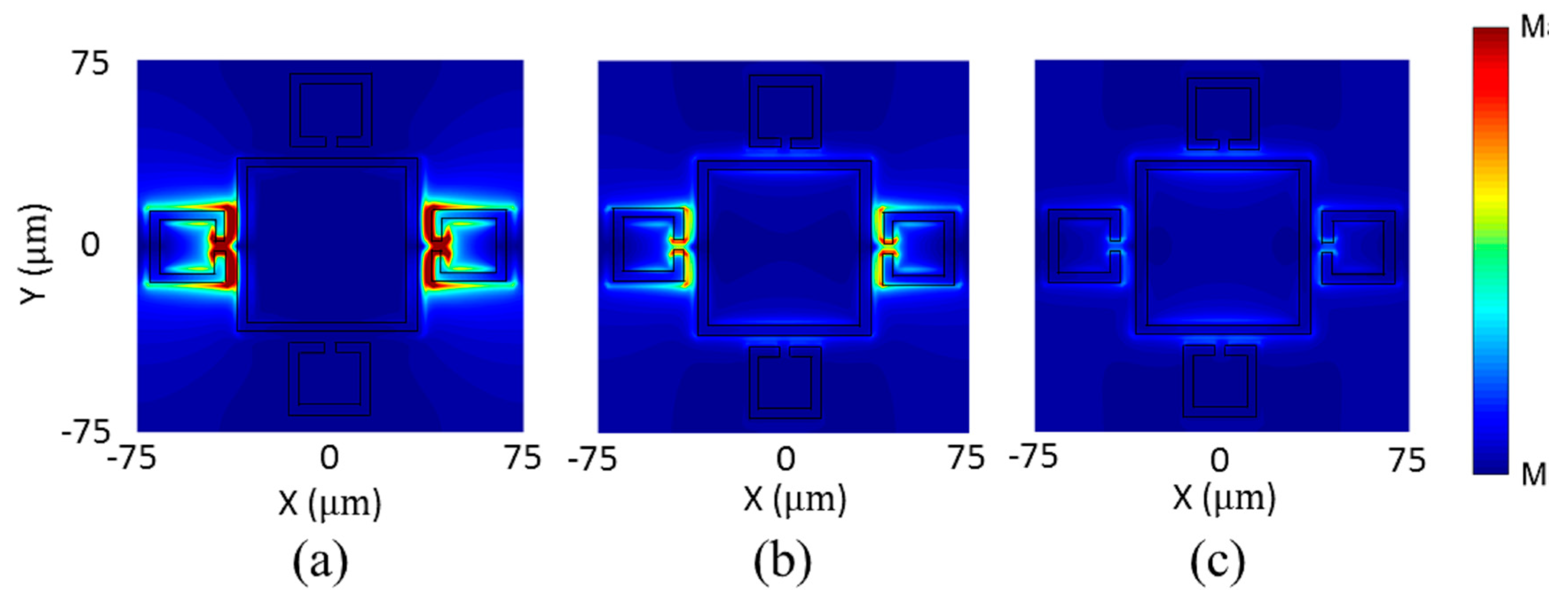
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Yang, Q.; Deng, B.; Qin, Y.; Wang, H. Experimental research on interferometric inverse synthetic aperture radar imaging with multi-channel terahertz radar system. Sensors 2019, 19, 2330. [Google Scholar] [CrossRef]
- Niessen, K.A.; Xu, M.; George, D.K.; Chen, M.C.; Ferré-D’Amaré, A.R.; Snell, E.H.; Cody, V.; Pace, J.; Schmidt, M.; Markelz, A.G. Protein and RNA dynamical fingerprinting. Nat. Commun. 2019, 10, 1026. [Google Scholar] [CrossRef] [PubMed]
- García-Muñoz, E.; Abdalmalak, K.A.; Santamaría, G.; Rivera-Lavado, A.; Segovia-Vargas, D.; Castillo-Araníbar, P.; Van Dijk, F.; Nagatsuma, T.; Brown, E.R.; Guzman, R.C.; et al. Photonic-based integrated sources and antenna arrays for broadband wireless links in terahertz communications. Semicond. Sci. Technol. 2019, 34, 054001. [Google Scholar] [CrossRef]
- Zheludev, N.I. The road ahead for metamaterials. Science 2010, 328, 582–583. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.T.; Padilla, W.J.; Zide, J.M.; Gossard, A.C.; Taylor, A.J.; Averitt, R.D. Active terahertz metamaterial devices. Nature 2006, 444, 597–600. [Google Scholar] [CrossRef]
- Chen, H.-T.; Padilla, W.J.; Cich, M.J.; Azad, A.K.; Averitt, R.D.; Taylor, A.J. A metamaterial solid-state terahertz phase modulator. Nat. Photonics 2009, 3, 148–151. [Google Scholar] [CrossRef]
- Liu, M.; Yang, Q.; Xu, Q.; Chen, X.; Tian, Z.; Gu, J.; Ouyang, C.; Zhang, X.; Han, J.; Zhang, W. Tailoring mode interference in plasmon-induced transparency metamaterials. J. Phys. D: Appl. Phys. 2018, 51, 174005. [Google Scholar] [CrossRef]
- Liu, M.; Tian, Z.; Zhang, X.; Gu, J.; Ouyang, C.; Han, J.; Zhang, W. Tailoring the plasmon-induced transparency resonances in terahertz metamaterials. Opt. Express 2017, 25, 19844–19855. [Google Scholar] [CrossRef]
- Cong, L.; Xu, N.; Chowdhury, D.R.; Manjappa, M.; Rockstuhl, C.; Zhang, W.; Singh, R. Nonradiative and radiative resonances in coupled metamolecules. Adv. Opt. Mater. 2016, 4, 252–258. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, H.; Guo, X.; Liu, S.; Zhang, Y. Tunable plasmon-induced transparency in H-shaped Dirac semimetal metamaterial. Appl. Opt. 2018, 57, 752–756. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; He, X.; Han, Y.; Zhang, J.; Huang, J.; Chen, D.; Xu, S. Plasmon-induced transparency based on aperture-coupled cascade resonators without gap. Superlattices Microstruct. 2018, 123, 138–143. [Google Scholar] [CrossRef]
- Hokmabadi, M.P.; Philip, E.; Rivera, E.; Kung, P.; Kim, S.M. Plasmon-induced transparency by hybridizing concentric-twisted double split ring resonators. Sci. Rep. 2015, 5, 15735. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Liu, P.; Bian, L.; Zhou, Q.; Li, G.; Liu, H. Dynamically tunable electromagnetically induced transparency analogy in terahertz metamaterial. Opt. Commun. 2018, 410, 17–24. [Google Scholar] [CrossRef]
- Wei, B.; Liu, H.; Ren, G.; Yang, Y.; Ye, S.; Pei, L.; Jian, S. Graphene based silicon–air grating structure to realize electromagnetically-induced-transparency and slow light effect. Phys. Lett. A 2017, 381, 160–165. [Google Scholar] [CrossRef]
- Zhang, S.; Genov, D.A.; Wang, Y.; Liu, M.; Zhang, X. Plasmon-induced transparency in metamaterials. Phys. Rev. Lett. 2008, 101, 047401. [Google Scholar] [CrossRef]
- Sun, C.; Si, J.; Dong, Z.; Deng, X. Tunable multispectral plasmon induced transparency based on graphene metamaterials. Opt. Express 2016, 24, 11466–11474. [Google Scholar] [CrossRef]
- Tassin, P.; Koschny, T.; Soukoulis, C.M. Applied physics. Graphene for terahertz applications. Science 2013, 341, 620–621. [Google Scholar] [CrossRef]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Li, X.; Tao, L.; Chen, Z.; Fang, H.; Li, X.; Wang, X.; Xu, J.-B.; Zhu, H. Graphene and related two-dimensional materials: Structure-property relationships for electronics and optoelectronics. Appl. Phys. Rev. 2017, 4, 021306. [Google Scholar] [CrossRef]
- Chen, D.-C.; Li, H.-J.; Xia, S.-X.; Qin, M.; Zhai, X.; Wang, L.-L. Dynamically tunable electromagnetically-induced-transparency–like resonances in graphene nanoring and nanodisk hybrid metamaterials. Europhys. Lett. 2017, 119, 47002. [Google Scholar] [CrossRef]
- Qian, Z.; Yang, D.; Wang, W. Terahertz modulation based on surface plasmon resonance by self-gated graphene. Opt. Commun. 2018, 414, 52–58. [Google Scholar] [CrossRef]
- He, X.; Yang, X.; Lu, G.; Yang, W.; Wu, F.; Yu, Z.; Jiang, J. Implementation of selective controlling electromagnetically induced transparency in terahertz graphene metamaterial. Carbon 2017, 123, 668–675. [Google Scholar] [CrossRef]
- Low, T.; Avouris, P. Graphene Plasmonics for Terahertz to Mid-Infrared Applications. ACS Nano 2014, 8, 1086–1101. [Google Scholar] [CrossRef]
- Degl’Innocenti, R.; Jessop, D.S.; Shah, Y.D.; Sibik, J.; Zeitler, J.A.; Kidambi, P.R.; Hofmann, S.; Beere, H.E.; Ritchie, D.A.; Zeitler, A. Low-bias terahertz amplitude modulator based on split-ring resonators and graphene. ACS Nano 2014, 8, 2548–2554. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, X.; Zhang, L.; Wei, X. Dynamically tunable plasmon-induced transparency based on radiative–radiative-coupling in a terahertz metal–graphene metamaterial. Crystals 2019, 9, 146. [Google Scholar] [CrossRef]
- Liu, T.; Wang, H.; Liu, Y.; Xiao, L.; Yi, Z.; Zhou, C.; Xiao, S. Active manipulation of electromagnetically induced transparency in a terahertz hybrid metamaterial. Opt. Commun. 2018, 426, 629–634. [Google Scholar] [CrossRef]
- Kakenov, N.; Ergoktas, M.S.; Balci, O.; Kocabas, C. Graphene based terahertz phase modulators. 2D Mater. 2018, 5, 035018. [Google Scholar] [CrossRef]
- Tasolamprou, A.C.; Koulouklidis, A.D.; Daskalaki, C.; Mavidis, C.P.; Kenanakis, G.; Deligeorgis, G.; Viskadourakis, Z.; Kuzhir, P.; Tzortzakis, S.; Kafesaki, M.; et al. Experimental demonstration of ultrafast THz modulation in a graphene-based thin film absorber through negative photoinduced conductivity. ACS Photonics 2019, 6, 720–727. [Google Scholar] [CrossRef]
- Dong, Z.; Sun, C.; Si, J.; Deng, X. Tunable polarization-independent plasmonically induced transparency based on metal-graphene metasurface. Opt. Express 2017, 25, 12251–12259. [Google Scholar] [CrossRef]
- Sun, C.; Dong, Z.; Si, J.; Deng, X. Independently tunable dual-band plasmonically induced transparency based on hybrid metal-graphene metamaterials at mid-infrared frequencies. Opt. Express 2017, 25, 1242–1250. [Google Scholar] [CrossRef]
- Huang, H.; Xia, H.; Guo, Z.; Li, H.; Xie, D. Polarization-insensitive and tunable plasmon induced transparency in a graphene-based terahertz metamaterial. Opt. Commun. 2018, 424, 163–169. [Google Scholar] [CrossRef]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical properties of fourteen metals in the infrared and far infrared: Al, co, cu, au, fe, pb, mo, ni, pd, pt, ag, ti, v, and w. Appl. Opt. 1985, 24, 4493–4499. [Google Scholar] [CrossRef]
- Ishikawa, A.; Tanaka, T. Plasmon hybridization in graphene metamaterials. Appl. Phys. Lett. 2013, 102, 253110. [Google Scholar] [CrossRef]
- Jnawali, G.; Rao, Y.; Yan, H.; Heinz, T.F. Observation of a transient decrease in terahertz conductivity of single-layer graphene induced by ultrafast optical excitation. Nano Lett. 2013, 13, 524–530. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Tan, Y.W.; Stormer, H.L.; Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 2005, 438, 201–204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manjappa, M.; Chiam, S.-Y.; Cong, L.; Bettiol, A.A.; Zhang, W.; Singh, R. Tailoring the slow light behavior in terahertz metasurfaces. Appl. Phys. Lett. 2015, 106, 181101. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.-Y.; Wu, Q.; Erni, D.; Wu, K.; Lee, J.-C. Polarization-independent metamaterial analog of electromagnetically induced transparency for a refractive-index-based sensor. IEEE Trans. Microw. Theory Tech. 2012, 60, 3013–3022. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Q.; Cao, W.; Gu, J.; Singh, R.; Tian, Z.; Han, J.; Zhang, W. Polarization-independent plasmon-induced transparency in a fourfold symmetric terahertz metamaterial. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 8400707. [Google Scholar] [CrossRef]
- Papasimakis, N.; Fu, Y.H.; Fedotov, V.A.; Prosvirnin, S.L.; Tsai, D.P.; Zheludev, N. Metamaterial with polarization and direction insensitive resonant transmission response mimicking electromagnetically induced transparency. Appl. Phys. Lett. 2009, 94, 211902. [Google Scholar] [CrossRef] [Green Version]
- Hu, S.; Liu, D.; Lin, H.; Chen, J.; Yi, Y.; Yang, H. Analogue of ultra-broadband and polarization-independent electromagnetically induced transparency using planar metamaterial. J. Appl. Phys. 2017, 121, 123103. [Google Scholar] [CrossRef]
- Duan, X.; Chen, S.; Yang, H.; Cheng, H.; Li, J.; Liu, W.; Gu, C.; Tian, J. Polarization-insensitive and wide-angle plasmonically induced transparency by planar metamaterials. Appl. Phys. Lett. 2012, 101, 143105. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Zhang, X.; Wei, X.; Zhang, G. Tunable and Polarization-Independent Plasmon-Induced Transparency in a Fourfold Symmetric Metal-Graphene Terahertz Metamaterial. Crystals 2019, 9, 632. https://doi.org/10.3390/cryst9120632
Wang G, Zhang X, Wei X, Zhang G. Tunable and Polarization-Independent Plasmon-Induced Transparency in a Fourfold Symmetric Metal-Graphene Terahertz Metamaterial. Crystals. 2019; 9(12):632. https://doi.org/10.3390/cryst9120632
Chicago/Turabian StyleWang, Guanqi, Xianbin Zhang, Xuyan Wei, and Gaoqi Zhang. 2019. "Tunable and Polarization-Independent Plasmon-Induced Transparency in a Fourfold Symmetric Metal-Graphene Terahertz Metamaterial" Crystals 9, no. 12: 632. https://doi.org/10.3390/cryst9120632
APA StyleWang, G., Zhang, X., Wei, X., & Zhang, G. (2019). Tunable and Polarization-Independent Plasmon-Induced Transparency in a Fourfold Symmetric Metal-Graphene Terahertz Metamaterial. Crystals, 9(12), 632. https://doi.org/10.3390/cryst9120632




