Nanowires for High-Efficiency, Low-Cost Solar Photovoltaics
Abstract
:1. Introduction
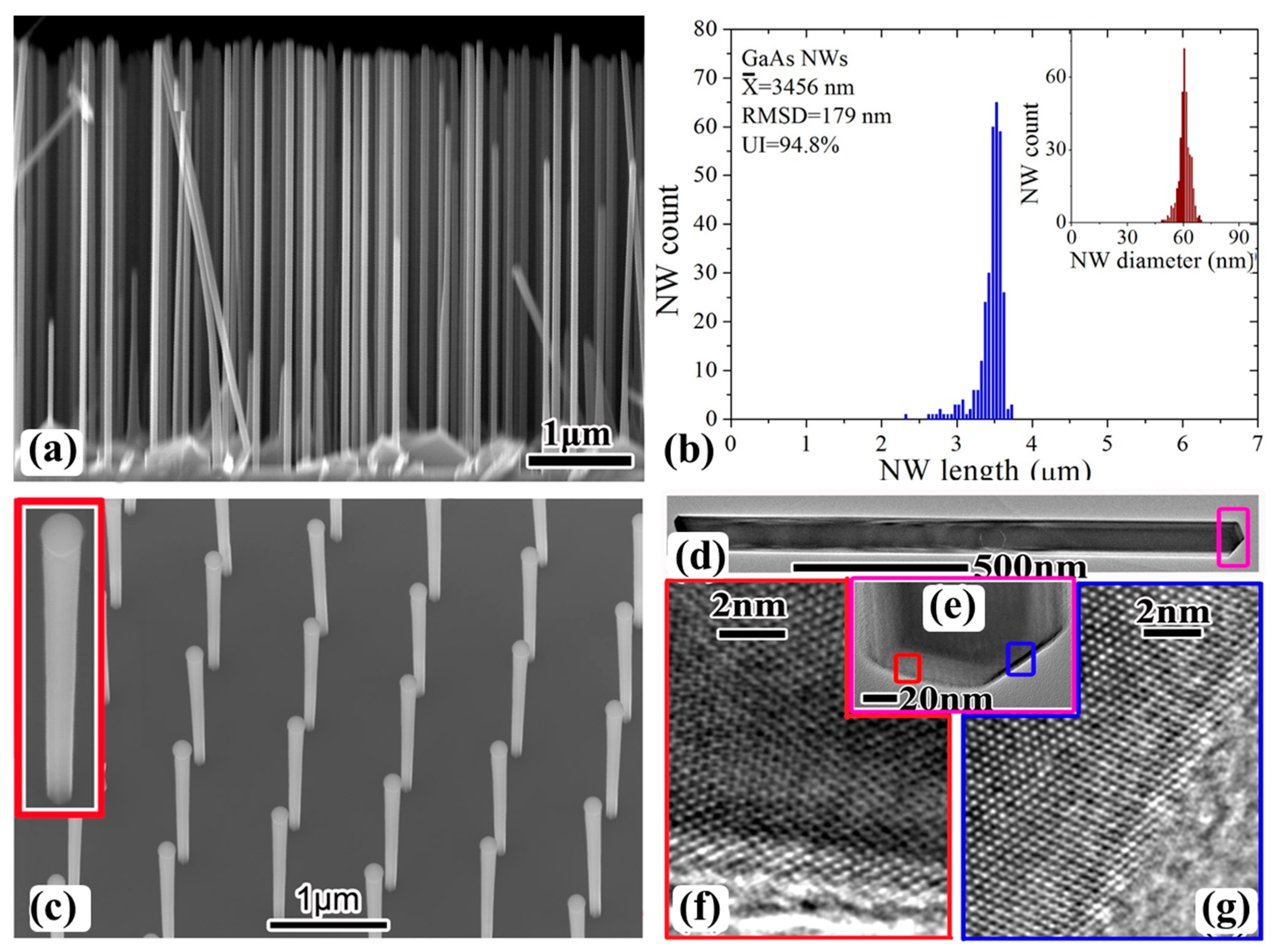
2. Integrating High-Quality III–Vs on Si
3. Superior Solar Photon Harvesting
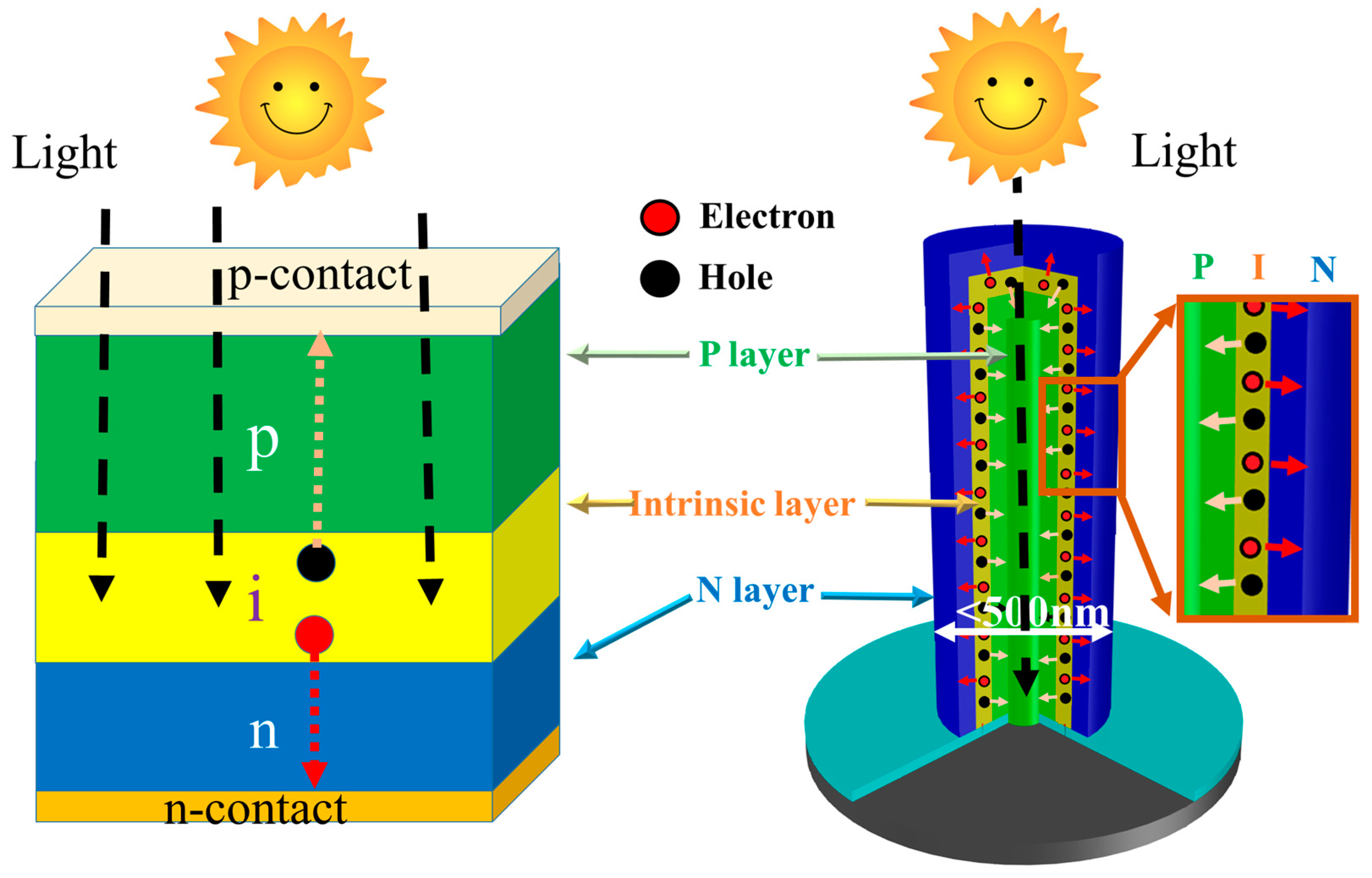
4. Superior Extraction Scheme for Photon-Generated Carriers
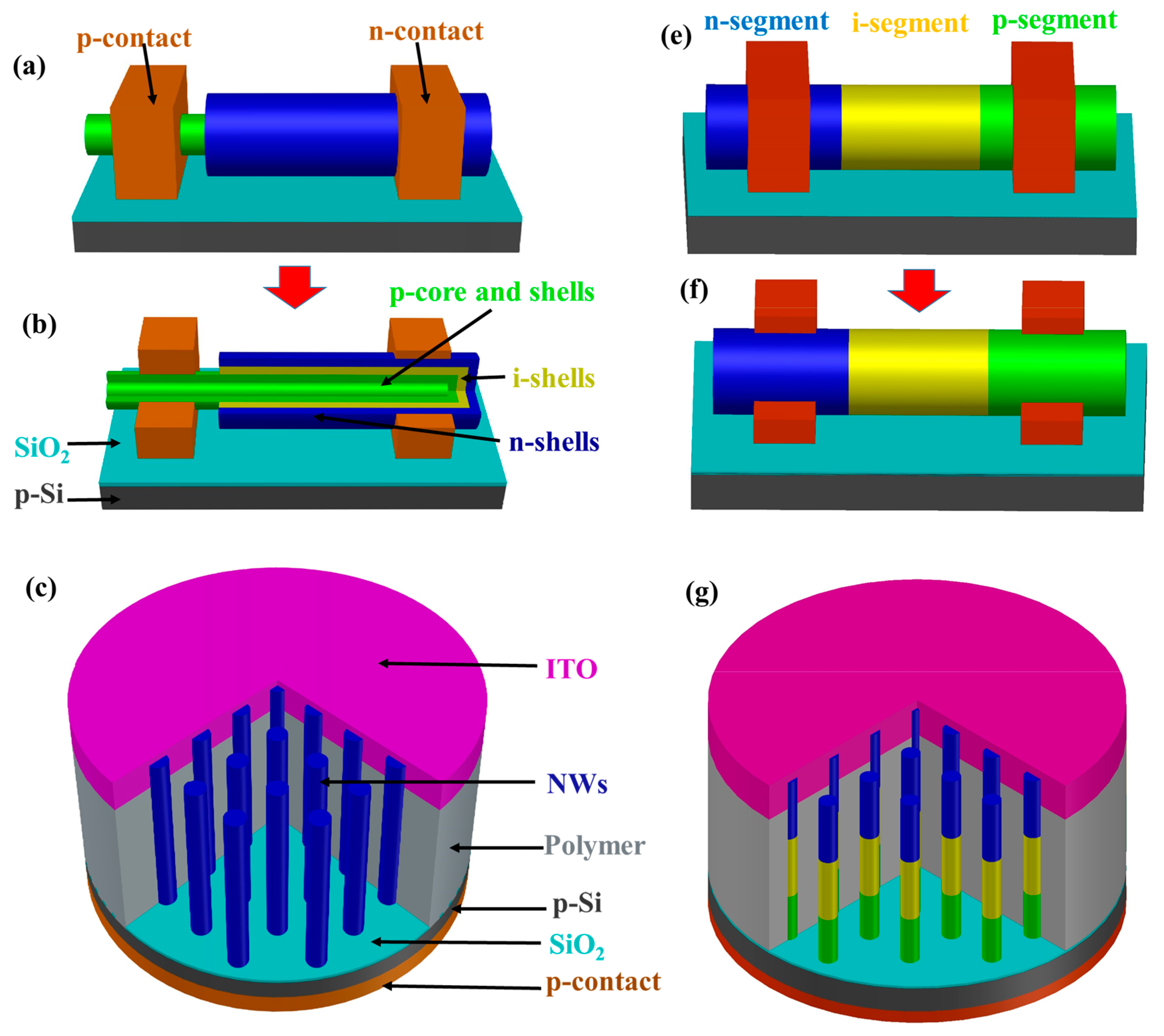
5. Single-Junction Solar Cells
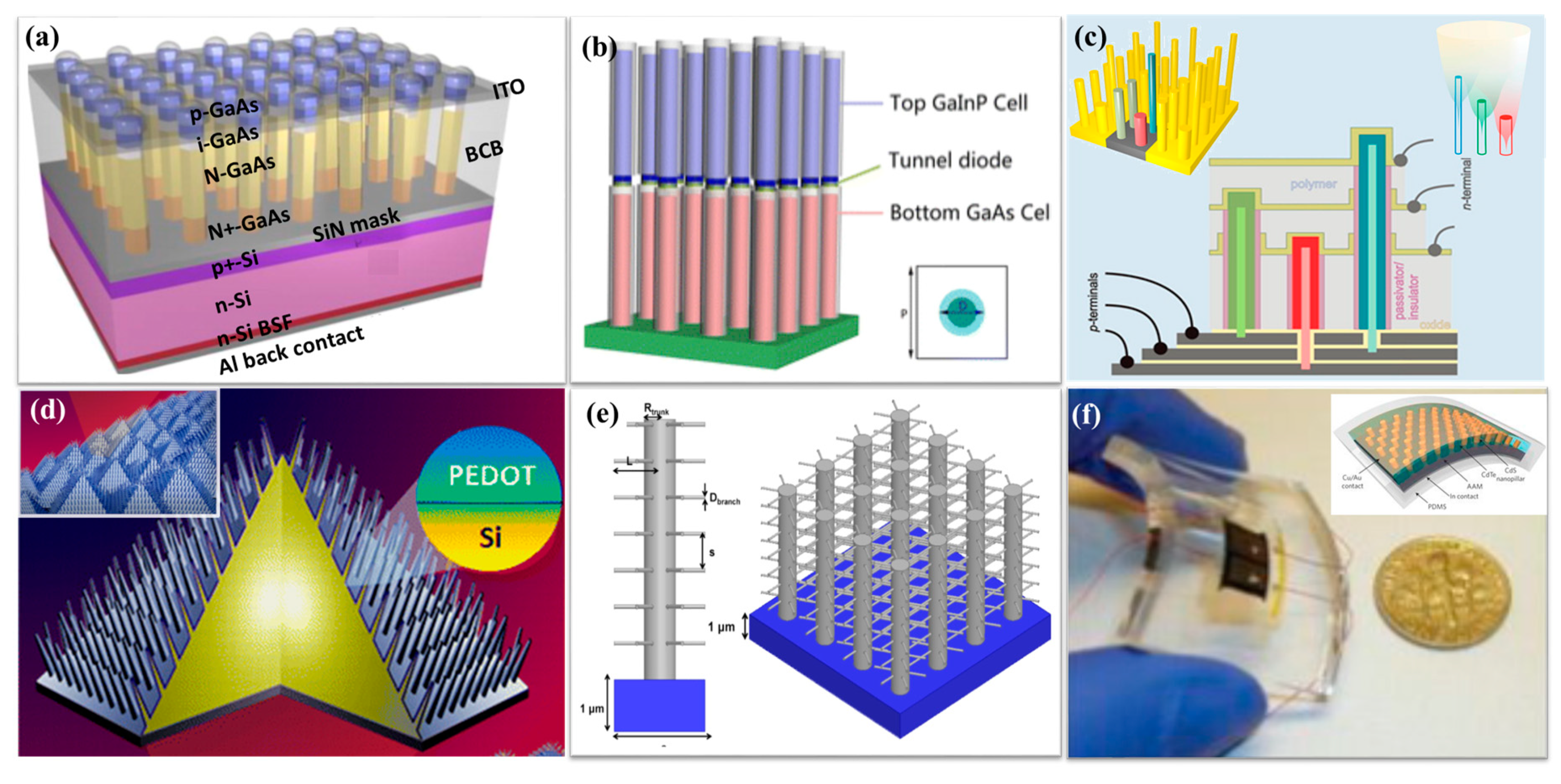
6. Design for Novel High-Efficiency and Low-Cost Solar Cells
7. Challenges in Making NW Solar Cells
8. Conclusions
Funding
Conflicts of Interest
References
- Husher, J.D. Beyond Global Warming: The Bigger Problem and Real Crisis; iUniverse, Inc.: Bloomington, IN, USA, 2007. [Google Scholar]
- Yu, K.; Chen, J. Enhancing solar cell efficiencies through 1-D nanostructures. Nanoscale Res. Lett. 2009, 4, 1. [Google Scholar] [CrossRef]
- Solar Cells Market Size—Industry Share Analysis Report 2024. Available online: https://www.gminsights.com/industry-analysis/solar-cells-market (accessed on 1 December 2016).
- Almansouri, I.; Ho-Baillie, A.; Bremner, S.P.; Green, M.A. Supercharging silicon solar cell performance by means of multijunction concept. IEEE J. Photovolt. 2015, 5, 968. [Google Scholar] [CrossRef]
- Essig, S.; Allebé, C.; Remo, T.; Geisz, J.F.; Steiner, M.A.; Horowitz, K.; Barraud, L.; Ward, J.S.; Schnabel, M.; Descoeudres, A.; et al. Raising the one-sun conversion efficiency of III–V/Si solar cells to 32.8% for two junctions and 35.9% for three junctions. Nat. Energy 2017, 2, 17144. [Google Scholar] [CrossRef]
- Abdul Hadi, S.; Fitzgerald, E.A.; Griffiths, S.; Nayfeh, A. III–V/Si dual junction solar cell at scale: Manufacturing cost estimates for step-cell based technology. J. Renew. Sustain. Energy 2018, 10, 015905. [Google Scholar] [CrossRef]
- Green, M.A.; Emery, K.; Hishikawa, Y.; Warta, W.; Dunlop, E.D. Solar cell efficiency tables (version 48). Prog. Photovolt. Res. Appl. 2016, 7, 905–913. [Google Scholar] [CrossRef]
- Marti, A.; Araújo, G.L. Limiting efficiencies for photovoltaic energy conversion in multigap systems. Sol. Energy Mater. Solar Cells 1996, 43, 203. [Google Scholar] [CrossRef]
- De Vos, A. Detailed balance limit of the efficiency of tandem solar cells. J. Phys. D Appl. Phys. 1980, 13, 839. [Google Scholar] [CrossRef]
- Abdul Hadi, S.; Fitzgerald, E.A.; Nayfeh, A. Theoretical efficiency limit for a two-terminal multijunction “step-cell” using detailed balance method. J. Appl. Phys. 2016, 119, 073104. [Google Scholar] [CrossRef]
- Kurtz, S.R.; Faine, P.; Olson, J.M. Modeling of two-junction, series-connected tandem solar cells using top-cell thickness as an adjustable parameter. J. Appl. Phys. 1990, 68, 1890. [Google Scholar] [CrossRef]
- Lieber, C.M.; Wang, Z.L. Functional nanowires. MRS Bull. 2007, 32, 99. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, J.; Aagesen, M.; Liu, H. III–V nanowires and nanowire optoelectronic devices. J. Phys. D Appl. Phys. 2015, 48, 463001. [Google Scholar] [CrossRef]
- Yan, R.; Gargas, D.; Yang, P. Nanowire photonics. Nat. Photonics 2009, 3, 569. [Google Scholar] [CrossRef]
- Dasgupta, N.P.; Sun, J.; Liu, C.; Brittman, S.; Andrews, S.C.; Lim, J.; Gao, H.; Yan, R.; Yang, P. 25th anniversary article: Semiconductor nanowires–synthesis, characterization, and applications. Adv. Mater. 2014, 26, 2137. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Yan, R.; Fardy, M. Semiconductor nanowire: what’s next? Nano Lett. 2010, 10, 1529. [Google Scholar] [CrossRef] [PubMed]
- Reimer, M.E.; Bulgarini, G.; Akopian, N.; Hocevar, M.; Bavinck, M.B.; Verheijen, M.A.; Bakkers, E.P.A.M.; Kouwenhoven, L.P.; Zwiller, V. Bright single-photon sources in bottom-up tailored nanowires. Nat. Commun. 2012, 3, 737. [Google Scholar] [CrossRef] [PubMed]
- LaPierre, R.R. Numerical model of current-voltage characteristics and efficiency of GaAs nanowire solar cells. J. Appl. Phys. 2011, 109, 034311. [Google Scholar] [CrossRef]
- Cui, Y.; Van Dam, D.; Mann, S.A.; Van Hoof, N.J.J.; Van Veldhoven, P.J.; Garnett, E.C.; Haverkort, J.E.M. Boosting solar cell photovoltage via nanophotonic engineering. Nano Lett. 2016, 16, 6467–6471. [Google Scholar] [CrossRef] [PubMed]
- Wallentin, J.; Anttu, N.; Asoli, D.; Huffman, M.; Åberg, I.; Magnusson, M.H.; Siefer, G.; Fuss-Kailuweit, P.; Dimroth, F.; Witzigmann, B.; et al. InP nanowire array solar cells achieving 13.8% efficiency by exceeding the ray optics limit. Science 2013, 339, 1057. [Google Scholar] [CrossRef]
- Service, R.F. Performance of Nanowire Solar Cells on the Rise. Science 2013, 339, 263. [Google Scholar] [CrossRef]
- Yu, R.; Lin, Q.; Leung, S.F.; Fan, Z. Nanomaterials and nanostructures for efficient light absorption and photovoltaics. Nano Energy 2012, 1, 57–72. [Google Scholar] [CrossRef]
- Kapadia, R.; Fan, Z.; Takei, K.; Javey, A. Nanopillar photovoltaics: Materials, processes, and devices. Nano Energy 2012, 1, 132–144. [Google Scholar] [CrossRef]
- Sun, K.; Kargar, A.; Park, N.; Madsen, K.N.; Naughton, P.W.; Bright, T.; Wang, D. Compound semiconductor nanowire solar cells. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 1033. [Google Scholar] [CrossRef]
- Hoang, S.; Gao, P.X. Nanowire array structures for photocatalytic energy conversion and utilization: A review of design concepts, assembly and integration, and function enabling. Adv. Energy Mater. 2016, 6, 1600683. [Google Scholar] [CrossRef]
- Ali, N.M.; Rafat, N.H. Modeling and simulation of nanorods photovoltaic solar cells: A review. Renew. Sustain. Energy Rev. 2017, 68, 212. [Google Scholar] [CrossRef]
- Haverkort, J.E.; Garnett, E.C.; Bakkers, E.P. Fundamentals of the nanowire solar cell: Optimization of the open circuit voltage. Appl. Phys. Rev. 2018, 5, 031106. [Google Scholar] [CrossRef]
- LaPierre, R.R.; Chia, A.C.E.; Gibson, S.J.; Haapamaki, C.M.; Boulanger, J.; Yee, R.; Rahman, K.M.A. III–V nanowire photovoltaics: Review of design for high efficiency. Phys. Status Solidi (RRL)–Rapid Res. Lett. 2013, 7, 815. [Google Scholar] [CrossRef]
- Mokkapati, S.; Jagadish, C. Review on photonic properties of nanowires for photovoltaics. Opt. Express 2016, 24, 17345. [Google Scholar] [CrossRef]
- Joyce, H.J.; Gao, Q.; Tan, H.H.; Jagadish, C.; Kim, Y.; Zou, J.; Smith, L.M.; Jackson, H.E.; Yarrison-Rice, J.M.; Parkinson, P.; et al. III–V semiconductor nanowires for optoelectronic device applications. Progr. Quantum Electron. 2011, 35, 23. [Google Scholar] [CrossRef]
- Wagner, R.S.; Ellis, W.C. Vapor-liquid-solid mechanism of single crystal growth. Appl. Phys. Lett. 1964, 4, 89. [Google Scholar] [CrossRef]
- Zhang, Y.; Sanchez, A.M.; Sun, Y.; Wu, J.; Aagesen, M.; Huo, S.; Kim, D.; Jurczak, P.; Xu, X.; Liu, H. Influence of droplet size on the growth of self-catalyzed ternary GaAsP nanowires. Nano Lett. 2016, 16, 1237. [Google Scholar] [CrossRef]
- Heiss, M.; Russo-Averchi, E.; Dalmau-Mallorquí, A.; Tütüncüoğlu, G.; Matteini, F.; Rüffer, D.; Conesa-Boj, S.; Demichel, O.; Alarcon-Lladó, E.; Fontcuberta i Morral, A. III–V nanowire arrays: Growth and light interaction. Nanotechnology 2014, 25, 014015. [Google Scholar] [CrossRef] [PubMed]
- Kelzenberg, M.D.; Boettcher, S.W.; Petykiewicz, J.A.; Turner-Evans, D.B.; Putnam, M.C.; Warren, E.L.; Spurgeon, J.M.; Briggs, R.M.; Lewis, N.S.; Atwater, H.A. Enhanced absorption and carrier collection in Si wire arrays for photovoltaic applications. Nat. Mater. 2010, 9, 239. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Povinelli, M.L. Optical absorption enhancement in silicon nanowire arrays with a large lattice constant for photovoltaic applications. Opt. Express 2009, 17, 19371. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wu, J.; Aagesen, M.; Holm, J.; Hatch, S.; Tang, M.; Huo, S.; Liu, H. Self-catalyzed ternary core–shell GaAsP nanowire arrays grown on patterned Si substrates by molecular beam epitaxy. Nano Lett. 2014, 14, 4542. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Fonseka, H.A.; Aagesen, M.; Gott, J.A.; Sanchez, A.M.; Wu, J.; Kim, D.; Jurczak, P.; Huo, S.; Liu, H. Growth of Pure Zinc-Blende GaAs (P) Core–Shell Nanowires with Highly Regular Morphology. Nano Lett. 2017, 17, 4946. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Yu, Z.; Fan, S.; Cui, Y. Nanostructured photon management for high performance solar cells. Mater. Sci. Eng. R Rep. 2010, 70, 330. [Google Scholar] [CrossRef]
- Sivasubramaniam, S.; Alkaisi, M.M. Inverted nanopyramid texturing for silicon solar cells using interference lithography. Microelectron. Eng. 2014, 119, 146. [Google Scholar] [CrossRef]
- Smith, A.W.; Rohatgi, A. Ray tracing analysis of the inverted pyramid texturing geometry for high efficiency silicon solar cells. Sol. Energy Mater. Sol. Cells 1993, 29, 37. [Google Scholar] [CrossRef]
- Mavrokefalos, A.; Han, S.E.; Yerci, S.; Branham, M.S.; Chen, G. Efficient light trapping in inverted nanopyramid thin crystalline silicon membranes for solar cell applications. Nano Lett. 2012, 12, 2792. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Chen, G. Analysis of optical absorption in silicon nanowire arrays for photovoltaic applications. Nano Lett. 2007, 7, 3249. [Google Scholar] [CrossRef] [PubMed]
- Rayleigh, L. On reflection of vibrations at the confines of two media between which the transition is gradual. Proc. Lond. Math. Soc. 1879, 1, 51. [Google Scholar] [CrossRef]
- Hiralal, P.; Chien, C.; Lal, N.N.; Abeygunasekara, W.; Kumar, A.; Butt, H.; Amaratunga, G.A. Nanowire-based multifunctional antireflection coatings for solar cells. Nanoscale 2014, 6, 14555–14562. [Google Scholar] [CrossRef] [PubMed]
- Diedenhofen, S.L.; Grzela, G.; Haverkamp, E.; Bauhuis, G.; Schermer, J.; Rivas, J.G. Broadband and omnidirectional antireflection layer for III/V multijunction solar cells. Sol. Energy Mater. Sol. Cells 2012, 101, 308–314. [Google Scholar] [CrossRef]
- Diedenhofen, S.L.; Vecchi, G.; Algra, R.E.; Hartsuiker, A.; Muskens, O.L.; Immink, G.; Bakkers, E.P.A.M.; Vos, W.L.; Rivas, J.G.; Rivas, J.G. Broad-band and Omnidirectional Antireflection Coatings Based on Semiconductor Nanorods. Adv. Mater. 2009, 21, 973. [Google Scholar] [CrossRef]
- Zhu, J.; Yu, Z.; Burkhard, G.F.; Hsu, C.M.; Connor, S.T.; Xu, Y.; Wang, Q.; McGehee, M.; Fan, S.; Cui, Y. Optical absorption enhancement in amorphous silicon nanowire and nanocone arrays. Nano Lett. 2008, 9, 279. [Google Scholar] [CrossRef] [PubMed]
- Garnett, E.; Yang, P. Light trapping in silicon nanowire solar cells. Nano Lett. 2010, 10, 1082. [Google Scholar] [CrossRef]
- Tsakalakos, L.; Balch, J.E.; Fronheiser, J.; Shih, M.Y.; LeBoeuf, S.F.; Pietrzykowski, M.; Codella, P.J.; Korevaar, B.A.; Sulima, O.; Rand, J.; et al. Strong broadband optical absorption in silicon nanowire films. J. Nanophotonics 2007, 1, 013552. [Google Scholar] [CrossRef]
- Muskens, O.L.; Rivas, J.G.; Algra, R.E.; Bakkers, E.P.; Lagendijk, A. Design of light scattering in nanowire materials for photovoltaic applications. Nano Lett. 2008, 8, 2638. [Google Scholar] [CrossRef]
- Strudley, T.; Zehender, T.; Blejean, C.; Bakkers, E.P.; Muskens, O.L. Mesoscopic light transport by very strong collective multiple scattering in nanowire mats. Nat. Photonics 2013, 7, 413. [Google Scholar] [CrossRef]
- Van Dam, D.; Abujetas, D.R.; Paniagua-Dominguez, R.; Sánchez-Gil, J.A.; Bakkers, E.P.; Haverkort, J.E.; Gómez Rivas, J. Directional and polarized emission from nanowire arrays. Nano Lett. 2015, 15, 4557. [Google Scholar] [CrossRef]
- Kupec, J.; Witzigmann, B. Dispersion, wave propagation and efficiency analysis of nanowire solar cells. Opt. Express 2009, 17, 10399. [Google Scholar] [CrossRef] [PubMed]
- Fountaine, K.T.; Whitney, W.S.; Atwater, H.A. Resonant absorption in semiconductor nanowires and nanowire arrays: Relating leaky waveguide modes to Bloch photonic crystal modes. J. Appl. Phys. 2014, 116, 153106. [Google Scholar] [CrossRef]
- Krogstrup, P.; Jørgensen, H.I.; Heiss, M.; Demichel, O.; Holm, J.V.; Aagesen, M.; Nygard, J.; i Morral, A.F. Single-nanowire solar cells beyond the Shockley–Queisser limit. Nat. Photonics 2013, 7, 306. [Google Scholar] [CrossRef]
- Cao, L.; White, J.S.; Park, J.S.; Schuller, J.A.; Clemens, B.M.; Brongersma, M.L. Engineering light absorption in semiconductor nanowire devices. Nat. Mater. 2009, 8, 643. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhan, Y. Enhanced external quantum efficiency in rectangular single nanowire solar cells. Appl. Phys. Lett. 2013, 102, 021101. [Google Scholar] [CrossRef]
- Wang, B.; Leu, P.W. Tunable and selective resonant absorption in vertical nanowires. Opt. Lett. 2012, 37, 3756. [Google Scholar] [CrossRef]
- Sandhu, S.; Yu, Z.; Fan, S. Detailed balance analysis and enhancement of open-circuit voltage in single-nanowire solar cells. Nano Lett. 2014, 14, 1011. [Google Scholar] [CrossRef]
- Cao, L.; Fan, P.; Vasudev, A.P.; White, J.S.; Yu, Z.; Cai, W.; Schuller, J.A.; Fan, S.; Brongersma, M.L.; Brongersma, M.L. Semiconductor nanowire optical antenna solar absorbers. Nano Lett. 2010, 10, 439. [Google Scholar] [CrossRef]
- Callahan, D.M.; Munday, J.N.; Atwater, H.A. Solar cell light trapping beyond the ray optic limit. Nano Lett. 2012, 12, 214. [Google Scholar] [CrossRef]
- Wen, L.; Zhao, Z.; Li, X.; Shen, Y.; Guo, H.; Wang, Y. Theoretical analysis and modeling of light trapping in high efficicency GaAs nanowire array solar cells. Appl. Phys. Lett. 2011, 99, 143116. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, X.H.; Huang, H.; Wang, X.; Huang, Y.; Ren, X. Optical absorption in InP/InGaAs/InP double-heterostructure nanopillar arrays for solar cells. Appl. Phys. Lett. 2014, 104, 061110. [Google Scholar] [CrossRef]
- Guo, H.; Wen, L.; Li, X.; Zhao, Z.; Wang, Y. Analysis of optical absorption in GaAs nanowire arrays. Nanoscale Res. Lett. 2011, 6, 617. [Google Scholar] [CrossRef]
- Anttu, N. Shockley–Queisser detailed balance efficiency limit for nanowire solar cells. ACS Photonics 2015, 2, 446. [Google Scholar] [CrossRef]
- Anttu, N.; Abrand, A.; Asoli, D.; Heurlin, M.; Åberg, I.; Samuelson, L.; Borgström, M. Absorption of light in InP nanowire arrays. Nano Res. 2014, 7, 816. [Google Scholar] [CrossRef]
- Xie, W.Q.; Oh, J.I.; Shen, W.Z. Realization of effective light trapping and omnidirectional antireflection in smooth surface silicon nanowire arrays. Nanotechnology 2011, 22, 065704. [Google Scholar] [CrossRef]
- Convertino, A.; Cuscuna, M.; Martelli, F. Optical reflectivity from highly disordered Si nanowire films. Nanotechnology 2010, 21, 355701. [Google Scholar] [CrossRef]
- Srivastava, S.K.; Kumar, D.; Singh, P.K.; Kar, M.; Kumar, V.; Husain, M. Excellent antireflection properties of vertical silicon nanowire arrays. Sol. Energy Mater. Sol. Cells 2010, 94, 1506. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Chen, T.; Tay, B.K.; Wang, J.; Yu, H. Periodically aligned Si nanopillar arrays as efficient antireflection layers for solar cell applications. Nanoscale Res. Lett. 2010, 5, 1721. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhao, F.; Yang, J.; Hu, X. Comparison of optical absorption in Si nanowire and nanoporous Si structures for photovoltaic applications. Appl. Phys. Lett. 2010, 96, 181903. [Google Scholar] [CrossRef]
- Li, J.; Yu, H.; Wong, S.M.; Zhang, G.; Sun, X.; Lo, P.G.Q.; Kwong, D.L. Si nanopillar array optimization on Si thin films for solar energy harvesting. Appl. Phys. Lett. 2009, 95, 033102. [Google Scholar] [CrossRef]
- Li, J.; Yu, H.; Wong, S.M.; Li, X.; Zhang, G.; Lo, P.G.Q.; Kwong, D.L. Design guidelines of periodic Si nanowire arrays for solar cell application. Appl. Phys. Lett. 2009, 95, 243113. [Google Scholar] [CrossRef]
- Fan, Z.; Kapadia, R.; Leu, P.W.; Zhang, X.; Chueh, Y.L.; Takei, K.; Wu, M. Ordered arrays of dual-diameter nanopillars for maximized optical absorption. Nano Lett. 2010, 10, 3823. [Google Scholar] [CrossRef]
- Anttu, N.; Xu, H.Q. Coupling of light into nanowire arrays and subsequent absorption. J. Nanosci. Nanotechnol. 2010, 10, 7183. [Google Scholar] [CrossRef]
- Kupec, J.; Stoop, R.L.; Witzigmann, B. Light absorption and emission in nanowire array solar cells. Opt. Express 2010, 18, 27589. [Google Scholar] [CrossRef]
- Hu, Y.; LaPierre, R.R.; Li, M.; Chen, K.; He, J.J. Optical characteristics of GaAs nanowire solar cells. J. Appl. Phys. 2012, 112, 104311. [Google Scholar] [CrossRef]
- Motohisa, J.; Hiruma, K. Light absorption in semiconductor nanowire arrays with multijunction cell structures. Jpn. J. Appl. Phys. 2012, 51, 11PE07. [Google Scholar] [CrossRef]
- Jeong, S.; Wang, S.; Cui, Y. Nanoscale photon management in silicon solar cells. J. Vac. Sci. Technol. A 2012, 30, 060801. [Google Scholar] [CrossRef]
- Du, Q.G.; Kam, C.H.; Demir, H.V.; Yu, H.Y.; Sun, X.W. Broadband absorption enhancement in randomly positioned silicon nanowire arrays for solar cell applications. Opt. Lett. 2011, 36, 1884–1886. [Google Scholar] [CrossRef]
- Diedenhofen, S.L.; Janssen, O.T.; Grzela, G.; Bakkers, E.P.; Gómez Rivas, J. Strong geometrical dependence of the absorption of light in arrays of semiconductor nanowires. ACS Nano 2011, 5, 2316. [Google Scholar] [CrossRef]
- Kayes, B.M.; Atwater, H.A.; Lewis, N.S. Comparison of the device physics principles of planar and radial p–n junction nanorod solar cells. J. Appl. Phys. 2005, 97, 114302. [Google Scholar] [CrossRef]
- Lam, P.; Hatch, S.; Wu, J.; Tang, M.; Dorogan, V.G.; Mazur, Y.I.; Salamo, G.J.; Ramiro, I.; Seeds, A.; Liu, H. Voltage recovery in charged InAs/GaAs quantum dot solar cells. Nano Energy 2014, 6, 159. [Google Scholar] [CrossRef]
- Cheng, Y.C.; Chen, T.G.; Chang, F.Y.; Huang, B.Y.; Pan, H.T.; Li, C.K.; Yu, P.; Wu, Y.R. Fabrication and modeling of large-scale silicon nanowire solar cells for thin-film photovoltaics. In Proceedings of the Photovoltaic Specialists Conference (PVSC), Austin, TX, USA, 3–8 June 2012. [Google Scholar]
- Pei, Z.; Chang, S.T.; Liu, C.W.; Chen, Y.C. Numerical simulation on the photovoltaic behavior of an amorphous-silicon nanowire-array solar cell. IEEE Electron Device Lett. 2009, 30, 1305. [Google Scholar]
- Christesen, J.D.; Zhang, X.; Pinion, C.W.; Celano, T.A.; Flynn, C.J.; Cahoon, J.F. Design principles for photovoltaic devices based on Si nanowires with axial or radial p–n junctions. Nano Lett. 2012, 12, 6024. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Roemer, F.; Witzigmann, B. Analysis of surface recombination in nanowire array solar cells. J. Photonics Energy 2012, 2, 028002. [Google Scholar] [CrossRef]
- Alekseev, P.A.; Dunaevskiy, M.S.; Cirlin, G.E.; Reznik, R.R.; Smirnov, A.N.; Kirilenko, D.A.; Davydov, V.Y.; Berkovits, V.L. Unified mechanism of the surface Fermi level pinning in III-As nanowires. Nanotechnology 2018, 29, 314003. [Google Scholar] [CrossRef] [PubMed]
- Ali, H.; Zhang, Y.; Tang, J.; Peng, K.; Sun, S.; Sun, Y.; Song, F.; Falak, A.; Wu, S.; Qian, C.; et al. High-Responsivity Photodetection by a Self-Catalyzed Phase-Pure p-GaAs Nanowire. Small 2018, 14, 1704429. [Google Scholar] [CrossRef] [PubMed]
- Demichel, O.; Heiss, M.; Bleuse, J.; Mariette, H.; Fontcuberta i Morral, A. Impact of surfaces on the optical properties of GaAs nanowires. Appl. Phys. Lett. 2010, 97, 201907. [Google Scholar] [CrossRef]
- Zhang, Y.; Sanchez, A.M.; Aagesen, M.; Huo, S.; Fonseka, H.A.; Gott, J.A.; Kim, D.; Yu, X.; Chen, X.; Xu, J.; et al. Growth and Fabrication of High-Quality Single-Nanowire Devices with Radial P–i–n junctions. Small 2018, 15, e1803684. [Google Scholar] [CrossRef] [PubMed]
- Åberg, I.; Vescovi, G.; Asoli, D.; Naseem, U.; Gilboy, J.P.; Sundvall, C.; Dahlgren, A.; Svensson, K.; Anttu, N.; Bjork, M.T.; et al. A GaAs nanowire array solar cell with 15.3% efficiency at 1 sun. IEEE J. Photovolt. 2016, 6, 185. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, J.; Plissard, S.R.; Cavalli, A.; Vu, T.T.; van Veldhoven, R.P.; Gao, L.; Trainor, M.; Verheijen, M.A.; Haverkort, J.E.M.; et al. Efficiency enhancement of InP nanowire solar cells by surface cleaning. Nano Lett. 2013, 13, 4113. [Google Scholar] [CrossRef] [PubMed]
- Yao, M.; Huang, N.; Cong, S.; Chi, C.Y.; Seyedi, M.A.; Lin, Y.T.; Cao, Y.; Povinelli, M.L.; Dapkus, P.D.; Zhou, C. GaAs nanowire array solar cells with axial p–i–n junctions. Nano Lett. 2014, 14, 3293. [Google Scholar] [CrossRef] [PubMed]
- Mariani, G.; Scofield, A.C.; Hung, C.H.; Huffaker, D.L. GaAs nanopillar-array solar cells employing in situ surface passivation. Nat. Commun. 2013, 4, 1497. [Google Scholar] [CrossRef] [PubMed]
- Mariani, G.; Wong, P.S.; Katzenmeyer, A.M.; Léonard, F.; Shapiro, J.; Huffaker, D.L. Patterned radial GaAs nanopillar solar cells. Nano Lett. 2011, 11, 2490. [Google Scholar] [CrossRef] [PubMed]
- Yao, M.; Cong, S.; Arab, S.; Huang, N.; Povinelli, M.L.; Cronin, S.B.; Dapkus, P.D.; Zhou, C. Tandem solar cells using GaAs nanowires on Si: Design, fabrication, and observation of voltage addition. Nano Lett. 2015, 15, 7217. [Google Scholar] [CrossRef] [PubMed]
- Tian, B.; Zheng, X.; Kempa, T.J.; Fang, Y.; Yu, N.; Yu, G.; Lieber, C.M. Coaxial silicon nanowires as solar cells and nanoelectronic power sources. Nature 2007, 449, 885. [Google Scholar] [CrossRef] [PubMed]
- Krishnamoorthy, A.V.; Ho, R.; Zheng, X.; Schwetman, H.; Lexau, J.; Koka, P.; Li, G.; Shubin, I.; Cunningham, J.E. Computer systems based on silicon photonic interconnects. Proc. IEEE 2009, 97, 1337. [Google Scholar] [CrossRef]
- Gutsche, C.; Lysov, A.; Braam, D.; Regolin, I.; Keller, G.; Li, Z.A.; Geller, M.; Spasova, M.; Prost, W.; Tegude, F.J. n-GaAs/InGaP/p-GaAs Core-Multishell Nanowire Diodes for Efficient Light-to-Current Conversion. Adv. Funct. Mater. 2012, 22, 929. [Google Scholar] [CrossRef]
- Dong, Y.; Tian, B.; Kempa, T.J.; Lieber, C.M. Coaxial group III− nitride nanowire photovoltaics. Nano Lett. 2009, 9, 2183. [Google Scholar] [CrossRef]
- Garcia, J.C.; Rosencher, E.; Collot, P.; Laurent, N.; Guyaux, J.L.; Vinter, B.; Nagle, J. Epitaxially stacked lasers with Esaki junctions: A bipolar cascade laser. Appl. Phys. Lett. 1997, 71, 3752. [Google Scholar] [CrossRef]
- Fang, H.; Li, X.; Song, S.; Xu, Y.; Zhu, J. Fabrication of slantingly-aligned silicon nanowire arrays for solar cell applications. Nanotechnology 2008, 19, 255703. [Google Scholar] [CrossRef]
- Colombo, C.; Heiβ, M.; Grätzel, M.; Fontcuberta i Morral, A. Gallium arsenide p-i-n radial structures for photovoltaic applications. Appl. Phys. Lett. 2009, 94, 173108. [Google Scholar] [CrossRef]
- Dai, X.; Zhang, S.; Wang, Z.; Adamo, G.; Liu, H.; Huang, Y.; Couteau, C.; Soci, C. GaAs/AlGaAs nanowire photodetector. Nano Lett. 2014, 14, 2688. [Google Scholar] [CrossRef] [PubMed]
- Otnes, G.; Borgström, M.T. Towards high efficiency nanowire solar cells. Nano Today 2017, 12, 31. [Google Scholar] [CrossRef]
- Barrigon, E.; Hultin, O.; Lindgren, D.; Yadegari, F.; Magnusson, M.H.; Samuelson, L.; Johansson, L.I.M.; Björk, M.T. GaAs nanowire pn-junctions produced by low-cost and high-throughput Aerotaxy. Nano Lett. 2017, 18, 1088. [Google Scholar] [CrossRef] [PubMed]
- Heurlin, M.; Wickert, P.; Fält, S.; Borgström, M.T.; Deppert, K.; Samuelson, L.; Magnusson, M.H. Axial InP nanowire tandem junction grown on a silicon substrate. Nano Lett. 2011, 11, 2028. [Google Scholar] [CrossRef] [PubMed]
- Holm, J.V.; Jørgensen, H.I.; Krogstrup, P.; Nygård, J.; Liu, H.; Aagesen, M. Surface-passivated GaAsP single-nanowire solar cells exceeding 10% efficiency grown on silicon. Nat. Commun. 2013, 4, 1498. [Google Scholar] [CrossRef] [PubMed]
- Ko, W.S.; Tran, T.T.D.; Bhattacharya, I.; Ng, K.W.; Sun, H.; Chang-Hasnain, C. Illumination angle insensitive single indium phosphide tapered nanopillar solar cell. Nano Lett. 2015, 15, 4961–4967. [Google Scholar] [CrossRef]
- Nakai, E.; Chen, M.; Yoshimura, M.; Tomioka, K.; Fukui, T. InGaAs axial-junction nanowire-array solar cells. Jpn. J. Appl. Phys. 2014, 54, 015201. [Google Scholar] [CrossRef]
- Hwang, I.; Um, H.D.; Kim, B.S.; Wober, M.; Seo, K. Flexible crystalline silicon radial junction photovoltaics with vertically aligned tapered microwires. Energy Environ. Sci. 2018, 11, 641–647. [Google Scholar] [CrossRef]
- Van Dam, D.; van Hoof, N.J.; Cui, Y.; van Veldhoven, P.J.; Bakkers, E.P.; Gómez Rivas, J.; Haverkort, J.E. High-efficiency nanowire solar cells with omnidirectionally enhanced absorption due to self-aligned indium–tin–oxide mie scatterers. ACS Nano 2016, 10, 11414. [Google Scholar] [CrossRef]
- Boulanger, J.P.; Chia, A.C.E.; Wood, B.; Yazdi, S.; Kasama, T.; Aagesen, M.; LaPierre, R.R. Characterization of a Ga-assisted GaAs nanowire array solar cell on Si substrate. IEEE J. Photovolt. 2016, 6, 661. [Google Scholar] [CrossRef]
- Shin, J.C.; Kim, K.H.; Yu, K.J.; Hu, H.; Yin, L.; Ning, C.Z.; Rogers, J.A.; Zuo, J.-M.; Li, X. In x Ga1-x As Nanowires on Silicon: One-Dimensional Heterogeneous Epitaxy, Bandgap Engineering, and Photovoltaics. Nano Lett. 2011, 11, 4831. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.B.; Chen, Z.H.; Song, H.S.; Lee, C.S.; Cong, H.T.; Cheng, H.M.; Zhang, W.J.; Bello, I.; Lee, S.T. Vertically aligned p-type single-crystalline GaN nanorod arrays on n-type Si for heterojunction photovoltaic cells. Nano Lett. 2008, 8, 4191. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.P.T.; Chang, Y.L.; Shih, I.; Mi, Z. InN pin nanowire solar cells on Si. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 1062. [Google Scholar] [CrossRef]
- Wei, W.; Bao, X.Y.; Soci, C.; Ding, Y.; Wang, Z.L.; Wang, D. Direct heteroepitaxy of vertical InAs nanowires on Si substrates for broad band photovoltaics and photodetection. Nano Lett. 2009, 9, 2926. [Google Scholar] [CrossRef] [PubMed]
- Han, N.; Wang, F.; Yip, S.; Hou, J.J.; Xiu, F.; Shi, X.; Hui, A.T.; Hung, T.; Ho, J.C. GaAs nanowire Schottky barrier photovoltaics utilizing Au–Ga alloy catalytic tips. Appl. Phys. Lett. 2012, 101, 013105. [Google Scholar] [CrossRef]
- Fukui, T.; Yoshimura, M.; Nakai, E.; Tomioka, K. Position-Controlled III–V Compound Semiconductor Nanowire Solar Cells by Selective-Area Metal–Organic Vapor Phase Epitaxy. Ambio 2012, 41, 119. [Google Scholar] [CrossRef]
- Goto, H.; Nosaki, K.; Tomioka, K.; Hara, S.; Hiruma, K.; Motohisa, J.; Fukui, T. Growth of core–shell InP nanowires for photovoltaic application by selective-area metal organic vapor phase epitaxy. Appl. Phys. Express 2009, 2, 035004. [Google Scholar] [CrossRef]
- Mariani, G.; Zhou, Z.; Scofield, A.; Huffaker, D.L. Direct-bandgap epitaxial core–multishell nanopillar photovoltaics featuring subwavelength optical concentrators. Nano Lett. 2013, 13, 1632. [Google Scholar] [CrossRef]
- Mohseni, P.K.; Behnam, A.; Wood, J.D.; Zhao, X.; Yu, K.J.; Wang, N.C.; Rockett, A.; Rogers, J.A.; Lyding, J.W.; Pop, E.; et al. Monolithic III-V nanowire solar cells on graphene via direct van der waals epitaxy. Adv. Mater. 2014, 26, 3755. [Google Scholar] [CrossRef]
- Yoshimura, M.; Nakai, E.; Tomioka, K.; Fukui, T. Indium phosphide core–shell nanowire array solar cells with lattice-mismatched window layer. Appl. Phys. Express 2013, 6, 052301. [Google Scholar] [CrossRef]
- Nowzari, A.; Heurlin, M.; Jain, V.; Storm, K.; Hosseinnia, A.; Anttu, N.; Borgström, M.T.; Pettersson, H.; Samuelson, L. A comparative study of absorption in vertically and laterally oriented InP core–shell nanowire photovoltaic devices. Nano Lett. 2015, 15, 1809. [Google Scholar] [CrossRef] [PubMed]
- Holm, J.V.; Aagesen, M.; Zhang, Y.; Wu, J.; Hatch, S.; Liu, H. Bandgap optimized III–V (GaAsP) nanowire on silicon tandem solar cell, device and data. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014. [Google Scholar]
- Bu, S.; Li, X.; Wen, L.; Zeng, X.; Zhao, Y.; Wang, W.; Wang, Y. Optical and electrical simulations of two-junction III–V nanowires on Si solar cell. Appl. Phys. Lett. 2013, 102, 031106. [Google Scholar] [CrossRef]
- Chen, Y.; Höhn, O.; Tucher, N.; Pistol, M.E.; Anttu, N. Optical analysis of a III–V-nanowire-array-on-Si dual junction solar cell. Opt. Express 2017, 25, A665–A679. [Google Scholar] [CrossRef] [PubMed]
- Maryasin, V.; Bucci, D.; Rafhay, Q.; Panicco, F.; Michallon, J.; Kaminski-Cachopo, A. Technological guidelines for the design of tandem III–V nanowire on Si solar cells from opto-electrical simulations. Sol. Energy Mater. Sol. Cells 2017, 172, 314–323. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Zhao, Z.; Bu, S.; Zeng, X.; Huang, J.H.; Wang, Y. Theoretical consideration of III–V nanowire/Si triple-junction solar cells. Nanotechnology 2012, 23, 505202. [Google Scholar] [CrossRef] [PubMed]
- Foster, A.P.; Wilson, L.R. Design parameters for nanowire-planar tandem solar cells. Phys. Status Solidi (A) 2013, 210, 425–429. [Google Scholar] [CrossRef]
- Guter, W.; Schöne, J.; Philipps, S.P.; Steiner, M.; Siefer, G.; Wekkeli, A.; Dimroth, F. Current-matched triple-junction solar cell reaching 41.1% conversion efficiency under concentrated sunlight. Appl. Phys. Lett. 2009, 94, 223504. [Google Scholar] [CrossRef]
- Benali, A.; Michallon, J.; Regreny, P.; Drouard, E.; Rojo, P.; Chauvin, N.; Gendry, M. Optical simulation of multijunction solar cells based on III–V nanowires on silicon. Energy Procedia 2014, 60, 109–115. [Google Scholar] [CrossRef]
- Hu, Y.; Li, M.; He, J.J.; LaPierre, R.R. Current matching and efficiency optimization in a two-junction nanowire-on-silicon solar cell. Nanotechnology 2013, 24, 065402. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.; Lin, C.; Povinelli, M.L. Limiting efficiencies of tandem solar cells consisting of III–V nanowire arrays on silicon. J. Appl. Phys. 2012, 112, 064321. [Google Scholar] [CrossRef]
- LaPierre, R.R. Theoretical conversion efficiency of a two-junction III–V nanowire on Si solar cell. J. Appl. Phys. 2011, 110, 014310. [Google Scholar] [CrossRef]
- Larsson, M.W.; Wagner, J.B.; Wallin, M.; Håkansson, P.; Fröberg, L.E.; Samuelson, L.; Wallenberg, L.R. Strain mapping in free-standing heterostructured wurtzite InAs/InP nanowires. Nanotechnology 2006, 18, 015504. [Google Scholar] [CrossRef]
- Glas, F. Critical dimensions for the plastic relaxation of strained axial heterostructures in free-standing nanowires. Phys. Rev. B 2006, 74, 121302. [Google Scholar] [CrossRef]
- Ye, H.; Lu, P.; Yu, Z.; Song, Y.; Wang, D.; Wang, S. Critical thickness and radius for axial heterostructure nanowires using finite-element method. Nano Lett. 2009, 9, 1921. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Tateno, K.; Gotoh, H.; Sogawa, T.; Nakano, H. Structural, compositional, and optical characterizations of vertically aligned AlAs/GaAs/GaP heterostructure nanowires epitaxially grown on Si substrate. Jpn. J. Appl. Phys. 2010, 49, 015001. [Google Scholar] [CrossRef]
- Ercolani, D.; Rossi, F.; Li, A.; Roddaro, S.; Grillo, V.; Salviati, G.; Beltram, F.; Sorba, L. InAs/InSb nanowire heterostructures grown by chemical beam epitaxy. Nanotechnology 2009, 20, 505605. [Google Scholar] [CrossRef] [PubMed]
- Hilse, M.; Takagaki, Y.; Ramsteiner, M.; Herfort, J.; Breuer, S.; Geelhaar, L.; Riechert, H. Strain in GaAs–MnAs core–shell nanowires grown by molecular beam epitaxy. J. Cryst. Growth 2011, 323, 307. [Google Scholar] [CrossRef]
- Søndergaard, N.; He, Y.; Fan, C.; Han, R.; Guhr, T.; Xu, H.Q. Strain distributions in lattice-mismatched semiconductor core–shell nanowires. J. Vac. Sci. Technol. 2009, 27, 827. [Google Scholar] [CrossRef]
- Grönqvist, J.; Søndergaard, N.; Boxberg, F.; Guhr, T.; Åberg, S.; Xu, H.Q. Strain in semiconductor core–shell nanowires. J. Appl. Phys. 2009, 106, 053508. [Google Scholar] [CrossRef]
- Biermanns, A.; Rieger, T.; Bussone, G.; Pietsch, U.; Grützmacher, D.; Ion Lepsa, M. Axial strain in GaAs/InAs core–shell nanowires. Appl. Phys. Lett. 2013, 102, 043109. [Google Scholar] [CrossRef]
- Montazeri, M.; Fickenscher, M.; Smith, L.M.; Jackson, H.E.; Yarrison-Rice, J.; Kang, J.H.; Gao, Q.; Tan, H.H.; Jagadish, C.; Guo, Y.; et al. Direct Measure of Strain and Electronic Structure in GaAs/GaP Core− Shell Nanowires. Nano Lett. 2010, 10, 880. [Google Scholar] [CrossRef] [PubMed]
- Sköld, N.; Karlsson, L.S.; Larsson, M.W.; Pistol, M.E.; Seifert, W.; Trägårdh, J.; Samuelson, L. Growth and Optical Properties of Strained GaAs− Ga x In1-x P Core− Shell Nanowires. Nano Lett. 2005, 5, 1943. [Google Scholar] [CrossRef] [PubMed]
- Raychaudhuri, S.; Yu, E.T. Calculation of critical dimensions for wurtzite and cubic zinc blende coaxial nanowire heterostructures. J. Vac. Sci. Technol. B 2006, 24, 2053. [Google Scholar] [CrossRef]
- Raychaudhuri, S.; Yu, E.T. Critical dimensions in coherently strained coaxial nanowire heterostructures. J. Appl. Phys. 2006, 99, 114308. [Google Scholar] [CrossRef]
- Nazarenko, M.V.; Sibirev, N.V.; Wei Ng, K.; Ren, F.; Son Ko, W.; Dubrovskii, V.G.; Chang-Hasnain, C. Elastic energy relaxation and critical thickness for plastic deformation in the core–shell InGaAs/GaAs nanopillars. J. Appl. Phys. 2013, 113, 104311. [Google Scholar] [CrossRef]
- Chen, Y.; Pistol, M.E.; Anttu, N. Design for strong absorption in a nanowire array tandem solar cell. Sci. Rep. 2016, 6, 32349. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Yan, X.; Zhang, X.; Li, J.; Ren, X. Axially connected nanowire core–shell pn junctions: A composite structure for high-efficiency solar cells. Nanoscale Res. Lett. 2015, 10, 22. [Google Scholar] [CrossRef]
- Hocevar, M.; Immink, G.; Verheijen, M.; Akopian, N.; Zwiller, V.; Kouwenhoven, L.; Bakkers, E. Growth and optical properties of axial hybrid III–V/silicon nanowires. Nat. Commun. 2012, 3, 1266. [Google Scholar] [CrossRef]
- Dorodnyy, A.; Alarcon-Lladó, E.; Shklover, V.; Hafner, C.; Fontcuberta i Morral, A.; Leuthold, J. Efficient multiterminal spectrum splitting via a nanowire array solar cell. ACS Photonics 2015, 2, 1284–1288. [Google Scholar] [CrossRef]
- Adikaari, A.D.T.; Dissanayake, D.N.M.; Silva, S.R.P. Organic–inorganic solar cells: Recent developments and outlook. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1595–1606. [Google Scholar] [CrossRef]
- Yan, L.; You, W. Real function of semiconducting polymer in GaAs/polymer planar heterojunction solar cells. ACS Nano 2013, 7, 6619–6626. [Google Scholar] [CrossRef] [PubMed]
- Sato, K.; Dutta, M.; Fukata, N. Inorganic/organic hybrid solar cells: Optimal carrier transport in vertically aligned silicon nanowire arrays. Nanoscale 2014, 6, 6092–6101. [Google Scholar] [CrossRef] [PubMed]
- Bi, H.; LaPierre, R.R. A GaAs nanowire/P3HT hybrid photovoltaic device. Nanotechnology 2009, 20, 465205. [Google Scholar] [CrossRef] [PubMed]
- Chao, J.J.; Shiu, S.C.; Hung, S.C.; Lin, C.F. GaAs nanowire/poly (3, 4-ethylenedioxythiophene): Poly (styrenesulfonate) hybrid solar cells. Nanotechnology 2010, 21, 285203. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Sun, B.; Liu, D.; Lee, S.T. Hybrid heterojunction solar cell based on organic–inorganic silicon nanowire array architecture. J. Am. Chem. Soc. 2011, 133, 19408–19415. [Google Scholar] [CrossRef] [PubMed]
- Tsai, S.H.; Chang, H.C.; Wang, H.H.; Chen, S.Y.; Lin, C.A.; Chen, S.A.; He, J.H. Significant efficiency enhancement of hybrid solar cells using core–shell nanowire geometry for energy harvesting. ACS Nano 2011, 5, 9501–9510. [Google Scholar] [CrossRef]
- Wang, J.; Wang, H.; Prakoso, A.B.; Togonal, A.S.; Hong, L.; Jiang, C. High efficiency silicon nanowire/organic hybrid solar cells with two-step surface treatment. Nanoscale 2015, 7, 4559–4565. [Google Scholar] [CrossRef]
- Yu, P.; Tsai, C.Y.; Chang, J.K.; Lai, C.C.; Chen, P.H.; Lai, Y.C.; Wu, C.I. 13% efficiency hybrid organic/silicon-nanowire heterojunction solar cell via interface engineering. ACS Nano 2013, 7, 10780–10787. [Google Scholar] [CrossRef]
- Um, H.D.; Choi, D.; Choi, A.; Seo, J.H.; Seo, K. Embedded Metal Electrode for Organic–Inorganic Hybrid Nanowire Solar Cells. ACS Nano 2017, 11, 6218–6224. [Google Scholar] [CrossRef]
- Wei, W.R.; Tsai, M.L.; Ho, S.T.; Tai, S.H.; Ho, C.R.; Tsai, S.H.; He, J.H. Above-11%-efficiency organic–inorganic hybrid solar cells with omnidirectional harvesting characteristics by employing hierarchical photon-trapping structures. Nano Lett. 2013, 13, 3658–3663. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Wang, J.; Sun, T.; Wang, M.; Wu, C.; Zou, H.; Song, T.; Zhang, X.; Lee, S.; Wang, Z.L.; et al. Silicon nanowire/polymer hybrid solar cell-supercapacitor: A self-charging power unit with a total efficiency of 10.5%. Nano Lett. 2017, 17, 4240. [Google Scholar] [CrossRef] [PubMed]
- Park, K.T.; Kim, H.J.; Park, M.J.; Jeong, J.H.; Lee, J.; Choi, D.G.; Choi, J.H. 13.2% efficiency Si nanowire/PEDOT: PSS hybrid solar cell using a transfer-imprinted Au mesh electrode. Sci. Rep. 2015, 5, 12093. [Google Scholar] [CrossRef] [PubMed]
- Chao, J.J.; Shiu, S.C.; Lin, C.F. GaAs nanowire/poly (3, 4-ethylenedioxythiophene): Poly (styrenesulfonate) hybrid solar cells with incorporating electron blocking poly (3-hexylthiophene) layer. Sol. Energy Mater. Sol. Cells 2012, 105, 40. [Google Scholar] [CrossRef]
- Mariani, G.; Wang, Y.; Wong, P.S.; Lech, A.; Hung, C.H.; Shapiro, J.; Prikhodko, S.; El-Kady, M.; Kaner, R.B.; Huffaker, D.L. Three-Dimensional Core–Shell Hybrid Solar Cells via Controlled in Situ Materials Engineering. Nano Lett. 2012, 12, 3581. [Google Scholar] [CrossRef] [PubMed]
- Lundgren, C.; Lopez, R.; Redwing, J.; Melde, K. FDTD modeling of solar energy absorption in silicon branched nanowires. Opt. Express 2013, 21, A392. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Fan, H.J. Branched nanowires: Synthesis and energy applications. Nano Today 2012, 7, 327. [Google Scholar] [CrossRef]
- Wang, D.; Qian, F.; Yang, C.; Zhong, Z.; Lieber, C.M. Rational growth of branched and hyperbranched nanowire structures. Nano Lett. 2004, 4, 871. [Google Scholar] [CrossRef]
- Baxter, J.B.; Aydil, E.S. Nanowire-based dye-sensitized solar cells. Appl. Phys. Lett. 2005, 86, 053114. [Google Scholar] [CrossRef]
- Cohin, Y.; Mauguin, O.; Largeau, L.; Patriarche, G.; Glas, F.; Søndergaård, E.; Harmand, J.C. Growth of vertical GaAs nanowires on an amorphous substrate via a fiber-textured Si platform. Nano Lett. 2013, 13, 2743. [Google Scholar] [CrossRef]
- Bakkers, E.P.; Borgström, M.T.; Verheijen, M.A. Epitaxial growth of III–V nanowires on group IV substrates. Mrs Bull. 2007, 32, 117. [Google Scholar] [CrossRef]
- Mohseni, P.K.; Lawson, G.; Couteau, C.; Weihs, G.; Adronov, A.; LaPierre, R.R. Growth and characterization of GaAs nanowires on carbon nanotube composite films: Toward flexible nanodevices. Nano Lett. 2008, 8, 4075. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.J.; Lee, W.H.; Wu, Y.; Ruoff, R.S.; Fukui, T. Van der Waals epitaxy of InAs nanowires vertically aligned on single-layer graphene. Nano Lett. 2012, 12, 1431. [Google Scholar] [CrossRef] [PubMed]
- Mårtensson, T.; Svensson, C.P.T.; Wacaser, B.A.; Larsson, M.W.; Seifert, W.; Deppert, K.; Gustafsson, A.; Wallenberg, L.R.; Samuelson, L. Epitaxial III− V nanowires on silicon. Nano Lett. 2004, 4, 1987. [Google Scholar] [CrossRef]
- Lohn, A.J.; Li, X.; Kobayashi, N.P. Epitaxial growth of ensembles of indium phosphide nanowires on various non-single crystal substrates using an amorphous template layer. J. Cryst. Growth 2011, 315, 157. [Google Scholar] [CrossRef]
- Mohseni, P.K.; Behnam, A.; Wood, J.D.; English, C.D.; Lyding, J.W.; Pop, E.; Li, X. In x Ga1–x As Nanowire Growth on Graphene: Van der Waals Epitaxy Induced Phase Segregation. Nano Lett. 2013, 13, 1153. [Google Scholar] [CrossRef] [PubMed]
- Munshi, A.M.; Dheeraj, D.L.; Fauske, V.T.; Kim, D.C.; van Helvoort, A.T.; Fimland, B.O.; Weman, H. Vertically aligned GaAs nanowires on graphite and few-layer graphene: Generic model and epitaxial growth. Nano Lett. 2012, 12, 4570. [Google Scholar] [CrossRef] [PubMed]
- Ikejiri, K.; Ishizaka, F.; Tomioka, K.; Fukui, T. GaAs nanowire growth on polycrystalline silicon thin films using selective-area MOVPE. Nanotechnol. 2013, 24, 115304. [Google Scholar] [CrossRef] [PubMed]
- Novotny, C.J.; Yu, E.T.; Yu, P.K. InP nanowire/polymer hybrid photodiode. Nano Lett. 2008, 8, 775. [Google Scholar] [CrossRef]
- Dhaka, V.; Haggren, T.; Jussila, H.; Jiang, H.; Kauppinen, E.; Huhtio, T.; Sopanen, M.; Lipsanen, H. High quality GaAs nanowires grown on glass substrates. Nano Lett. 2012, 12, 1912. [Google Scholar] [CrossRef]
- O’Donnell, B.; Yu, L.; Foldyna, M.; i Cabarrocas, P.R. Silicon nanowire solar cells grown by PECVD. J. Non-Cryst. Solids 2012, 358, 2299–2302. [Google Scholar] [CrossRef]
- Schubert, M.B.; Werner, J.H. Flexible Solar Cells for Clothing. Mater. Today 2006, 9, 42. [Google Scholar] [CrossRef]
- Valente, J.; Godde, T.; Zhang, Y.; Mowbray, D.J.; Liu, H. Light Emitting GaAs Nanowires on a Flexible Substrate. Nano Lett. 2018, 18, 4206. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Razavi, H.; Do, J.W.; Moriwaki, A.; Ergen, O.; Chueh, Y.L.; Leu, P.W.; Ho, J.C.; Takahashi, T.; Reichertz, L.A.; et al. Three-dimensional nanopillar-array photovoltaics on low-cost and flexible substrates. Nat. Mater. 2009, 8, 648. [Google Scholar] [CrossRef] [PubMed]
- Kwon, J.Y.; Lee, D.H.; Chitambar, M.; Maldonado, S.; Tuteja, A.; Boukai, A. High efficiency thin upgraded metallurgical-grade silicon solar cells on flexible substrates. Nano Lett. 2012, 12, 5143. [Google Scholar] [CrossRef] [PubMed]
- Han, N.; Yang, Z.X.; Wang, F.; Dong, G.; Yip, S.; Liang, X.; Hung, T.F.; Chen, Y.; Ho, J.C. High-performance GaAs nanowire solar cells for flexible and transparent photovoltaics. ACS Appl. Mater. Interfaces 2015, 7, 20454. [Google Scholar] [CrossRef] [PubMed]
- Blömers, C.; Grap, T.; Lepsa, M.I.; Moers, J.; Trellenkamp, S.; Grützmacher, D.; Lüth, H.; Schäpers, T. Hall effect measurements on InAs nanowires. Appl. Phys. Lett. 2012, 101, 152106. [Google Scholar] [CrossRef]
- Storm, K.; Halvardsson, F.; Heurlin, M.; Lindgren, D.; Gustafsson, A.; Wu, P.M.; Monemar, B.; Samuelson, L. Spatially resolved Hall effect measurement in a single semiconductor nanowire. Nat. Nanotechnol. 2012, 7, 718. [Google Scholar] [CrossRef] [PubMed]
- Wunnicke, O. Gate capacitance of back-gated nanowire field-effect transistors. Appl. Phys. Lett. 2006, 89, 083102. [Google Scholar] [CrossRef]
- Bertness, K.A.; Sanford, N.A.; Davydov, A.V. GaN nanowires grown by molecular beam epitaxy. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 847. [Google Scholar] [CrossRef]
- Ashkenasy, G.; Cahen, D.; Cohen, R.; Shanzer, A.; Vilan, A. Molecular engineering of semiconductor surfaces and devices. Acc. Chem. Res. 2002, 35, 121. [Google Scholar] [CrossRef] [PubMed]
- Dalmau Mallorquí, A.; Epple, F.M.; Fan, D.; Demichel, O.; Fontcuberta i Morral, A. Effect of the pn junction engineering on Si microwire-array solar cells. Phys. Status Solidi (A) 2012, 209, 1588–1591. [Google Scholar] [CrossRef]
- Tajik, N.; Peng, Z.; Kuyanov, P.; LaPierre, R.R. Sulfur passivation and contact methods for GaAs nanowire solar cells. Nanotechnology 2011, 22, 225402. [Google Scholar] [CrossRef] [PubMed]
- Garnett, E.C.; Yang, P. Silicon nanowire radial p− n junction solar cells. J. Am. Chem. Soc. 2008, 130, 9224–9225. [Google Scholar] [CrossRef]
- Parkinson, P.; Joyce, H.J.; Gao, Q.; Tan, H.H.; Zhang, X.; Zou, J.; Jagadish, C.; Her, L.M.; Johnston, M.B. Carrier lifetime and mobility enhancement in nearly defect-free core− shell nanowires measured using time-resolved terahertz spectroscopy. Nano Lett. 2009, 9, 3349. [Google Scholar] [CrossRef]
- Czaban, J.A.; Thompson, D.A.; LaPierre, R.R. GaAs core− shell nanowires for photovoltaic applications. Nano Lett. 2008, 9, 148. [Google Scholar] [CrossRef] [PubMed]
- Nakai, E.; Yoshimura, M.; Tomioka, K.; Fukui, T. GaAs/InGaP core–multishell nanowire-array-based solar cells. Japanese J. Appl. Phys. 2013, 52, 055002. [Google Scholar] [CrossRef]
- Zhang, G.; Jiang, S.; Lin, Y.; Ren, W.; Cai, H.; Wu, Y.; Zhang, Q.; Pan, N.; Luo, Y.; Wang, X. Improving the photovoltaic performance of solid-state ZnO/CdTe core–shell nanorod array solar cells using a thin CdS interfacial layer. J. Mater. Chem. A 2014, 2, 5675. [Google Scholar] [CrossRef]
- Kartopu, G.; Turkay, D.; Ozcan, C.; Hadibrata, W.; Aurang, P.; Yerci, S.; Unalan, H.E.; Barrioz, V.; Qu, Y.; Bowen, L.; et al. Photovoltaic performance of CdS/CdTe junctions on ZnO nanorod arrays. Sol. Energy Mater. Sol. Cells 2018, 176, 100. [Google Scholar] [CrossRef]
- Dan, Y.; Seo, K.; Takei, K.; Meza, J.H.; Javey, A.; Crozier, K.B. Dramatic reduction of surface recombination by in situ surface passivation of silicon nanowires. Nano Lett. 2011, 11, 2527. [Google Scholar] [CrossRef]
- Wang, X.; Peng, K.Q.; Pan, X.J.; Chen, X.; Yang, Y.; Li, L.; Lee, S.T. High-Performance Silicon Nanowire Array Photoelectrochemical Solar Cells through Surface Passivation and Modification. Angew. Chem. Int. Ed. 2011, 50, 9861. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, J.; Kerr, M.; Cuevas, A. Surface passivation of silicon solar cells using plasma-enhanced chemical-vapour-deposited SiN films and thin thermal SiO2/plasma SiN stacks. Semicond. Sci. Technol. 2001, 16, 164. [Google Scholar] [CrossRef]
- Schmidt, J.; Merkle, A.; Brendel, R.; Hoex, B.; de Sanden, M.V.; Kessels, W.M.M. Surface passivation of high-efficiency silicon solar cells by atomic-layer-deposited Al2O3. Prog. Photovolt. 2008, 16, 461. [Google Scholar] [CrossRef]
- Chang, C.C.; Chi, C.Y.; Yao, M.; Huang, N.; Chen, C.C.; Theiss, J.; Bushmaker, A.W.; LaLumondiere, S.; Yeh, T.; Povinelli, M.L.; et al. Electrical and optical characterization of surface passivation in GaAs nanowires. Nano Lett. 2012, 12, 4484. [Google Scholar] [CrossRef] [PubMed]
- Goktas, N.I.; Fiordaliso, E.M.; LaPierre, R.R. Doping assessment in GaAs nanowires. Nanotechnology 2018, 29, 234001. [Google Scholar] [CrossRef]
- Chia, A.C.E.; LaPierre, R.R. Electrostatic model of radial pn junction nanowires. J. Appl. Phys. 2013, 114, 074317. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Z.; Sanchez, A.M.; Ramsteiner, M.; Aagesen, M.; Wu, J.; Kim, D.; Jurczak, P.; Huo, S.; Lauhon, L.J.; et al. Doping of Self-Catalyzed Nanowires under the Influence of Droplets. Nano Lett. 2018, 18, 81. [Google Scholar] [CrossRef]
- Björk, M.T.; Schmid, H.; Knoch, J.; Riel, H.; Riess, W. Donor deactivation in silicon nanostructures. Nat. Nanotechnol. 2009, 4, 103. [Google Scholar] [CrossRef]
- Dalpian, G.M.; Chelikowsky, J.R. Self-purification in semiconductor nanocrystals. Phys. Rev. Lett. 2006, 96, 226802. [Google Scholar] [CrossRef]
- Norris, D.J.; Efros, A.L.; Erwin, S.C. Doped nanocrystals. Science 2008, 319, 1776. [Google Scholar] [CrossRef]
- Chia, A.C.; LaPierre, R.R. Analytical model of surface depletion in GaAs nanowires. J. Appl. Phys. 2012, 112, 063705. [Google Scholar] [CrossRef]
- Amit, I.; Givan, U.; Connell, J.G.; Paul, D.F.; Hammond, J.S.; Lauhon, L.J.; Rosenwaks, Y. Spatially resolved correlation of active and total doping concentrations in VLS grown nanowires. Nano Lett. 2013, 13, 2598. [Google Scholar] [CrossRef] [PubMed]
- Fiordaliso, E.M.; Balogh, Z.I.; Kasama, T.; LaPierre, R.; Aagesen, M. Mapping electrostatic potentials across the p-n junction in GaAs nanowires by off-axis electron holography. In Proceedings of the European Microscopy Congress 2016, 28 August–2 September 2016, Lyon, France; Wiley-VCH Verlag GmbH and Co. KGaA: Weinheim, Germany, 2016; pp. 743–744. [Google Scholar]
- Shin, J.C.; Lee, A.; Katal Mohseni, P.; Kim, D.Y.; Yu, L.; Kim, J.H.; Li, X. Wafer-Scale Production of Uniform InAs y P1–y Nanowire Array on Silicon for Heterogeneous Integration. ACS Nano 2013, 7, 5463. [Google Scholar] [CrossRef] [PubMed]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, H. Nanowires for High-Efficiency, Low-Cost Solar Photovoltaics. Crystals 2019, 9, 87. https://doi.org/10.3390/cryst9020087
Zhang Y, Liu H. Nanowires for High-Efficiency, Low-Cost Solar Photovoltaics. Crystals. 2019; 9(2):87. https://doi.org/10.3390/cryst9020087
Chicago/Turabian StyleZhang, Yunyan, and Huiyun Liu. 2019. "Nanowires for High-Efficiency, Low-Cost Solar Photovoltaics" Crystals 9, no. 2: 87. https://doi.org/10.3390/cryst9020087
APA StyleZhang, Y., & Liu, H. (2019). Nanowires for High-Efficiency, Low-Cost Solar Photovoltaics. Crystals, 9(2), 87. https://doi.org/10.3390/cryst9020087



