Site-Preference, Electronic, Magnetic, and Half-Metal Properties of Full-Heusler Sc2VGe and a Discussion on the Uniform Strain and Tetragonal Deformation Effects
Abstract
:1. Introduction
2. Calculation Methods
3. Results and Discussions
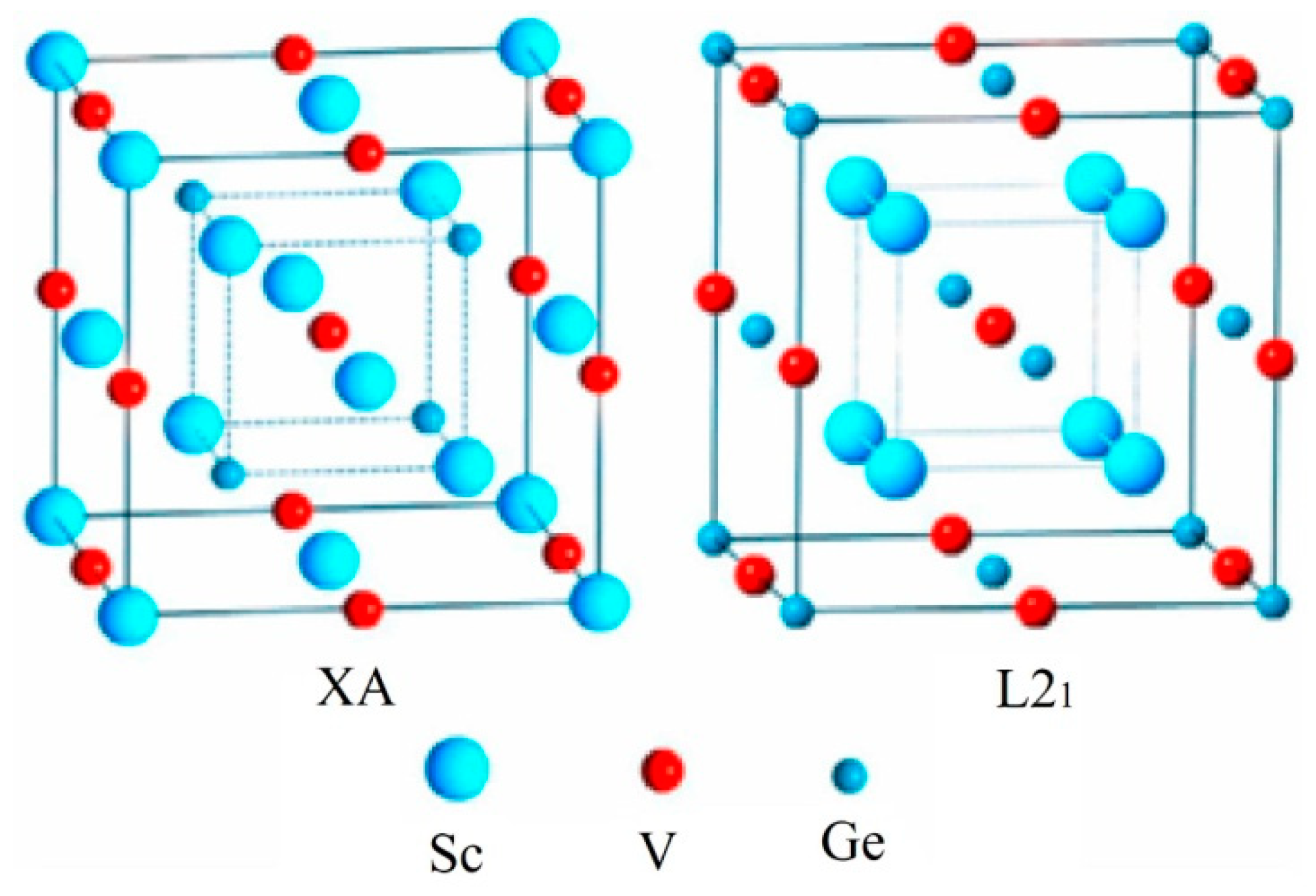
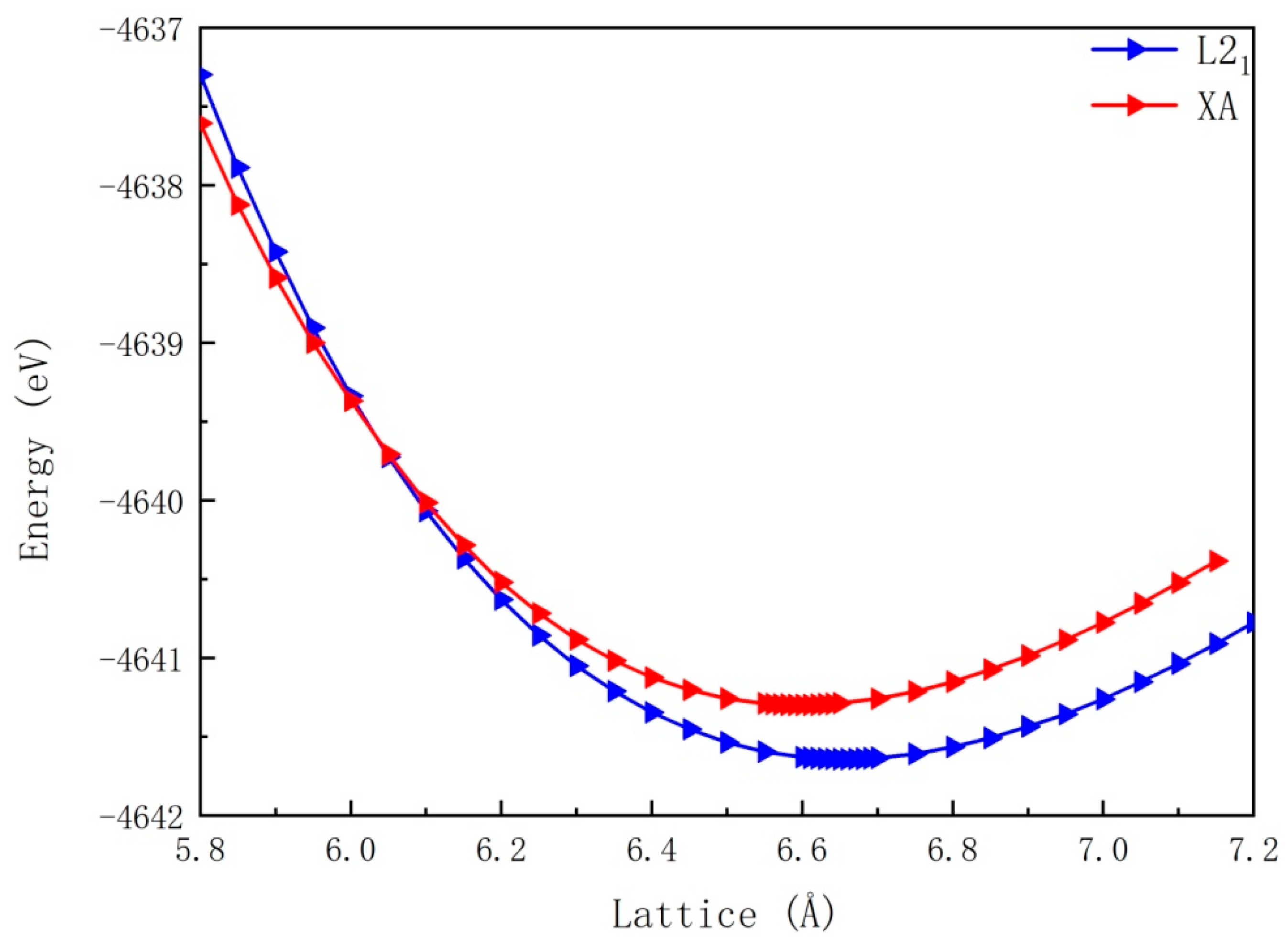
3.1. Competition of L21 and XA Structurein Full-Heusler Sc2VGe
3.2. Thermal Stability of XA-Type Sc2VGe
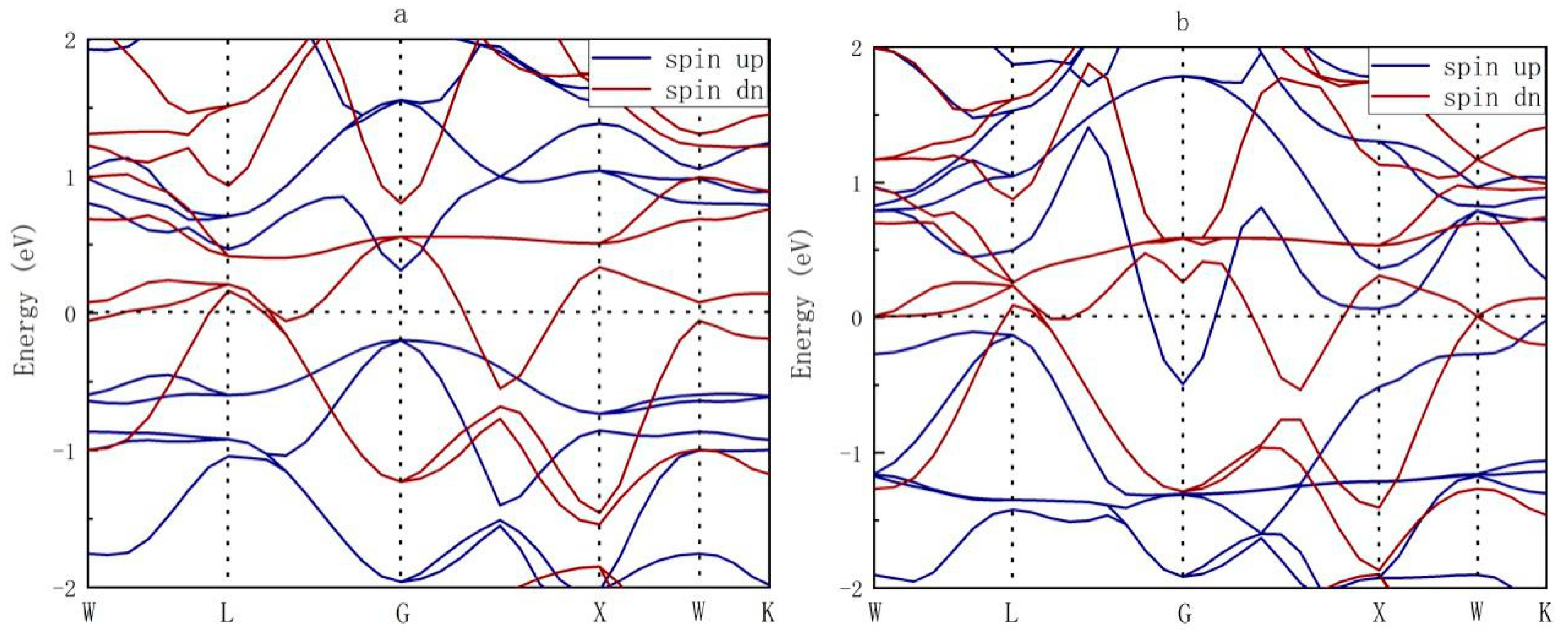
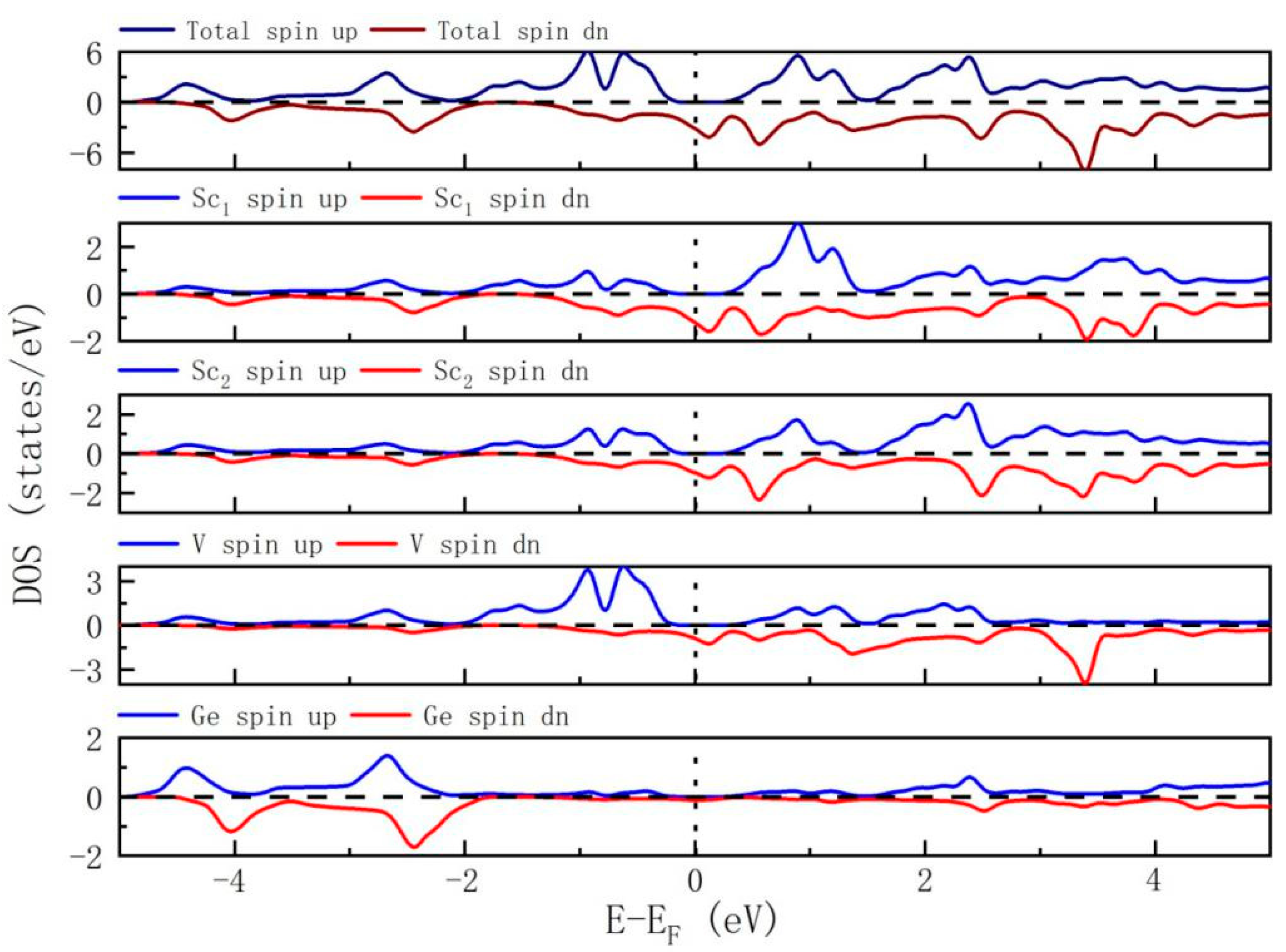
3.3. Total and Partial Density of States of XA-Type Sc2VGe
3.4. Effect of Uniform Strain on XA-Type Sc2VGe
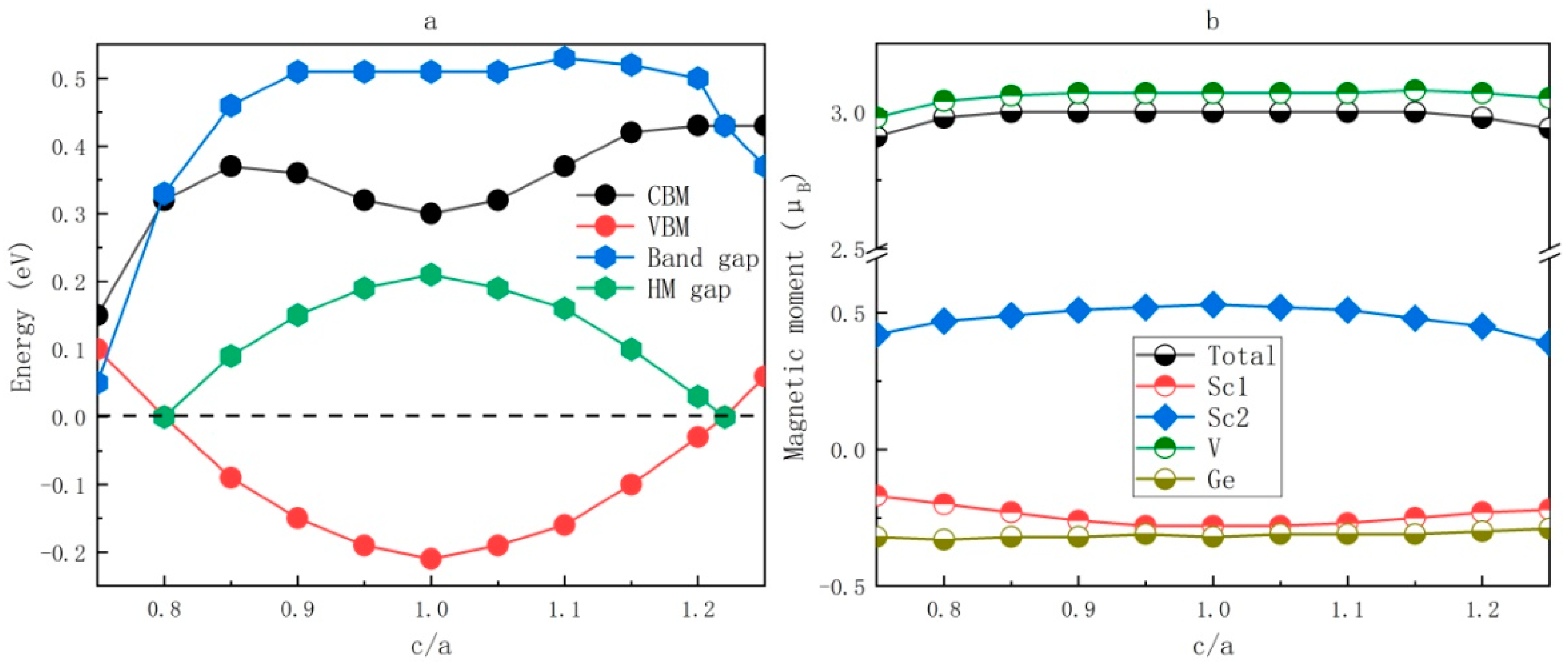
3.5. The effect of Tetragonal Lattice Distortion on XA-Type Sc2VGe
4. Conclusions
- (i)
- The site-preference of FH alloy Sc2VGe was examined, and results showed that the L21 type is more stable than the XA type. We further calculated the electronic structures of both types of Sc2VGe and found that the XA-type alloy was an excellent half-metallic material, whereas the L21-type alloy was a magnetic metal. XA-type Sc2VGe can intrinsically provide single spin channel electrons, and therefore this material can be used for pure spin generation and injection.
- (ii)
- When XA-type Sc2VGe is at its equilibrium lattice parameter, its total magnetic moment is 3 μB, which is in accordance with the well-known Slater–Pauling rule, and the main contribution to the total magnetism came from V atoms.
- (iii)
- The effects of uniform strain and tetragonal lattice distortion on the electronic structures of XA-type Sc2VGe were also studied. We found that the half-metallic state can be maintained in a large area of the lattice parameter and the c/a ratio, indicating that XA-type Sc2VGe is a robust half-metallic material.
- (iv)
- The formation energy and cohesive energy were calculated and results showed that this alloy has extensive scope for use in experiments.
- (v)
- The half-metallic band gap and the band gap in the spin-up channel as a function of the lattice parameter and the c/a ratio were taken into consideration for XA-type Sc2VGe, and we found that the maximum half-metallic band gap around 6.6 Å was approximately 0.2 eV. Such a large value ensures that the half-metallic property of this material is not affected by external factors.
- (vi)
- All the aforementioned results indicate that XA-type Sc2VGe would be an ideal candidate in spintronics.
Author Contributions
Funding
Conflicts of Interest
References
- Groot, R.A.D.; Mueller, F.M.; Engen, P.G.V.; Buschow, K.H.J. New class of materials: Half-metallic ferromagnets. Phys. Rev. Lett. 1983, 50, 2024–2027. [Google Scholar] [CrossRef]
- Haque, E.; Hossain, M.A. First-principles study of elastic, electronic, thermodynamic, and thermoelectric transport properties of TaCoSn. Results Phys. 2018, 10, 458–465. [Google Scholar] [CrossRef]
- Tang, Y.; Li, X.; Martin, H.J.; Reyes, E.C.; Ivas, T.; Leinenbach, C.; Anand, S.; Peters, M.; Snyde, G.; Battaglia, C. Impact of Ni content on the thermoelectric properties of half-Heusler TiNiSn. Energy Environ. Sci. 2018, 11, 311–320. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, C.; Xia, K.; Yu, J.; Zhao, X.; Pan, H.; Felser, C.; Zhu, T.J. Lanthanide Contraction as a Design Factor for High-Performance Half-Heusler Thermoelectric Materials. Adv. Mater. 2018, 30, 1800881. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.J.; Liu, Z.H.; Wu, Z.G.; Ma, X.Q. Prediction of fully compensated ferrimagnetic spin-gapless semiconducting FeMnGa/Al/In half Heusler alloys. IUCrJ 2019, 6, 610–618. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, Y.; Bouhemadou, A.; Khenata, R.; Cheng, Z.; Yang, T.; Wang, X. Prediction of possible martensitic transformations in all-d-metal Zinc-based Heusler alloys from first-principles. J. Magn. Magn. Mater. 2019, 471, 49–55. [Google Scholar] [CrossRef]
- Anjami, A.; Boochani, A.; Elahi, S.M.; Akbari, H. Ab-initio study of mechanical, half-metallic and optical properties of Mn2ZrX (X= Ge, Si) compounds. Results Phys. 2017, 7, 3522–3529. [Google Scholar] [CrossRef]
- Faleev, S.V.; Ferrante, Y.; Jeong, J.; Samant, M.G.; Jones, B.; Stuart, P. Origin of the tetragonal ground state of Heusler compounds. Phys. Rev. Appl. 2017, 7, 034022. [Google Scholar] [CrossRef]
- Sanvito, S.; Oses, C.; Xue, J.; Tiwari, A.; Zic, M.; Archer, T.; Tozman, P.; Venkatesan, M.; Coey, M.; Curtarolo, S. Accelerated discovery of new magnets in the Heusler alloy family. Sci. Adv. 2017, 3, e1602241. [Google Scholar] [CrossRef] [PubMed]
- Xin, Y.; Ma, Y.; Hao, H.; Luo, H.; Meng, F.; Liu, H.; Liu, E.; Wu, G. Structure and magnetic properties of Heusler alloy Co2RuSi melt-spun ribbons. J. Magn. Magn. Mater. 2017, 435, 76–80. [Google Scholar] [CrossRef]
- Li, T.; Wu, Y.; Han, Y.; Wang, X. Tuning the topological nontrivial nature in a family of alkali-metal-based inverse Heusler compounds: A first-principles study. J. Magn. Magn. Mater. 2018, 463, 44–49. [Google Scholar] [CrossRef]
- Galdun, L.; Ryba, T.; Prida, V.M.; Zhukova, V.; Zhukov, A.; Diko, P.; Kavečanský, V.; Vargova, Z.; Varga, R. Monocrystalline Heusler Co2FeSi alloy glass-coated microwires: Fabrication and magneto-structural characterization. J. Magn. Magn. Mater. 2018, 453, 96–100. [Google Scholar] [CrossRef]
- Marchenkov, V.V.; Perevozchikova, Y.A.; Kourov, N.I.; Irkhin, V.Y.; Eisterer, M.; Gao, T. Peculiarities of the electronic transport in half-metallic Co-based Heusler alloys. J. Magn. Magn. Mater. 2018, 459, 211–214. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Zhang, J.M. First-principles study of the Hf-based Heusler alloys: Hf2CoGa and Hf2CoIn. J. Magn. Magn. Mater. 2017, 421, 1–6. [Google Scholar] [CrossRef]
- Ahmad, N.; Ahmed, N.; Han, X.F. Analysis of electronic, magnetic and half-metallic properties of L21-type (Co2Mn0.5Fe0.5Sn) Heusler alloy nanowires synthesized by AC-electrodeposition in AAO templates. J. Magn. Magn. Mater. 2018, 460, 120–127. [Google Scholar]
- Djefal, A.; Amari, S.; Obodo, K.O.; Beldi, L.; Bendaoud, H.; Evans, R.F.L.; Bouhafs, B. Half-metallic ferromagnetism in double perovskite Ca2CoMoO6 compound: DFT + U calculations. Spin 2017, 7, 1750009. [Google Scholar] [CrossRef]
- Yan, W.; Zhang, X.; Shi, Q.; Yu, X.; Zhang, Z.; Wang, Q. Study of magnetocaloric effect in half-metallic ferromagnet Co3Sn2S2. Results Phys. 2018, 11, 1004–1007. [Google Scholar]
- Li, Y.; Liu, G.D.; Wang, X.T.; Liu, E.K.; Xi, X.K.; Wang, W.H.; Wu, G.H.; Wang, L.Y.; Dai, X.F. First-principles study on electronic structure, magnetism and half-metallicity of the NbCoCrAl and NbRhCrAl compounds. Results Phys. 2017, 7, 2248–2254. [Google Scholar] [CrossRef]
- Akbar, W.; Nazir, S. Origin of p-type half-metallic ferromagnetism in carbon-doped BeS: First-principles characterization. J. Alloy. Compd. 2018, 743, 83–86. [Google Scholar] [CrossRef]
- Yousuf, S.; Gupta, D.C. Insight into half-metallicity, spin-polarization and mechanical properties of L21 structured MnY2Z (Z = Al, Si, Ga, Ge, Sn, Sb) Heusler alloys. J. Alloy. Compd. 2018, 735, 1245–1252. [Google Scholar] [CrossRef]
- Boehnke, A.; Martens, U.; Sterwerf, C.; Niesen, A.; Huebner, T.; Ehe, M.; Meinert, M.; Kuschel, T.; Thomas, A.; Heiliger, C.; et al. Large magneto-Seebeck effect in magnetic tunnel junctions with half-metallic Heusler electrodes. Nat. Commun. 2017, 8, 1626. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Cheng, Z. Electronic, magnetic, mechanical, half-metallic and highly dispersive zero-gap half-metallic properties of rare-earth-element-based quaternary Heusler compounds. J. Alloy. Compd. 2017, 718, 63–74. [Google Scholar] [CrossRef]
- Chadov, S.; Wu, S.C.; Felser, C.; Galanakis, I. Stability of Weyl points in magnetic half-metallic Heusler compounds. Phys. Rev. B 2017, 96, 024435. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Gao, G.Y.; Yao, K.L.; Song, M.H. Half-metallic ferromagnetism in the half-Heusler compounds GeKCa and SnKCa from first-principles calculations. J. Alloy. Compd. 2011, 509, 10172–10178. [Google Scholar] [CrossRef]
- Yao, Z.; Zhang, Y.S.; Yao, K.L. Large half-metallic gap in ferromagnetic semi-Heusler alloys CoCrP and CoCrAs. Appl. Phys. Lett. 2012, 101, 062402. [Google Scholar] [CrossRef]
- Hirohata, A.; Sagar, J.; Lari, L.; Fleet, L.R.; Lazarov, V.K. Heusler-alloy films for spintronic devices. Appl. Phys. A 2013, 111, 423–430. [Google Scholar] [CrossRef]
- Azadani, J.; Munira, K.; Romero, J.; Ma, J.; Sivakumar, C.; Ghosh, A.W.; Butler, W.H. Anisotropy in layered half-metallic Heusler alloy superlattices. J. Appl. Phys. 2016, 119, 043904. [Google Scholar] [CrossRef] [Green Version]
- Nazemi, N.; Ahmadian, F. Half-Metallic Characteristic in the New Full–Heusler SrYO2 (Y = Sc, Ti, V, and Cr). Phys. Solid State 2019, 61, 1–10. [Google Scholar] [CrossRef]
- Kogachi, M.; Fujiwara, T.; Kikuchi, S. Atomic disorder and magnetic property in Co-based heusler alloys Co2MnZ (Z = Si, Ge, Sn). J. Alloy. Compd. 2009, 475, 723–729. [Google Scholar] [CrossRef]
- Liu, G.D.; Dai, X.F.; Liu, H.Y.; Chen, J.L.; Li, Y.X.; Xiao, G.; Wu, G.H. Mn2CoZ (Z = Al, Ga, In, Si, Ge, Sn, Sb) compounds: Structural, electronic, and magnetic properties. Phys. Rev. B 2008, 77, 117–119. [Google Scholar] [CrossRef]
- Wang, X.T.; Cui, Y.T.; Liu, X.F.; Liu, G.D. Electronic structures and magnetism in the Li2AgSb-type heusler alloys, Zr2CoZ (Z = Al, Ga, In, Si, Ge, Sn, Sb, Pb, Sb): A first-principles study. J. Magn. Magn. Mater. 2015, 394, 50–59. [Google Scholar] [CrossRef]
- Wang, X.T.; Cheng, Z.X.; Yuan, H.K.; Khenata, R. L21 and XA ordering competition in Titanium-based full-heusler alloys. J. Mater. Chem. C 2017, 5, 11559–11564. [Google Scholar] [CrossRef]
- Wang, X.T.; Cheng, Z.X.; Wang, W.H. L21 and XA ordering competition in hafnium-based full-heusler alloys Hf2VZ (Z = Al, Ga, In, Tl, Si, Ge, Sn, Pb). Materials 2017, 10, 1200. [Google Scholar] [CrossRef]
- Zhang, X.M.; Liu, E.K.; Liu, Z.Y.; Liu, G.D.; Wu, G.H.; Wang, W.H. Prediction of topological insulating behavior in inverse Heusler compounds from first principles. Comput. Mater. Sci. 2013, 70, 145–149. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Yang, G.; Yang, Y.; Ma, H.; Zhang, Q.; Zhang, Z.; Fang, W.; Yin, F.; Li, J. Electronic and thermoelectric properties of nonmagnetic inverse Heusler semiconductors Sc2FeSi and Sc2FeGe. J. Magn. Magn. Mater. 2017, 442, 151–158. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.; Probert, M.A.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. 2002, 14, 2717. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Maximoff, S.N.; Ernzerhof, M.; Scuseria, G.E. Current-dependent extension of the Perdew-Burke-Ernzerhof exchange-correlation functional. J. Chem. Phys. 2004, 120, 2105–2109. [Google Scholar] [CrossRef]
- Chen, Z.; Rozale, H.; Gao, Y.; Xu, H. Strain Control of the Tunable Physical Nature of a Newly Designed Quaternary Spintronic Heusler Compound ScFeRhP. Appl. Sci. 2018, 8, 1581. [Google Scholar] [CrossRef]
- Galanakis, I.; Dederichs, P.H.; Papanikolaou, N. Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 2002, 66, 174429. [Google Scholar] [CrossRef] [Green Version]
- Skaftouros, S.; Özdoğan, K.; Şaşıoğlu, E.; Galanakis, I. Generalized Slater-Pauling rule for the inverse Heusler compounds. Phys. Rev. B 2013, 87, 024420. [Google Scholar] [CrossRef]
- Meng, F.; Hao, H.; Ma, Y.; Guo, X.; Luo, H. Site preference of Zr in Heusler alloys Zr2YAl (Y = Cr, Mn, Fe, Co, Ni) and its influence on the electronic properties. J. Alloy. Compd. 2017, 695, 2995–3001. [Google Scholar] [CrossRef]
- Ni, Z.; Ma, Y.; Liu, X.; Luo, H.; Liu, H.; Meng, F. Site preference, electronic structure and possible martensitic transformation in Heusler alloys Ni2CoZ (Z = Al, Ga, In, Si, Ge, Sn, Sb). Intermetallics 2017, 81, 1–8. [Google Scholar]
- Ma, Y.; Hao, H.; Xin, Y.; Luo, H.; Liu, H.; Meng, F.; Liu, E. Atomic ordering and magnetic properties of quaternary Heusler alloys NiCuMnZ (Z = In, Sn, Sb). Intermetallics 2017, 86, 121–125. [Google Scholar] [CrossRef]
- Luo, H.; Xin, Y.; Liu, B.; Men, F.; Li, H.; Liu, E.; Wu, G. Competition of L21 and XA structural ordering in Heusler alloys X2CuAl (X = Sc, Ti, V, Cr, Mn, Fe, Co, Ni). J. Alloy. Compd. 2016, 665, 180–185. [Google Scholar] [CrossRef]
- Wang, J.X.; Chen, Z.B.; Gao, Y.C. Phase stability, magnetic, electronic, half-metallic and mechanical properties of a new equiatomic quaternary Heusler compound ZrRhTiIn: A first-principles investigation. J. Phys. Chem. Solids 2018, 116, 72–78. [Google Scholar] [CrossRef]
- Han, Y.; Wu, Y.; Li, T.; Khenata, R.; Yang, T.; Wang, X. Electronic, magnetic, half-metallic, and mechanical properties of a new equiatomic quaternary Heusler compound YRhTiGe: A first-principles study. Materials 2018, 11, 797. [Google Scholar] [CrossRef] [PubMed]
- Chandra, A.R.; Jain, V.; Lakshmi, N.; Jain, V.K.; Jain, R.; Venugopalan, K. Spin polarization in Co2CrAl/GaAs 2D-slabs: A computational study. J. Magn. Magn. Mater. 2018, 448, 75–81. [Google Scholar] [CrossRef]
- Bhat, T.M.; Gupta, D.C. First-principles study of high spin-polarization and thermoelectric efficiency of ferromagnetic CoFeCrAs quaternary Heusler alloy. J. Magn. Magn. Mater. 2018, 449, 493–499. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Z.; Liu, G.; Dai, X.; Bouhemadou, A. Rare earth-based quaternary Heusler compounds MCoVZ (M = Lu, Y.; Z= Si, Ge) with tunable band characteristics for potential spintronic applications. IUCrJ 2017, 4, 758–768. [Google Scholar] [CrossRef] [PubMed]


| Type | Mtotal () | MSc () | MSc () | Energy (eV) | ||
|---|---|---|---|---|---|---|
| XA | 3.00 | −0.28 | 0.53 | 3.07 | −0.32 | −4641.30 |
| L21 | 2.93 | −0.01 | −0.01 | 3.22 | −0.27 | −4641.64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xu, H.; Gao, Y.; Wang, X.; Yang, T. Site-Preference, Electronic, Magnetic, and Half-Metal Properties of Full-Heusler Sc2VGe and a Discussion on the Uniform Strain and Tetragonal Deformation Effects. Crystals 2019, 9, 445. https://doi.org/10.3390/cryst9090445
Chen Z, Xu H, Gao Y, Wang X, Yang T. Site-Preference, Electronic, Magnetic, and Half-Metal Properties of Full-Heusler Sc2VGe and a Discussion on the Uniform Strain and Tetragonal Deformation Effects. Crystals. 2019; 9(9):445. https://doi.org/10.3390/cryst9090445
Chicago/Turabian StyleChen, Zongbin, Heju Xu, Yongchun Gao, Xiaotian Wang, and Tie Yang. 2019. "Site-Preference, Electronic, Magnetic, and Half-Metal Properties of Full-Heusler Sc2VGe and a Discussion on the Uniform Strain and Tetragonal Deformation Effects" Crystals 9, no. 9: 445. https://doi.org/10.3390/cryst9090445
APA StyleChen, Z., Xu, H., Gao, Y., Wang, X., & Yang, T. (2019). Site-Preference, Electronic, Magnetic, and Half-Metal Properties of Full-Heusler Sc2VGe and a Discussion on the Uniform Strain and Tetragonal Deformation Effects. Crystals, 9(9), 445. https://doi.org/10.3390/cryst9090445






