Figure 1.
Schematic diagram of the rheometer with parallel-plate geometry.
Figure 1.
Schematic diagram of the rheometer with parallel-plate geometry.
Figure 2.
The schematic of a TPG measurement.
Figure 2.
The schematic of a TPG measurement.
Figure 3.
The schematic of a typical polymer flooding experiment.
Figure 3.
The schematic of a typical polymer flooding experiment.
Figure 4.
The rheological charts of the polymer solution with a concentration of 2000 mg/L and the original heavy oil.
Figure 4.
The rheological charts of the polymer solution with a concentration of 2000 mg/L and the original heavy oil.
Figure 5.
The viscosities of the polymer solution with a concentration of 2000 mg/L and the original heavy oil at different shear rates.
Figure 5.
The viscosities of the polymer solution with a concentration of 2000 mg/L and the original heavy oil at different shear rates.
Figure 6.
The relationship between the viscosity of the polymer solution and polymer concentration.
Figure 6.
The relationship between the viscosity of the polymer solution and polymer concentration.
Figure 7.
The relationship between the TPG and mobility.
Figure 7.
The relationship between the TPG and mobility.
Figure 8.
The grid system, well location and 3D distributions of initial oil saturation of Case 1.
Figure 8.
The grid system, well location and 3D distributions of initial oil saturation of Case 1.
Figure 9.
The relative permeabilities used in Case 1.
Figure 9.
The relative permeabilities used in Case 1.
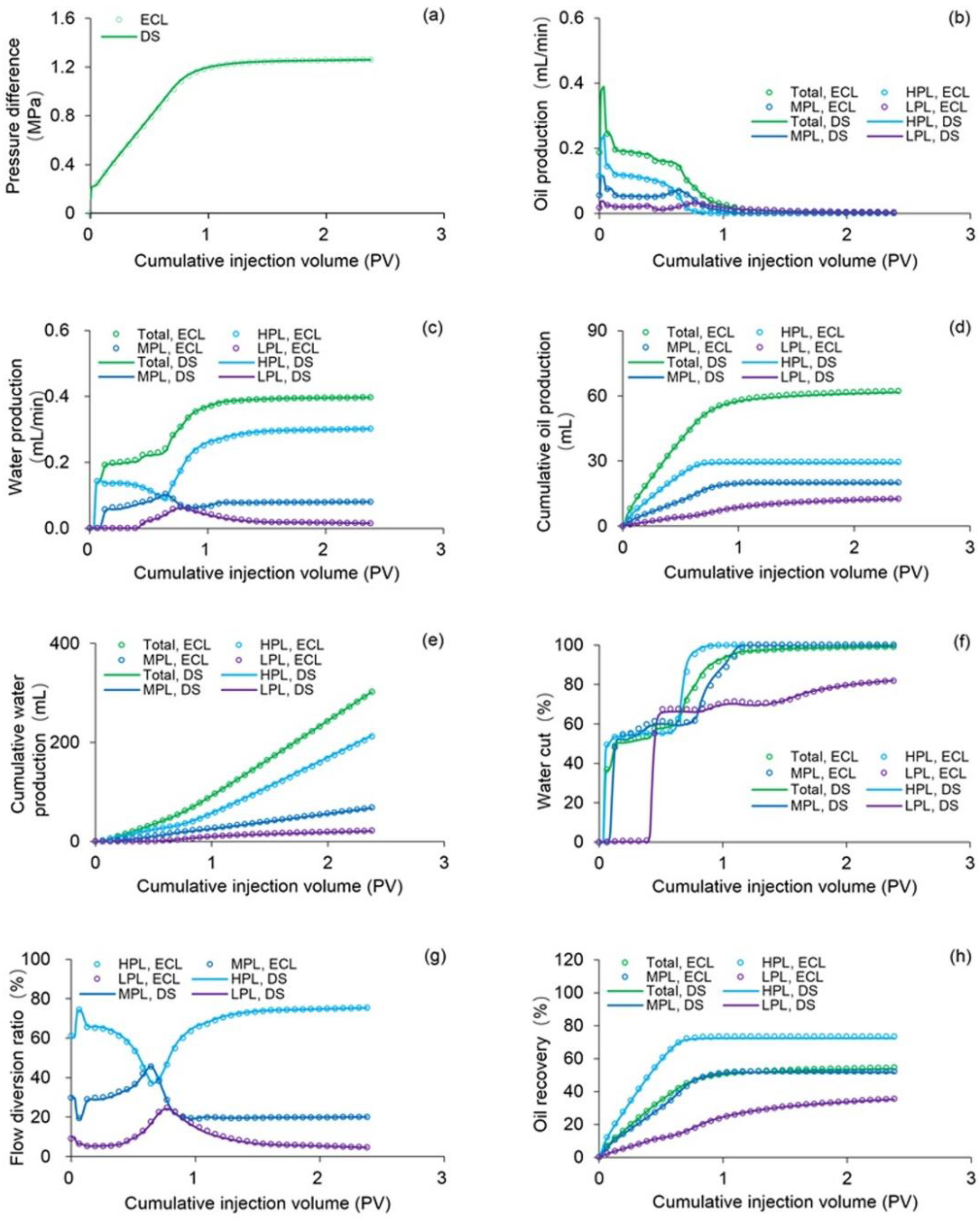
Figure 10.
Comparison results of (a) pressure difference, (b) oil production, (c) water production, (d) cumulative oil production, (e) cumulative water production, (f) water cut, (g) flow diversion ratio and (h) oil recovery of Case 1 simulated by the ECLIPSE V2013.1 software and the designed simulator.
Figure 10.
Comparison results of (a) pressure difference, (b) oil production, (c) water production, (d) cumulative oil production, (e) cumulative water production, (f) water cut, (g) flow diversion ratio and (h) oil recovery of Case 1 simulated by the ECLIPSE V2013.1 software and the designed simulator.
Figure 11.
Comparison of 3D remaining oil saturation distributions after cumulative injection volume of 2.4 PV based on (a) ECLIPSE V2013.1 software and (b) the designed simulator for running Case 1.
Figure 11.
Comparison of 3D remaining oil saturation distributions after cumulative injection volume of 2.4 PV based on (a) ECLIPSE V2013.1 software and (b) the designed simulator for running Case 1.
Figure 12.
Comparison results of (a) pressure difference, (b) oil production, (c) water production, (d) water cut, (e) cumulative oil production and (f) cumulative water production of Case 2 simulated by the designed simulator and the TPF experiment.
Figure 12.
Comparison results of (a) pressure difference, (b) oil production, (c) water production, (d) water cut, (e) cumulative oil production and (f) cumulative water production of Case 2 simulated by the designed simulator and the TPF experiment.
Figure 13.
Comparison results of (a) pressure difference, (b) water cut, (c) LPL flow diversion ratio and (d) oil recovery of Cases 1 and 3–5, and those of (e) pressure difference, (f) water cut, (g) LPL flow diversion ratio and (h) oil recovery of Cases 6–9.
Figure 13.
Comparison results of (a) pressure difference, (b) water cut, (c) LPL flow diversion ratio and (d) oil recovery of Cases 1 and 3–5, and those of (e) pressure difference, (f) water cut, (g) LPL flow diversion ratio and (h) oil recovery of Cases 6–9.
Figure 14.
3D remaining oil saturation distributions after polymer flooding of (a) Case 3 and (b) Case 5.
Figure 14.
3D remaining oil saturation distributions after polymer flooding of (a) Case 3 and (b) Case 5.
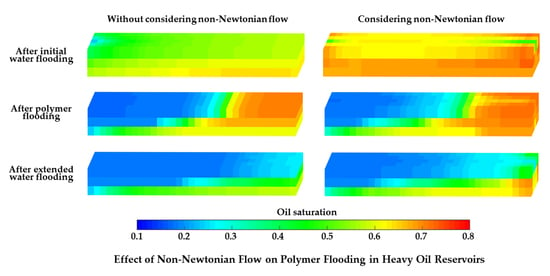
Figure 15.
3D remaining oil saturation distributions after (a) initial water flooding, (b) polymer flooding and (c) extended water flooding of Case 6, and those results after (d) initial water flooding, (e) polymer flooding and (f) extended water flooding of Case 9.
Figure 15.
3D remaining oil saturation distributions after (a) initial water flooding, (b) polymer flooding and (c) extended water flooding of Case 6, and those results after (d) initial water flooding, (e) polymer flooding and (f) extended water flooding of Case 9.
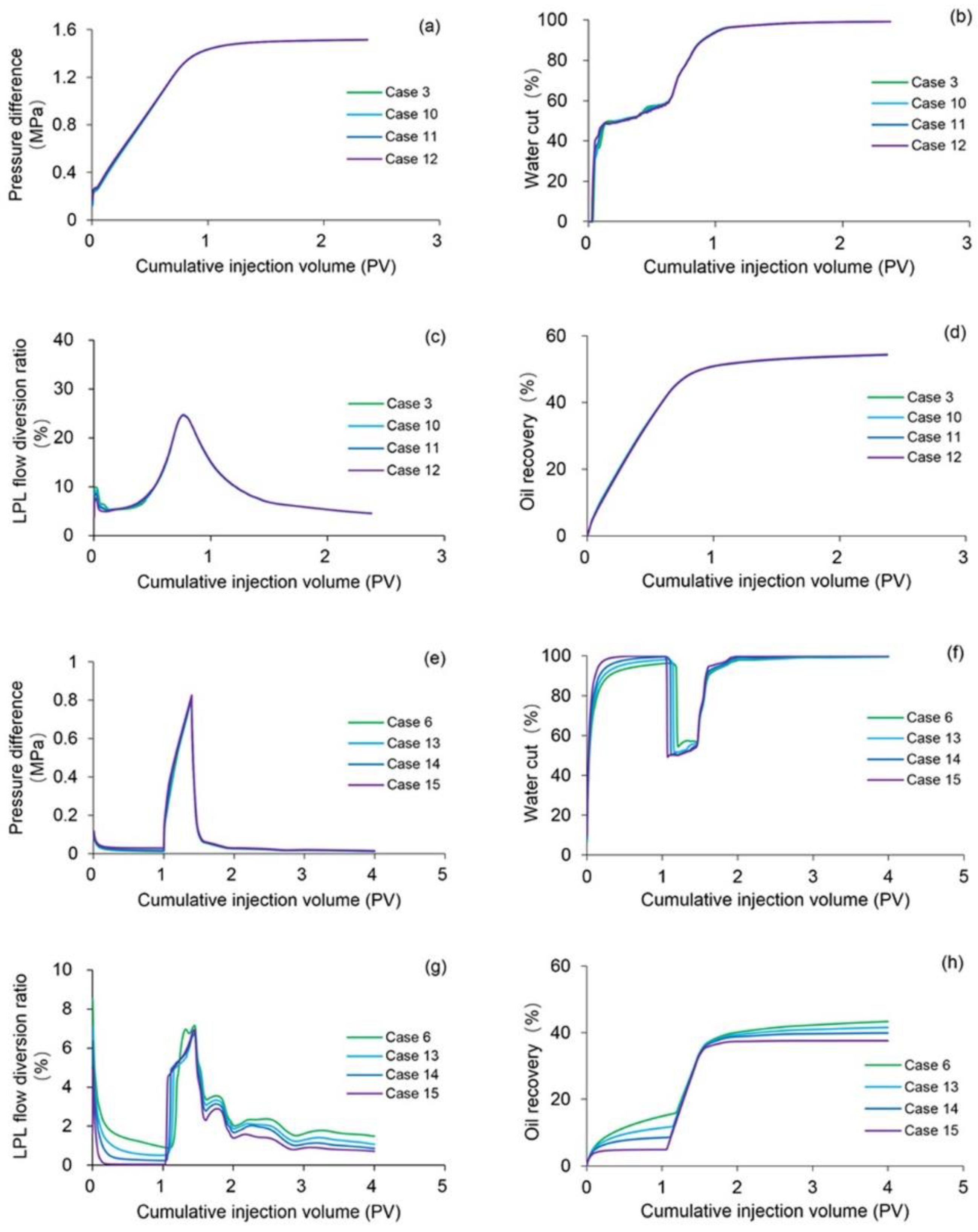
Figure 16.
Comparison results of (a) pressure difference, (b) water cut, (c) LPL flow diversion ratio and (d) oil recovery of Cases 3 and 10–12, and those of (e) pressure difference, (f) water cut, (g) LPL flow diversion ratio, and (h) oil recovery of Cases 6 and 13–15.
Figure 16.
Comparison results of (a) pressure difference, (b) water cut, (c) LPL flow diversion ratio and (d) oil recovery of Cases 3 and 10–12, and those of (e) pressure difference, (f) water cut, (g) LPL flow diversion ratio, and (h) oil recovery of Cases 6 and 13–15.
Figure 17.
3D remaining oil saturation distributions after polymer flooding of Case 12.
Figure 17.
3D remaining oil saturation distributions after polymer flooding of Case 12.
Figure 18.
3D remaining oil saturation distributions after (a) initial water flooding, (b) polymer flooding and (c) extended water flooding of Case 15.
Figure 18.
3D remaining oil saturation distributions after (a) initial water flooding, (b) polymer flooding and (c) extended water flooding of Case 15.
Figure 19.
Comparison results of (a) pressure difference, (b) water cut, (c) LPL flow diversion ratio and (d) oil recovery of Cases 3 and 16, and those of (e) pressure difference, (f) water cut, (g) LPL flow diversion ratio and (h) oil recovery of Cases 6 and 17.
Figure 19.
Comparison results of (a) pressure difference, (b) water cut, (c) LPL flow diversion ratio and (d) oil recovery of Cases 3 and 16, and those of (e) pressure difference, (f) water cut, (g) LPL flow diversion ratio and (h) oil recovery of Cases 6 and 17.
Figure 20.
3D remaining oil saturation distributions after polymer flooding of Case 16.
Figure 20.
3D remaining oil saturation distributions after polymer flooding of Case 16.
Figure 21.
3D remaining oil saturation distributions after (a) initial water flooding, (b) polymer flooding and (c) extended water flooding of Case 17.
Figure 21.
3D remaining oil saturation distributions after (a) initial water flooding, (b) polymer flooding and (c) extended water flooding of Case 17.
Table 1.
Polymer properties.
Table 1.
Polymer properties.
| Properties | Description/Value |
|---|
| Type | HPAM |
| Molecular weight | 2.52 × 107 |
| Solid content, wt % | 91 |
| Hydrolysis degree, % | 26 |
| Filtration factor | 1.4 |
| Dissolution rate, hour | <2 |
| Insoluble matter, wt % | 0.15 |
| Granularity ≥ 1.0 mm, % | 4.9 |
| Granularity ≤ 0.2 mm, % | 2.5 |
Table 2.
Ion component concentrations in brine.
Table 2.
Ion component concentrations in brine.
| Ion Components | Concentration, mg/L |
|---|
| Na+ and K+ | 217.73 |
| Ca2+ | 61.16 |
| Mg2+ | 27.66 |
| HCO3− | 309.59 |
| CO32− | 76.13 |
| SO42− | 158.35 |
| Cl− | 135.00 |
| TDS | 985.60 |
Table 3.
Original heavy oil composition and basic physical properties.
Table 3.
Original heavy oil composition and basic physical properties.
| Parameters | Saturate, wt % | Aromatic, wt % | Resin, wt % | Asphaltene, wt % | Density (25 °C), kg/m3 | Viscosity (25 °C), mPa·s |
|---|
| Value | 56.15 | 28.87 | 13.52 | 1.46 | 938.30 | 202.70 |
Table 4.
Parameters of core samples used to study the relationship between TPG and mobility.
Table 4.
Parameters of core samples used to study the relationship between TPG and mobility.
| Core Number | Length, cm | Diameter, cm | Porosity, % | Permeability, mD |
|---|
| #1 | 25.06 | 2.49 | 19.42 | 103 |
| #2 | 25.10 | 2.51 | 19.44 | 104 |
| #3 | 25.08 | 2.50 | 19.41 | 103 |
| #4 | 25.07 | 2.49 | 19.44 | 105 |
| #5 | 25.18 | 2.50 | 21.62 | 458 |
| #6 | 25.16 | 2.51 | 21.60 | 456 |
| #7 | 25.17 | 2.49 | 21.60 | 455 |
| #8 | 25.16 | 2.50 | 21.61 | 457 |
| #9 | 25.05 | 2.50 | 23.38 | 863 |
| #10 | 25.08 | 2.49 | 23.40 | 864 |
| #11 | 25.02 | 2.48 | 23.36 | 862 |
| #12 | 25.04 | 2.49 | 23.36 | 862 |
| #13 | 25.12 | 2.50 | 25.04 | 1683 |
| #14 | 25.09 | 2.49 | 25.08 | 1685 |
| #15 | 25.06 | 2.50 | 25.12 | 1686 |
| #16 | 25.11 | 2.51 | 25.10 | 1685 |
Table 5.
Parameters of core samples used to perform polymer flooding experiment.
Table 5.
Parameters of core samples used to perform polymer flooding experiment.
| Parameters | Core Name |
|---|
| High Permeability Layer (HPL) | Middle Permeability Layer (MPL) | Low Permeability Layer (LPL) |
|---|
| Length, cm | 30 | 30 | 30 |
| Width, cm | 4.5 | 4.5 | 4.5 |
| Height, cm | 1.5 | 1.5 | 1.5 |
| Porosity, % | 26.2 | 25.6 | 25 |
| Permeability, mD | 1800 | 900 | 300 |
Table 6.
The measured TPG of heavy oil.
Table 6.
The measured TPG of heavy oil.
| Core Number | Permeability, mD | Oil Sample | Viscosity, mPa·s | TPG, Pa/m |
|---|
| #1 | 103 | #1 | 202.7 | 1442.23 |
| #2 | 104 | #2 | 162.2 | 1198.81 |
| #3 | 103 | #3 | 118.7 | 1055.87 |
| #4 | 105 | #4 | 73.8 | 868.76 |
| #5 | 458 | #1 | 202.7 | 690.13 |
| #6 | 456 | #2 | 162.2 | 675.27 |
| #7 | 455 | #3 | 118.7 | 663.83 |
| #8 | 457 | #4 | 73.8 | 570.80 |
| #9 | 863 | #1 | 202.7 | 627.70 |
| #10 | 864 | #2 | 162.2 | 633.98 |
| #11 | 862 | #3 | 118.7 | 552.12 |
| #12 | 862 | #4 | 73.8 | 368.76 |
| #13 | 1683 | #1 | 202.7 | 470.51 |
| #14 | 1685 | #2 | 162.2 | 466.65 |
| #15 | 1686 | #3 | 118.7 | 370.64 |
| #16 | 1685 | #4 | 73.8 | 342.32 |
Table 7.
The reservoir property, fluid property, initial conditions and production data of Case 1.
Table 7.
The reservoir property, fluid property, initial conditions and production data of Case 1.
| Parameters | Value |
|---|
| Initial porosity in HPL, MPL and LPL, fraction | 0.262, 0.256, 0.25 |
| Initial permeability in x direction in HPL, MPL and LPL, mD | 1800, 900, 300 |
| Initial permeability in y direction in HPL, MPL and LPL, mD | 1800, 900, 300 |
| Initial permeability in z direction in HPL, MPL and LPL, mD | 180, 90, 30 |
| Reservoir temperature, °C | 25 |
| Rock density in HPL, MPL and LPL, kg/m3 | 2570, 2590, 2610 |
| Rock compressibility in HPL, MPL and LPL, MPa−1 | 2.82 × 10−3, 2.78 × 10−3, 2.72 × 10−3 |
| Stock tank oil density, kg/m3 | 938.3 |
| Initial oil viscosity, mPa·s | 202.7 |
| Oil compressibility, MPa−1 | 1.18 × 10−3 |
| Oil formation volume factor | 1.068 |
| Initial water density, kg/m3 | 1000 |
| Water viscosity, mPa·s | 0.69 |
| Water compressibility, MPa−1 | 4.26 × 10−4 |
| Water formation volume factor | 1.016 |
| Polymer concentration, mg/L | 2500 |
| Inaccessible pore volume factor in HPL, MPL and LPL, fraction | 0.05, 0.06, 0.08 |
| Maximum polymer absorption in HPL, MPL and LPL, kg/kg | 6.88 × 10−5, 7.67 × 10−5, 8.66 × 10−5 |
| Residual resistance factor in HPL, MPL and LPL | 2.80, 3.60, 5.20 |
| Initial reservoir pressure, MPa | 0 |
| Initial water saturation in HPL, MPL and LPL, fraction | 0.24, 0.26, 0.3 |
| Initial oil saturation in HPL, MPL and LPL, fraction | 0.76, 0.74, 0.70 |
| Bottom hole pressure of production well, MPa | 0 |
| Injected polymer solution during polymer flooding, PV | 2.4 |
Table 8.
The different parameters of Case 2 when compared with Case 1.
Table 8.
The different parameters of Case 2 when compared with Case 1.
| Parameters | Value |
|---|
| TPG in HPL, MPL and LPL, Pa/m | 469.45, 603.75, 899.61 |
| Injected water during water flooding, PV | 1 |
| Injected polymer solution during polymer flooding, PV | 0.4 |
| Injected water during subsequent water flooding after polymer flooding, PV | 2.6 |
Table 9.
Production indicator reductions of Cases 1, 4 and 5 vs. Case 3, and those of Cases 7–9 vs. Case 6.
Table 9.
Production indicator reductions of Cases 1, 4 and 5 vs. Case 3, and those of Cases 7–9 vs. Case 6.
| Production Indictors | Case Number |
|---|
| 1 | 4 | 5 | 7 | 8 | 9 |
|---|
| After initial water flooding | Pressure difference, MPa | - | - | - | 0.0000 | 0.0000 | 0.0000 |
| Water cut, % | - | - | - | 0.0000 | 0.0000 | 0.0000 |
| LPL flow diversion ratio, % | - | - | - | 0.0000 | 0.0000 | 0.0000 |
| Oil recovery, % | - | - | - | 0.0000 | 0.0000 | 0.0000 |
| After polymer flooding | Pressure difference, MPa | 0.2540 | 0.6155 | 0.7371 | 0.1355 | 0.2973 | 0.3529 |
| Water cut, % | −0.0480 | −0.0508 | −0.0728 | −1.3499 | −2.3286 | −2.7385 |
| LPL flow diversion ratio, % | 0.0033 | 0.1814 | 0.4382 | 0.0316 | 0.1320 | 0.1946 |
| Oil recovery, % | 0.4566 | 1.2515 | 1.6614 | 0.7086 | 1.0095 | 1.2173 |
| After extended water flooding | Pressure difference, MPa | - | - | - | 0.0024 | 0.0029 | 0.0029 |
| Water cut, % | - | - | - | −0.0753 | −0.1943 | −0.2024 |
| LPL flow diversion ratio, % | - | - | - | 0.2932 | 0.4682 | 0.4969 |
| Oil recovery, % | - | - | - | 0.8670 | 1.9394 | 2.4850 |
Table 10.
Production indicator reductions of Cases 10–12 vs. Case 3, and those of Cases 13–15 vs. Case 6.
Table 10.
Production indicator reductions of Cases 10–12 vs. Case 3, and those of Cases 13–15 vs. Case 6.
| Production Indictors | Case Number |
|---|
| 10 | 11 | 12 | 13 | 14 | 15 |
|---|
| After initial water flooding | Pressure difference, MPa | - | - | - | −0.0013 | −0.0048 | −0.0167 |
| Water cut, % | - | - | - | −1.9711 | −3.2508 | −3.8929 |
| LPL flow diversion ratio, % | - | - | - | 0.4186 | 0.6880 | 0.8840 |
| Oil recovery, % | - | - | - | 3.5002 | 6.4676 | 10.0672 |
| After polymer flooding | Pressure difference, MPa | −0.0001 | −0.0002 | −0.0003 | −0.0041 | −0.0083 | −0.0167 |
| Water cut, % | −0.0026 | −0.0042 | −0.0066 | 1.5416 | 3.3325 | 4.0417 |
| LPL flow diversion ratio, % | 0.0004 | 0.0031 | 0.0119 | 0.4061 | 0.4852 | 0.4864 |
| Oil recovery, % | 0.0437 | 0.0196 | 0.0141 | 0.2837 | 0.5885 | 0.9841 |
| After extended water flooding | Pressure difference, MPa | - | - | - | −0.0001 | −0.0005 | −0.0015 |
| Water cut, % | - | - | - | −0.2863 | −0.5018 | −0.5916 |
| LPL flow diversion ratio, % | - | - | - | 0.4132 | 0.6257 | 0.7701 |
| Oil recovery, % | - | - | - | 1.7753 | 3.4951 | 5.7741 |
Table 11.
Production indicator reductions of Case 16 vs. Case 3, and those of Case 17 vs. Case 6.
Table 11.
Production indicator reductions of Case 16 vs. Case 3, and those of Case 17 vs. Case 6.
| Production Indicators | Case Number |
|---|
| 16 | 17 |
|---|
| After first water flooding | Pressure difference, MPa | - | 0.0167 |
| Water cut, % | - | −3.8929 |
| LPL flow diversion ratio, % | - | 0.8840 |
| Oil recovery, % | - | 10.0672 |
| After polymer flooding | Pressure difference, MPa | 0.7366 | 0.3443 |
| Water cut, % | −0.0104 | 2.1395 |
| LPL flow diversion ratio, % | 0.5591 | 0.4370 |
| Oil recovery, % | 1.7407 | 2.0819 |
| After second water flooding | Pressure difference, MPa | - | 0.0013 |
| Water cut, % | - | −0.5918 |
| LPL flow diversion ratio, % | - | 0.7901 |
| Oil recovery, % | - | 8.3466 |