Multiscale Modeling of Structure, Transport and Reactivity in Alkaline Fuel Cell Membranes: Combined Coarse-Grained, Atomistic and Reactive Molecular Dynamics Simulations
Abstract
1. Introduction
2. System Description and Methodology
2.1. System
2.2. Multiscale Modeling Approach
2.3. Coarse Grained Simulations
2.4. Atomistic Non-Reactive Simulations (APPLE&P)
2.5. Atomistic Reactive Simulations (ReaxFF)
3. Results and Discussion
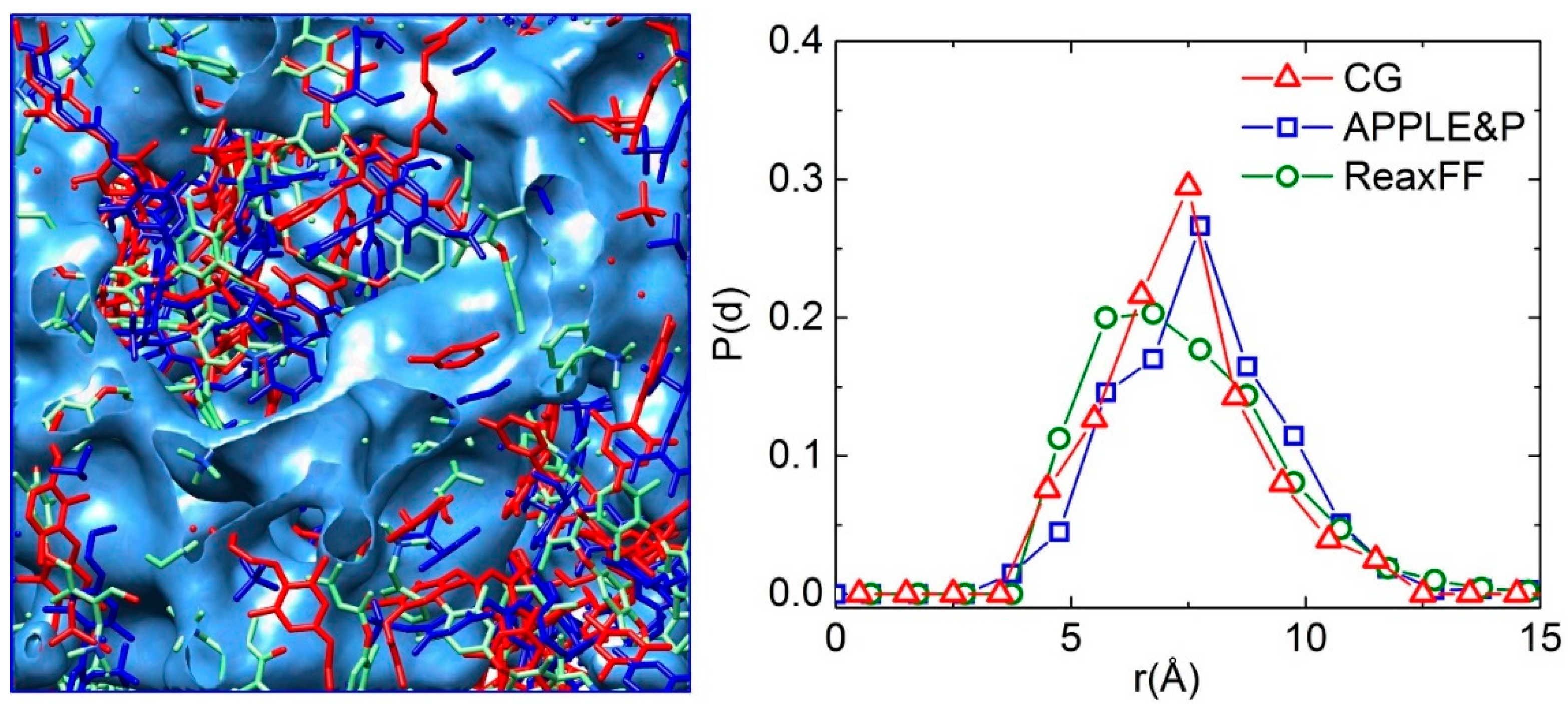
3.1. Morphology of the Hydrated Membrane
3.2. Structural Properties
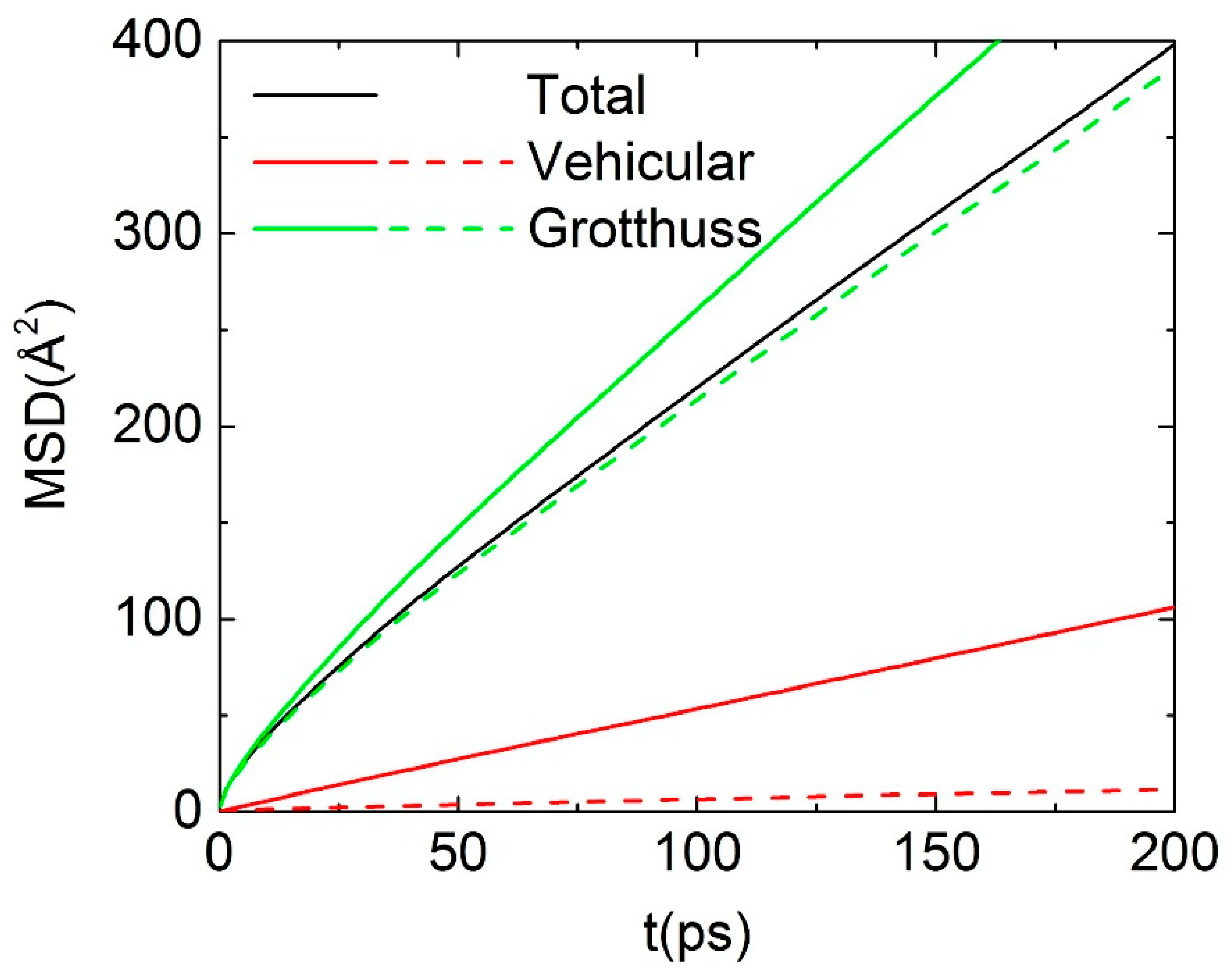
3.3. Dynamical Properties
3.4. Degradation Mechanism of AEM (ReaxFF)
4. Conclusions
Author Contributions
Acknowledgement
Conflicts of Interest
References
- Yanagi, H.; Fukuta, K. Anion Exchange Membrane and Ionomer for Alkaline Membrane Fuel Cells (AMFCs). ECS Trans. 2008, 16, 257–262. [Google Scholar] [CrossRef]
- Merle, G.; Wessling, M.; Nijmeijer, K. Anion Exchange Membranes for Alkaline Fuel Cells: A Review. J. Membr. Sci. 2011, 377, 1–35. [Google Scholar] [CrossRef]
- Pan, J.; Chen, C.; Zhuang, L.; Lu, J. Designing Advanced Alkaline Polymer Electrolytes for Fuel Cell Applications. Acc. Chem. Res. 2011, 45, 473–481. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Leng, Y.; Hickner, M.A.; Wang, C.Y. Highly Stable, Anion Conductive, Comb-Shaped Copolymers for Alkaline Fuel Cells. J. Am. Chem. Soc. 2013, 135, 10124–10133. [Google Scholar] [CrossRef] [PubMed]
- Hagesteijn, K.F.; Jiang, S.; Ladewig, B.P. A Review of The Synthesis and Characterization of Anion Exchange Membranes. J. Mater. Sci. 2018, 53, 11131–11150. [Google Scholar] [CrossRef]
- Ran, J.; Wu, L.; He, Y.; Yang, Z.; Wang, Y.; Jiang, C.; Ge, L.; Bakangura, E.; Xu, T. Ion Exchange Membranes: New Developments and Applications. J. Membr. Sci. 2017, 522, 267–291. [Google Scholar] [CrossRef]
- Lu, S.; Pan, J.; Huang, A.; Zhuang, L.; Lu, J. Alkaline Polymer Electrolyte Fuel Cells Completely Free from Noble Metal Catalysts. Proc. Natl. Acad. Sci. USA 2008, 105, 20611–20614. [Google Scholar] [CrossRef]
- Kruusenberg, I.; Matisen, L.; Shah, Q.; Kannan, A.M.; Tammeveski, K. Non-platinum Cathode Catalysts for Alkaline Membrane Fuel Cells. Int. J. Hydrog. Energy 2012, 37, 4406–4412. [Google Scholar] [CrossRef]
- Liu, F.H.; Lin, C.X.; Hu, E.N.; Yang, Q.; Zhang, Q.G.; Zhu, A.M.; Liu, Q.L. Anion Exchange Membranes with Well-Developed Conductive Channels: Effect of The Functional Groups. J. Membr. Sci. 2018, 564, 298–307. [Google Scholar] [CrossRef]
- Nuñez, S.A.; Capparelli, C.; Hickner, M.A. N-Alkyl Interstitial Spacers and Terminal Pendants Influence the Alkaline Stability of Tetraalkylammonium Cations for Anion Exchange Membrane Fuel Cells. Chem. Mater. 2016, 28, 2589–2598. [Google Scholar] [CrossRef]
- Pan, J.; Chen, C.; Li, Y.; Wang, L.; Tan, L.; Li, G.; Tang, X.; Xiao, L.; Lu, J.; Zhuang, L. Constructing Ionic Highway in Alkaline Polymer Electrolytes. Energy Environ. Sci. 2014, 7, 354–360. [Google Scholar] [CrossRef]
- Dong, D.; Wei, X.; Hooper, J.B.; Pan, H.; Bedrov, D. Role of Cationic Groups on Structural and Dynamical Correlations in Hydrated Quaternary Ammonium-Functionalized Poly (P-Phenylene Oxide)-Based Anion Exchange Membranes. Phys. Chem. Chem. Phys. 2018. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Zimudzi, T.J.; Wang, Y.; Yu, X.; Pan, J.; Han, J.; Kushner, D.I.; Zhuang, L.; Hickner, M.A. Mechanically Robust Anion Exchange Membranes via Long Hydrophilic Cross-Linkers. Macromolecules 2017, 50, 2329–2337. [Google Scholar] [CrossRef]
- Han, J.; Zhu, L.; Pan, J.; Zimudzi, T.J.; Wang, Y.; Peng, Y.; Hickner, M.A.; Zhuang, L. Elastic Long-Chain Multication Cross-Linked Anion Exchange Membranes. Macromolecules 2017, 50, 3323–3332. [Google Scholar] [CrossRef]
- Katzfuß, A.; Gogel, V.; Jörissen, L.; Kerres, J. The Application of Covalently Cross-Linked BrPPO as AEM in Alkaline DMFC. J. Membr. Sci. 2013, 425, 131–140. [Google Scholar] [CrossRef]
- Zhang, J.; Qiao, J.; Jiang, G.; Liu, L.; Liu, Y. Cross-linked Poly(vinyl alcohol)/poly(diallyldimethylammonium chloride) as Anion-exchange Membrane for Fuel Cell Applications. J. Power Sources 2013, 240, 359–367. [Google Scholar] [CrossRef]
- Liu, L.; Chu, X.; Liao, J.; Huang, Y.; Li, Y.; Ge, Z.; Hickner, M.A.; Li, N. Tuning The Properties of Poly (2, 6-Dimethyl-1,4-Phenylene Oxide) Anion Exchange Membranes and Their Performance in H2/O2 Fuel Cells. Energy Environ. Sci. 2018, 11, 435–446. [Google Scholar] [CrossRef]
- Li, N.; Zhang, Q.; Wang, C.; Lee, Y.M.; Guiver, M.D. Phenyltrimethylammonium Functionalized Polysulfone Anion Exchange Membranes. Macromolecules 2012, 45, 2411–2419. [Google Scholar] [CrossRef]
- He, G.; Li, Z.; Zhao, J.; Wang, S.; Wu, H.; Guiver, M.D.; Jiang, Z. Nanostructured Ion-Exchange Membranes for Fuel Cells: Recent Advances and Perspectives. Adv. Mater. 2015, 27, 5280–5295. [Google Scholar] [CrossRef] [PubMed]
- Merinov, B.V.; Goddard, W.A., III. Computational Modeling of Structure and OH-Anion Diffusion in Quaternary Ammonium Polysulfone Hydroxide–Polymer Electrolyte for Application in Electrochemical Devices. J. Membr. Sci. 2013, 431, 79–85. [Google Scholar] [CrossRef]
- Chen, C.; Tse, Y.L.S.; Lindberg, G.E.; Knight, C.; Voth, G.A. Hydroxide Solvation and Transport in Anion Exchange Membranes. J. Am. Chem. Soc. 2016, 138, 991–1000. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Jacobson, L.C.; Perez Sirkin, Y.A.; Molinero, V. High-Resolution Coarse-Grained Model of Hydrated Anion-Exchange Membranes that Accounts for Hydrophobic and Ionic Interactions through Short-Ranged Potentials. J. Chem. Theory Comput. 2016, 13, 245–264. [Google Scholar] [CrossRef] [PubMed]
- Dong, D.; Zhang, W.; Van Duin, A.C.; Bedrov, D. Grotthuss versus Vehicular Transport of Hydroxide in Anion-Exchange Membranes: Insight from Combined Reactive and Nonreactive Molecular Simulations. J. Phys. Chem. Lett. 2018, 9, 825–829. [Google Scholar] [CrossRef] [PubMed]
- van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Zhang, W.; Van Duin, A.C. Reaxff Reactive Molecular Dynamics Simulation of Functionalized Poly(Phenylene Oxide) Anion Exchange Membrane. J. Phys. Chem. C 2015, 19, 27727–27736. [Google Scholar] [CrossRef]
- Dong, D.; Hooper, J.B.; Bedrov, D. Structural and Dynamical Properties of Tetraalkylammonium Bromide Aqueous Solutions: A Molecular Dynamics Simulation Study Using a Polarizable Force Field. J. Phys. Chem. B 2017, 121, 4853–4863. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Miller, C.; Molinero, V. Parameterization of a Coarse-Grained Model with Short-Ranged Interactions for Modeling Fuel Cell Membranes with Controlled Water Uptake. Phys. Chem. Chem. Phys. 2017, 19, 17698–17707. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Xiao, H.; Lackner, K.S.; Chen, X. Capture CO2 from Ambient Air Using Nanoconfined Ion Hydration. Angew. Chem. Int. Ed. 2016, 55, 4026–4029. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Xiao, H.; Liao, X.; Armstrong, M.; Chen, X.; Lackner, K.S. Humidity Effect on Ion Behaviors of Moisture-Driven CO2 sorbents. J. Chem. Phys. 2018, 149, 164708. [Google Scholar] [CrossRef] [PubMed]
- Molinero, V.; Moore, E.B. Water Modeled as an Intermediate Element Between Carbon and Silicon. J. Phys. Chem. B 2009, 113, 4008–4016. [Google Scholar] [CrossRef] [PubMed]
- DeMille, R.C.; Molinero, V. Coarse-grained Ions Without Charges: Reproducing the Solvation Structure of Nacl in Water Using Short-Ranged Potentials. J. Chem. Phys. 2009, 131, 034107. [Google Scholar] [CrossRef] [PubMed]
- Stillinger, F.H.; Weber, T.A. Computer-Simulation of Local Order in Condensed Phases of Silicon. Phys. Rev. B 1985, 31, 5262–5271. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Borodin, O. Polarizable Force Field Development and Molecular Dynamics Simulations of Ionic Liquids. J. Phys. Chem. B 2009, 113, 11463–11478. [Google Scholar] [CrossRef] [PubMed]
- Palmer, B.J. Direct Application of Shake to The Velocity Verlet Algorithm. J. Comput. Phys. 1993, 104, 470–472. [Google Scholar] [CrossRef]
- Yeh, I.C.; Berkowitz, M.L. Ewald Summation for Systems with Slab Geometry. J. Chem. Phys. 1999, 111, 3155–3162. [Google Scholar] [CrossRef]
- Zhang, W.; Van Duin, A.C. Improvement of the ReaxFF Description for Functionalized Hydrocarbon/Water Weak Interactions in the Condensed Phase. J. Phys. Chem. B 2018, 122, 4083–4092. [Google Scholar] [CrossRef] [PubMed]
- Te Velde, G.T.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 2, 931–967. [Google Scholar]
- Bhattacharya, S.; Gubbins, K.E. Fast Method for Computing Pore Size Distributions of Model Materials. Langmuir 2006, 22, 7726–7731. [Google Scholar] [CrossRef] [PubMed]
- Ufimtsev, I.S.; Kalinichev, A.G.; Martinez, T.J.; Kirkpatrick, R.J.A. Charged Ring Model for Classical OH−(Aq) Simulations. Chem. Phys. Lett. 2007, 442, 128–133. [Google Scholar] [CrossRef]
- Kale, S.; Herzfeld, J. Proton Defect Solvation and Dynamics in Aqueous Acid and Base. Angew. Chem. Int. Ed. 2012, 51, 11029–11032. [Google Scholar] [CrossRef] [PubMed]
- Atkins, P.; De Paula, J.; Keeler, J. Atkins’ Physical Chemistry; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Hillyer, M.B.; Gibb, B.C. Molecular Shape and The Hydrophobic Effect. Annu. Rev. Phys. Chem. 2016, 67, 307–329. [Google Scholar] [CrossRef] [PubMed]
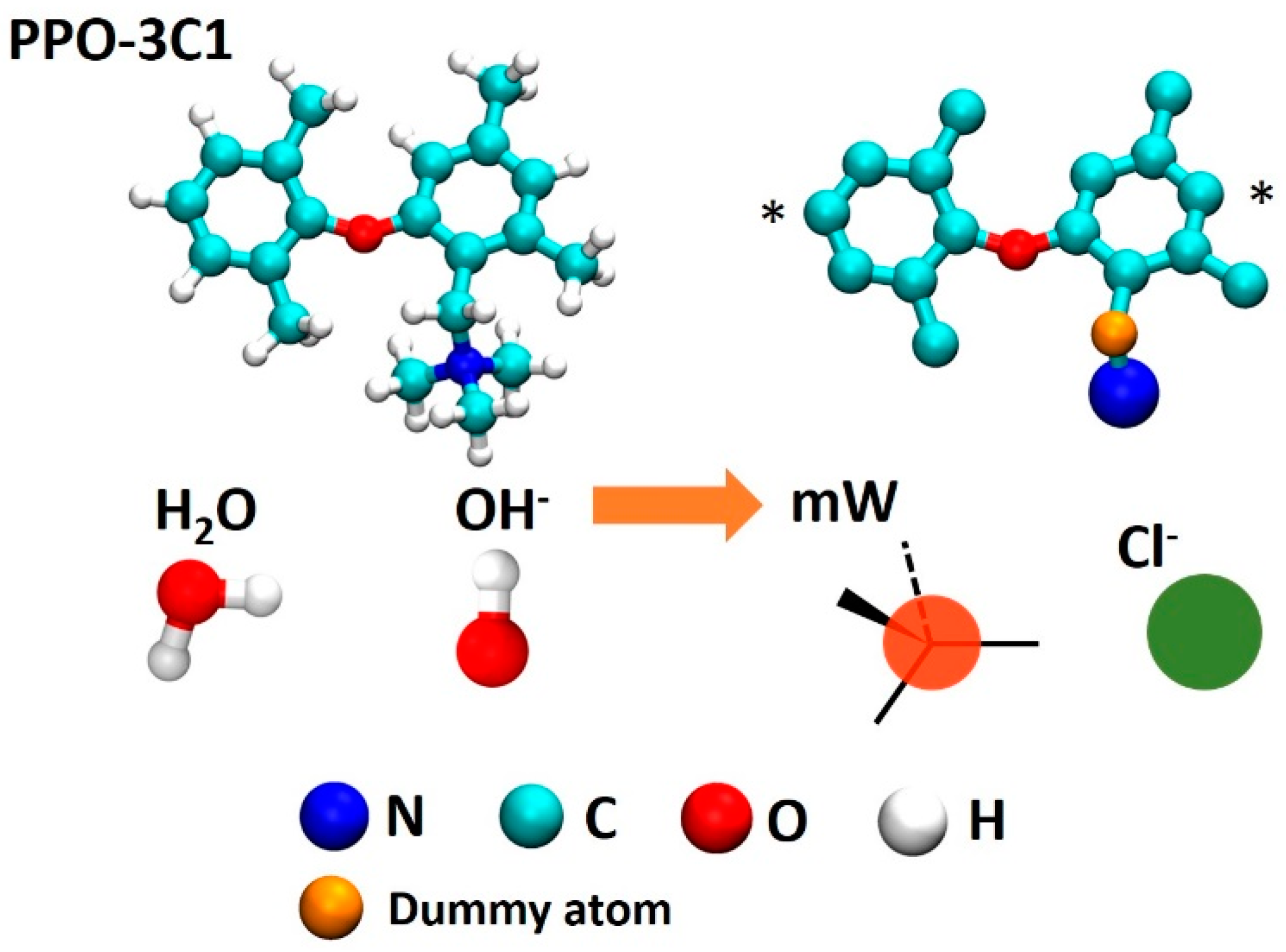





| Capability | Reactive Atomistic MD | Non-Reactive Atomistic MD | Coarse Grained MD |
|---|---|---|---|
| Water uptake | - | ? | ✔ |
| Nanoscale morphology of short oligomers | ✔ | ✔ | ✔ |
| Nanoscale morphology of long chains | - | - | ✔ |
| Local dynamics (a few ns timescale) | ✔ | ✔ | ? |
| Global dynamics (up to microsecond) | ? | ✔ | ✔ |
| Thermodynamics | ✔ | ✔ | ✔ |
| Local structure | ✔ | ✔ | - |
| Grotthuss mechanism | ✔ | - | - |
| Membrane chemical stability | ✔ | - | - |
| Residence Time | |||
|---|---|---|---|
| CG | 934.5 * | 98.0 | 9.5 |
| APPLE&P | 2285.6 | 567.5 | 4.0 |
| ReaxFF | 38.9 | 102.6 | 0.38 |
| Diffusion Coefficient in Membrane | Diffusion Coefficients in Bulk Water | |||||
|---|---|---|---|---|---|---|
| DOH− (Å2/ps) | DH2O (Å2/ps) | DOH−/DH2O | DOH− (Å2/ps) | DH2O (Å2/ps) | DOH−/DH2O | |
| EXP | - | - | - | 0.53 | 0.23 | 2.3 |
| CG | 0.0140 * | 0.0770 | 0.18 | 0.30 * | 0.65 | 0.46 |
| APPLE&P | 0.0025 | 0.0083 | 0.30 | 0.19 | 0.23 | 0.81 |
| ReaxFF | 0.2980 | 0.0521 | 5.72 | 1.48 | 0.25 | 5.9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, D.; Zhang, W.; Barnett, A.; Lu, J.; Van Duin, A.C.T.; Molinero, V.; Bedrov, D. Multiscale Modeling of Structure, Transport and Reactivity in Alkaline Fuel Cell Membranes: Combined Coarse-Grained, Atomistic and Reactive Molecular Dynamics Simulations. Polymers 2018, 10, 1289. https://doi.org/10.3390/polym10111289
Dong D, Zhang W, Barnett A, Lu J, Van Duin ACT, Molinero V, Bedrov D. Multiscale Modeling of Structure, Transport and Reactivity in Alkaline Fuel Cell Membranes: Combined Coarse-Grained, Atomistic and Reactive Molecular Dynamics Simulations. Polymers. 2018; 10(11):1289. https://doi.org/10.3390/polym10111289
Chicago/Turabian StyleDong, Dengpan, Weiwei Zhang, Adam Barnett, Jibao Lu, Adri C. T. Van Duin, Valeria Molinero, and Dmitry Bedrov. 2018. "Multiscale Modeling of Structure, Transport and Reactivity in Alkaline Fuel Cell Membranes: Combined Coarse-Grained, Atomistic and Reactive Molecular Dynamics Simulations" Polymers 10, no. 11: 1289. https://doi.org/10.3390/polym10111289
APA StyleDong, D., Zhang, W., Barnett, A., Lu, J., Van Duin, A. C. T., Molinero, V., & Bedrov, D. (2018). Multiscale Modeling of Structure, Transport and Reactivity in Alkaline Fuel Cell Membranes: Combined Coarse-Grained, Atomistic and Reactive Molecular Dynamics Simulations. Polymers, 10(11), 1289. https://doi.org/10.3390/polym10111289






