Modelling of Rod-Like Fillers’ Rotation and Translation near Two Growing Cells in Conductive Polymer Composite Foam Processing
Abstract
1. Introduction
2. Theoretical Estimation
2.1. One-Cell Model Approach
2.2. Two-Cell model Approach
3. Results and Discussion
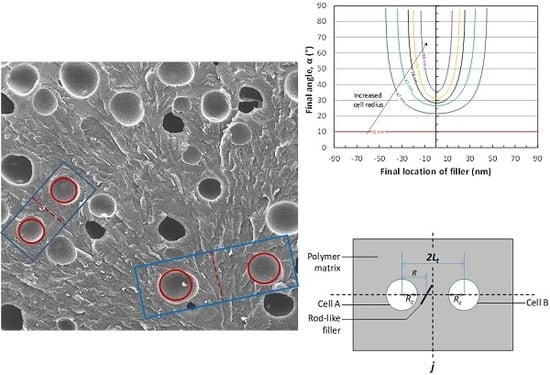
3.1. Single Cell-Filler Interaction
3.2. Two Cell-Filler Interactions
3.2.1. Effect of Initial Filler Location and Void Fraction
3.2.2. Effect of the Initial Filler Angle
3.2.3. Effect of the Relative Size of the Filler and the Cell
3.3. Illustration of the Two-Cell Growth
3.4. Experimental Verification
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Pang, H.; Xu, L.; Yan, D.-X.; Li, Z.-M. Conductive polymer composites with segregated structures. Prog. Polym. Sci. 2014, 39, 1908–1933. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.B.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef] [PubMed]
- Katsura, T.; Kamal, M.R.; Utracki, L.A. Electrical and thermal properties of polypropylene filled with steel fibers. Adv. Polym. Technol. 1985, 5, 193–202. [Google Scholar] [CrossRef]
- Zhang, W.; Dehghani-Sanij, A.A.; Blackburn, R.S. Carbon based conductive polymer composites. J. Mater. Sci. 2007, 42, 3408–3418. [Google Scholar] [CrossRef]
- Liu, H.; Shen, Y.; Song, Y.; Nan, C.-W.; Lin, Y.; Yang, X. Carbon nanotube array/polymer core/shell structured composites with high dielectric permittivity, low dielectric loss, and large energy density. Adv. Mater. 2011, 23, 5104–5108. [Google Scholar] [CrossRef] [PubMed]
- Dang, Z.-M.; Zheng, M.-S.; Zha, J.-W. 1d/2d carbon nanomaterial-polymer dielectric composites with high permittivity for power energy storage applications. Small 2016, 12, 1688–1701. [Google Scholar] [CrossRef] [PubMed]
- Song, S.; Zhai, Y.; Zhang, Y. Bioinspired graphene oxide/polymer nanocomposite paper with high strength, toughness, and dielectric constant. ACS Appl. Mater. Interfaces 2016, 8, 31264–31272. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Wang, P.; Zheng, P.; Liu, X. Core-shell structured batio3@polymer hybrid nanofiller for poly(arylene ether nitrile) nanocomposites with enhanced dielectric properties and high thermal stability. Compos. Sci. Technol. 2016, 123, 134–142. [Google Scholar] [CrossRef]
- Zhao, B.; Zhao, C.; Li, R.; Hamidinejad, S.M.; Park, C.B. Flexible, ultrathin, and high-efficiency electromagnetic shielding properties of poly(vinylidene fluoride)/carbon composite films. ACS Appl. Mater. Interfaces 2017, 9, 20873–20884. [Google Scholar] [CrossRef] [PubMed]
- Jia, L.-C.; Yan, D.-X.; Yang, Y.; Zhou, D.; Cui, C.-H.; Bianco, E.; Lou, J.; Vajtai, R.; Li, B.; Ajayan, P.M.; et al. High strain tolerant EMI shielding using carbon nanotube network stabilized rubber composite. Adv. Mater. Technol. 2017, 2, 1700078. [Google Scholar] [CrossRef]
- Ren, F.; Shi, Y.; Ren, P.; Si, X.; Wang, H. Cyanate ester resin filled with graphene nanosheets and NiFe2O4–reduced graphene oxide nanohybrids for efficient electromagnetic interference shielding. Nano 2017, 12, 1750066. [Google Scholar] [CrossRef]
- Lyu, J.; Zhao, X.; Hou, X.; Zhang, Y.; Li, T.; Yan, Y. Electromagnetic interference shielding based on a high strength polyaniline-aramid nanocomposite. Compos. Sci. Technol. 2017, 149, 159–165. [Google Scholar] [CrossRef]
- Adloo, A.; Sadeghi, M.; Masoomi, M.; Pazhooh, H.N. High performance polymeric bipolar plate based on polypropylene/graphite/graphene/nano-carbon black composites for pem fuel cells. Renew. Energy 2016, 99, 867–874. [Google Scholar] [CrossRef]
- Iwan, A.; Malinowski, M.; Pasciak, G. Polymer fuel cell components modified by graphene: Electrodes, electrolytes and bipolar plates. Renew. Sust. Energy Rev. 2015, 49, 954–967. [Google Scholar] [CrossRef]
- Lopes De Oliveira, M.C.; Sayeg, I.J.; Ett, G.; Antunes, R.A. Corrosion behavior of polyphenylene sulfide-carbon black-graphite composites for bipolar plates of polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2014, 39, 16405–16418. [Google Scholar] [CrossRef]
- Ameli, A.; Nofar, M.; Wang, S.; Park, C.B. Lightweight polypropylene/stainless-steel fiber composite foams with low percolation for efficient electromagnetic interference shielding. ACS Appl. Mater. Interfaces 2014, 6, 11091–11100. [Google Scholar] [CrossRef] [PubMed]
- Ansari, S.; Giannelis, E.P. Functionalized graphene sheet-poly(vinylidene fluoride) conductive nanocomposites. J. Polym. Sci. Pol. Phys. 2009, 47, 888–897. [Google Scholar] [CrossRef]
- Chen, M.; Duan, S.; Zhang, L.; Wang, Z.; Li, C. Three-dimensional porous stretchable and conductive polymer composites based on graphene networks grown by chemical vapour deposition and pedot: Pss coating. Chem. Commun. 2015, 51, 3169–3172. [Google Scholar] [CrossRef] [PubMed]
- Noël, A.; Faucheu, J.; Rieu, M.; Viricelle, J.-P.; Bourgeat-Lami, E. Tunable architecture for flexible and highly conductive graphene-polymer composites. Comp. Sci. Technol. 2014, 95, 82–88. [Google Scholar] [CrossRef]
- Shaayegan, V.; Ameli, A.; Wang, S.; Park, C.B. Experimental observation and modeling of fiber rotation and translation during foam injection molding of polymer composites. Compos. Part A 2016, 88, 67–74. [Google Scholar] [CrossRef]
- Yang, Y.; Gupta, M.C.; Dudley, K.L.; Lawrence, R.W. Conductive carbon nanofiber polymer faom structures. Adv. Mater. 2005, 17, 1999–2003. [Google Scholar] [CrossRef]
- Harikrishnan, G.; Singh, S.N.; Kiesel, E.; Macosko, C.W. Nanodispersions of carbon nanofiber for polyurethane foaming. Polymer 2010, 51, 3349–3353. [Google Scholar] [CrossRef]
- Al-Saleh, M.H.; Sundararaj, U. A review of vapor grown carbon nanofiber/polymer conductive composites. Carbon 2009, 47, 2–22. [Google Scholar] [CrossRef]
- Buys, Y.F.; Lokman, N.A.S. Conductive polymer composites from polylactic acid/natural rubber filled with carbon black. Adv. Mat. Res. 2015, 1115, 253–257. [Google Scholar] [CrossRef]
- Wang, J.; Dai, J.; Yarlagadda, T. Carbon nanotube-conducting-polymer composite nanowires. Langmuir 2005, 21, 9–12. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Cho, E.; Jeon, S.H.; Youn, J.R. Rheological and electrical properties of polypropylene composites containing functionalized multi-walled carbon nanotubes and compatibilizers. Carbon 2007, 45, 2810–2822. [Google Scholar] [CrossRef]
- Yang, Y.; Gupta, M.C. Novel carbon nanotube PS foam composites for electromagnetic interference shielding. Nano Lett. 2005, 5, 2131–2134. [Google Scholar] [CrossRef] [PubMed]
- Pötschke, P.; Bhattacharyya, A.R.; Janke, A. Carbon nanotube-filled polycarbonate composites produced by melt mixing and their use in blends with polyethylene. Carbon 2004, 42, 965–969. [Google Scholar] [CrossRef]
- Xu, X.B.; Li, Z.M.; Shi, L.; Bian, X.C.; Xiang, Z.D. Ultralight conductive carbon-nanotube-polymer composite. Small 2007, 3, 408–411. [Google Scholar] [CrossRef] [PubMed]
- Al-Saleh, M.H.; Sundararaj, U. Electrically conductive carbon nanofiber/polyethylene composite: Effect of melt mixing conditions. Polym. Adv. Technol. 2011, 22, 246–253. [Google Scholar] [CrossRef]
- Villmow, T.; Pötschke, P.; Pegel, S.; Häussler, L.; Kretzschmar, B. Influence of twin-screw extrusion conditions on the dispersion of multi-walled carbon nanotubes in a poly(lactic acid) matrix. Polymer 2008, 49, 3500–3509. [Google Scholar] [CrossRef]
- Ameli, A.; Kazemi, Y.; Wang, S.; Park, C.B.; Pötschke, P. Process-microstructure-electrical conductivity relationships in injection-molded polypropylene/carbon nanotube nanocomposite foams. Compos. Part A 2017, 96, 28–36. [Google Scholar] [CrossRef]
- Antunes, M.; Mudarra, M.; Velasco, J.G. Broad-band electrical conductivity of carbon nanofibre-reinforced polypropylene foams. Carbon 2011, 49, 708–717. [Google Scholar] [CrossRef]
- Ameli, A.; Wang, S.; Kazemi, Y.; Park, C.B.; Pötschke, P. A facile method to increase the charge storage capability of polymer nanocomposites. Nano Energy 2015, 15, 54–65. [Google Scholar] [CrossRef]
- Motlagh, G.H.; Hrymak, A.N.; Thompson, M.R. Improved through-plane electrical conductivity in a carbon-filled thermoplastic via foaming. Polym. Eng. Sci. 2008, 48, 687–696. [Google Scholar] [CrossRef]
- Ameli, A.; Jung, P.U.; Park, C.B. Through-plane electrical conductivity of injection-molded polypropylene/carbon-fiber composite foams. Comp. Sci. Technol. 2013, 76, 37–44. [Google Scholar] [CrossRef]
- Okamoto, M.; Nam, P.H.; Maiti, P.; Kotaka, T.; Nakayama, T.; Takada, M.; Ohshima, M.; Usuki, A.; Hasegawa, N.; Okamoto, H. Biaxial flow-induced alignment of silicate layers in polypropylene/clay nanocomposite foam. Nano Lett. 2001, 1, 503–505. [Google Scholar] [CrossRef]
- Tran, M.-P.; Detrembleur, C.; Alexandre, M.; Jerome, C.; Thomassin, J.-M. The influence of foam morphology of multi-walled carbon nanotubes/poly(methyl methacrylate) nanocomposites on electrical conductivity. Polymer 2013, 54, 3261–3270. [Google Scholar] [CrossRef]
- Rizvi, R.; Naguib, H. Porosity and composition dependence on electrical and piezoresistive properties of thermoplastic polyurethane nanocomposites. J. Mater. Res. 2013, 28, 2415–2425. [Google Scholar] [CrossRef]
- Sun, Y.-C.; Terakita, D.; Tseng, A.C.; Naguib, H.E. Study on the thermoelectric properties of pvdf/mwcnt and pvdf/gnp composite foam. Smart Mater. Struct. 2015, 24, 085034. [Google Scholar] [CrossRef]
- Kazemi, Y.; Kakroodi, A.R.; Wang, S.; Ameli, A.; Filleter, T.; Pötschke, P.; Park, C.B. Conductive network formation and destruction in polypropylene/carbon nanotube composites via crystal control using supercritical carbon dioxide. Polymer 2017, 129, 179–188. [Google Scholar] [CrossRef]
- Ameli, A.; Nofar, M.; Park, C.B.; Pötschke, P.; Rizvi, G. Polypropylene/carbon nanotube nano/microcellular structures with high dielectric permittivity, low dielectric loss, and low percolation threshold. Carbon 2014, 71, 206–217. [Google Scholar] [CrossRef]
- Du, F.; Fischer, J.; Winey, K. Effect of nanotube alignment on percolation conductivity in carbon nanotube/polymer composites. Phys. Rev. B 2005, 72, 121404. [Google Scholar] [CrossRef]
- Gong, S.; Zhu, Z.H.; Meguid, S.A. Anisotropic electrical conductivity of polymer composites with aligned carbon nanotubes. Polymer 2015, 56, 498–506. [Google Scholar] [CrossRef]
- Chang, E.; Ameli, A.; Mark, L.H.; Park, C.B. Effects of uniaxial and biaxial orientation on fiber percolation in conductive polymer composites. AIP Conf. Proc. 2015, 1693, 020027. [Google Scholar]










© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Ameli, A.; Shaayegan, V.; Kazemi, Y.; Huang, Y.; Naguib, H.E.; Park, C.B. Modelling of Rod-Like Fillers’ Rotation and Translation near Two Growing Cells in Conductive Polymer Composite Foam Processing. Polymers 2018, 10, 261. https://doi.org/10.3390/polym10030261
Wang S, Ameli A, Shaayegan V, Kazemi Y, Huang Y, Naguib HE, Park CB. Modelling of Rod-Like Fillers’ Rotation and Translation near Two Growing Cells in Conductive Polymer Composite Foam Processing. Polymers. 2018; 10(3):261. https://doi.org/10.3390/polym10030261
Chicago/Turabian StyleWang, Sai, Amir Ameli, Vahid Shaayegan, Yasamin Kazemi, Yifeng Huang, Hani E. Naguib, and Chul B. Park. 2018. "Modelling of Rod-Like Fillers’ Rotation and Translation near Two Growing Cells in Conductive Polymer Composite Foam Processing" Polymers 10, no. 3: 261. https://doi.org/10.3390/polym10030261
APA StyleWang, S., Ameli, A., Shaayegan, V., Kazemi, Y., Huang, Y., Naguib, H. E., & Park, C. B. (2018). Modelling of Rod-Like Fillers’ Rotation and Translation near Two Growing Cells in Conductive Polymer Composite Foam Processing. Polymers, 10(3), 261. https://doi.org/10.3390/polym10030261