Hydrophobicity Tuning by the Fast Evolution of Mold Temperature during Injection Molding
Abstract
:1. Introduction
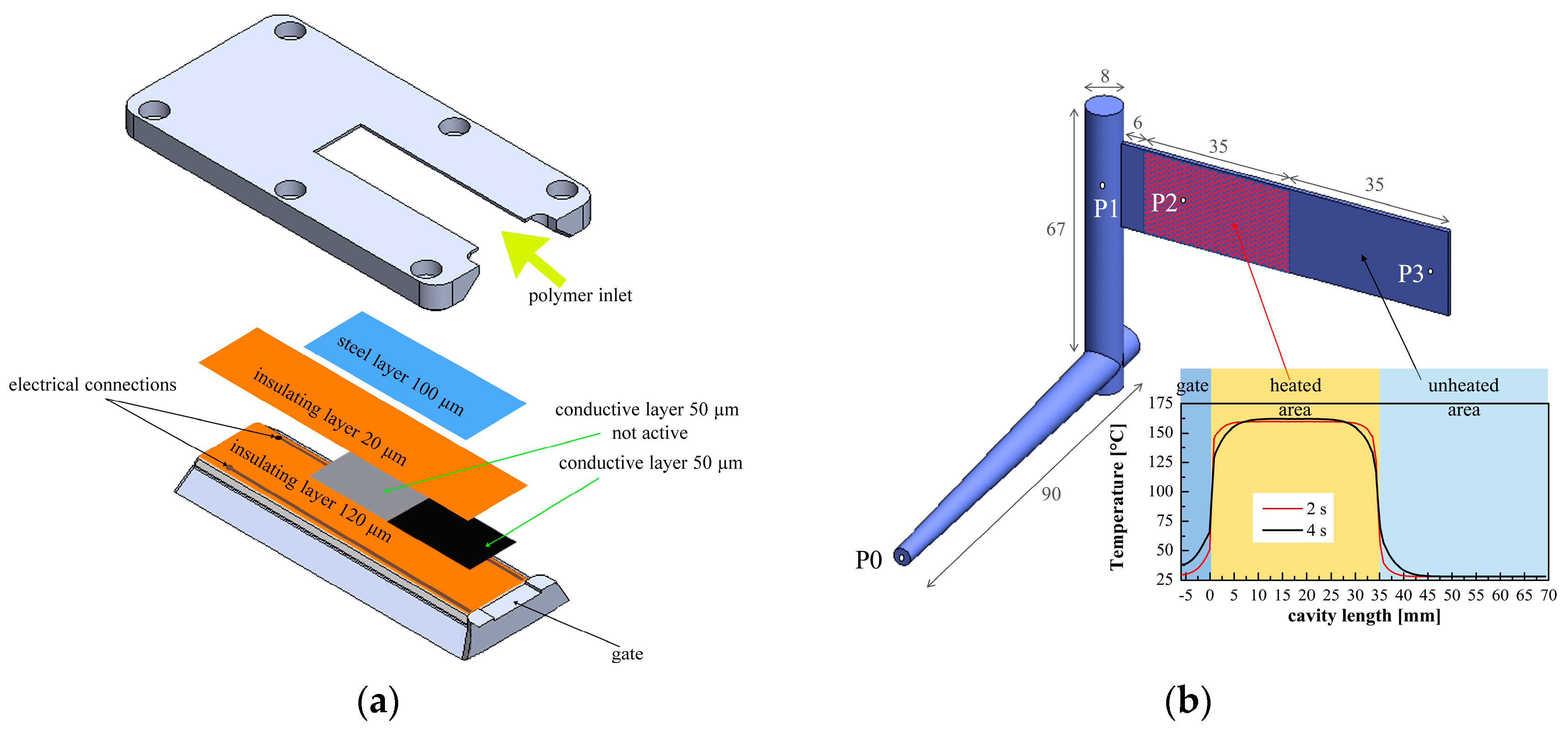
2. Materials and Methods
3. Results
3.1. The Process
3.2. Contact Angle Distribution
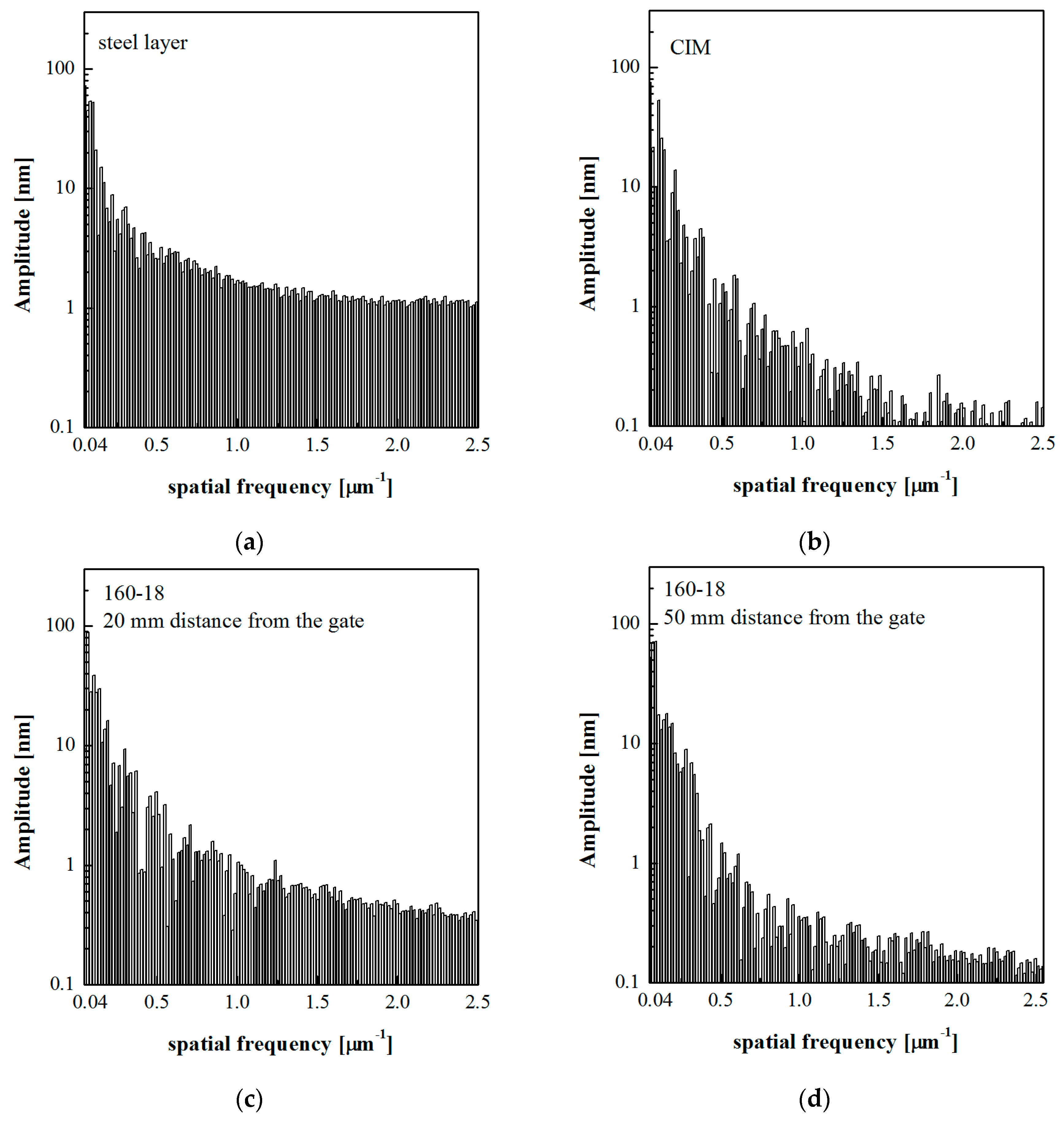
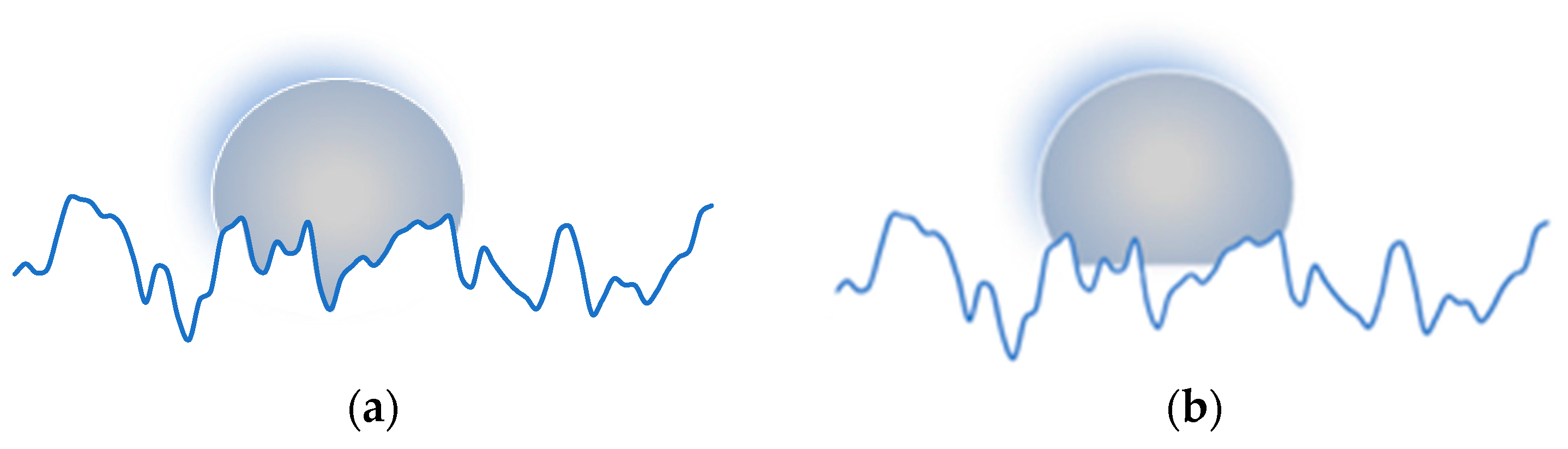
3.3. Analysis of the Topography of the Molded Surface
3.4. Determination of Relevant Sample Surface Parameters
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Marmur, A. The Lotus Effect: Superhydrophobicity and Metastability. Langmuir 2004, 20, 3517–3519. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Verho, T.; Ras, R.H.A. Moving superhydrophobic surfaces toward real-world applications. Science 2016, 352, 142–143. [Google Scholar] [CrossRef] [PubMed]
- Kojevnikova, S.; Marmur, A. Multi-scale roughness and the Lotus effect: Discontinuous liquid-air interfaces. Colloids Surf. A Physicochem. Eng. Asp. 2017, 521, 78–85. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Y.; Hu, Z.; Zhang, X.; Wu, S.; Wang, R.; Zhu, Y. A novel electrodeposition route for fabrication of the superhydrophobic surface with unique self-cleaning, mechanical abrasion and corrosion resistance properties. Chem. Eng. J. 2016, 303, 37–47. [Google Scholar] [CrossRef]
- Quan, Y.-Y.; Zhang, L.-Z.; Qi, R.-H.; Cai, R.-R. Self-cleaning of Surfaces: The Role of Surface Wettability and Dust Types. Sci. Rep. 2016, 6, 38239. [Google Scholar] [CrossRef] [PubMed]
- Förstner, R.; Barthlott, W.; Neinhuis, C.; Walzel, P. Wetting and Self-Cleaning Properties of Artificial Superhydrophobic Surfaces. Langmuir 2005, 21, 956–961. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yao, W.; Yin, X.; Wang, H.; Han, Z.; Ren, L. Controlling Wettability for Improved Corrosion Inhibition on Magnesium Alloy as Biomedical Implant Materials. Adv. Mater. Interfaces 2016, 3, 1500723. [Google Scholar] [CrossRef]
- Falde, E.J.; Yohe, S.T.; Colson, Y.L.; Grinstaff, M.W. Superhydrophobic materials for biomedical applications. Biomaterials 2016, 104, 87–103. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Seo, J.; Han, H.; Kang, S.; Kim, H.; Lee, T. Bio-Inspired Extreme Wetting Surfaces for Biomedical Applications. Materials 2016, 9, 116. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Frank, M.A.; Yang, Y.; Boccaccini, A.R.; Virtanen, S. A novel local drug delivery system: Superhydrophobic titanium oxide nanotube arrays serve as the drug reservoir and ultrasonication functions as the drug release trigger. Mater. Sci. Eng. C 2018, 82, 277–283. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Liu, S.; Zhu, C.; Tao, J.; Wang, G. Facile fabrication of hierarchical structured superhydrophobic surface and its ultra dynamic water repellency. Chem. Eng. J. 2017, 313, 47–55. [Google Scholar] [CrossRef]
- Gray-Munro, J.; Campbell, J. Mimicking the hierarchical surface topography and superhydrophobicity of the lotus leaf on magnesium alloy AZ31. Mater. Lett. 2017, 189, 271–274. [Google Scholar] [CrossRef]
- MacGregor-Ramiasa, M.N.; Vasilev, K. Questions and Answers on the Wettability of Nano-Engineered Surfaces. Adv. Mater. Interfaces 2017, 4, 1700381. [Google Scholar] [CrossRef]
- Rogers, J.A.; Lee, H.H. Unconventional Nanopatterning Techniques and Applications; Wiley: Hoboken, NJ, USA, 2008; ISBN 9780470099575. [Google Scholar]
- Cesca, F.; Limongi, T.; Accardo, A.; Rocchi, A.; Orlando, M.; Shalabaeva, V.; Di Fabrizio, E.; Benfenati, F. Fabrication of biocompatible free-standing nanopatterned films for primary neuronal cultures. RSC Adv. 2014, 4, 45696–45702. [Google Scholar] [CrossRef]
- Limongi, T.; Tirinato, L.; Pagliari, F.; Giugni, A.; Allione, M.; Perozziello, G.; Candeloro, P.; Di Fabrizio, E. Fabrication and Applications of Micro/Nanostructured Devices for Tissue Engineering. Nano-Micro Lett. 2017, 9, 1. [Google Scholar] [CrossRef]
- Yang, C.; Huang, H.-X.; Castro, J.M.; Yi, A.Y. Replication characterization in injection molding of microfeatures with high aspect ratio: Influence of layout and shape factor. Polym. Eng. Sci. 2011, 51, 959–968. [Google Scholar] [CrossRef]
- Limongi, T.; Schipani, R.; Di Vito, A.; Giugni, A.; Francardi, M.; Torre, B.; Allione, M.; Miele, E.; Malara, N.; Alrasheed, S.; et al. Photolithography and micromolding techniques for the realization of 3D polycaprolactone scaffolds for tissue engineering applications. Microelectron. Eng. 2015, 141, 135–139. [Google Scholar] [CrossRef]
- Hwa, K.-Y.; Chang, V.H.S.; Cheng, Y.-Y.; Wang, Y.-D.; Jan, P.-S.; Subramani, B.; Wu, M.-J.; Wang, B.-K. Analyzing polymeric matrix for fabrication of a biodegradable microneedle array to enhance transdermal delivery. Biomed. Microdevices 2017, 19, 84. [Google Scholar] [CrossRef] [PubMed]
- Calaon, M.; Tosello, G.; Hansen, H.N.; Nøregaard, J. Influence of process parameters on edge replication quality of lab-on-a-chip micro fluidic systems geometries. In Proceedings of the Annual Technical Conference—ANTEC Conference Proceedings, Cincinnati, OH, USA, 22–24 April 2013; Volume 2, pp. 1084–1088. [Google Scholar]
- Baruffi, F.; Calaon, M.; Tosello, G. Effects of micro-injection moulding process parameters on accuracy and precision of thermoplastic elastomer micro rings. Precis. Eng. 2017. [Google Scholar] [CrossRef]
- Calaon, M.; Tosello, G.; Garnaes, J.; Hansen, H.N. Injection and injection-compression moulding replication capability for the production of polymer lab-on-a-chip with nano structures. J. Micromech. Microeng. 2017, 27, 105001. [Google Scholar] [CrossRef]
- Menotti, S.; Hansen, H.N.; Bissacco, G.; Calaon, M.; Tang, P.T.; Ravn, C. Injection molding of nanopatterned surfaces in the sub-micrometer range with induction heating aid. Int. J. Adv. Manuf. Technol. 2014, 74, 907–916. [Google Scholar] [CrossRef]
- Speranza, V.; Liparoti, S.; Calaon, M.; Tosello, G.; Pantani, R.; Titomanlio, G. Replication of micro and nano-features on iPP by injection molding with fast cavity surface temperature evolution. Mater. Des. 2017, 133, 559–569. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Sasaki, S.; Suzuki, S.; Nakayama, Y. Injection-molded plastic plate with hydrophobic surface by nanoperiodic structure applied in uniaxial direction. J. Adhes. Sci. Technol. 2015, 29, 24–35. [Google Scholar] [CrossRef]
- Puukilainen, E.; Rasilainen, T.; Suvanto, M.; Pakkanen, T.A. Superhydrophobic polyolefin surfaces: Controlled micro- and nanostructures. Langmuir 2007, 23, 7263–7268. [Google Scholar] [CrossRef] [PubMed]
- Yoo, Y.E.; Kim, T.H.; Choi, D.S.; Hyun, S.M.; Lee, H.J.; Lee, K.H.; Kim, S.K.; Kim, B.H.; Seo, Y.H.; Lee, H.G.; et al. Injection molding of a nanostructured plate and measurement of its surface properties. Curr. Appl. Phys. 2009, 9, e12–e18. [Google Scholar] [CrossRef]
- Puukilainen, E.; Koponen, H.K.; Xiao, Z.; Suvanto, S.; Pakkanen, T.A. Nanostructured and chemically modified hydrophobic polyolefin surfaces. Colloids Surf. A Physicochem. Eng. Aspects 2006, 287, 175–181. [Google Scholar] [CrossRef]
- Liparoti, S.; Sorrentino, A.; Speranza, V.; Titomanlio, G. Multiscale mechanical characterization of iPP injection molded samples. Eur. Polym. J. 2017, 90, 79–91. [Google Scholar] [CrossRef]
- Chen, S.-C.; Lin, Y.-W.; Chien, R.-D.; Li, H.-M. Variable mold temperature to improve surface quality of microcellular injection molded parts using induction heating technology. Adv. Polym Technol. 2008, 27, 224–232. [Google Scholar] [CrossRef]
- Lin, H.L.; Chen, S.C.; Jeng, M.C.; Minh, P.S.; Chang, J.A.; Hwang, J.R. Induction heating with the ring effect for injection molding plates. Int. Commun. Heat Mass Transf. 2012, 39, 514–522. [Google Scholar] [CrossRef]
- Yao, D.; Kimerling, T.E.; Kim, B. High-frequency proximity heating for injection molding applications. Polym Eng. Sci. 2006, 46, 938–945. [Google Scholar] [CrossRef]
- Su, Q.; Zhang, N.; Gilchrist, M.D. The use of variotherm systems for microinjection molding. J. Appl. Polym Sci. 2016, 133. [Google Scholar] [CrossRef]
- Kim, B.M.; Niemeyer, M.F. Insulated Mold Structure for Injection Molding of Optical Disks. U.S. Patent 5,458,818A, 31 August 1993. [Google Scholar]
- Pantani, R.; Speranza, V.; Titomanlio, G. Simultaneous morphological and rheological measurements on polypropylene: Effect of crystallinity on viscoelastic parameters. J. Rheol. 2015, 59, 377–390. [Google Scholar] [CrossRef]
- Pantani, R.; Speranza, V.; Titomanlio, G. Evolution of iPP Relaxation Spectrum during Crystallization. Macromol. Theory Simul. 2014, 23, 300–306. [Google Scholar] [CrossRef]
- Liparoti, S.; Landi, G.; Sorrentino, A.; Speranza, V.; Cakmak, M.; Neitzert, H.C. Flexible Poly(Amide-Imide)-Carbon Black Based Microheater with High-Temperature Capability and an Extremely Low Temperature Coefficient. Adv. Electron. Mater. 2016, 2, 1600126. [Google Scholar] [CrossRef]
- Leach, R. Characterisation of Areal Surface Texture; Leach, R., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-36457-0. [Google Scholar]
- Vietri, U.; Sorrentino, A.; Speranza, V.; Pantani, R. Improving the predictions of injection molding simulation software. Polym Eng. Sci. 2011, 51, 2542–2551. [Google Scholar] [CrossRef]
- Wu, P.H.; Cheng, C.W.; Chang, C.P.; Wu, T.M.; Wang, J.K. Fabrication of large-area hydrophobic surfaces with femtosecond-laser-structured molds. J. Micromech. Microeng. 2011, 21. [Google Scholar] [CrossRef]
- Belaud, V.; Valette, S.; Stremsdoerfer, G.; Bigerelle, M.; Benayoun, S. Wettability versus roughness: Multi-scales approach. Tribol. Int. 2015, 82, 343–349. [Google Scholar] [CrossRef]
- Lucchetta, G.; Fiorotto, M.; Bariani, P.F. Influence of rapid mold temperature variation on surface topography replication and appearance of injection-molded parts. CIRP Ann. Manuf. Technol. 2012, 61, 539–542. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of Solid Surfaces to Wetting by Water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546. [Google Scholar] [CrossRef]
- Erbil, H.Y.; Demirel, A.L.; Avci, Y.; Mert, O. Transformation of a Simple Plastic into a Superhydrophobic Surface. Science 2003, 299, 1377–1380. [Google Scholar] [CrossRef] [PubMed]
- Vogler, E.A. Structure and reactivity of water at biomaterial surfaces. Adv. Colloid Interface Sci. 1998, 74, 69–117. [Google Scholar] [CrossRef]
- Zitzenbacher, G.; Längauer, M.; Holzer, C. Modeling Temperature and Time Dependence of the Wetting of Tool Steel Surfaces by Polymer Melts. Int. Polymer Process. 2017, 32, 245–252. [Google Scholar] [CrossRef]
- Rytka, C.; Opara, N.; Andersen, N.K.; Kristiansen, P.M.; Neyer, A. On The Role of Wetting, Structure Width, and Flow Characteristics in Polymer Replication on Micro- and Nanoscale. Macromol. Mater. Eng. 2016, 301, 597–609. [Google Scholar] [CrossRef] [Green Version]







| Test | Tmelt [°C] | Tmold [°C] | Pholding [MPa] | Holding time [s] | Tlevel [°C] | Heating time [s] |
|---|---|---|---|---|---|---|
| CIM | 220 | 28 | 26 | 2 | 28 | 0 |
| 80-07 | 220 | 28 | 26 | 2 | 80 | 0.7 |
| 120-07 | 220 | 28 | 26 | 2 | 120 | 0.7 |
| 160-07 | 220 | 28 | 26 | 2 | 160 | 0.7 |
| 80-18 | 220 | 28 | 26 | 2 | 80 | 18 |
| 120-18 | 220 | 28 | 26 | 2 | 120 | 18 |
| 140-18 | 220 | 28 | 26 | 2 | 140 | 18 |
| 160-18 | 220 | 28 | 26 | 2 | 160 | 18 |
| Test | Filter | 5 mm | 20 mm | 55 mm |
|---|---|---|---|---|
| Steel layer | flattened | 164 ± 30 nm | ||
| 0.1 µm−1 | 64 ± 10 nm | |||
| 0.2 µm−1 | 25 ± 5 nm | |||
| CIM | flattened | 113 ± 25 nm | 139 ± 10 nm | 116 ± 10 nm |
| 0.1 µm−1 | 48 ± 3 nm | 38 ± 5 nm | 48 ± 3 nm | |
| 0.2 µm−1 | 26 ± 3 nm | 20 ± 2 nm | 25 ± 2 nm | |
| 160-18 | flattened | 77 ± 5 nm | 136 ± 15 nm | 106 ± 12 nm |
| 0.1 µm−1 | 25 ± 5 nm | 40 ± 6 nm | 24 ± 2 nm | |
| 0.2 µm−1 | 23 ± 5 nm | 27 ± 3 nm | 23 ± 2 nm | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liparoti, S.; Pantani, R.; Sorrentino, A.; Speranza, V.; Titomanlio, G. Hydrophobicity Tuning by the Fast Evolution of Mold Temperature during Injection Molding. Polymers 2018, 10, 322. https://doi.org/10.3390/polym10030322
Liparoti S, Pantani R, Sorrentino A, Speranza V, Titomanlio G. Hydrophobicity Tuning by the Fast Evolution of Mold Temperature during Injection Molding. Polymers. 2018; 10(3):322. https://doi.org/10.3390/polym10030322
Chicago/Turabian StyleLiparoti, Sara, Roberto Pantani, Andrea Sorrentino, Vito Speranza, and Giuseppe Titomanlio. 2018. "Hydrophobicity Tuning by the Fast Evolution of Mold Temperature during Injection Molding" Polymers 10, no. 3: 322. https://doi.org/10.3390/polym10030322
APA StyleLiparoti, S., Pantani, R., Sorrentino, A., Speranza, V., & Titomanlio, G. (2018). Hydrophobicity Tuning by the Fast Evolution of Mold Temperature during Injection Molding. Polymers, 10(3), 322. https://doi.org/10.3390/polym10030322









