Water Absorption and Distribution in a Pultruded Unidirectional Carbon/Glass Hybrid Rod under Hydraulic Pressure and Elevated Temperatures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Raw Materials
2.2. Water Uptake Test
3. Results and Discussion
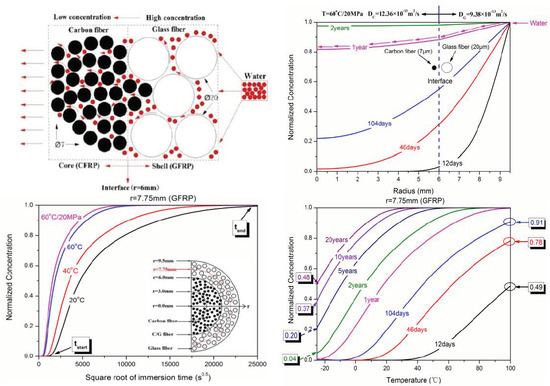
3.1. Water Absorption and Diffusion in the Hybrid Rod
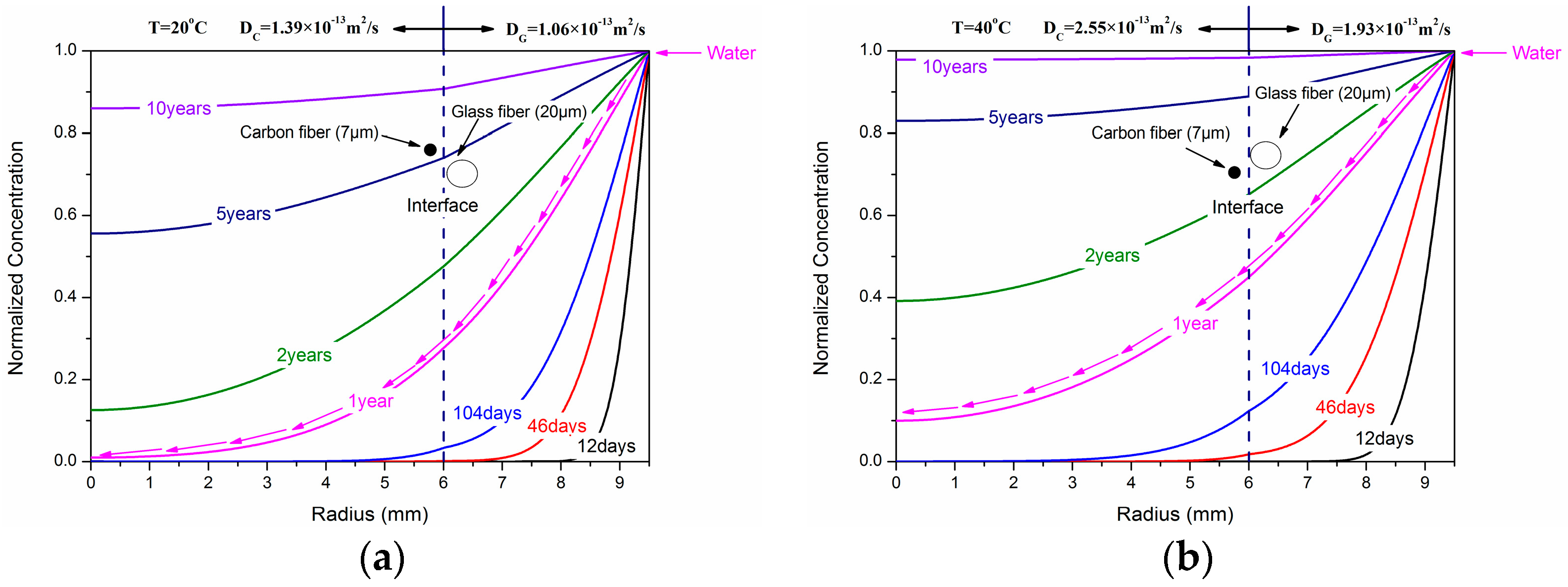
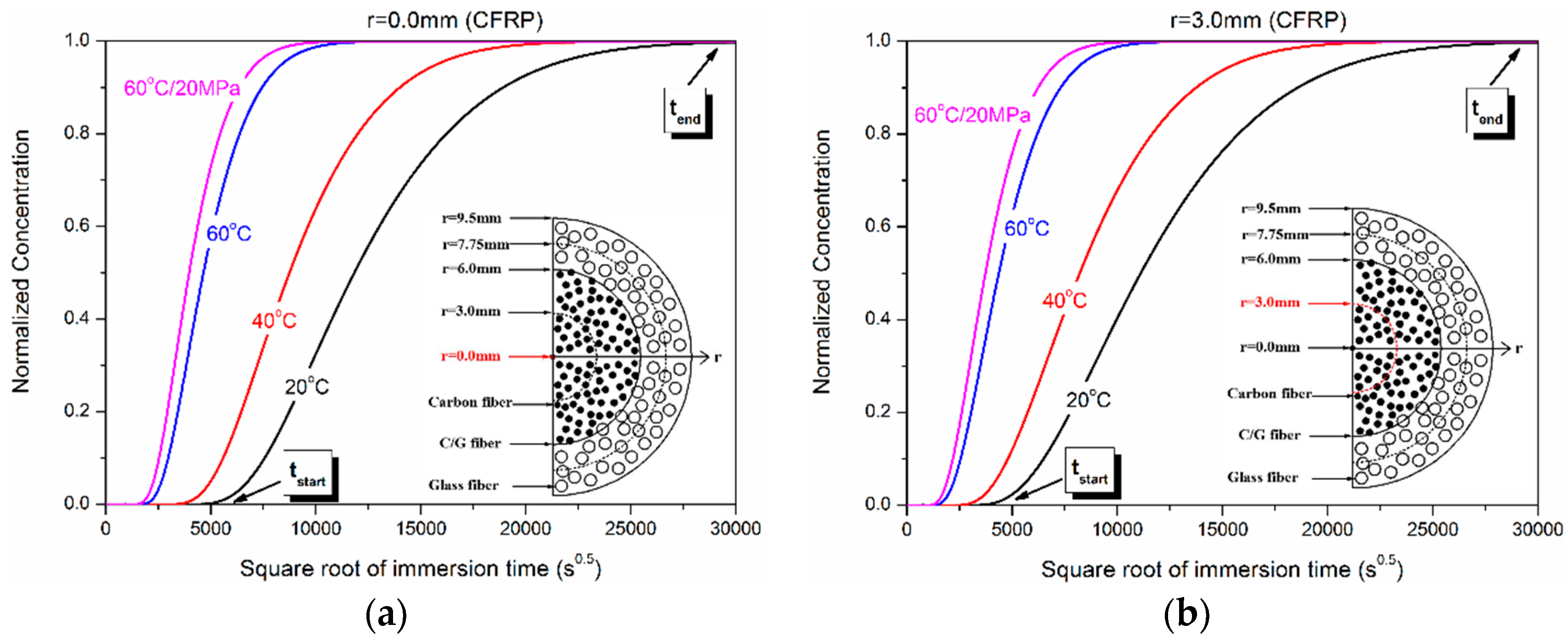
3.2. Water Concentration Distribution in the Hybrid Rod
4. Conclusions
- (1)
- Water absorption curves of the hybrid FRP rod complied with Fickian law. The exposure temperatures and hydraulic pressure accelerated the water absorption and diffusion in the hybrid FRP rod. This was attributed to initial defects (such as resin matrix voids, fiber microcracks, and fiber/resin interface imperfections) inside the hybrid rod being rapidly filled by water molecules under the actions of exposure temperature and hydraulic pressure.
- (2)
- By means of the diffusion mathematics theory, the equation of the water concentration distributions in the hybrid rod was deduced as a function of immersion time and temperature.
- (3)
- The temperature and hydraulic pressure acceleration factor of water absorption were obtained, and the immersion time to reach saturation under various immersion conditions was predicted.
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Carra, G.; Carvelli, V. Long-term bending performance and service life prediction of pultruded glass fibre reinforced polymer composites. Compos. Struct. 2015, 127, 308–315. [Google Scholar] [CrossRef]
- Jiang, X.; Kolstein, H.; Bijlaard, F.S.K. Moisture diffusion and hygrothermal aging in pultruded fibre reinforced polymer composites of bridge decks. Mater. Des. 2012, 37, 304–312. [Google Scholar] [CrossRef]
- Won, J.P.; Park, C.G.; Lee, S.J.; Hong, B.T. Durability of hybrid FRP reinforcing bars in concrete structures exposed to marine environments. In Proceedings of the 2nd International Conference on Durability of Concrete Structures (ICDCS 2010), Sapporo, Japan, 24–26 November 2010; pp. 431–438. [Google Scholar]
- Santhosh, K.; Muniraju, M.; Shivakumar, N.D. Hygrothermal durability and failure modes of FRP for marine applications. J. Compos. Mater. 2012, 46, 1889–1896. [Google Scholar] [CrossRef]
- Nakada, M.; Miyano, Y. Accelerated testing for long-term fatigue strength of various FRP laminates for marine use. Compos. Sci. Technol. 2009, 69, 805–813. [Google Scholar] [CrossRef]
- Miyano, Y.; Nakada, M.; Sekine, N. Accelerated testing for long-term durability of FRP laminates for marine use. J. Compos. Mater. 2005, 39, 5–20. [Google Scholar] [CrossRef]
- Humeau, C.; Davies, P.; Jacquemin, F. Moisture diffusion under hydrostatic pressure in composites. Mater. Des. 2016, 96, 90–98. [Google Scholar] [CrossRef]
- Barjasteh, E.; Nutt, S.R. Moisture absorption of unidirectional hybrid composites. Compos. Part A 2012, 43, 158–164. [Google Scholar] [CrossRef]
- Garcia-Espinel, J.D.; Castro-Fresno, D.; Gayo, P.P.; Ballester-Muñoz, F. Effects of sea water environment on glass fiber reinforced plastic materials used for marine civil engineering constructions. Mater. Des. 2015, 66, 46–50. [Google Scholar] [CrossRef]
- Hawa, A.; Abdul-Majid, M.S.; Afendi, M.; Marzuki, H.F.A.; Amin, N.A.M.; Mat, F.; Gibson, A.G. Burst strength and impact behaviour of hydrothermally aged glass fibre/epoxy composite pipes. Mater. Des. 2016, 89, 455–464. [Google Scholar] [CrossRef]
- Assarar, M.; Scida, D.; EI-Mahi, A.; Poilânec, C.; Ayada, R. Influence of water ageing on mechanical properties and damage events of two reinforced composite materials: Flax-fibres and glass-fibres. Mater. Des. 2011, 32, 788–795. [Google Scholar] [CrossRef]
- Berketis, K.; Tzetzis, D.; Hogg, P.J. The influence of long term water immersion ageing on impact damage behaviour and residual compression strength of glass fibre reinforced polymer (GFRP). Mater. Des. 2008, 29, 1300–1310. [Google Scholar] [CrossRef]
- Davies, P.; Mazéas, D.C.F. Composites underwater. In Proceedings of the Progress in Durability Analysis of Composites Systems, Rotterdam, The Netherlands, 14–17 September 1997; pp. 19–24. [Google Scholar]
- Avena, A.; Bunsell, A.R. Effect of hydrostatic-pressure on the water-absorption of glass fiber-reinforced epoxy-Resin. Composites 1988, 19, 355–357. [Google Scholar] [CrossRef]
- Derrien, K.; Gilormini, P. The effect of moisture-induced swelling on the absorption capacity of transversely isotropic elastic polymer-matrix composites. Int. J. Solids Struct. 2009, 46, 1547–1553. [Google Scholar] [CrossRef]
- Sar, B.E.; Fréoura, S.; Davies, P.; Jacquemin, F. Coupling moisture diffusion and internal mechanical states in polymers—A thermodynamical approach. Eur. J. Mech. A-Solids 2012, 36, 38–43. [Google Scholar] [CrossRef]
- Pollard, A.; Baggott, R.; Wostenholm, G.H.; Yates, B.; George, A.P. Influence of hydrostatic-pressure on the moisture absorption of glass fiber-reinforced polyester. J. Mater. Sci. 1989, 24, 1665–1669. [Google Scholar] [CrossRef]
- Whitaker, G.; Darby, M.I.; Wostenholm, G.H.; Yates, B.; Collins, M.H.; Lyle, A.R.; Brown, B. Influence of temperature and hydrostatic-pressure on moisture absorption in polymer resins. J. Mater. Sci. 1991, 26, 49–55. [Google Scholar] [CrossRef]
- Sugiyama, M.; Uomoto, T. Research on strength and durability of GFRP rods for prestressed concrete tendons. In Proceedings of the Fibre-Reinforcement Polymer Reinforcement for Concrete Structures, Singapore, July 2003. [Google Scholar]
- Uomoto, T. Durability design of GFRP rods for concrete reinforcement. In Proceedings of the Fibre-Reinforcement Polymer Reinforcement for Concrete Structures, Singapore, July 2003. [Google Scholar]
- Filippo, M.D.; Alessi, S.; Pitarresi, G.; Sabatino, M.A.; Zucchelli, A.; Dispenzaac, C. Hydrothermal aging of carbon reinforced epoxy laminates with nanofibrous mats as toughening interlayers. Polym. Degrad. Stabil. 2016, 126, 188–195. [Google Scholar] [CrossRef]
- Tanks, J.; Sharp, S.; Harris, D.; Ozyildirim, C. Durability of CFRP cables exposed to simulated concrete environments. Adv. Compos. Mater. 2017, 26, 245–258. [Google Scholar] [CrossRef]
- Koyanagi, J.; Nakada, M.; Miyano, Y. Prediction of long-term durability of unidirectional CFRP. J. Reinf. Plast. Compos. 2011, 30, 1305–1313. [Google Scholar] [CrossRef]
- Kobayashi, S.; Terada, K.; Takeda, N. Evaluation of long-term durability in high temperature resistant CFRP laminates under thermal fatigue loading. Compos. B Eng. 2003, 34, 753–759. [Google Scholar] [CrossRef]
- Lubineau, G.; Ladeveze, P.; Violeau, D. Durability of CFRP laminates under thermomechanical loading: A micro-meso damage model. Compos. Sci. Technol. 2006, 66, 983–992. [Google Scholar] [CrossRef]
- Swolfs, Y.; Gorbatikh, L.; Verpoest, I. Fibre hybridisation in polymer composites: A review. Compos. Part A 2014, 67, 181–200. [Google Scholar] [CrossRef] [Green Version]
- Tsai, Y.I.; Bosze, E.J.; Barjasteh, E.; Nutt, S.R. Influence of hygrothermal environment on thermal and mechanical properties of carbon fiber/fiberglass hybrid composites. Compos. Sci. Technol. 2009, 69, 432–437. [Google Scholar] [CrossRef]
- Selzer, R.; Friedrich, K. Mechanical properties and failure behaviour of carbon fibre-reinforced polymer composites under the influence of moisture. Compos. Part A 1997, 28, 595–604. [Google Scholar] [CrossRef]
- Ellyin, F.; Maser, R. Environmental effects on the mechanical properties of glass-fiber epoxy composite tubular specimens. Compos. Sci. Technol. 2004, 64, 1863–1874. [Google Scholar] [CrossRef]
- Kar, N.K.; Barjasteh, E.; Hu, Y.; Nutt, S.R. Bending fatigue of hybrid composite rods. Compos. Part A 2011, 42, 328–336. [Google Scholar] [CrossRef]
- Karbhari, V.M.; Xian, G.J. Hygrothermal effects on high V-F pultruded unidirectional carbon/epoxy composites: Moisture uptake. Compos. B Eng. 2009, 40, 41–49. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1975; Volume 2. [Google Scholar]
- Tsenoglou, C.J.; Pavlidou, S.; Papaspyrides, C.D. Evaluation of interfacial relaxation due to water absorption in fiber-polymer composites. Compos. Sci. Technol. 2006, 66, 2855–2864. [Google Scholar] [CrossRef]



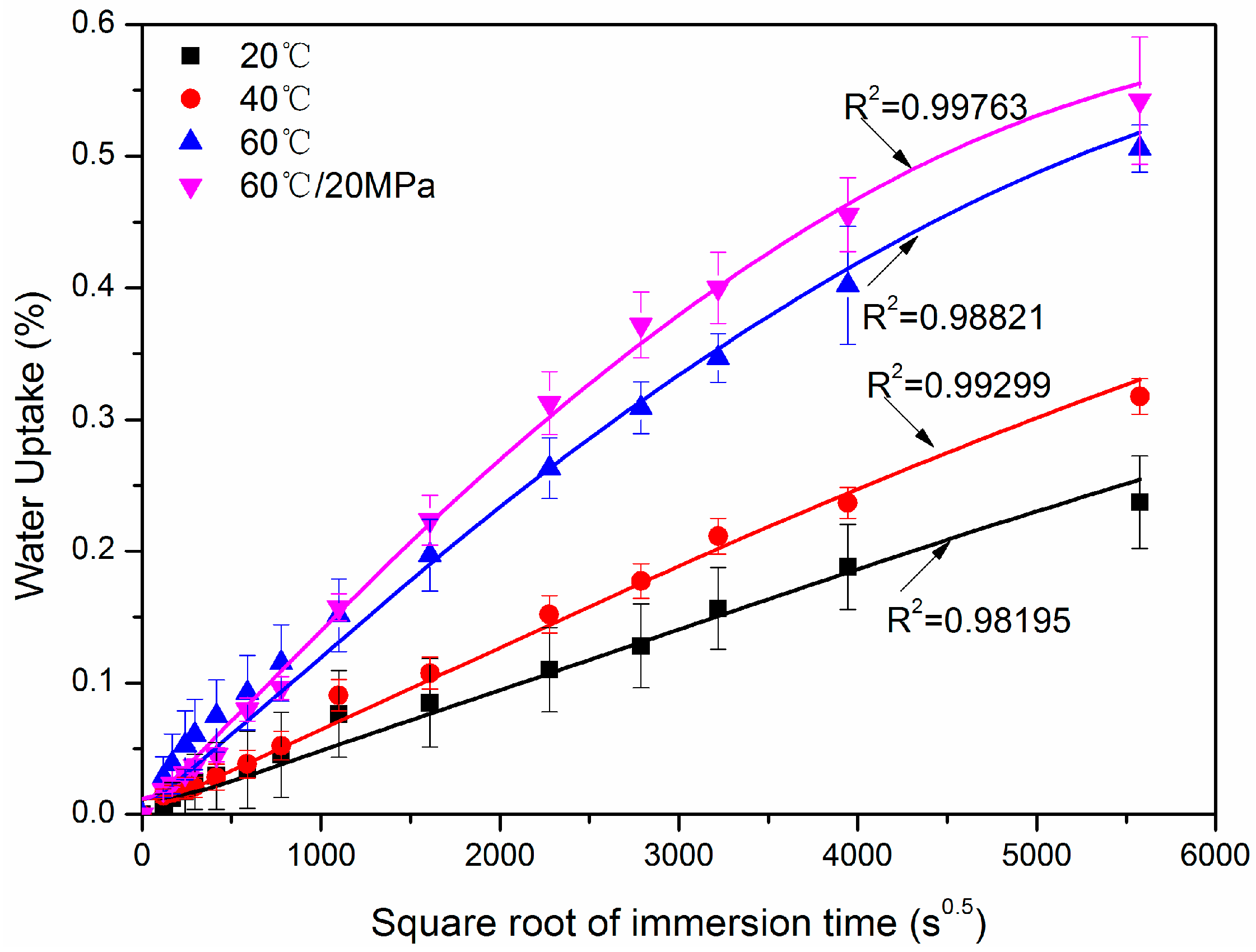









| Temperatures (°C) | 20 | 40 | 60 | 60/20 MPa |
|---|---|---|---|---|
| Dav (m2/s) | 1.26 × 10−13 | 2.30 × 10−13 | 8.14 × 10−13 | 11.17 × 10−13 |
| Temperature (°C) | 20 | 40 | 60 | 60/20 MPa |
|---|---|---|---|---|
| DC (m2/s) | 1.39 × 10−13 | 2.55 × 10−13 | 9.01 × 10−13 | 12.36 × 10−13 |
| DG (m2/s) | 1.06 × 10−13 | 1.93 × 10−13 | 6.84 × 10−13 | 9.38 × 10−13 |
| Conditions | 20 °C | 40 °C | 60 °C | 60 °C/20 MPa | ||||
|---|---|---|---|---|---|---|---|---|
| tstart (day) | tend (year) | tstart (day) | tend (year) | tstart (day) | tend (year) | tstart (day) | tend (year) | |
| r = 0 mm (CFRP) | 362 | 21.4 * | 198 | 11.8 * | 56 | 3.3 * | 41 | 2.4 * |
| r = 3.0 mm (CFRP) | 231 | 21.2 | 126 | 11.6 | 35.5 | 3.3 | 26 | 2.4 |
| r = 6.0 mm (CFRP/GFRP) | 73 | 20.4 | 40 | 11.2 | 11 | 3.2 | 8 | 2.3 |
| r = 7.75 mm (GFRP) | 25 | 17.1 | 13 | 9.4 | 4 | 2.6 | 2 | 1.9 |
| Conditions | t (C40°C/C20°C = max) (day) | t (C60°C/C20°C = max) (day) | t (C60°C/20MPa/C60°C = max) (day) |
|---|---|---|---|
| r = 0.0 mm | 127.3 | 111.7 | 20.8 |
| r = 3.0 mm | 71.8 | 62.5 | 11.6 |
| r = 7.75 mm | 12.2 | 11.0 | 2.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Xian, G.; Li, H. Water Absorption and Distribution in a Pultruded Unidirectional Carbon/Glass Hybrid Rod under Hydraulic Pressure and Elevated Temperatures. Polymers 2018, 10, 627. https://doi.org/10.3390/polym10060627
Li C, Xian G, Li H. Water Absorption and Distribution in a Pultruded Unidirectional Carbon/Glass Hybrid Rod under Hydraulic Pressure and Elevated Temperatures. Polymers. 2018; 10(6):627. https://doi.org/10.3390/polym10060627
Chicago/Turabian StyleLi, Chenggao, Guijun Xian, and Hui Li. 2018. "Water Absorption and Distribution in a Pultruded Unidirectional Carbon/Glass Hybrid Rod under Hydraulic Pressure and Elevated Temperatures" Polymers 10, no. 6: 627. https://doi.org/10.3390/polym10060627
APA StyleLi, C., Xian, G., & Li, H. (2018). Water Absorption and Distribution in a Pultruded Unidirectional Carbon/Glass Hybrid Rod under Hydraulic Pressure and Elevated Temperatures. Polymers, 10(6), 627. https://doi.org/10.3390/polym10060627