3.2. Network-Theory-Based Modeling
Recently, the heuristic pumping models have been tested successfully against additional numerical solutions not used in their design [
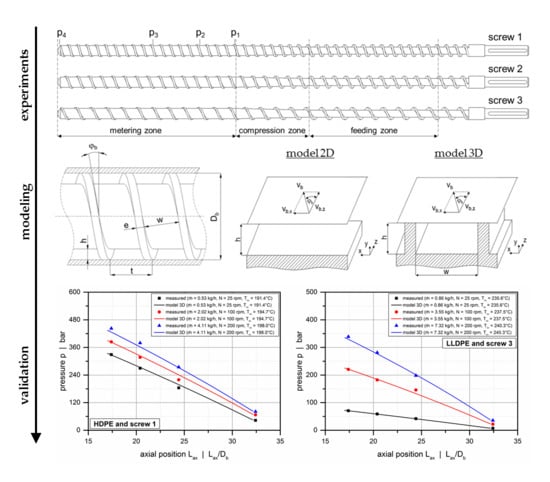
25]. To further validate the methods against experimental data, a network-theory-based simulation routine was written in MATLAB. The objective was to replicate the flow in the metering zones experimentally analyzed in the first part of the study by predicting the axial pressure profile along the metering section for the experimental setups shown in
Table A1.
Network theory originates from the field of electrical engineering [
34], but has also proven useful in predicting the flow in extrusion dies [
35] and in investigating the pumping behavior of barrier-screws [
36]. The main idea is to model the flow in complex geometries by subdividing the system into geometrically simpler, interconnected elements for which analytical equations are available. The resulting two-dimensional equivalent circuit diagram is solved numerically by means of nodal analysis in which the currents are replaced with flow rates and the voltages with pressure differences. For non-Newtonian flows, an iterative procedure is additionally required to obtain converging solutions. Network theory provides a convenient modeling approach to consider local changes in geometry or material properties in the flow calculation.
Note that the heuristic melt-conveying models examined in this study consider an isothermal, incompressible, fully-developed flow of a power-law fluid in a screw channel of constant channel height, as indicated in
Table 6. Thus, the application of network theory is required, for two reasons. First, our analysis is based on a pressure-dependent density. Since the pressure varies with the position in the screw channel, the melt density must be calculated incrementally. Second, our analysis includes leakage flow over the screw flights. Applying network theory allows us to capture the change in channel height at the flight clearances and consequently to describe the entire channel geometry accurately.
Our simulation routine is based on the procedure illustrated in
Figure 7. In the first step, basic simulation settings are defined. These include screw geometry (metering section), material of interest and input processing parameters, such as screw speed, mass flow rate, and melt temperature, which were evaluated experimentally. The last of these is used to shift the viscosity data to the desired temperature. For convenience, the geometric parameters of the metering sections (
Table 5) and the flow properties of the materials (
Table 3) are stored in an external library. To describe the shear-thinning nature of the polymer melts, the Carreau-Yasuda model in Equations (1) and (2) is applied. Further, the pvT behavior of the testing materials is approximated by the Tait model in Equations (3)–(6). To finalize definition of the setup, the coefficients of the heuristic melt-conveying models are imported, including 51 and 69 constants in model 2D and model 3D, respectively.
In the second step, the geometry of the melt-conveying section is subdivided into a network of smaller segments of constant geometry. These sections are indicated by network elements (shown schematically in
Figure 8, each of which consists of a source and a resistance that represent the local drag and pressure flows. The mass flow rate of each element is thus calculated by:
where the pressure flow is given by the conductance k and the pressure difference Δ
p. Analogously to electrical circuits, the elements are connected by nodal points, whose axial and down-channel positions along the screw are functions of the outer screw diameter, the pitch angle and the number of elements per revolution. The last of these can be adjusted and defines the resolution of the grid. At each nodal point, the geometry of the screw channel is calculated. Note that this study includes the cross-channel flow over the screw flights, as captured by the network elements positioned perpendicular to the screw channel. To accurately describe the channel geometry in this direction, each cross-channel connection is initialized with three elements (with
h1 =
h and
w1 =
w/2,
h2 =
δ and
w2 =
e,
h3 =
h and
w3 =
w/2), which are then replaced by one equivalent element. The total conductance and drag flow for three elements connected in series is given by:
To identify the pairs of nodal points connected in the cross-channel direction, a characteristic parameter was introduced based on geometric considerations. This parameter, which is referred to as
Noff, counts the number of down-channel elements between two nodal points that are connected in the cross-channel direction. The equivalent circuit diagram of the flow network is shown in
Figure 9. At the beginning of the calculation, the pressures at the nodal points and the properties and flow rates of the network elements are initialized with zeroes.
In the third step, the equivalent circuit diagram is solved iteratively by means of nodal analysis. Assuming that the mass flow rates incident at a nodal point add up to zero (cf. Kirchhoff’s current law), the network equations are built at each node, as demonstrated by the following relationship for an arbitrary node with index
i:
Taking all nodal points into account, the network equations are summarized in matrix form:
where
is the drag flow vector,
K the conductance matrix,
p the pressure vector, and
includes the boundary conditions. For each simulation, we predefined the mass flow rate and calculated the pressure vector. The system is thus rearranged into:
To solve the linear set of equations, the drag flow and conductance of each network element are determined as follows. First, the element dimensions are defined by using the geometric parameters known at each nodal point. The local flow properties are then evaluated. To this end, the Carreau-Yasuda data are converted into equivalent power-law parameters. On a log-log scale, the power law is a linear function and can be considered as the tangent of the Carreau-Yasuda model at a specific shear rate [
35]. It is thus possible to determine the local power-law parameters from the Carreau-Yasuda parameters as follows:
where the local effective shear rate is given by:
and the shear-rate components in the cross- and down-channel directions are specified by a linear combination of a drag flow and a pressure flow.
Finally, with the melt densities in the discretized screw channel being defined by the Tait equation, the local operating point (
Πp,z,
Πv) is evaluated using our melt-conveying models. For models 2D and 3D, a linearization of the screw characteristic curve is derived at this point, as shown in
Figure 10a. For each element, theoretical drag flow and conductance are obtained from the initial value and the slope of the linearization, respectively. Considering the restrictive influence of the screw flights in model 2D requires these element properties to be corrected. To this end, the local shape factors obtained from Equations (12) and (13) are used.
Note that in the first iteration the flow in the metering section is governed solely by the drag flow components, as all pressure differences are set to zero. In each iterative step, the element properties and the nodal pressures are updated. A simulation was considered converged if the pressure difference between the first and the final nodal point was smaller than 0.01 bar. For all simulations, we used 200 elements per revolution to discretize the screw channel.
The section above explains the theoretical background of our modeling approach, combining the heuristic melt-conveying models and network theory. Due to the complexity of the analysis, however, presenting an example case of how the theory is applied for a particular set of input parameters goes beyond the scope of this contribution. The conductance matrix, for example, has more than 1,000,000 entries in the analysis presented, which is moreover updated each iteration.