Micelle Structure Details and Stabilities of Cyclic Block Copolymer Amphiphile and Its Linear Analogues
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Micelle Formation
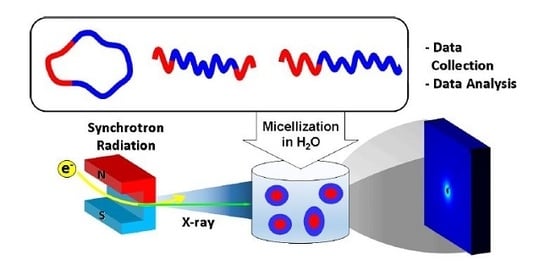
2.3. Synchrotron X-ray Scattering Measurements
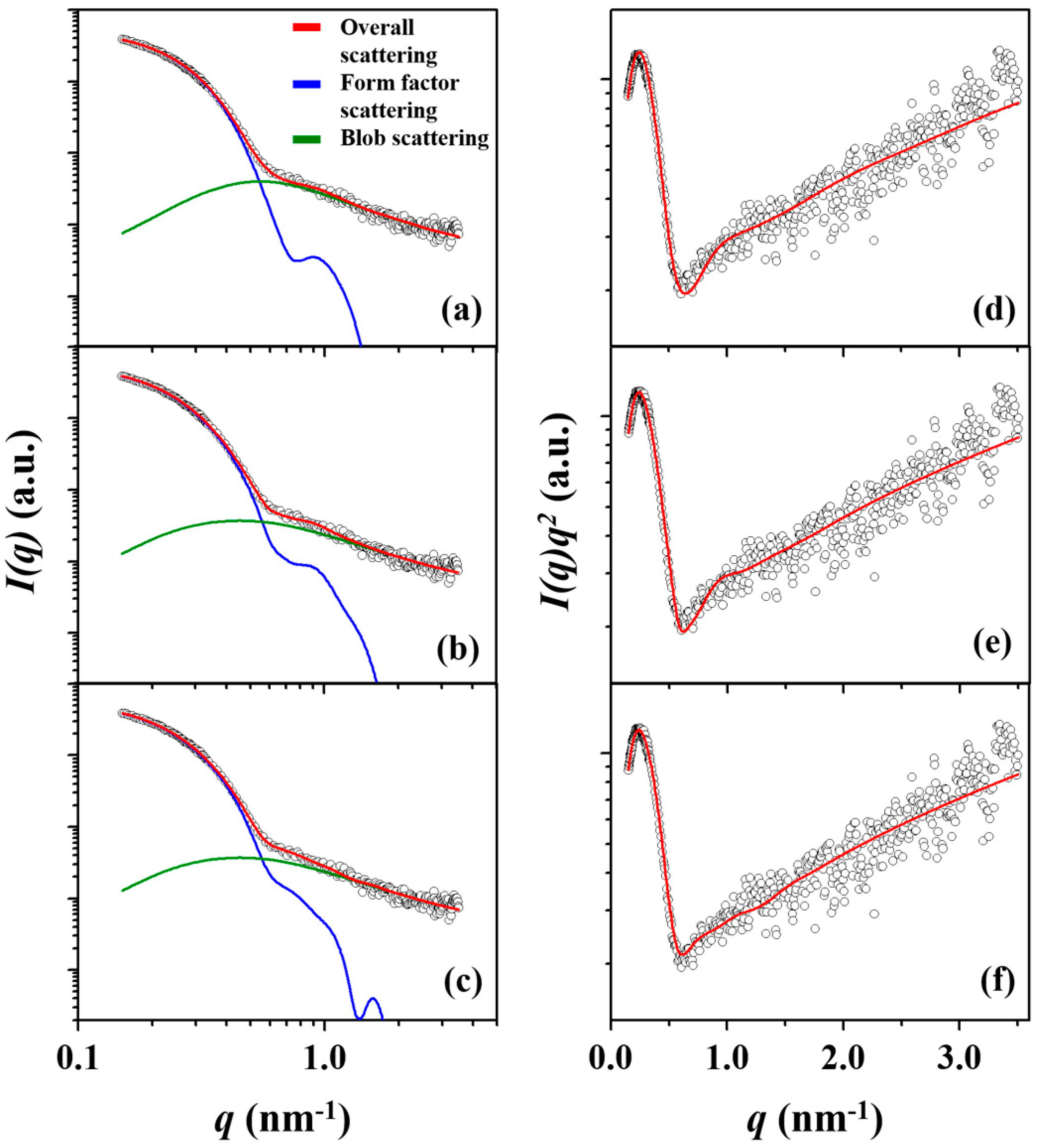
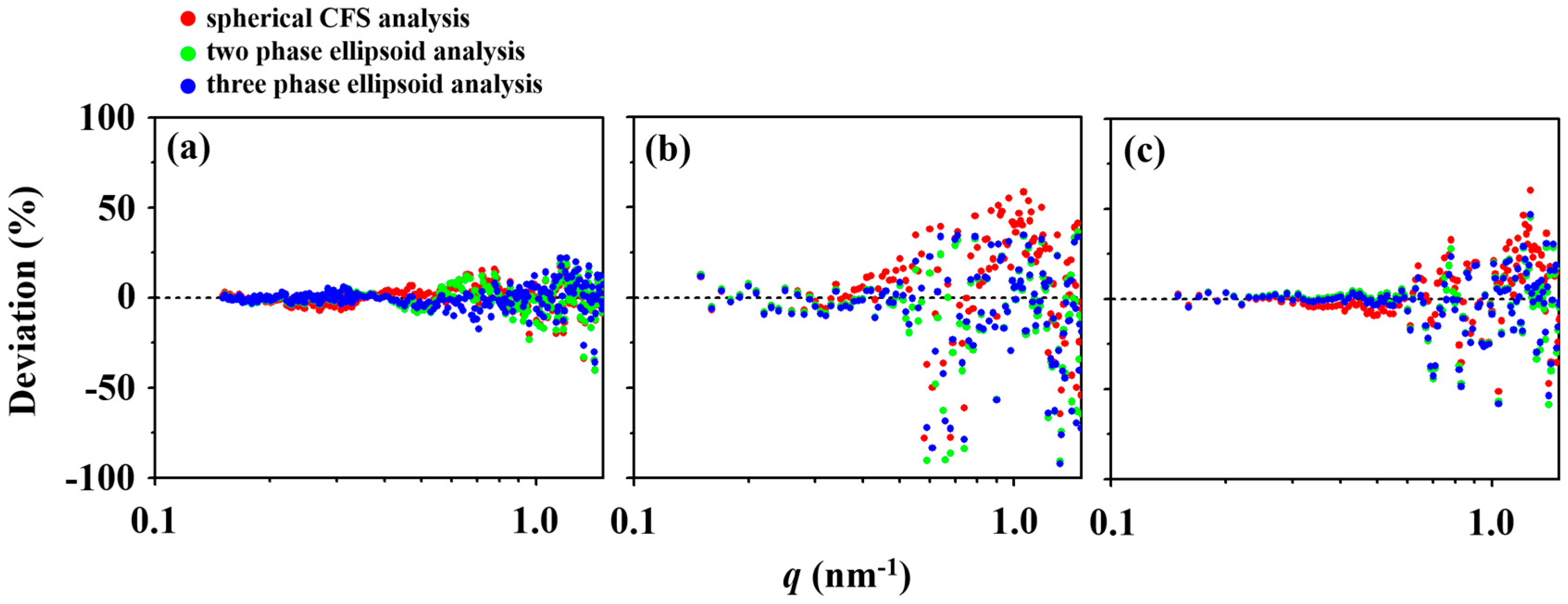
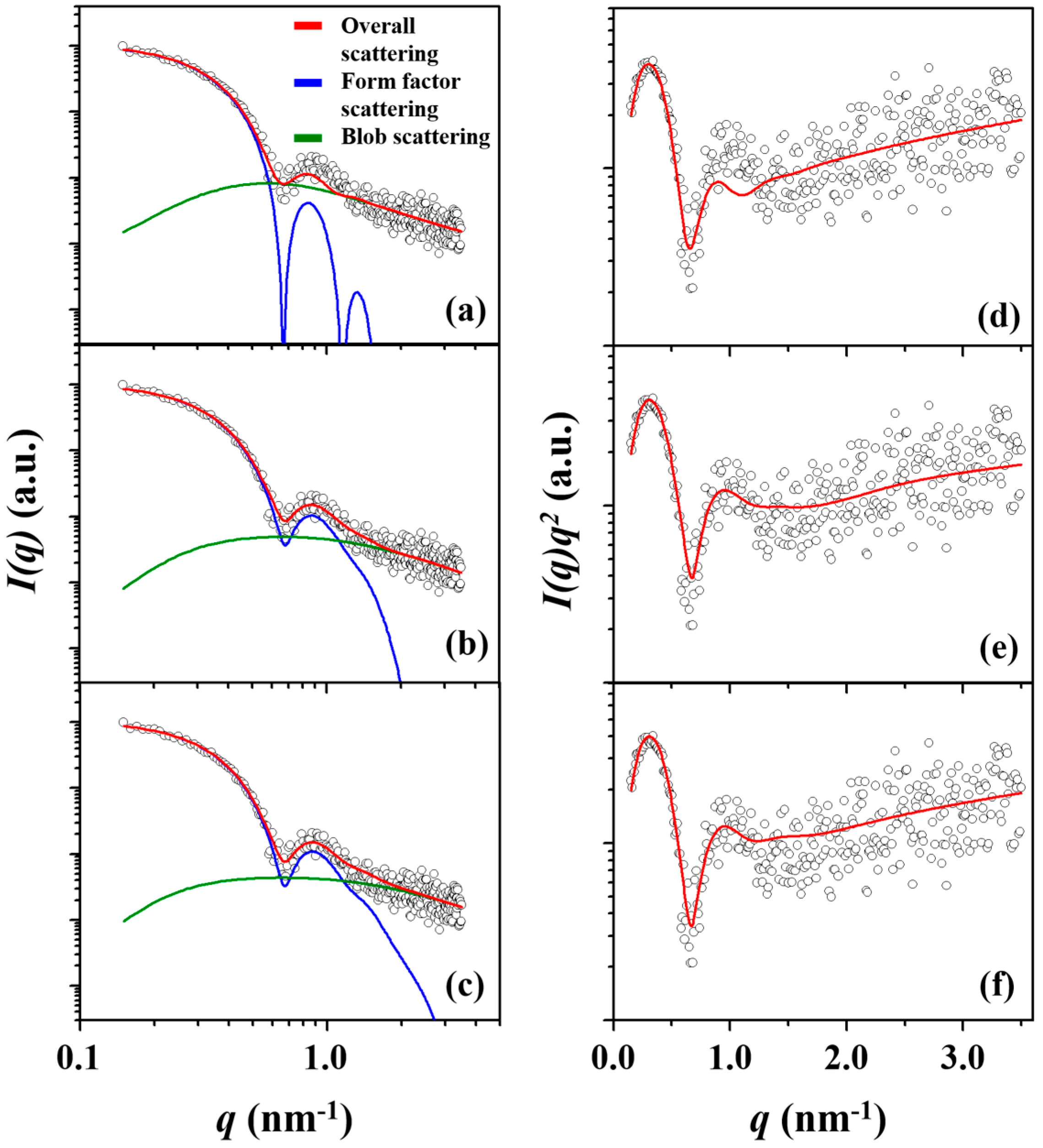
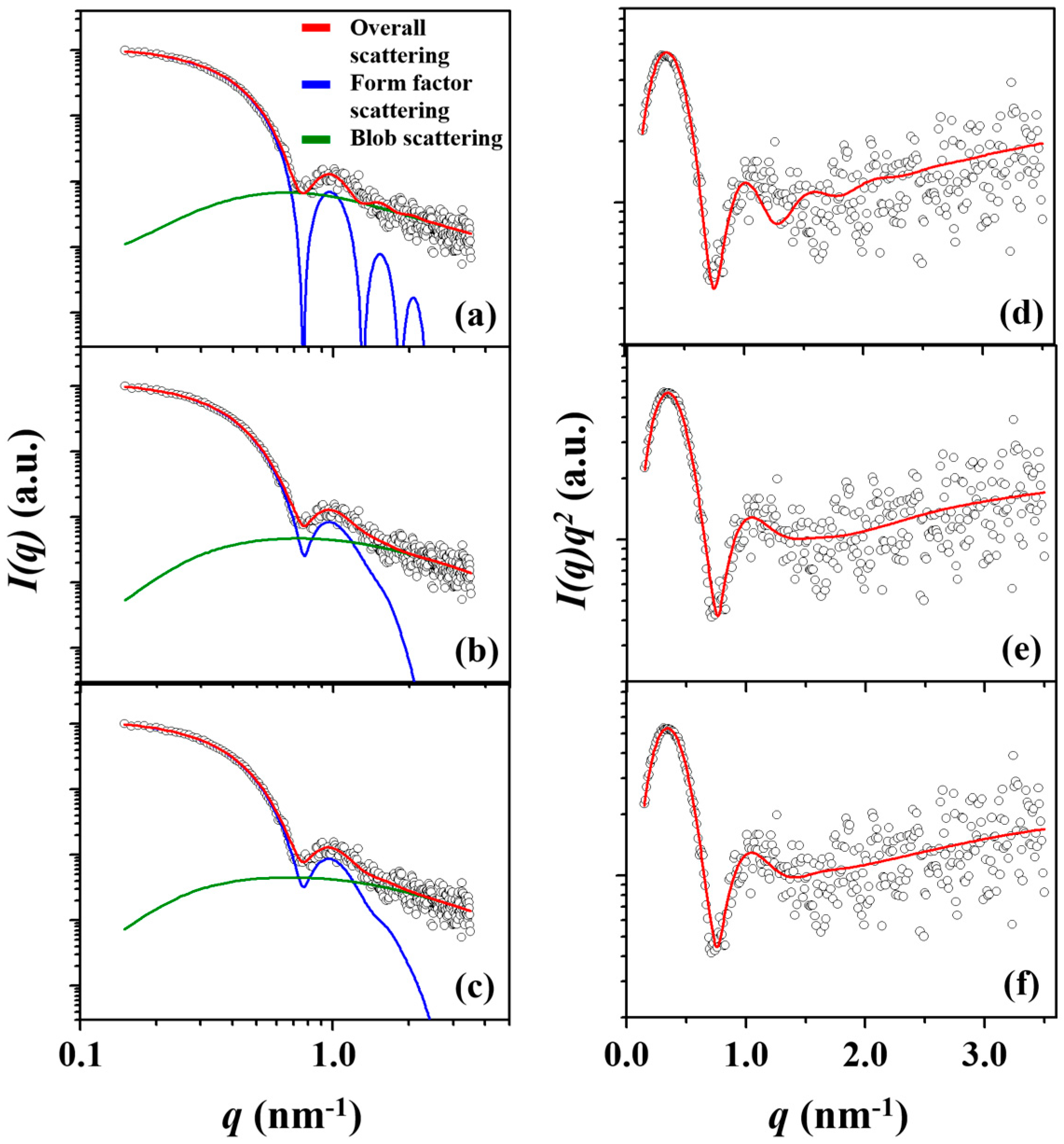
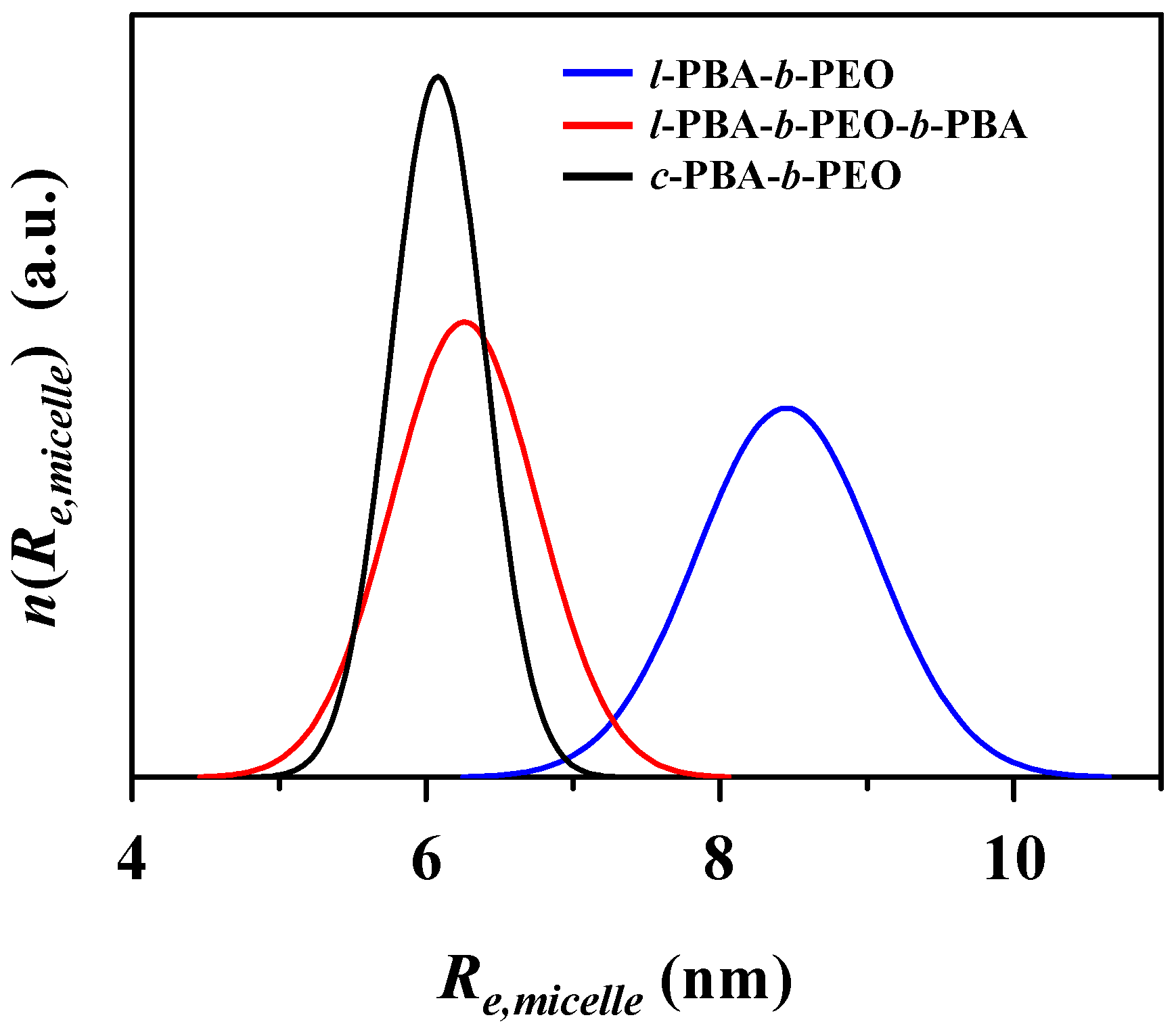
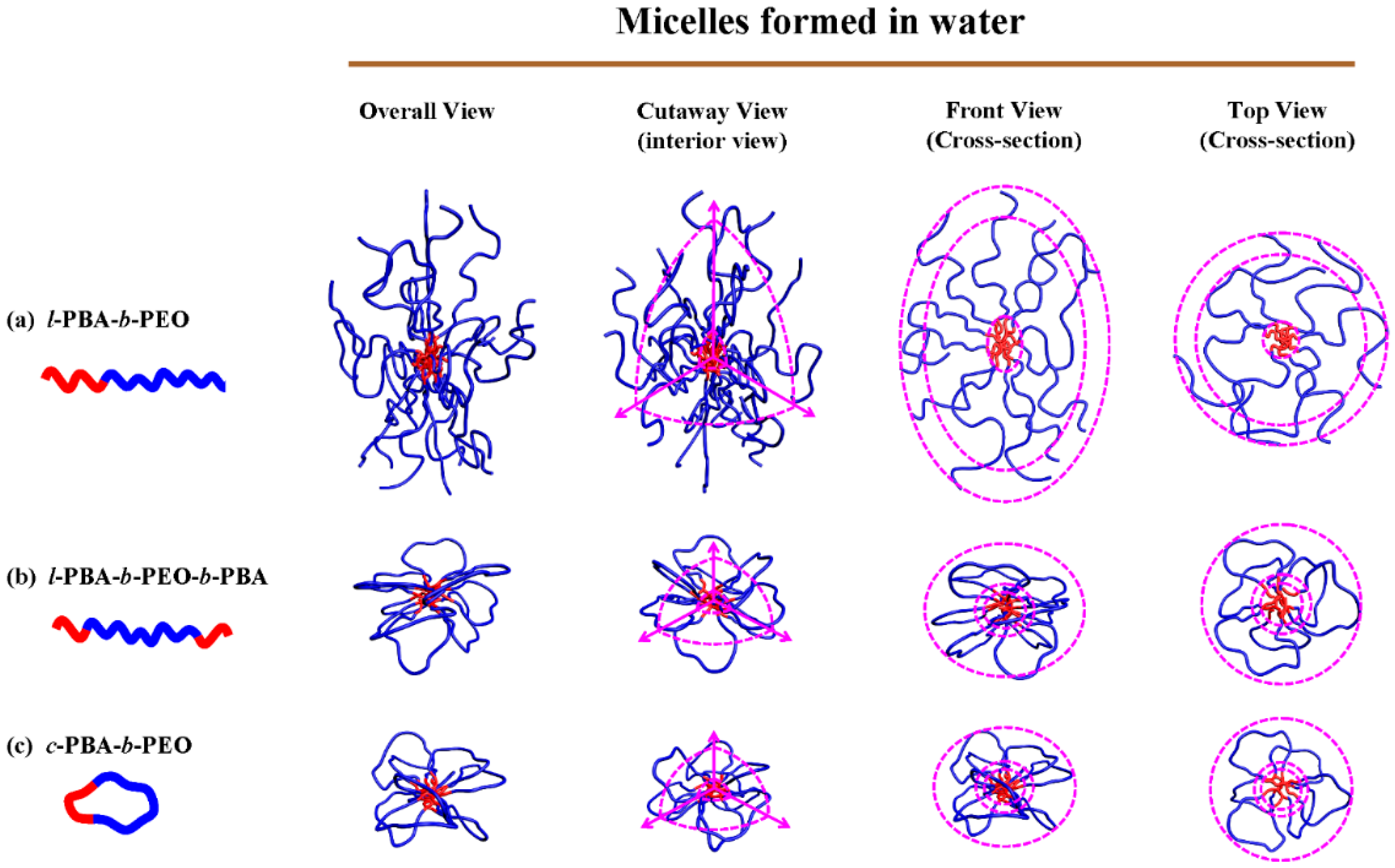
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schlueter, A.D.; Hawker, C.; Sakamoto, J. (Eds.) Synthesis of Polymers; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Hadjichristidis, N.; Hirao, A.; Tezuka, Y.; Du Prez, F. (Eds.) Complex Macromolecular Architectures, Synthesis, Characterization and Self-Assembly; Wiley: Singapore, 2011. [Google Scholar]
- Hirao, A.; Watanabe, T.; Ishizu, K.; Ree, M.; Jin, S.; Jin, K.S.; Deffieux, A.; Schappacher, M.; Carlott, S. Precise synthesis and characterization of fourth-generation dendrimer-like star-branched poly(methyl methacrylate)s and block copolymers by iterative methodology based on living anionic polymerization. Macromolecules 2009, 42, 682–693. [Google Scholar] [CrossRef]
- Kwon, W.; Rho, Y.; Kamoshida, K.; Kwon, K.H.; Jeong, Y.C.; Kim, J.; Misaka, H.; Shin, T.J.; Kim, J.; Kim, K.-W.; et al. Well-defined functional linear aliphatic diblock copolyethers: A versatile linear aliphatic polyether platform for selective functionalizations and various nanostructures. Adv. Funct. Mater. 2012, 22, 5194–5208. [Google Scholar] [CrossRef]
- Kim, G.; Park, S.; Jung, J.; Heo, K.; Yoon, J.; Kim, H.; Kim, I.J.; Kim, J.R.; Lee, J.I.; Ree, M. Novel brush polymers with phosphorylcholine bristle ends: Synthesis, structure, properties, and biocompatibility. Adv. Funct. Mater. 2009, 19, 1631–1644. [Google Scholar] [CrossRef]
- Semlyen, J.A. (Ed.) Cyclic Polymers, 2nd ed.; Kluwer: Dordorecht, The Netherlands, 2000. [Google Scholar]
- Yamamoto, T.; Tezuka, Y. Topological Polymer Chemistry: A cyclic approach toward novel polymer properties and functions. Polym. Chem. 2011, 2, 1930–1941. [Google Scholar] [CrossRef]
- Laurent, B.A.; Grayson, S.M. Synthetic approaches for the preparation of cyclic polymers. Chem. Soc. Rev. 2009, 38, 2202–2213. [Google Scholar] [CrossRef]
- Kricheldorf, H.R. Cyclic polymers: Synthetic Strategies and Physical Properties. J. Polym. Sci. Part A Polym. Chem. Ed. 2010, 48, 251–284. [Google Scholar] [CrossRef]
- Castro-Osma, J.A.; Alonso-Moreno, C.; García-Martinez, J.C.; Fernández-Baeza, J.; Sánchez-Barba, L.F.; Lara-Sánchez, A.; Otero, A. ring-opening (ROP) versus ring-extension (REP) polymerization of ε-caprolactone to give linear or cyclic polycaprolatones. Macromolecules 2013, 46, 6388–6394. [Google Scholar] [CrossRef]
- Cortez, M.A.; Godbey, W.T.; Fang, Y.; Payne, M.E.; Cafferty, B.J.; Kosakowska, K.A.; Grayson, S.M. The synthesis of cyclic poly(ethylene imine) and exact linear analogues: An evaluation of gene delivery comparing polymer architectures. J. Am. Chem. Soc. 2015, 137, 6541–6549. [Google Scholar] [CrossRef]
- Lonsdale, D.E.; Monteiro, M.J. Synthesis and self-assembly of amphiphilic macrocyclic block copolymer topologies. J. Polym. Sci. Part A Polym. Chem. 2011, 49, 4603–4612. [Google Scholar] [CrossRef]
- Isono, T.; Satoh, Y.; Miyachi, K.; Chen, Y.; Sato, S.-I.; Tajima, K.; Satoh, T.; Kakuchi, T. Synthesis of linear, cyclic, figure-eight-shaped, and tadpole-shaped amphiphilic block copolyethers via t-Bu-P4-catalyzed ring-opening polymerization of hydrophilic and hydrophobic glycidyl ethers. Macromolecules 2014, 47, 2853–2863. [Google Scholar] [CrossRef]
- Satoh, Y.; Matsuno, H.; Yamamoto, T.; Tajima, K.; Isono, T.; Satoh, T. Synthesis of well-defined three- and four-amed cage-shaped polymers via “Topological Conversion” from trefoil- and quatrefoil-shaped polymers. Macromolecules 2017, 50, 97–106. [Google Scholar] [CrossRef]
- McLeish, T. Polymers without beginning or end. Science 2002, 297, 2005–2006. [Google Scholar] [CrossRef] [PubMed]
- Deffieux, A.; Borsali, R. Controlled Synthesis and Properties of Cyclic Polymers; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Xiang, L.; Ryu, W.; Kim, H.; Ree, M. Precise synthesis, properties, and structures of cyclic poly(ε caprolactone)s. Polymers 2018, 10, 577. [Google Scholar]
- Yamamoto, T.; Tezuka, Y. Cyclic polymers revealing topology effects upon self-assemblies, dynamics and responses. Soft Matter 2015, 11, 7458–7468. [Google Scholar] [CrossRef] [PubMed]
- Williams, R.J.; Dove, A.P.; O’Reilly, R.K. Self-assembly of cyclic polymers. Polym. Chem. 2015, 6, 2998–3008. [Google Scholar] [CrossRef]
- Shin, E.J.; Jeong, W.; Brown, H.A.; Koo, B.J.; Hedrick, J.L.; Waymouth, R.M. Crystallization of cyclic polymers: Synthesis and crystallization behaviour of high molecular weight cyclic poly(ε-caprolactone)s. Macromolecules 2011, 44, 2773–2779. [Google Scholar] [CrossRef]
- Su, H.; Chen, H.; Díaz, A.; Casas, M.T.; Ouiggalí, J.; Hoskins, J.N.; Grayson, S.M.; Pérez, R.A.; Müller, A.J. New insight on the crystallization and melting of cyclic PCL chains on the basis of a modified Thomson-Gibbs equation. Polymer 2013, 54, 846–859. [Google Scholar] [CrossRef]
- Qiu, X.-P.; Tanaka, F.; Winnik, F.M. Temperature-induced phase transition of well-defined cyclic poly(N-isopropylacrylamide)s in aqueous solution. Macromolecules 2007, 40, 7069–7071. [Google Scholar] [CrossRef]
- Takeshita, H.; Poovarodom, M.; Kiya, T.; Arai, F.; Takenaka, K.; Miya, M.; Shiomi, T. Crystallization behavior and chain folding manner of cyclic, star and linear poly(tetrahydrofuran)s. Polymer 2012, 53, 5375–5384. [Google Scholar] [CrossRef]
- Zhu, Y.; Gido, S.P.; Iatrou, H.; Hadjichristidis, N.; Mays, J.M. Microphase separation of cyclic block copolymers of styrene and butadiene and of their corresponding linear triblock copolymers. Macromolecules 2003, 36, 148–152. [Google Scholar] [CrossRef]
- Honda, S.; Yamamoto, T.; Tezuka, Y. Topology-directed control on thermal stability: Micelles formed from linear and cyclized amphiphilic block copolymers. J. Am. Chem. Soc. 2010, 132, 10251–10253. [Google Scholar] [CrossRef] [PubMed]
- Honda, S.; Yamamoto, T.; Tezuka, Y. Tuneable enhancement of the salt and thermal stability of polymeric micelles by cyclized amphiphiles. Nat. Commun. 2013, 4, 1574. [Google Scholar] [CrossRef] [PubMed]
- Minatti, E.; Borsali, R.; Schappacher, M.; Deffieux, A.; Soldi, V.; Narayanan, T.; Putaux, J.-L. Effect of cyclization of polystyrene/polyisoprene block copolymers on their micellar morphology. Macromol. Rapid Commun. 2002, 23, 978–982. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Borisov, O.V. Effect of block copolymer architecture on morphology of self-assembled aggregates in solution. ACS Macro Lett. 2013, 2, 292–295. [Google Scholar] [CrossRef]
- Atanase, L.I.; Desbrieres, J.; Riess, G. Micellization of synthetic and polysaccharides-based graft copolymers in aqueous media. Prog. Polym. Sci. 2017, 73, 32–60. [Google Scholar] [CrossRef]
- Atanase, L.I.; Riess, G. Self-assembly of block and graft copolymers in organic solvents: An overview of recent advances. Polymers 2018, 10, 62. [Google Scholar] [CrossRef]
- Heo, K.; Kim, Y.Y.; Kitazawa, Y.; Kim, M.; Jin, K.S.; Yamamoto, T.; Ree, M. Structural characteristics of amphiphilic cyclic and linear block copolymer micelles in aqueous solutions. ACS Macro Lett. 2014, 3, 233–239. [Google Scholar] [CrossRef]
- Akiba, I.; Takechi, A.; Sakou, M.; Handa, M.; Shinohara, Y.; Amemiya, Y.; Yagi, N.; Sakurai, K. Anomalous small-angle X-ray scattering study of structure of polymer micelles having bromines in hydrophobic core. Macromolecules 2012, 45, 6150–6157. [Google Scholar] [CrossRef]
- Sasaki, S.; Machida, G.; Nakanishi, R.; Kinoshita, M.; Akiba, I. Elucidation of spatial distribution of hydrophobic aromatic compounds encapsulated in polymer micelles by anomalous small-angle X-ray scattering. Polymers 2018, 10, 180. [Google Scholar] [CrossRef]
- Szymusiak, M.; Kalkowski, J.; Luo, H.; Donovan, A.J.; Zhang, P.; Liu, C.; Shang, W.; Irving, T.; Herrera-Alonso, M.; Liu, Y. Core-shell structure and aggregation number of micelles composed of mphiphilic block copolymers and amphiphilic heterografted polymer brushes determined by small-angle X-ray scattering. ACS Macro Lett. 2017, 6, 1005–1012. [Google Scholar] [CrossRef]
- Ree, B.J.; Satoh, Y.; Jin, K.S.; Isono, T.; Kim, W.J.; Kakuchi, T.; Satoh, T.; Ree, M. Well-defined stable nanomicelles self-assembled by brush cyclic and tadpole copolymer amphiphiles: A versatile smart carrier platform. NPG Asia Mater. 2017, 9, e453. [Google Scholar] [CrossRef]
- Adachi, K.; Honda, S.; Hayashi, S.; Tezuka, Y. ATRP-RCM synthesis of cyclic diblock copolymers. Macromolecules 2008, 41, 7898–7903. [Google Scholar] [CrossRef]
- Kim, M.; Rho, Y.; Jin, K.S.; Ahn, B.; Jung, S.; Kim, H.; Ree, M. pH-Depedent structures of ferritin and apoferrin in solution: Disassembly and reassembly. Biomacromolecules 2011, 12, 1629–1640. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.R.; Jin, K.S.; Lee, C.K.; Kim, S.I.; Spinks, G.M.; So, I.; Jeon, J.-H.; Kang, T.M.; Mun, J.Y.; Han, S.-S.; et al. Fullerene attachment enhances performance of a DNA nanomachine. Adv. Mater. 2009, 21, 1907–1910. [Google Scholar] [CrossRef]
- Jin, S.; Higashihara, T.; Jin, K.S.; Yoon, J.; Rho, Y.; Ahn, B.; Kim, J.; Hirao, A.; Ree, M. Synchrotron X-ray Scattering Characterization of the Molecular Structures of Star Polystyrenes with Varying Numbers of Arms. J. Phys. Chem. B 2010, 114, 6247–6257. [Google Scholar] [CrossRef] [PubMed]
- Jin, S.; Jin, K.S.; Yoon, J.; Heo, K.; Kim, J.; Kim, K.-W.; Ree, M.; Higashihara, T.; Watanabe, T.; Hirao, A. X-ray scattering studies on molecular structures of star and dendritic polymers. Macromol. Res. 2008, 16, 686–694. [Google Scholar] [CrossRef]
- Rathgeber, S.; Monkenbusch, M.; Kreitschmann, M.; Urban, V.; Brulet, A. Dynamics of star-burst dendrimers in solution in relation to their structural properties. J. Chem. Phys. 2002, 117, 4047–4062. [Google Scholar] [CrossRef]
- Daoud, M.; Cotton, J. Star Shaped Polymers: A model for the conformation and its concentration dependence. J. Phys. 1982, 43, 531–538. [Google Scholar] [CrossRef]
- Hayter, J.B.; Penfold, J. Determination of micelle structure and charge by neutron small-angle scattering. Coll. Polym. Sci. 1983, 261, 1022–1030. [Google Scholar] [CrossRef]
- Roe, R.-J. Methods of X-ray and Neutron Scattering in Polymer Science; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Guinier, A.; Fournet, G. Small Angle Scattering X-ray; Wiley: New York, NY, USA, 1955. [Google Scholar]
- Glatter, O. A new method for the evaluation of small-angle scattering data. J. Appl. Crystallogr. 1977, 10, 415–421. [Google Scholar] [CrossRef]
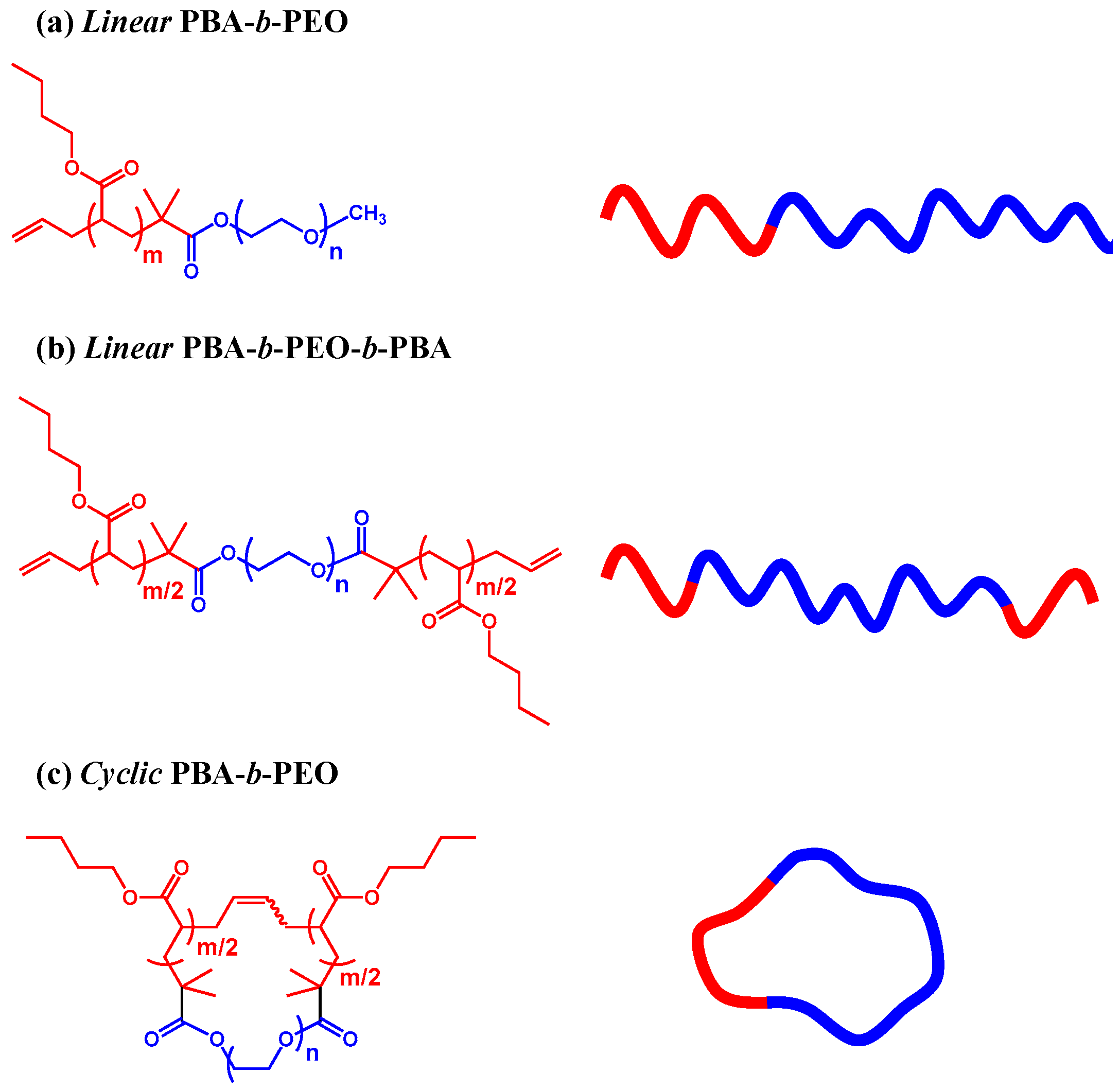
| Amphiphilic Block Copolymer | PDIb | PBA Block | PEO Block | |||
|---|---|---|---|---|---|---|
| φPBAd | e | φPEOf | ||||
| l-PBA-b-PEO | 6830 | 1.07 | 9 | 0.177 | 126 | 0.823 |
| l-PBA-b-PEO-b-PBA | 5850 | 1.11 | 10 | 0.331 | 69 | 0.669 |
| c-PBA-b-PEO | 4700 | 1.18 | 10 | 0.334 | 68 | 0.666 |
| Structural Parameter | l-PBA-b-PEO Micelle | |||||
|---|---|---|---|---|---|---|
| Spherical CFS | Two-Phase Ellipsoid | Three-Phase Ellipsoid | ||||
| Re,micellea (nm) | 7.10 | 7.20 | 8.50 | |||
| rcoreb (nm) | 2.80 | 2.10 | 1.90 | |||
| tf,corec (nm) | 1.00 | 0.50 | ||||
| tcoronad (nm) | 4.30 | 5.10 | 6.60 | |||
| tf.coronae (nm) | 3.66 | 2.55 | ||||
| td,coronaf (nm) | 4.80 | |||||
| tf,d.coronag (nm) | 0.72 | |||||
| ts.coronah (nm) | 1.80 | |||||
| tf,s.coronai (nm) | 0.90 | |||||
| εj | 1.0 | 1.5 | 1.5 | |||
| ξk (nm) | 3.00 | 1.70 | 1.70 | |||
| Rgl (nm) | 5.50 | 6.64 | 7.84 | |||
| ρcorem (g/cm3) | 1.08 | 1.08 | 1.08 | |||
| ρcoronan (g/cm3) | 0.348 | 0.013 | 0.059 | |||
| Naggo | 51.9 | 32.9 | 24.3 | |||
| Structural Parameter | l-PBA-b-PEO-b-PBA Micelle | |||||
|---|---|---|---|---|---|---|
| Spherical CFS | Two-Phase Ellipsoid | Three-Phase Ellipsoid | ||||
| Re,micellea (nm) | 6.50 | 6.30 | 6.26 | |||
| rcoreb (nm) | 1.85 | 2.30 | 1.73 | |||
| tf,corec (nm) | 0.60 | 0.40 | ||||
| tcoronad (nm) | 4.65 | 4.00 | 4.45 | |||
| tf.coronae (nm) | 0.89 | 1.95 | ||||
| td,coronaf (nm) | 0.80 | |||||
| tf,d.coronag (nm) | 0.31 | |||||
| ts.coronah (nm) | 3.65 | |||||
| tf,s.coronai (nm) | 1.74 | |||||
| εj | 1.0 | 0.79 | 0.83 | |||
| ξk (nm) | 1.71 | 0.70 | 0.55 | |||
| Rgl (nm) | 5.03 | 4.56 | 4.59 | |||
| ρcorem (g/cm3) | 1.08 | 1.08 | 1.08 | |||
| ρcoronan (g/cm3) | 0.060 | 0.013 | 0.054 | |||
| Naggo | 13.5 | 20.5 | 9.1 | |||
| Structural Parameter | c-PBA-b-PEO Micelle | |||||
|---|---|---|---|---|---|---|
| Spherical CFS | Two-Phase Ellipsoid | Three-Phase Ellipsoid | ||||
| Re,micellea (nm) | 5.96 | 5.75 | 6.05 | |||
| rcoreb (nm) | 1.69 | 2.20 | 1.65 | |||
| tf,corec (nm) | 0.50 | 0.30 | ||||
| tcoronad (nm) | 4.27 | 3.55 | 4.40 | |||
| tf.coronae (nm) | 0.64 | 1.73 | ||||
| td,coronaf (nm) | 0.60 | |||||
| tf,d.coronag (nm) | 0.12 | |||||
| ts.coronah (nm) | 3.80 | |||||
| tf,s.coronai (nm) | 1.44 | |||||
| εj | 1.0 | 0.78 | 0.82 | |||
| ξk (nm) | 1.23 | 0.70 | 0.60 | |||
| Rgl (nm) | 4.62 | 4.15 | 4.42 | |||
| ρcorem (g/cm3) | 1.23 | 1.23 | 1.23 | |||
| ρcoronan (g/cm3) | 0.067 | 0.016 | 0.058 | |||
| Naggo | 11.7 | 20.1 | 8.9 | |||
| Structural Parameter | Amphiphilic Block Copolymer Micelle | ||||
|---|---|---|---|---|---|
| l-PBA-b-PEO | l-PBA-b-PEO-b-PBA | c-PBA-b-PEO | |||
| Re,micellea (nm) | 8.50 (0.61) b | 6.26 (0.49) | 6.05 (0.32) | ||
| rcoreb (nm) | 1.90 (0.35) | 1.73 (0.25) | 1.65 (0.15) | ||
| tf,cored (nm) | 1.90 (0.35) | 1.73 (0.25) | 1.65 (0.15) | ||
| td,coronae (nm) | 0.50 | 0.40 | 0.30 | ||
| tf,d.coronaf (nm) | 4.80 (0.40) | 0.80 (0.15) | 0.60 (0.05) | ||
| ts.coronag (nm) | 0.72 | 0.31 | 0.12 | ||
| tf,s.coronah (nm) | 1.80 (0.30) | 3.65 (0.40) | 3.80 (0.10) | ||
| εi | 1.50 | 0.83 | 0.82 | ||
| ξj (nm) | 1.70 | 0.55 | 0.60 | ||
| Rgk (nm) | 7.84 | 4.59 | 4.42 | ||
| ρcorel (g/cm3) | 1.08 | 1.08 | 1.23 m | ||
| ρcoronan (g/cm3) | 0.059 | 0.054 | 0.058 | ||
| Naggo | 24.3 | 9.1 | 8.9 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ree, B.J.; Satoh, T.; Yamamoto, T. Micelle Structure Details and Stabilities of Cyclic Block Copolymer Amphiphile and Its Linear Analogues. Polymers 2019, 11, 163. https://doi.org/10.3390/polym11010163
Ree BJ, Satoh T, Yamamoto T. Micelle Structure Details and Stabilities of Cyclic Block Copolymer Amphiphile and Its Linear Analogues. Polymers. 2019; 11(1):163. https://doi.org/10.3390/polym11010163
Chicago/Turabian StyleRee, Brian J., Toshifumi Satoh, and Takuya Yamamoto. 2019. "Micelle Structure Details and Stabilities of Cyclic Block Copolymer Amphiphile and Its Linear Analogues" Polymers 11, no. 1: 163. https://doi.org/10.3390/polym11010163
APA StyleRee, B. J., Satoh, T., & Yamamoto, T. (2019). Micelle Structure Details and Stabilities of Cyclic Block Copolymer Amphiphile and Its Linear Analogues. Polymers, 11(1), 163. https://doi.org/10.3390/polym11010163