Calculated Terahertz Spectra of Glycine Oligopeptide Solutions Confined in Carbon Nanotubes
Abstract
:1. Introduction
2. Model and Method
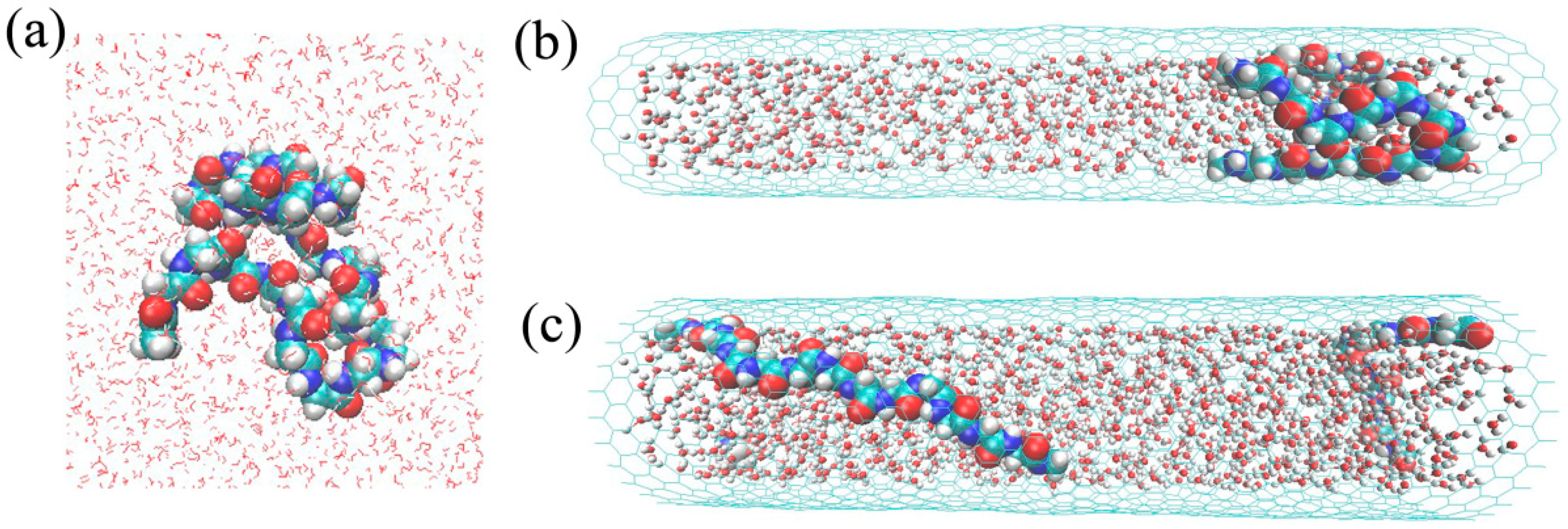
2.1. The Free and Confined Gly23 Solution Systems
2.2. Radius of Gyration and Diffusion Coefficient
2.3. THz Absorption Spectroscopy
3. Results and Discussion
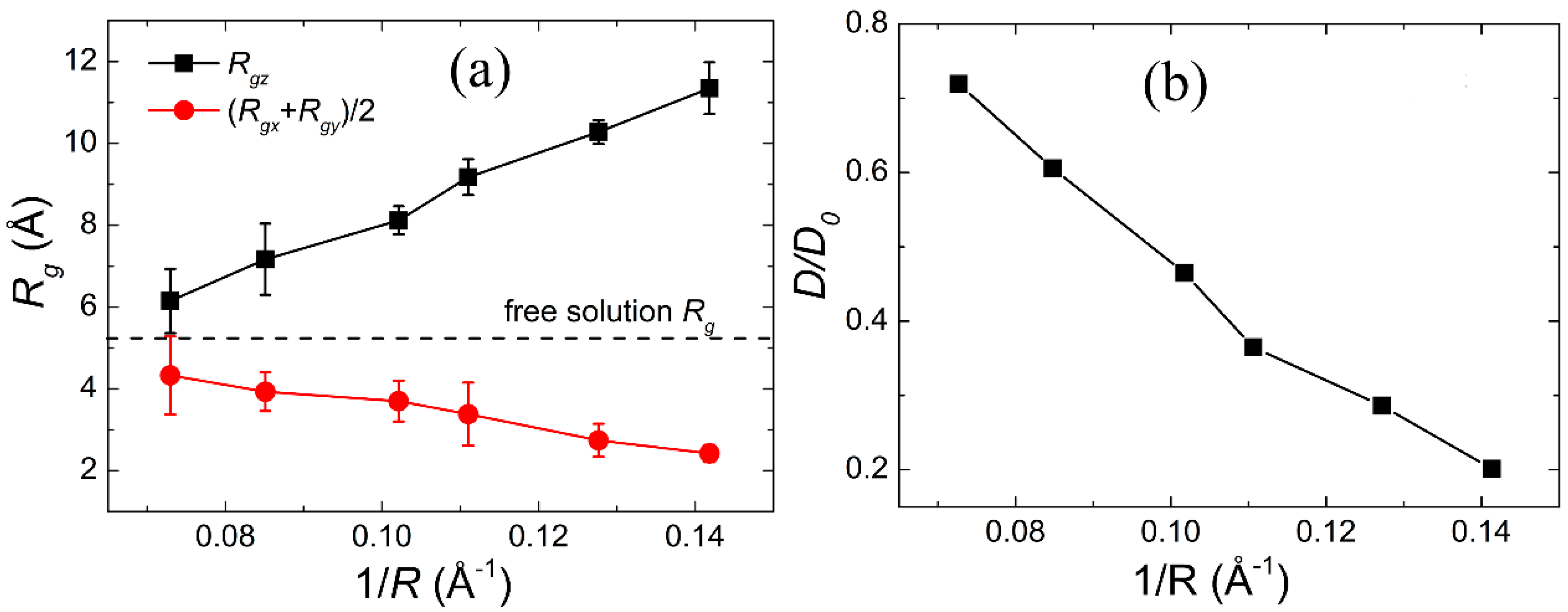
3.1. Confinement Effects on the Size of Gly23 Oligopeptide and the Water Diffusion Dynamics
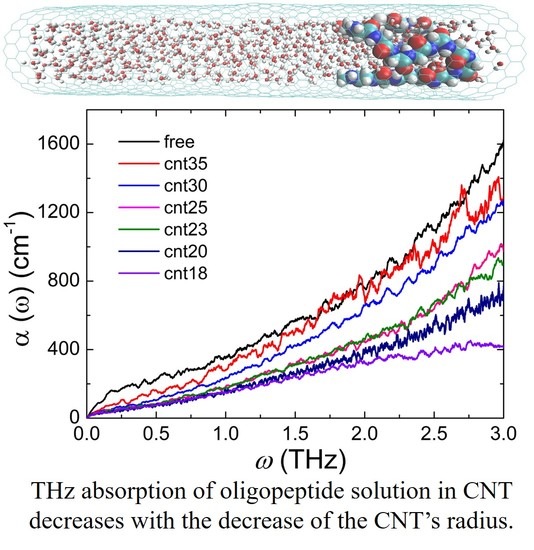
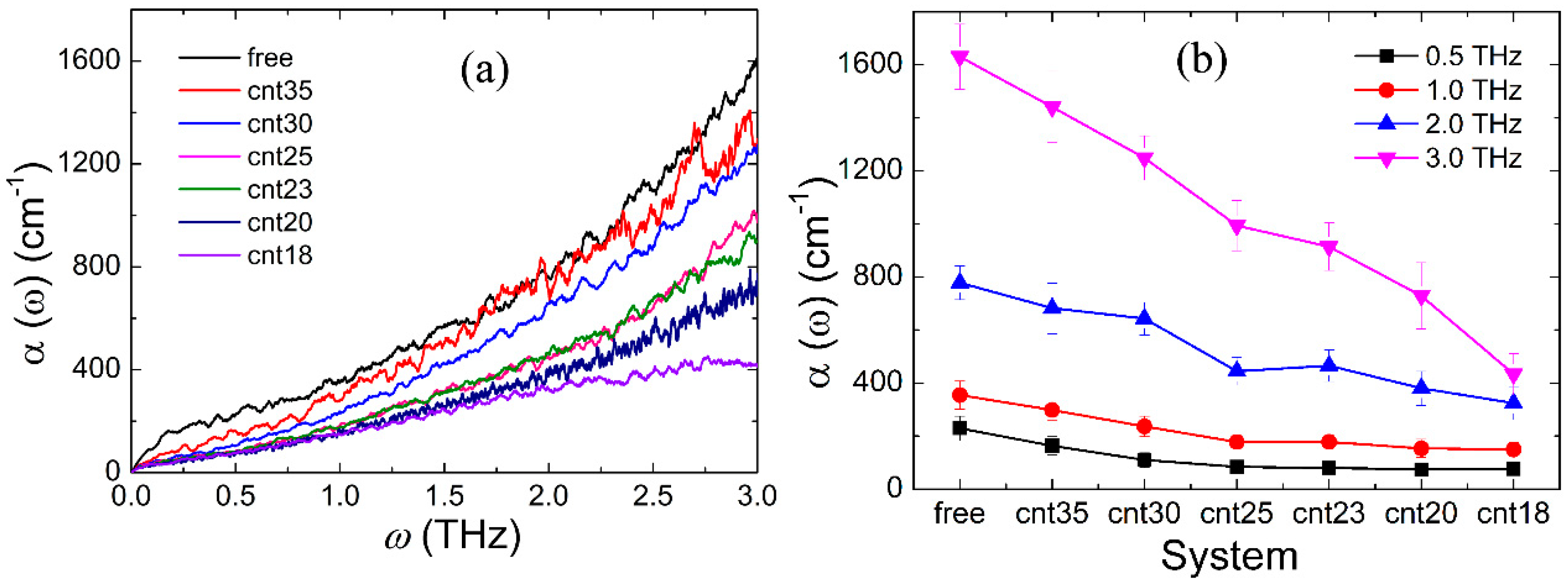
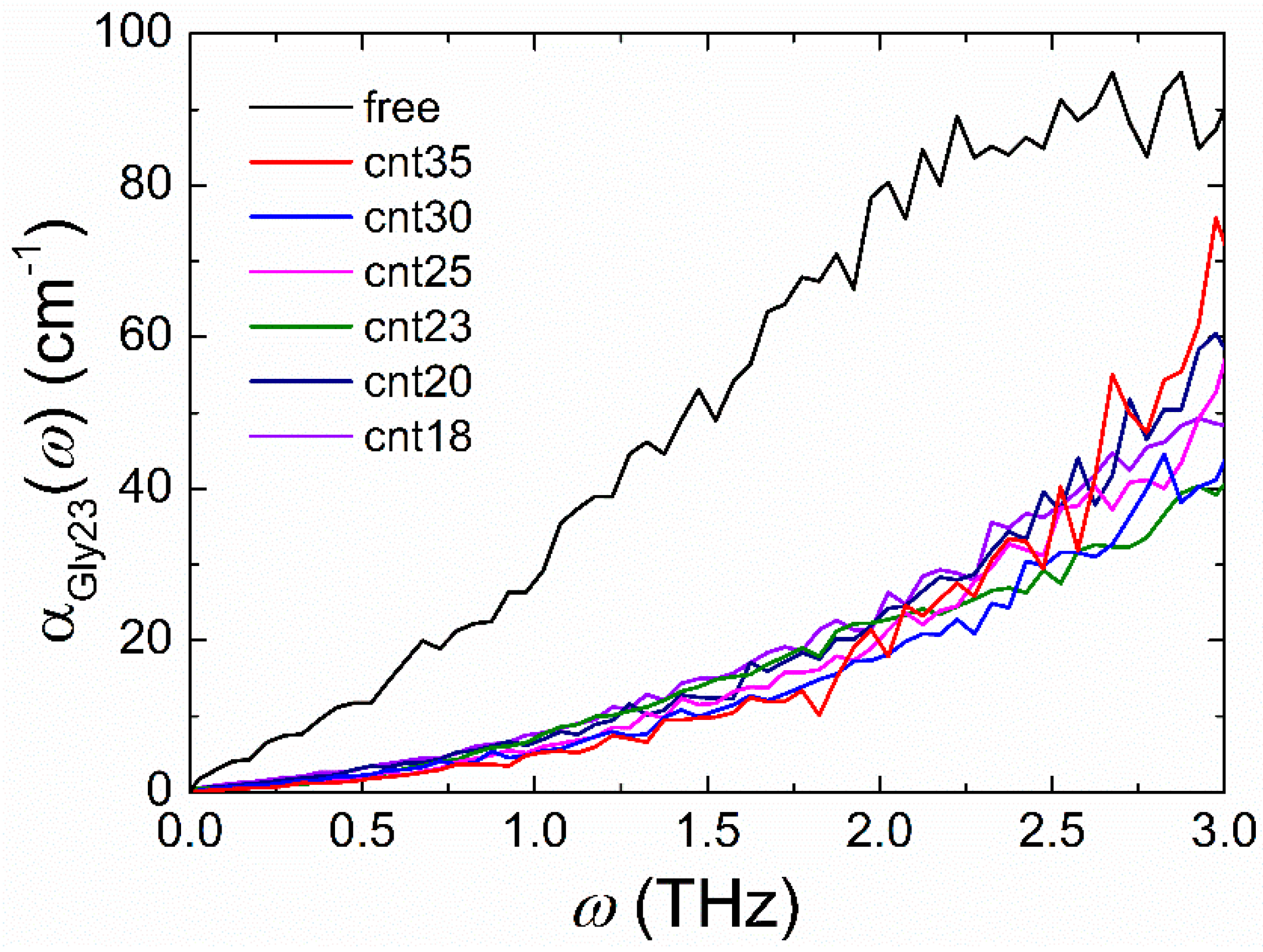
3.2. Confinement Effect on the Terahertz Absorption Spectrum of Gly23
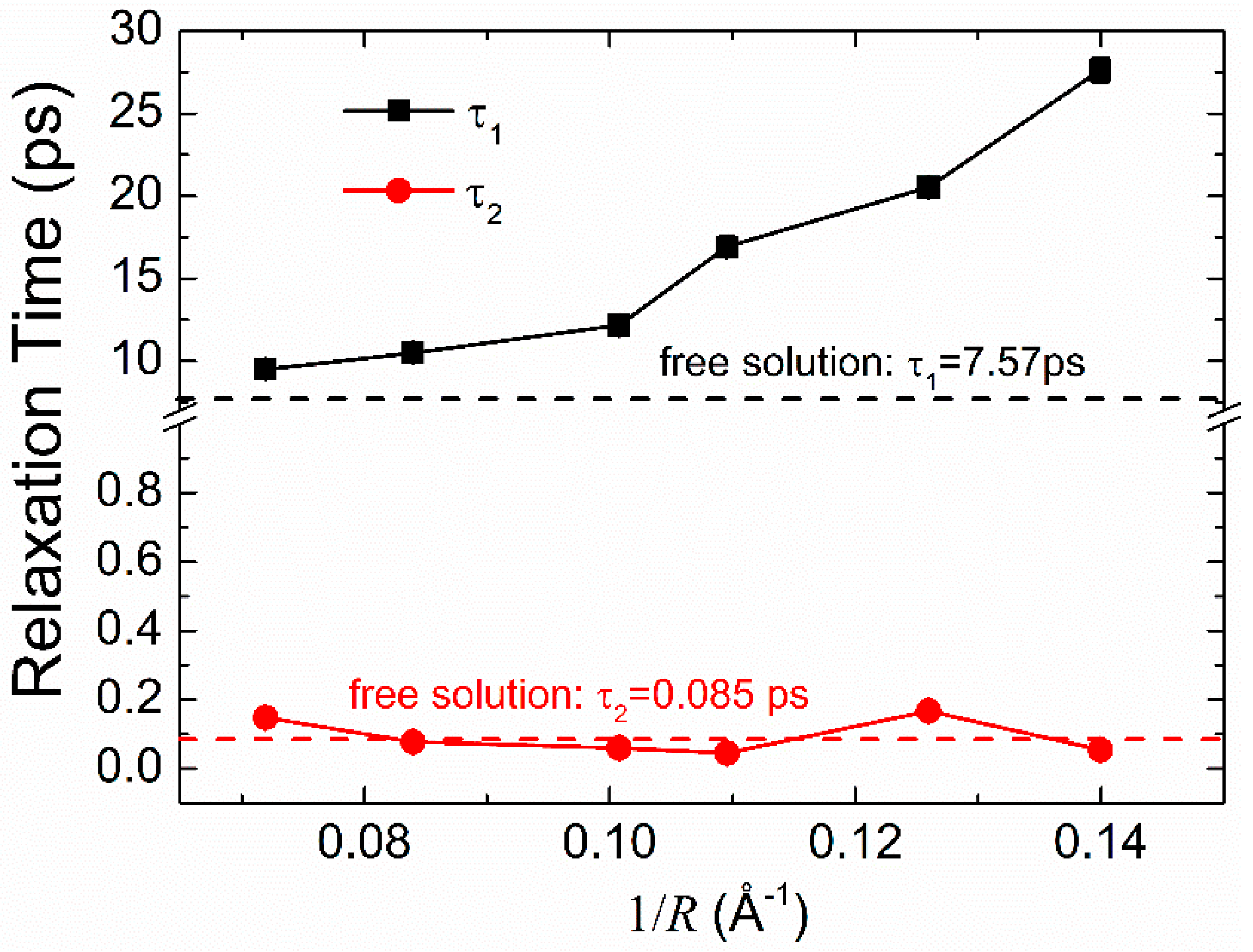
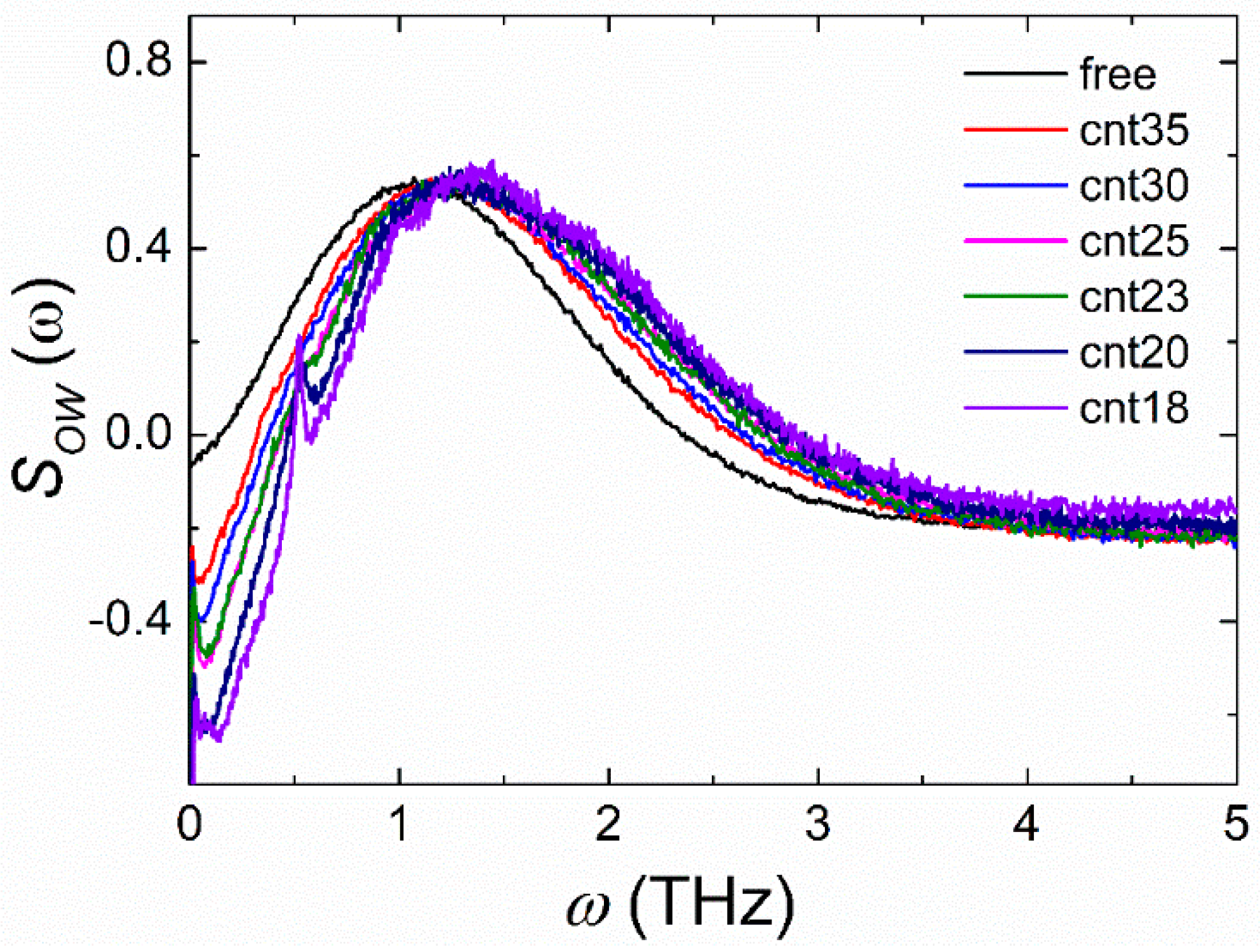
3.3. Dielectric Relaxation Dynamics of Water
3.4. Hydrogen Bond Dynamics
3.5. Vibration Density of States
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sakai, K.; Tani, M. Introduction to terahertz pulses. Terahertz Optoelectron. 2005, 97, 1–30. [Google Scholar]
- Leitner, D.M.; Havenith, M.; Gruebele, M. Biomolecule large-amplitude motion and solvation dynamics: Modelling and probes from THz to X-rays. Int. Rev. Phys. Chem. 2006, 25, 553–582. [Google Scholar] [CrossRef]
- Dexheimer, S.L. Terahertz Spectroscopy: Principles and Applications; Taylor & Francis: London, UK, 2007. [Google Scholar]
- Leitner, D.M.; Gruebele, M.; Havenith, M. Solvation dynamics of biomolecules: Modeling and terahertz experiments. HFSP J. 2008, 2, 314–323. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Markelz, A.G. Terahertz Dielectric Sensitivity to Biomolecular Structure and Function. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 180–190. [Google Scholar] [CrossRef]
- Zhang, W.; Brown, E.R.; Rahman, M.; Norton, M.L. Observation of terahertz absorption signatures in microliter DNA solutions. Appl. Phys. Lett. 2013, 102, 023701. [Google Scholar] [CrossRef]
- Sun, J.; Niehues, G.; Forbert, H.; Decka, D.; Schwaab, G.; Marx, D.; Havenith, M. Understanding THz Spectra of Aqueous Solutions: Glycine in Light and Heavy Water. J. Am. Chem. Soc. 2014, 136, 5031–5038. [Google Scholar] [CrossRef] [PubMed]
- George, P.A.; Hui, W.; Rana, F.; Hawkins, B.G.; Smith, A.E.; Kirby, B.J. Microfluidic devices for terahertz spectroscopy of biomolecules. Opt. Express 2008, 16, 1577–1582. [Google Scholar] [CrossRef] [PubMed]
- Brown, E.R.; Mendoza, E.A.; Xia, D.; Brueck, S.R.J. Narrow THz Spectral Signatures Through an RNA Solution in Nanofluidic Channels. IEEE Sens. J. 2010, 10, 755–759. [Google Scholar] [CrossRef] [Green Version]
- Brown, E.R.; Zhang, W.; Mendoza, E.A.; Kuznetsova, Y.; Brueck, S.R.J.; Rahman, M.; Norton, M.L. Concentration methods for high-resolution THz spectroscopy of nucleic-acid biomolecules and crystals. In Proceedings of the SPIE BiOS, San Francisco, CA, USA, 21–26 January 2012; p. 9. [Google Scholar]
- Xia, D.; Yan, J.; Hou, S. Fabrication of Nanofluidic Biochips with Nanochannels for Applications in DNA Analysis. Small 2012, 8, 2787–2801. [Google Scholar] [CrossRef] [PubMed]
- Douville, N.; Huh, D.; Takayama, S. DNA linearization through confinement in nanofluidic channels. Anal. Bioanal. Chem. 2008, 391, 2395–2409. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.-G.; Niu, H. Nanofluidic Channel Fabrication and Manipulation of DNA Molecules. In Micro and Nano Technologies in Bioanalysis: Methods and Protocols; Foote, R.S., Lee, J.W., Eds.; Humana Press: Totowa, NJ, USA, 2009; pp. 17–27. [Google Scholar]
- Odijk, T. The statistics and dynamics of confined or entangled stiff polymers. Macromolecules 1983, 16, 1340–1344. [Google Scholar] [CrossRef]
- Daoud, M.; De Gennes, P.-G. Statistics of macromolecular solutions trapped in small pores. J. Phys. (Paris) 1977, 38, 85. [Google Scholar] [CrossRef]
- Reisner, W.; Morton, K.J.; Riehn, R.; Wang, Y.M.; Yu, Z.; Rosen, M.; Sturm, J.C.; Chou, S.Y.; Frey, E.; Austin, R.H. Statics and Dynamics of Single DNA Molecules Confined in Nanochannels. Phys. Rev. Lett. 2005, 94, 196101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krivov, S.V.; Chekmarev, S.F.; Karplus, M. Potential Energy Surfaces and Conformational Transitions in Biomolecules: A Successive Confinement Approach Applied to a Solvated Tetrapeptide. Phys. Rev. Lett. 2002, 88, 038101. [Google Scholar] [CrossRef] [PubMed]
- Keten, S.; Xu, Z.; Ihle, B.; Buehler, M.J. Nanoconfinement controls stiffness, strength and mechanical toughness of β-sheet crystals in silk. Nat. Mater. 2010, 9, 359. [Google Scholar] [CrossRef] [PubMed]
- Brinker, A.; Pfeifer, G.; Kerner, M.J.; Naylor, D.J.; Hartl, F.U.; Hayer-Hartl, M. Dual Function of Protein Confinement in Chaperonin-Assisted Protein Folding. Cell 2001, 107, 223–233. [Google Scholar] [CrossRef] [Green Version]
- Konopka, M.C.; Shkel, I.A.; Cayley, S.; Record, M.T.; Weisshaar, J.C. Crowding and Confinement Effects on Protein Diffusion In Vivo. J. Bacteriol. 2006, 188, 6115–6123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roosen-Runge, F.; Hennig, M.; Zhang, F.; Jacobs, R.M.J.; Sztucki, M.; Schober, H.; Seydel, T.; Schreiber, F. Protein self-diffusion in crowded solutions. Proc. Natl. Acad. Sci. USA 2011, 108, 11815–11820. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.-Q.; Cheung, M.S. Manipulating Biopolymer Dynamics by Anisotropic Nanoconfinement. Nano Lett. 2007, 7, 3438–3442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lucent, D.; Vishal, V.; Pande, V.S. Protein folding under confinement: A role for solvent. Proc. Natl. Acad. Sci. USA 2007, 104, 10430–10434. [Google Scholar] [CrossRef] [PubMed]
- Rasaiah, J.C.; Garde, S.; Hummer, G. Water in Nonpolar Confinement: From Nanotubes to Proteins and Beyond. Annu. Rev. Phys. Chem. 2008, 59, 713–740. [Google Scholar] [CrossRef] [PubMed]
- Andrea, M.; Scott, W.; Jay, H.; Robert, B. THz time domain spectroscopy of biomolecular conformational modes. Phys. Med. Biol. 2002, 47, 3797. [Google Scholar]
- Zhang, M.; Wei, D.; Tang, M.; Shi, C.; Cui, H.-l.; Du, C. Molecular dynamics simulations of conformation and chain length dependent terahertz spectra of alanine polypeptides. Mol. Simul. 2016, 42, 398–404. [Google Scholar] [CrossRef]
- Sushko, O.; Dubrovka, R.; Donnan, R.S. Terahertz Spectral Domain Computational Analysis of Hydration Shell of Proteins with Increasingly Complex Tertiary Structure. J. Phys. Chem. B 2013, 117, 16486–16492. [Google Scholar] [CrossRef] [PubMed]
- Globus, T.; Khromova, T.; Lobo, R.; Woolard, D.; Swami, N.; Fernandez, E. THz characterization of lysozyme at different conformation. In Proceedings of the SPIE 5790, Terahertz for Military and Security Applications III, Orlando, FL, USA, 28 March–1 April 2005. [Google Scholar]
- Heyden, M.; Tobias, D.J. Spatial Dependence of Protein-Water Collective Hydrogen-Bond Dynamics. Phys. Rev. Lett. 2013, 111, 218101. [Google Scholar] [CrossRef] [PubMed]
- Born, B.; Weingärtner, H.; Bründermann, E.; Havenith, M. Solvation Dynamics of Model Peptides Probed by Terahertz Spectroscopy. Observation of the Onset of Collective Network Motions. J. Am. Chem. Soc. 2009, 131, 3752–3755. [Google Scholar] [CrossRef] [PubMed]
- Ebbinghaus, S.; Kim, S.J.; Heyden, M.; Yu, X.; Heugen, U.; Gruebele, M.; Leitner, D.M.; Havenith, M. An extended dynamical hydration shell around proteins. Proc. Natl. Acad. Sci. USA 2007, 104, 20749–20752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bye, J.W.; Meliga, S.; Ferachou, D.; Cinque, G.; Zeitler, J.A.; Falconer, R.J. Analysis of the Hydration Water around Bovine Serum Albumin Using Terahertz Coherent Synchrotron Radiation. J. Phys. Chem. A 2014, 118, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Heyden, M.; Sun, J.; Funkner, S.; Mathias, G.; Forbert, H.; Havenith, M.; Marx, D. Dissecting the THz spectrum of liquid water from first principles via correlations in time and space. Proc. Natl. Acad. Sci. USA 2010, 107, 12068–12073. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M.C.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003, 24, 1999–2012. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Song, Y.; Wang, F. A simple molecular mechanics potential for μm scale graphene simulations from the adaptive force matching method. J. Chem. Phys. 2011, 134, 184704. [Google Scholar] [CrossRef] [PubMed]
- Li, J.C.; Wang, F. Water graphene contact surface investigated by pairwise potentials from force-matching PAW-PBE with dispersion correction. J. Chem. Phys. 2017, 146, 054702. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.S.; Wang, F. Graphene: A partially ordered non-periodic solid. J. Chem. Phys. 2014, 141, 144701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, W.; Yong, C.W.; Rodger, P.M. DL_POLY: Application to molecular simulation. Mol. Simul. 2002, 28, 385–471. [Google Scholar] [CrossRef]
- Gam, S.; Meth, J.S.; Zane, S.G.; Chi, C.Z.; Wood, B.A.; Seitz, M.E.; Winey, K.I.; Clarke, N.; Composto, R.J. Macromolecular Diffusion in a Crowded Polymer Nanocomposite. Macromolecules 2011, 44, 3494–3501. [Google Scholar] [CrossRef]
- Chen, Y.-L.; Lin, Y.-H.; Chang, J.-F.; Lin, P.-K. Dynamics and Conformation of Semiflexible Polymers in Strong Quasi-1D and -2D Confinement. Macromolecules 2014, 47, 1199–1205. [Google Scholar] [CrossRef]
- Bonthuis, D.J.; Meyer, C.; Stein, D.; Dekker, C. Conformation and Dynamics of DNA Confined in Slitlike Nanofluidic Channels. Phys. Rev. Lett. 2008, 101, 108303. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Levy, S.L.; Trahan, D.W.; Jones, J.J.; Craighead, H.G.; Doyle, P.S. Revisiting the Conformation and Dynamics of DNA in Slitlike Confinement. Macromolecules 2010, 43, 7368–7377. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, M.; Wei, D.; Wang, Y.; Yan, S.; Liu, M.; Yang, X.; Yang, K.; Cui, H.-L.; Fu, W. Label-free sensing of the binding state of MUC1 peptide and anti-MUC1 aptamer solution in fluidic chip by terahertz spectroscopy. Biomed. Opt. Express 2017, 8, 4427–4437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, M.; Zhang, M.; Yan, S.; Xia, L.; Yang, Z.; Du, C.; Cui, H.-L.; Wei, D. Detection of DNA oligonucleotides with base mutations by terahertz spectroscopy and microstructures. PLoS ONE 2018, 13, e0191515. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Chang, T.; Wei, D.; Tang, M.; Yan, S.; Du, C.; Cui, H.-L. Label-free detection of anti-estrogen receptor alpha and its binding with estrogen receptor peptide alpha by terahertz spectroscopy. RSC Adv. 2017, 7, 24338–24344. [Google Scholar] [CrossRef] [Green Version]
- Flory, P.J. The Configuration of Real Polymer Chains. J. Chem. Phys. 1949, 17, 303–310. [Google Scholar] [CrossRef]
- Heyden, M.; Havenith, M. Combining THz spectroscopy and MD simulations to study protein-hydration coupling. Methods 2010, 52, 74–83. [Google Scholar] [CrossRef] [PubMed]
- Garg, S.K.; Smyth, C.P. Microwave Absorption and Molecular Structure in Liquids. LXVI. The Dielectric Relaxation of the Water—Dioxane System and the Structure of Water. J. Chem. Phys. 1965, 43, 2959–2965. [Google Scholar] [CrossRef]
- Schrödle, S.; Hefter, G.; Buchner, R. Dielectric Spectroscopy of Hydrogen Bond Dynamics and Microheterogenity of Water + Dioxane Mixtures. J. Phys. Chem. B 2007, 111, 5946–5955. [Google Scholar] [CrossRef] [PubMed]
- Venables, D.S.; Schmuttenmaer, C.A. Spectroscopy and dynamics of mixtures of water with acetone, acetonitrile, and methanol. J. Chem. Phys. 2000, 113, 11222–11236. [Google Scholar] [CrossRef]
- Luong, T.Q.; Verma, P.K.; Mitra, R.K.; Havenith, M. Onset of Hydrogen Bonded Collective Network of Water in 1,4-Dioxane. J. Phys. Chem. A 2011, 115, 14462–14469. [Google Scholar] [CrossRef] [PubMed]
- Fukasawa, T.; Sato, T.; Watanabe, J.; Hama, Y.; Kunz, W.; Buchner, R. Relation between Dielectric and Low-Frequency Raman Spectra of Hydrogen-Bond Liquids. Phys. Rev. Lett. 2005, 95, 197802. [Google Scholar] [CrossRef] [PubMed]
- Buchner, R.; Barthel, J.; Stauber, J. The dielectric relaxation of water between 0 °C and 35 °C. Chem. Phys. Lett. 1999, 306, 57–63. [Google Scholar] [CrossRef]
- Qi, W.; Chen, J.; Yang, J.; Lei, X.; Song, B.; Fang, H. Anisotropic Dielectric Relaxation of the Water Confined in Nanotubes for Terahertz Spectroscopy Studied by Molecular Dynamics Simulations. J. Phys. Chem. B 2013, 117, 7967–7971. [Google Scholar] [CrossRef] [PubMed]
- Rapaport, D.C. Hydrogen bonds in water. Mol. Phys. 1983, 50, 1151–1162. [Google Scholar] [CrossRef]
- Milischuk, A.A.; Ladanyi, B.M. Structure and dynamics of water confined in silica nanopores. J. Chem. Phys. 2011, 135, 174709. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Sinha, S.K.; Bandyopadhyay, S. Low-Frequency Vibrational Spectrum of Water in the Hydration Layer of a Protein: A Molecular Dynamics Simulation Study. J. Phys. Chem. B 2007, 111, 13626–13631. [Google Scholar] [CrossRef] [PubMed]
- Niehues, G.; Heyden, M.; Schmidt, D.A.; Havenith, M. Exploring hydrophobicity by THz absorption spectroscopy of solvated amino acids. Faraday Discuss. 2011, 150, 193–207. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, D.; Zhang, M.; Song, J.; Wei, D. Calculated Terahertz Spectra of Glycine Oligopeptide Solutions Confined in Carbon Nanotubes. Polymers 2019, 11, 385. https://doi.org/10.3390/polym11020385
Ling D, Zhang M, Song J, Wei D. Calculated Terahertz Spectra of Glycine Oligopeptide Solutions Confined in Carbon Nanotubes. Polymers. 2019; 11(2):385. https://doi.org/10.3390/polym11020385
Chicago/Turabian StyleLing, Dongxiong, Mingkun Zhang, Jianxun Song, and Dongshan Wei. 2019. "Calculated Terahertz Spectra of Glycine Oligopeptide Solutions Confined in Carbon Nanotubes" Polymers 11, no. 2: 385. https://doi.org/10.3390/polym11020385
APA StyleLing, D., Zhang, M., Song, J., & Wei, D. (2019). Calculated Terahertz Spectra of Glycine Oligopeptide Solutions Confined in Carbon Nanotubes. Polymers, 11(2), 385. https://doi.org/10.3390/polym11020385