Direct Numerical Simulation of Gas-Liquid Drag-Reducing Cavity Flow by the VOSET Method
Abstract
1. Introduction
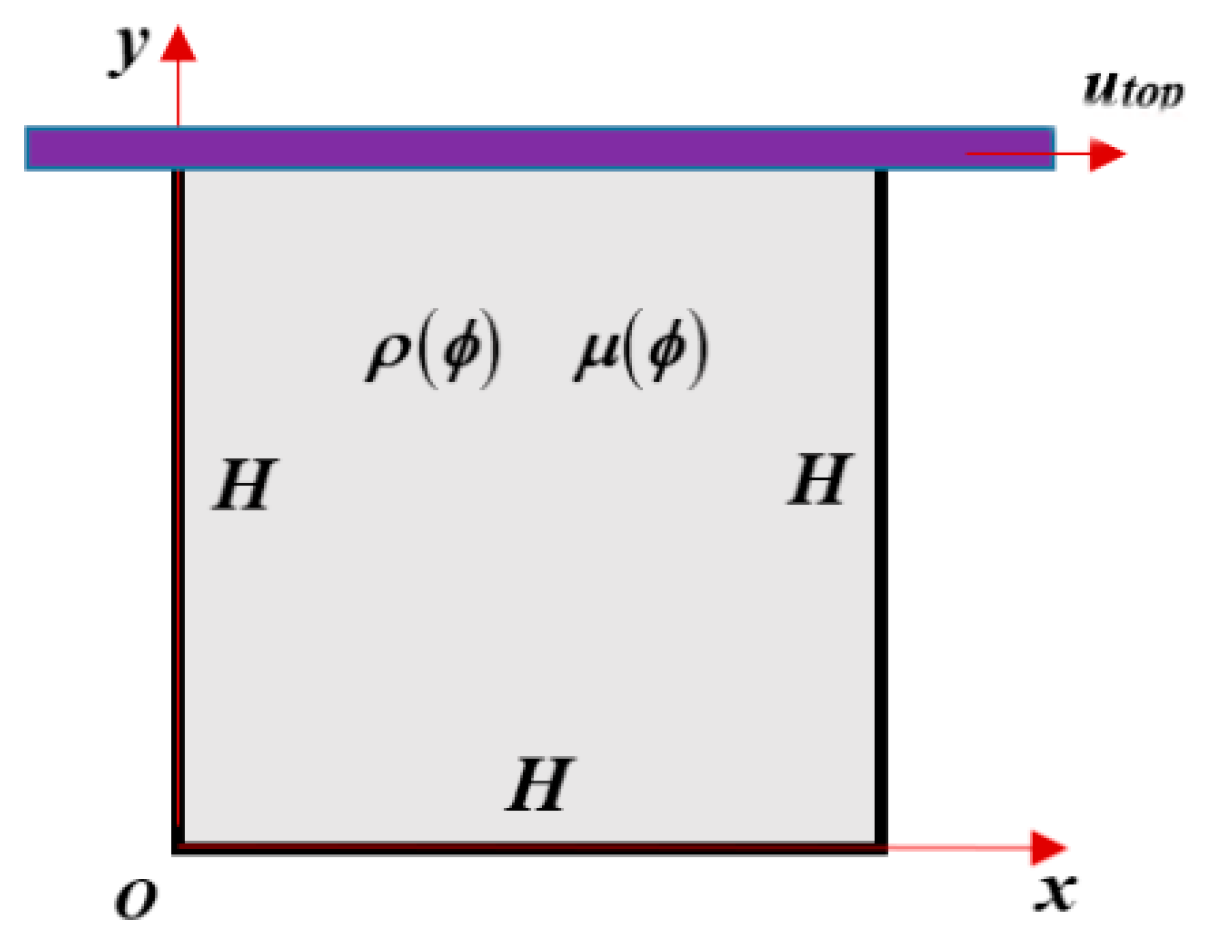
2. Governing Equations
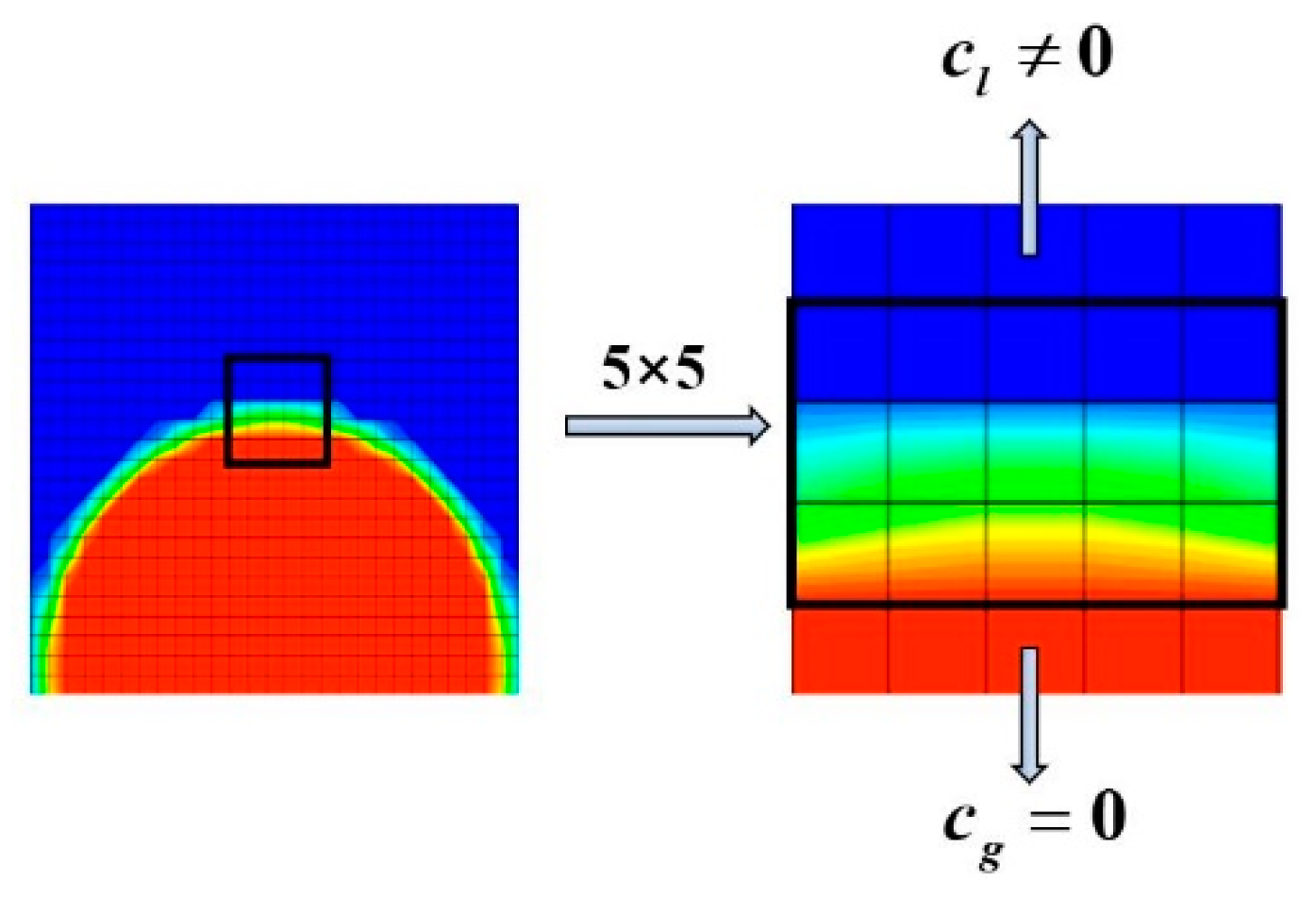
3. Numerical Methods
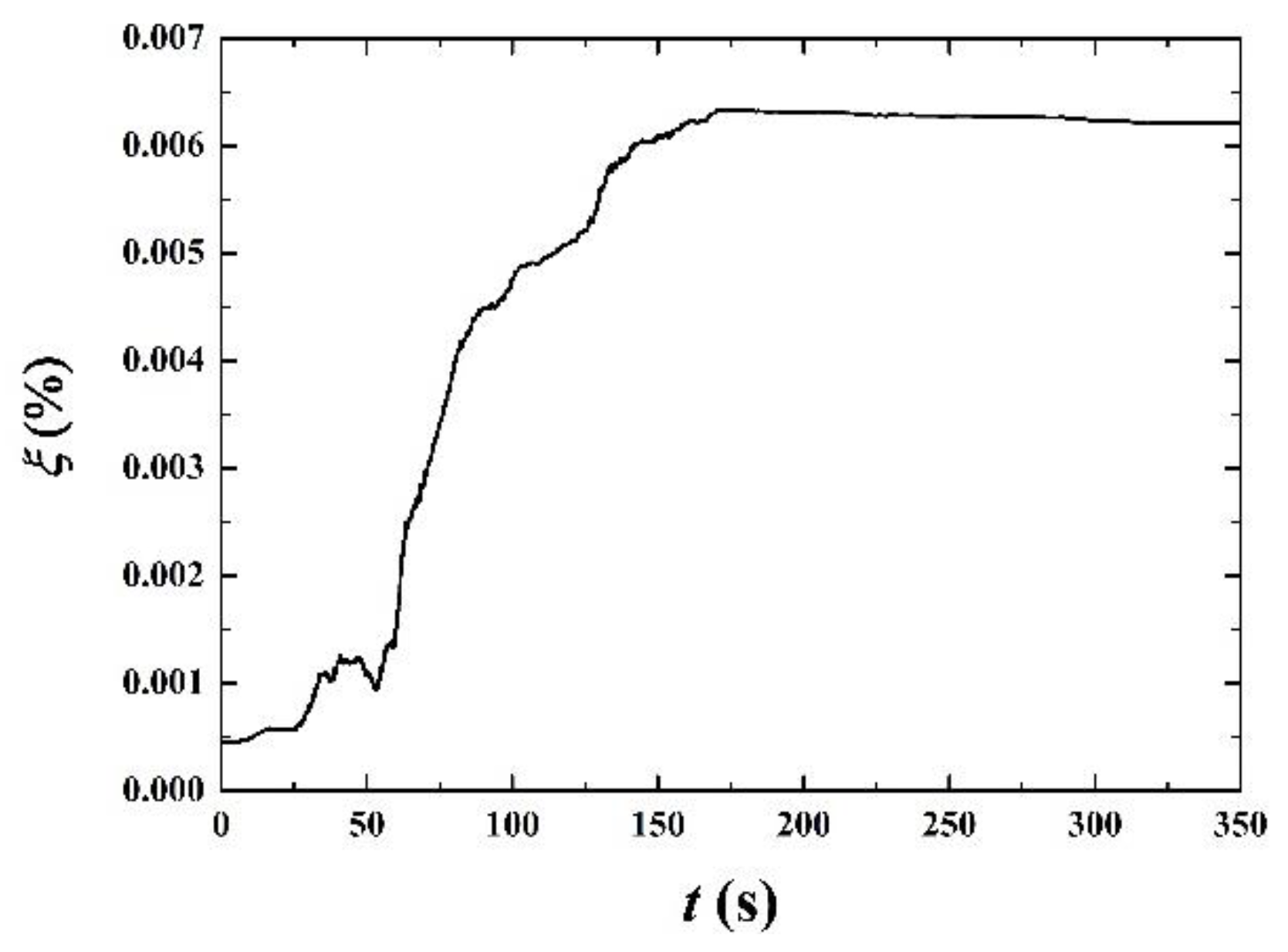
4. Results and Discussion
5. Conclusions
- (1)
- DNS of the polymeric drag reduction for gas-liquid turbulent flow is practical. Conformation tensor induced by the polymer should be smoothed near the two-phase interface to greatly enhance the numerical stability thus that the DNS can be made at much wider scopes of parameters. This is the first helpful attempt for the DNS of two-phase gas-liquid drag-reducing flow.
- (2)
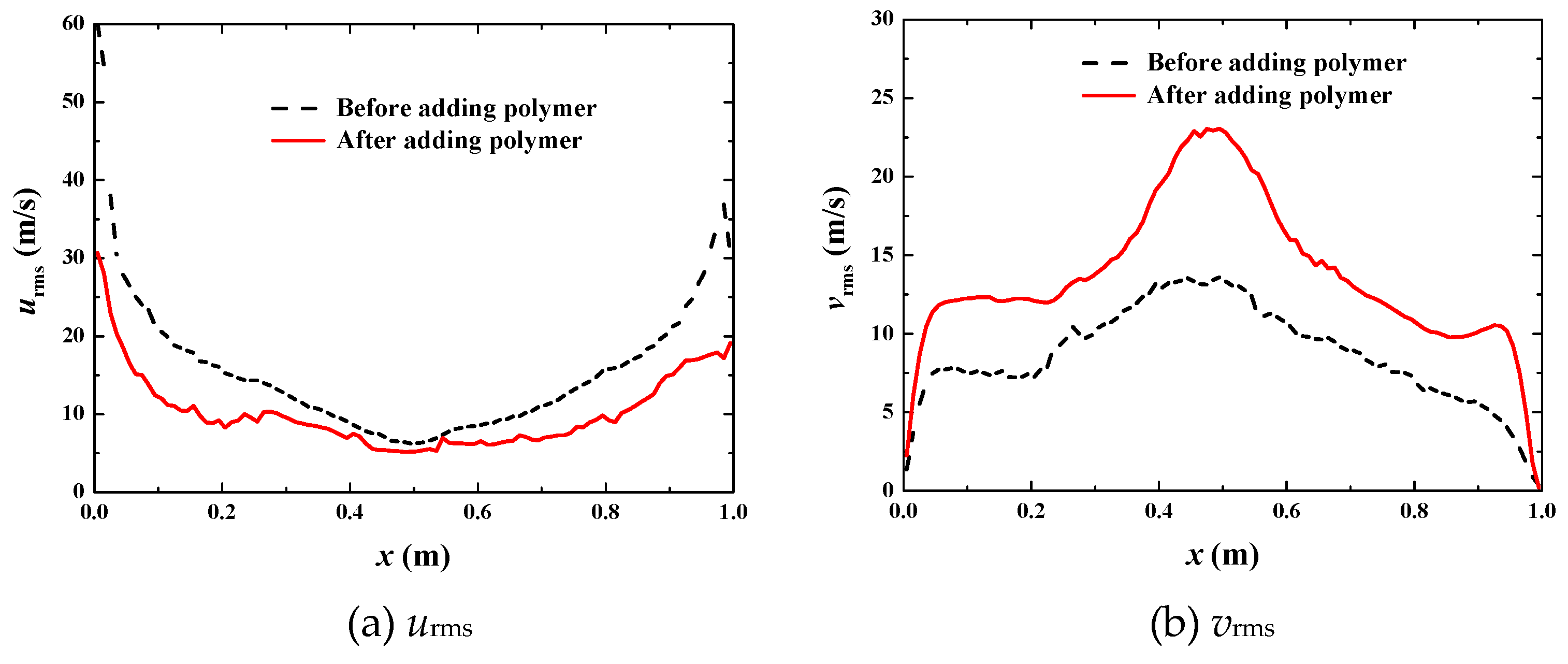
- The drag reduction mechanism of gas-liquid drag-reducing flow can be the global suppression of turbulent fluctuations. This is the same as a single-phase drag-reducing flow. The mechanism can also be due to local enhancement in the core region with local suppression near the walls of turbulent fluctuations. This is the special feature of gas-liquid drag-reducing flow.
- (3)
- High shear of flow depresses the efficiency of the gas-liquid drag reduction, while a high concentration of polymer promotes the efficiency. To guarantee efficient drag reduction, it is better to use a high concentration of polymer DRAs.
Author Contributions
Funding
Conflicts of Interest
Appendix A
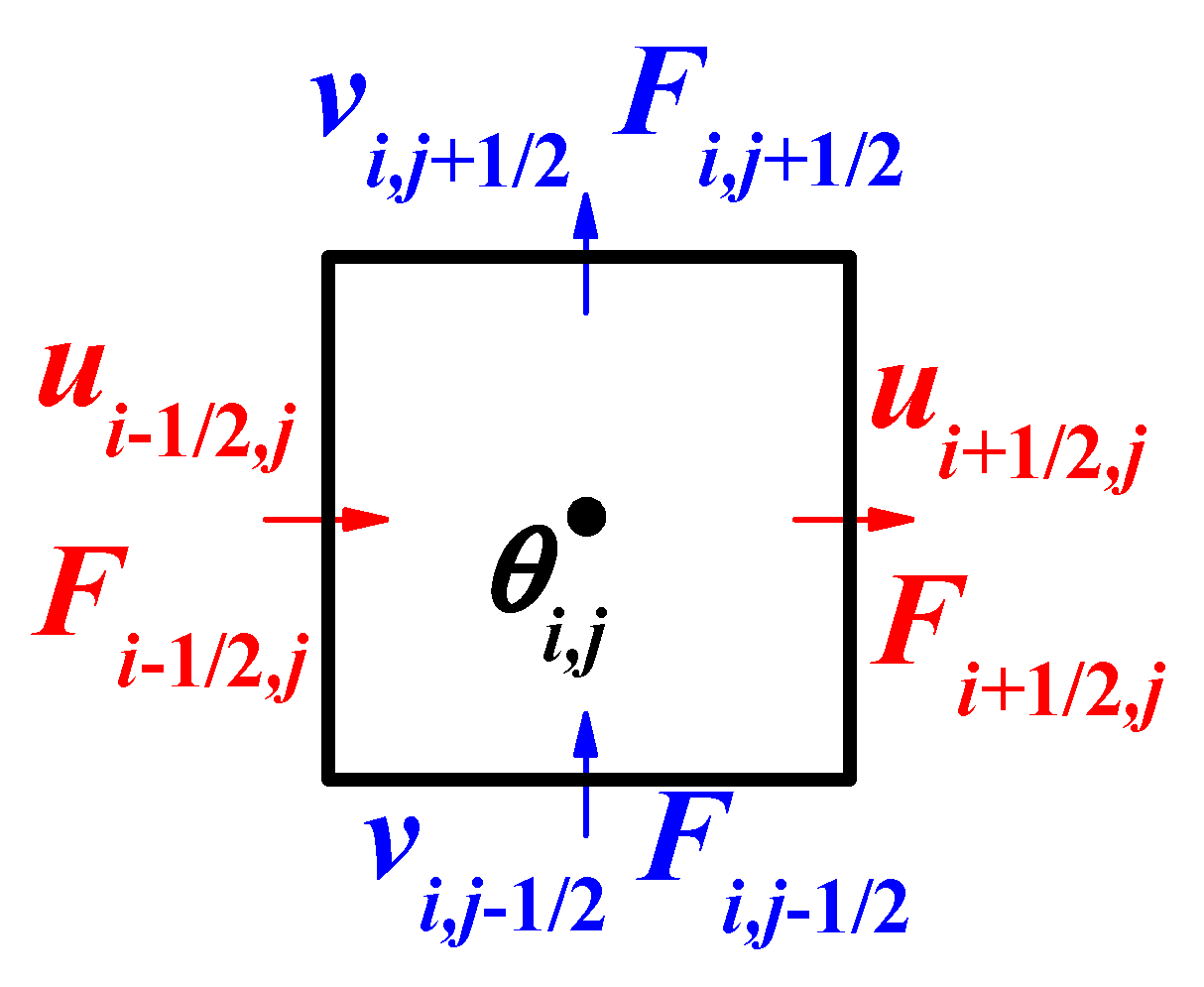

References
- Toms, B.A. Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proceedings of the International Congress on Rheology, Scheveningen, The Netherlands, 21–24 September 1948. [Google Scholar]
- Savins, J.G. Drag reductions characteristics of solutions of macromolecules in turbulent pipe flow. SPE J. 1964, 4, 203. [Google Scholar] [CrossRef]
- Burger, E.D.; Munk, W.R.; Wahl, H.A. Flow increase in the Trans Alaska Pipeline through use of a polymeric drag reducing additive. J. Petrol. Technol. 1982, 34, 377–386. [Google Scholar] [CrossRef]
- Virk, P.S. The effect of polymer concentration on drag reduction. Chem. Eng. Sci. 1970, 25, 1183–1189. [Google Scholar] [CrossRef]
- Warholic, M.D.; Massah, H.; Hanratty, T.J. Influence of drag-reducing polymers on turbulence: Effects of Reynolds number, concentration and mixing. Exp. Fluids 1999, 27, 461–472. [Google Scholar] [CrossRef]
- Housiadas, K.D.; Beris, A.N. Polymer-induced drag reduction: Effects of the variations in elasticity and inertia in turbulent viscoelastic channel flow. Phys. Fluids 2003, 15, 2369–2384. [Google Scholar] [CrossRef]
- Li, C.F.; Sureshkumar, R.; Khomami, B. Influence of rheological parameters on polymer induced turbulent drag reduction. J. Nonnewton. Fluid Mech. 2006, 140, 23–40. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, B.; Wu, X.; Wang, P. POD and wavelet analyses on the flow structures of a polymer drag-reducing flow based on DNS data. Int. J. Heat Mass Transf. 2012, 55, 4849–4861. [Google Scholar] [CrossRef]
- Cai, W.H.; Wei, T.Z.; Tang, X.J.; Liu, Y.; Li, B.; Li, F.C. The polymer effect on turbulent Rayleigh-Bénard convection based on PIV experiments. Exp. Therm. Fluid Sci. 2019, 103, 214–221. [Google Scholar] [CrossRef]
- Chen, J.P.; Zhang, H.N.; Cai, W.H.; Li, S.N.; Li, F.C. Effect of polymer additives on heat transport and large-scale circulation in turbulent Rayleigh-Bénard convection. Phys. Rev. E 2017, 96, 013111. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Cai, W.H.; Zheng, X.; Zhang, H.N.; Wang, L.; Li, F.C. Experimental study on two-oscillating grid turbulence with viscoelastic fluids based on PIV. Can. J. Phys. 2017, 95, 1271–1277. [Google Scholar] [CrossRef]
- Liu, L. A new method for evaluating drag reduction in gas-liquid two-phase flow based on energy dissipation. Chem. Eng. Sci. 2013, 95, 54–64. [Google Scholar] [CrossRef]
- Oliver, D.R.; Young, H.A. Two-phase non-Newtonian flow. Trans. Inst. Chem. Eng. 1968, 46, T106. [Google Scholar]
- Greskovich, E.J.; Shrier, A.L. Drag reduction in two-phase flows. Ind. Eng. Chem. Fundam. 1971, 10, 646–648. [Google Scholar] [CrossRef]
- Sylvester, N.D.; Brill, J.P. Drag-reduction in two-phase annular mist flow of air and water. AIChE J. 1976, 22, 615–617. [Google Scholar] [CrossRef]
- Kang, C.; Jepson, W.P. Multiphase flow conditioning using drag-reducing agents. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999. [Google Scholar]
- Kang, C.; Jepson, W.P. Effect of drag-reducing agents in multiphase oil/gas horizontal flow. In Proceedings of the SPE International Petroleum Conference and Exhibition in Mexico, Villahermosa, Mexico, 1–3 February 2000. [Google Scholar]
- Daas, M.; Kang, C.; Jepson, W.P. Quantitative analysis of drag reduction in horizontal slug flow. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Kang, C.; Jepson, W.P.; Gopal, M. Effect of drag-reducing agent on slug characteristics in multiphase flow in inclined pipes. J. Energy Resour. Technol. 1999, 121, 86–90. [Google Scholar] [CrossRef]
- Al-Sarkhi, A.; Hanratty, T.J. Effect of drag-reducing polymer on annular gas-liquid flow in a horizontal pipe. Int. J. Multiph. Flow 2001, 27, 1151–1162. [Google Scholar] [CrossRef]
- Soleimani, A.; Al-Sarkhi, A.; Hanratty, T.J. Effect of drag reducing polymers on pseudo-slugs-interfacial drag and transition to slug flow. Int. J. Multiph. Flow 2002, 28, 1911–1927. [Google Scholar] [CrossRef]
- Al-Sarkhi, A.; Soleimani, A. Effect of drag reducing polymers on two-phase gas-liquid flows in a horizontal pipe. Chem. Eng. Res. Des. 2004, 82, 1583–1588. [Google Scholar] [CrossRef]
- Pouranfard, A.R.; Mowla, D.; Esmaeilzadeh, F. An experimental study of drag reduction by nanofluids in slug two-phase flow of air and water through horizontal pipes. Chin. J. Chem. Eng. 2015, 23, 471–475. [Google Scholar] [CrossRef]
- Alsurakji, I.H.; Al-Sarkhi, A.; Habib, M.; Badr, H.M. An experimental study on the performance of drag-reducing polymers in single- and multiphase horizontal flow using particle image velocimetry. J. Energy Resour. Technol. 2018, 140, 052005. [Google Scholar] [CrossRef]
- Nesyn, G.V.; Sunagatullin, R.Z.; Shibaev, V.P.; Malkin, A.Y. Drag reduction in transportation of hydrocarbon liquids: From fundamentals to engineering applications. J. Petrol. Sci. Eng. 2018, 161, 715–725. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Noh, W.F.; Woodward, P. SLIC (simple line interface calculation). Lect. Notes Phys. 1976, 59, 273–285. [Google Scholar]
- Youngs, D.L. Time-dependent multi-material flow with large fluid distortion. In Numerical Methods in Fluid Dynamics; Morton, K.W., Baines, M.J., Eds.; Academic Press: New York, NY, USA, 1982; pp. 273–285. [Google Scholar]
- Ashgriz, N.; Poo, J.Y. FLAIR: Flux line-segment model for advection and interface reconstruction. J. Comput. Phys. 1991, 93, 449–468. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Gomez, P.; Hernandez, J.; Lopez, J. On the reinitialization procedure in a narrow band locally refined level set method for interfacial flows. Int. J. Numer. Meth. Eng. 2005, 63, 1478–1512. [Google Scholar] [CrossRef]
- Sussman, M.; Fatemi, E.; Smereka, P. An improved level set method for incompressible two-phase flows. Comput. Fluids 1997, 27, 663–680. [Google Scholar] [CrossRef]
- Nourgaliev, R.R.; Wiri, S.; Dinh, N.T. On improving mass conservation of level set by reducing spatial discretization errors. Int. J. Multiph. Flow 2005, 31, 1329–1336. [Google Scholar] [CrossRef]
- Sethian, J.A. Fast marching methods. SIAM Rev. 1999, 41, 199–235. [Google Scholar] [CrossRef]
- Moghadam, A.M.; Shafieefar, M.; Panahi, R. Development of a high-order level set method: Compact conservative level set (CCLS). Comput. Fluids 2016, 129, 79–90. [Google Scholar] [CrossRef]
- Shao, C.X.; Luo, K.; Song, C. A mass conserving level set method for simulation of liquid atomization. J. Eng. Thermophys. 2015, 298, 495–519. [Google Scholar]
- Sun, D.L.; Tao, W.Q. A coupled volume-of-fluid and level set (VOSET) method for computing incompressible two-phase flows. Int. J. Heat Mass Transf. 2010, 53, 645–655. [Google Scholar] [CrossRef]
- Ahn, J.; Na, S.J. Three-dimensional thermal simulation of nanosecond laser ablation for semitransparent material. Appl. Surf. Sci. 2013, 283, 115–127. [Google Scholar] [CrossRef]
- Chiu, P.H.; Lin, Y.T. A conservative phase field method for solving incompressible two-phase flows. J. Comput. Phys. 2011, 230, 185–204. [Google Scholar] [CrossRef]
- Ansari, M.R.; Azadi, R.; Salimi, E. Capturing of interface topological changes in two-phase gas–liquid flows using a coupled volume-of-fluid and level-set method (VOSET). Comput. Fluids 2016, 125, 82–100. [Google Scholar] [CrossRef]
- Wang, T.; Li, H.; Feng, Y. A coupled volume-of-fluid and level set (VOSET) method on dynamically adaptive quadtree grids. Int. J. Heat Mass Transf. 2013, 67, 70–73. [Google Scholar] [CrossRef]
- Cao, Z.; Sun, D.L.; Yu, B. A coupled volume-of-fluid and level set (VOSET) method based on remapping algorithm for unstructured triangular grids. Int. J. Heat Mass Transf. 2017, 111, 232–245. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, B.; Wei, J.J.; Li, F.C.; Kawaguchi, Y. Direct numerical simulation on drag-reducing flow by polymer additives using a spring-dumbbell model. Progr. Comput. Fluid Dyn. 2009, 9, 217–224. [Google Scholar] [CrossRef]
- Yu, B.; Kawaguchi, Y. Direct numerical simulation of viscoelastic drag-reducing flow—A faithful finite-difference method. J. Nonnewton. Fluid Mech. 2004, 116, 431–466. [Google Scholar] [CrossRef]
- Cai, W.H.; Li, F.C.; Zhang, H.N. DNS study of decaying homogeneous isotropic turbulence with polymer additives. J. Fluid Mech. 2010, 665, 334–356. [Google Scholar] [CrossRef]
- Li, F.C.; Cai, W.H.; Zhang, H.N. Influence of polymer additives on turbulent energy cascading in forced homogeneous isotropic turbulence studied by DNS. Chin. Phys. B 2012, 21, 114701. [Google Scholar] [CrossRef]
- Cai, W.H.; Li, F.C.; Zhang, H.N.; Wang, Y.; Wang, L. Analysis of coherent structures in drag-reducing polymer solution flow based on proper orthogonal decomposition. Sci. China E 2012, 55, 854–860. [Google Scholar] [CrossRef]
- Sun, D.L.; Qu, Z.G.; He, Y.L. An efficient segregated algorithm for incompressible fluid flow and heat transfer problems-IDEAL (inner doubly iterative efficient algorithm for linked equations) part I: Mathematical formulation and solution procedure. Numer. Heat Transf. B Fundam. 2008, 53, 1–17. [Google Scholar] [CrossRef]
- Mirzakhanlari, S.; Shirvan, K.M.; Mamourian, M.; Chamkh, A.J. Increment of mixed convection heat transfer and decrement of drag coefficient in a lid-driven nanofluid-filled cavity with a conductive rotating circular cylinder at different horizontal locations: A sensitivity analysis. Powder Technol. 2017, 305, 495–508. [Google Scholar] [CrossRef]
- Alinia, M.; Ganji, D.D.; Gorji-Bandpy, M. Numerical study of mixed convection in an inclined two sided lid driven cavity filled with nanofluid using two-phase mixture model. Int. Commun. Heat Mass Transf. 2011, 38, 1428–1435. [Google Scholar] [CrossRef]
- Alsbery, A.I.; Ismael, M.A.; Chamkha, A.J.; Hashim, I. Mixed convection of Al2O3-water nanofluid in a double lid-driven square cavity with a solid inner insert using Buongiorno’s two-phase model. Int. J. Heat Mass Transf. 2018, 119, 939–961. [Google Scholar] [CrossRef]
- Kefayati, G.H.R. Mixed convection of non-Newtonian nanofluid in an enclosure using Buongiorno’s mathematical model. Int. J. Heat Mass Transf. 2017, 108, 1481–1500. [Google Scholar] [CrossRef]
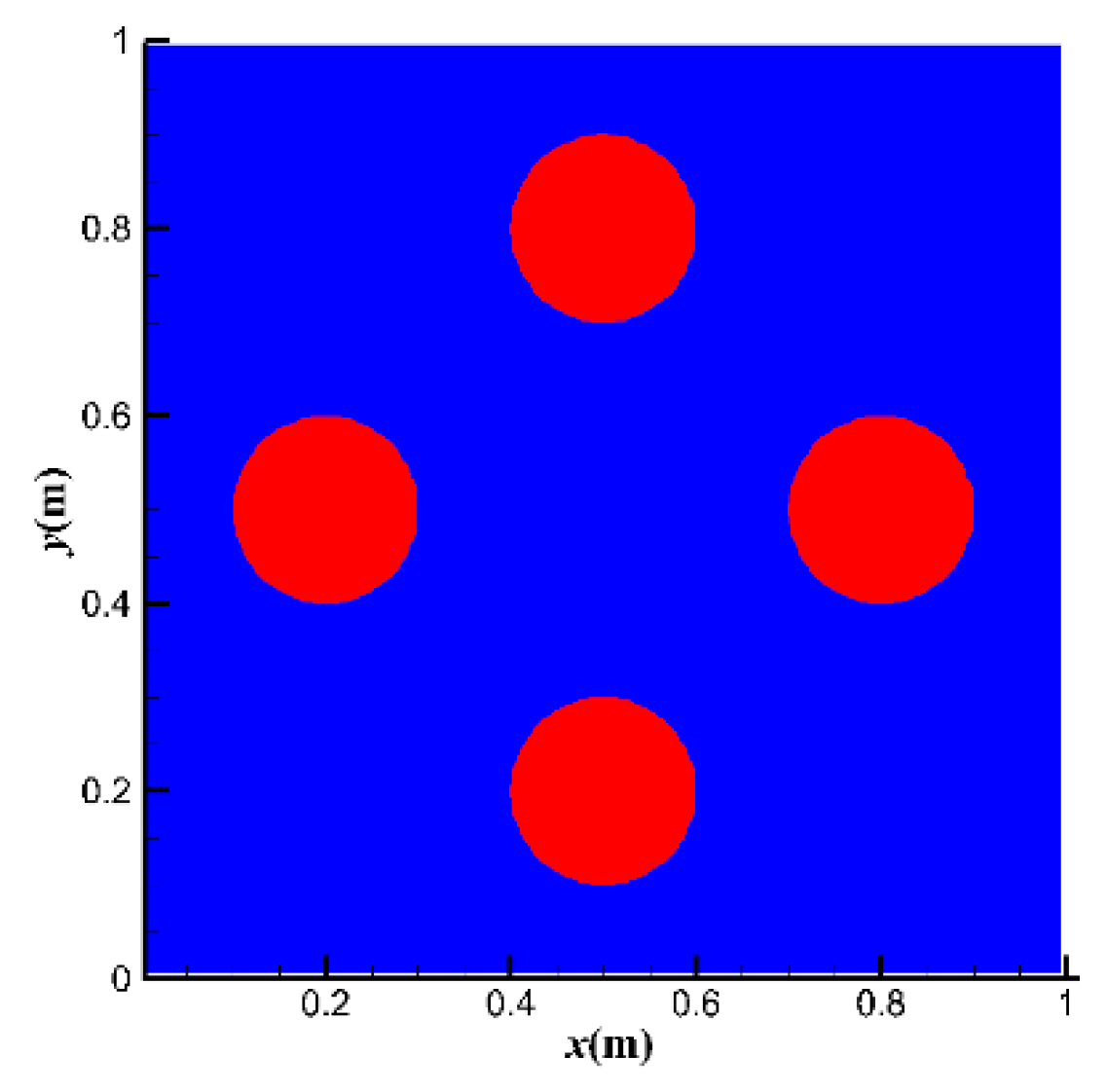
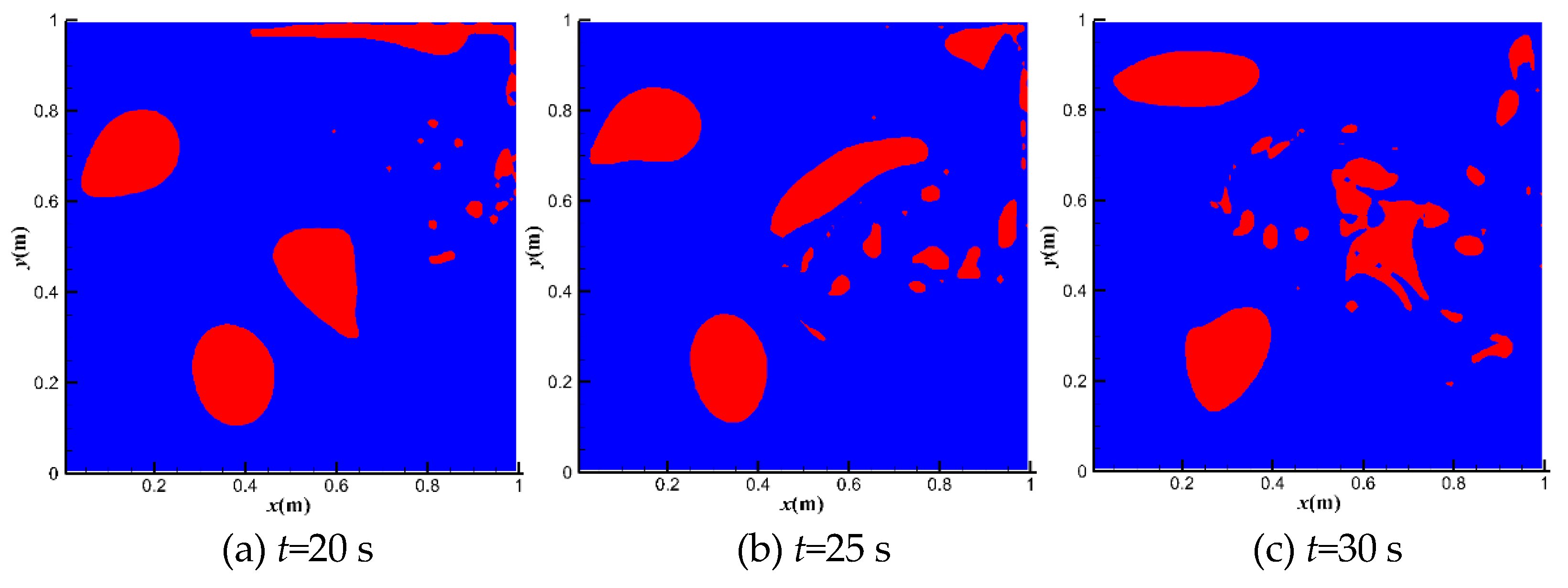
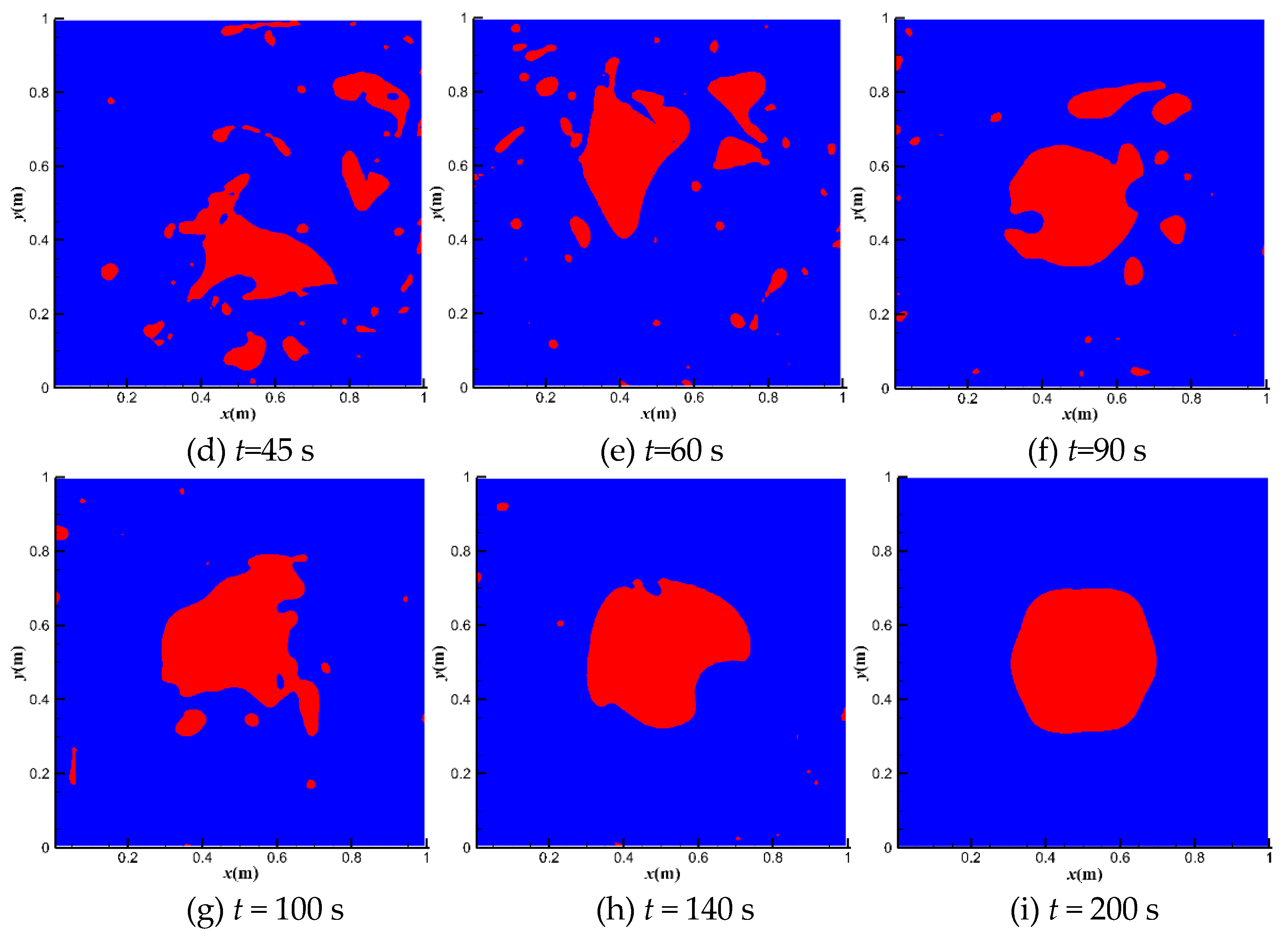


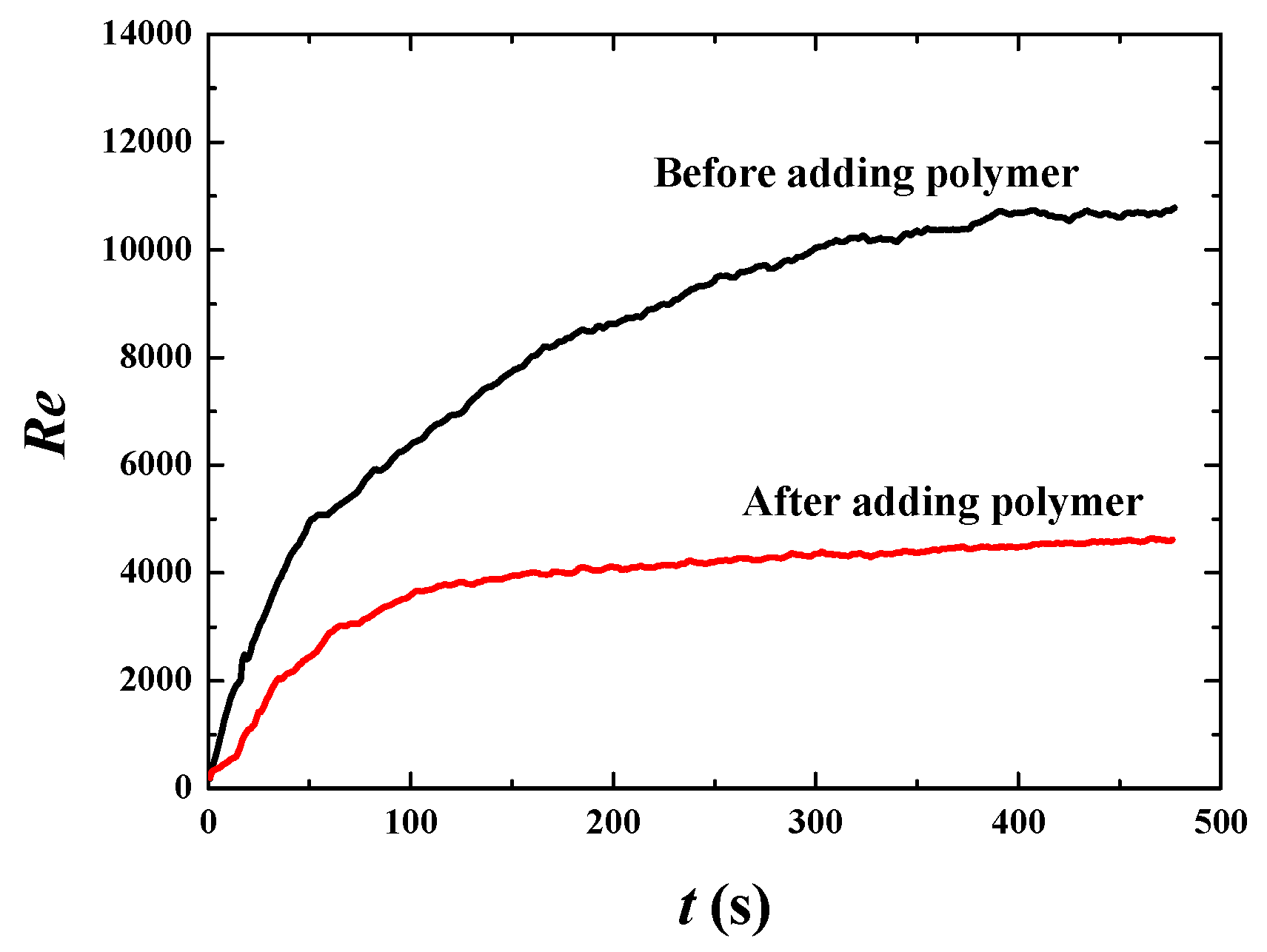

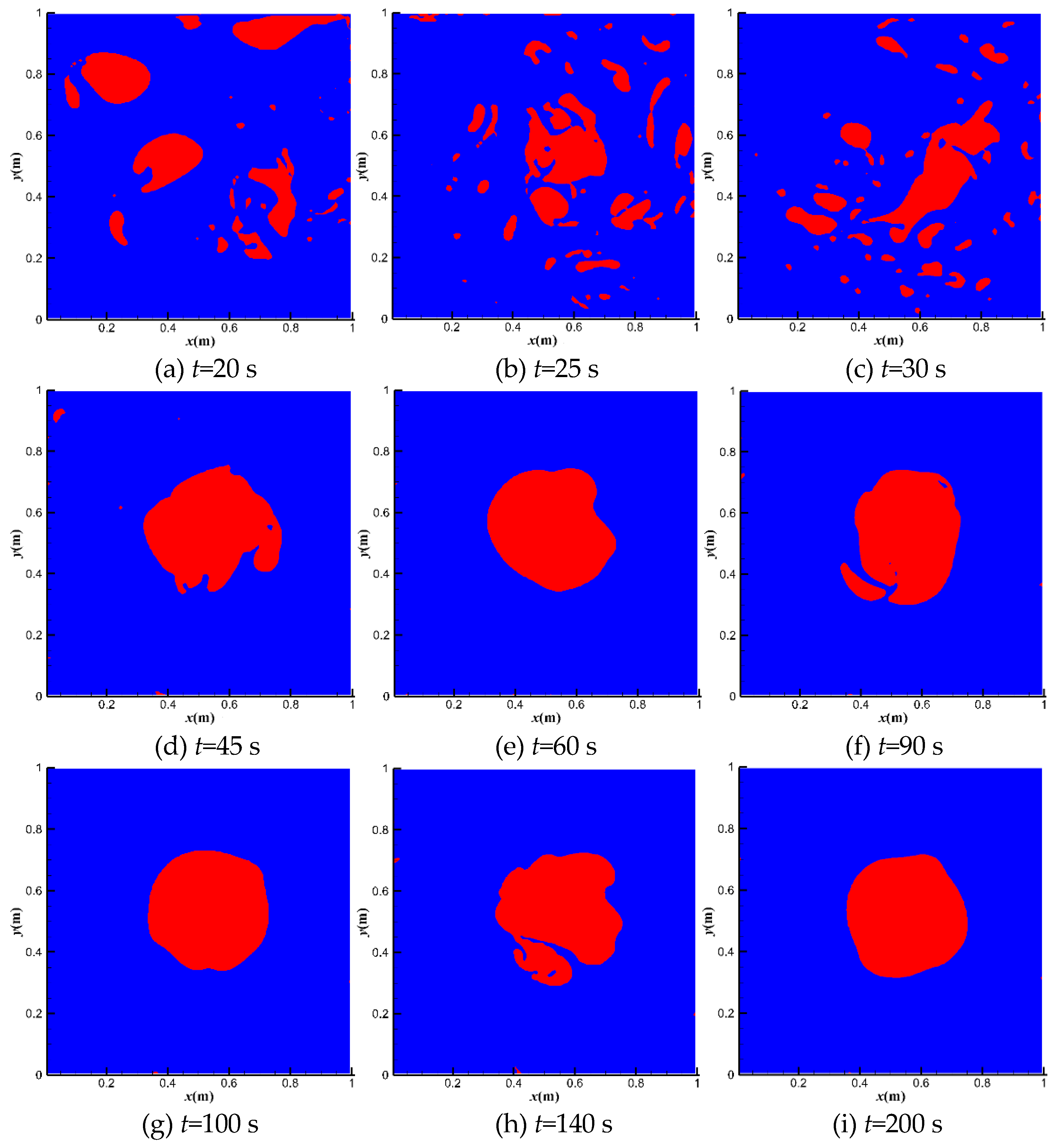
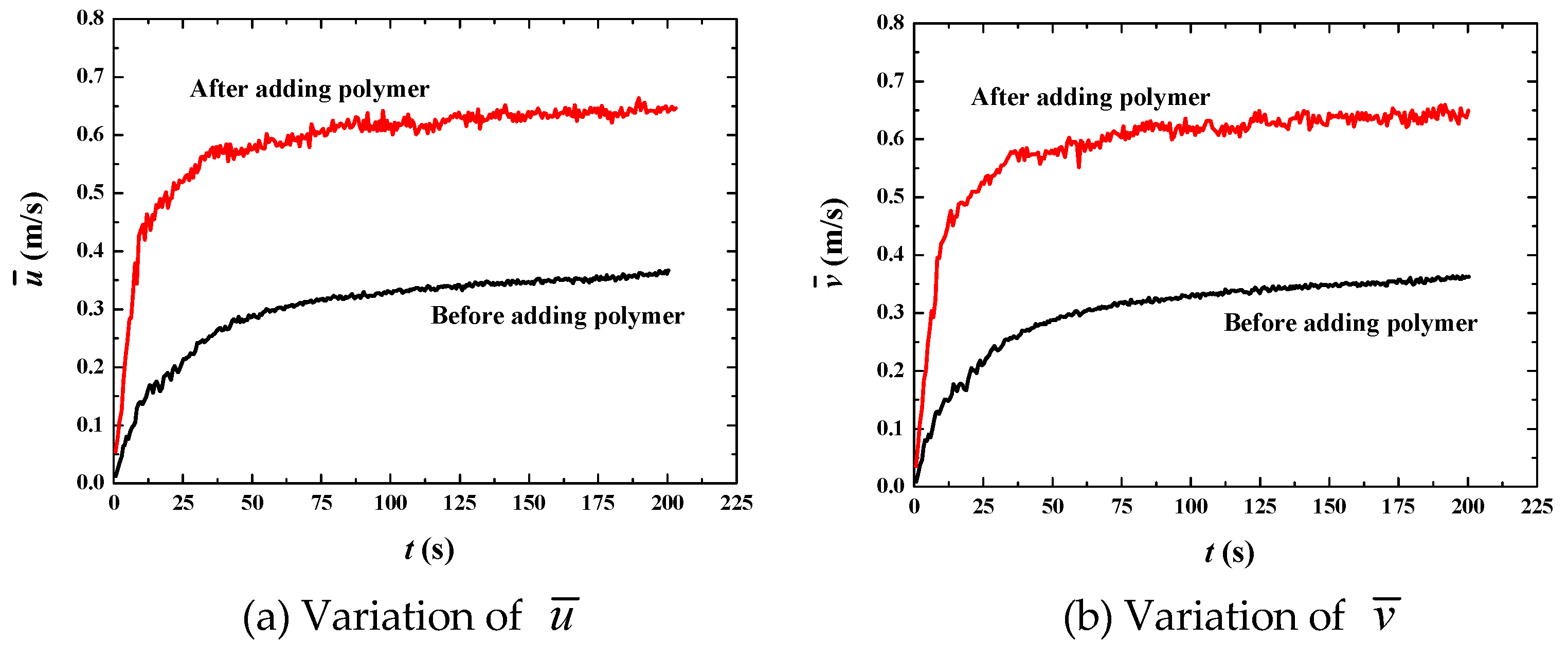
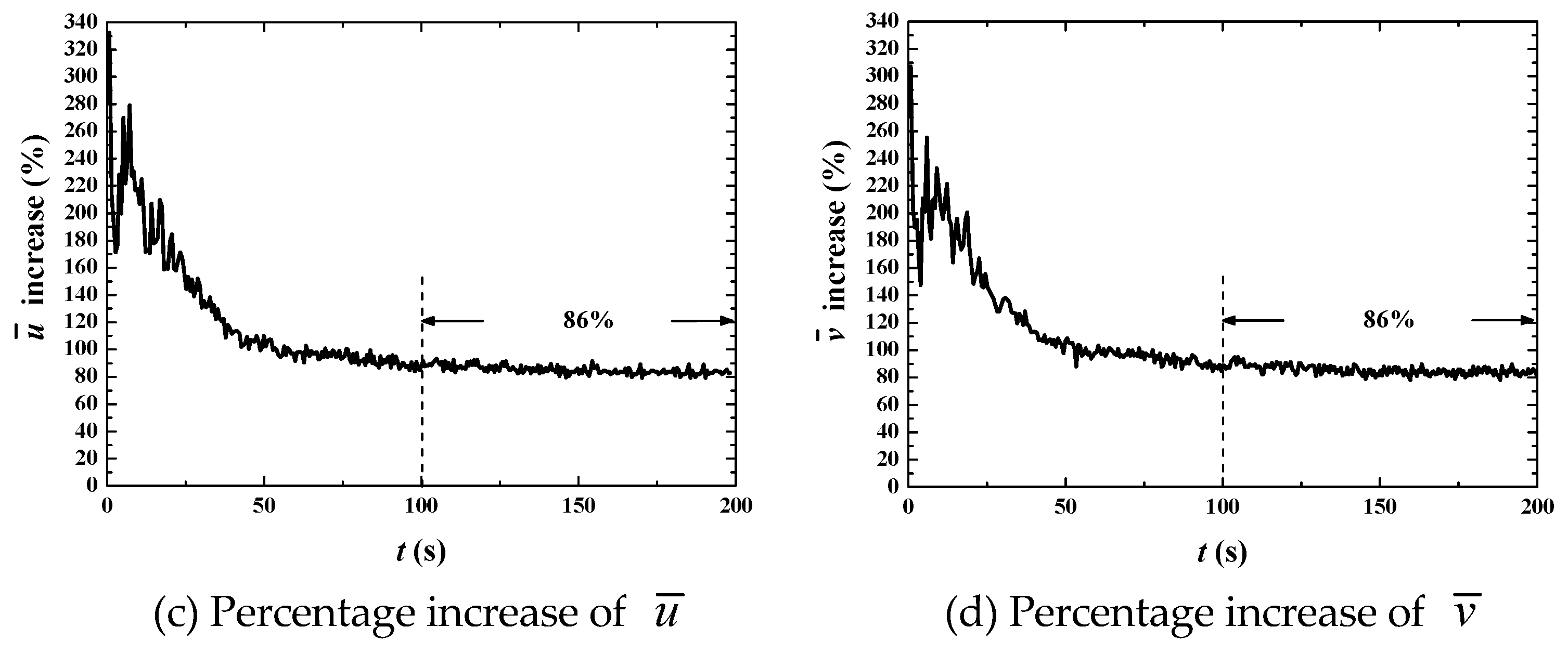

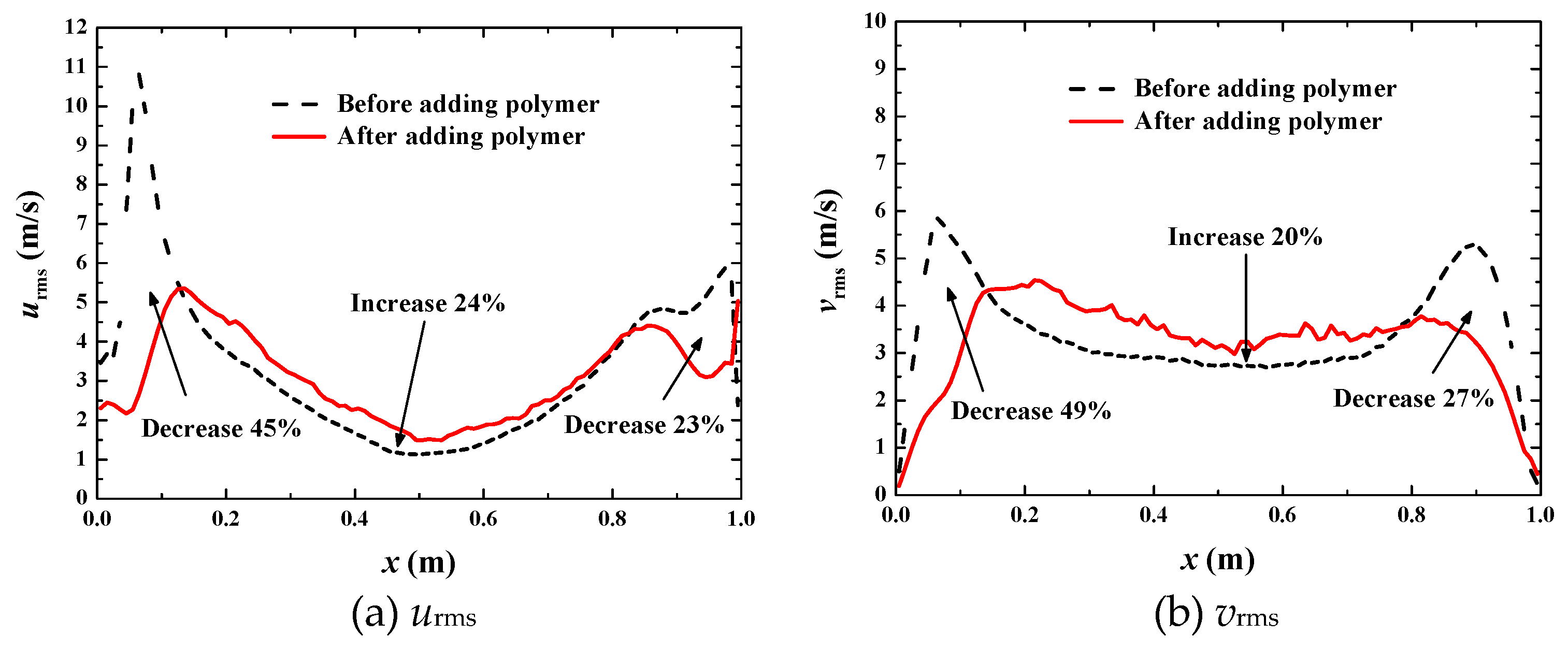


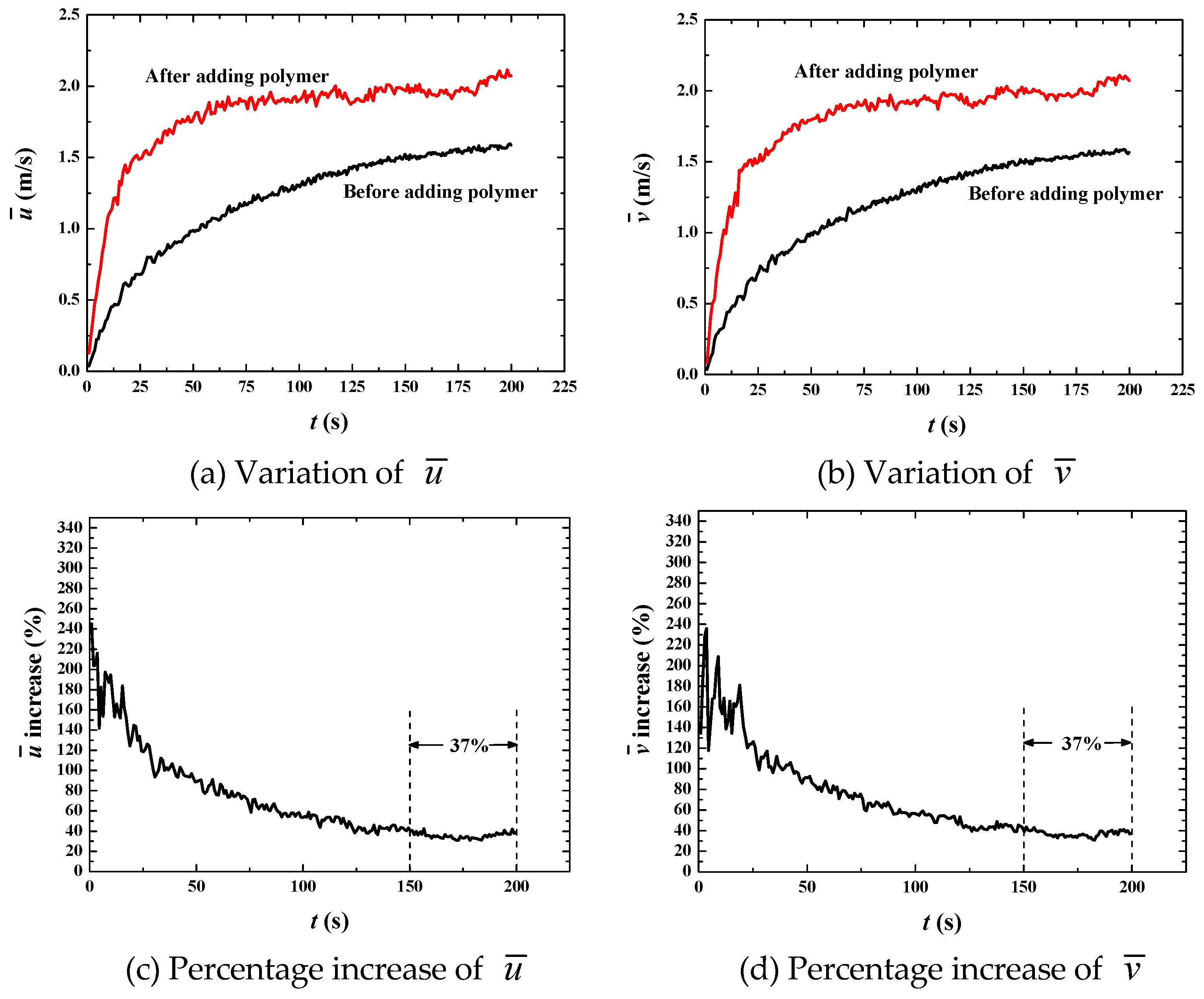
| β | utop = 1 m·s−1 | utop = 10 m·s−1 | utop = 50 m·s−1 |
|---|---|---|---|
| 0.4 | 20% | 8% | 0% |
| 0.6 | 40% | 45% | 30% |
| 0.8 | 70% | 86% | 37% |
| 0.95 | 80% | 87% | 89% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, Y.; Cheng, Z. Direct Numerical Simulation of Gas-Liquid Drag-Reducing Cavity Flow by the VOSET Method. Polymers 2019, 11, 596. https://doi.org/10.3390/polym11040596
Wang Y, Wang Y, Cheng Z. Direct Numerical Simulation of Gas-Liquid Drag-Reducing Cavity Flow by the VOSET Method. Polymers. 2019; 11(4):596. https://doi.org/10.3390/polym11040596
Chicago/Turabian StyleWang, Yi, Yan Wang, and Zhe Cheng. 2019. "Direct Numerical Simulation of Gas-Liquid Drag-Reducing Cavity Flow by the VOSET Method" Polymers 11, no. 4: 596. https://doi.org/10.3390/polym11040596
APA StyleWang, Y., Wang, Y., & Cheng, Z. (2019). Direct Numerical Simulation of Gas-Liquid Drag-Reducing Cavity Flow by the VOSET Method. Polymers, 11(4), 596. https://doi.org/10.3390/polym11040596






