Radial Basis Function Neural Network-Based Modeling of the Dynamic Thermo-Mechanical Response and Damping Behavior of Thermoplastic Elastomer Systems
Abstract
1. Introduction
1.1. Thermoplastic Elastomers
1.2. Thermoplastic Polyurethanes
1.3. Viscoelastic Behavior of Thermoplastic Polyurethanes
1.4. Dynamic meChanical Analysis of Polymers
1.5. Artificial Neural Networks Modeling
1.6. Radial Basis Function Artificial Neural Network
2. Materials and Methods
2.1. Sample Preparation
2.2. DMA Testing
2.3. RBF-ANN Modeling
3. Results and Discussion
3.1. Results of Dynamic Mechanical Analysis
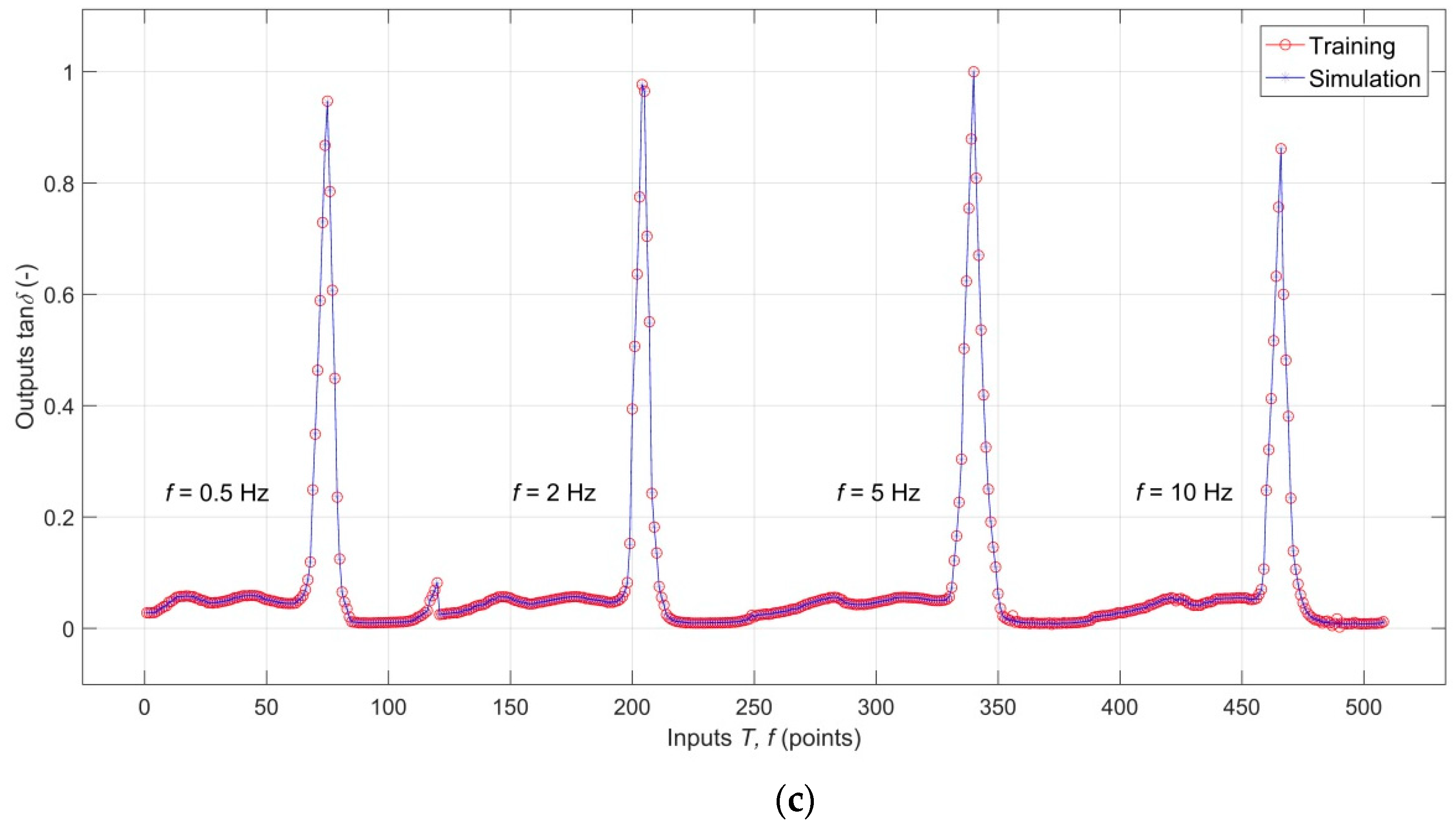
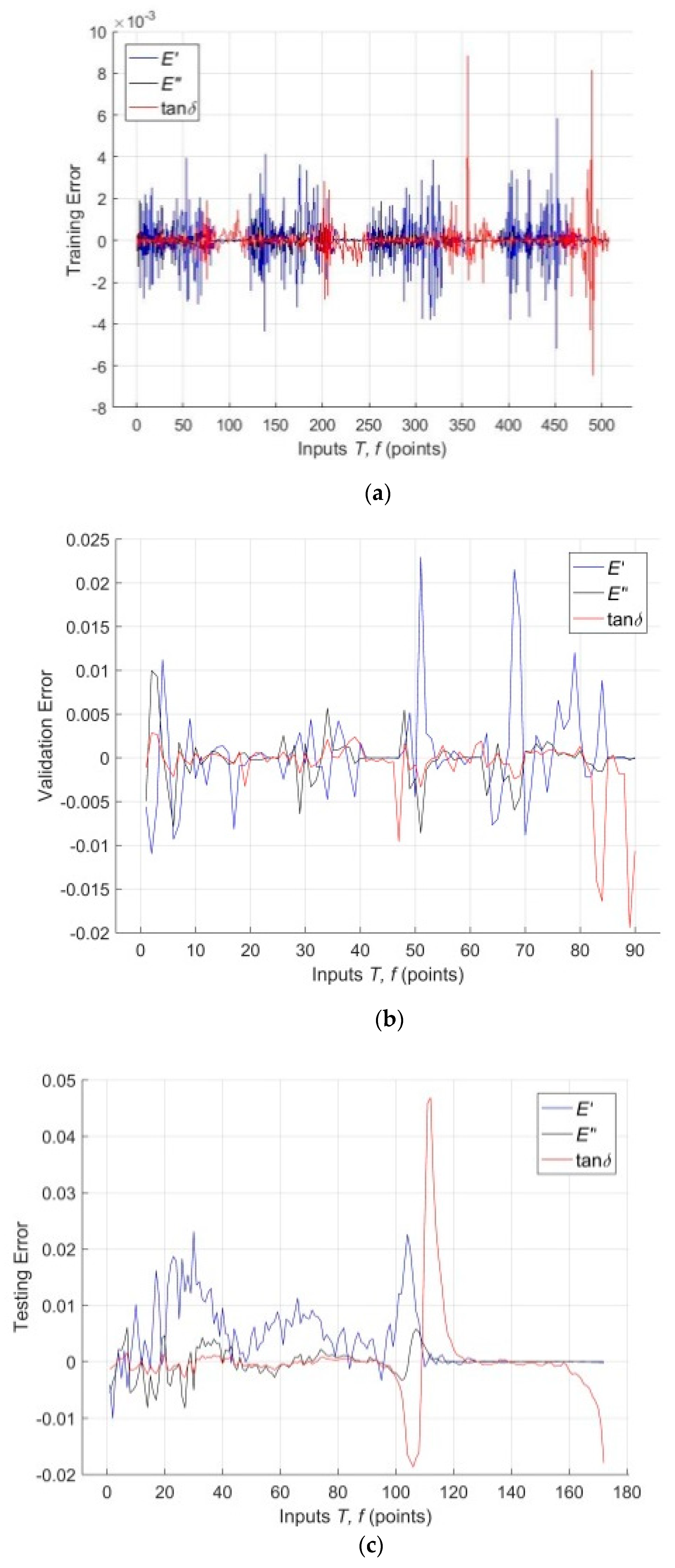
3.2. Analysis of the RBF-ANN Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Drobny, J.G. Handbook of Thermoplastic Elastomers, 2nd ed.; Elsevier: Oxford, UK, 2014. [Google Scholar]
- Olagoke, O.; Kolapo, A. Handbook of Thermoplastics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Coveney, V.A. Elastomers and Components; Elsevier: Oxforf, UK, 2006. [Google Scholar]
- Prisacariu, C. Polyurethane Elastomers: From Morphology to Mechanical Aspects; Springer: Wien, Austria, 2011. [Google Scholar]
- Spontak, R.J.; Patel, N.P. Thermoplastic elastomers: Fundamentals and applications. Curr. Opin. Colloid Interface Sci. 2000, 5, 333–340. [Google Scholar] [CrossRef]
- Kopal, I.; Vršková, J.; Labaj, I.; Ondrušová, D.; Hybler, P.; Harničárová, M.; Valíček, J.; Kušnerová, M. The Effect of High-Energy Ionizing Radiation on the Mechanical Properties of a Melamine Resin, Phenol-Formaldehyde Resin, and Nitrile Rubber Blend. Procedia Eng. 2017, 11, 2405. [Google Scholar] [CrossRef] [PubMed]
- Roylance, D. Engineering Viscoelasticity; MIT: Cambridge, MA, USA, 2001. [Google Scholar]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity, 2nd ed.; Springer: Berlin, Germany, 2014. [Google Scholar]
- Randall, D.; Lee, S. The Polyurethanes Book; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Koštial, P.; Bakošová, D.; Jančíková, Z.; Ružiak, I.; Valíček, J. Thermo-Mechanical Analysis of Rubber Compounds Filled by Carbon Nanotubes. Defect Diffus. Forum 2013, 336, 1–10. [Google Scholar] [CrossRef]
- Ward, I.M.; Sweeney, J. An Introduction to the Mechanical Properties of Solid Polymers, 2nd ed.; Wiley: Chichester, UK, 2004. [Google Scholar]
- Ashby, M.F.; Jones, H.R.D. Engineering Materials 2. An Introduction to Microstructures, Processing and Design; Elsevier/Butterworth-Heinemann: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Riande, E.; Diaz-Calleja, R.; Prolongo, M.G.; Masegosa, R.M.; Salom, C. Polymer viscoelasticity: stress and strain in practice; Marcel Dekker, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Gabbott, P. Principles and Applications of Thermal Analysis; Blackwell Publishing: Oxford, UK, 2008. [Google Scholar]
- Menard, K. Dynamic Mechanical Analysis: A Practical Introduction, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Fried, J.R. Polymer Science and Technology, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2014. [Google Scholar]
- Kopal, I.; Harničárová, M.; Valíček, J.; Koštial, P.; Jančíková, Z.K. Determination of activation energy of relaxation events in thermoplastic polyurethane by dynamic mechanical analysis. Materialwiss. Werkstofftech. 2018, 49, 627–634. [Google Scholar] [CrossRef]
- Mahieux, C.A.; Reifsnider, K.L. Property modeling across transition temperatures in polymers: A robust stiffness-temperature model. Polymer 2001, 42, 3281–3291. [Google Scholar] [CrossRef]
- Richeton, J.; Schlatter, G.; Vecchio, K.S.; Rémond, Y.; Ahzi, S. Unified model for stiffness modulus of amorphous polymers across transition temperatures and strain rates. Polymer 2005, 46, 8194–8201. [Google Scholar] [CrossRef]
- Kopal, I.; Bakošová, D.; Koštial, P.; Jančíková, Z.; Valíček, J.; Harničárová, M. Weibull distribution application on temperature dependence of polyurethane storage modulus. Int. J. Mater. Res. 2016, 107, 472–476. [Google Scholar] [CrossRef]
- Kopal, I.; Labaj, I.; Harničárová, M.; Valíček, J.; Hrubý, D. Prediction of the Tensile Response of Carbon Black Filled Rubber Blends by Artificial Neural Network. Polymers 2018, 10, 644. [Google Scholar] [CrossRef] [PubMed]
- Aliev, R.; Bonfig, K.; Aliew, F. Soft Computing; Verlag Technic: Berlin, Germany, 2000. [Google Scholar]
- Zhang, Z.; Friedrich, K. Artificial neural networks applied to polymer composites: A review. Compos. Sci. Technol. 2003, 63, 2029–2044. [Google Scholar] [CrossRef]
- Al-Haik, M.S.; Hussaini, M.Y.; Rogan, C.S. Artificial Intelligence Techniques in Simulation of Viscoplasticity of Polymeric Composites. Polym. Compos. 2009, 30, 1701–1708. [Google Scholar] [CrossRef]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H.; De Jesús, O. Neural Network Design, 2nd ed.; Martin Hagan: Jersey, NJ, USA, 2014. [Google Scholar]
- Rao, M.A. Neural Networks: Algorithms and Applications; Alpha Science International: Oxford, UK, 2003. [Google Scholar]
- Livingstone, D.J. Artificial Neural Networks Methods and Applications (Methods in Molecular Biology); Humana Press: Totowa, NJ, USA, 2013. [Google Scholar]
- Kopal, I.; Harničárová, M.; Valíček, J.; Kušnerová, M. Modeling the Temperature Dependence of Dynamic Mechanical Properties and Visco-Elastic Behavior of Thermoplastic Polyurethane Using Artificial Neural Network. Polymers 2017, 9, 519. [Google Scholar] [CrossRef] [PubMed]
- Seidl, D.; Jančíková, Z.; Koštial, P.; Ružiak, I.; Kopal, I.; Kreislova, K. Exploitation of Artificial Intelligence Methods for Prediction of Atmospheric Corrosion. Defect Diffus. Forum 2012, 326, 65–68. [Google Scholar] [CrossRef]
- Ružiak, I.; Koštial, P.; Jančíková, Z.; Gajtanska, M.; Krišťák, Ľ.; Kopal, I.; Polakovič, P. Artificial Neural Networks Prediction of Rubber Mechanical Properties in Aged and Nonaged State. In Improved Performance of Materials; Öchsner, A., Altenbach, H., Eds.; Springer: Berlin, Germany, 2018; Volume 72, pp. 27–35. [Google Scholar]
- Nguyen, L.T.K.; Keip, M.A. A data-driven approach to nonlinear elasticity. Comput. Struct. 2018, 194, 97–115. [Google Scholar] [CrossRef]
- Davydov, O.; Oanh, D.T. On the optimal shape parameter for Gaussian radial basis function finite difference approximation of the Poisson equation. Comput. Math. Appl. 2011, 62, 2143–2161. [Google Scholar] [CrossRef]
- Pislaru, C.; Shebani, A. Identification of Nonlinear Systems Using Radial Basis Function Neural Network. Int. J. Comput. Inf. Syst. Control Eng. 2014, 8, 1528–1533. [Google Scholar]
- Xu, X.; Gupta, N. Artificial neural network approach to predict the elastic modulus from dynamic mechanical analysis results. Adv. Theory Simul. 2019, 2, 1800131. [Google Scholar] [CrossRef]
- Xu, X.; Gupta, N. Application of radial basis neural network to transform viscoelastic to elastic properties for materials with multiple thermal transitions. J. Mater. Sci. 2019, 54, 8401–8413. [Google Scholar] [CrossRef]
- Trebar, M.; Susteric, Z.; Lotric, U. Predicting mechanical properties of elastomers with neural networks. Polymer 2007, 48, 5340–5347. [Google Scholar] [CrossRef]
- Bhowmick, A.K.; Stephens, H.L. Handbook of Elastomers, 2nd ed.; CRC-Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Shi, F.; Wang, X.C.; Yu, L.; Li, Y. MATLAB 30 Case Analysis of MATLAB Neural Network; Beijing University Press: Beijing, China, 2009. [Google Scholar]
- Paliwal, M.; Kumar, U.A. Neural networks and statistical techniques: A review of applications. Expert Syst. Appl. 2009, 36, 2–17. [Google Scholar] [CrossRef]
- Wang, H.; Xu, X. Applying RBF Neural Networks and Genetic Algorithms to Nonlinear System Optimization. Adv. Mater. Res. 2012, 605, 2457–2460. [Google Scholar] [CrossRef]


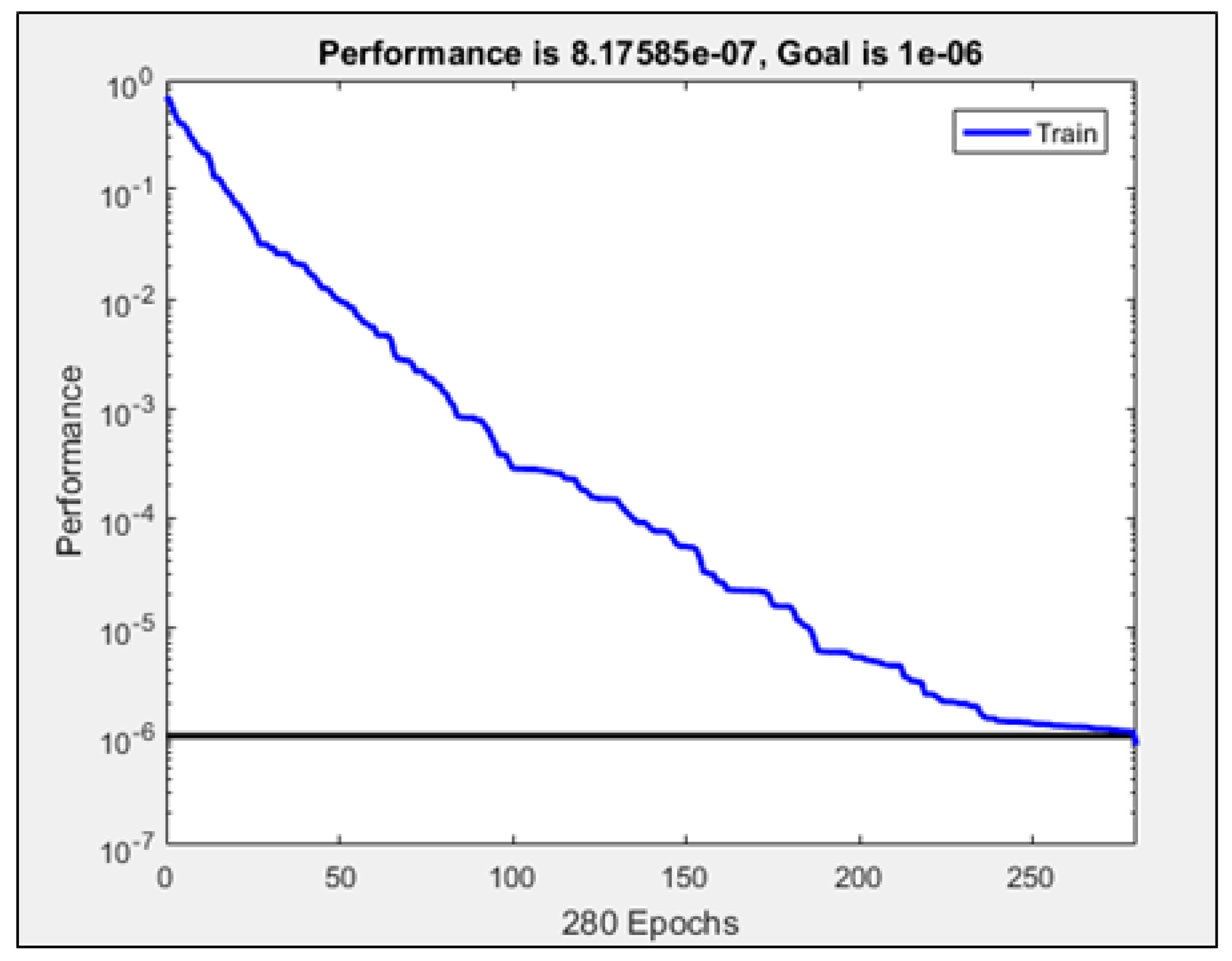






| IL | HL | OL | TF | DDF | PF | MN | Spread | Goal |
|---|---|---|---|---|---|---|---|---|
| 2 | 268 | 3 | Gaussian RBF, linear | dividerand | MSE | 103 | 7 | 10−6 |
| Data Division | Samples | MSE | R | Intercept | |
|---|---|---|---|---|---|
| Training | 0.85 | 1016 | 8.176 × 10−7 | 1 | 4.9 × 10−7 |
| Validation | 0.15 | 180 | - | 0.99999 | 3 × 10−4 |
| Testing | 1 | 344 | - | 0.99999 | 3.9 × 10×5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kopal, I.; Harničárová, M.; Valíček, J.; Krmela, J.; Lukáč, O. Radial Basis Function Neural Network-Based Modeling of the Dynamic Thermo-Mechanical Response and Damping Behavior of Thermoplastic Elastomer Systems. Polymers 2019, 11, 1074. https://doi.org/10.3390/polym11061074
Kopal I, Harničárová M, Valíček J, Krmela J, Lukáč O. Radial Basis Function Neural Network-Based Modeling of the Dynamic Thermo-Mechanical Response and Damping Behavior of Thermoplastic Elastomer Systems. Polymers. 2019; 11(6):1074. https://doi.org/10.3390/polym11061074
Chicago/Turabian StyleKopal, Ivan, Marta Harničárová, Jan Valíček, Jan Krmela, and Ondrej Lukáč. 2019. "Radial Basis Function Neural Network-Based Modeling of the Dynamic Thermo-Mechanical Response and Damping Behavior of Thermoplastic Elastomer Systems" Polymers 11, no. 6: 1074. https://doi.org/10.3390/polym11061074
APA StyleKopal, I., Harničárová, M., Valíček, J., Krmela, J., & Lukáč, O. (2019). Radial Basis Function Neural Network-Based Modeling of the Dynamic Thermo-Mechanical Response and Damping Behavior of Thermoplastic Elastomer Systems. Polymers, 11(6), 1074. https://doi.org/10.3390/polym11061074








