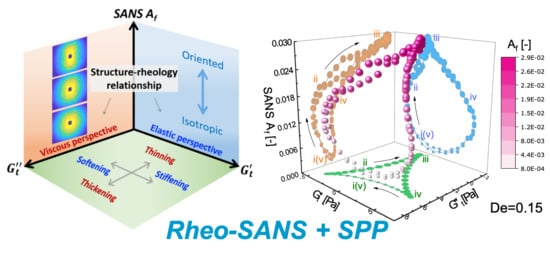
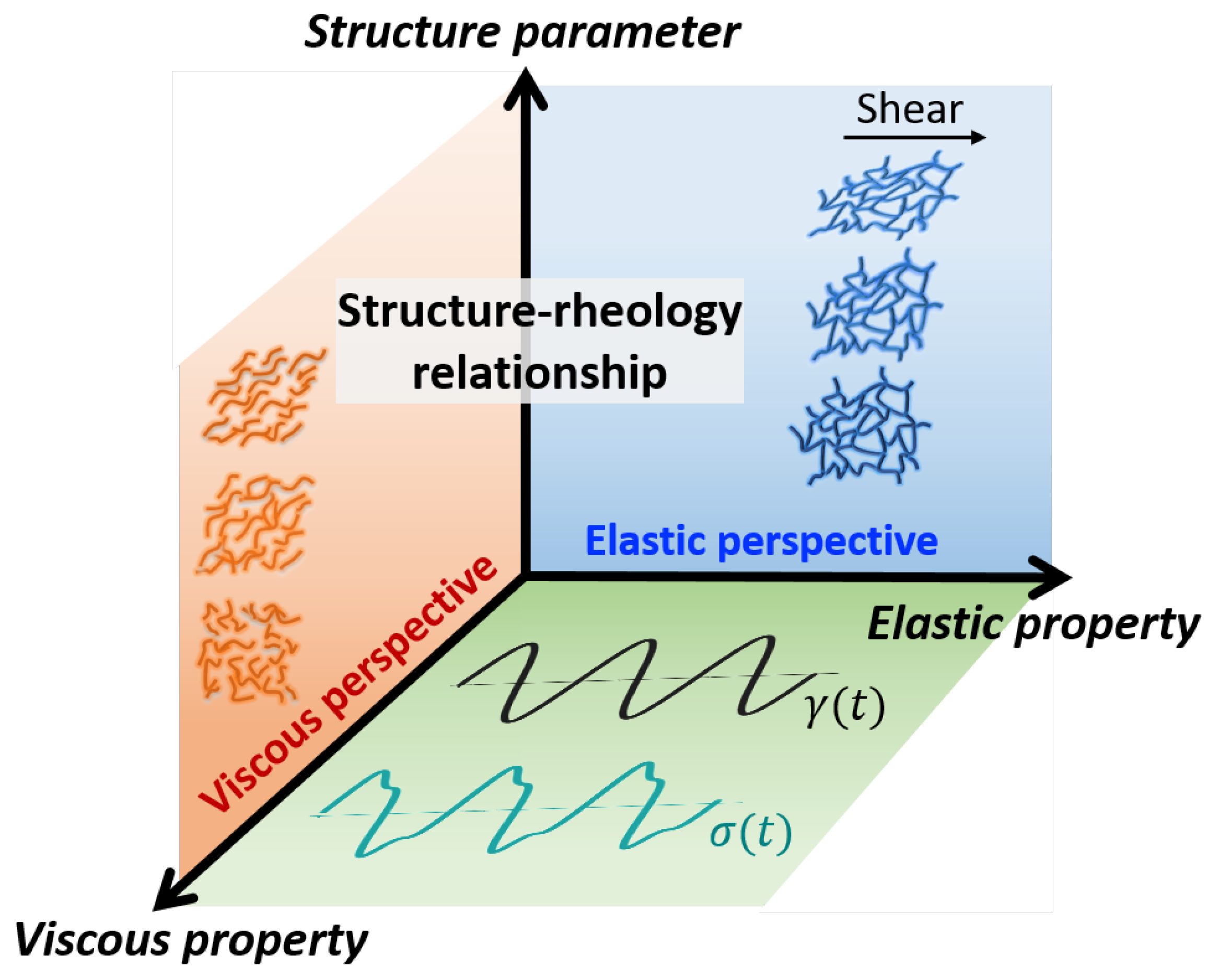
Unveiling Temporal Nonlinear Structure–Rheology Relationships under Dynamic Shearing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Rheo-Small-Angle Neutron Scattering
2.3. Sequence of Physical Processes (SPP)
3. Results
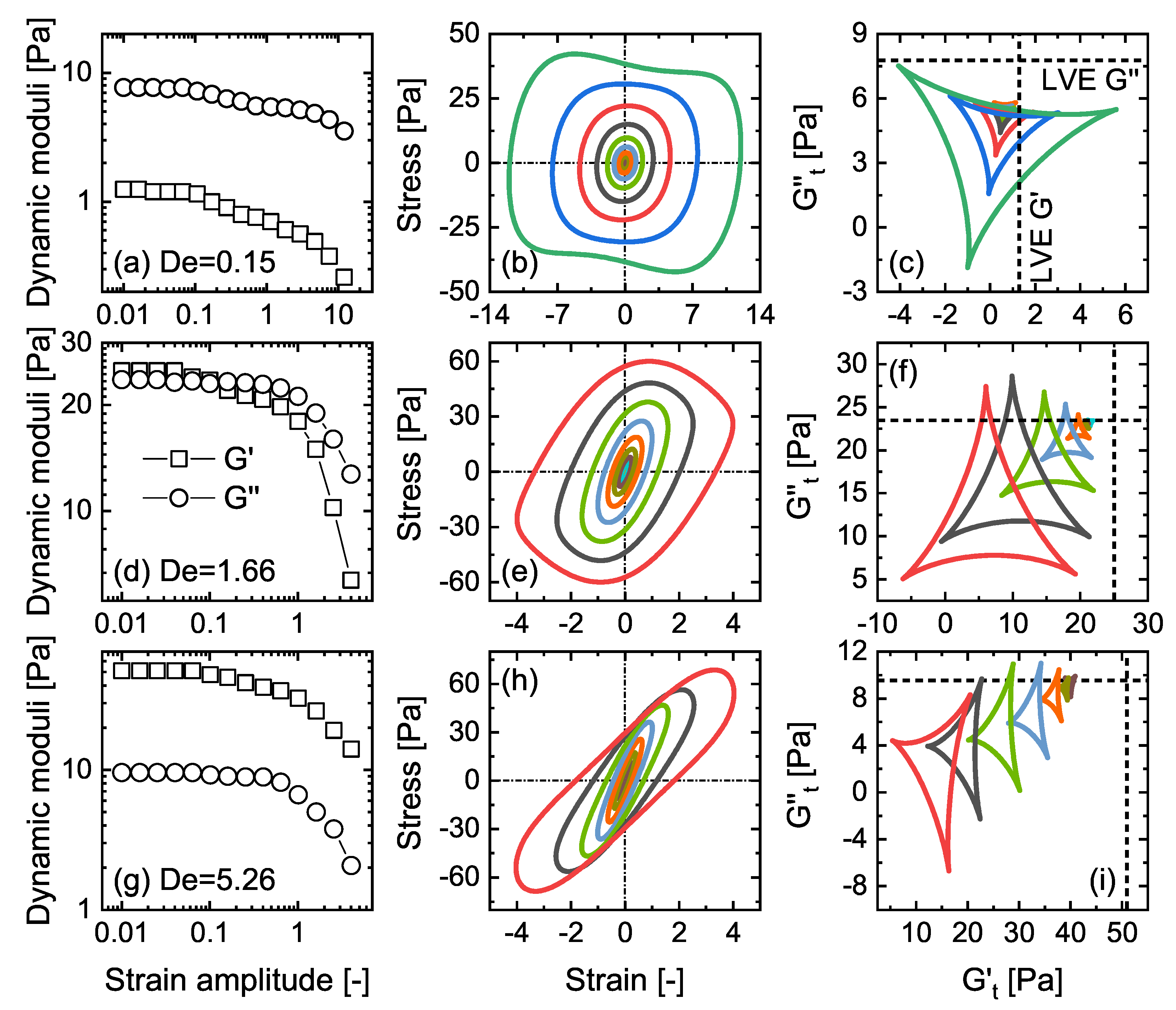
3.1. Linear Viscoelasticity
3.2. LAOS as a Model Protocol
3.3. Temporal Structure–Rheology Relationships
3.4. Low-Frequency Regime ()
3.5. Intermediate-Frequency Regime ()
3.6. High-Frequency Regime ()
3.7. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Amplitude Dependence of Oscillatory Shear Responses
References
- Zhao, X.; Lv, L.; Pan, B.; Zhang, W.; Zhang, S.; Zhang, Q. Polymer-supported nanocomposites for environmental application: A review. Chem. Eng. J. 2011, 170, 381–394. [Google Scholar] [CrossRef]
- Sukhorukov, G.B.; Rogach, A.L.; Garstka, M.; Springer, S.; Parak, W.J.; Muñoz-Javier, A.; Kreft, O.; Skirtach, A.G.; Susha, A.S.; Ramaye, Y.; et al. Multifunctionalized polymer microcapsules: Novel tools for biological and pharmacological applications. Small 2007, 3, 944–955. [Google Scholar] [CrossRef]
- Friedrich, K.; Almajid, A.A. Manufacturing aspects of advanced polymer composites for automotive applications. Appl. Compos. Mater. 2013, 20, 107–128. [Google Scholar] [CrossRef]
- Guilherme, M.R.; Aouada, F.A.; Fajardo, A.R.; Martins, A.F.; Paulino, A.T.; Davi, M.F.; Rubira, A.F.; Muniz, E.C. Superabsorbent hydrogels based on polysaccharides for application in agriculture as soil conditioner and nutrient carrier: A review. Eur. Polym. J. 2015, 72, 365–385. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Jiang, M.; Zhou, Z.; Gou, J.; Hui, D. 3D printing of polymer matrix composites: A review and prospective. Compos. Part B Eng. 2017, 110, 442–458. [Google Scholar] [CrossRef]
- Cordier, P.; Tournilhac, F.; Soulié-Ziakovic, C.; Leibler, L. Self-healing and thermoreversible rubber from supramolecular assembly. Nature 2008, 451, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Koos, E.; Willenbacher, N. Capillary forces in suspension rheology. Science 2011, 331, 897–900. [Google Scholar] [CrossRef]
- Mangal, R.; Srivastava, S.; Archer, L.A. Phase stability and dynamics of entangled polymer-nanoparticle composites. Nat. Commun. 2015, 6, 7198. [Google Scholar] [CrossRef] [PubMed]
- Sun Han Chang, R.; Lee, J.C.W.; Pedron, S.; Harley, B.A.C.; Rogers, S.A. Rheological Analysis of the Gelation Kinetics of an Enzyme Cross-linked PEG Hydrogel. Biomacromolecules 2019, 20, 2198–2206. [Google Scholar] [CrossRef]
- Leblanc, J.L. Large amplitude oscillatory shear experiments to investigate the nonlinear viscoelastic properties of highly loaded carbon black rubber compounds without curatives. J. Appl. Polym. Sci. 2008, 109, 1271–1293. [Google Scholar] [CrossRef]
- Lettinga, M.P.; Holmqvist, P.; Ballesta, P.; Rogers, S.; Kleshchanok, D.; Struth, B. Nonlinear Behavior of Nematic Platelet Dispersions in Shear Flow. Phys. Rev. Lett. 2012, 109, 246001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- López-Barrón, C.R.; Porcar, L.; Eberle, A.P.R.; Wagner, N.J. Dynamics of melting and recrystallization in a polymeric micellar crystal subjected to large amplitude oscillatory shear flow. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef] [PubMed]
- Rogers, M.C.; Chen, K.; Pagenkopp, M.J.; Mason, T.G.; Narayanan, S.; Harden, J.L.; Leheny, R.L. Microscopic signatures of yielding in concentrated nanoemulsions under large-amplitude oscillatory shear. Phys. Rev. Mater. 2018, 2, 095601. [Google Scholar] [CrossRef]
- Boukany, P.E.; Wang, S.Q. Use of particle-tracking velocimetry and flow birefringence to study nonlinear flow behavior of entangled wormlike micellar solution: From wall slip, bulk disentanglement to chain scission. Macromolecules 2008, 41, 1455–1464. [Google Scholar] [CrossRef]
- Smith, P.A.; Petekidis, G.; Egelhaaf, S.U.; Poon, W.C. Yielding and crystallization of colloidal gels under oscillatory shear. Phys. Rev. E 2007, 76. [Google Scholar] [CrossRef] [PubMed]
- Rogers, M.C.; Chen, K.; Andrzejewski, L.; Narayanan, S.; Ramakrishnan, S.; Leheny, R.L.; Harden, J.L. Echoes in X-ray speckles track nanometer-scale plastic events in colloidal gels under shear. Phys. Rev. E 2014, 90, 62310. [Google Scholar] [CrossRef] [PubMed]
- Park, J.D.; Rogers, S.A. The transient behavior of soft glassy materials far from equilibrium. J. Rheol. 2018, 62, 869–888. [Google Scholar] [CrossRef]
- Leheny, R.L.; Rogers, M.C.; Chen, K.; Narayanan, S.; Harden, J.L. Rheo-XPCS. Curr. Opin. Colloid Interface Sci. 2015, 20, 261–271. [Google Scholar] [CrossRef] [Green Version]
- McMullan, J.M.; Wagner, N.J. Directed self-assembly of suspensions by large amplitude oscillatory shear flow. J. Rheol. 2009, 53, 575–588. [Google Scholar] [CrossRef]
- Calabrese, M.A.; Rogers, S.A.; Porcar, L.; Wagner, N.J. Understanding steady and dynamic shear banding in a model wormlike micellar solution. J. Rheol. 2016, 60, 1001–1017. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Schroeder, C.M. Single polymer dynamics under large amplitude oscillatory extension. Phys. Rev. Fluids 2016, 1, 053301. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. (Oxf.) 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Cho, K.S.; Hyun, K.; Ahn, K.H.; Lee, S.J. A geometrical interpretation of large amplitude oscillatory shear response. J. Rheol. 2005, 49, 747–758. [Google Scholar] [CrossRef]
- Ewoldt, R.H.; Hosoi, A.E.; McKinley, G.H. New measures for characterizing nonlinear viscoelasticity in large amplitude oscillatory shear. J. Rheol. 2008, 52, 1427–1458. [Google Scholar] [CrossRef] [Green Version]
- Eberle, A.P.R.; Porcar, L. Flow-SANS and Rheo-SANS applied to soft matter. Curr. Opin. Colloid Interface Sci. 2012, 17, 33–43. [Google Scholar] [CrossRef]
- Rogers, S.; Kohlbrecher, J.; Lettinga, M.P. The molecular origin of stress generation in worm-like micelles, using a rheo-SANS LAOS approach. Soft Matter 2012, 8, 7831–7839. [Google Scholar] [CrossRef] [Green Version]
- Thompson, R.L.; Alicke, A.A.; de Souza Mendes, P.R. Model-based material functions for SAOS and LAOS analyses. J. Non-Newton. Fluid Mech. 2015, 215, 19–30. [Google Scholar] [CrossRef]
- Lee, J.C.W.; Weigandt, K.M.; Kelley, E.G.; Rogers, S.A. Structure-property relationships via recovery rheology in viscoelastic materials. Phys. Rev. Lett. 2019, 122, 248003. [Google Scholar] [CrossRef]
- Somani, R.H.; Yang, L.; Hsiao, B.S.; Agarwal, P.K.; Fruitwala, H.A.; Tsou, A.H. Shear-induced precursor structures in isotactic polypropylene melt by in-situ rheo-SAXS and rheo-WAXD studies. Macromolecules 2002, 35, 9096–9104. [Google Scholar] [CrossRef]
- Callaghan, P.T. Rheo-NMR and velocity imaging. Curr. Opin. Colloid Interface Sci. 2006, 11, 13–18. [Google Scholar] [CrossRef]
- Medronho, B.; Brown, J.; Miguel, M.G.; Schmidt, C.; Olsson, U.; Galvosas, P. Planar lamellae and onions: A spatially resolved rheo-NMR approach to the shear-induced structural transformations in a surfactant model system. Soft Matter 2011, 7, 4938–4947. [Google Scholar] [CrossRef]
- Herle, V.; Fischer, P.; Windhab, E.J. Stress driven shear bands and the effect of confinement on their structures—A rheological, flow visualization, and rheo-SALS study. Langmuir 2005, 21, 9051–9057. [Google Scholar] [CrossRef] [PubMed]
- Boukany, P.E.; Wang, S.Q.; Ravindranath, S.; Lee, L.J. Shear banding in entangled polymers in the micron scale gap: A confocal-rheoscopic study. Soft Matter 2015, 11, 8058–8068. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.C.; Hsiao, L.C.; Doyle, P.S. Multiple particle tracking study of thermally-gelling nanoemulsions. Soft Matter 2017, 13, 6606–6619. [Google Scholar] [CrossRef] [PubMed]
- Tschoegl, N.W. The Phenomenological Theory of Linear Viscoelastic Behavior; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Onck, P.R.; Koeman, T.; van Dillen, T.; van der Giessen, E. Alternative Explanation of Stiffening in Cross-Linked Semiflexible Networks. Phys. Rev. Lett. 2005, 95, 178102. [Google Scholar] [CrossRef] [Green Version]
- Mackintosh, F.C.; Kas, J.; Janmey, P.A. Elasticity of Semiflexible Biopolymer Networks. Phys. Rev. Lett. 1995, 75, 4425. [Google Scholar] [CrossRef] [PubMed]
- Gurnon, A.K.; Lopez-Barron, C.R.; Eberle, A.P.; Porcar, L.; Wagner, N.J. Spatiotemporal stress and structure evolution in dynamically sheared polymer-like micellar solutions. Soft Matter 2014, 10, 2889–2898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Förster, S.; Konrad, M.; Lindner, P. Shear thinning and orientational ordering of Wormlike Micelles. Phys. Rev. Lett. 2005, 94, 017803. [Google Scholar] [CrossRef] [PubMed]
- Weigandt, K.M.; Porcar, L.; Pozzo, D.C. In situ neutron scattering study of structural transitions in fibrin networks under shear deformation. Soft Matter 2011, 7, 9992–10000. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Fielding, S.M. Shear Banding of Soft Glassy Materials in Large Amplitude Oscillatory Shear. Phys. Rev. Lett. 2016, 117, 188001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanso, M.A.; Jbara, L.; Giacomin, A.J.; Saengow, C.; Gilbert, P.H. Order in polymeric liquids under oscillatory shear flow. Phys. Fluids 2019, 31, 033103. [Google Scholar] [CrossRef]
- Rogers, S.A. In search of physical meaning: Defining transient parameters for nonlinear viscoelasticity. Rheol. Acta 2017, 56, 501–525. [Google Scholar] [CrossRef]
- Lee, J.C.W.; Park, J.D.; Rogers, S.A. Studying large amplitude oscillatory shear response of soft materials. J. Vis. Exp. 2019, 146, e58707. [Google Scholar]
- Donley, G.J.; de Bruyn, J.R.; McKinley, G.H.; Rogers, S.A. Time-resolved dynamics of the yielding transition in soft materials. J. Non-Newton. Fluid Mech. 2019, 264, 117–134. [Google Scholar] [CrossRef]
- Tirtaatmadja, V.; Tam, K.C.; Jenkins, R.D. Superposition of oscillations on steady shear flow as a technique for investigating the structure of associative polymers. Macromolecules 1997, 30, 1426–1433. [Google Scholar] [CrossRef]
- Cates, M.E.; Candau, S.J. Statics and dynamics of worm-like surfactant micelles. J. Phys.-Condens. Matter 1990, 2, 6869–6892. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Spenley, N.A.; Cates, M.E.; McLeish, T.C.B. Nonlinear rheology of wormlike micelles. Phys. Rev. Lett. 1993, 71, 939–942. [Google Scholar] [CrossRef] [PubMed]
- In, M.; Warr, G.G.; Zana, R. Dynamics of branched threadlike micelles. Phys. Rev. Lett. 1999, 82, 2278–2281. [Google Scholar] [CrossRef]
- Cardiel, J.J.; Dohnalkova, A.C.; Dubash, N.; Zhao, Y.; Cheung, P.; Shen, A.Q. Microstructure and rheology of a flow-induced structured phase in wormlike micellar solutions. Proc. Natl. Acad. Sci. USA 2013, 110, 1653–1660. [Google Scholar] [CrossRef]
- Helgeson, M.E.; Vasquez, P.A.; Kaler, E.W.; Wagner, N.J. Rheology and spatially resolved structure of cetyltrimethylammonium bromide wormlike micelles through the shear banding transition. J. Rheol. 2009, 53, 727–756. [Google Scholar] [CrossRef]
- Calabrese, M.A.; Wagner, N.J.; Rogers, S.A. An optimized protocol for the analysis of time-resolved elastic scattering experiments. Soft Matter 2016, 12, 2301–2308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, Y.T.; Lips, A. Kinetics and mechanism of shear banding in an entangled micellar solution. J. Rheol. 2005, 49, 1001–1027. [Google Scholar] [CrossRef]
- Rogers, S.A.; Erwin, B.M.; Vlassopoulos, D.; Cloitre, M. A sequence of physical processes determined and quantified in LAOS: Application to a yield stress fluid. J. Rheol. 2011, 55, 435–458. [Google Scholar] [CrossRef]
- Kim, J.; Merger, D.; Wilhelm, M.; Helgeson, M.E. Microstructure and nonlinear signatures of yielding in a heterogeneous colloidal gel under large amplitude oscillatory shear. J. Rheol. 2014, 58, 1359–1390. [Google Scholar] [CrossRef]
- Lee, C.W.; Rogers, S.A. A sequence of physical processes quantified in LAOS by continuous local measures. Korea-Aust. Rheol. J. 2017, 29, 269–279. [Google Scholar] [CrossRef]
- Ramya, K.A.; Kodavaty, J.; Dorishetty, P.; Setti, M.; Deshpande, A.P. Characterizing the yielding processes in pluronic-hyaluronic acid thermoreversible gelling systems using oscillatory rheology. J. Rheol. 2019, 63, 215–228. [Google Scholar] [CrossRef]
- Deshpande, A.P. Oscillatory Shear Rheology for Probing Nonlinear Viscoelasticity of Complex Fluids: Large Amplitude Oscillatory Shear; Springer: New York, NY, USA, 2010. [Google Scholar]
- Inoue, T.; Inoue, Y.; Watanabe, H. Nonlinear rheology of CTAB/NaSal aqueous solutions: Finite extensibility of a network of wormlike micelles. Langmuir 2005, 21, 1201–1208. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.Q. Exploring stress overshoot phenomenon upon startup deformation of entangled linear polymeric liquids. J. Rheol. 2010, 53, 1389–1401. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.Q. From elastic deformation to terminal flow of a monodisperse entangled melt in uniaxial extension. J. Rheol. 2008, 52, 1275–1290. [Google Scholar] [CrossRef]
- Wang, S.Q.; Wang, Y.; Cheng, S.; Li, X.; Zhu, X.; Sun, H. New experiments for improved theoretical description of nonlinear rheology of entangled polymers. Macromolecules 2013, 46, 3147–3159. [Google Scholar] [CrossRef]
- Rogers, S.A.; Park, J.D.; Lee, C.W.J. Instantaneous dimensionless numbers for transient nonlinear rheology. Rheol. Acta 2019. [Google Scholar] [CrossRef]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.C.-W.; Porcar, L.; Rogers, S.A. Unveiling Temporal Nonlinear Structure–Rheology Relationships under Dynamic Shearing. Polymers 2019, 11, 1189. https://doi.org/10.3390/polym11071189
Lee JC-W, Porcar L, Rogers SA. Unveiling Temporal Nonlinear Structure–Rheology Relationships under Dynamic Shearing. Polymers. 2019; 11(7):1189. https://doi.org/10.3390/polym11071189
Chicago/Turabian StyleLee, Johnny Ching-Wei, Lionel Porcar, and Simon A. Rogers. 2019. "Unveiling Temporal Nonlinear Structure–Rheology Relationships under Dynamic Shearing" Polymers 11, no. 7: 1189. https://doi.org/10.3390/polym11071189
APA StyleLee, J. C.-W., Porcar, L., & Rogers, S. A. (2019). Unveiling Temporal Nonlinear Structure–Rheology Relationships under Dynamic Shearing. Polymers, 11(7), 1189. https://doi.org/10.3390/polym11071189