Two-Step Energy Transfer Dynamics in Conjugated Polymer and Dye-Labeled Aptamer-Based Potassium Ion Detection Assay
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Time-Integrated Fluorescence and Quantum Yield Measurement
2.3. Time-Resolved Fluorescence Measurement
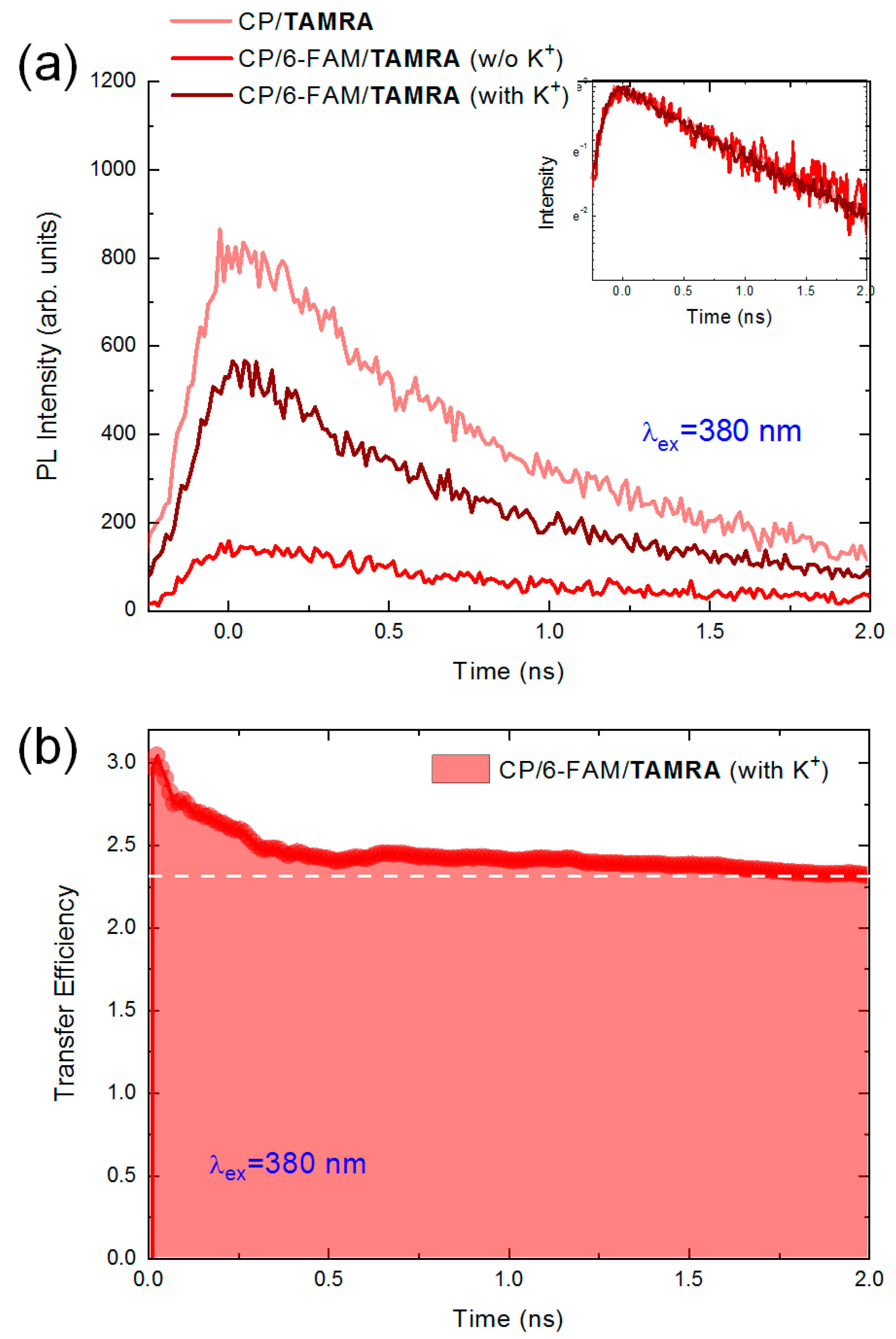
3. Results and Discussion
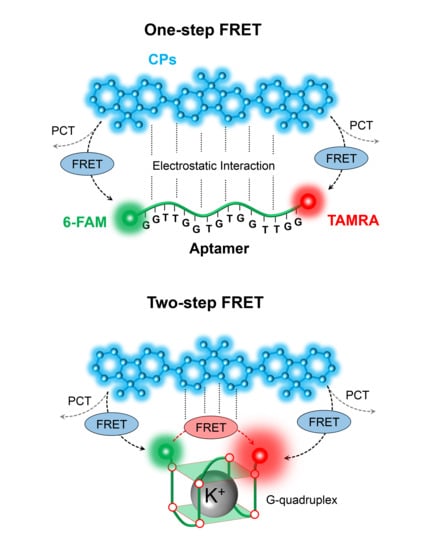
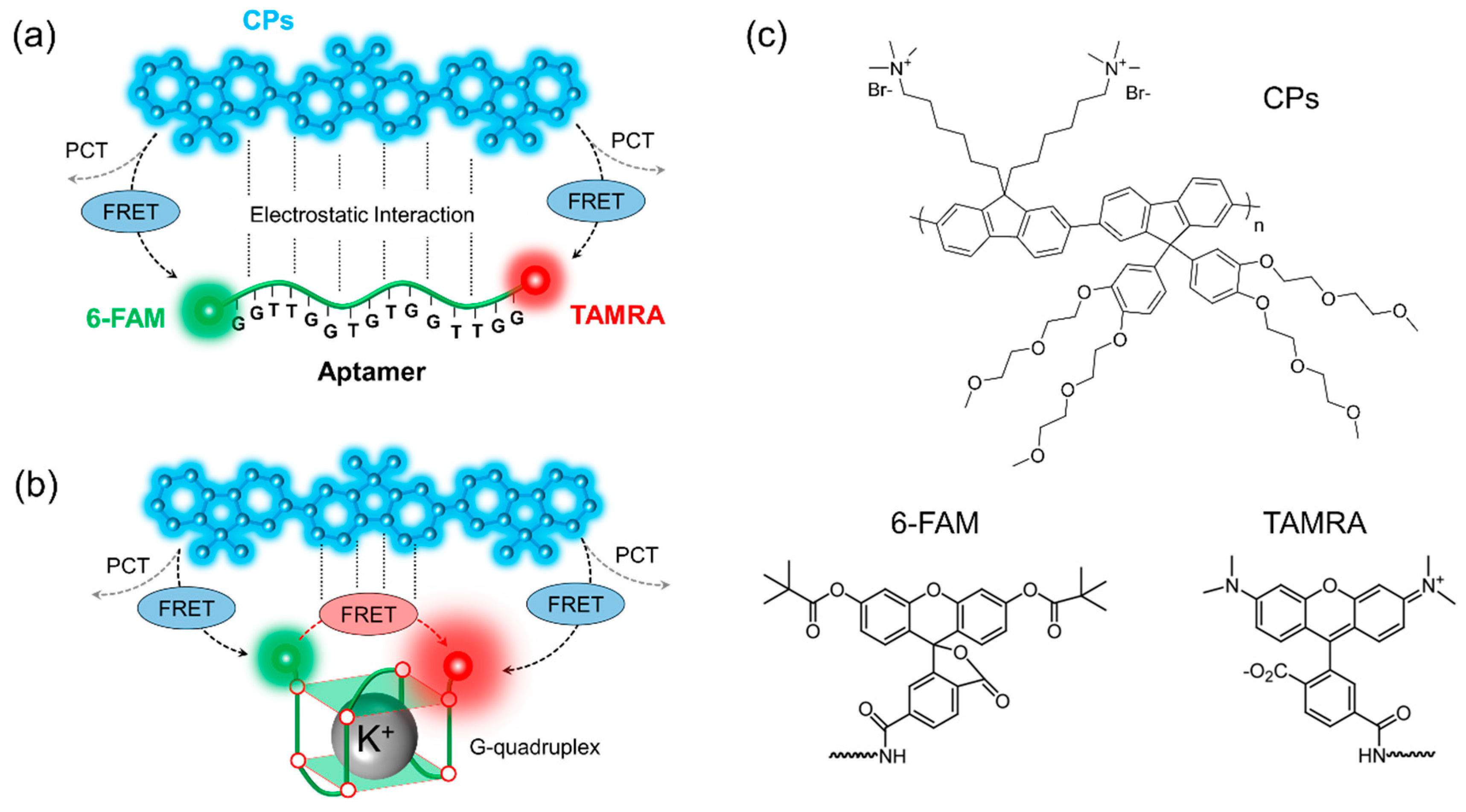
3.1. Two-Step FRET Process in CPs and Two-Dye-Labeled Aptamer Complex
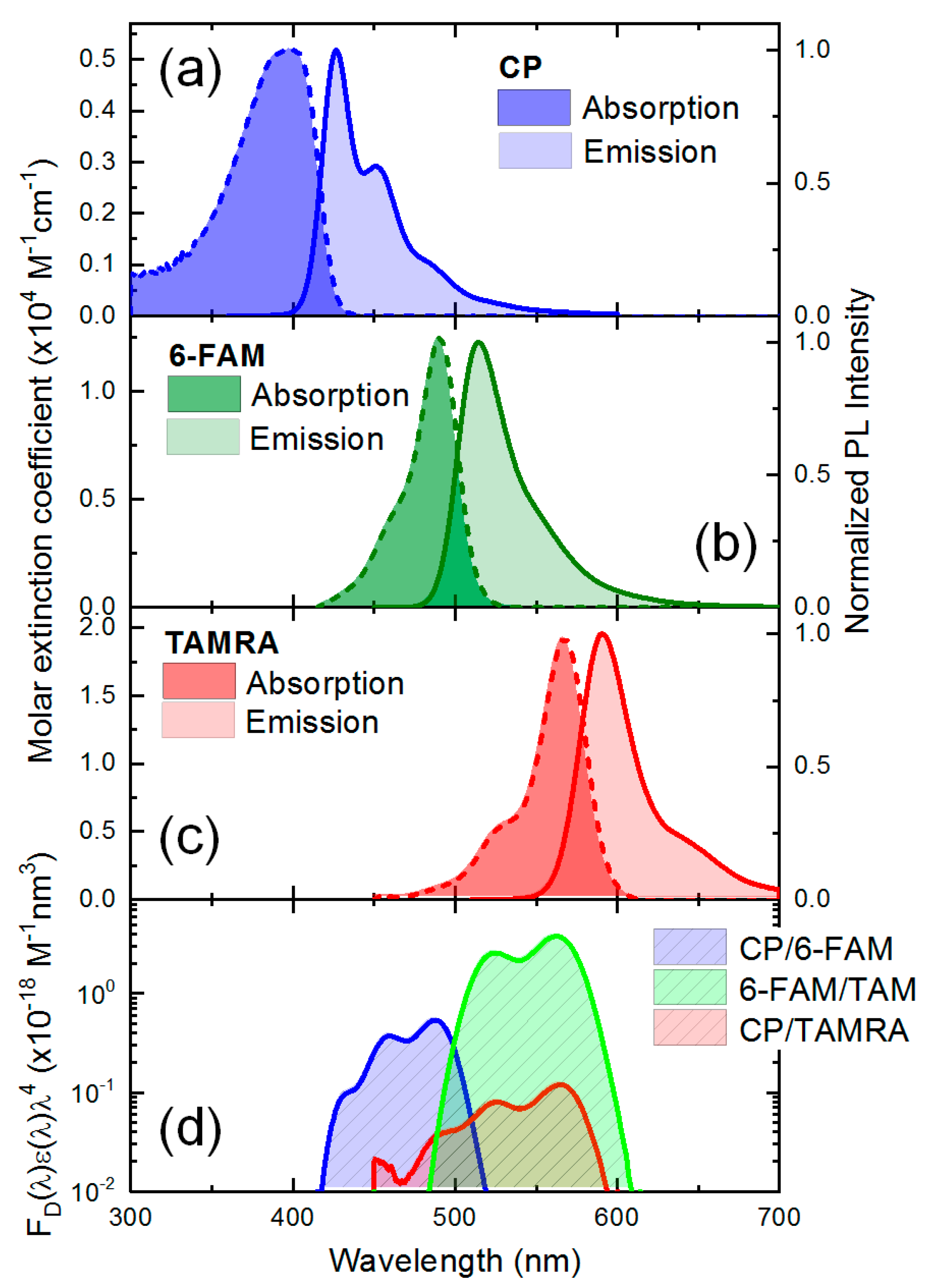
3.2. The Spectral Overlap between Conjugated Polymer, 6-FAM, and TAMRA
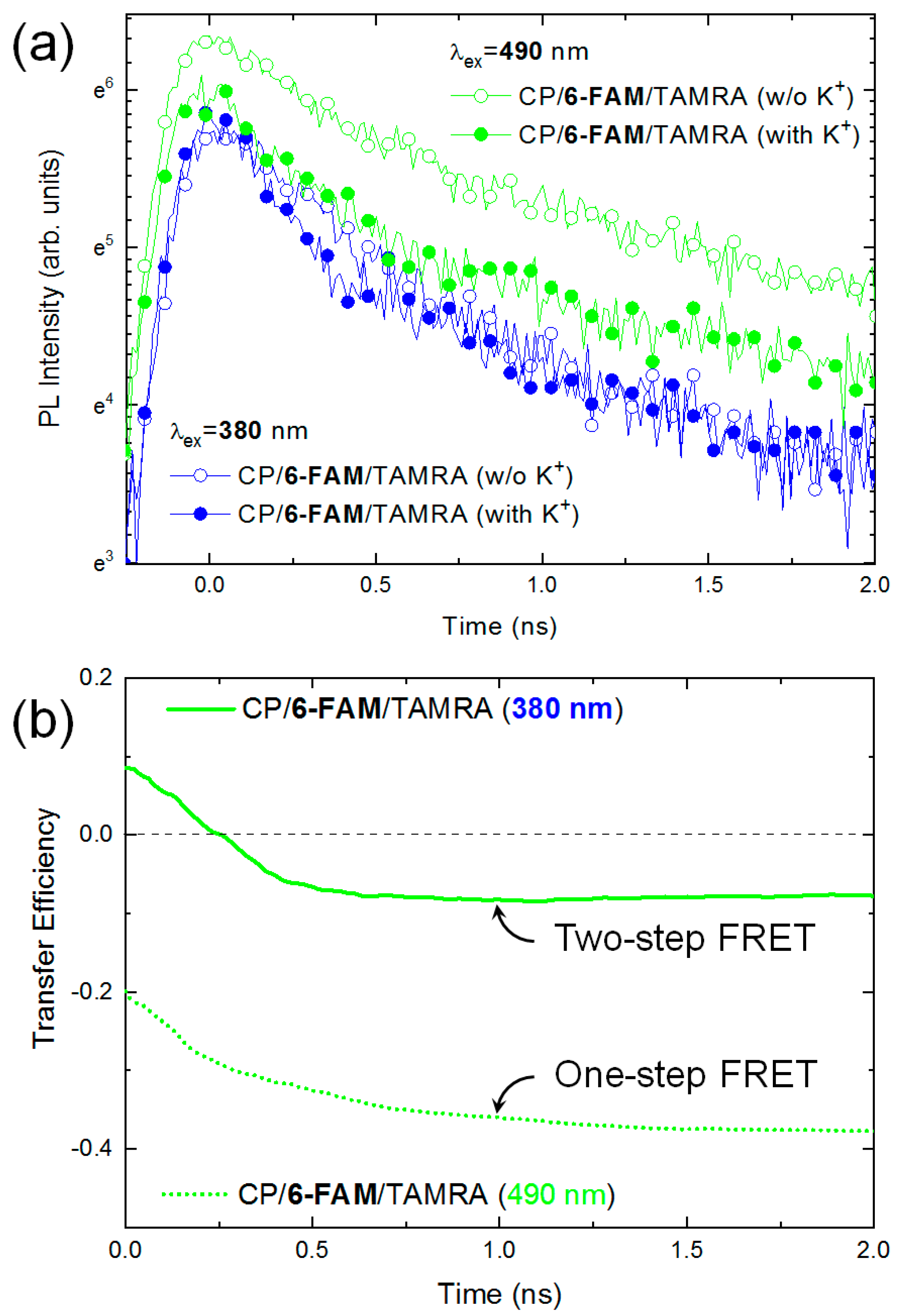
3.3. The Fluorescence Decay Dynamics of the Conjugated Polymer, 6-FAM, and TAMRA
3.3.1. The Fluorescence Decay of Conjugated Polymers
3.3.2. The Fluorescence Decay of 6-FAM
3.3.3. The Fluorescence Decay of TAMRA
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nguyen, B.L.; Jeong, J.E.; Jung, I.H.; Kim, B.; Le, V.S.; Kim, I.; Kyhm, K.; Woo, H.Y. Conjugated polyelectrolyte and aptamer based potassium assay via single- and two-Step fluorescence energy transfer with a tunable dynamic detection range. Adv. Funct. Mater. 2014, 24, 1748–1757. [Google Scholar] [CrossRef]
- Gaylord, B.S.; Heeger, A.J.; Bazan, G.C. DNA detection using water-soluble conjugated polymers and peptide nucleic acid probes. Proc. Natl. Acad. Sci. USA 2002, 99, 10954–10957. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Medintz, I.L.; Clapp, A.R.; Mattousi, H.; Goldman, E.R.; Fisher, B.; Mauro, J.M. Self-assembled nanoscale biosensors based on quantum dot FRET donors. Nat. Mater. 2003, 2, 630–683. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.-Y.; Yeh, H.-C.; Kuroki, M.T.; Wang, T.-H. Single-quantum-dot-based DNA nanosensor. Nat. Mater. 2005, 4, 826–831. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.; Nag, O.K.; Nayak, R.R.; Hwang, S.; Suh, H.; Woo, H.Y. Signal amplification by changing counterions in conjugated polyelectrolyte-based FRET DNA detection. Macromolecules 2009, 42, 2708–2714. [Google Scholar] [CrossRef]
- Clapp, A.R.; Medintz, I.L.; Mauro, J.M.; Fisher, B.R.; Bawendi, M.G.; Mattoussi, H. Fluorescence resonance energy transfer between quantum dot donors and dye-labeled protein acceptors. J. Am. Chem. Soc. 2004, 126, 301–310. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, D.; Zhang, P.; Gong, P.; Chen, C.; Gao, G.; Cai, L. A near infrared fluorescence resonance energy transfer based aptamer biosensor for insulin detection in human plasma. Chem. Commun. 2014, 50, 811–813. [Google Scholar] [CrossRef]
- Sapsford, K.E.; Berti, L.; Medintz, I.L. Materials for fluorescence resonance energy transfer analysis: beyond traditional donor–acceptor combinations. Angew. Chem. Int. Ed. 2006, 45, 4562–4588. [Google Scholar] [CrossRef]
- McQuade, D.T.; Pullen, A.E.; Swager, T.M. Conjugated polymer-based chemical sensors. Chem. Rev. 2000, 100, 2537–2574. [Google Scholar] [CrossRef]
- Liu, B.; Bazan, G.C. Homogeneous fluorescence-based DNA detection with water-soluble conjugated polymers. Chem. Mater. 2004, 16, 4467–4476. [Google Scholar] [CrossRef]
- Wang, S.; Gaylord, B.S.; Bazan, G.C. Fluorescein provides a resonance gate for FRET from conjugated polymers to DNA intercalated dyes. J. Am. Chem. Soc. 2004, 126, 5446–5451. [Google Scholar] [CrossRef] [PubMed]
- Jiang, G.; Susha, A.S.; Lutich, A.A.; Stefani, F.D.; Feldmann, J.; Rogach, A.L. Cascaded FRET in conjugated polymer/quantum dot/dye-labeled DNA complexes for DNA hybridization. ACS Nano 2009, 12, 4127–4131. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Hu, Y.; Zhang, Q.; Guo, Z.; Ge, G.; Wang, S.; Zhai, C.; Zhu, M. Competition-derived FRET-switching cationic conjugated polymer-Ir(III) complex probe for thrombin detection. Biosens. Bioelectron. 2018, 100, 132–138. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, L.; Shao, M.; Wu, Y.; Zeng, D.; Cai, X.; Duan, J.; Zhang, X.; Gao, X. Fine-tuning the quasi-3D geometry: Enabling efficient nonfullerene organic solar cells based on perylene diimides. ACS Appl. Mater. Interfaces 2018, 10, 762–768. [Google Scholar] [CrossRef] [PubMed]
- Wen, S.; Wu, Y.; Wang, Y.; Li, Y.; Liu, L.; Jiang, H.; Liu, Z.; Yang, R. Pyran-bridged indacenodithiophene as a building block for constructing efficient A-D-A-type nonfullerene acceptors for polymer solar cells. ChemSusChem 2018, 11, 360–366. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Wu, Y.; Zhang, Q.; Gao, X. Non-fullerene small molecule acceptors based on perylene diimides. J. Mater. Chem. A 2016, 4, 17604–17622. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Y.; Dong, J.; Yang, M.; Liu, M.; Zhang, Y.; Wen, J.; Ma, H.; Gao, X.; Chen, W.; et al. Chlorinated wide-bandgap donor polymer enabling annealing free nonfullerene solar cells with the efficiency of 11.5%. J. Phys. Chem. Lett. 2018, 9, 6955–6962. [Google Scholar] [CrossRef]
- Liu, Z.; Zeng, D.; Gao, X.; Li, P.; Zhang, Q.; Peng, X. Non-fullerene polymer acceptors based on perylene diimides in all-polymer solar cells. Sol. Energ. Mat. Sol. C. 2019, 189, 103–117. [Google Scholar] [CrossRef]
- Dunn, M.D.; Jimenez, R.M.; Chaput, J.C. Analysis of aptamer discovery and technology. Nat. Rev. Chem. 2017, 1, 1–16. [Google Scholar] [CrossRef]
- Song, S.; Wang, L.; Li, J.; Zhao, J.; Fan, C. Aptamer-based biosensors. TrAC-Trend Anal. Chem. 2008, 27, 108–117. [Google Scholar] [CrossRef]
- Han, K.; Liang, Z.; Zhou, N. Design strategies for aptamer-based biosensors. Sensors 2010, 10, 4541–4557. [Google Scholar] [CrossRef] [PubMed]
- Song, K.-M.; Lee, S.; Ban, C. Aptamers and their biological applications. Sensors 2012, 12, 612–631. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.T. G-quartets 40 years later: From 5′-GMP to molecular biology and supramolecular chemistry. Angew. Chem. Int. Ed. 2004, 43, 668–698. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Sugiyama, H. Formation of the G-quadruplex and i-motif structures in retinoblastoma susceptibility genes (Rb). Nucleic Acids Res. 2006, 34, 949–954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, S.P.; Canzoniero, L.M.; Choi, D.W. Ion homeostasis and apoptosis. Curr. Opin. Cell Biol. 2001, 13, 405–411. [Google Scholar] [CrossRef]
- Walz, W. Role of astrocytes in the clearance of excess extracellular potassium. Neurochem. Int. 2000, 36, 291–300. [Google Scholar] [CrossRef]
- Lippard, S.L.; Berg, J.M. Principles of Bioinorganic Chemistry, Chapter 1; University Science Books: Mill Valley, CA, USA, 1994. [Google Scholar]
- Schwartz, A.B. Potassium-related cardiac arrhythmias and their treatment. Angiology 1978, 29, 194–205. [Google Scholar] [CrossRef]
- Lakowicz, J.R.; Szmacinski, H. Fluorescence lifetime-based sensing of pH, Ca2+, KS and glucose. Sensor Actuat. B 1993, 11, 133–143. [Google Scholar] [CrossRef]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Gopich, I.V.; Szabo, A. Theory of the energy transfer efficiency and fluorescence lifetime distribution in single-molecule FRET. Proc. Natl. Acad. Sci. USA. 2012, 109, 7747–7752. [Google Scholar] [CrossRef] [Green Version]
- Kawahara, S.I.; Uchimaru, T.; Murata, S. Sequential multistep energy transfer: enhancement of efficiency of long-range fluorescence resonance energy transfer. Chem. Commun. 1999, 563–564. [Google Scholar] [CrossRef]
- Song, X.; Shi, J.; Nolan, J.; Swanson, B. Detection of multivalent interactions through two-tiered energy transfer. Anal. Biochem. 2001, 291, 133–141. [Google Scholar] [CrossRef]
- Watrob, H.M.; Pan, C.-P.; Barkley, M.D. Two-step FRET as a structural tool. J. Am. Chem. Soc. 2003, 125, 7336–7343. [Google Scholar] [CrossRef]
- Dale, R.E.; Eisinger, J.; Blumberg, W.E. The orientational freedom of molecular probes. The orientation factor in intramolecular energy transfer. Biophys. J. 1979, 26, 161–194. [Google Scholar] [CrossRef]
- Khrenova, M.; Topol, I.; Collins, J.; Nemukhin, A. Estimating orientation factors in the FRET theory of fluorescent proteins: The TagRFP-KFP pair and beyond. Biophys. J. 2015, 108, 126–132. [Google Scholar] [CrossRef]
- Woo, H.Y.; Vak, D.; Korystov, D.; Mikhailovsky, A.; Bazan, G.C.; Kim, D.-Y. Cationic conjugated polyelectrolytes with molecular spacers for efficient fluorescence energy transfer to dye-labeled DNA. Adv. Funct. Mater. 2007, 17, 290–295. [Google Scholar] [CrossRef]
- Bardeen, C. Exciton quenching and migration in single conjugated polymers. Science 2011, 331, 544–545. [Google Scholar] [CrossRef]
- Kim, I.; Kyhm, K.; Kang, M.; Woo, H.Y. Ultrafast combined dynamics of Förster resonance energy transfer and transient quenching in cationic polyfluorene/fluorescein-labelled single-stranded DNA complex. J. Lumin. 2014, 149, 185–189. [Google Scholar] [CrossRef]
- Cao, Q.; Li, Y.; Freisinger, E.; Qin, P.Z.; Sigel, R.K.O.; Mao, Z.-W. G-quadruplex DNA targeted metal complexes acting as potential anticancer drugs. Inorg. Chem. Front. 2017, 4, 10–32. [Google Scholar] [CrossRef]
- Lane, A.N.; Chaires, J.B.; Gray, R.D.; Trent, J.O. Stability and kinetics of G-quadruplex structures. Nucleic Acids Res. 2008, 36, 5482–5515. [Google Scholar] [CrossRef] [Green Version]
- Fox, M. Optical Properties of Solids.; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Clegg, R.M. The history of FRET: From conception through the labors of birth. In Reviews in Fluorescence; Springer: New York, NY, USA, 2006; Volume 3, pp. 1–45. [Google Scholar]
- Clegg, R.M. Fluorescence resonance energy transfer. Curr. Opin. Biotech. 1995, 6, 103–110. [Google Scholar] [CrossRef]
- Kyhm, K.; Kim, I.; Kang, M.; Woo, H.Y. Ultrafast dynamics of Förster resonance energy transfer and photo-induced charge transfer in cationic polyfluorene/dye-labeled DNA complex. J. Nanosci. Nanotechnol. 2012, 12, 7733–7738. [Google Scholar] [CrossRef]

| Fluorophores | Free | w/o K+ | with K+ | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (nm) | (ns) | (ns) | (ns) | (ns) | (ns) | |||||
| CPs | 380 | 0.43 (with K+) | 0.94 | 0.35 | 0.06 | 1.76 | 0.73 | 0.19 | 0.27 | 1.46 |
| 6-FAM | 380 | - | - | 0.49 | - | - | - | 0.33 | - | - |
| 490 | 3.72 | 0.51 | 0.36 | 0.49 | 2.09 | 0.61 | 0.25 | 0.39 | 2.18 | |
| TAMRA | 380 | 1.01 (with CPs) | - | 0.87 | - | - | - | 0.90 | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, I.; Jung, J.-E.; Lee, W.; Park, S.; Kim, H.; Jho, Y.-D.; Woo, H.Y.; Kyhm, K. Two-Step Energy Transfer Dynamics in Conjugated Polymer and Dye-Labeled Aptamer-Based Potassium Ion Detection Assay. Polymers 2019, 11, 1206. https://doi.org/10.3390/polym11071206
Kim I, Jung J-E, Lee W, Park S, Kim H, Jho Y-D, Woo HY, Kyhm K. Two-Step Energy Transfer Dynamics in Conjugated Polymer and Dye-Labeled Aptamer-Based Potassium Ion Detection Assay. Polymers. 2019; 11(7):1206. https://doi.org/10.3390/polym11071206
Chicago/Turabian StyleKim, Inhong, Ji-Eun Jung, Woojin Lee, Seongho Park, Heedae Kim, Young-Dahl Jho, Han Young Woo, and Kwangseuk Kyhm. 2019. "Two-Step Energy Transfer Dynamics in Conjugated Polymer and Dye-Labeled Aptamer-Based Potassium Ion Detection Assay" Polymers 11, no. 7: 1206. https://doi.org/10.3390/polym11071206
APA StyleKim, I., Jung, J.-E., Lee, W., Park, S., Kim, H., Jho, Y.-D., Woo, H. Y., & Kyhm, K. (2019). Two-Step Energy Transfer Dynamics in Conjugated Polymer and Dye-Labeled Aptamer-Based Potassium Ion Detection Assay. Polymers, 11(7), 1206. https://doi.org/10.3390/polym11071206