Addition of Graphite Filler to Enhance Electrical, Morphological, Thermal, and Mechanical Properties in Poly (Ethylene Terephthalate): Experimental Characterization and Material Modeling
Abstract
1. Introduction
2. Experimental Details
2.1. Materials
2.2. Preparation of PET/Graphite Micro-Composites
2.3. Characterization of Micro-Composites
3. Results and Discussions
3.1. Morphological Characterization of PET/Graphite Micro-Composites
3.2. Electrical Properties of PET/Graphite Micro-Composites
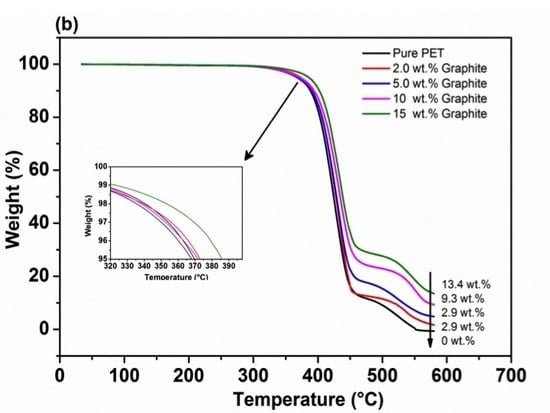
3.3. Thermal Analyses of PET/Graphite Micro-Composites
3.3.1. Crystallization Behavior
3.3.2. Thermal Stability of the Micro-Composites
4. Mechanical Characterization and Modeling of Filled Polymers
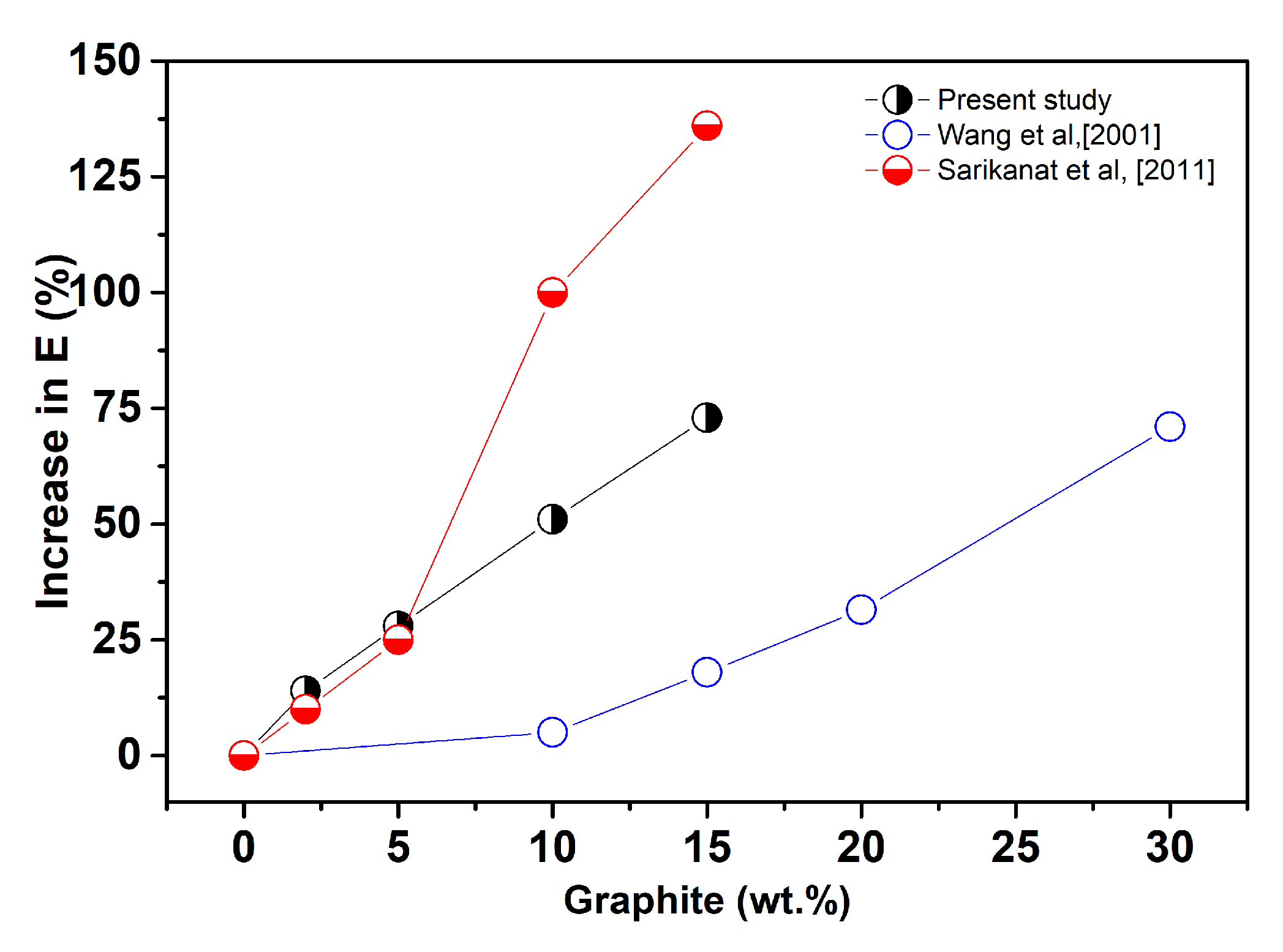
4.1. Mechanical Characterization
4.2. Constitutive Modeling of Filled Polymer
4.2.1. Small Strain-Based Particle-Filled Polymer Models
4.2.2. Large Strain-Based Particle-Filled Polymer Models
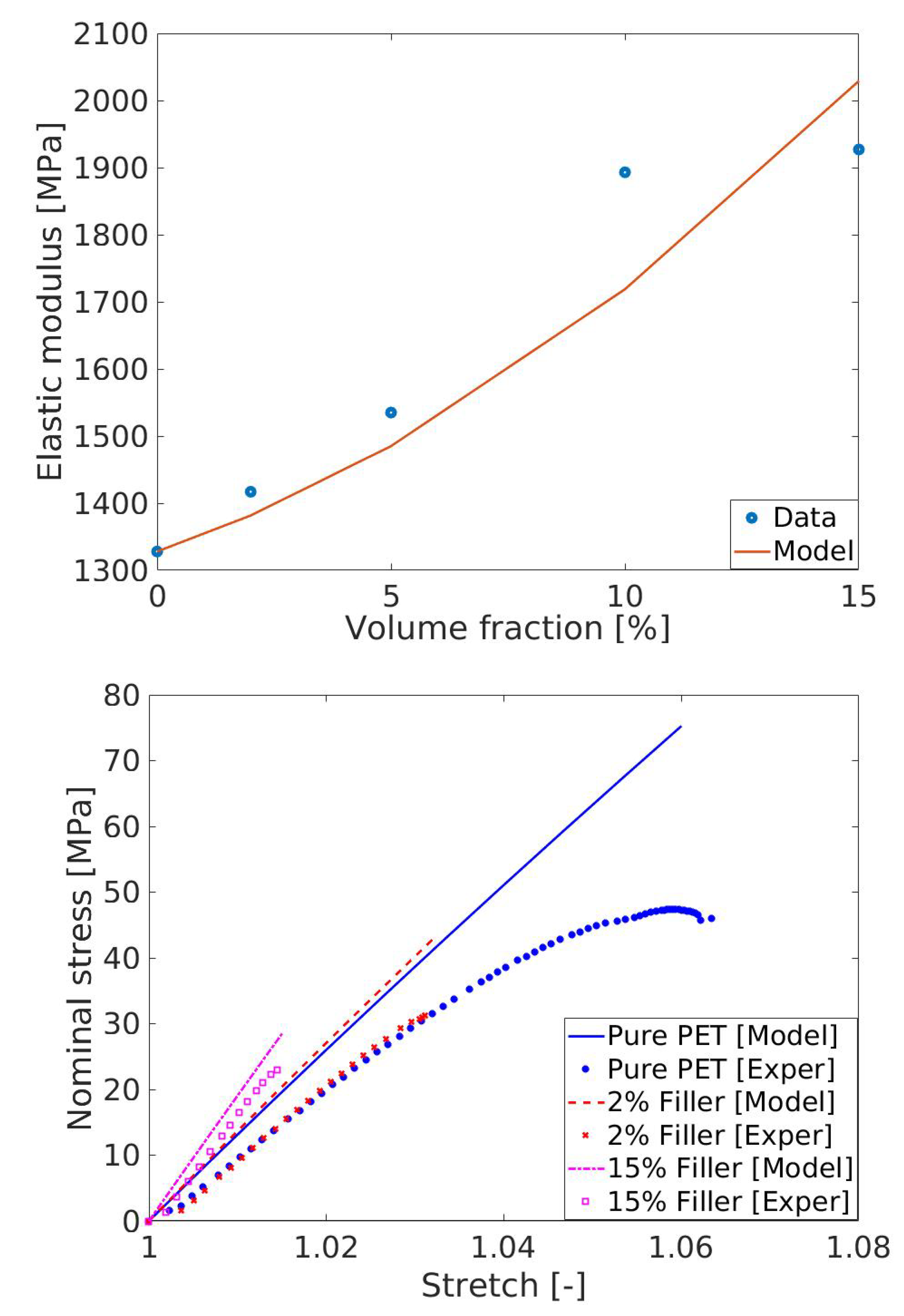
4.3. Parameter Identification and Model Validation
4.3.1. Linear Models
4.3.2. Non-Linear Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Karim, M.R.; Lee, C.J.; Lee, M.S. Synthesis and the characterization of conducting polythiophene/carbon nanotube composites. J. Polym. Sci. Part A Polym. Chem. 2006, 44, 5283–5290. [Google Scholar] [CrossRef]
- Jordan, J.; Jacob, K.I.; Tannenbaum, R.; Sharaf, M.A.; Jasiuk, I. Experimental trends in polymer nanocomposites-a review. Mater. Sci. Eng. A 2005, 393, 1–11. [Google Scholar] [CrossRef]
- Schadler, L.; Brinson, L.; Sawyer, W. Polymer nanocomposites: A small Part of The Story. JOM 2007, 59, 53–60. [Google Scholar] [CrossRef]
- Sun, X.; Sun, H.; Li, H.; Peng, H. Developing polymer composite materials: Carbon nanotubes or graphene? Adv. Mater. 2013, 25, 5153–5176. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.L.; Zhang, M.Q.; Rong, M.Z.; Friedrich, K. Tensile performance improvement of low nanoparticles filled-polypropylene composites. Compos. Sci. Technol. 2002, 62, 1327–1340. [Google Scholar] [CrossRef]
- Magaraphan, R.; Lilayuthalert, W.; Sirivat, A.; Schwank, J.W. Preparation, structure, properties and thermal behavior of rigid-rod polyimide/montmorillonite nanocomposites. Compos. Sci. Technol. 2001, 61, 1253–1264. [Google Scholar] [CrossRef]
- Xing, W.; Yang, W.; Yang, W.; Hu, Q.; Si, J.; Lu, H.; Yang, B.; Song, L.; Hu, Y.; Yuen, R.K.K. Functionalized Carbon Nanotubes with Phosphorus- and Nitrogen-Containing Agents: Effective Reinforcer for Thermal, Mechanical, and Flame-Retardant Properties of Polystyrene Nanocomposites. ACS Appl. Mater. Interfaces 2016, 8, 26266–26274. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.E.; Wang, L.L.; Chen, H.; Yang, W.; Yuen, A.C.Y.; Chen, T.B.Y.; Luo, C.; Bi, W.M.; Hu, E.Z.; Zhang, J.; et al. Comparative Studies on Thermal, Mechanical, and Flame Retardant Properties of PBT Nanocomposites via Different Oxidation State Phosphorus-Containing Agents Modified Amino-CNTs. Nanomaterials 2018, 8, 70. [Google Scholar] [CrossRef]
- Sahoo, N.G.; Rana, S.; Cho, J.W.; Li, L.; Chan, S.H. Polymer nanocomposites based on functionalized carbon nanotubes. Prog. Polym. Sci. 2010, 35, 837–867. [Google Scholar] [CrossRef]
- Margolis, J.M. Conductive Polymers and Plastics; Chapman & Hall: London, UK, 1989. [Google Scholar]
- Rupprecht, L. Conductive Polymers and Plastics: In Industrial Applications; William Andrew: NewYork, NY, USA, 1999. [Google Scholar]
- Chung, D. Electrical applications of carbon materials. J. Mater. Sci. 2004, 39, 2645–2661. [Google Scholar] [CrossRef]
- Sengupta, R.; Bhattacharya, M.; Bandyopadhyay, S.; Bhowmick, A.K. A review on the mechanical and electrical properties of graphite and modified graphite reinforced polymer composites. Prog. Polym. Sci. 2011, 36, 638–670. [Google Scholar] [CrossRef]
- Brydson, J. Plastic Materials, 7th ed.; Butterworth-Heineman Linacre House: Oxford, UK, 1999. [Google Scholar]
- Harper, C.A.; Petrie, E.M. Plastics Materials and Processes: A Concise Encyclopedia; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Li, M.; Jeong, Y.G. Poly (ethylene terephthalate)/exfoliated graphite nanocomposites with improved thermal stability, mechanical and electrical properties. Compos. Part A Appl. Sci. Manuf. 2011, 42, 560–566. [Google Scholar] [CrossRef]
- Paul, S.; Kim, D.-W. Preparation and characterization of highly conductive transparent films with single-walled carbon nanotubes for flexible display applications. Carbon 2009, 47, 2436–2441. [Google Scholar] [CrossRef]
- Hussain, F.; Hojjati, M.; Okamoto, M.; Gorga, R.E. Review article: Polymer matrix nanocomposites, processing, manufacturing, and application: An overview. J. Compos. Mater. 2006, 40, 1511–1575. [Google Scholar] [CrossRef]
- Calixto, C.M.F.; Mendes, R.K.; Oliveira, A.C.d.; Ramos, L.A.; Cervini, P.; Cavalheiro, É.T.G. Development of graphite-polymer composites as electrode materials. Mater. Res. 2007, 10, 109–114. [Google Scholar] [CrossRef]
- Sun, C.; Zhao, W.; Chen, S. Studies on the comprehensive performance of graphite and additives filled high density polyethylene composites. J. Appl. Polym. Sci. 2008, 107, 4000–4004. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, J.; Wang, R.; Hua, Z. Mechanical and rheological properties of HDPE/graphite composite with enhanced thermal conductivity. Polym. Compos. 2001, 22, 97–103. [Google Scholar] [CrossRef]
- Krupa, I.; Novák, I.; Chodák, I. Electrically and thermally conductive polyethylene/graphite composites and their mechanical properties. Synth. Met. 2004, 145, 245–252. [Google Scholar] [CrossRef]
- Akinci, A. Mechanical and structural properties of polypropylene composites filled with graphite flakes. Arch. Mater. Sci. Eng. 2009, 35, 91–94. [Google Scholar]
- Page, D.J.; Gopakumar, T.G. Properties and crystallization of maleated polypropylene/graphite flake nanocomposites. Polym. J. 2006, 38, 920–929. [Google Scholar] [CrossRef]
- He, F.; Fan, J.; Lau, S. Thermal, mechanical, and dielectric properties of graphite reinforced poly(vinylidene fluoride) composites. Polym. Test. 2008, 27, 964–970. [Google Scholar] [CrossRef]
- Wakabayashi, K.; Brunner, P.J.; Masuda, J.I.; Hewlett, S.A.; Torkelson, J.M. Polypropylene-graphite nanocomposites made by solid-state shear pulverization: Effects of significantly exfoliated, unmodified graphite content on physical, mechanical and electrical properties. Polymer 2010, 51, 5525–5531. [Google Scholar] [CrossRef]
- Kelly, B.T. Physics of Graphite; Applied Science Publishers: London, UK, 1981. [Google Scholar]
- Lee, S.M. Handbook of Composite Reinforcements; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Krupa, I.; Chodák, I. Physical properties of thermoplastic/graphite composites. Eur. Polym. J. 2001, 37, 2159–2168. [Google Scholar] [CrossRef]
- Ramanathan, T.; Stankovich, S.; Dikin, D.A.; Liu, H.; Shen, H.; Nguyen, S.T.; Brinson, L.C. Graphitic nanofillers in PMMA nanocomposites-An investigation of particle size and dispersion and their influence on nanocomposite properties. J. Polym. Sci. Part B Polym. Phys. 2007, 45, 2097–2112. [Google Scholar] [CrossRef]
- Xin, F.; Li, L.; Chan, S.H.; Zhao, J. Influences of carbon fillers on electrical conductivity and crystallinity of polyethylene terephthalate. J. Compos. Mater. 2012, 46, 1091–1099. [Google Scholar] [CrossRef]
- Guth, L. Theory of filler reinforcement. J. Appl. Phys. 1945, 16, 20–25. [Google Scholar] [CrossRef]
- Guth, L.; Gold, O. On the hydrodynamical theory of the viscosity of suspensions. Phys. Rev. 1938, 53, 322. [Google Scholar]
- Bergstroem, J.; Boyce, M.C. Mechanical behaviour of particle filled elastomers. Rubber Chem. Technol. 1999, 72, 633. [Google Scholar] [CrossRef]
- Production Information of LIGHTER93: Polyethylene Terephthalate (PET) Resins. Available online: https://www.equipolymers.com/pdf/technicaldatasheetc93en.pdf (accessed on 12 August 2019).
- Sandler, J.; Kirk, J.; Kinloch, I.; Shaffer, M.; Windle, A. Ultra-low electrical percolation threshold in carbon-nanotube-epoxy composites. Polymer 2003, 44, 5893–5899. [Google Scholar] [CrossRef]
- Sandler, J.; Shaffer, M.; Prasse, T.; Bauhofer, W.; Schulte, K.; Windle, A. Development of a dispersion process for carbon nanotubes in an epoxy matrix and the resulting electrical properties. Polymer 1999, 40, 5967–5971. [Google Scholar] [CrossRef]
- Pang, H.; Xu, L.; Yan, D.-X.; Li, Z.-M. Conductive polymer composites with segregated structures. Prog. Polym. Sci. 2014, 39, 1908–1933. [Google Scholar] [CrossRef]
- Clingerman, M.L.; Weber, E.H.; King, J.A.; Schulz, K.H. Development of an additive equation for predicting the electrical conductivity of carbon-filled composites. J. Appl. Polym. Sci. 2003, 88, 2280–2299. [Google Scholar] [CrossRef]
- Young, R.J.; Lovell, P.A. Introduction to Polymers, 3rd ed.; CRC: Boca Raton, FL, USA, 2011. [Google Scholar]
- Bauhofer, W.; Kovacs, J.Z. A review and analysis of electrical percolation in carbon nanotube polymer composites. Compos. Sci. Technol. 2009, 69, 1486–1498. [Google Scholar] [CrossRef]
- She, Y.; Chen, G.; Wu, D. Fabrication of polyethylene/graphite nanocomposite from modified expanded graphite. Polym. Int. 2007, 56, 679–685. [Google Scholar] [CrossRef]
- Hossain, M. Modelling the curing process in particle-filled electro-active polymers with a dispersion anisotropy. Contin. Mech. Thermodyn. 2019, 1–17. [Google Scholar] [CrossRef]
- Mehnert, M.; Hossain, M.; Steinmann, P. Experimental and numerical investigations of the electro-viscoelastic behaviour of VHB 4905. Eur. J. Mech. A/Solids 2019, 77, 103797. [Google Scholar] [CrossRef]
- Zhang, M.; Li, D.J.; Wu, D.F.; Yan, C.H.; Lu, P.; Qiu, G.M. Poly (ethylene erephthalate)/expanded graphite conductive composites: Structure, properties, and transport behavior. J. Appl. Polym. Sci. 2008, 108, 1482–1489. [Google Scholar] [CrossRef]
- Hu, G.; Feng, X.; Zhang, S.; Yang, M. Crystallization behavior of poly (ethylene terephthalate)/multiwalled carbon nanotubes composites. J. Appl. Polym. Sci. 2008, 108, 4080–4089. [Google Scholar] [CrossRef]
- Yoo, H.J.; Jung, Y.C.; Cho, J.W. Effect of interaction between poly(ethylene terephthalate) and carbon nanotubes on the morphology and properties of their nanocomposites. J. Polym. Sci. Part B Polym. Phys. 2008, 46, 900–910. [Google Scholar] [CrossRef]
- Al-Jabareen, A.; Al-Bustami, H.; Harel, H.; Marom, G. Improving the oxygen barrier properties of polyethylene terephthalate by graphite nanoplatelets. J. Appl. Polym. Sci. 2013, 128, 1534–1539. [Google Scholar] [CrossRef]
- Yesil, S.; Bayram, G. Poly (ethylene terephthalate)/carbon nanotube composites prepared with chemically treated carbon nanotubes. Polym. Eng. Sci. 2011, 51, 1286–1300. [Google Scholar] [CrossRef]
- Antoniadis, G.; Paraskevopoulos, K.; Bikiaris, D.; Chrissafis, K. Meltcrystallization mechanism of poly (ethylene terephthalate)/multi-walled carbon nanotubes prepared by in situ polymerization. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 1452–1466. [Google Scholar] [CrossRef]
- Brup, J.; Immergut, E.H.; Grulke, E.A.; Abe, A.; Bloch, D.R. (Eds.) Polymer Handbook, 4th ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Wang, Y.; Deng, J.; Wang, K.; Zhang, Q.; Fu, Q. Morphology, crystallization, and mechanical properties of poly (ethylene terephthalate)/multiwall carbon nanotube nanocomposites via in situ polymerization with very low content of multiwall carbon nanotubes. J. Appl. Polym.Sci. 2007, 104, 3695–3701. [Google Scholar] [CrossRef]
- Zaman, H.U.; Hun, P.D.; Khan, R.A.; Yoon, K.B. Effect of Multi-walled Carbon Nanotubes on Morphology, Mechanical and Thermal Properties of Poly (ethylene Terephthalate) Nanocomposites. Fuller. Nanotub. Carbon Nanostruct. 2013, 21, 701–711. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, R.; Dong, Z.; Huang, X.; Zhang, D. Morphology, crystallization, and mechanical properties of poly (ethylene terephthalate)/multiwalled carbon nanotubes composites. J. Appl. Polym. Sci. 2011, 120, 3460–3468. [Google Scholar] [CrossRef]
- Agarwal, U.S.; Nisal, A.; Joseph, R. PET-SWNT nanocomposites through ultrasound assisted dissolution- evaporation. Eur. Polym. J. 2007, 43, 2279–2285. [Google Scholar]
- Anoop, K.; Agarwal, A.U.; Joseph, R. Carbon nanotubes induced crystallization of poly (ethylene terephthalate). Polymer 2006, 47, 3976–3980. [Google Scholar] [CrossRef]
- Campbell, D.; Pethrick, R.A.; White, J.R. Polymer Characterization: Physical Techniques; CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Gao, Y.; Wang, Y.; Shi, J.; Bai, H.; Song, B. Functionalized multi-walled carbon nanotubes improve nonisothermal crystallization of poly (ethylene terephthalate). Polym. Test. 2008, 27, 179–188. [Google Scholar] [CrossRef]
- Cho, D.; Lee, S.; Yang, G.; Fukushima, H.; Drzal, L.T. Dynamic Mechanical and Thermal Properties of Phenylethynyl-Terminated Polyimide Composites Reinforced With Expanded Graphite Nanoplatelets. Macromol. Mater. Eng. 2005, 290, 179–187. [Google Scholar] [CrossRef]
- Lee, H.J.; Oh, S.J.; Choi, J.Y.; Kim, J.W.; Han, J.; Tan, L.S.; Baek, J.B. In situ synthesis of poly (ethylene terephthalate)(PET) in ethylene glycol containing terephthalic acid and functionalized multiwalled carbon nanotubes (MWNTs) as an approach to MWNT/PET nanocomposites. Chem. Mater. 2005, 17, 5057–5064. [Google Scholar] [CrossRef]
- Bandyopadhyay, J.; Ray, S.S.; Bousmina, M. Thermal and Thermomechanical Properties of Poly (ethylene terephthalate) Nanocomposites. J. Ind. Eng. Chem. 2007, 13, 614–623. [Google Scholar]
- Otieno, G.; Kim, J.Y. Conductive graphite/polyurethane composite films using amphiphilic reactive dispersant: Synthesis and characterization. J. Ind. Eng. Chem. 2008, 14, 187–193. [Google Scholar] [CrossRef]
- Steinmann, P.; Hossain, M.; Possart, G. Hyperelastic models for rubber-like materials: Consistent tangent operators and suitability for Treloar’s data. Arch. Appl. Mech. 2012, 82, 1183–1217. [Google Scholar] [CrossRef]
- Hossain, M.; Steinmann, P. More hyperelastic models for rubber-like materials: Consistent tangent operator and comparative study. J. Mech. Behav. Mater. 2013, 22, 27–50. [Google Scholar] [CrossRef]
- Hossain, M.; Kabir, N.; Amin, A.F.M.S. Eight-chain and full-network models and their modified versions for rubber hyperelasticity: A comparative study. J. Mech. Behav. Mater. 2015, 24, 11–24. [Google Scholar] [CrossRef]
- Ahret, A.E. On a molecular statistical basis for Ogden’s model of rubber elasticity. J. Mech. Phys. Solids 2015, 78, 249–268. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Hossain, M.; Vu, D.K.; Steinmann, P. Experimental study and numerical modelling of VHB 4910 polymer. Comput. Mater. Sci. 2012, 59, 65–74. [Google Scholar] [CrossRef]
- Liao, Z.; Yao, X.; Zhang, L.; Hossain, M.; Wang, J.; Zang, S. Temperature and strain rate dependent large tensile deformation and tensile failure behavior of transparent polyurethane at intermediate strain rates. Int. J. Impact Eng. 2019, 129, 152–167. [Google Scholar] [CrossRef]
- Mullins, L.; Tobin, N.R. Stress softening of rubber vulcanizates: Part 1. Use of a strain amplification factor to describe the elastic behavior of filler-reinforced vulcanized rubber. J. Appl. Polym. Sci. 1965, 9, 2993–3009. [Google Scholar] [CrossRef]








| Graphite (wt.%) | ||||||
|---|---|---|---|---|---|---|
| 0 | 72.9 ± 1.2 | 133.5 ± 0.1 | 253.4 ± 0.4 | 245.9 ± 0.9 | 209.2 ± 0.1 | 11.8 ± 1.8 |
| 2 | 73.9 ± 0.1 | 122.6 ± 0.5 | 254.4 ± 0.9 | 249.1 ± 0.1 | 218.1 ± 0.8 | 15.9 ± 2.0 |
| 5 | 74.2 ± 0.1 | 120.5 ± 1.5 | 254.9 ± 1.0 | 249.2 ± 0.4 | 220.5 ± 0.5 | 15.6 ± 1.6 |
| 10 | 73.8 ± 0.1 | 119.1 ± 0.5 | 253.5 ± 1.7 | 249.8 ± 0.2 | 220.1 ± 0.4 | 15.8 ± 2.0 |
| 15 | 65.0 ± 0.5 | 116.5 ± 0.1 | 253.7 ± 1.0 | 249.9 ± 0.4 | 221.2 ± 0.2 | 19.8 ± 1.1 |
| 20 | 64.1 ± 0.1 | 111.6 ± 0.7 | 253.0 ± 0.9 | 250.5 ± 0.2 | 223.4 ± 0.1 | 21.3 ± 2.8 |
| Graphite (wt.%) | Air | |
|---|---|---|
| 0 | 382.3 ± 1.4 | 370.1 ± 1.0 |
| 2 | 389.8 ± 0.8 | 373.1 ± 6.0 |
| 5 | 387.7 ± 0.4 | 368.0 ± 4.3 |
| 10 | 386.7 ± 3.0 | 372.7 ± 2.6 |
| 15 | 391.7 ± 0.5 | 383.7 ± 1.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, B.A.; Al-Mubaddel, F.S.; Karim, M.R.; Hossain, M.; Al-Mutairi, A.S.; Wilkinson, A.N. Addition of Graphite Filler to Enhance Electrical, Morphological, Thermal, and Mechanical Properties in Poly (Ethylene Terephthalate): Experimental Characterization and Material Modeling. Polymers 2019, 11, 1411. https://doi.org/10.3390/polym11091411
Alshammari BA, Al-Mubaddel FS, Karim MR, Hossain M, Al-Mutairi AS, Wilkinson AN. Addition of Graphite Filler to Enhance Electrical, Morphological, Thermal, and Mechanical Properties in Poly (Ethylene Terephthalate): Experimental Characterization and Material Modeling. Polymers. 2019; 11(9):1411. https://doi.org/10.3390/polym11091411
Chicago/Turabian StyleAlshammari, Basheer A., Fahad S. Al-Mubaddel, Mohammad Rezaul Karim, Mokarram Hossain, Abdullah S. Al-Mutairi, and Arthur N. Wilkinson. 2019. "Addition of Graphite Filler to Enhance Electrical, Morphological, Thermal, and Mechanical Properties in Poly (Ethylene Terephthalate): Experimental Characterization and Material Modeling" Polymers 11, no. 9: 1411. https://doi.org/10.3390/polym11091411
APA StyleAlshammari, B. A., Al-Mubaddel, F. S., Karim, M. R., Hossain, M., Al-Mutairi, A. S., & Wilkinson, A. N. (2019). Addition of Graphite Filler to Enhance Electrical, Morphological, Thermal, and Mechanical Properties in Poly (Ethylene Terephthalate): Experimental Characterization and Material Modeling. Polymers, 11(9), 1411. https://doi.org/10.3390/polym11091411