Dielectric Spectroscopy and Thermal Properties of Poly(lactic) Acid Reinforced with Carbon-Based Particles: Experimental Study and Design Theory
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Nanocomposites and Test Samples
2.2. Experimental Methods
2.2.1. Scanning Electron Microscopy (SEM)
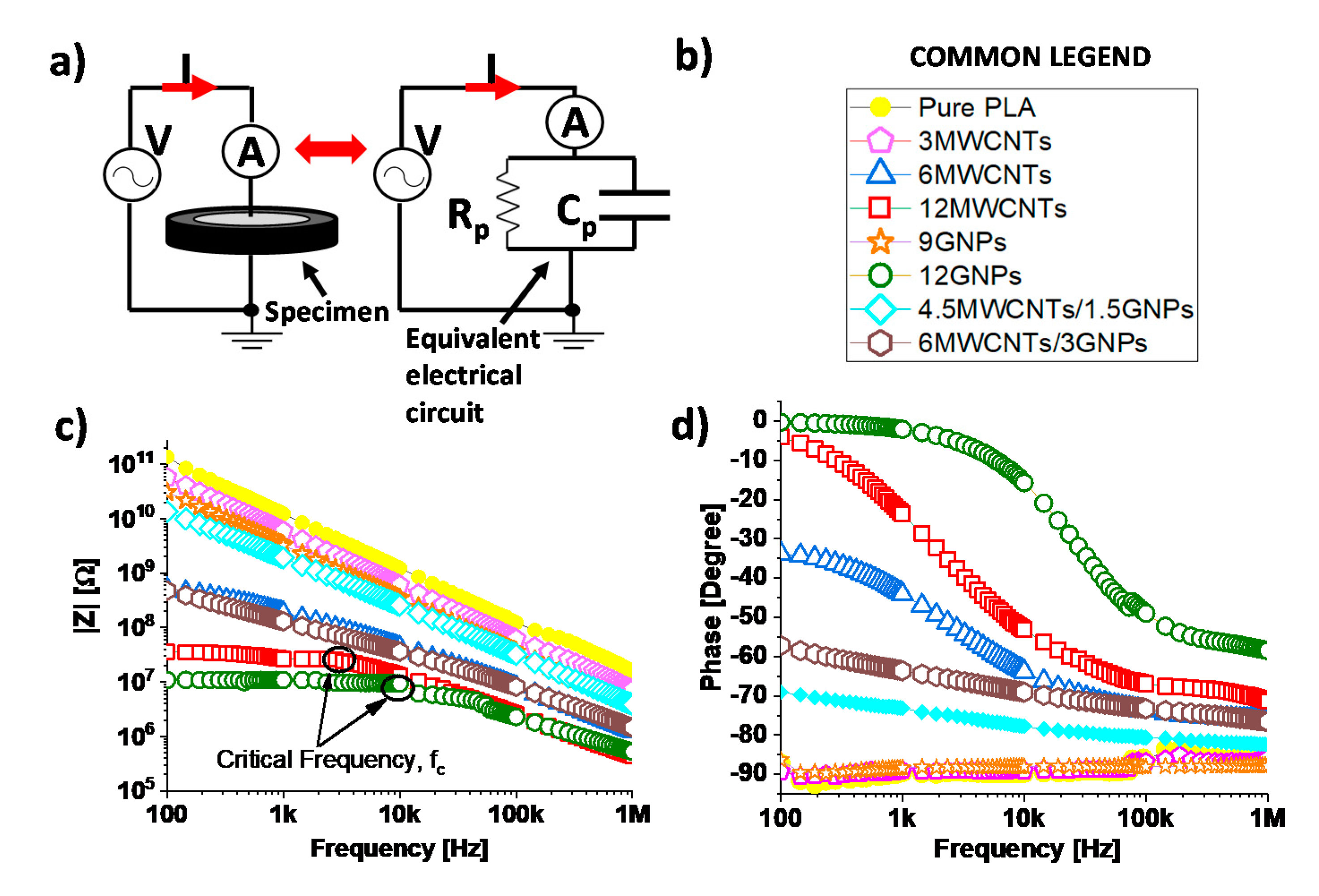
2.2.2. Electrical Impedance Spectroscopy (EIS)
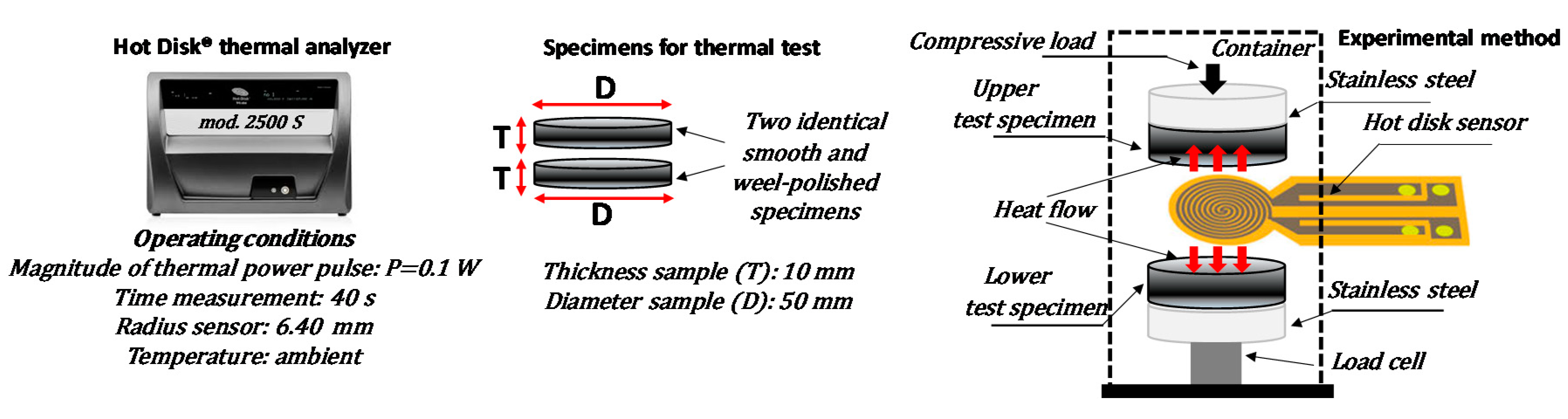
2.2.3. Thermal Measurements
2.2.4. Design of Experiment (DoE)
3. Results and Discussion
3.1. Morphological Analysys
3.2. Dieletric Spectroscopy
3.2.1. AC Electrical Conductivity and Electrical Percolation Threshold
3.2.2. Electrical Impedance: Modulus and Phase
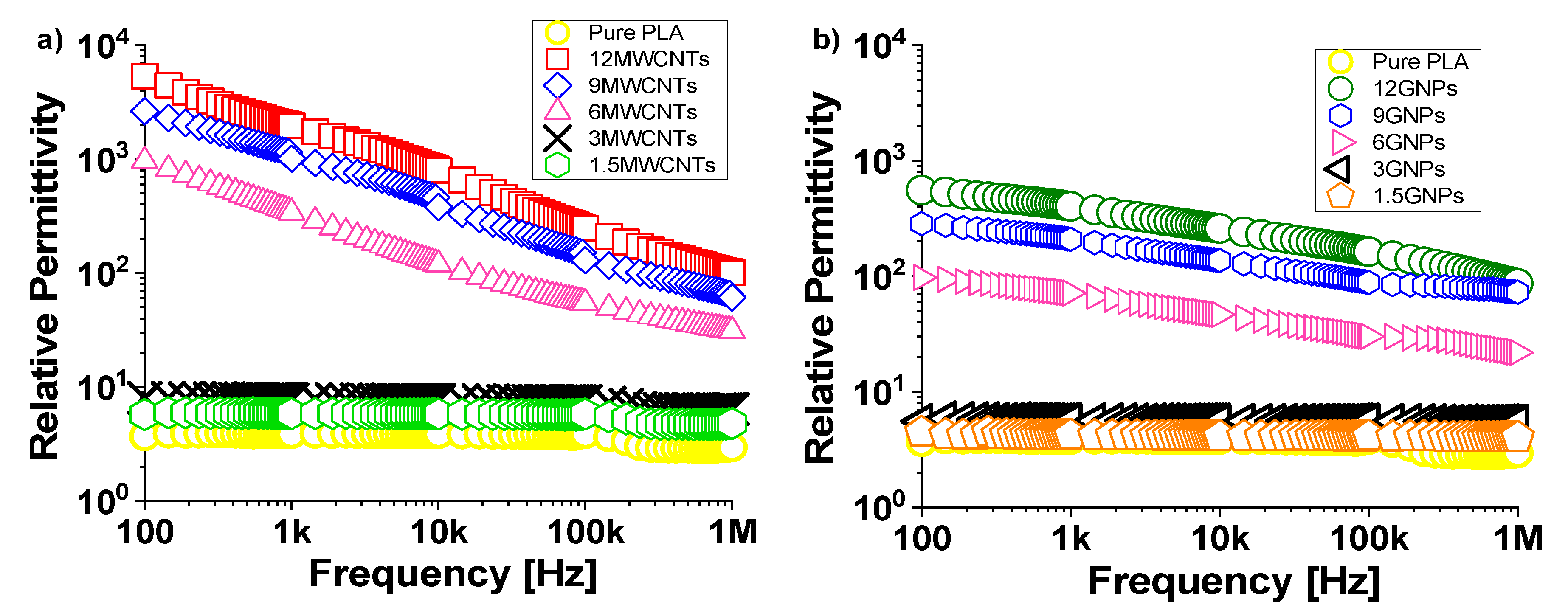
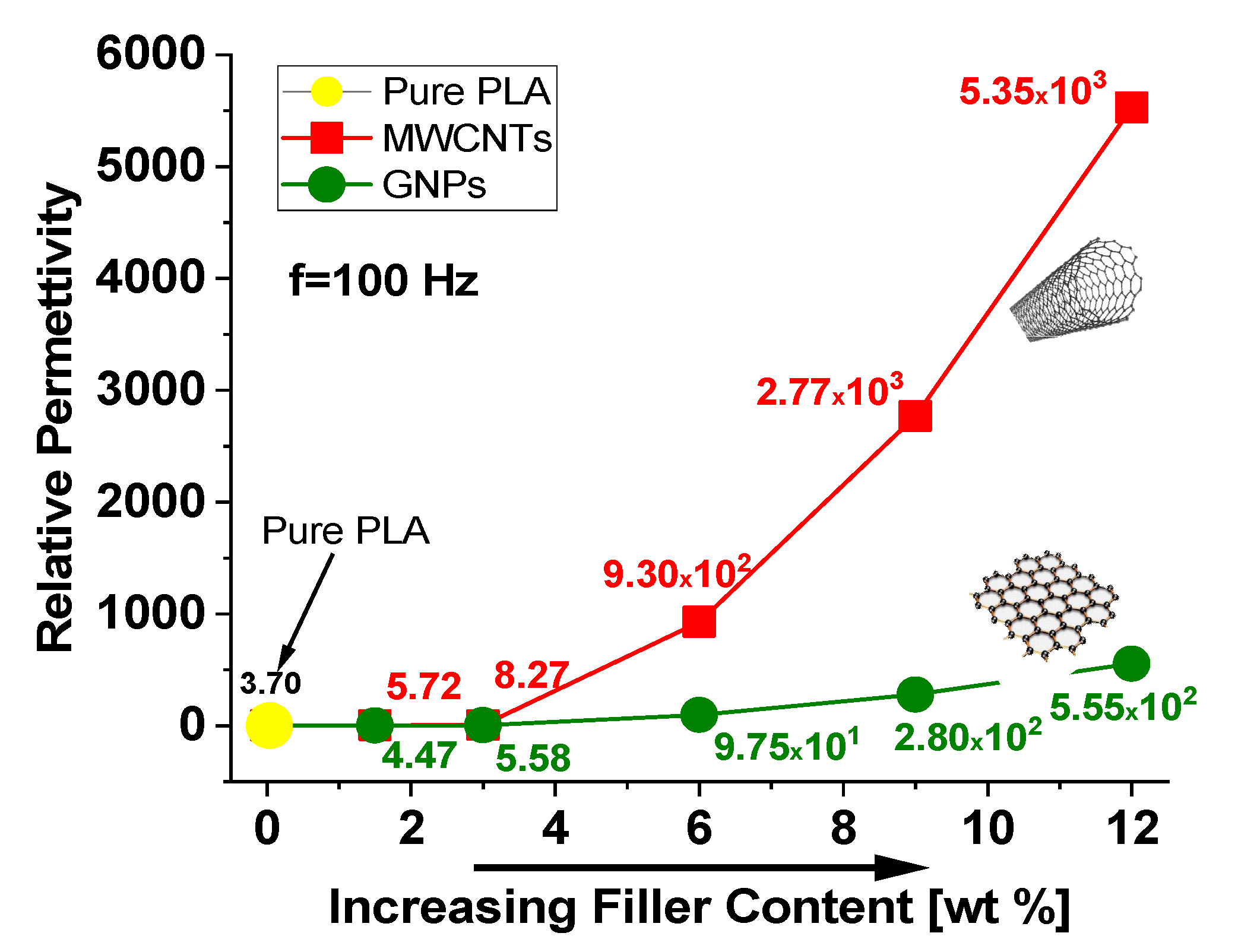
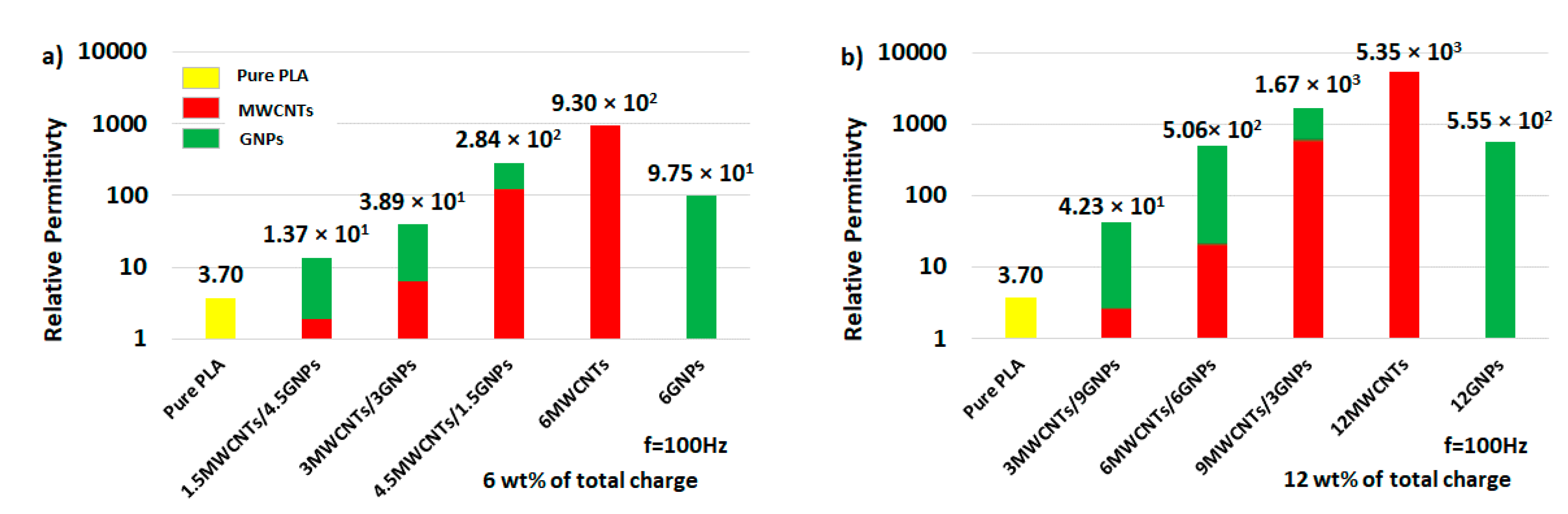
3.2.3. Dielectric Properties: Relative Permittivity
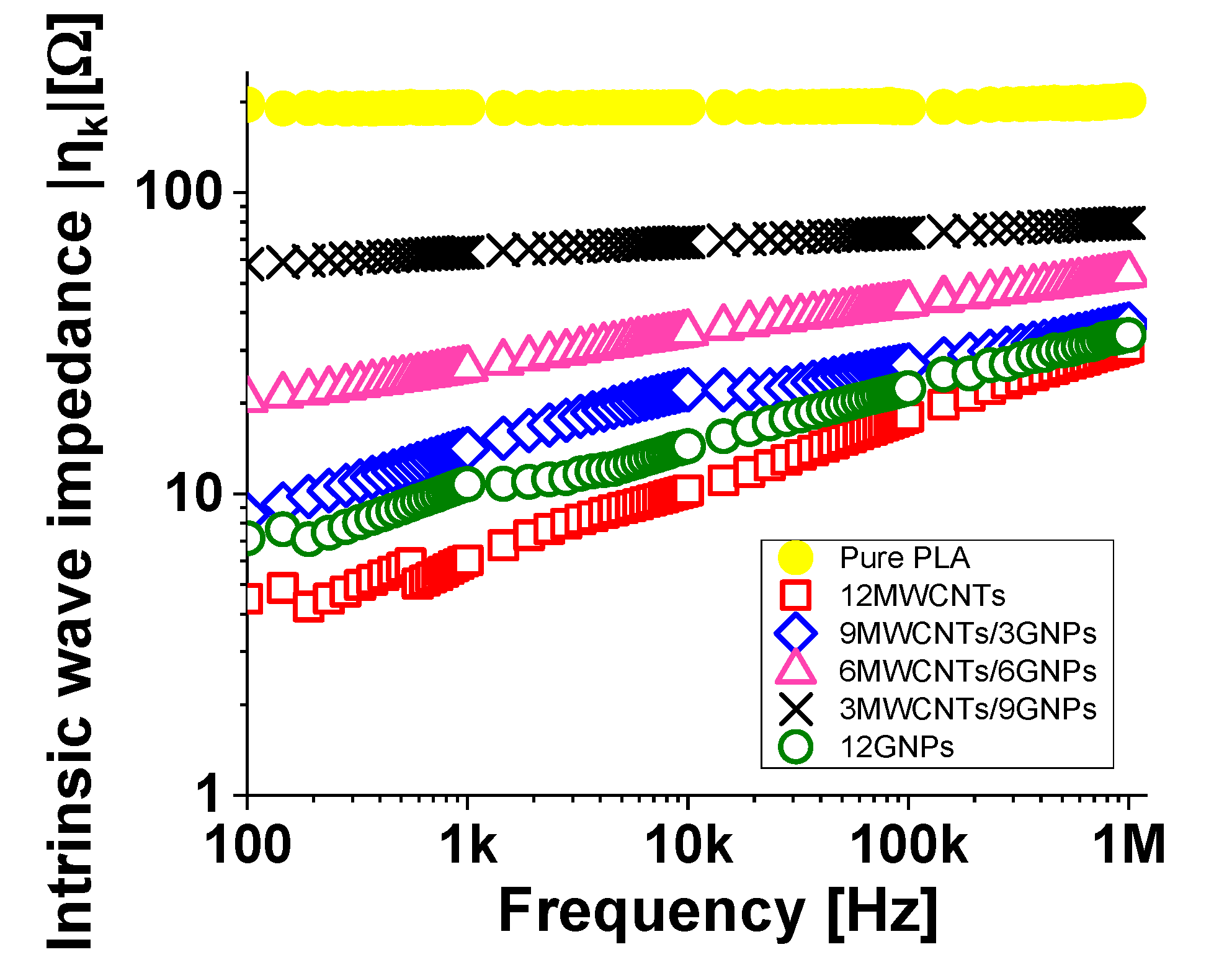
3.2.4. Dielectric Properties: Intrinsic Wave Impedance
3.3. Thermal Properties
3.4. Design of Experiment (DoE): Dex Scatter Plot and Main Factor Plot for the Relative Permettivity and the Thermal Conductivity
3.5. Response Surface Methodology (RSM)
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, S.H.; Liu, P.; Mokasdar, A.; Hou, L. Additive manufacturing and its societal impact: A literature review. Int. J. Adv. Manuf. Technol. 2013, 67, 1191–1203. [Google Scholar] [CrossRef]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L. Optimization of fused deposition modeling process parameters: A review of current research and future prospects. Adv. Manuf. 2015, 3, 42–53. [Google Scholar] [CrossRef]
- Durakovic, B. Design for Additive Manufacturing: Benefits, Trends and Challenges. Period. Eng. Nat. Sci. 2018, 6, 179–191. [Google Scholar] [CrossRef] [Green Version]
- Singamneni, S.; Yifan, L.V.; Hewitt, A.; Chalk, R.; Thomas, W.; Jordison, D. Additive Manufacturing for the Aircraft Industry: A Review. J. Aeronaut. Aerosp. Eng. 2019, 8, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Jamróz, W.; Szafraniec, J.; Kurek, M.; Jachowicz, R. 3D printing in pharmaceutical and medical applications–recent achievements and challenges. Pharm. Res. 2018, 35, 176. [Google Scholar] [CrossRef] [Green Version]
- Farré-Guasch, E.; Wolff, J.; Helder, M.N.; Schulten, E.A.; Forouzanfar, T.; Klein-Nulend, J. Application of additive manufacturing in oral and maxillofacial surgery. J. Oral Maxillofac. Surg. 2015, 7, 2408–2418. [Google Scholar]
- Hoerber, J.; Glasschroeder, J.; Pfeffer, M.; Schilp, J.; Zaeh, M.; Franke, J. Approaches for additive manufacturing of 3D electronic applications. Procedia CIRP 2014, 17, 806–811. [Google Scholar] [CrossRef] [Green Version]
- Kruth, J.P.; Leu, M.C.; Nakagawa, T. Progress in additive manufacturing and rapid prototyping. CIRP Ann. Manuf. Technol. 1998, 47, 525–540. [Google Scholar] [CrossRef]
- Kruth, J.P.; Wang, X.; Laoui, T.; Froyen, L. Lasers and materials in selective laser sintering. Assem. Autom. 2003, 23, 357–371. [Google Scholar] [CrossRef]
- Guo, S.Z.; Gosselin, F.; Guerin, N.; Lanouette, A.M.; Heuzey, M.C.; Therriault, D. Solvent-Cast Three-Dimensional Printing of Multifunctional Microsystems. Small 2013, 9, 4118–4122. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, X.N.; Sun, C. Micro-stereolithography of polymeric and ceramic microstructure. Sens. Actuators A 1999, 77, 149–156. [Google Scholar] [CrossRef]
- Ivanova, O.; Williams, C.; Campbell, T. Additive manufacturing (AM) and nanotechnology: Promises and challenges. Rapid Protot. J. 2013, 19, 353–364. [Google Scholar] [CrossRef] [Green Version]
- Francis, V.; Prashant, K.J. Advances in nanocomposite materials for additive manufacturing. Int. J. Rapid Manuf. 2015, 5, 215–233. [Google Scholar] [CrossRef]
- Woźniak, M.J.; Chlanda, A.; Oberbek, P.; Heljak, M.; Czarnecka, K.; Janeta, M.; John, Ł. Binary bioactive glass composite scaffolds for bone tissue engineering—Structure and mechanical properties in micro and nano scale. A preliminary study. Micron 2019, 119, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Chlanda, A.; Oberbek, P.; Heljak, M.; Kijeńska-Gawrońska, E.; Bolek, T.; Gloc, M.; John, Ł.; Janeta, M.; Woźniak, M.J. Fabrication, multi-scale characterization and in-vitro evaluation of porous hybrid bioactive glass polymer-coated scaffolds for bone tissue engineering. Mater. Sci. Eng. C 2019, 94, 516–523. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Shi, Q.; Guo, W.; Terrell, L.; Qureshi, A.T.; Hayes, D.J.; Wu, Q. Electrospun bio-nanocomposite scaffolds for bone tissue engineering by cellulose nanocrystals reinforcing maleic anhydride grafted PLA. ACS Appl. Mater. Interfaces 2013, 5, 3847–3854. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A. Additive manufacturing applications in medical cases: A literature based review. Alex. J. Med. 2018, 54, 411–422. [Google Scholar] [CrossRef] [Green Version]
- Arif, M.F.; Alhashmi, H.; Varadarajan, K.M.; Koo, J.H.; Hart, A.J.; Kumar, S. Multifunctional performance of carbon nanotubes and graphene nanoplatelets reinforced PEEK composites enabled via FFF additive manufacturing. Compos. Part B 2020, 184, 107625. [Google Scholar] [CrossRef]
- Cholleti, E.R.; Gibson, I. ABS Nano Composite Materials in Additive Manufacturing. IOP Conf. Ser. Mater. Sci. Eng. 2018, 455, 012038. [Google Scholar] [CrossRef]
- Huber, E.; Mirzaee, M.; Bjorgaard, J.; Hoyack, M.; Noghanian, S.; Chang, I. Dielectric property measurement of PLA. In Proceedings of the 2016 IEEE International Conference on Electro Information Technology (EIT), Grand Forks, ND, USA, 19–21 May 2016. [Google Scholar]
- Yingwei, W.; Isakov, D.; Grant, P.G. Fabrication of composite filaments with high dielectric permittivity for fused deposition 3D printing. Materials 2017, 10, 1218. [Google Scholar]
- Li, N.; Huang, S.; Zhang, G.; Qin, R.; Liu, W.; Xiong, H.; Shi, G.; Blackburn, J. Progress in additive manufacturing on new materials: A review. J. Mater. Sci. Technol. 2019, 35, 242–269. [Google Scholar] [CrossRef]
- Lamberti, P.; Spinelli, G.; Kuzhir, P.; Guadagno, L.; Naddeo, C.; Romano, V.; Kotsilkova, R.; Angelova, P.; Georgiev, V. Evaluation of thermal and electrical conductivity of carbon-based PLA nanocomposites for 3D printing. In Proceedings of the AIP Conference Proceedings of 9th International Conference on Times of Polymers and Composites: From Aerospace to Nanotechnology, Ischia, Italy, 17–21 June 2018. [Google Scholar]
- Spinelli, G.; Lamberti, P.; Tucci, V.; Kotsilkova, R.; Ivanov, E.; Menseidov, D.; Naddeo, C.; Romano, V.; Guadagno, L.; Adami, R.; et al. Nanocarbon/poly(lactic) acid for 3D printing: Effect of fillers content on electromagnetic and thermal properties. Materials 2019, 12, 2369. [Google Scholar] [CrossRef] [Green Version]
- Tereshchenko, O.V.; Buesink, F.J.K.; Leferink, F.B.J. An overview of the techniques for measuring the dielectric properties of materials. In Proceedings of the 2011 XXXth URSI General Assembly and Scientific Symposium, Istanbul, Turkey, 13–20 August 2011. [Google Scholar]
- (ISO 22007-2:2015). Plastic—Determination of Thermal Conductivity and Thermal Diffusivity—Part 2: Transient Plane Heat Source (Hot Disc) Method; Swedish Standards Institute: Stockholm, Sweden, 2015. [Google Scholar]
- Gustafsson, S.E. Transient plane source techniques for thermal conductivity and thermal diffusivity measurements of solid materials. Rev. Sci. Instrum. 1991, 62, 797–804. [Google Scholar] [CrossRef]
- Wagner, J.R.; Mount, E.M.; Giles, H.F. Design of Experiments; William Andrew Publishing: New York, NY, USA, 2014; pp. 291–308. [Google Scholar]
- Berk, J.; Berk, S. Cahpter Anova, Taguchi, and Other Design of Experiments Techniques: Finding needles in haystacks. In Quality Management for the Technology Sector; Butterworth-Heinemann: Woburn, MA, USA, 2000; pp. 106–123. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 5th ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Vicario, G. Computer experiments: Promising new frontiers in analysis and design of experiments. Stat. Appl. 2006, 18, 231–249. [Google Scholar]
- Maxwel-Garnett, J. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. 1904, 203, 385–420. [Google Scholar]
- McLachlan, D.S.; Blaszkiewicz, M.; Newnham, R.E. Electrical resistivity of composites. J. Am. Ceram. Soc. 1990, 73, 2187–2203. [Google Scholar] [CrossRef]
- Myroshnychenko, V.; Brosseau, C. Finite-element modeling method for the prediction of the complex effective permittivity of two-phase random statistically isotropic heterostructures. J. Appl. Phys. 2005, 97, 044101. [Google Scholar] [CrossRef]
- Myroshnychenko, V.; Brosseau, C. Finite-element method for calculation of the effective permittivity of random inhomogeneous media. Phys. Rev. E 2005, 71, 016701. [Google Scholar] [CrossRef] [PubMed]
- De Vivo, B.; Lamberti, P.; Spinelli, G.; Tucci, V. Numerical investigation on the influence factors of the electrical properties of carbon nanotubes-filled composites. J. Appl. Phys. 2013, 113, 244301. [Google Scholar] [CrossRef]
- De Vivo, B.; Lamberti, P.; Spinelli, G.; Tucci, V. A morphological and structural approach to evaluate the electromagnetic performances of composites based on random networks of carbon nanotubes. J. Appl. Phys. 2014, 115, 154311. [Google Scholar] [CrossRef]
- Nan, C.W.; Shen, Y.; Ma, J. Physical properties of composites near percolation. Annu. Rev. Mater. Res. 2010, 40, 131–151. [Google Scholar] [CrossRef]
- De Vivo, B.; Guadagno, L.; Lamberti, P.; Raimondo, M.; Spinelli, G.; Tucci, V.; Vertuccio, L.; Vittoria, V. Electrical properties of multi-walled carbon nanotube/tetrafunctional epoxy-amine composites. In Proceedings of the 6th International Conference on Times of Polymers (Top) And Composites, Ischia, Italy, 10–14 June 2012. [Google Scholar]
- De Vivo, B.; Lamberti, P.; Spinelli, G.; Tucci, V.; Guadagno, L.; Raimondo, M. The effect of filler aspect ratio on the electromagnetic properties of carbon-nanofibers reinforced composites. J. Appl. Phys. 2015, 118, 064302-9. [Google Scholar] [CrossRef]
- Balberg, I.; Binenbaum, N.; Wagner, N. Percolation thresholds in the three-dimensional sticks system. Phys. Rev. Lett. 1984, 52, 1465. [Google Scholar] [CrossRef]
- Almond, D.; Duncan, G.; West, A. The determination of hopping rates and carrier concentrations in ionic conductors by a new analysis of ac conductivity. Solid State Ion. 1983, 8, 159–164. [Google Scholar] [CrossRef]
- Kilbride, B.E.; Coleman, J.; Fraysse, J.; Fournet, P.; Cadek, M.; Drury, A.; Hutzler, S.; Roth, S.; Blau, W. Experimental observation of scaling laws for alternating current and direct current conductivity in polymer-carbon nanotube composite thin films. J. Appl. Phys. 2002, 92, 4024–4030. [Google Scholar] [CrossRef]
- Li, C.; Thostenson, E.T.; Chou, T.-W. Dominant role of tunneling resistance in the electrical conductivity of carbon nanotube—Based composites. Appl. Phys. Lett. 2007, 91, 223114. [Google Scholar] [CrossRef]
- Connor, M.T.; Roy, S.; Ezquerra, T.A.; Calleja, F.J.B. Broadband ac conductivity of conductor-polymer composites. Phys. Rev. B 1998, 57, 2286. [Google Scholar] [CrossRef] [Green Version]
- Nelson, J.K. Dielectric Polymer Nanocomposites; Springer: New York, NY, USA, 2010. [Google Scholar]
- Jonscher, A.K. Universal Relaxation in Solids; Chelsea Dielectrics Press Limited: London, UK, 1983. [Google Scholar]
- Jonscher, A.K. Dielectric relaxation in solids. J. Phys. D Appl. Phys. 1999, 32, R57. [Google Scholar] [CrossRef]
- Mdarhri, A.; Carmona, F.; Brosseau, C.; Delhaes, P. Direct current electrical and microwave properties of polymer-multiwalled carbon nanotubes composites. J. Appl. Phys. 2008, 103, 054303. [Google Scholar] [CrossRef]
- Psarras, G.C. Conductivity and dielectric characterization of polymer nanocomposites. In Physical Properties and Applications of Polymer Nanocomposites; Woodhead Publishing: Cambridge, UK, 2010; Chapter 2; pp. 31–69. [Google Scholar]
- Debye, P.J.W. Polar Molecules; Chemical Catalog Company, Incorporated: Manhattan, NY, USA, 1929. [Google Scholar]
- Garcia-Belmonte, G.; Bisquert, J. Chapter 9—Anomalous Charge Transport and Polarization in Semiconductors Oxides and Porous Film Electrodes. In Supramolecular Photosensitive and Electroactive Materials; Nalwa, H.S., Ed.; Stanford Scientific Corporation: Los Angeles, CA, USA, 2001; Chapter 10; pp. 727–779. [Google Scholar]
- Micheli, D.; Apollo, C.; Pastore, R.; Marchetti, M. X-Band microwave characterization of carbon-based nanocomposite material, absorption capability comparison and RAS design simulation. Compos. Sci. Technol. 2010, 70, 400–409. [Google Scholar] [CrossRef]
- Bellucci, S.; Bistarelli, S.; Cataldo, A.; Micciulla, F.; Kranauskaite, I.; Macutkevic, J.; Banys, J.; Volynets, N.; Paddubskaya, A.; Bychanok, D. Broadband dielectric spectroscopy of composites filled with various carbon materials. IEEE Trans. Microw. Theory 2015, 63, 2024–2031. [Google Scholar] [CrossRef]
- Ramo, S.; Whinnery, J.R.; Van Duzer, T. Fields and Waves in Communication Electronics, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
- D’Aloia, A.; Marra, F.; Tamburrano, A.; De Bellis, G.; Sarto, M.S. Electromagnetic absorbing properties of graphene–polymer composite shields. Carbon 2014, 73, 175–184. [Google Scholar] [CrossRef]
- D’Aloia, A.G.; D’Amore, M.; Sarto, M.S. Terahertz shielding effectiveness of graphene-based multilayer screens controlled by electric field bias in a reverberating environment. IEEE Trans. Terahertz Sci. Technol. 2015, 5, 628–636. [Google Scholar] [CrossRef]
- Chae, H.G.; Kumar, S. Making strong fibers. Science 2008, 319, 908–909. [Google Scholar] [CrossRef]
- Chen, H.; Ginzburg, V.V.; Yang, J.; Yang, Y.; Liu, W.; Huang, Y.; Du, L.; Chen, B. Thermal conductivity of polymer-based composites: Fundamentals and applications. Prog. Polym. Sci. 2016, 59, 41–85. [Google Scholar] [CrossRef]
- Huang, C.; Qian, X.; Yang, R. Thermal conductivity of polymers and polymer nanocomposites. Mater. Sci. Eng. R 2018, 132, 1–22. [Google Scholar] [CrossRef] [Green Version]
- White, C.C.; Hunston, D.L.; Tan, K.T.; Filliben, J.J.; Pintar, A.; Schueneman, G. A Systematic Approach to the Study of Accelerated Weathering of Building Joint Sealants. J. ASTM Int. 2012, 9, 1–17. [Google Scholar] [CrossRef]
- Croarkin, C.; Tobias, P.; Filliben, J.J.; Hembree, B.; Guthrie, W. NIST/SEMATECH e-Handbook of Statistical Methods; NIST/SEMATECH: Gaithersburg, MD, USA, 2006. [Google Scholar]
- Kuehl, R.O. Design of Experiment: Statistical Principles of Research Design and Analysis, 2nd ed.; Duxbury/Thomson Learning: Pacific Grove, CA, USA, 2000. [Google Scholar]
- Ghosh, S.; Rao, C.R. Design and Analysis of Experiments. Handbook of Statistics Vol. 13; Elsevier Science: Amsterdam, North-Holland, The Netherlands, 1996. [Google Scholar]
- Draper, N.R.; Lin, D.K.J. Response surface designs. In Design and Analysis of Experiments; Elsevier Science: Amsterdam, North-Holland, The Netherlands, 1996; pp. 343–375. [Google Scholar]
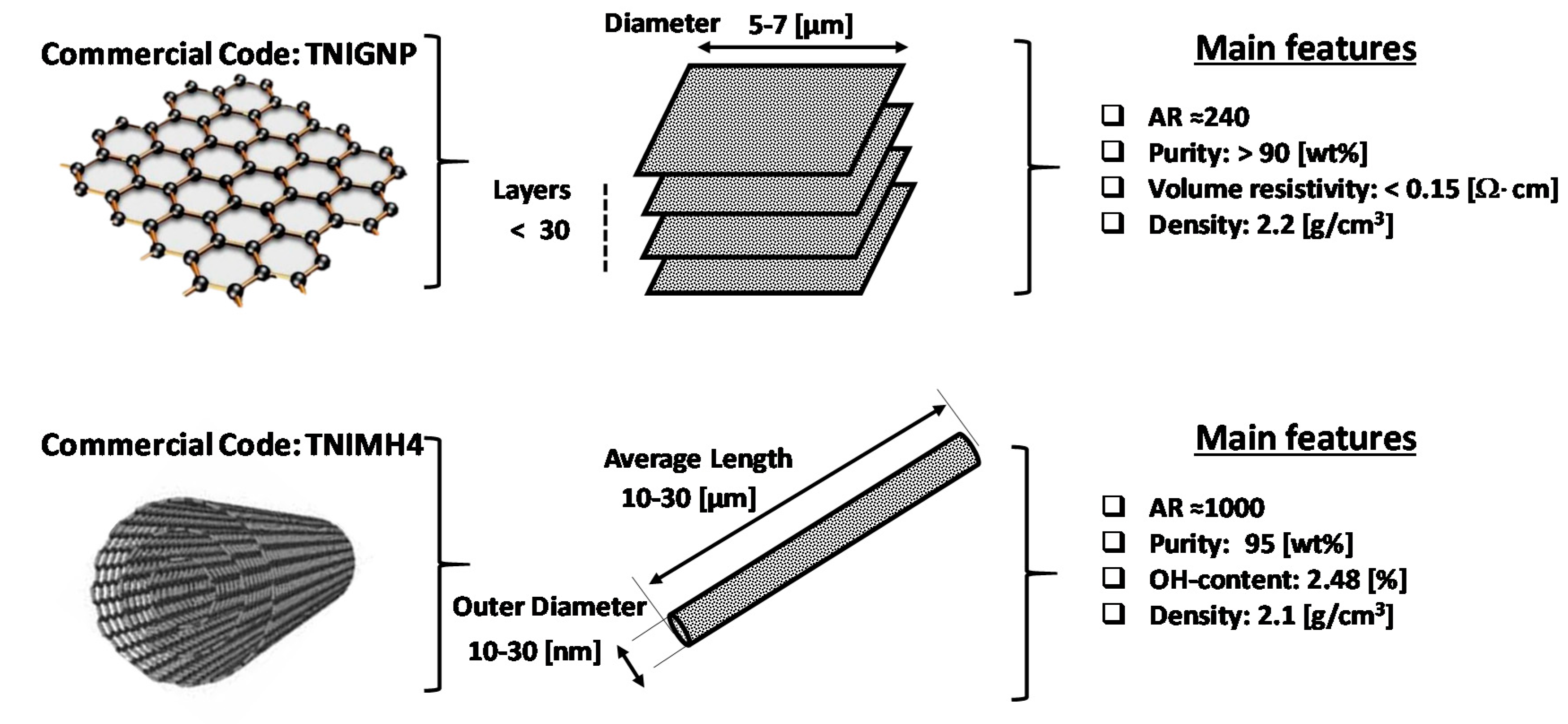

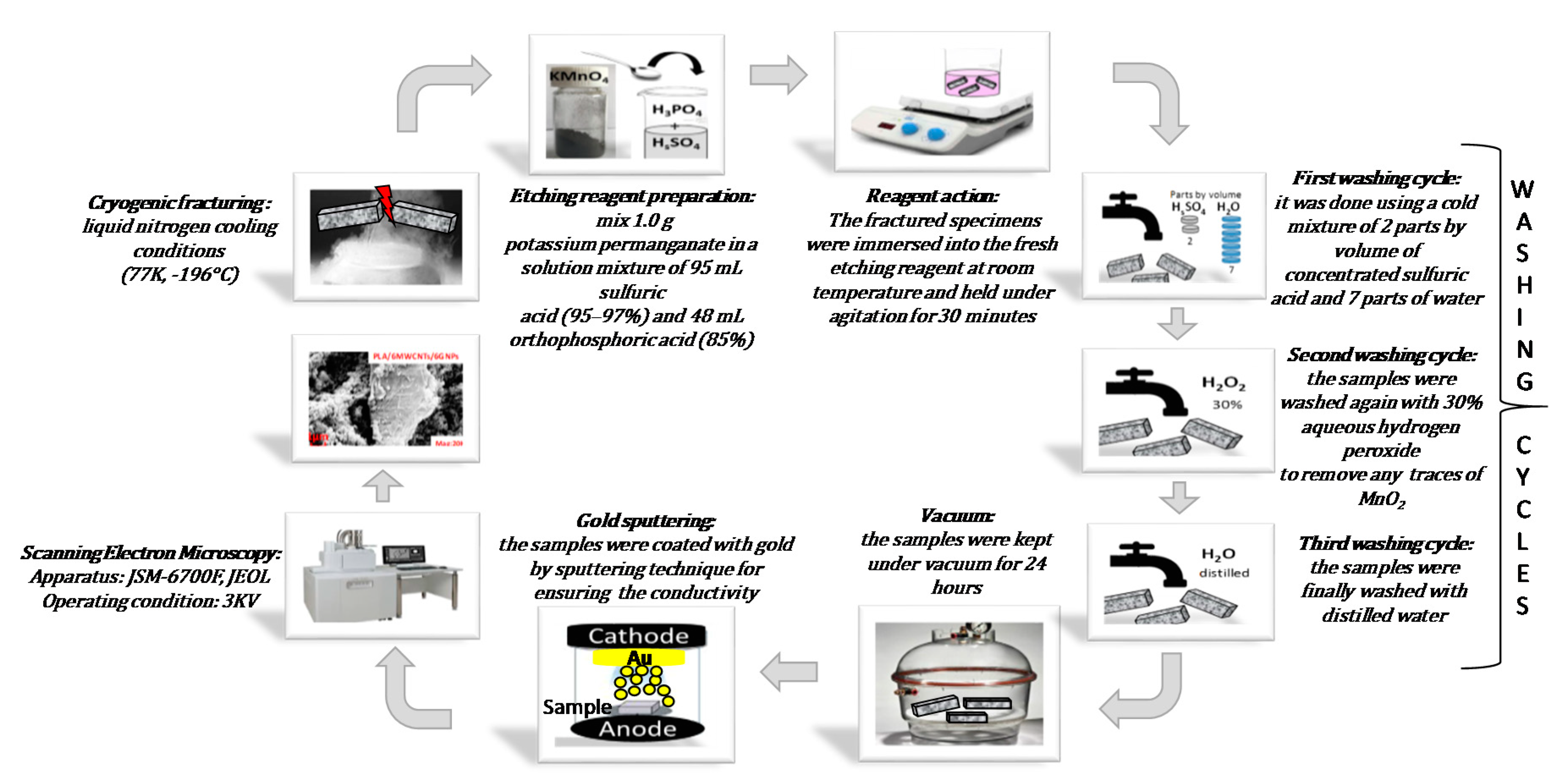

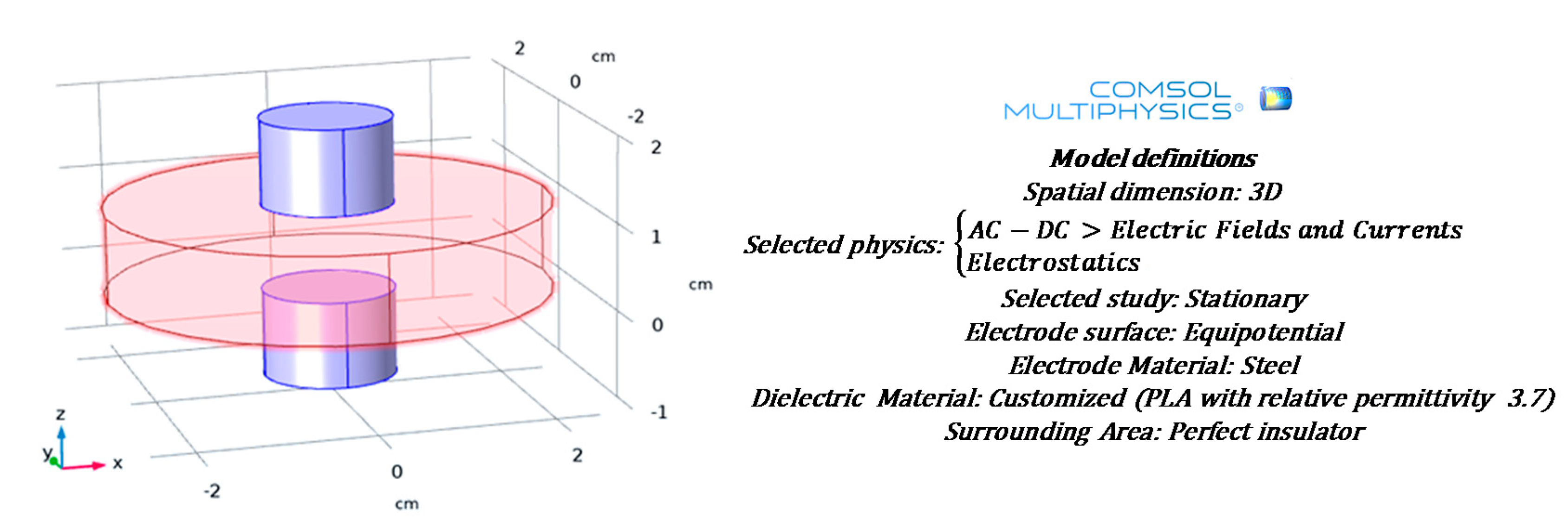
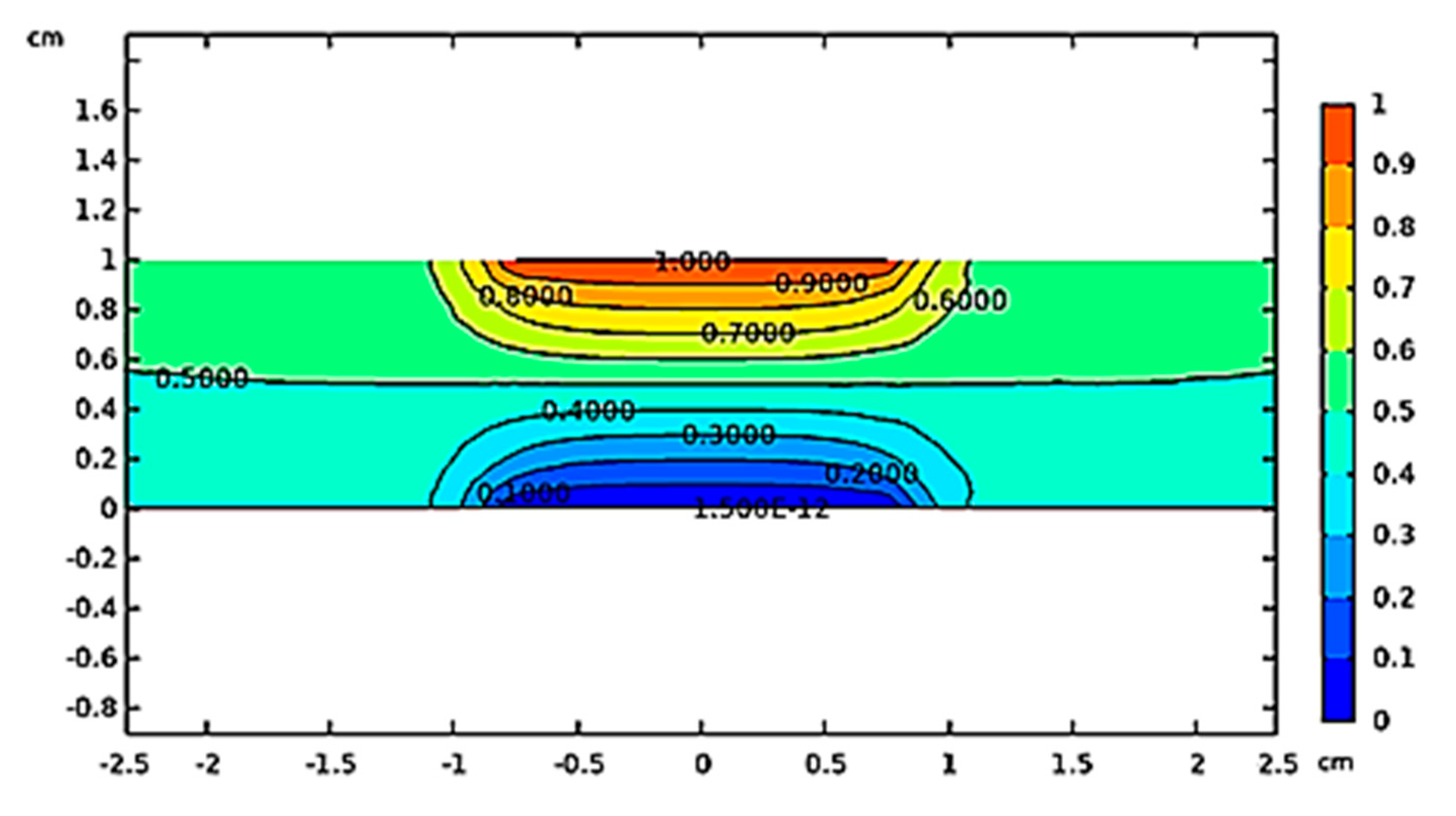










| Parameter | Value | Unit |
|---|---|---|
| Nozzle Temperature | 210–220 | °C |
| Nozzle Diameter | 0.4 (PLA)–0.5 (PLA with filler) | mm |
| Bed Temperature | 65 | °C |
| Extrusion Speed | 17 | mm/s |
| Extrusion Multiplier | 0.8 | - |
| Extrusion Width | 0.4 | mm |
| Primary Layer Height | 0.25 | mm |
| Internal Infill Pattern | Rectangular | - |
| External Infill Pattern | Rectangular | - |
| Retraction Length (Distance) | 1 | mm |
| Retraction Speed | 30 | mm/s |
| Infill Density | 100 | % |
| Cooling | 100 | % |
| Sample | Filler Content wt % | GNP Content wt % | MWCNT Content wt % | GNP:MWCNT Ratio |
|---|---|---|---|---|
| PLA | 0 | - | - | 0 |
| 1.5GNP | 1.5 | 1.5 | - | 0 |
| 3GNP | 3 | 3 | - | 0 |
| 6GNP | 6 | 6 | - | 0 |
| 9GNP | 9 | 9 | - | 0 |
| 12GNP | 12 | 12 | - | 0 |
| 1.5MWCNT | 1.5 | - | 1.5 | 0 |
| 3MWCNT | 3 | - | 3 | 0 |
| 6MWCNT | 6 | - | 6 | 0 |
| 9MWCNT | 9 | - | 9 | 0 |
| 12MWCNT | 12 | - | 12 | 0 |
| 1.5GNP/1.5MWCNT | 3 | 1.5 | 1.5 | 1:1 |
| 3GNP/3MWCNT | 6 | 3 | 3 | 1:1 |
| 1.5GNP/4.5MWCNT | 6 | 1.5 | 4.5 | 1:3 |
| 4.5GNP/1.5MWCNT | 6 | 4.5 | 1.5 | 3:1 |
| 3GNP/6MWCNT | 9 | 3 | 6 | 1:2 |
| 3GNP/9MWCNT | 12 | 3 | 9 | 1:3 |
| 6GNP/6MWCNT | 12 | 6 | 6 | 1:1 |
| 9GNP/3MWCNT | 12 | 9 | 3 | 3:1 |
| Coefficient | β0 | β1 | β2 | β12 | β11 | β22 |
|---|---|---|---|---|---|---|
| Value for ɛr: | +3.7 | −151.4827 | −14.5239 | −9.0489 | +51.0020 | +5.0502 |
| Value for : | +0.1892 | +0.0153 | +0.0360 | +9.1667 × 10−4 | −0.0015 | +0.0014 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spinelli, G.; Kotsilkova, R.; Ivanov, E.; Georgiev, V.; Ivanova, R.; Naddeo, C.; Romano, V. Dielectric Spectroscopy and Thermal Properties of Poly(lactic) Acid Reinforced with Carbon-Based Particles: Experimental Study and Design Theory. Polymers 2020, 12, 2414. https://doi.org/10.3390/polym12102414
Spinelli G, Kotsilkova R, Ivanov E, Georgiev V, Ivanova R, Naddeo C, Romano V. Dielectric Spectroscopy and Thermal Properties of Poly(lactic) Acid Reinforced with Carbon-Based Particles: Experimental Study and Design Theory. Polymers. 2020; 12(10):2414. https://doi.org/10.3390/polym12102414
Chicago/Turabian StyleSpinelli, Giovanni, Rumiana Kotsilkova, Evgeni Ivanov, Vladimir Georgiev, Radost Ivanova, Carlo Naddeo, and Vittorio Romano. 2020. "Dielectric Spectroscopy and Thermal Properties of Poly(lactic) Acid Reinforced with Carbon-Based Particles: Experimental Study and Design Theory" Polymers 12, no. 10: 2414. https://doi.org/10.3390/polym12102414
APA StyleSpinelli, G., Kotsilkova, R., Ivanov, E., Georgiev, V., Ivanova, R., Naddeo, C., & Romano, V. (2020). Dielectric Spectroscopy and Thermal Properties of Poly(lactic) Acid Reinforced with Carbon-Based Particles: Experimental Study and Design Theory. Polymers, 12(10), 2414. https://doi.org/10.3390/polym12102414








