Effects of Topological Constraints on Penetration Structures of Semi-Flexible Ring Polymers
Abstract
:1. Introduction
2. Simulation Model and Method
2.1. Model
2.2. Molecule Dynamics Simulation
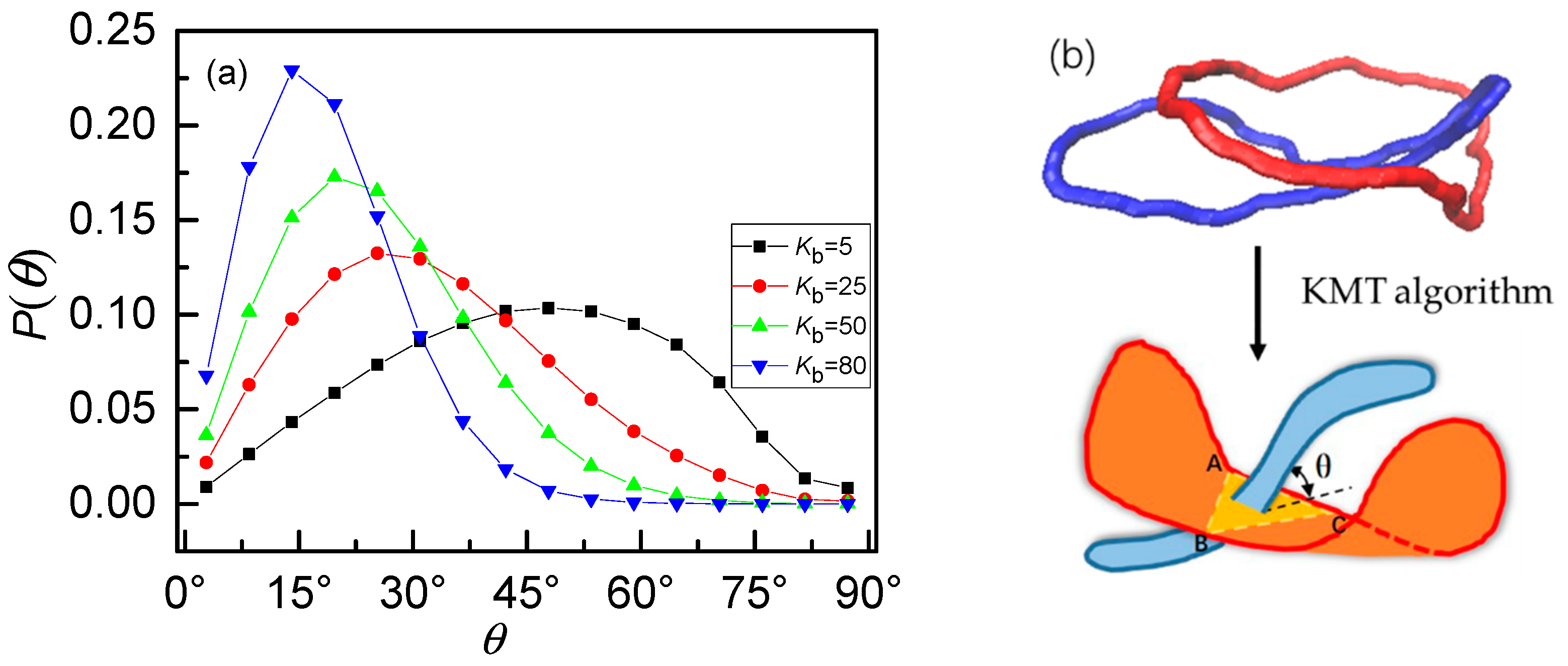
2.3. KMT Algorithm
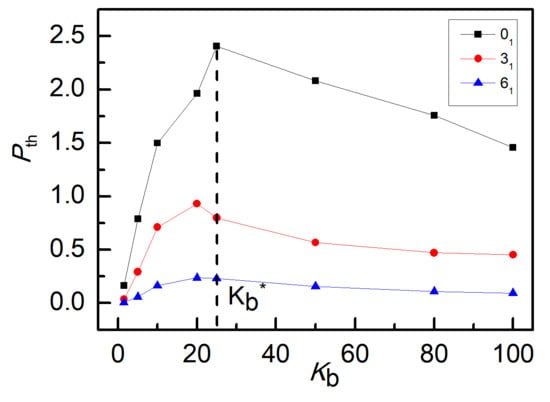
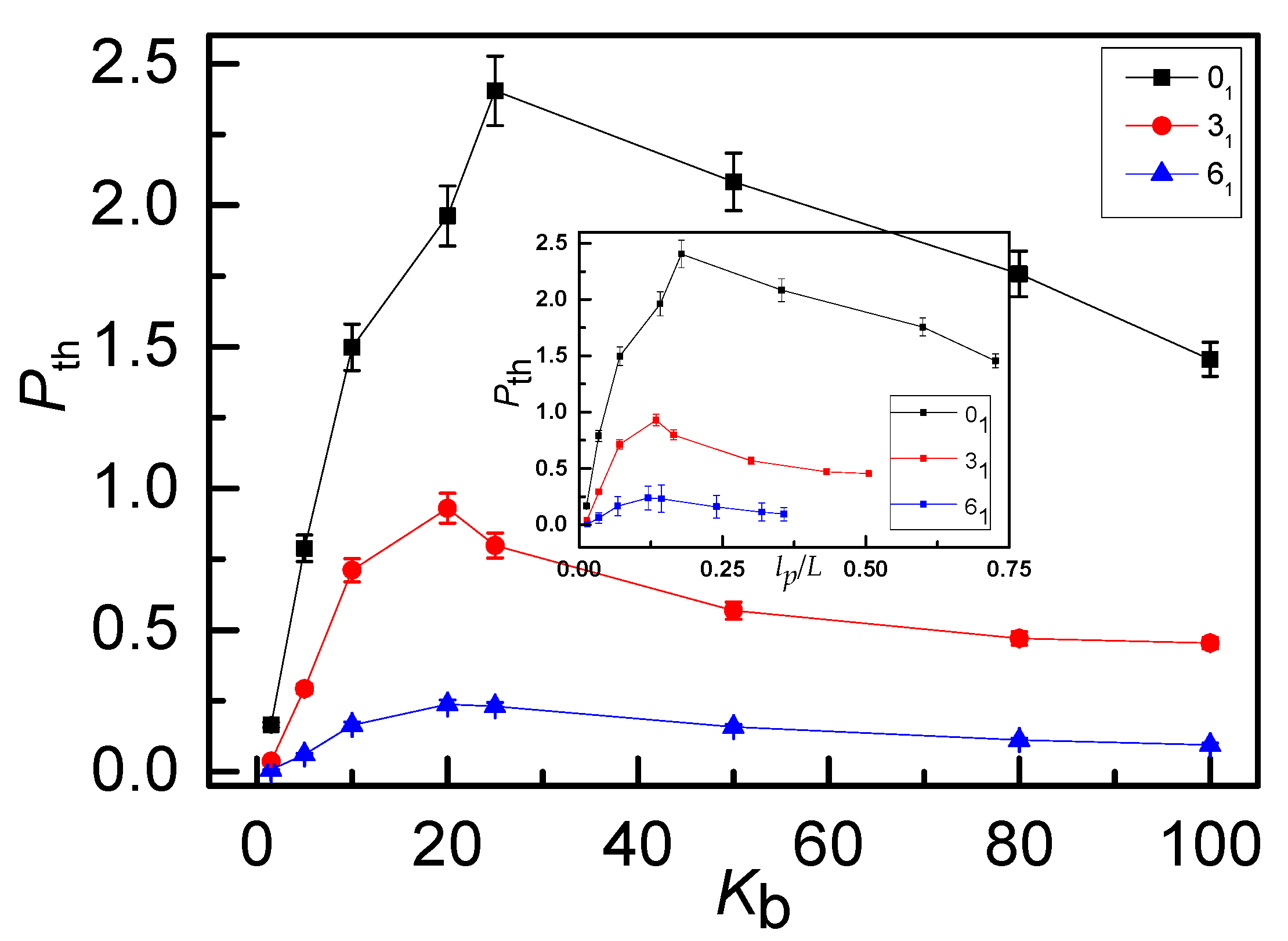
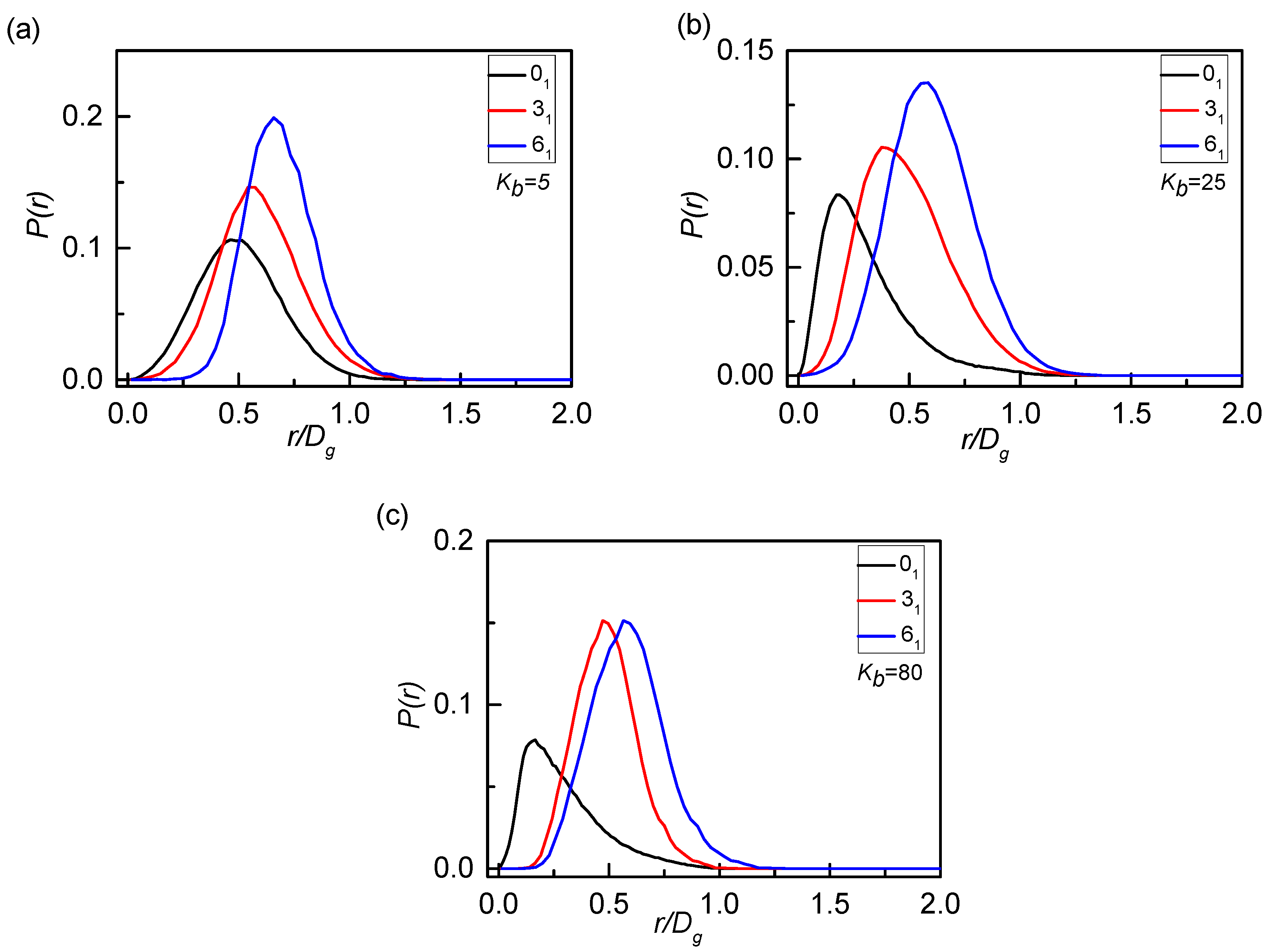
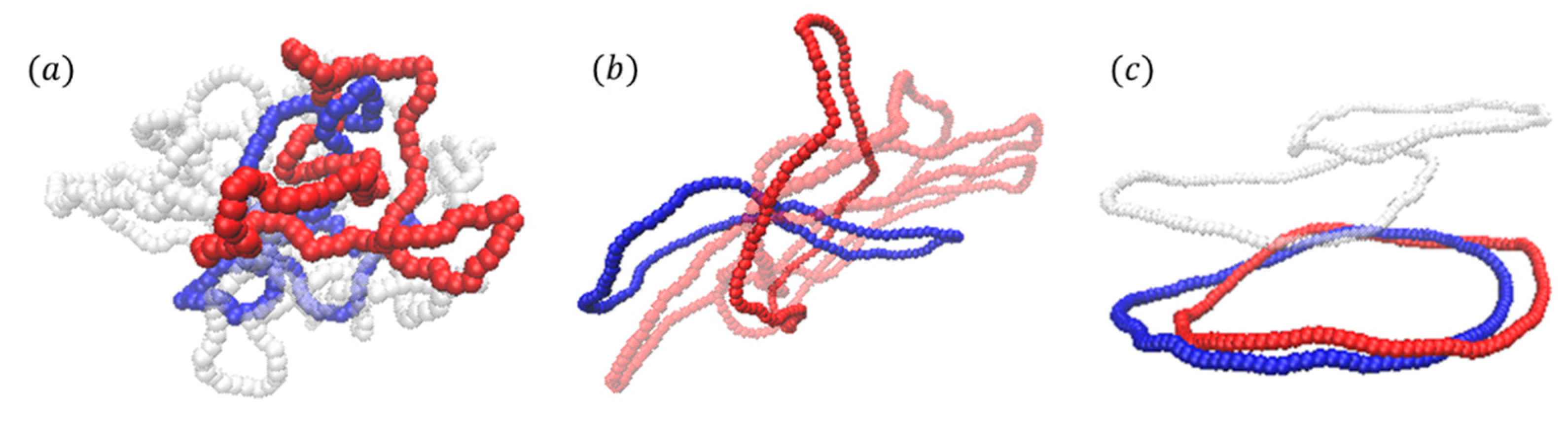
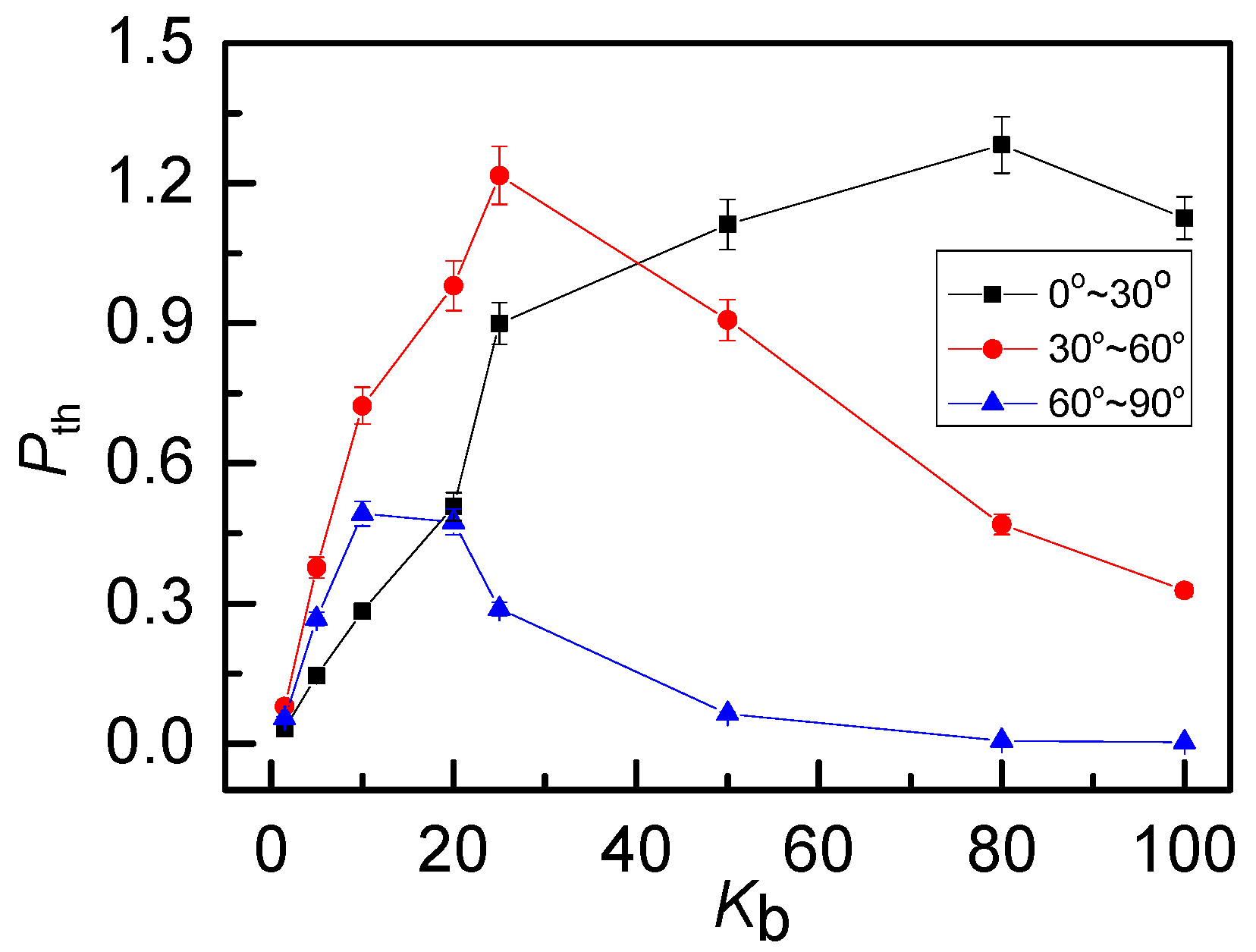
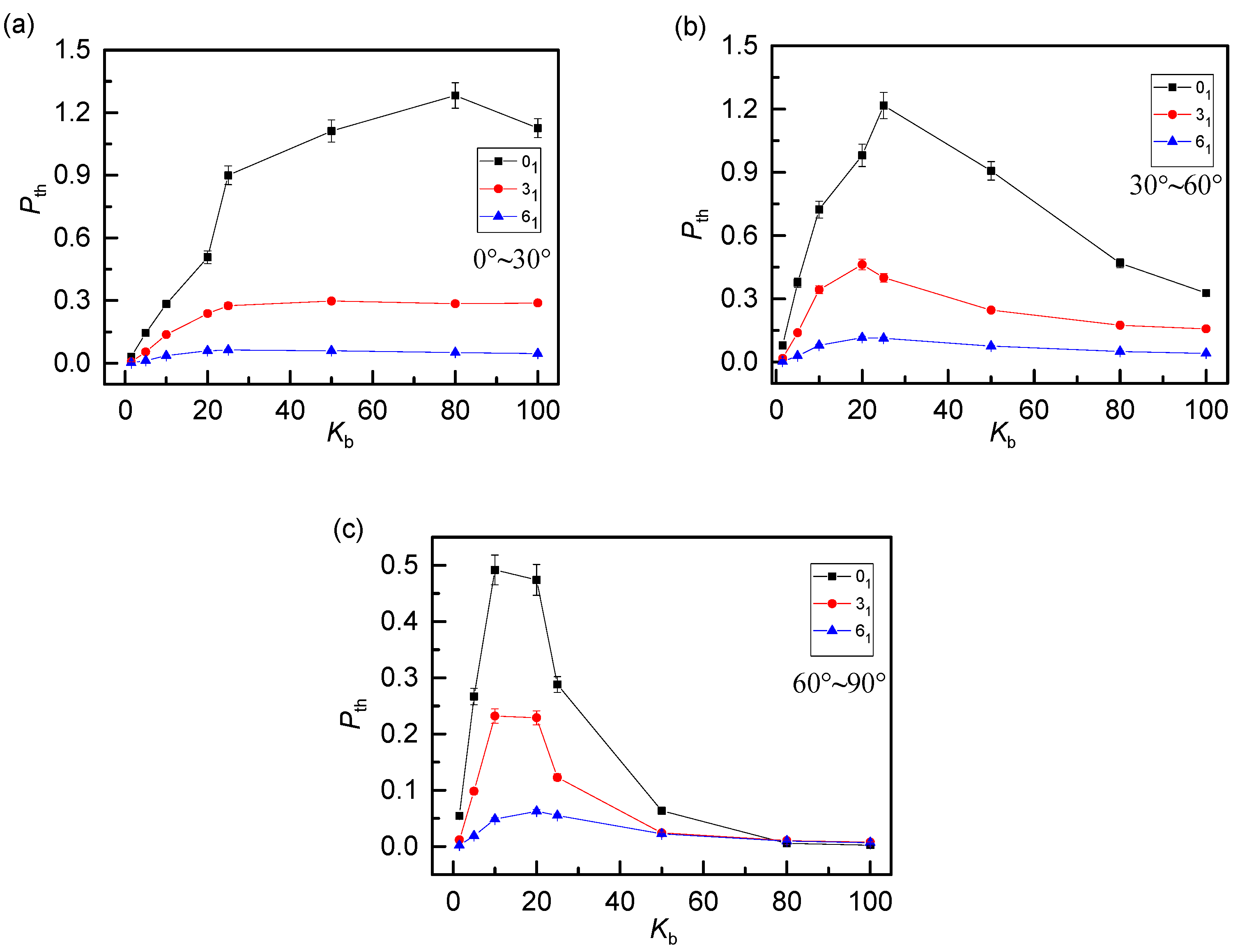
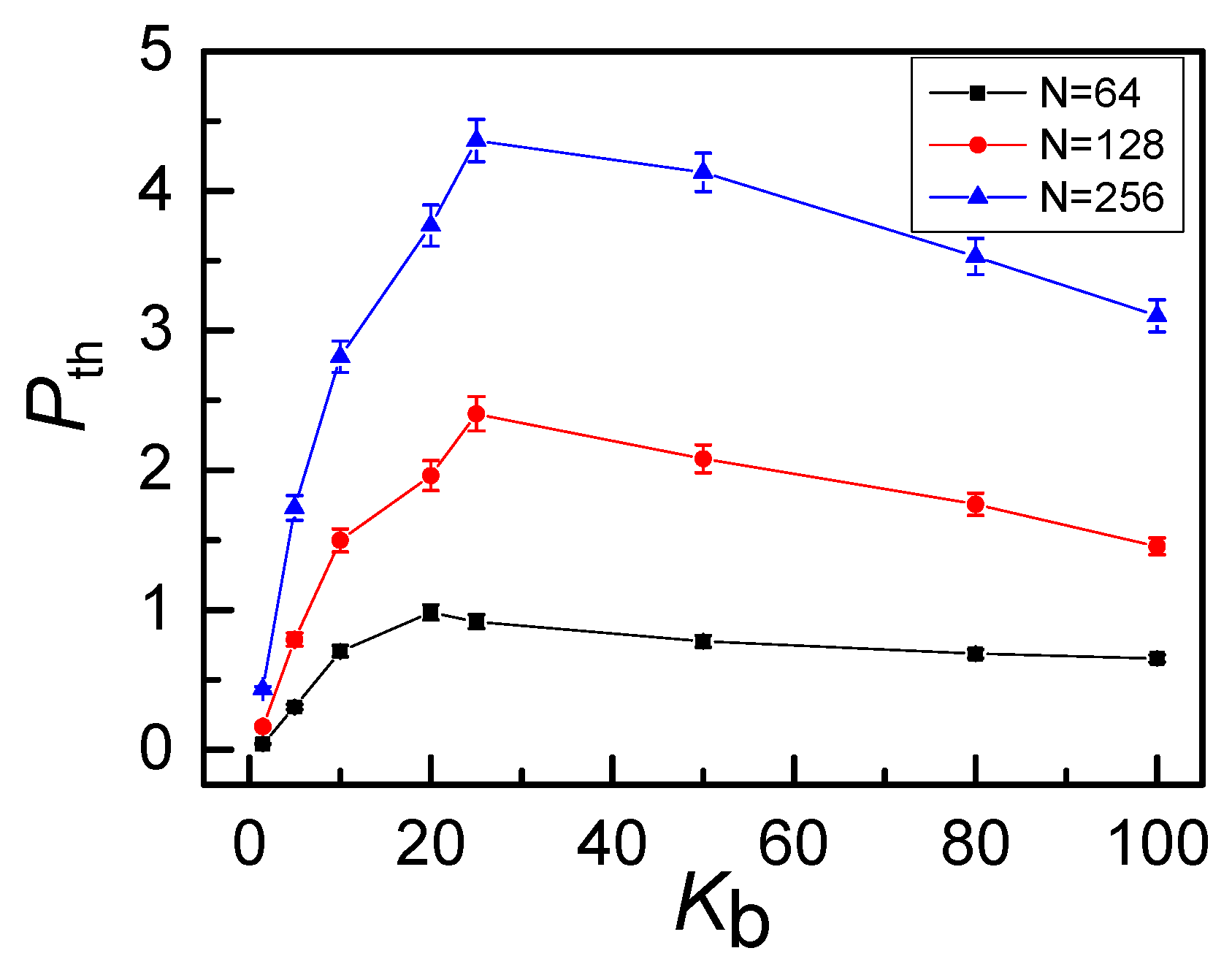
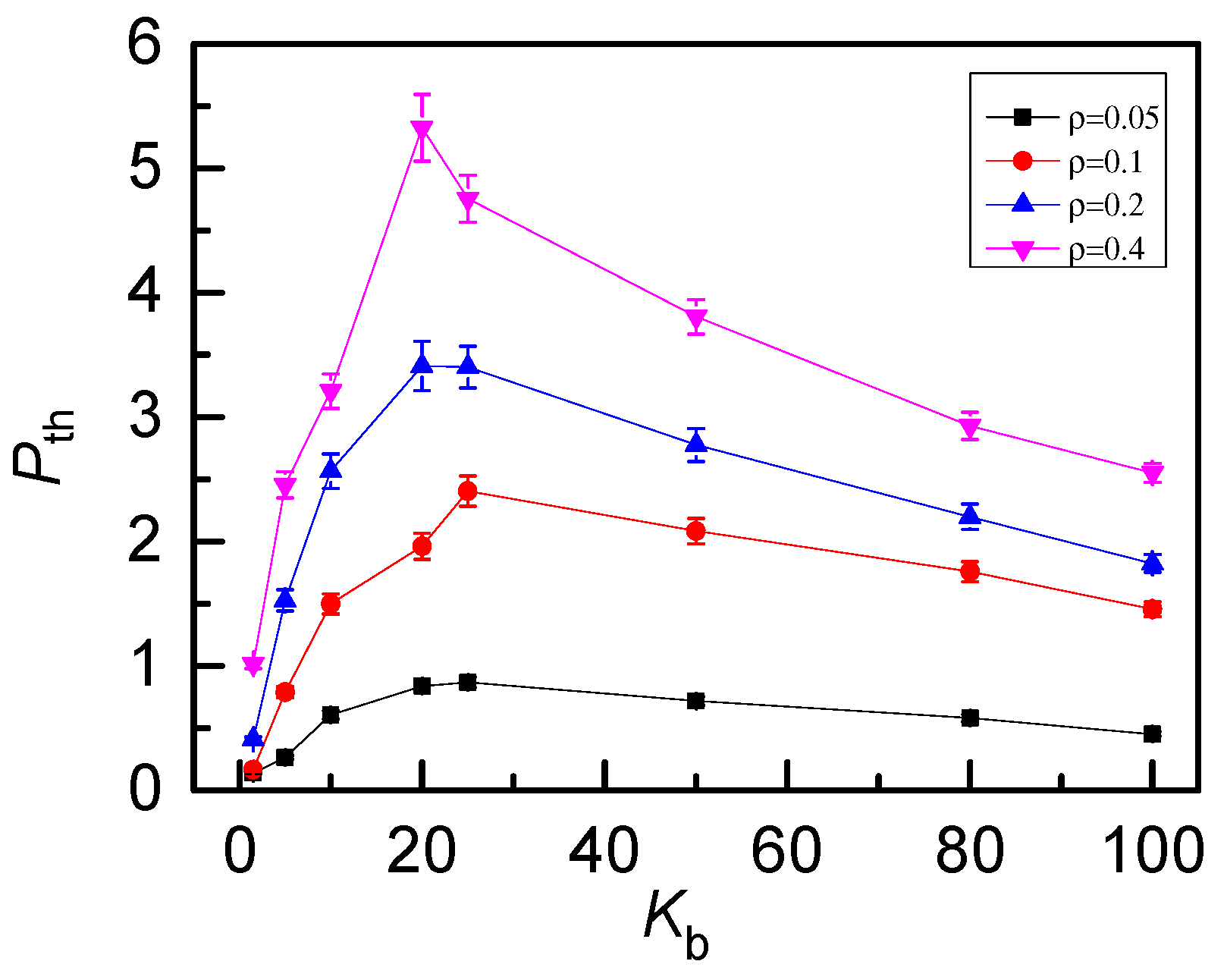
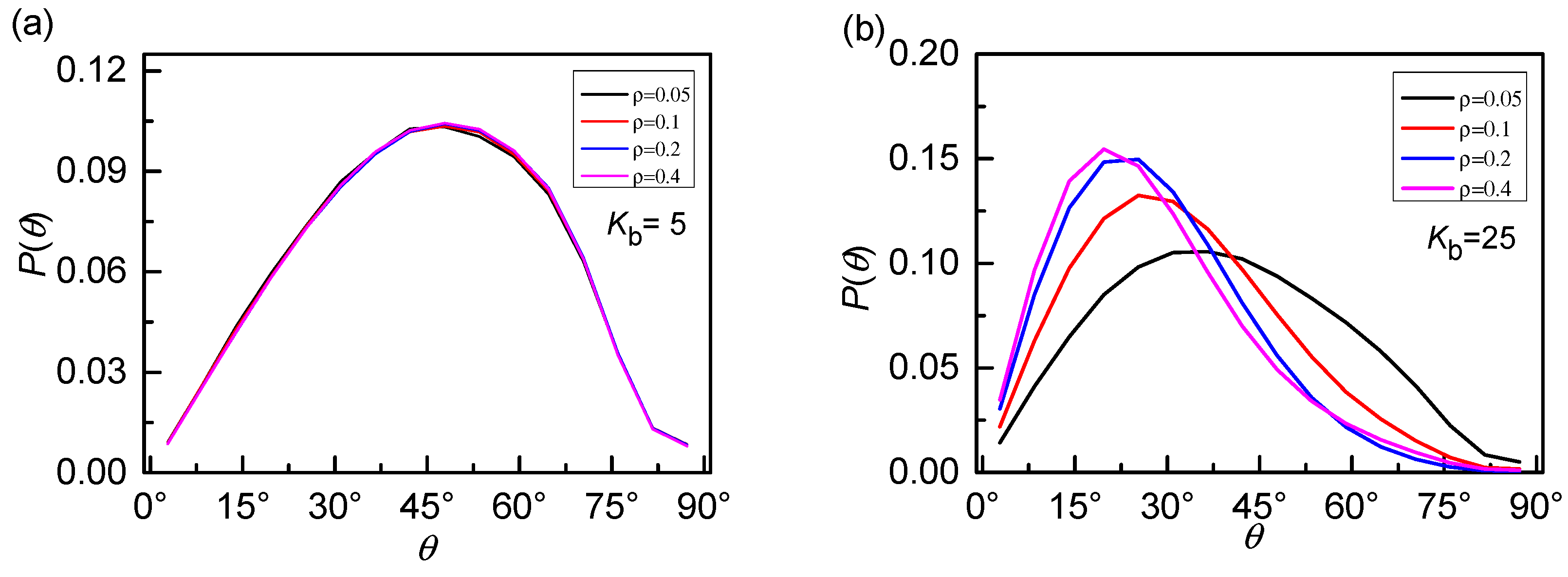
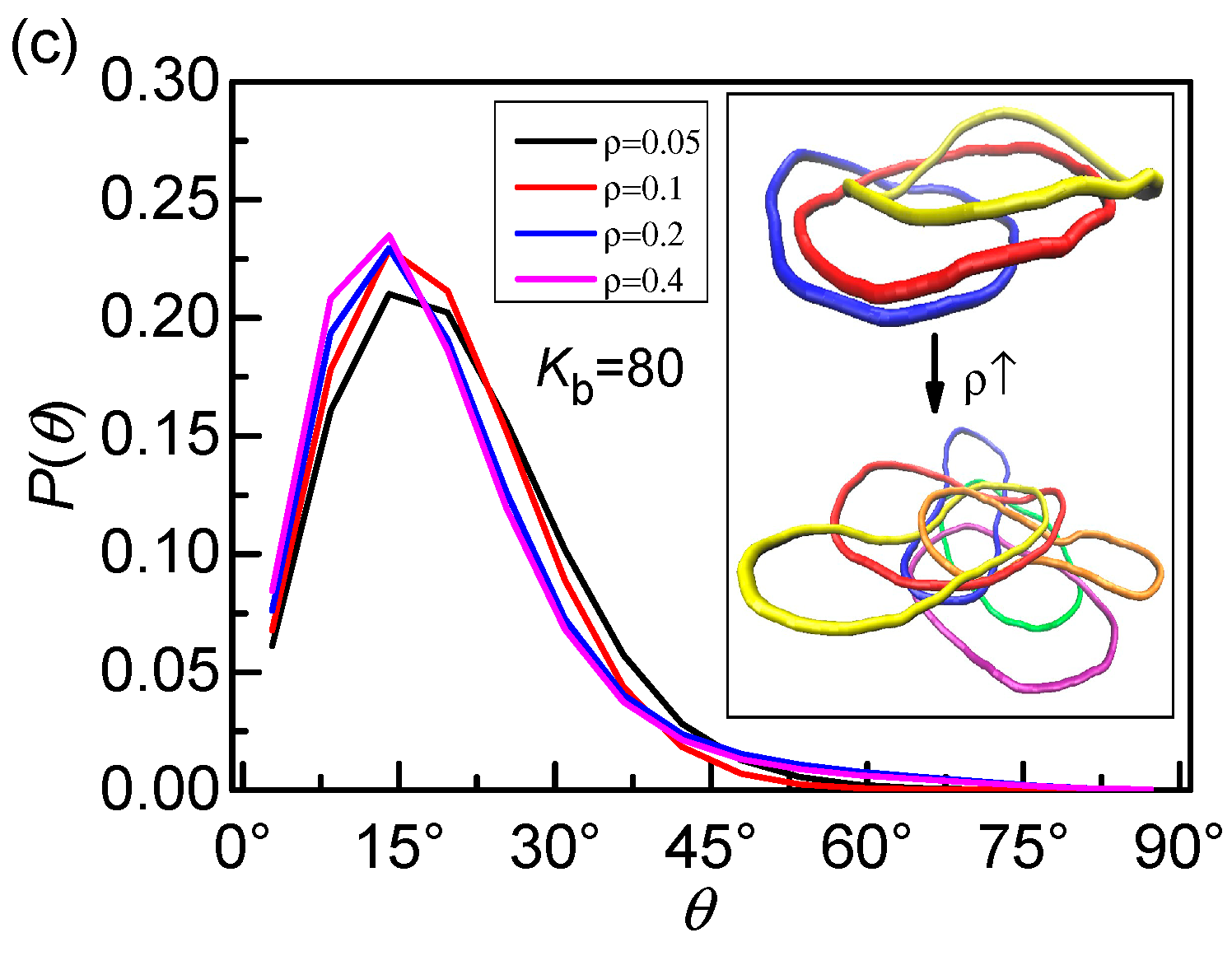
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Guo, H.; Mao, R.; Block, T.M.; Guo, J.T. Production and function of the cytoplasmic deproteinized relaxed circular DNA of hepadnaviruses. J. Virol. 2010, 84, 387–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Conway, J.H. An enumeration of knots and links and some of their related properties. In Computational Problems in Abstract Algebra; Leech, J., Ed.; Pergamon Press: Oxford, UK, 1967; pp. 329–358. [Google Scholar]
- Narros, A.; Moreno, A.J.; Likos, C.N. Influence of topology on effective potentials: Coarse-graining ring polymers. Soft Matter 2010, 6, 2435–2441. [Google Scholar] [CrossRef]
- Daichi, I. Semiflexible ring polymers in dilute solutions. React. Funct. Polym. 2018, 130, 111–117. [Google Scholar]
- Hiroki, A.; Daichi, I. Mean-square radius of gyration and scattering function of semiflexible ring Polymers of the trefoil knot. Polymers 2016, 8, 271. [Google Scholar]
- Moore, N.T.; Grosberg, A.Y. Limits of analogy between self-avoidance and topology-driven swelling of polymer loops. Phys. Rev. E 2005, 72, 061803. [Google Scholar] [CrossRef] [Green Version]
- Halverson, J.D.; Lee, W.B.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. I. Statics. J. Chem. Phys. 2011, 134, 204904. [Google Scholar] [CrossRef] [Green Version]
- Reigh, S.Y.; Yoon, D.Y. Concentration dependence of ring polymer conformations from Monte Carlo simulations. ACS Macro. Lett. 2013, 2, 296–300. [Google Scholar] [CrossRef]
- Zhou, X.L.; Jiang, Y.W.; Deng, Z.Y.; Zhang, L.X. Glassy dynamics of nanoparticles in semiflexible ring polymer nanocomposite melts. Sci. Rep. 2017, 7, 44325. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.L.; Jiang, Y.W.; Chen, J.M.; He, L.L.; Zhang, L.X. Size-dependent nanoparticle dynamics in semiflexible ring polymer nanocomposites. Polymer 2017, 131, 243–251. [Google Scholar] [CrossRef]
- Doi, Y.; Matsubara, K.; Ohta, Y.; Nakano, T.; Kawaguchi, D.; Takahashi, Y.; Takano, A.; Matsushita, Y. Melt rheology of ring polystyrenes with ultrahigh purity. Macromolecules 2015, 48, 3140–3147. [Google Scholar] [CrossRef]
- Yan, Z.C.; Costanzo, S.; Jeong, Y.; Chang, T.; Vlassopoulos, D. Linear and nonlinear shear rheology of a marginally entangled ring polymer. Macromolecules 2016, 49, 1444–1453. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]
- Kapnistos, M.; Lang, M.; Vlassopoulos, D.; Pyckhout-Hintzen, W.; Richter, D.; Cho, D.; Chang, T.; Rubinstein, M. Unexpected power-law stress relaxation of entangled ring polymers. Nat. Mater. 2008, 7, 997–1002. [Google Scholar] [CrossRef] [PubMed]
- Narros, A.; Moreno, A.J.; Likos, C.N. Effects of knots on ring polymers in solvents of varying quality. Macromolecules 2013, 46, 9437–9445. [Google Scholar] [CrossRef]
- Narros, A.; Moreno, A.J.; Likos, C.N. Effective Interactions of knotted ring polymers. Biochem. Soc. Trans. 2013, 41, 630–634. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.L.; Guo, F.C.; Li, K.; He, L.L.; Zhang, L.X. Entropy-induced separation of binary semiflexible ring polymer mixture in spherical confinement. Polymers 2019, 11, 1992. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khokhlov, A.R.; Nechaev, S.K. Polymer chain in an array of obstacles. Phys. Lett. A 1985, 112, 156–160. [Google Scholar] [CrossRef]
- Obukhov, S.P.; Rubinstein, M.; Duke, T. Dynamics of a ring polymer in a gel. Phys. Rev. Lett. 1994, 73, 1263–1266. [Google Scholar] [CrossRef]
- Grosberg, A.Y. Annealed lattice animal model and Flory theory for the melt of non-concatenated rings: Towards the physics of crumpling. Soft Matter 2014, 10, 560–565. [Google Scholar] [CrossRef] [Green Version]
- Smrek, J.; Grosberg, A.Y. Understanding the dynamics of rings in the melt in terms of the annealed tree model. J. Phys. Condens. Matter 2015, 27, 064117. [Google Scholar] [CrossRef]
- Michieletto, D.; Marenduzzo, D.; Orlandini, E.; Alexander, G.P.; Turner, M.S. Threading dynamics of ring polymers in a gel. ACS Macro. Lett. 2014, 3, 255–259. [Google Scholar] [CrossRef]
- Michieletto, D.; Nahali, N.; Rosa, A. Glassiness and heterogeneous dynamics in dense solutions of ring polymers. Phys. Rev. Lett. 2017, 119, 197801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, E.; Kim, S.; Jung, Y. Slowing down of ring polymer diffusion caused by inter-ring threading. Macromol. Rapid Commun. 2015, 36, 1115–1121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smrek, J.; Grosberg, A.Y. Minimal surfaces on unconcatenated polymer rings in melt. ACS Macro. Lett. 2016, 5, 750–754. [Google Scholar] [CrossRef]
- Halverson, J.D.; Smrek, J.; Kremer, K.; Grosberg, A.Y. From a melt of rings to chromosome territories: The role of topological constraints in genome folding. Rep. Prog. Phys. 2014, 77, 022601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marenduzzo, D.; Micheletti, C.; Orlandini, E. Biopolymer organization upon confinement. J. Phys. Condens. Matter 2010, 22, 283102. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- Grest, G.S.; Kremer, K. Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Jiang, Y.W.; Zhang, D.; He, L.L.; Zhang, L.X. Entropic interactions in semiflexible polymer nanocomposite melts. J. Phys. Chem. B 2016, 120, 572–582. [Google Scholar] [CrossRef]
- Souaille, M.; Roux, B. Extension to the weighted histogram analysis method: Combining umbrella sampling with free energy calculations. Comput. Phys. Commun. 2001, 135, 40–57. [Google Scholar] [CrossRef]
- Deng, Z.Y.; Jiang, Y.W.; He, L.L.; Zhang, L.X. Aggregation–dispersion transition for nanoparticles in semiflexible ring polymer nanocomposite melts. J. Phys. Chem. B 2016, 120, 11574–11581. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Ferrenberg, A.M.; Swendsen, R.H. Optimized Monte Carlo data analysis. Phys. Rev. Lett. 1989, 63, 1195. [Google Scholar] [CrossRef] [PubMed]
- Koniaris, K.; Muthukumar, M. Knottedness in ring polymers. Phys. Rev. Lett. 1991, 66, 2211–2214. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W.R. A deeply knotted protein structure and how it might fold. Nature 2000, 406, 916–919. [Google Scholar] [CrossRef]
- Virnau, P.; Kantor, Y.; Kardar, M. Knots in globule and coil phases of a model polyethylene. J. Am. Chem. Soc. 2005, 127, 15102–15106. [Google Scholar] [CrossRef]
- Gómez, L.R.; García, N.A.; Pöschel, T. Packing structure of semiflexible rings. Proc. Natl. Acad. Sci. USA 2020, 117, 3382–3387. [Google Scholar] [CrossRef] [Green Version]
- Bernabei, M.; Bacova, P.; Moreno, A.J.; Narros, A.; Likos, C.N. Fluids of semiflexible ring polymers: Effective potentials and clustering. Soft Matter 2013, 9, 1287–1300. [Google Scholar] [CrossRef] [Green Version]
- Poier, P.; Likos, C.N.; Moreno, A.J.; Blaak, R. An Anisotropic effective model for the simulation of semiflexible ring polymers. Macromolecules 2015, 9, 4983–4997. [Google Scholar] [CrossRef] [Green Version]
- Heermann, B. Topological interactions between ring polymers: Implications for chromatin loops. J. Chem. Phys. 2010, 132, 044904. [Google Scholar]
- Mladek, P.B.M.; Kahl, G.; Likos, C.N. Computer assembly of cluster-forming amphiphilic dendrimers. Phys. Rev. Lett. 2008, 100, 028301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
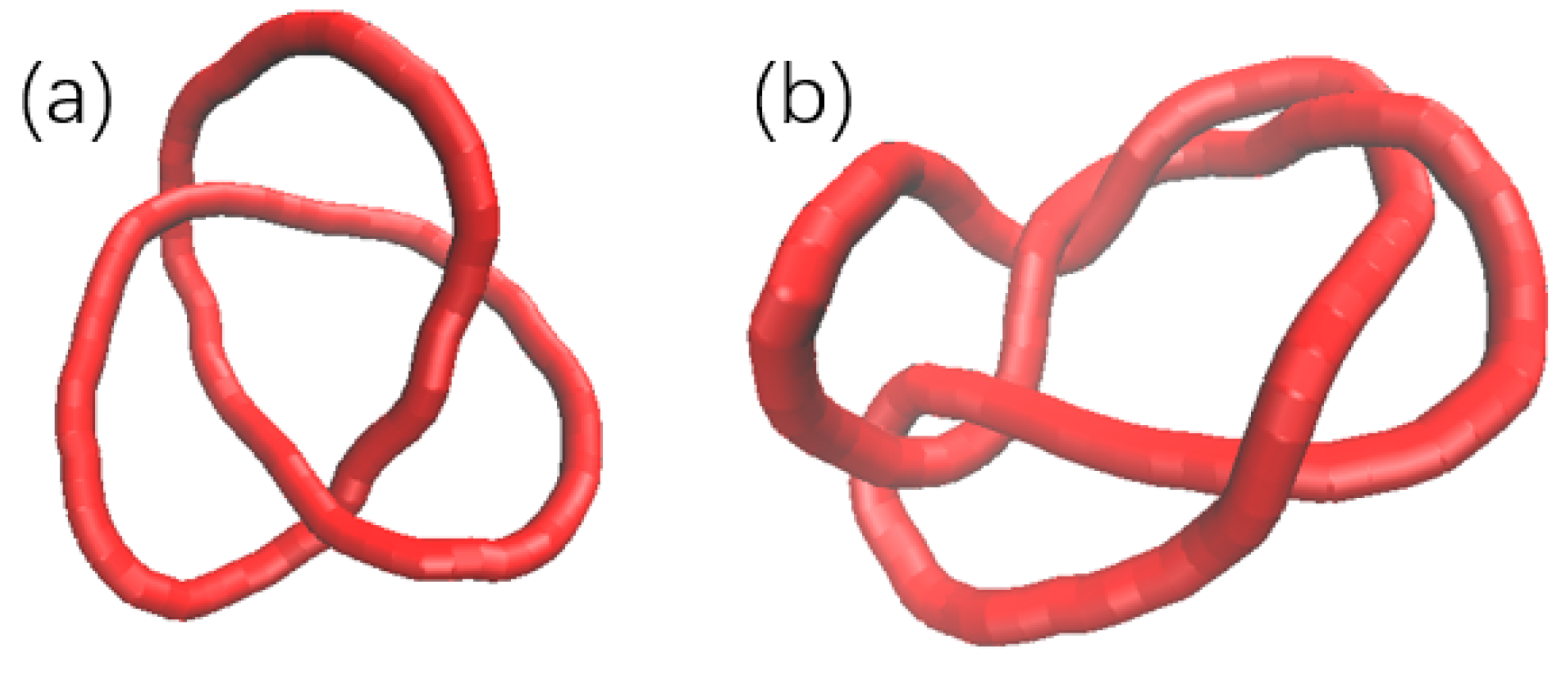



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Li, K.; Wu, J.; He, L.; Zhang, L. Effects of Topological Constraints on Penetration Structures of Semi-Flexible Ring Polymers. Polymers 2020, 12, 2659. https://doi.org/10.3390/polym12112659
Guo F, Li K, Wu J, He L, Zhang L. Effects of Topological Constraints on Penetration Structures of Semi-Flexible Ring Polymers. Polymers. 2020; 12(11):2659. https://doi.org/10.3390/polym12112659
Chicago/Turabian StyleGuo, Fuchen, Ke Li, Jiaxin Wu, Linli He, and Linxi Zhang. 2020. "Effects of Topological Constraints on Penetration Structures of Semi-Flexible Ring Polymers" Polymers 12, no. 11: 2659. https://doi.org/10.3390/polym12112659
APA StyleGuo, F., Li, K., Wu, J., He, L., & Zhang, L. (2020). Effects of Topological Constraints on Penetration Structures of Semi-Flexible Ring Polymers. Polymers, 12(11), 2659. https://doi.org/10.3390/polym12112659