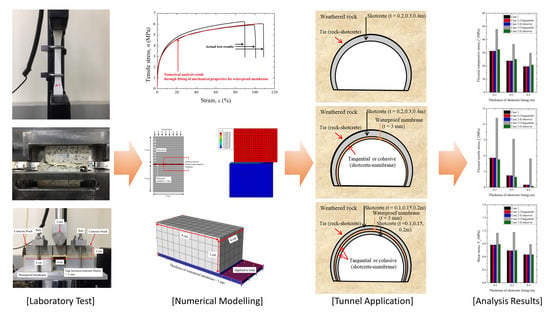
Numerical Analysis of the Contact Behavior of a Polymer-Based Waterproof Membrane for Tunnel Lining
Abstract
:1. Introduction
2. Characteristics of the Waterproof Membrane
2.1. Composition of the Waterproof Membrane and Water Tightness
2.2. Mechanical Properties of the Waterproof Membrane
3. Contact Properties between the Membrane and Shotcrete
3.1. Tangential Behavior Model
3.1.1. Direct Shear Test
3.1.2. Numerical Analysis Based on the Direct Shear Test
3.1.3. Estimation of Parameters for Tangential Contact Behavior
3.2. Cohesive Behavior Model
3.2.1. Linear Block Support Tests
3.2.2. Numerical Analysis Based on the Linear Block Support Test
3.2.3. Estimation of Parameters for Cohesive Contact Behavior
3.3. Analysis of General Beam Members in Different Contact Conditions
4. Implementation of a Membrane and Shotcrete Lining in a Tunnel
4.1. Numerical Analysis Procedure
4.2. Results of Numerical Analysis
4.3. Examination of Shotcrete Lining According to the Waterproof Membrane Construction
5. Conclusions
- (1)
- Tensile tests established that the membrane shows elastic and plastic behavior, so an elasto-plastic model was applied in the numerical analysis. Direct shear tests and linear block tests determined the contact condition between the membrane and shotcrete. The former obtained a tangential behavior model, and the latter obtained a cohesive behavior model.
- (2)
- Analysis of the forces acting on the shotcrete lining (axial load, shear load, and moment) and the lateral and vertical displacements revealed insignificant differences regardless of the application of a waterproof membrane and contact condition. The stresses used in tunnel stability analysis (flexural compressive, flexural tensile, and shear) were similarly unchanged. Therefore, attaching the membrane to the bottom of the shotcrete does not affect the overall tunnel stability, so it need not be considered at the design stage.
- (3)
- Inserting the membrane inside the shotcrete greatly influenced the forces acting on the shotcrete, its displacement, and the stresses used to assess tunnel stability. The different contact conditions gave significantly different results. Those for tangential behavior were discounted as abnormal, and excessive stress was generated in comparison to analysis results in which the membrane was not applied.
- (4)
- The non-conforming results for tangential behavior and the properties of the waterproof membrane itself (such as cohesion and adhesion) indicate that the contact between the shotcrete and membrane is cohesive. With regard to the overall tunnel stability, the membrane increases flexural compressive stress and decreases flexural tensile stress. Shear stress increases or decreases, depending on the shotcrete’s thickness. Therefore, tunnel design must consider the shotcrete structure when planning the placement of a waterproof membrane.
- (5)
- Tunnel design must rely on numerical analysis because actual experiments are impossible in reality. However, results can be verified using model experiments. Further to the work of this study, which considered only a waterproof membrane of 3 mm thickness, subsequent studies are expected to test different membrane thicknesses.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nakashima, M.; Hammer, A.L.; Thewes, M.; Elshafie, M.; Soga, K. Mechanical Behavior of a Sprayed Concrete Lining Isolated by a Sprayed Waterproofing Membrane. Tunn. Undergr. Space Technol. 2015, 47, 143–152. [Google Scholar] [CrossRef] [Green Version]
- ITA. Design Guidance for Spray Applied Waterproofing Membranes; ITAtech Report No 2; International tunneling Association: Avignon, France, 2013. [Google Scholar]
- Tannant, D.D. Thin Spray-on Liners for Underground Rock Support. In Proceedings of the 17th International Mining Congress and Exhibition of Turkey-IMCET, Ankara, Turkey, 19–22 June 2001; pp. 57–73. [Google Scholar]
- Holter, K.G. Performance of EVA-Based Membranes for SCL in Hard Rock. Rock Mech. Rock Eng. 2016, 49, 1329–1358. [Google Scholar] [CrossRef] [Green Version]
- Verani, C.A.; Aldrian, W. Composite Linings: Ground Support and Waterproofing through the Use of a Fully Bonded Membrane. In Shotcrete: Element of a System; Taylor & Francis: London, UK, 2010; pp. 269–282. [Google Scholar]
- Johnson, R.P.; Swallow, F.E.; Psomas, S. Structural properties and durability of a sprayed waterproofing membrane for tunnels. Tunn. Undergr. Space Technol. 2016, 60, 41–48. [Google Scholar] [CrossRef]
- Su, J.; Bloodworth, A. Interface Parameters of Composite Sprayed Concrete Linings in Soft Ground with Spray-Applied Waterproofing. Tunn. Undergr. Space Technol. 2016, 59, 170–182. [Google Scholar] [CrossRef]
- Lee, K.; Kim, D.; Chang, S.H.; Choi, S.W.; Park, B.; Lee, C. Numerical Approach to Assessing the Contact Characteristics of a Polymer-Based Waterproof Membrane. Tunn. Undergr. Space Technol. 2018, 79, 242–249. [Google Scholar] [CrossRef]
- Lee, K.; Choi, S.W.; Kim, D.; Lee, C. Numerical Study on Direct Shear Test of Composite Shotcrete with Sprayable Waterproofing Membrane. J. Korean Geosynth. Soc. 2018, 17, 189–197. (In Korean) [Google Scholar]
- EFNARC. Specification and Guidelines on Thin Spray-on Liners for Mining and Tunneling; European Federation of National Associations Representing for Concrete: Surrey, UK, 2008. [Google Scholar]
- Park, P.; Lee, C.; Choi, S.W.; Kang, T.H.; Kim, J.; Choi, M.S.; Jeon, S.; Chang, S.H. Interfacial Properties of Composite Shotcrete Containing Sprayed Waterproofing Membrane. Geomech. Eng. 2018, 16, 385–397. [Google Scholar]
- ASTM D638. Standard Test Method for Tensile Properties of Plastics; American Society for Testing of Materials: West Conshohocken, PA, USA, 2010. [Google Scholar]
- SIMULIA. ABAQUS 6.14 Scripting User’s Manual; SIMULIA: Maastricht, The Netherlands, 2014. [Google Scholar]
- Kim, Y.S. Modeling Contact with Abaqus/Standard, V-Eng.; Next Printing: Gyeonggi-do, Korea, 2014. (In Korean) [Google Scholar]
- Park, J.J.; Kim, Y.M.; Hwang, T.J.; Jeong, S.S. Numerical Analysis of Tunnel Lining under Loosening Load. J. Korean Geotech. Soc. 2011, 27, 35–45. (In Korean) [Google Scholar] [CrossRef] [Green Version]
- MOLIT. Standard of Shotcrete and Structure; Ministry of Land, Transport and Maritime Affairs: Sejong, Korea, 2012. (In Korean) [Google Scholar]

















| Materials | Prototype 1 (Two-Component) | Prototype 2 (One-Component) |
|---|---|---|
| Alumina cement | 30.0 | 15.0 |
| Calcium sulfo-aluminate | 30.0 | - |
| Calcium carbonate | 19.5 | 14.1 |
| Slag | 15.0 | - |
| Nano silica | 4.0 | - |
| Lithium carbonate | 0.1 | - |
| Citric acid | 0.3 | - |
| Anhydrous gtpsum | - | 5.0 |
| Hydroxypropyl methylcellulose | 0.5 | - |
| Antifoaming agent | 0.3 | - |
| Aluminum hydroxide | - | 10 |
| Thickener | - | 0.85 |
| Promoter | - | 0.05 |
| Synthetic fiber | 0.3 | - |
| Powder-type EVA (ethylene-vinyl acetate) polymer | - | 55.0 |
| Material Property | Density (kg/m3) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|
| Value | 1070 | 486.54 | 0.3 |
| Cohesive Contact Property | Value |
|---|---|
| Cohesive stiffness | 2.7 GPa |
| Maximum nominal stress at damage initiation | 1.2 MPa |
| Evolution energy | 1.0 kJ/m2 |
| Material | Density (kN/m3) | Elastic Modulus (MPa) | Poisson’s Ratio | Cohesion (kPa) | Friction Angle (°) |
|---|---|---|---|---|---|
| Weathered rock | 22.0 | 250 | 0.3 | 50 | 35 |
| Shotcrete lining | 23.5 | 25,800 | 0.2 | - | - |
| Case | Thickness of Shotcrete Lining (m) | Contact Property | Max. Axial Load (MN) | Max. Shear Force (MN) | Max. Moment (MNm) | Max. Displacement (cm) | |
|---|---|---|---|---|---|---|---|
| Lateral | Vertical | ||||||
| 1 | 0.2 | - | 3.945 | 0.175 | 0.394 | 0.327 | 2.609 |
| 0.3 | - | 4.146 | 0.222 | 0.516 | 0.357 | 2.501 | |
| 0.4 | - | 4.258 | 0.260 | 0.613 | 0.365 | 2.441 | |
| 2 | 0.2 | Tangential | 3.942 | 0.174 | 0.393 | 0.327 | 2.613 |
| Cohesive | 3.942 | 0.175 | 0.394 | 0.327 | 2.601 | ||
| 0.3 | Tangential | 4.143 | 0.222 | 0.515 | 0.358 | 2.505 | |
| Cohesive | 4.142 | 0.222 | 0.515 | 0.358 | 2.503 | ||
| 0.4 | Tangential | 4.255 | 0.259 | 0.611 | 0.366 | 2.445 | |
| Cohesive | 4.254 | 0.259 | 0.612 | 0.365 | 2.443 | ||
| 3 | 0.2 | Tangential | 3.467 | 0.115 | 0.220 | 0.224 | 2.897 |
| Cohesive | 2.083 | 0.089 | 0.195 | 0.325 | 2.622 | ||
| 0.3 | Tangential | 3.725 | 0.175 | 0.290 | 0.250 | 2.701 | |
| Cohesive | 2.243 | 0.112 | 0.254 | 0.354 | 2.514 | ||
| 0.4 | Tangential | 3.887 | 0.177 | 0.349 | 0.347 | 2.696 | |
| Cohesive | 2.357 | 0.130 | 0.302 | 0.362 | 2.453 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.; Kim, D.; Choi, S.-W.; Chang, S.-H.; Kang, T.-H.; Lee, C. Numerical Analysis of the Contact Behavior of a Polymer-Based Waterproof Membrane for Tunnel Lining. Polymers 2020, 12, 2704. https://doi.org/10.3390/polym12112704
Lee K, Kim D, Choi S-W, Chang S-H, Kang T-H, Lee C. Numerical Analysis of the Contact Behavior of a Polymer-Based Waterproof Membrane for Tunnel Lining. Polymers. 2020; 12(11):2704. https://doi.org/10.3390/polym12112704
Chicago/Turabian StyleLee, Kicheol, Dongwook Kim, Soon-Wook Choi, Soo-Ho Chang, Tae-Ho Kang, and Chulho Lee. 2020. "Numerical Analysis of the Contact Behavior of a Polymer-Based Waterproof Membrane for Tunnel Lining" Polymers 12, no. 11: 2704. https://doi.org/10.3390/polym12112704
APA StyleLee, K., Kim, D., Choi, S.-W., Chang, S.-H., Kang, T.-H., & Lee, C. (2020). Numerical Analysis of the Contact Behavior of a Polymer-Based Waterproof Membrane for Tunnel Lining. Polymers, 12(11), 2704. https://doi.org/10.3390/polym12112704