Numerical Study of Using FRP and Steel Rebars in Simply Supported Prestressed Concrete Beams with External FRP Tendons
Abstract
:1. Introduction
2. Numerical Program and Verification
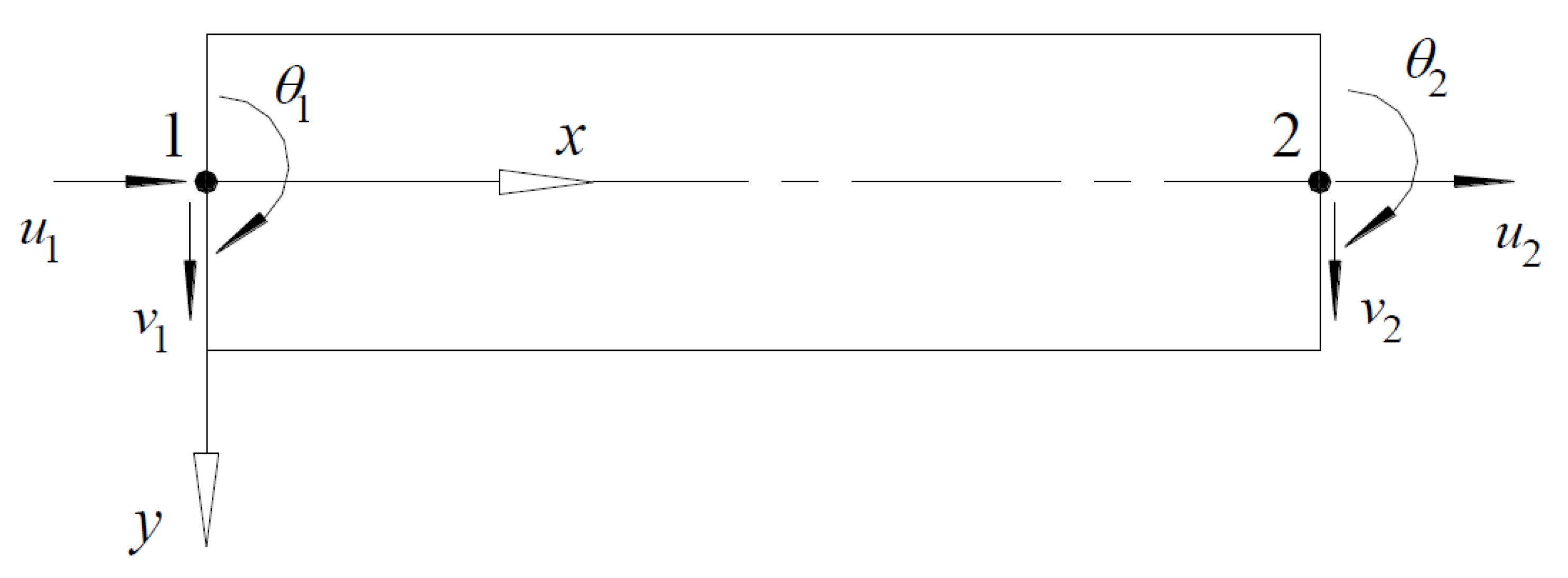
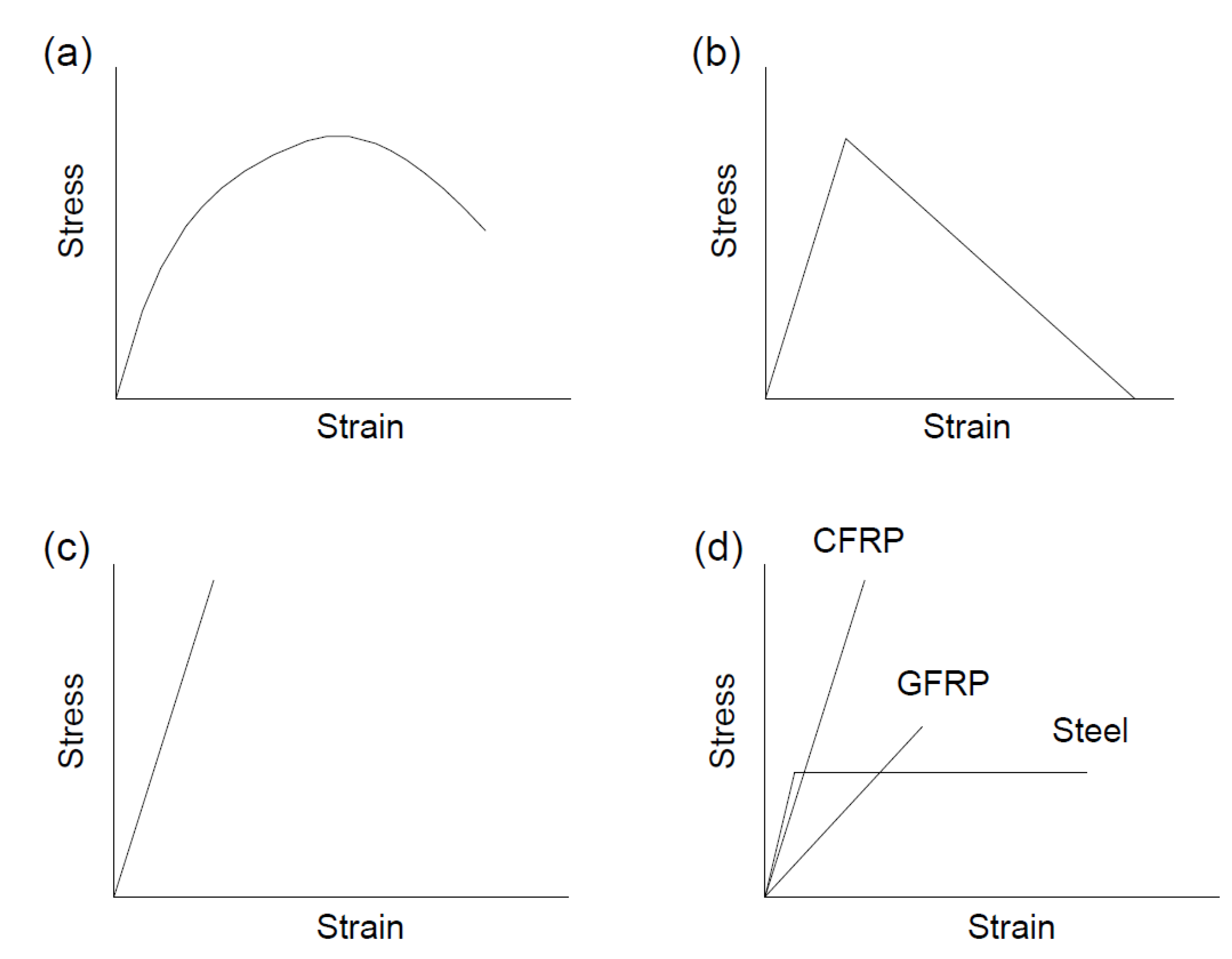
2.1. Numerical Program
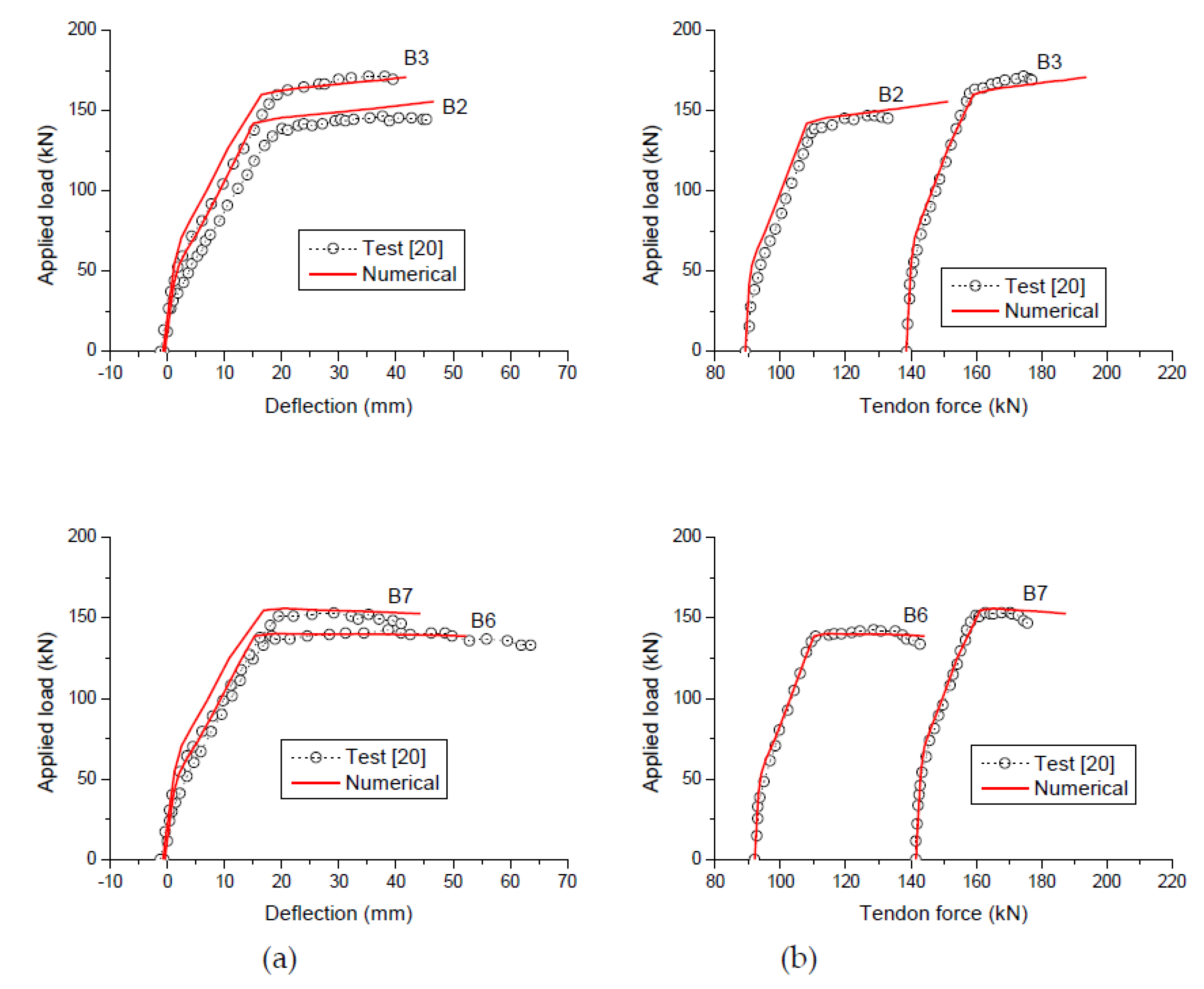
2.2. Verification with Experimental Results
3. Numerical Evaluation
3.1. Failure and Cracking Modes
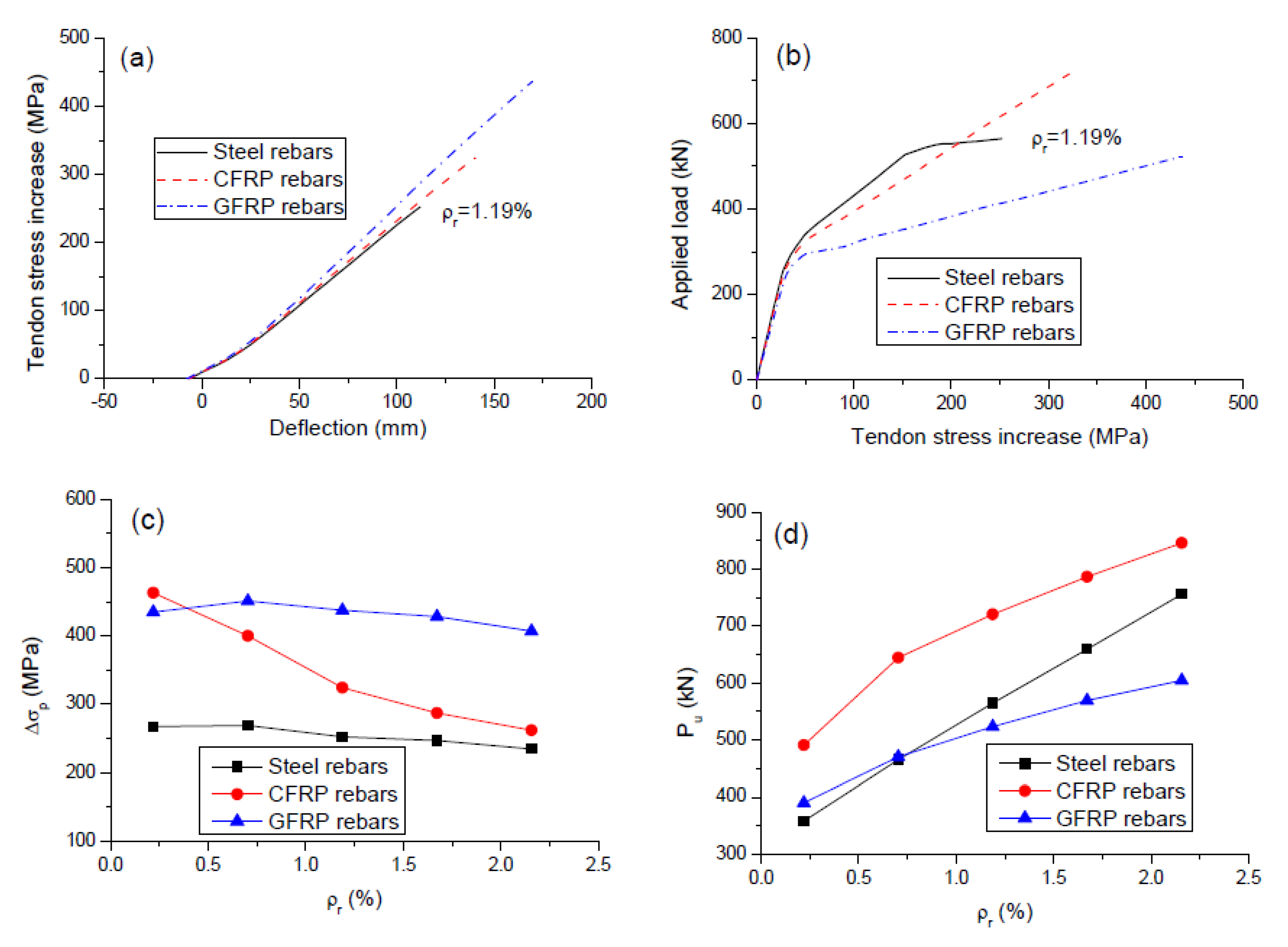
3.2. Tendon Stress Development
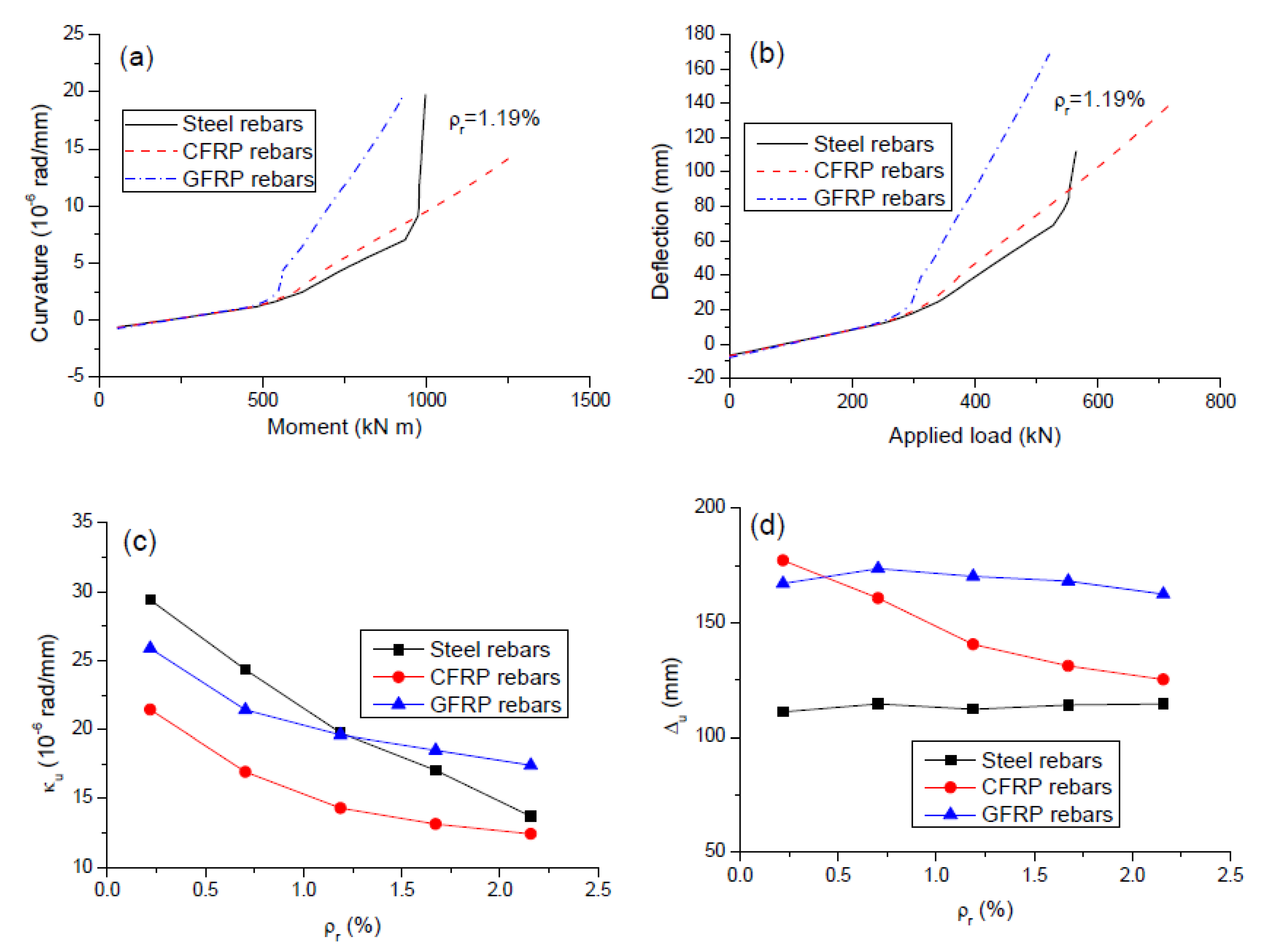
3.3. Deformation Behavior
3.4. Neutral Axis Depth and Rebar Strain
4. Analytical Modeling
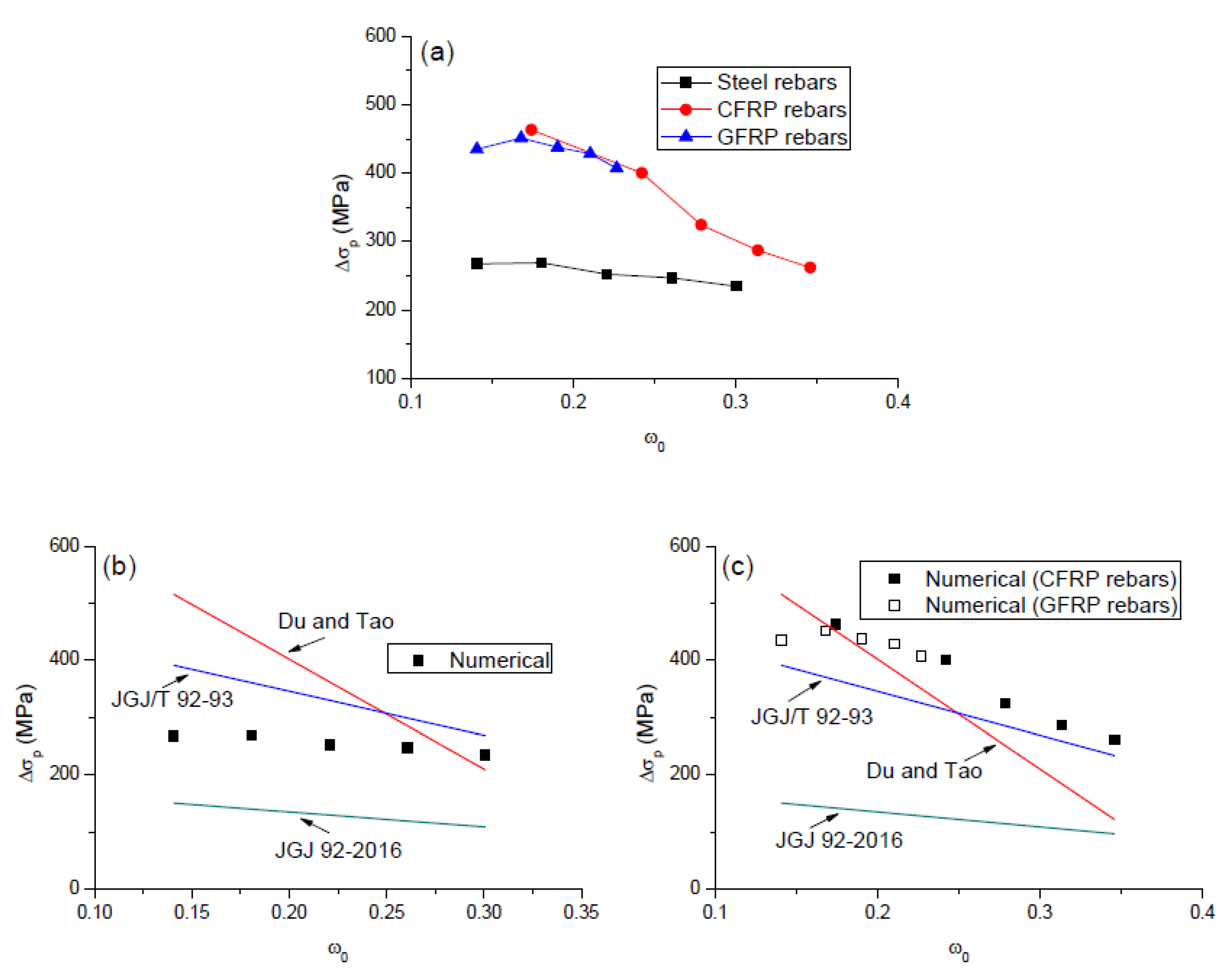
4.1. Existing Models Using Combined Reinforcing Index for Prediction of Ultimate Stress in Unbonded Tendons
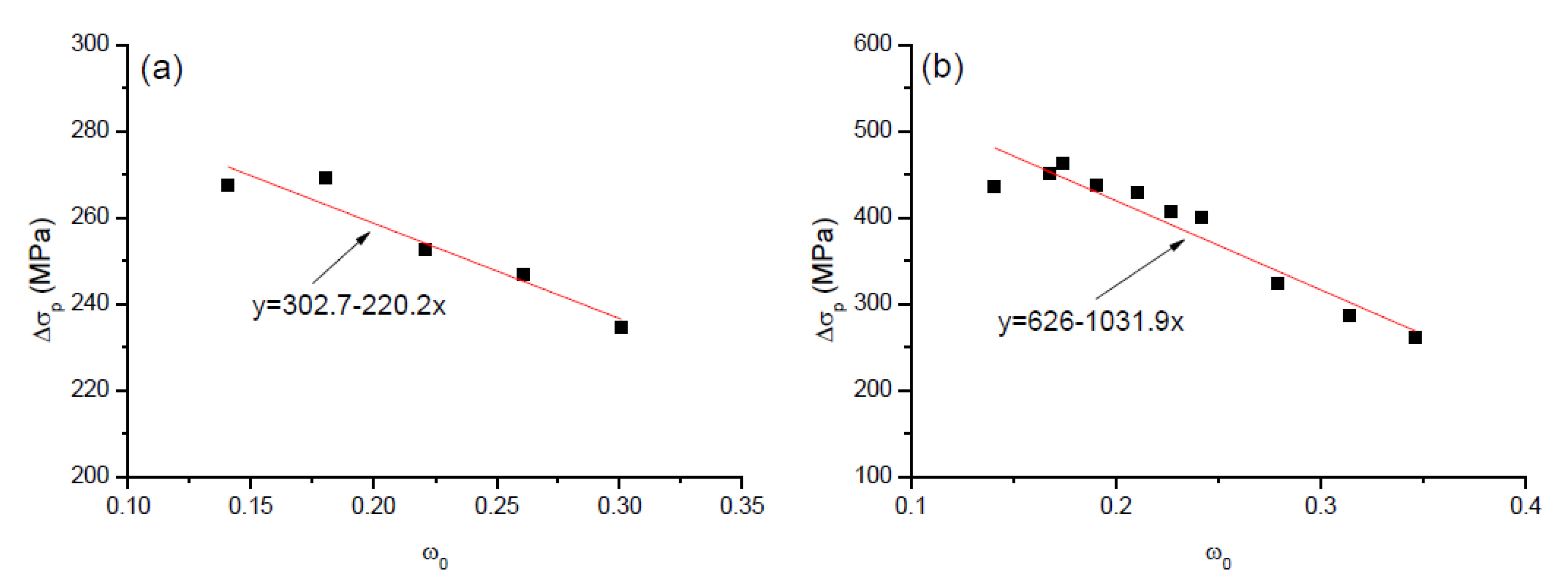
4.2. Proposed Model
5. Conclusions
- FRP (especially CFRP) rebars lead to better exploitation of noncritical sections than steel rebars, particularly notable at a low ρr level. The crack mode is improved by providing a minimum amount of rebars, while the improvement is more effective using CFRP rebars than using GFRP or steel rebars.
- CFRP rebars lead to larger ultimate load and neutral axis depth but smaller ultimate curvature and tensile rebar strain than steel rebars. Such values registered by GFRP rebars could be larger or smaller than those by steel rebars, depending on the ρr level.
- GFRP rebars mobilize substantially higher ultimate deflection and tendon stress increment than steel rebars. CFRP rebars lead to similar observation at a low ρr level, while the difference between the values for the beams with CFRP and steel rebars diminishes as ρr increases.
- Both JGJ/T 92-93 and JGJ 92-2016 underestimated the influence of combined reinforcing index on external tendons’ stress at ultimate in the beams with FRP rebars. Moreover, JGJ 92-2016 appears to be overly conservative for predicting the ultimate tendon stress.
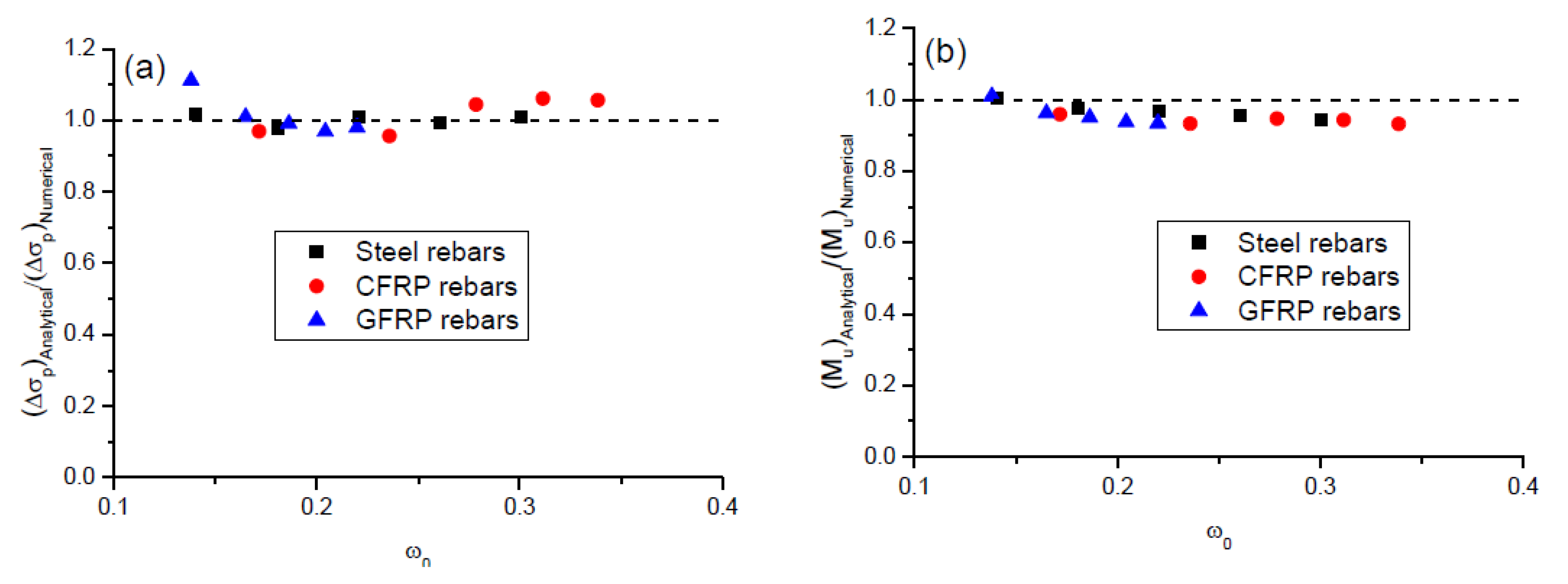
- An analytical model was proposed to predict the tendon stress at ultimate and flexural strength in externally PCBs with steel and FRP rebars. The model predictions are in good agreement with the numerical results.
Author Contributions
Funding
Conflicts of Interest
References
- Ahmad, S. Reinforcement corrosion in concrete structures, its monitoring and service life prediction—A review. Cem. Concr. Compos. 2003, 25, 459–471. [Google Scholar]
- Lou, T.; Karavasilis, T.L. Numerical evaluation of prestressed steel-concrete composite girders with external FRP or steel tendons. J. Constr. Steel Res. 2019, 162, 105698. [Google Scholar]
- Lou, T.; Peng, C.; Karavasilis, T.L.; Min, D.; Sun, W. Moment redistribution versus neutral axis depth in continuous PSC beams with external CFRP tendons. Eng. Struct. 2020, 209, 109927. [Google Scholar]
- Sun, W.; Jirsa, J.O.; Ghannoum, W.M. Behavior of anchored carbon fiber-reinforced polymer strips used for strengthening concrete structures. ACI Mater. J. 2016, 113, 163–172. [Google Scholar]
- Sun, W.; He, T.; Wang, X.; Zhang, J.; Lou, T. Developing an anchored near-surface mounted (NSM ) FRP system for fuller use of FRP material with less epoxy filler. Compos. Struct. 2019, 226, 111251. [Google Scholar]
- Mostofinejad, D.; Hosseini, S.M.; Tehrani, B.N.; Eftekhar, M.R.; Dyari, M. Innovative warp and woof strap (WWS) method to anchor the FRP sheets in strengthened concrete beams. Constr. Build. Mater. 2019, 218, 351–364. [Google Scholar]
- Wang, L.; Kawaguchi, K.; Xu, J.; Han, Q. Effects of transverse constraints on the longitudinal compressive strength of unidirectional CFRP pultruded plates and rods. Compos. Struct. 2019, 207, 740–751. [Google Scholar]
- Xu, J.; Wang, W.; Han, Q.; Liu, X. Damage pattern recognition and damage evolution analysis of unidirectional CFRP tendons under tensile loading using acoustic emission technology. Compos. Struct. 2020, 238, 111948. [Google Scholar]
- ACI committee 440. Guide for the Design and Construction of Structural Concrete Reinforced with FRP Bars; ACI 440.1R-06: Farmington Hills, MI, USA, 2006. [Google Scholar]
- ACI committee 440. Prestressing Concrete Structures with FRP Tendons; ACI 440.4R-04: Farmington Hills, MI, USA, 2004. [Google Scholar]
- El Refai, A.; Abed, F.; Altalmas, A. Bond durability of basalt fiber–reinforced polymer bars embedded in concrete under direct pullout conditions. ASCE J. Compos. Constr. 2015, 19, 04014078. [Google Scholar]
- Altalmas, A.; El Refai, A.; Abed, F. Bond degradation of basalt fiber-reinforced polymer (BFRP) bars exposed to accelerated aging conditions. Constr. Build. Mater. 2015, 81, 162–171. [Google Scholar]
- Al-Tamimi, A.; Abed, F.H.; Al-Rahmani, A. Effects of harsh environmental exposures on the bond capacity between concrete and GFRP reinforcing bars. Adv. Concr. Constr. 2014, 2, 1–11. [Google Scholar]
- Grace, N.F.; Abdel-Sayed, G. Behavior of externally draped CFRP tendons in prestressed concrete bridges. PCI J. 1998, 43, 88–101. [Google Scholar]
- Ghallab, A.; Beeby, A.W. Factors affecting the external prestressing stress in externally strengthened prestressed concrete beams. Cem. Concr. Compos. 2005, 27, 945–957. [Google Scholar]
- Abdel Aziz, M.; Abdel-Sayed, G.; Ghrib, F.; Grace, N.F.; Madugula, M.K.S. Analysis of concrete beams prestressed and post-tensioned with externally unbonded carbon fiber reinforced polymer tendons. Can. J. Civ. Eng. 2005, 31, 1138–1151. [Google Scholar]
- Wang, X.; Shi, J.; Wu, G.; Yang, L.; Wu, Z. Effectiveness of basalt FRP tendons for strengthening of RC beams through the external prestressing technique. Eng. Struct. 2015, 101, 34–44. [Google Scholar]
- Zhu, H.; Dong, Z.; Wu, G.; Chen, H.; Li, J.; Liu, Y. Experimental Evaluation of Bent FRP Tendons for Strengthening by External Prestressing. ASCE J. Compos. Constr. 2017, 21, 04017032. [Google Scholar]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. Numerical analysis of behaviour of concrete beams with external FRP tendons. Constr. Build. Mater. 2012, 35, 970–978. [Google Scholar]
- Bennitz, A.; Schmidt, J.W.; Nilimaa, J.; Taljsten, B.; Goltermann, P.; Ravn, D.L. Reinforced concrete T-beams externally prestressed with unbonded carbon fiber-reinforced polymer tendons. ACI Struct. J. 2012, 109, 521–530. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary (ACI 318R-14); American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Abed, F.; Oucif, C.; Awera, Y.; Mhanna, H.H.; Alkhraisha, H. FE modeling of concrete beams and columns reinforced with FRP composites. Def. Technol. 2020. [Google Scholar] [CrossRef]
- Abed, F.; El Refai, A.; Abdalla, S. Experimental and finite element investigation of the shear performance of BFRP-RC short beams. Structures 2019, 20, 689–701. [Google Scholar]
- Al-Rahmani, A.; Abed, F.H. Numerical investigation of hybrid FRP reinforced beams. In Proceedings of the 5th International Conference on Modeling, Simulation and Applied Optimization (ICMSAO), Hammamet, Tunisia, 28–30 April 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Ju, M.; Park, Y.; Park, C. Cracking control comparison in the specifications of serviceability in cracking for FRP reinforced concrete beams. Compos. Struct. 2018, 182, 674–684. [Google Scholar]
- Alam, M.S.; Hussein, A. Relationship between the shear capacity and the flexural cracking load of FRP reinforced concrete beams. Constr. Build. Mater. 2017, 154, 819–828. [Google Scholar]
- Barris, C.; Torres, L.; Vilanova, I.; Mias, C.; Llorens, M. Experimental study on crack width and crack spacing for Glass-FRP reinforced concrete beams. Eng. Struct. 2017, 131, 231–242. [Google Scholar]
- Dundar, C.; Tanrikulu, A.K.; Frosch, R.J. Prediction of load-deflection behavior of multi-span FRP and steel reinforced concrete beams. Compos. Struct. 2015, 132, 680–693. [Google Scholar]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. Neutral axis depth and moment redistribution in FRP and steel reinforced concrete continuous beams. Compos. Part B Eng. 2015, 70, 44–52. [Google Scholar]
- Mahroug, M.E.M.; Ashour, A.F.; Lam, D. Experimental response and code modelling of continuous concrete slabs reinforced with BFRP bars. Compos. Struct. 2014, 107, 664–674. [Google Scholar]
- Lou, T.; Xiang, Y. Finite element modeling of concrete beams prestressed with external tendons. Eng. Struct. 2006, 28, 1919–1926. [Google Scholar]
- CEN. Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. EN 1992-1-1; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Bernardo, L.; Nepomuceno, M.; Pinto, H. Neutral axis depth versus ductility and plastic rotation capacity on bending in lightweight-aggregate concrete beams. Materials 2019, 12, 3479. [Google Scholar]
- Du, G.C.; Tao, X.K. Ultimate stress of unbonded tendons in partially prestressed concrete beams. PCI J. 1985, 30, 72–91. [Google Scholar]
- JGJ/T 92-93. Technical Specification for Concrete Structures Prestressed with Unbonded Tendons; China Planning Press: Beijing, China, 1993. [Google Scholar]
- JGJ 92-2016. Technical Specification for Concrete Structures Prestressed with Unbonded Tendons; China Architecture & Building Press: Beijing, China, 2016. [Google Scholar]
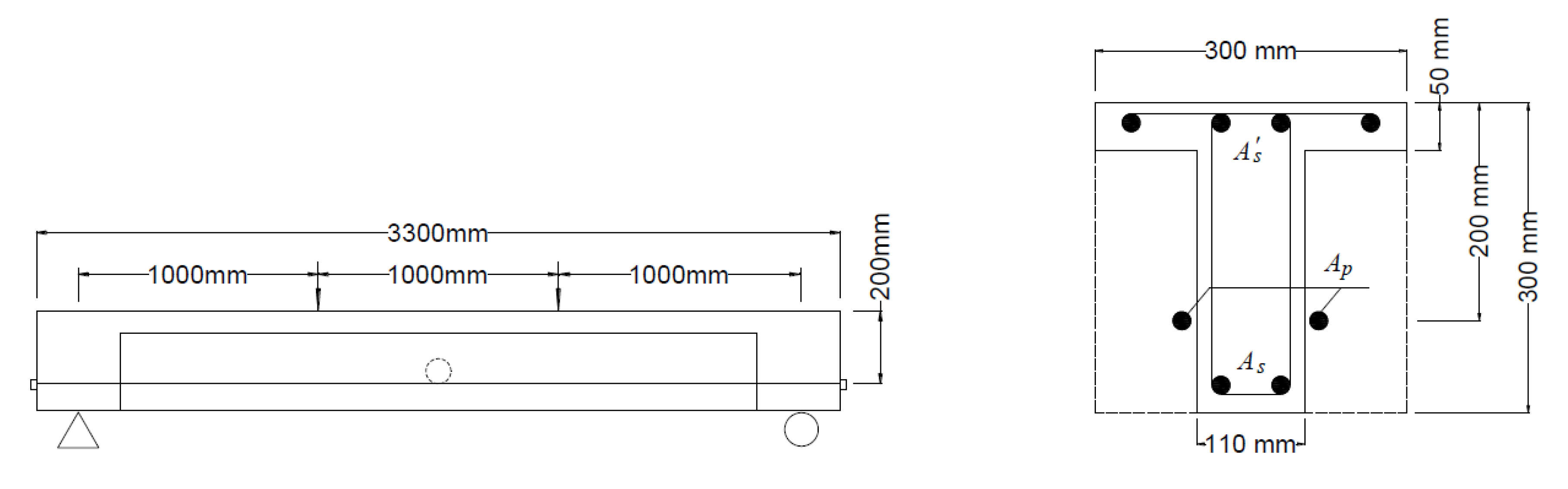
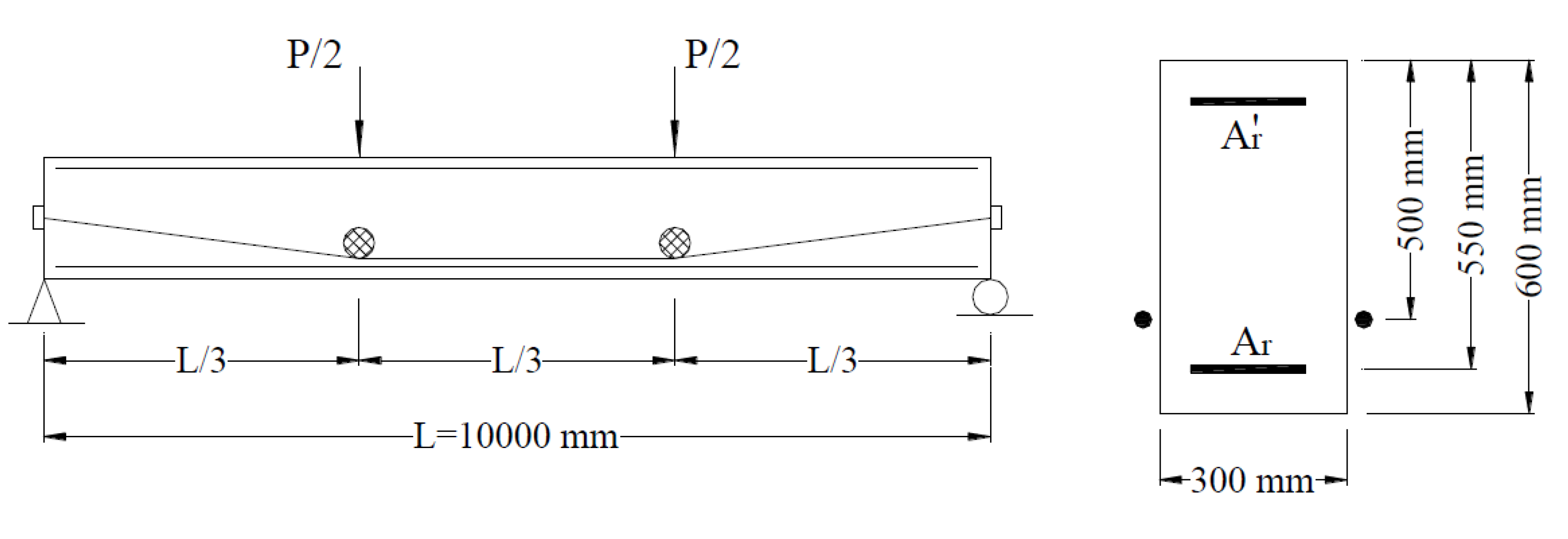


| Beam | Steel Rebars | FRP Tendons | Concrete | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| As (mm2) | fy (MPa) | Es (GPa) | (mm2) | (MPa) | (GPa) | Ap (mm2) | Ef (GPa) | ff (MPa) | σpe (MPa) | fck (MPa) | |
| B2 | 402 | 560 | 172 | 201 | 510 | 187 | 100.5 | 158 | 2790 | 895 | 35.2 |
| B3 | 402 | 560 | 172 | 201 | 510 | 187 | 100.5 | 158 | 2790 | 1382 | 33.4 |
| B6 | 402 | 560 | 172 | 201 | 510 | 187 | 100.5 | 158 | 2790 | 917 | 40.6 |
| B7 | 402 | 560 | 172 | 201 | 510 | 187 | 100.5 | 158 | 2790 | 1407 | 35.9 |
| Rebars | Tensile Strength (MPa) | Yield Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|
| Steel | 450 | 450 | 200 |
| CFRP | 1840 | - | 147 |
| GFRP | 750 | - | 40 |
| Rebars | ρr (%) | Δσp (MPa) | Mu (kN m) | ||||
|---|---|---|---|---|---|---|---|
| Analytical | Numerical | Error (%) | Analytical | Numerical | Error (%) | ||
| Steel | 0.22 | 272.05 | 267.60 | 1.66 | 654.40 | 653.12 | 0.20 |
| 0.70 | 263.25 | 269.05 | −2.15 | 812.72 | 831.63 | −2.27 | |
| 1.19 | 254.45 | 252.44 | 0.80 | 962.98 | 997.08 | −3.42 | |
| 1.67 | 245.65 | 246.93 | −0.52 | 1105.17 | 1154.67 | −4.29 | |
| 2.16 | 236.85 | 234.63 | 0.95 | 1239.31 | 1315.42 | −5.79 | |
| CFRP | 0.22 | 448.74 | 463.02 | −3.09 | 837.89 | 874.32 | −4.17 |
| 0.70 | 382.53 | 400.19 | −4.41 | 1054.40 | 1129.98 | −6.69 | |
| 1.19 | 338.41 | 324.23 | 4.37 | 1189.31 | 1256.83 | −5.37 | |
| 1.67 | 304.47 | 287.09 | 6.05 | 1288.01 | 1366.46 | −5.74 | |
| 2.16 | 276.65 | 261.86 | 5.65 | 1365.57 | 1466.04 | −6.85 | |
| GFRP | 0.22 | 483.51 | 435.02 | 11.15 | 713.43 | 706.31 | 1.01 |
| 0.70 | 455.67 | 451.08 | 1.02 | 808.85 | 840.51 | −3.77 | |
| 1.19 | 433.69 | 437.72 | −0.92 | 882.11 | 928.20 | −4.97 | |
| 1.67 | 415.19 | 428.42 | −3.09 | 942.27 | 1004.81 | −6.22 | |
| 2.16 | 399.09 | 407.03 | −1.95 | 993.58 | 1063.79 | −6.60 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, M.; Li, Z.; Lou, T. Numerical Study of Using FRP and Steel Rebars in Simply Supported Prestressed Concrete Beams with External FRP Tendons. Polymers 2020, 12, 2773. https://doi.org/10.3390/polym12122773
Pang M, Li Z, Lou T. Numerical Study of Using FRP and Steel Rebars in Simply Supported Prestressed Concrete Beams with External FRP Tendons. Polymers. 2020; 12(12):2773. https://doi.org/10.3390/polym12122773
Chicago/Turabian StylePang, Miao, Zhangxiang Li, and Tiejiong Lou. 2020. "Numerical Study of Using FRP and Steel Rebars in Simply Supported Prestressed Concrete Beams with External FRP Tendons" Polymers 12, no. 12: 2773. https://doi.org/10.3390/polym12122773
APA StylePang, M., Li, Z., & Lou, T. (2020). Numerical Study of Using FRP and Steel Rebars in Simply Supported Prestressed Concrete Beams with External FRP Tendons. Polymers, 12(12), 2773. https://doi.org/10.3390/polym12122773





